Integration Capability Evaluation of Wind and Photovoltaic Generation in Power Systems Based on Temporal and Spatial Correlations
Abstract
:1. Introduction
2. Aggregated Renewable Generation Model Based on the Copula Function
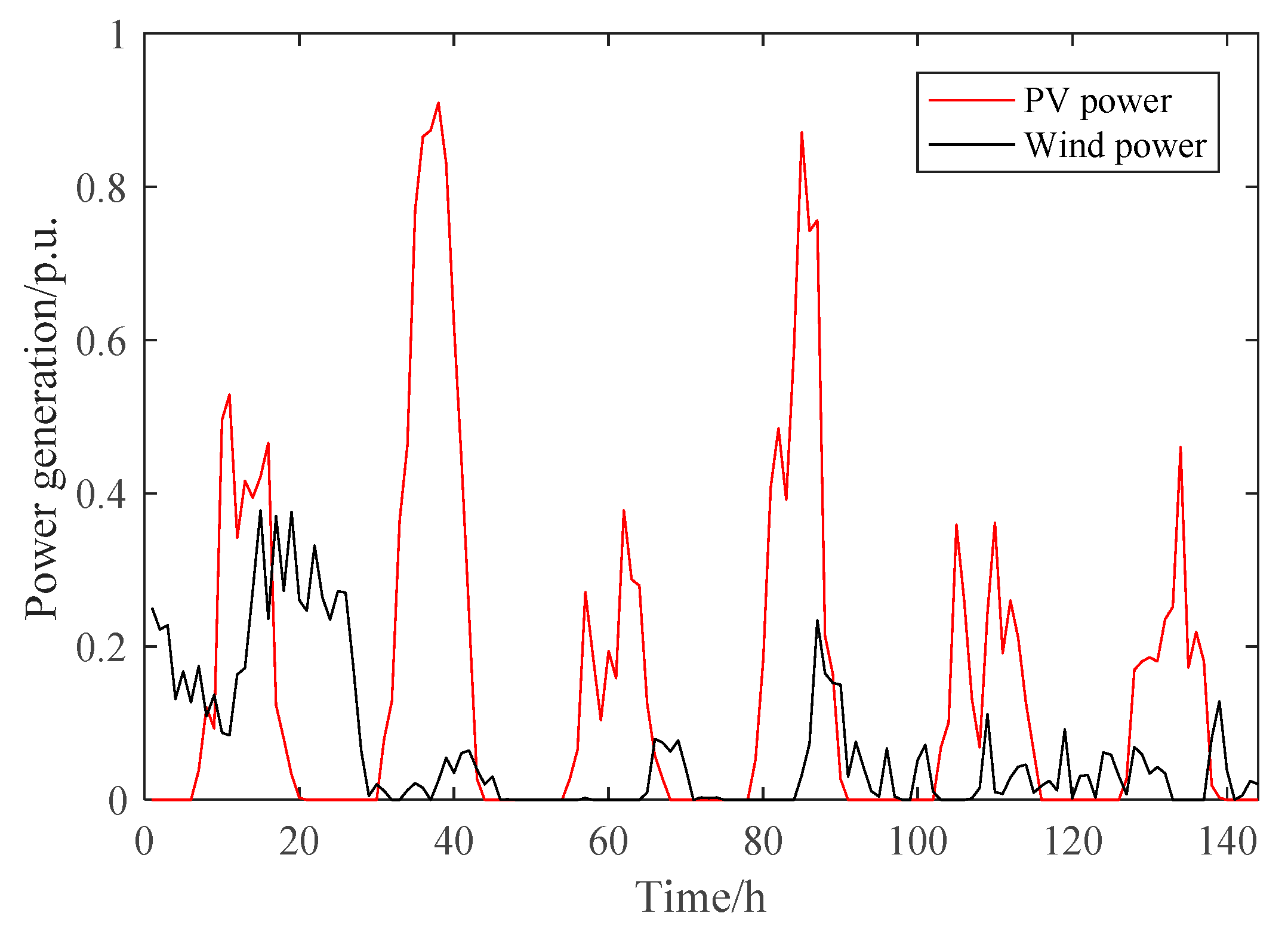
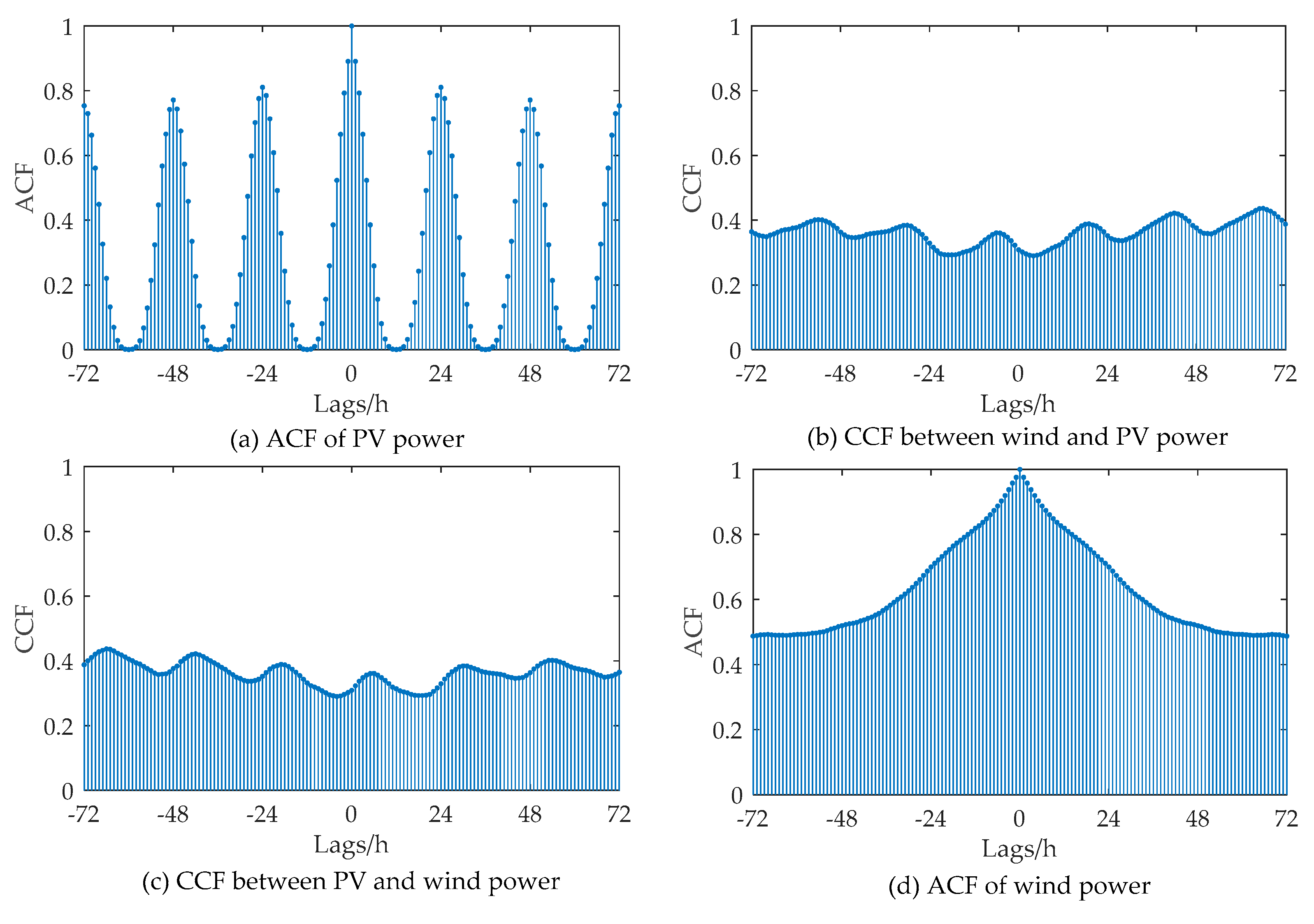
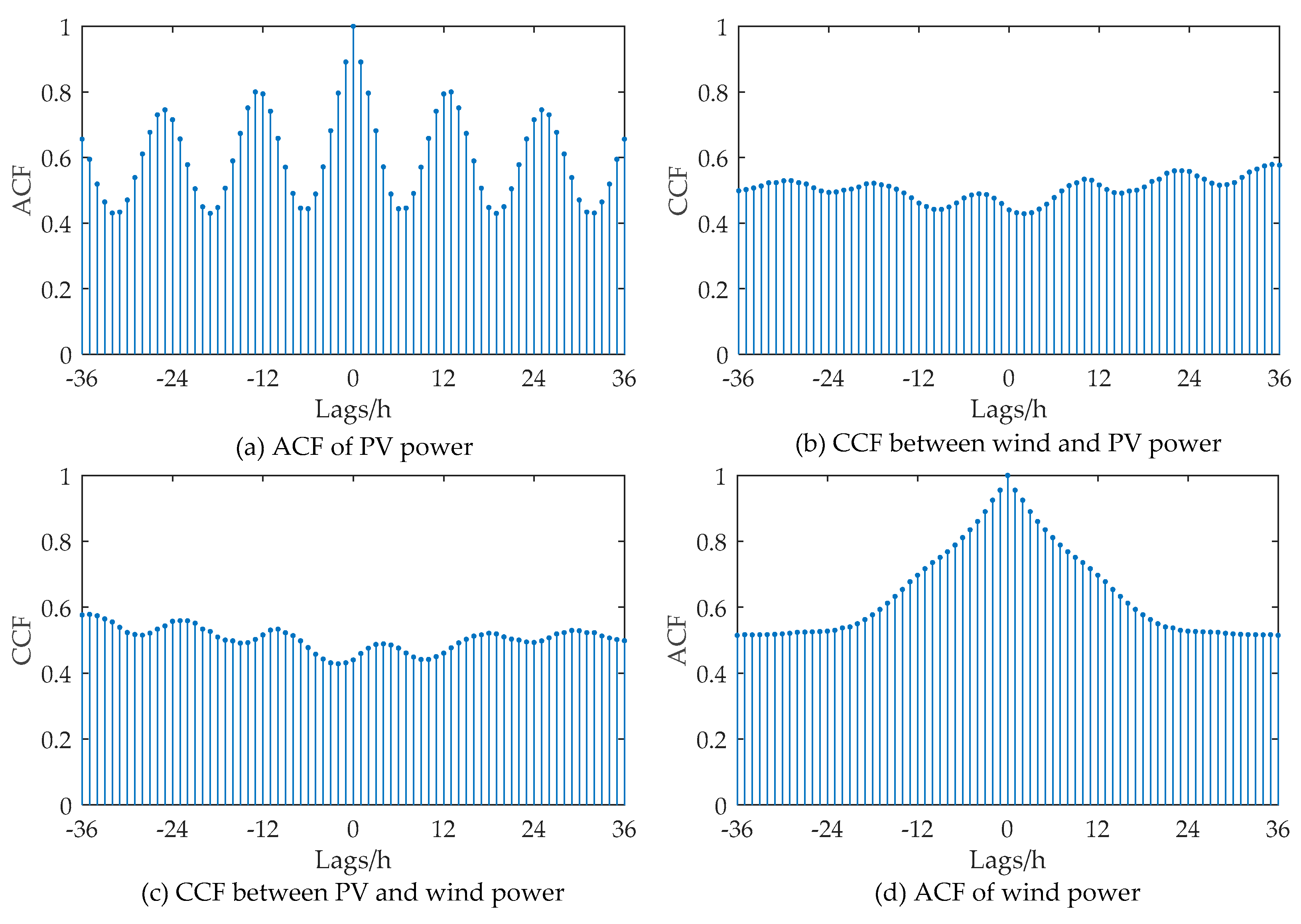
2.1. Correlation Analysis
2.2. Aggregated Generation Distribution of Wind Power and PV Power Based on the Copula Function
2.2.1. Basics of the Copula Function
2.2.2. Copula-Based Renewable Generation Aggregation
- Step 1: Sample V groups of the two-dimensional uniform random variables PV and wind power forecast errors based on the joint CDF estimated by the Gaussian copula model in (4). The groups of these samples can be represented by .
- Step 2: Transform the above V groups of sample to V groups of error samples through the inverse transformationwhere and are the inverse functions of and , respectively.
- Step 3: Generate V groups of the two-dimensional scenarios of PV and wind power generation. The jth scenario can be achieved bywhere is the forecasted PV and wind power generated by the SBL prediction model.
3. Optimization Model for Exploiting the Integration Capacity of Wind Power and PV Power
4. Overall Simulation Frame Work of the Proposed Model
| Algorithm 1 Pseudocodes for the overall simulation process |
| Function: spot forecast (PV power and wind power) |
| Model: SBL model; |
| Inputs: historical wind power/PV power measurements in the last 4 h at t − 1, t − 2, t − 3 and t − 4; |
| Outputs: wind power/PV power spot forecasting results at time t. |
| Function: copula-based distribution of PV power and wind power |
| Model: Gaussian copula; |
| Inputs: wind power/PV power spot forecasting results; forecast error series of wind power and PV power; correlation matrix; |
| Outputs: aggregated wind power and PV power scenarios. |
| Function: reliability evaluation model |
| Model: shown in equations in (8)~(17); |
| Inputs: varying integration capacities of wind and PV farms; aggregated wind power and PV power scenarios; data of IEEE RTS-24 system; |
| Outputs: LOLP values. |
5. Case Study
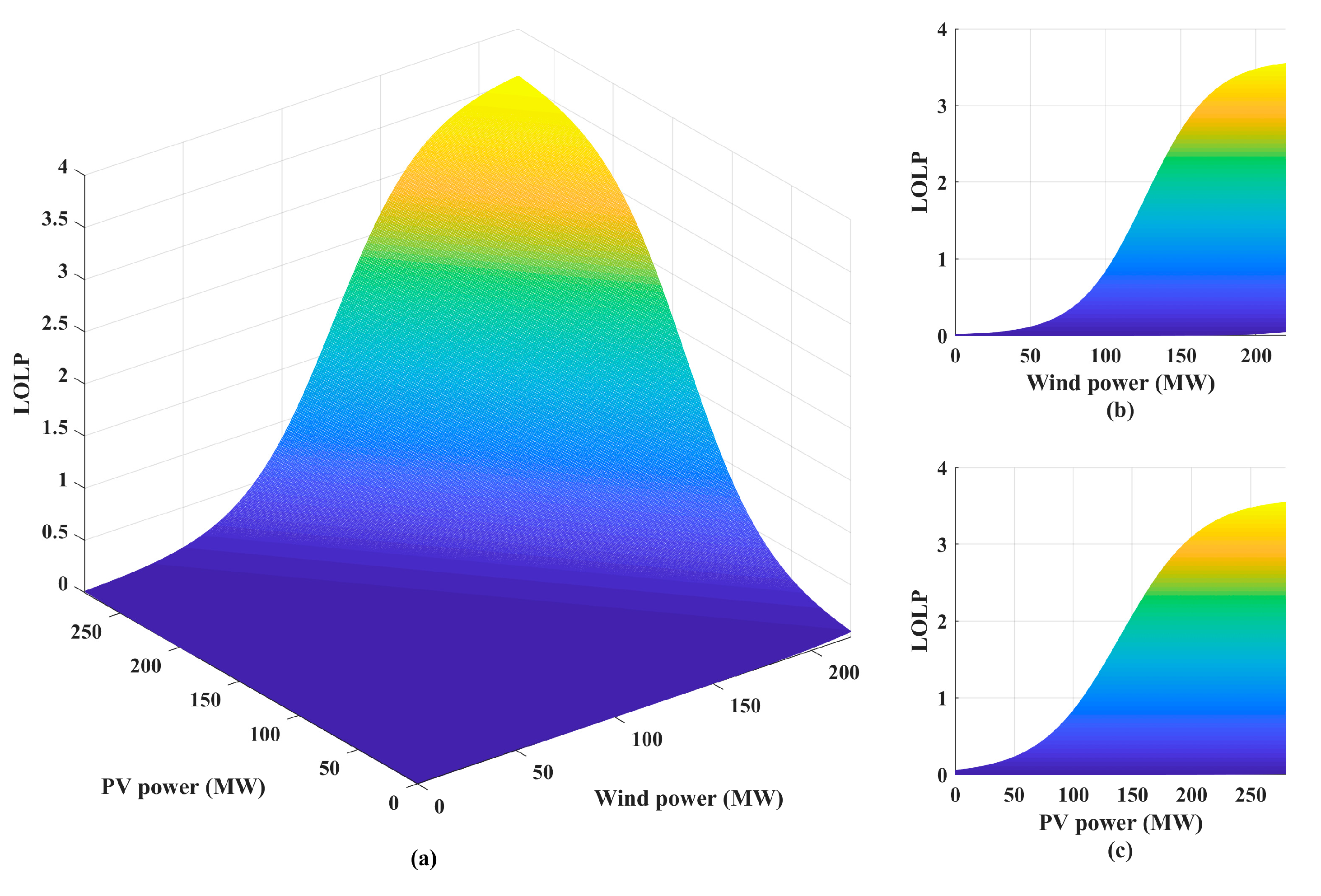
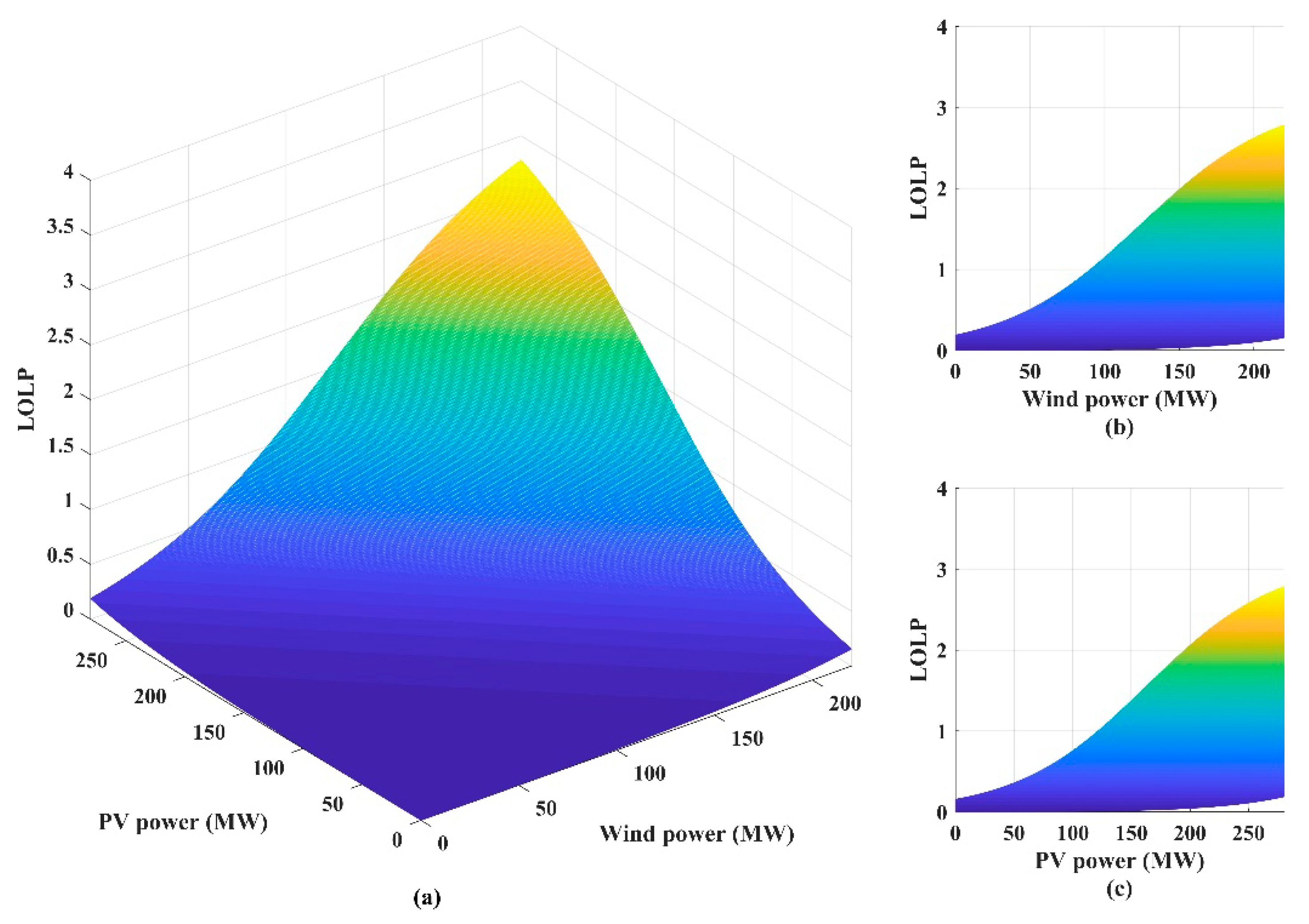
5.1. Reliability Evaluation
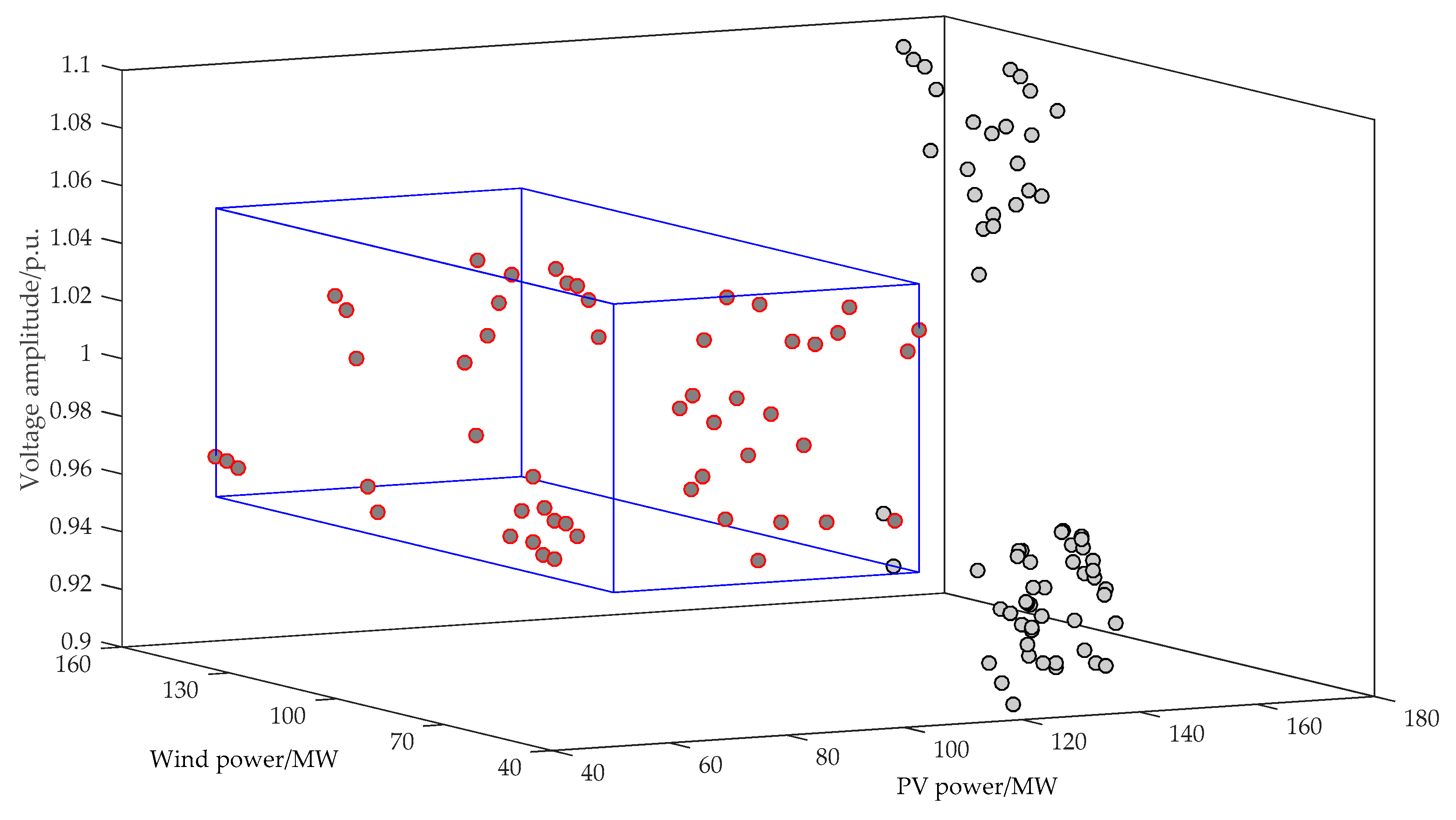
5.2. Voltage Variation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Council, G.W.E. Global Wind Report 2018; GWEC: Brussels, Belgium, 2018. [Google Scholar]
- SolarPower Europe. Global Market Outlook For Solar Power 2018–2022; SolarPower Europe: Brussels, Belgium, 2018. [Google Scholar]
- Lin, Y.; Yang, M.; Wan, C.; Wang, J.; Song, Y. A Multi-model Combination Approach for Probabilistic Wind Power Forecasting. IEEE Trans. Sustain. Energy 2018, 10, 226–237. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Song, Y.; Xu, Z.; Yang, G. Probabilistic forecasting of photovoltaic generation: An efficient statistical approach. IEEE Trans. Power Syst. 2017, 32, 2471–2472. [Google Scholar] [CrossRef]
- Yang, X.; Song, Y.; Wang, G.; Wang, W. A comprehensive review on the development of sustainable energy strategy and implementation in China. IEEE Trans. Sustain. Energy 2010, 1, 57–65. [Google Scholar] [CrossRef]
- Heydt, G.T. The next generation of power distribution systems. IEEE Trans. Smart Grid 2010, 1, 225–235. [Google Scholar] [CrossRef]
- Lin, Y.; Ding, Y.; Song, Y.; Guo, C. A Multi-State Model for Exploiting the Reserve Capability of Wind Power. IEEE Trans. Power Syst. 2018, 33, 3358–3372. [Google Scholar] [CrossRef]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef] [Green Version]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Impact of increased penetration of photovoltaic generation on power systems. IEEE Trans. Power Syst. 2013, 28, 893–901. [Google Scholar] [CrossRef]
- Shaaban, M.F.; El-Saadany, E. Accommodating high penetrations of PEVs and renewable DG considering uncertainties in distribution systems. IEEE Trans. Power Syst. 2014, 29, 259–270. [Google Scholar] [CrossRef]
- Divya, K.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Liu, Y.; Bebic, J.; Kroposki, B.; De Bedout, J.; Ren, W. Distribution system voltage performance analysis for high-penetration PV. In Proceedings of the Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–8. [Google Scholar]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef] [Green Version]
- Tahir, S.; Wang, J.; Baloch, M.H.; Kaloi, G.S. Digital control techniques based on voltage source inverters in renewable energy applications: A Review. Electronics 2018, 7, 18. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Widén, J. Correlations between large-scale solar and wind power in a future scenario for Sweden. IEEE Trans. Sustain. Energy 2011, 2, 177–184. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’isidoro, M.; Lacal-Arántegui, R. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Chatfield, C. The Analysis of Time Series: An Introduction; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energ. Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Bessa, R.J.; Miranda, V.; Botterud, A.; Zhou, Z.; Wang, J. Time-adaptive quantile-copula for wind power probabilistic forecasting. Renew. Energy 2012, 40, 29–39. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Angus, J.E. The probability integral transform and related results. SIAM Rev. 1994, 36, 652–654. [Google Scholar] [CrossRef]
- Li, D.X. On default correlation: A copula function approach. J. Fixed Income 2000. [Google Scholar] [CrossRef]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power App. Syst. 1979, 98, 2047–2054. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wu, H.; Ye, C.; Xiao, S.; Zhang, J.; He, X.; Wang, B. Integration Capability Evaluation of Wind and Photovoltaic Generation in Power Systems Based on Temporal and Spatial Correlations. Energies 2019, 12, 171. https://doi.org/10.3390/en12010171
Zhou H, Wu H, Ye C, Xiao S, Zhang J, He X, Wang B. Integration Capability Evaluation of Wind and Photovoltaic Generation in Power Systems Based on Temporal and Spatial Correlations. Energies. 2019; 12(1):171. https://doi.org/10.3390/en12010171
Chicago/Turabian StyleZhou, Hua, Huahua Wu, Chengjin Ye, Shijie Xiao, Jun Zhang, Xu He, and Bo Wang. 2019. "Integration Capability Evaluation of Wind and Photovoltaic Generation in Power Systems Based on Temporal and Spatial Correlations" Energies 12, no. 1: 171. https://doi.org/10.3390/en12010171
APA StyleZhou, H., Wu, H., Ye, C., Xiao, S., Zhang, J., He, X., & Wang, B. (2019). Integration Capability Evaluation of Wind and Photovoltaic Generation in Power Systems Based on Temporal and Spatial Correlations. Energies, 12(1), 171. https://doi.org/10.3390/en12010171




