Investigation on Heat Extraction Performance of Fractured Geothermal Reservoir Using Coupled Thermal-Hydraulic-Mechanical Model Based on Equivalent Continuum Method
Abstract
:1. Introduction
2. Methodology
2.1. Simulation Methods of Flow in Fractured Rock
2.2. Basic Assumptions
- The fluid flow in heat reservoir is in laminar regime and the Reynolds number is sufficiently low to meet the conditions of the Darcy law. Ignoring inertial loss, the pressure drop caused by porous resistance is proportional to velocity. This greatly simplifies the complexity of pores and throats in rock.
- The heat transmission fluid (i.e., water) always remains liquid. The temperature is always lower than 500 K, yet below the supercritical point of water (647 K, 22.064 MPa) [12], therefore it is reasonable to assume the water is always in liquid state.
- The porous heat reservoir is always fluid saturated, no immiscible gas is trapped in the rock and only single-phase flow is considered.
- There do not exist any fluid-structure interactions, including chemical dissolution, deposition, physical pressing, etc.
- The heat transmission fluid (i.e., water) is incompressible. The rock in this study is considered as thermo-poroelastic systems [13] based on a small strain assumption and obeys the generalized Hooke’s law.
2.3. The Governing Equations
2.3.1. Basic Flow Governing Equations
2.3.2. Energy Equations
2.3.3. Geo-Mechanical Equations
2.4. Coupling Method
2.5. Solving Method
3. Model Analysis
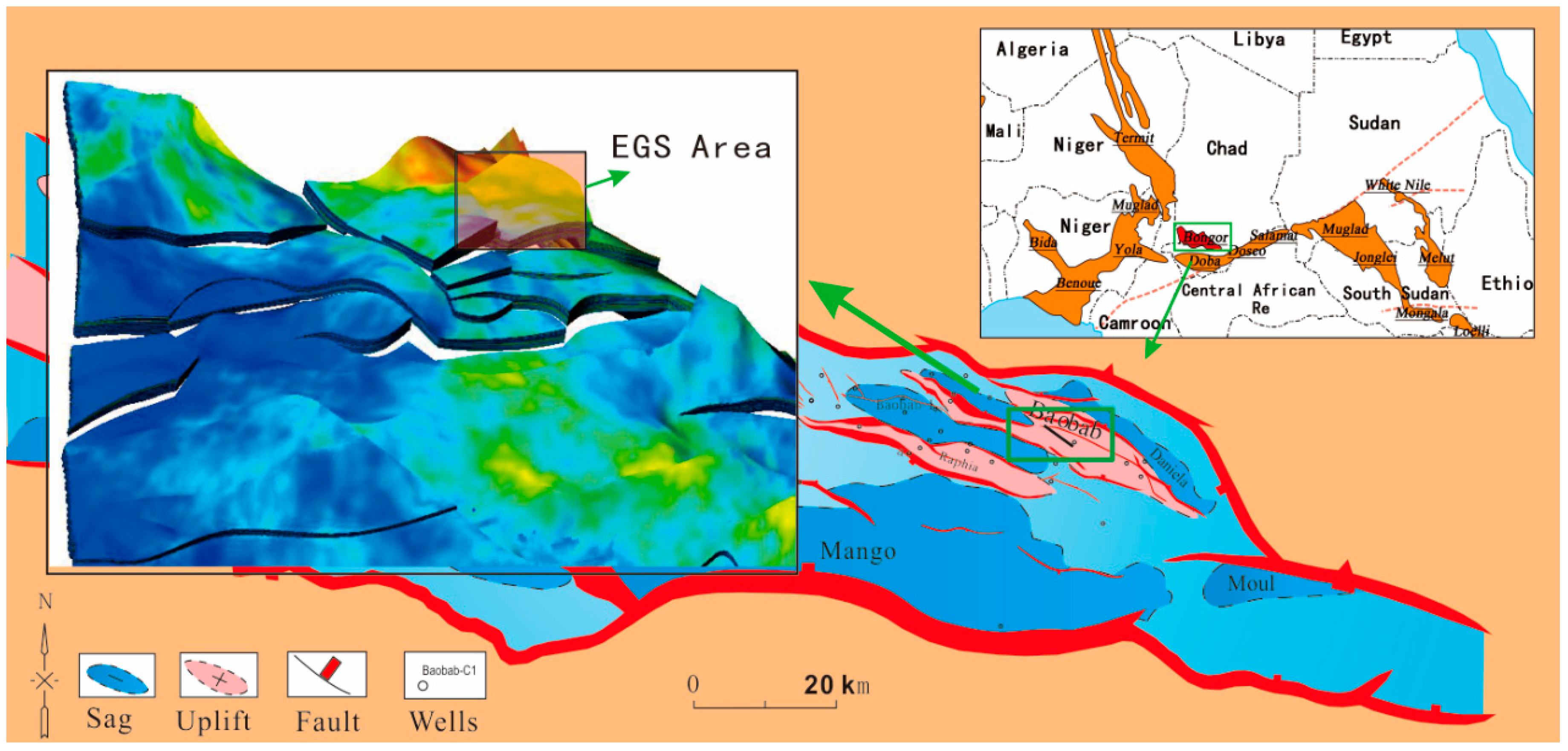
3.1. Background of Field-Scale Model
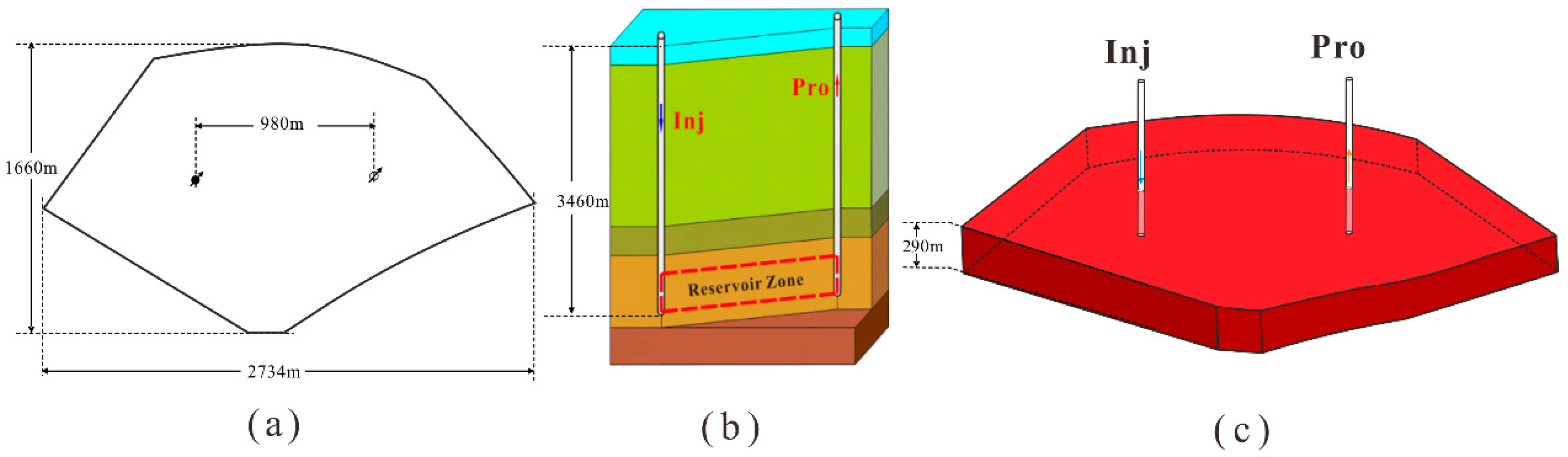
3.2. Boundary Conditions and Geometrical Parameters
3.3. Physics Parameters and Properties
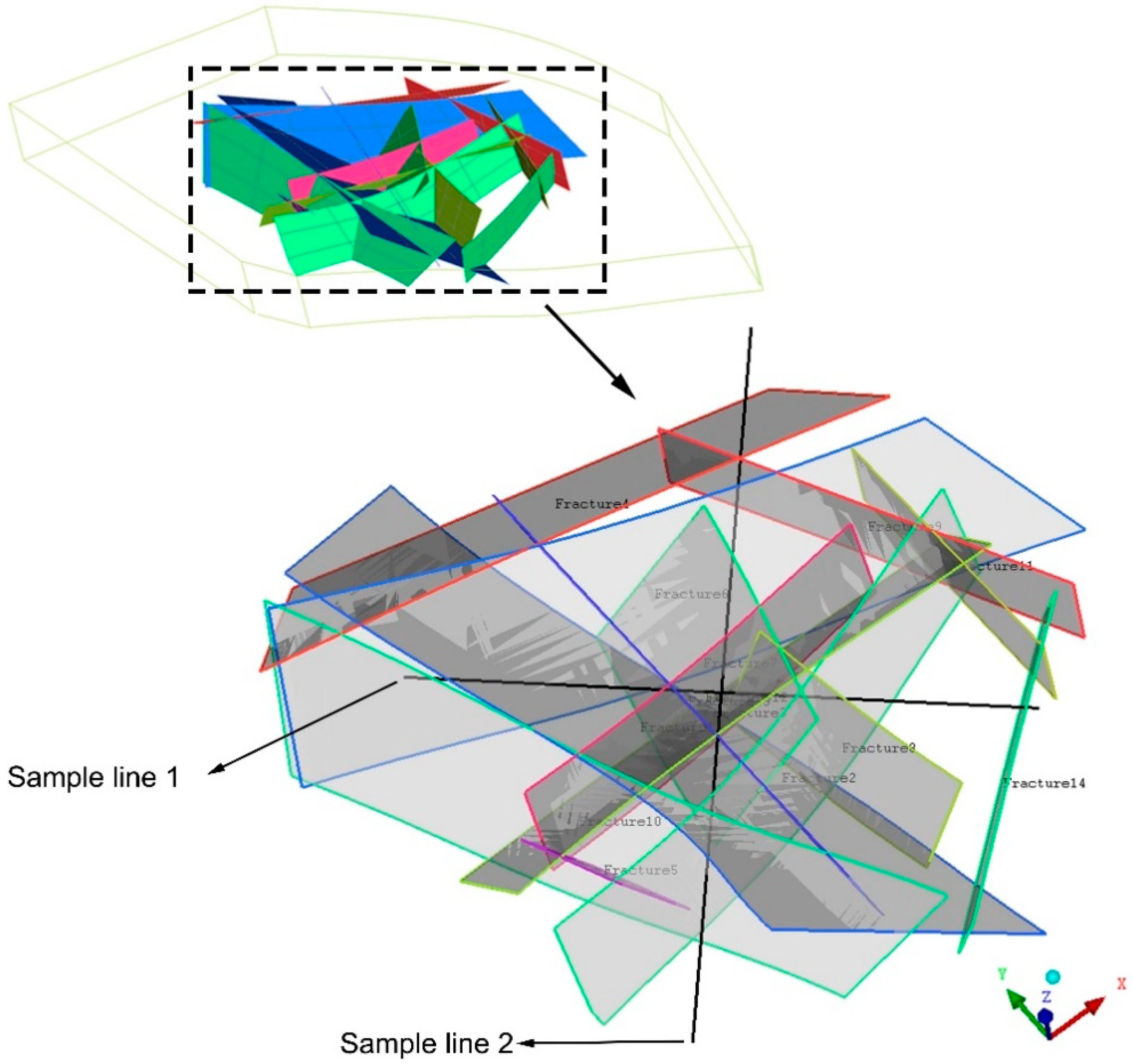
3.3.1. Initial Distribution of Permeability
3.3.2. Physics Parameters of Rock and Fluid
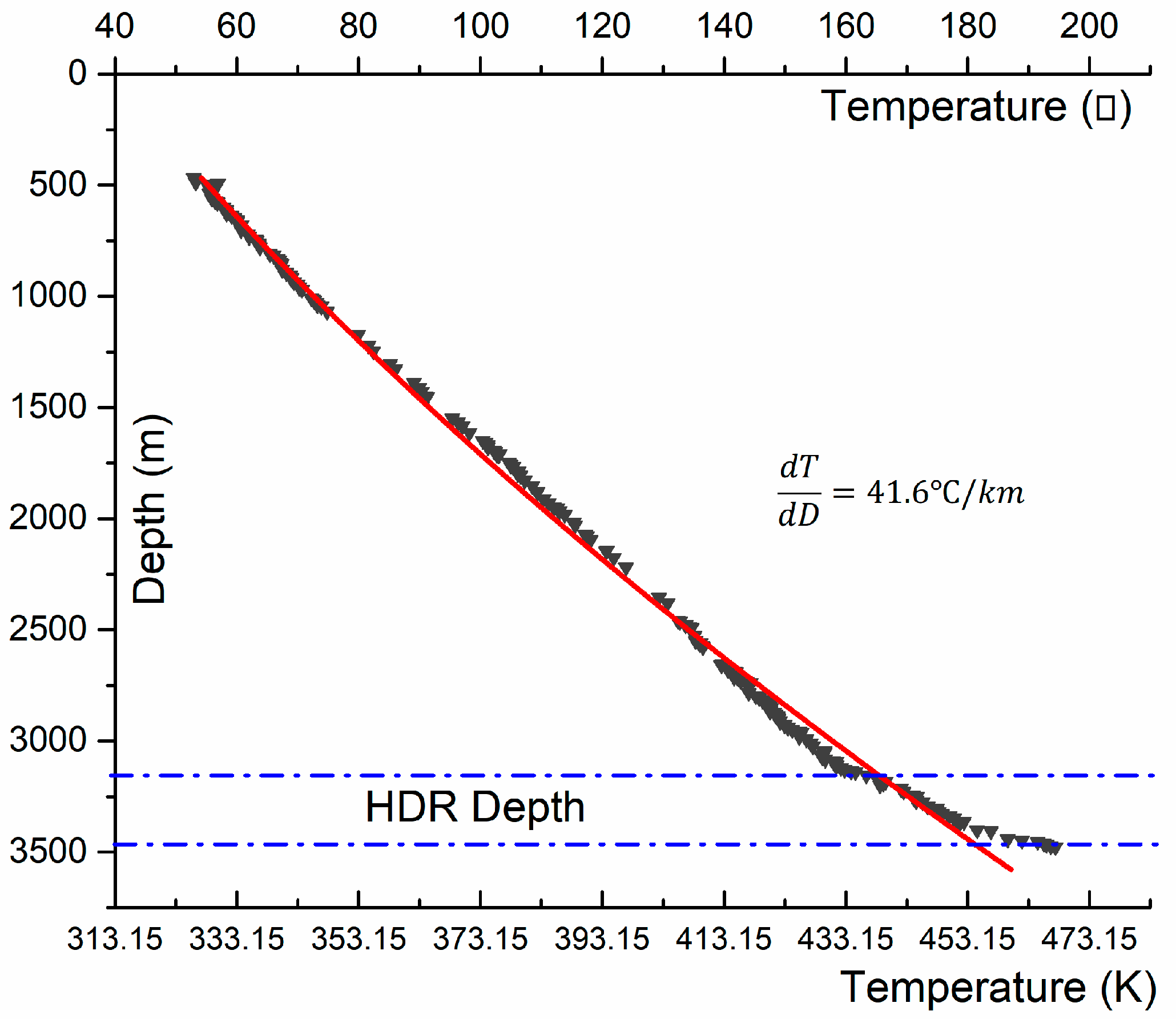
3.3.3. Initial Temperature Distribution
3.4. Equivalent Continuum Method for Discrete Fractures
3.4.1. Equivalent Continuum Method
3.4.2. Mapping Permeability Tensor from Discrete Fractures
5. Results and Discussion
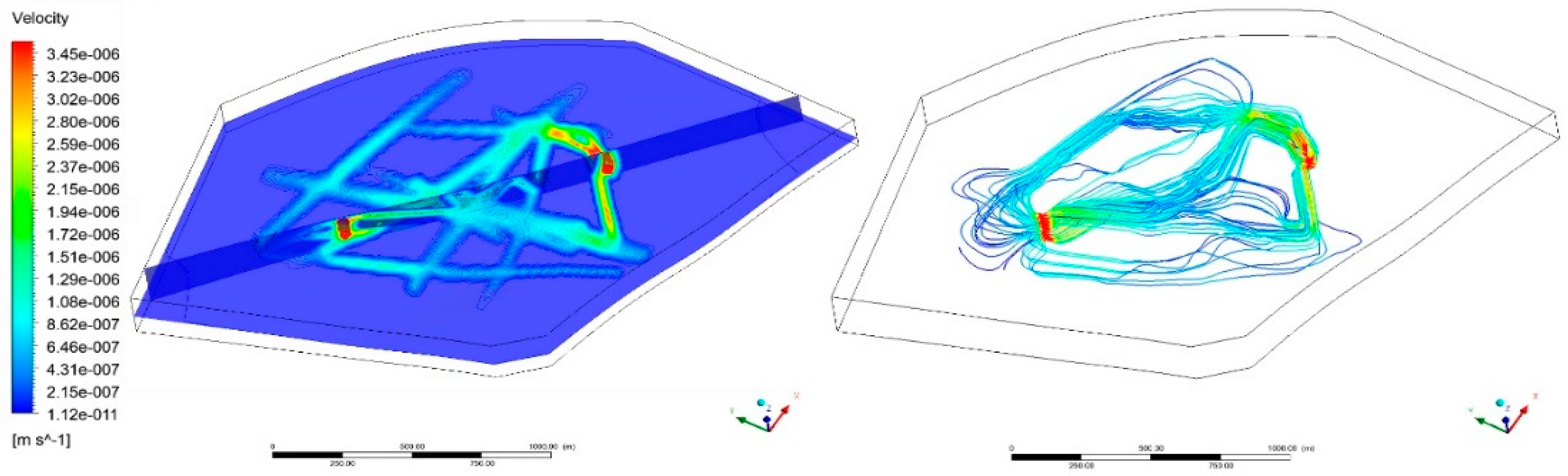
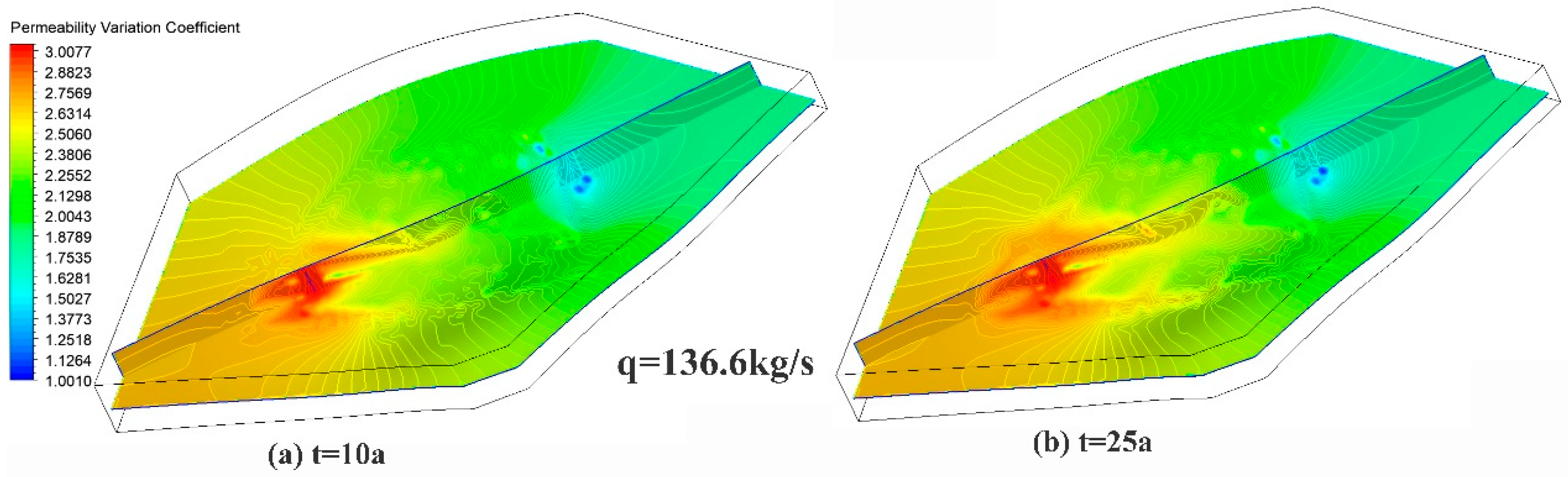
5.1. Analysis of Hydraulic Process
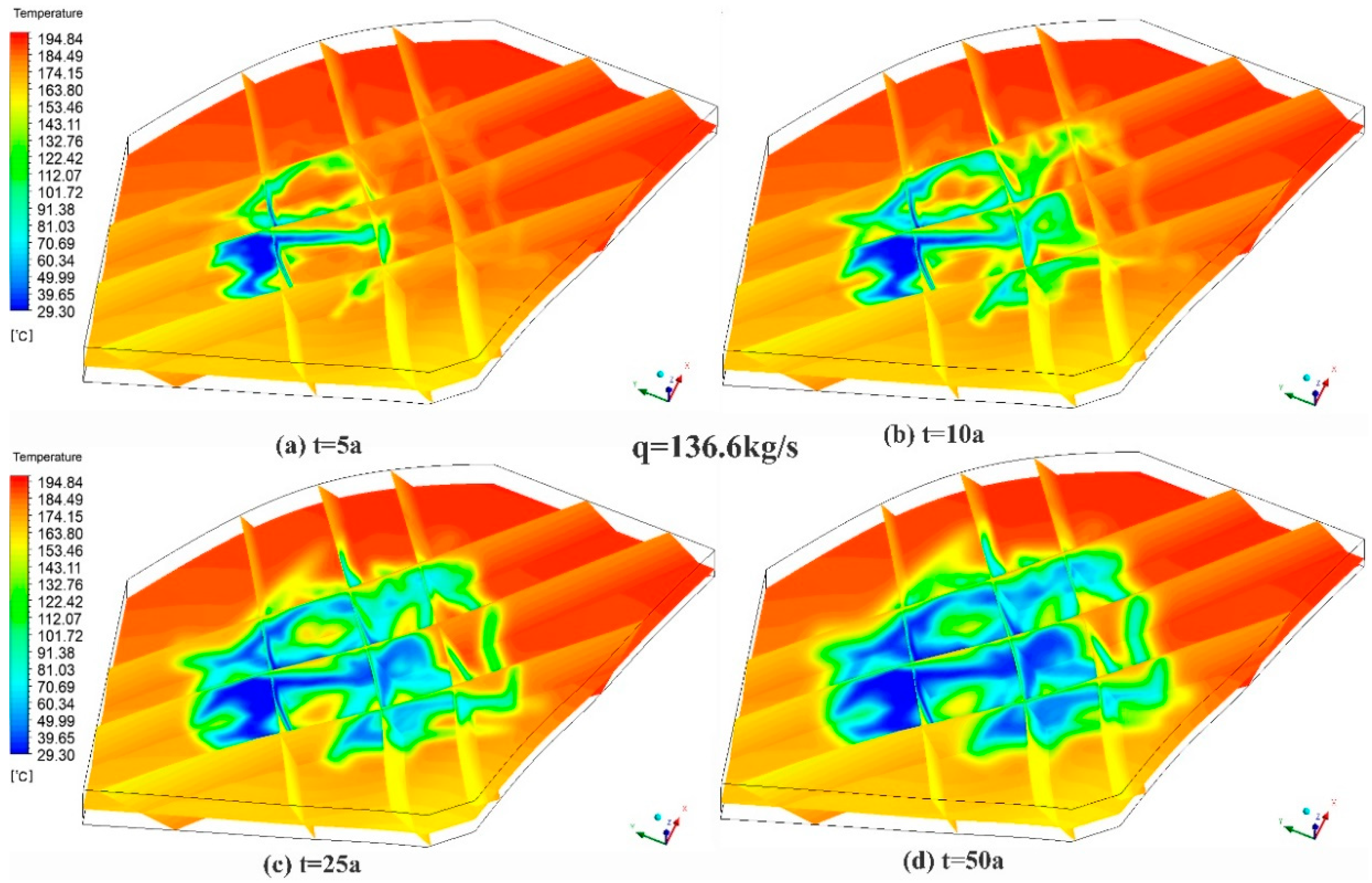
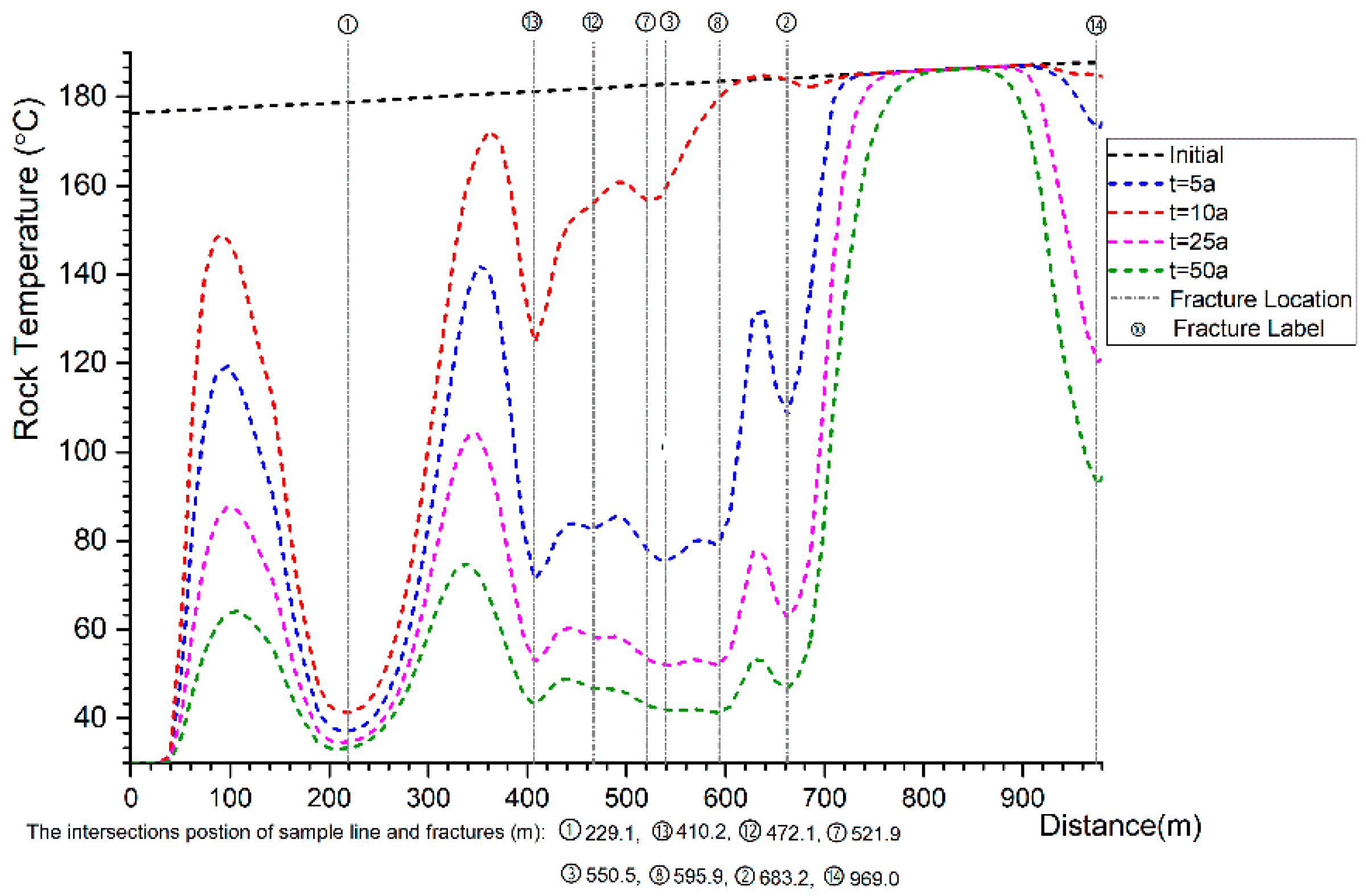
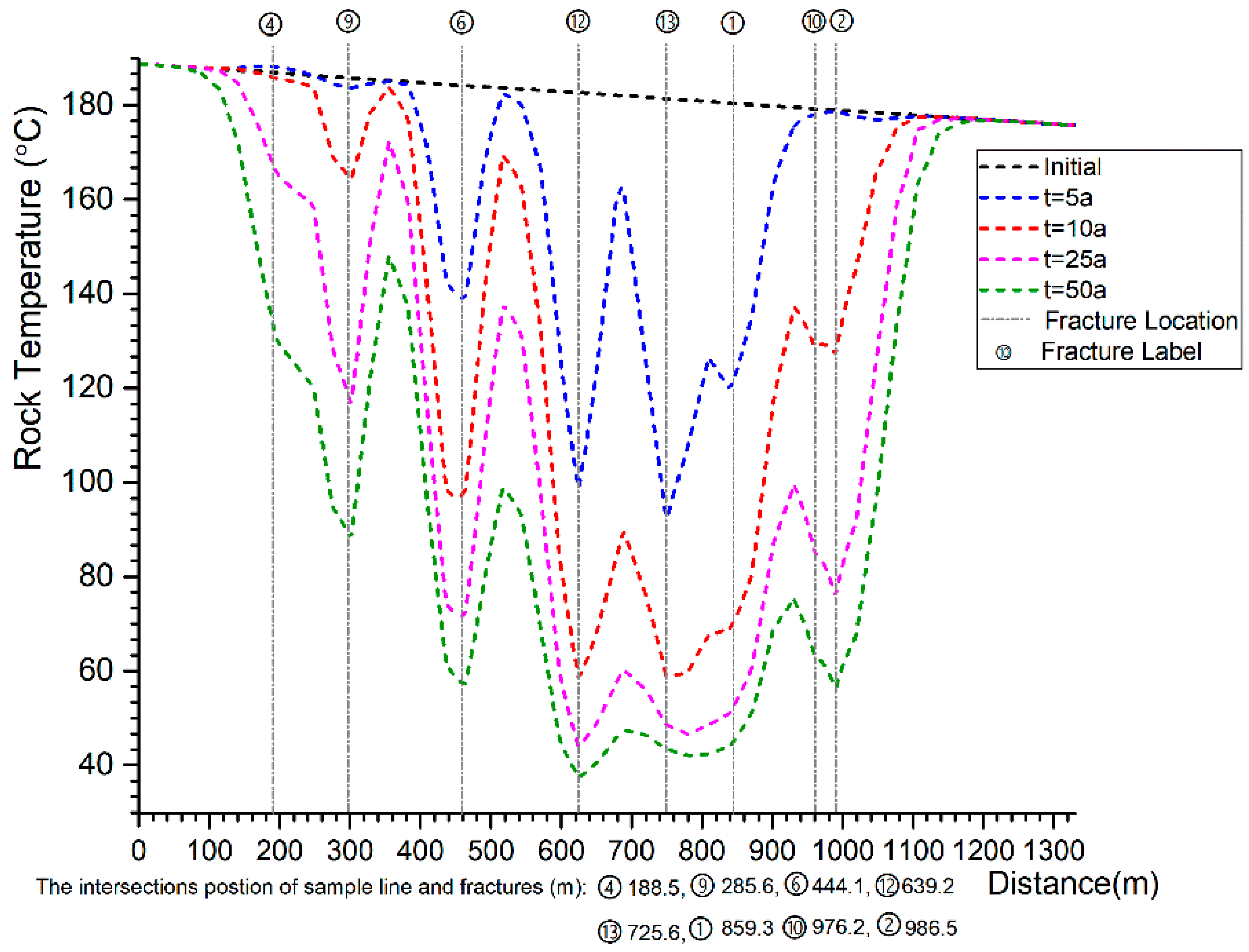
5.2. Analysis of Heat Transfer in Different Conditions
5.3. Analysis of Stress Sensitivity
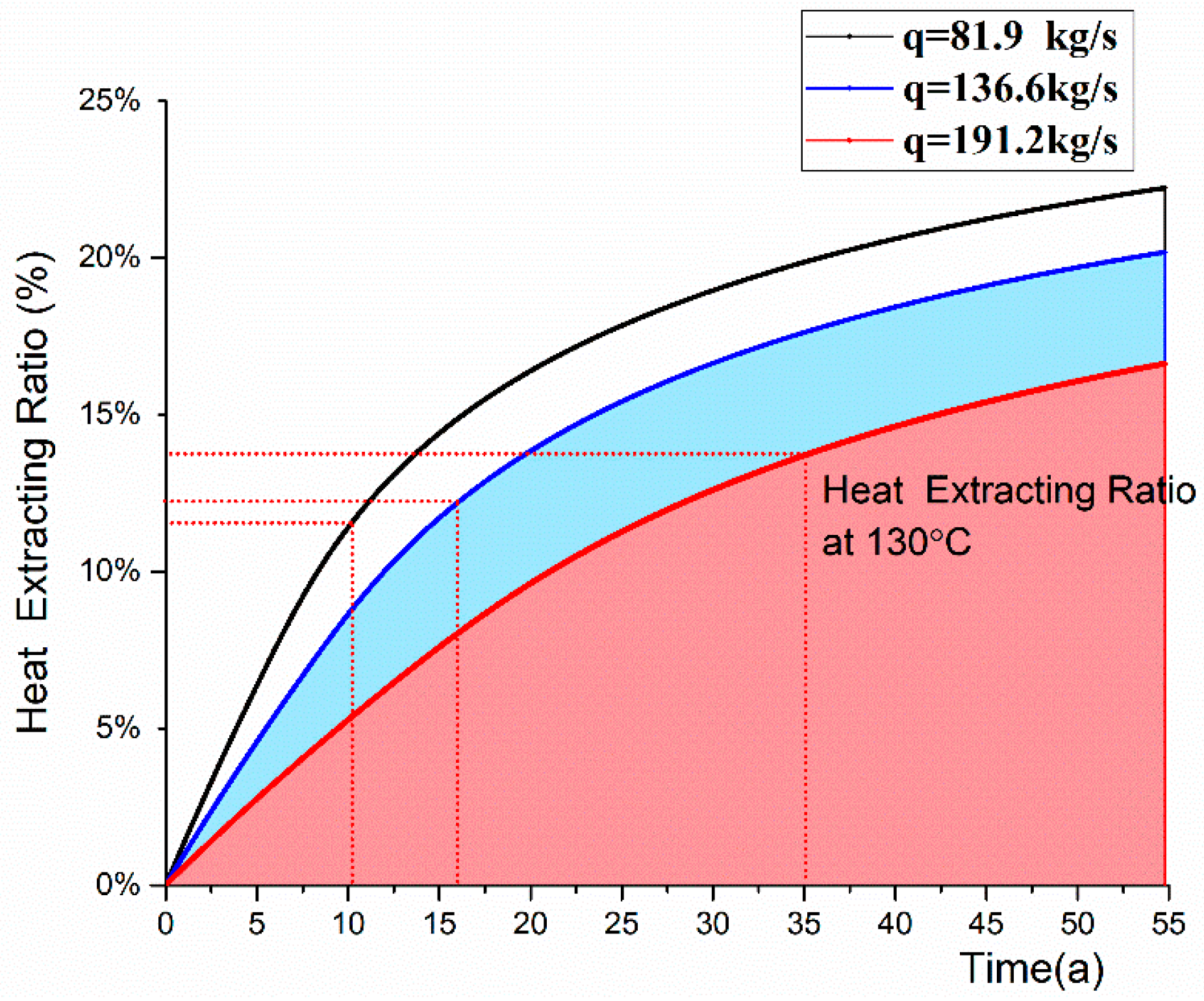
5.4. Analysis of Enhanced Geothermal System (EGS) Operation Prediction
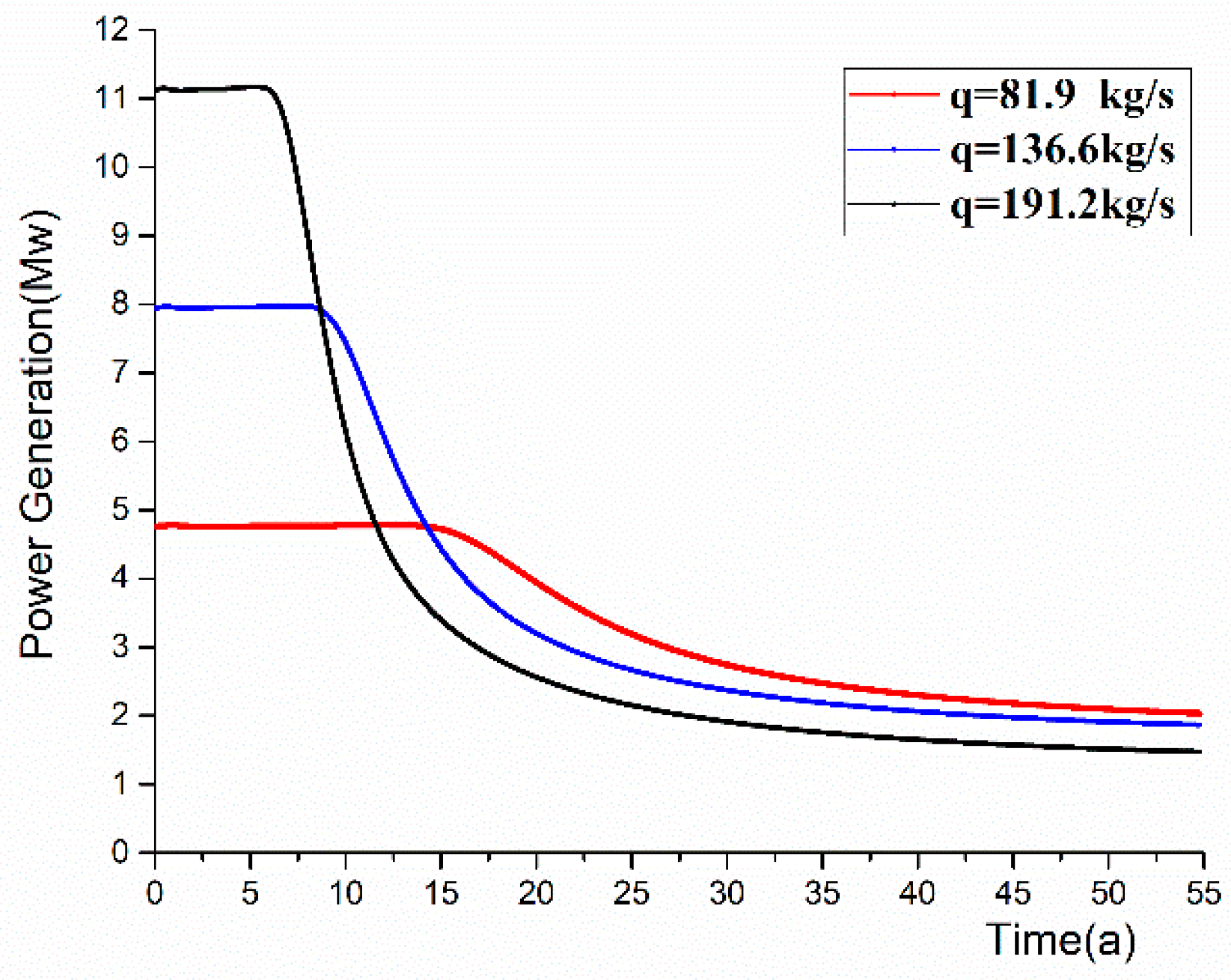
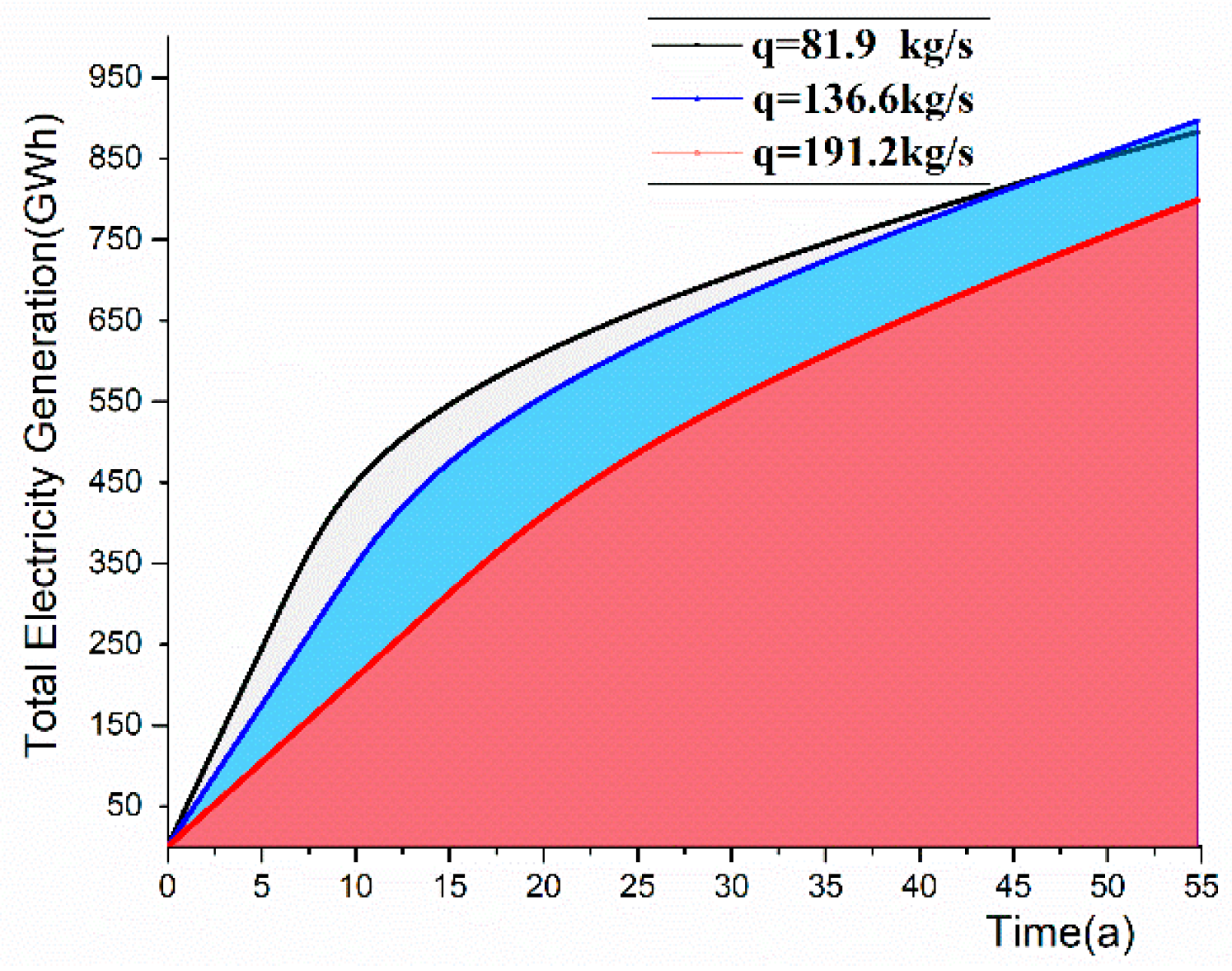
5.5. Analysis of Power Generation Prediction
6. Conclusions
- The equivalent continuum method is adopted in order to reduce computational overhead. The permeability tensor calculated from discrete fractures is employed to characterize the fractures. The thermal-hydraulic-mechanical process is coupled by a logarithmic stress sensitivity model.
- Strong heterogeneity is shown in the THM process because of the heterogenous distribution of fractures. In the heat transfer process, fractures are the dominant regions in which water transfers heat from the rock matrix by convection, in addition, the fractures have an impact on the pore pressure distribution, which increase the heterogeneity of geo-mechanical process.
- The EGS operation prediction data has a quantitative description of the subsurface evolving with time in different conditions. The case with high injection rates can rapidly extract heat, and has a relatively lower efficiency and unstable production temperature, however, occur in the late stage of operation. Heat conduction is not able to sufficiently transfer heat from the tight original rock to the fractures. This illustrates the necessity of well pattern optimization and intensive stimulation in the late stage of EGS operation.
- Most of the parameters used in the simulation are taken from actual field data, which includes geometrical data, geothermal gradient data, rock mechanical properties. Therefore, this model can better reflect actual geological physical properties and the simulation results are closer to actual reservoir operation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| superficial velocity (m/s) | |
| permeability tensor (m2) | |
| body force per unit volume in the i-coordinate (i = x, y, z in 3D) (Pa) | |
| elastic modulus (Pa) | |
| Poisson’s ratio | |
| hydraulic pressure (Pa) | |
| Biot’s constant | |
| rock temperature (K) | |
| water temperature in fracture (K) | |
| thermal expansion coefficient | |
| total stress of rock (Pa) | |
| effective stress of fracture (Pa) | |
| t | time (s) |
| dynamic viscosity of fluid (Pa·s) | |
| fracture length (m) | |
| water density (kg/m3) | |
| thermal conductivity of rock mass (W/m/K) | |
| thermal conductivity of water (W/m/K) | |
| heat capacity of rock block (J/kg/K) | |
| stress sensitivity coefficient | |
| heat capacity of water (J/kg/K) | |
| a | Specific surface area (1/m) |
| convection coefficient (W/m2/K) | |
| absolute temperature (K) | |
| initial permeability (m2) | |
| rock porosity (%) | |
| fracture aperture (m) | |
| injection specific enthalpy (kJ/kg) | |
| production specific enthalpy (kJ/kg) | |
| total production rate (kg/s) | |
| predicted output power (Mw) | |
| reinjection temperature of injection well (K) | |
| depth of injection well (m) | |
| depth of production well (m) | |
| geothermal power conversion efficiency | |
| heat recovery rate | |
| predicted total electricity generation (GWh) | |
| outflowing water temperature (K) | |
| average production temperature (K) | |
| average reservoir temperature (K) | |
| temperature of the injected fluid (K) |
References
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R. The Future of Geothermal Energy—Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; 358p. [Google Scholar]
- Lu, S.M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Breede, K.; Dzebisashvili, K.; Liu, X.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: past, present and future. Geotherm. Energy 2013, 1. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Tian, Z.F. A simplified coupled hydro-thermal model for enhanced geothermal systems. Appl. Energy 2015, 140, 135–145. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, J.; Huang, W.; Luo, L. A three-dimensional transient model for EGS subsurface thermo-hydraulic process. Energy 2014, 72, 300–310. [Google Scholar] [CrossRef]
- Shaik, A.R.; Rahman, S.S.; Tran, N.H.; Tran, T. Numerical simulation of Fluid-Rock coupling heat transfer in naturally fractured geothermal system. Appl. Therm. Eng. 2011, 31, 1600–1606. [Google Scholar] [CrossRef]
- Bahrami, D.; Danko, G.; Fu, P.; Guo, B.; Podgorney, R.; White, M.; Xia, Y. Poroelastic and Self-Propped Single Fracture THM Models for EGS Studies. In Proceedings of the 40th Stanford Geothermal Workshop, Stanford, CA, USA, 26–28 January 2015; pp. 1–20. [Google Scholar]
- Zhao, Y.; Feng, Z.; Feng, Z.; Yang, D.; Liang, W. THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573 K and buried depth 6000–7000 M. Energy 2015, 82, 193–205. [Google Scholar] [CrossRef]
- Guo, B.; Fu, P.; Hao, Y.; Peters, C.A.; Carrigan, C.R. Thermal drawdown-induced flow channeling in a single fracture in EGS. Geothermics 2016, 61, 46–62. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, X.; Xu, Y.; Yao, J.; Wang, H.; Lv, S.; Sun, Z.; Huang, Y.; Cai, M.; Huang, X. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 2017, 120, 20–33. [Google Scholar] [CrossRef]
- Dou, H.; Zhang, H.; Yao, S.; Zhu, D.; Sun, T.; Ma, S.; Wang, X. Measurement and evaluation of the stress sensitivity in tight reservoirs. Pet. Explor. Dev. 2016, 43, 1116–1123. [Google Scholar] [CrossRef]
- Thomson, G.W. The Antoine Equation for Vapor-pressure Data. Chem. Rev. 1946, 38, 1–39. [Google Scholar] [CrossRef]
- Hu, L.; Winterfeld, P.H.; Fakcharoenphol, P.; Wu, Y.S. A novel fully-coupled flow and geomechanics model in enhanced geothermal reservoirs. J. Pet. Sci. Eng. 2013, 107, 1–11. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 3-319-99691-6. [Google Scholar]
- Burke, K. The Chad Basin: An Active Intra-Continental Basin. Tectonophysics 1976, 36, 197–206. [Google Scholar] [CrossRef]
- Dou, L.; Xiao, K.; Hu, Y.; Song, H.; Cheng, D.; Du, Y. Petroleum geology and a model of hydrocarbon accumulations in the Bongor Basin, the Republic of Chad. Shiyou Xuebao Acta Pet. Sin. 2011, 32, 379–386. [Google Scholar]
- Genik, G.J. Regional framework, structural and petroleum aspects of rift basins in Niger, Chad and Central African Republic (C.A.R.). Tectonophysics 1992, 213, 169–185. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, J.; Gong, Y.; Wang, Y.; Ma, W. Energy efficiency comparison between geothermal power systems. Therm. Sci. 2016, 21, 74. [Google Scholar] [CrossRef]
- Oda, M. Frabric Tensor for Discontinuous Geological Material. Soil Found. 1982, 22, 96–108. [Google Scholar] [CrossRef]
- Oda, M. Similarity rule of crack geometry in statistically homogeneous rock masses. Mech. Mater. 1984, 3, 119–129. [Google Scholar] [CrossRef]
- Oda, M. Permeability tensor for discontinuous rock masses. Géotechnique 1985, 35, 483–495. [Google Scholar] [CrossRef]
- Kaviany, M. Principle of Heat Transfer in Porous Media; Springer: New York, NY, USA, 1995. [Google Scholar]
- Yari, M. Exergetic analysis of various types of geothermal power plants. Renew. Energy 2010, 35, 112–121. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, Z.W.; Guo, L.L.; Gao, P.; Jin, X.P.; Xu, T.F. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]
- Zarrouk, S.J.; Moon, H. Efficiency of geothermal power plants: A worldwide review. Geothermics 2014, 51, 142–153. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Injection well depth, () | 3460 |
| Production well depth, () | 3590 |
| Geothermal reservoir length, | 2734 |
| Geothermal reservoir width, | 1660 |
| Geothermal reservoir thickness, | 290 |
| Interwell separation, | 980 |
| Borehole size, | 0.3 |
| Average temperature, | |
| Initial average permeability, | |
| Initial average porosity, | |
| Reservoir total heat, |
| Parameter | Value |
|---|---|
| Rock thermal conductivity, () | 3.42 |
| Rock density, () | 2700 |
| Rock specific heat, | 1125 |
| Elastic modulus, | 41 |
| Poisson ratio, | 0.23 |
| Biot coefficient, | 1 |
| Rock linear thermal expansion, | |
| Fluid thermal conductivity, () | 0.6 |
| Fluid density, () | 1000 |
| Fluid specific heat, | 4200 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Sun, Z.; Zhang, K.; Jiang, C.; Xin, Y.; Mao, Q. Investigation on Heat Extraction Performance of Fractured Geothermal Reservoir Using Coupled Thermal-Hydraulic-Mechanical Model Based on Equivalent Continuum Method. Energies 2019, 12, 127. https://doi.org/10.3390/en12010127
Wang T, Sun Z, Zhang K, Jiang C, Xin Y, Mao Q. Investigation on Heat Extraction Performance of Fractured Geothermal Reservoir Using Coupled Thermal-Hydraulic-Mechanical Model Based on Equivalent Continuum Method. Energies. 2019; 12(1):127. https://doi.org/10.3390/en12010127
Chicago/Turabian StyleWang, Tong, Zhixue Sun, Kai Zhang, Chuanyin Jiang, Ying Xin, and Qiangqiang Mao. 2019. "Investigation on Heat Extraction Performance of Fractured Geothermal Reservoir Using Coupled Thermal-Hydraulic-Mechanical Model Based on Equivalent Continuum Method" Energies 12, no. 1: 127. https://doi.org/10.3390/en12010127
APA StyleWang, T., Sun, Z., Zhang, K., Jiang, C., Xin, Y., & Mao, Q. (2019). Investigation on Heat Extraction Performance of Fractured Geothermal Reservoir Using Coupled Thermal-Hydraulic-Mechanical Model Based on Equivalent Continuum Method. Energies, 12(1), 127. https://doi.org/10.3390/en12010127






