1. Introduction
A plethora of studies have been conducted to enhance understanding of electric vehicle connection to the grid [
1], and to define expectations for electricity grid performance when distributed generation also plays its own important role [
2,
3]. These two, relatively new components require wise consideration [
4] in order to enhance grids’ productivity; this has to be done in a manner which is interconnected [
5]. One approach could be electric vehicles that are aggregated to a virtual power plant [
6]; in conjunction to renewables generation, the degree to which they are able to increase grid capacity factors is investigated. Moreover, aggregation offers operational benefits to the system operator [
7], who is then able to take faster and safer operational decisions. Electric vehicles batteries can present energy storage opportunities for the grid if customer comfort is lightly compromised. Under these conditions, it can provide short-term reserves and offer additional grid flexibility [
8].
The increase of available computational power has also transferred to power system applications, thereby advancing the capability of researchers and operators to improve grid performance. This is a one-way path, due to the existing and increasing complexity of the addition of smart devices to the grid. Electric transportation is considered an important factor in this field [
9]. Special attention is given to high performance computing (HPC) applications that use probabilistic methods, which are demanding in terms of calculations, but necessary to understand specific phenomena with adequate accuracy. Electric vehicle connections to the grid and the Monte Carlo method is an example [
10]. However, stochastic methods, and especially Monte Carlo [
11], is computationally demanding even for today’s standards; hence, specific operational points are developed in this study for a specific network [
12].
Electric vehicles charging would also require a grid expansion design factor [
13]. Current research on electric vehicles, as far as the distribution network is concerned, gives emphasis to probabilistic methods in order to predict charging patterns, and predict the expected charging behavior. This also affects the connection points for distributed generations, that could be optimally different if connected points are based on probabilistic methods, taking into consideration their intermittency [
14]. As far as electric vehicles are concerned, the first step is to characterize their charging demand [
15]. In some cases, the system is simulated as a whole, and the operational benefits are optimized based on electric charging owners’ behavior [
16]. Alternatively, they are connected in a way that relieves distribution system constraints [
17]. Active distribution network management could be done by aggregating electric vehicle behavior in a probabilistic manner [
12]. Probabilistic studies have also shown good correlation between electric vehicles and renewables [
18]. In this research, electric vehicle and load aggregation is performed on the level of a secondary distribution system, at the point of medium voltage (MV)/low voltage (LV) connection, and it is fully controlled.
Having mentioned the above, several studies have researched the emerging phenomenon of electric vehicles. All of them are consumer oriented, giving emphasis to electric vehicles per se, and showing minimal consideration for the electricity grid. On the other hand, the research presented in the current paper is electric grid oriented. It is focused in the procedure of creating optimal electric grid operation points for electric vehicle charging for a real distribution network [
19], i.e., as it operates today, based on objective equations, solved with Monte Carlo using high performance computing.
2. Line under Investigation
This method is applied to a real representative distribution network [
19]. Details of the network are available at the online dataset (
http://dx.doi.org/10.7910/DVN/1I6MKU). Source code and data sets are open sourced to all users. This network spans fifty-five kilometers (55 km), a typical size for distribution rural lines, and its total installed load capacity is twelve mega-volt-amperes (12MVA). It is radially organized, and all conductors are optimized based on the expectation that higher currents appear near the feeder at the high to medium voltage substation.
It has forty-five (45) medium-to-low voltage transformers that are used to supply low voltage loads. These are the expected points for the aggregated connection of electric vehicles. The electric vehicles are connected to the secondary distribution network at low voltage levels, i.e., after the medium to low voltage transformers. It is assumed that the maximum load, including electric vehicles’, does not exceed the maximum observed active and reactive power of the existing installations. In this manner, the maximum utilization of the network is achieved.
Given that distribution network is limited, solar irradiation does not change significantly across the line. According to this assumption, production from photovoltaic plants could be safely assumed to be similar. Hence, the plants connected to the line under investigation would operate at the same percentage of installed capacity. There are also twenty-four (24) photovoltaic plants with an installed capacity totaling to 6929 ΜW. This network is not connected to any other type of distributed generation. The network in detail is available at [
19].
3. Monte Carlo and Power Flow Methods
The Monte Carlo method is applied to numerically stochastic processes, and is used to simulate probabilistic physical phenomena. For this research, it is assumed that each of the forty-five (45) loading nodes of the line under consideration in this analysis can independently receive an active load Sn of up to 1 pu of its capacity:
To achieve this input, a one-dimension table with 45 rows is defined that is assigned continuous random variables with values from 0 to 1. According to the following definition, a continuous random variable
x has the properties of the function:
In other words, probability is uniform across all applicable values. However, in the reality of modern computing, absolute random numbers cannot be produced. Pseudorandom numbers are used, with satisfactory results. Pseudorandom number also demonstrate additional research related benefits. The same procedure has always been used to produce them, i.e., they are always the same for a given application. Therefore, results are replicable, hence better benchmarked and controlled.
AC power flow is the typical procedure for solving problems of power systems steady state analysis, which is also applied to this research [
20]; it is a widely used and well-known procedure [
21]. A typical element has the following admittance
Yij:
and the voltage of a given bus is given as:
the current of this bus is given from:
and its active and reactive power:
which makes:
at every time the scheduled power needs to be similar to the calculated:
and consequently
the total active power loss is calculated by subtracting from the total generation the total load
and similarly, for the reactive power
Newton-Raphson is the numerical method used to solve the above-mentioned equations. A short description is provided below. If two equations are considered:
then, the solutions
and
can be yielded from:
And then expanding in Taylor series:
which can be rewritten as:
where the Jacobian matrix is:
this gives:
and the new estimates are:
4. Simulation Procedure
The source code for this publication has been simulated on Mathworks Matlab Runtime v92, 2017a [
22], compiled on Unix operating system and run on Aris high performance computing [
23]. High performance computing was not necessary to achieve the research goals; however, it reduces computational time and provides the capability of scaling up to larger electricity networks. Power load flow analysis is conducted on Matpower 6.0 code [
24,
25]. The source code and the results are provided in the
supplementary materials of this manuscript, available on Harvard Dataverse [
26].
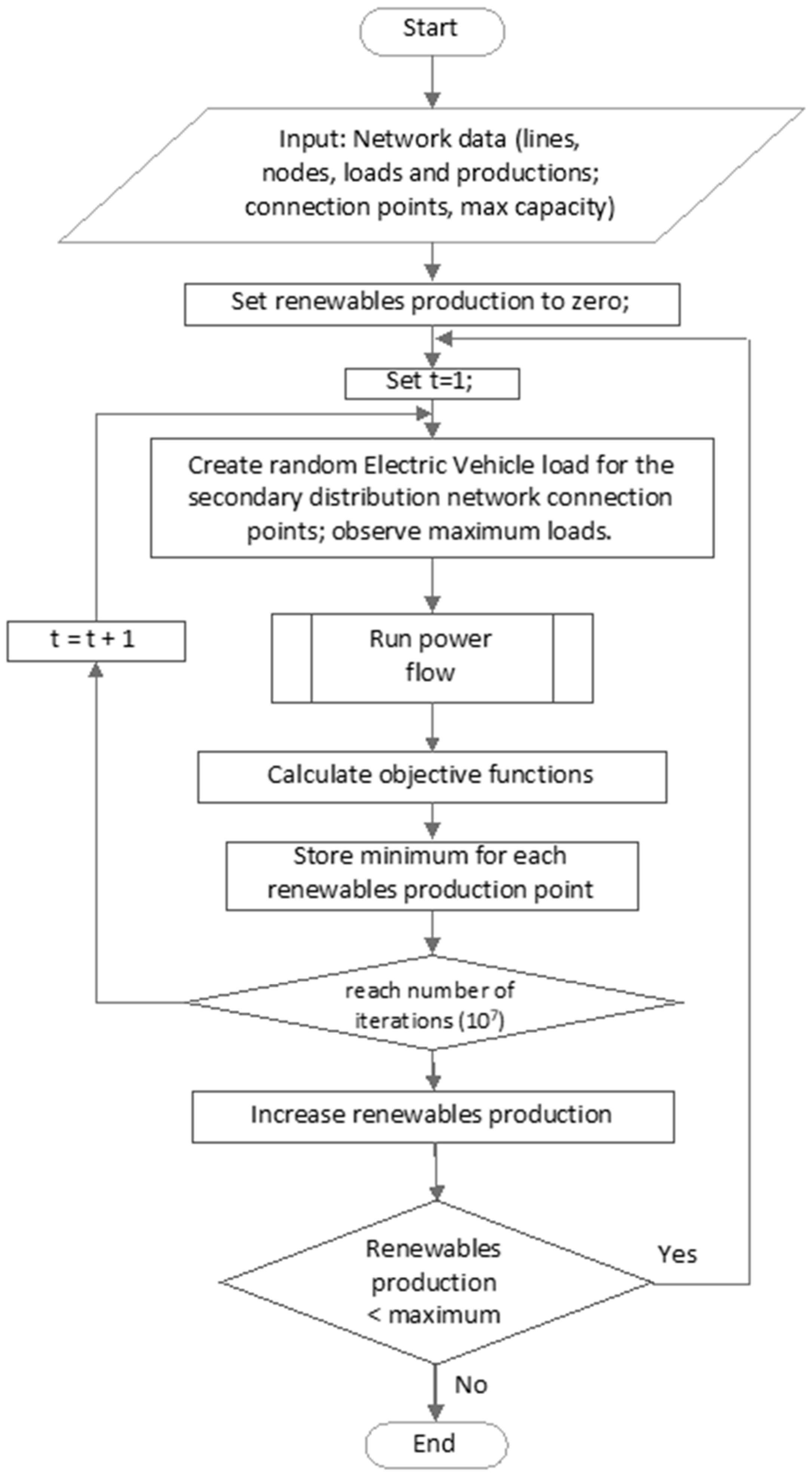
Figure 1 presents the flow chart for the proposed calculation method. Initially, the algorithm inputs the distribution network data. This includes information of its load and production nodes connection, line characteristics, as well as their impedance and reactance to perform load flow calculations. Then the system creates random loading using the Monte Carlo method [
11] for all applicable nodes, and performs load flow analysis.
The procedure repeats numerous times in order to cover all applicable cases, and the best result is stored for each operational point. An ARIS high performance computer was able to simulate each one of the operational points, using one processor, in 48 h [
23]. Source code total calculation time can be improved if the number of Monte Carlo iterations are reduced, but this could lead to suboptimal results. This source code may also run on personal computers, but usually higher computational times are required.
The default solver uses Newton’s method [
20]. This type of analysis is adequate to perform load aggregation and production analysis in a steady state.
The objective functions applied to this research take into consideration the maximum electric vehicle charging load and the minimum voltage across the network, based on the available production from distributed generation. From these two aspects, the charging load is more important to the analysis, and consequently, it receives a higher contribution factor. The final objective is achieved by minimizing the following equations:
where:
Pev stands for the total active load of the line. It is assumed that
.
and
Vmin is the minimum voltage observed at any node of the line.
All the above are calculated for increasing production from the connected-to-the-network distributed generation sources, such as photovoltaic plants. Then ten optimal operational points for each optimization equation were created, increasing renewables’ production from zero to maximum. These are operational points for a given network based on the availability of energy produced from renewables that meet the above-mentioned objective functions.
5. Results and Discussion
Simulation results have shown consistency across all applications to this work’s minimization formulas. According to the conducted simulations, there are repeating loading optimization patterns, unique for each line according to the imposed constraints in terms of distributed generation production and minimization requirements.
For
there are five (5) operational points (
Table 1 and
Table 2) across the installed capacity of the distributed generation connected to the line. For each transformer connection node, the load percentage in conjunction to the maximum observed load has been calculated. It was observed that in some cases, this percentage is very low. This is due to the specific characteristics of the line, and hence, reinforcement is suggested near these transformers.
The exact manner in which this reinforcement shall be done is not currently clear to the researchers. A probabilistic approach can be applied, which can be part of future work. To achieve better performance, it is proposed that messed, instead of radial, topology be applied; however, issues of protection may arise.
For
, there are three (3) operational points (
Table 3 and
Table 4) across the installed capacity of the distributed generation connected to the line. To a certain degree, these are similar to the operational points derived from the other equations. This observation further supports the possibility of having line-specific optimal operation points across a wide range of operating conditions. This is to be further investigated.
For
, there are three (3) operational points (
Table 5) across the installed capacity of the distributed generation connected to the line.
For
there are two (2) operational points (
Table 6) across the installed capacity of the distributed generation connected to the line.
It must be noted that, even if the equation results show an increasing value, the optimal line operation points remain, to a certain degree, of the same value. It appears that these are unique for each line, and can be pre-calculated. System operators, being able to affect electric vehicles’ load, can adjust grid’s operation near to these points. Grid reinforcements can be constructed on the objective of optimizing the optimization points, thereby achieving even better line performance when electric vehicles are to be connected. Moreover, in an effort to validate the obtained results, a genetic algorithm is applied in order to minimize the objective functions (25)–(28). Genetic algorithms are widely applied in science and engineering for solving practical search and optimization problems. The same algorithm gives excellent results in several other optimization problems [
27,
28,
29]. The obtained results of the two applied methodologies (
Table 7 and
Table 8) present adequate convergence, confirming the appropriateness of the proposed methodology.
6. Conclusions
This analysis provides specific operational points based on the production of the connected distributed generators. Based on these findings, potential charging service providers are able to optimize the charging of electric vehicles connected to the line under investigation. In this way, optimal operations could be achieved. It should be mentioned that it is possible to provide optimization formulas for minimizing line losses or maximizing transferred energy using the provided algorithm.
Loading patterns appear to be consistent across all performed calculations. It is believed that they are connected to the topology of the line, and are to a certain degree unconnected to the load. This is an important observation that requires further investigation.
It is observed that several transformer connection nodes display low percentages of optimal load. To the authors’ understanding, these are the areas of the grid that need reinforcement. The reinforcement can be done in a manner for the grid whereby the radial configuration is lost. In this case, new calculations are required.
Simulation results have shown improving performance of the grid for increasing production from distributed generators. This is an expected observation; however, the performed simulations are able to provide quantification.
Future work will include the creation of active protection systems based on pragmatic conditions operational system diagnosis, and further probabilistic analysis for possible reinforcements.