Cavitation Effects on the Structural Resonance of Hydraulic Turbines: Failure Analysis in a Real Francis Turbine Runner
Abstract
1. Introduction
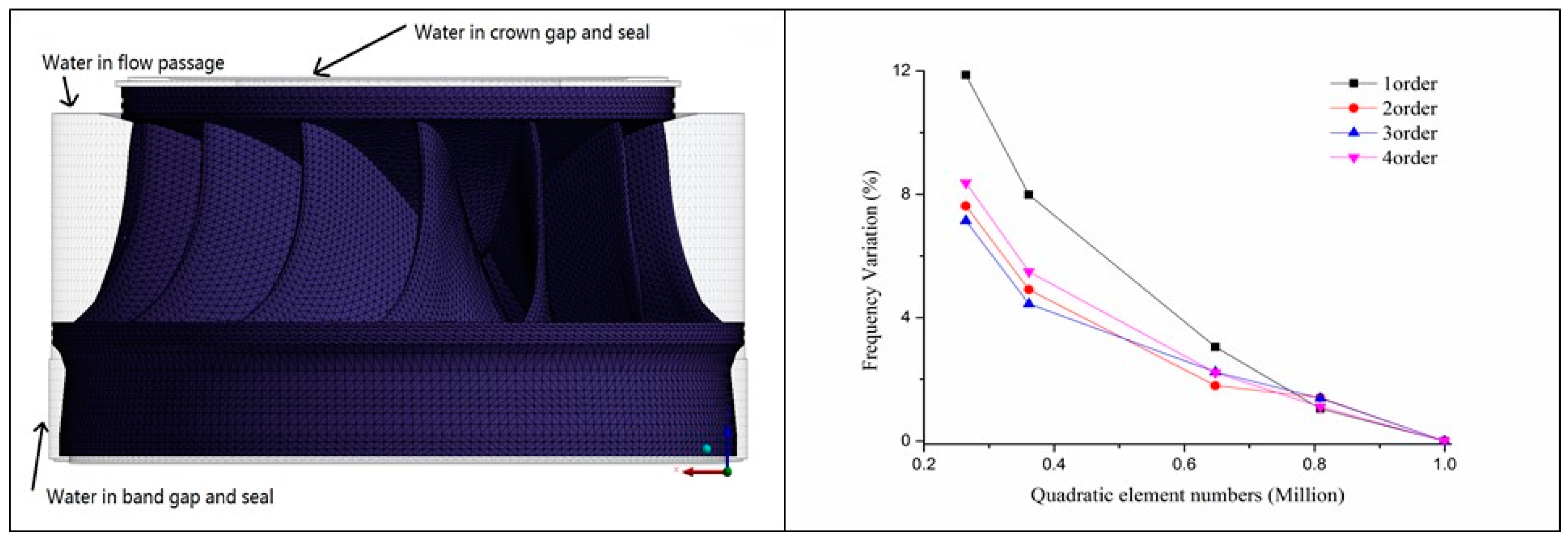
2. Finite Element Formulation for FSI
3. Description of Francis Turbine and Failure
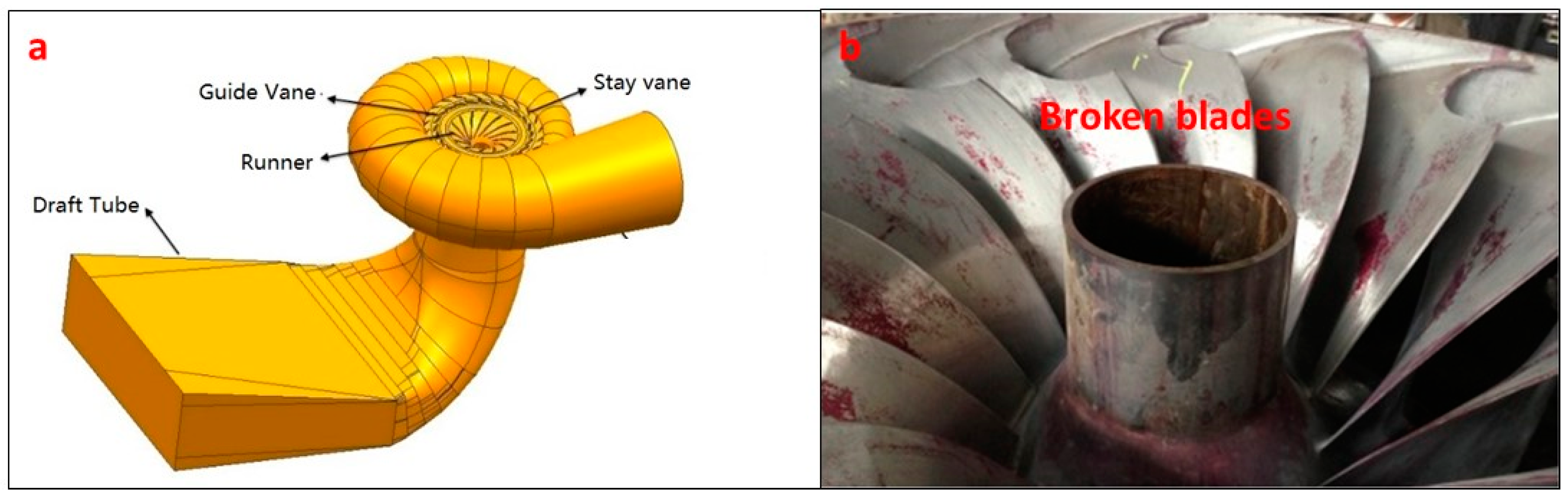
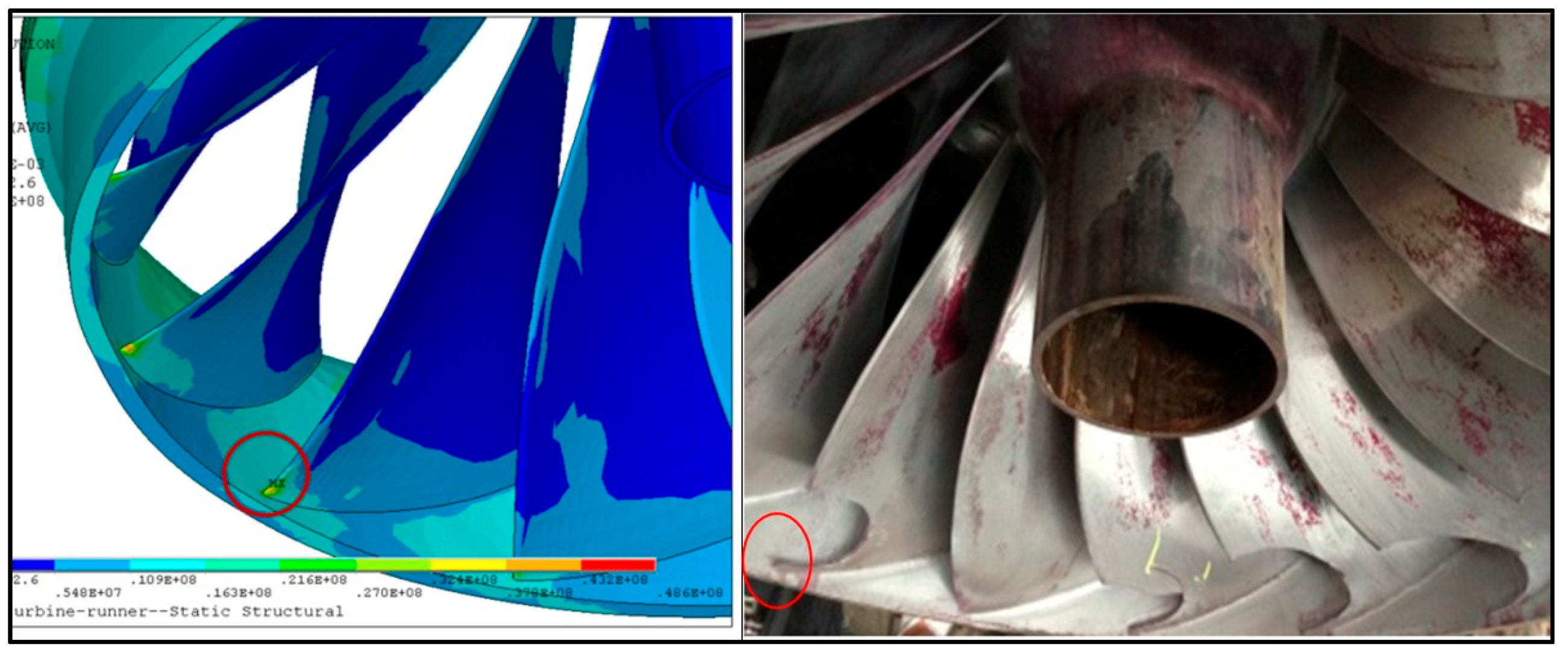
3.1. Unit Description and Damage Found
3.2. Operating Conditions before and after the Damage
3.3. Hydraulic Excitations
3.3.1. Deep Part Load Flow and Inter Blade Vortices
3.3.2. Vortex Rope
3.3.3. Von Karman Vortices
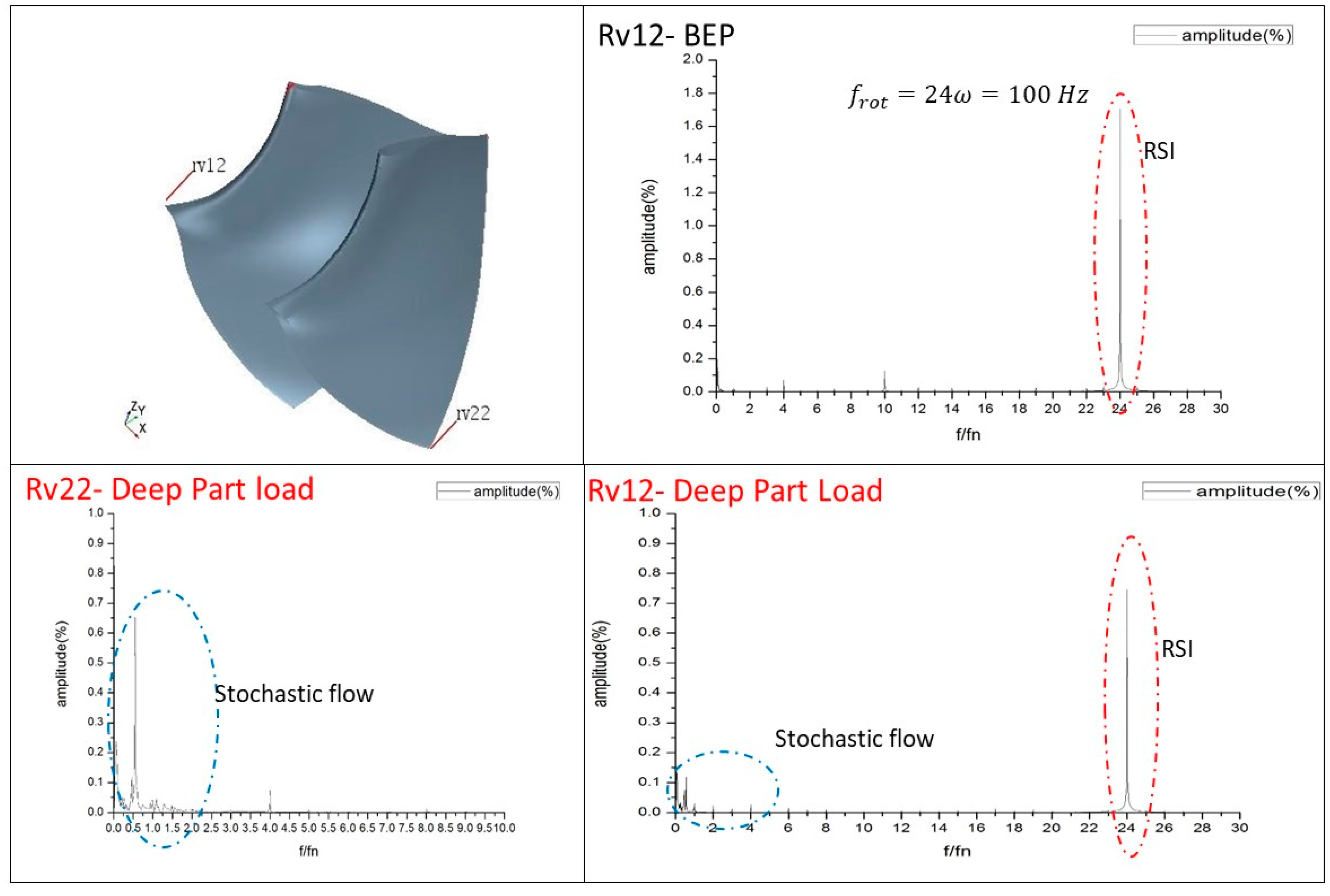
3.3.4. RSI
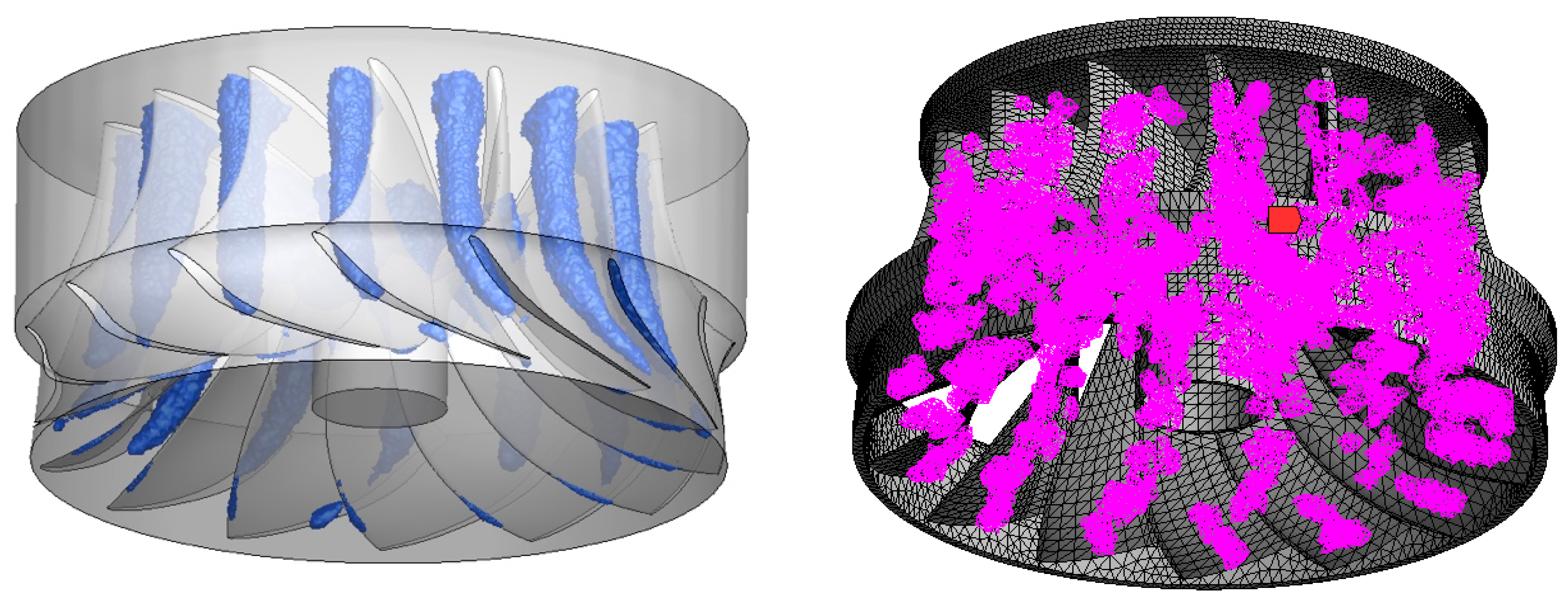
4. Flow Conditions through CFD Simulation
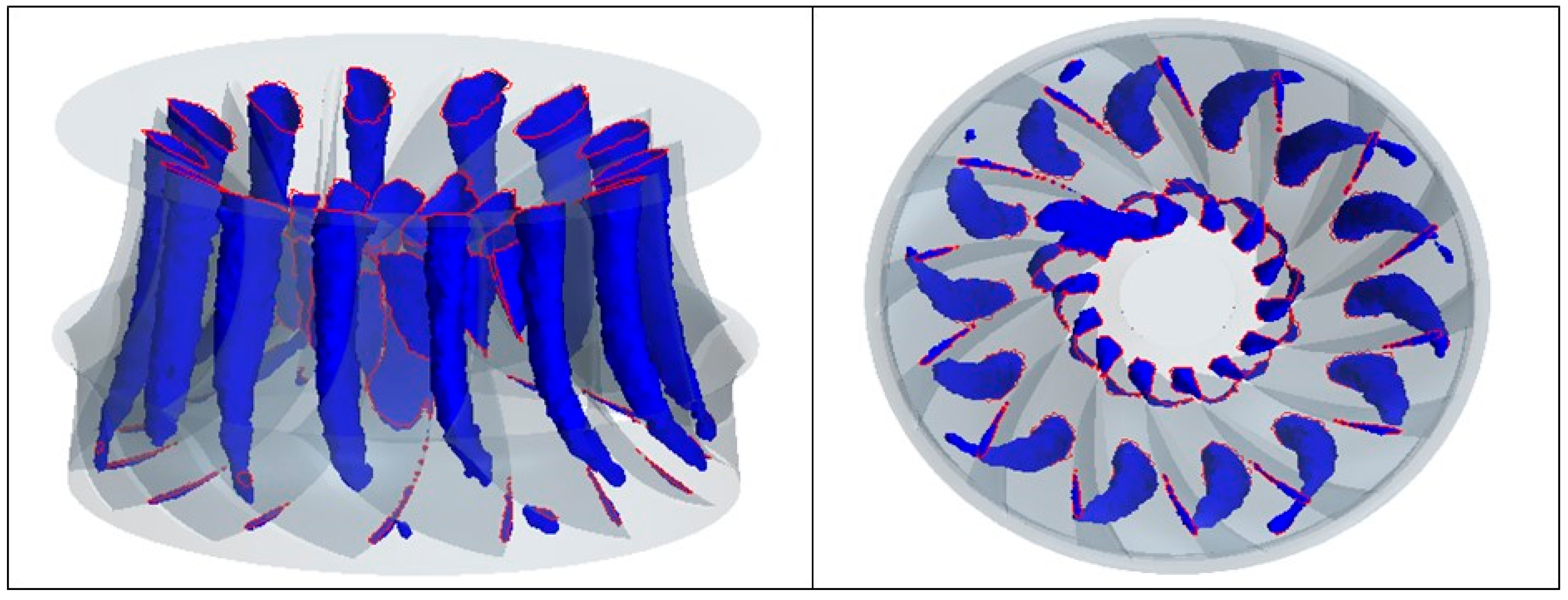
4.1. Simulated Cavities at Deep Part Load
4.2. Hydraulic Excitations from the CFD
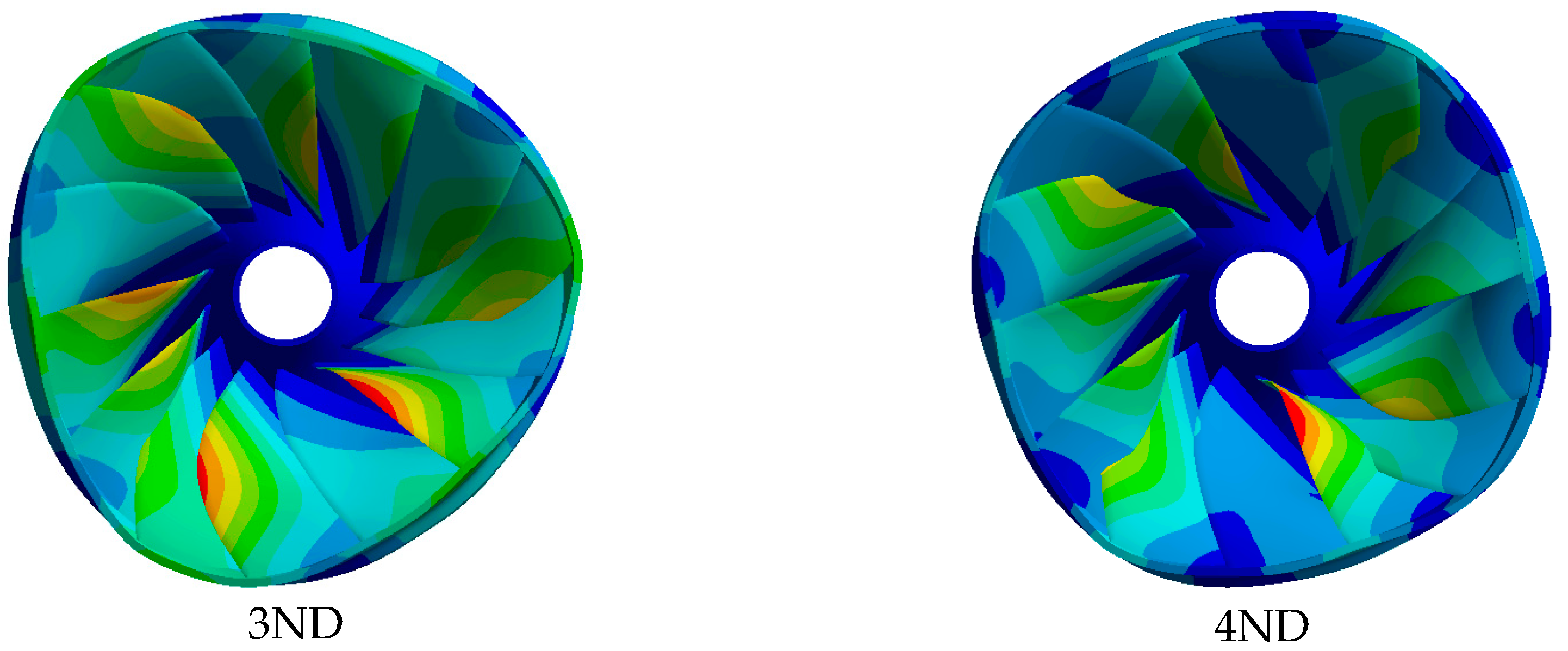
5. Natural Frequencies and Mode Shapes of the Runner without and with Cavitation Effects
5.1. Without Cavitation Effects (Conditions Close to BEP)
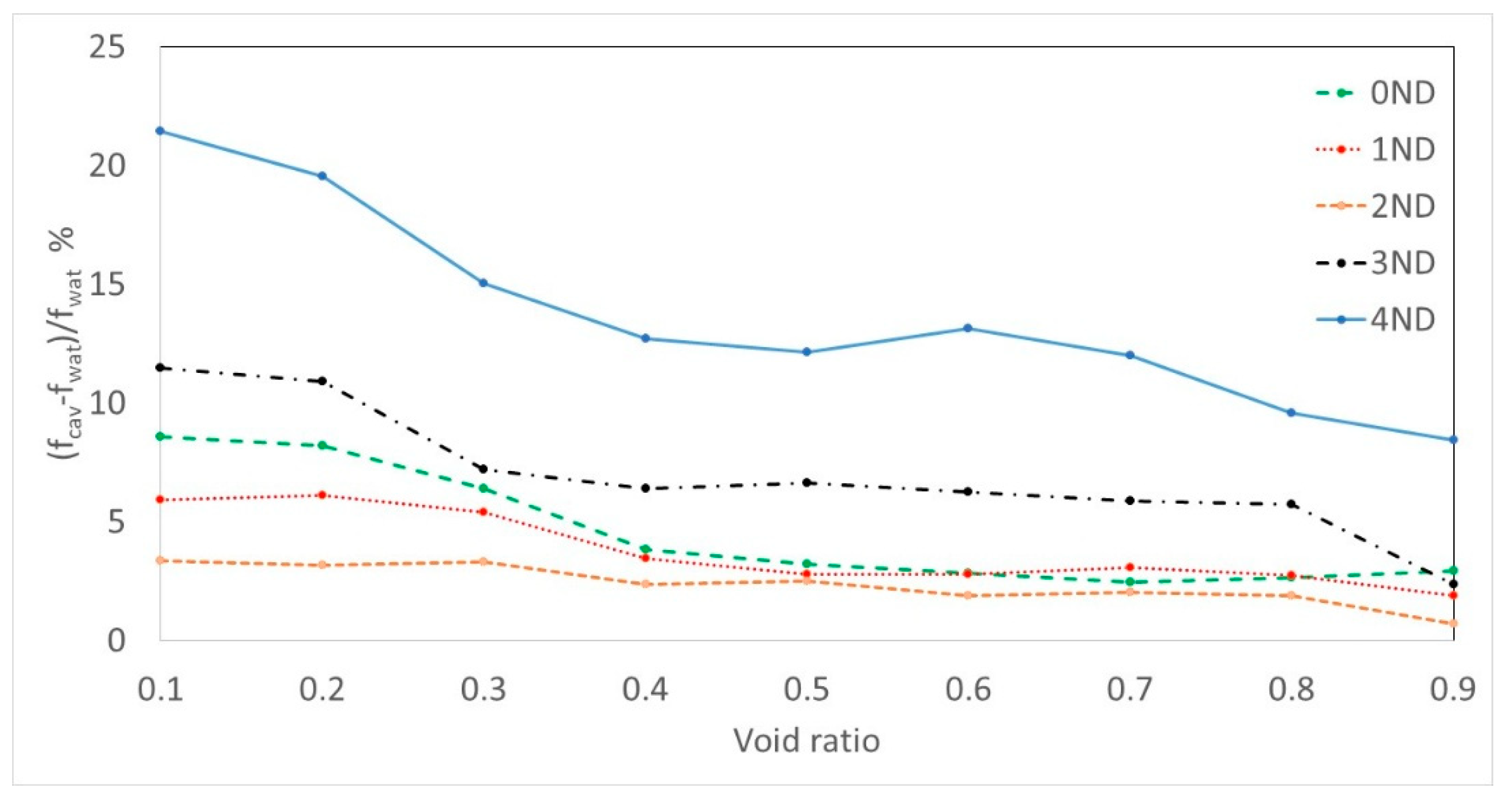
5.2. With Interblade Vortices (Deep Part Load Condition)
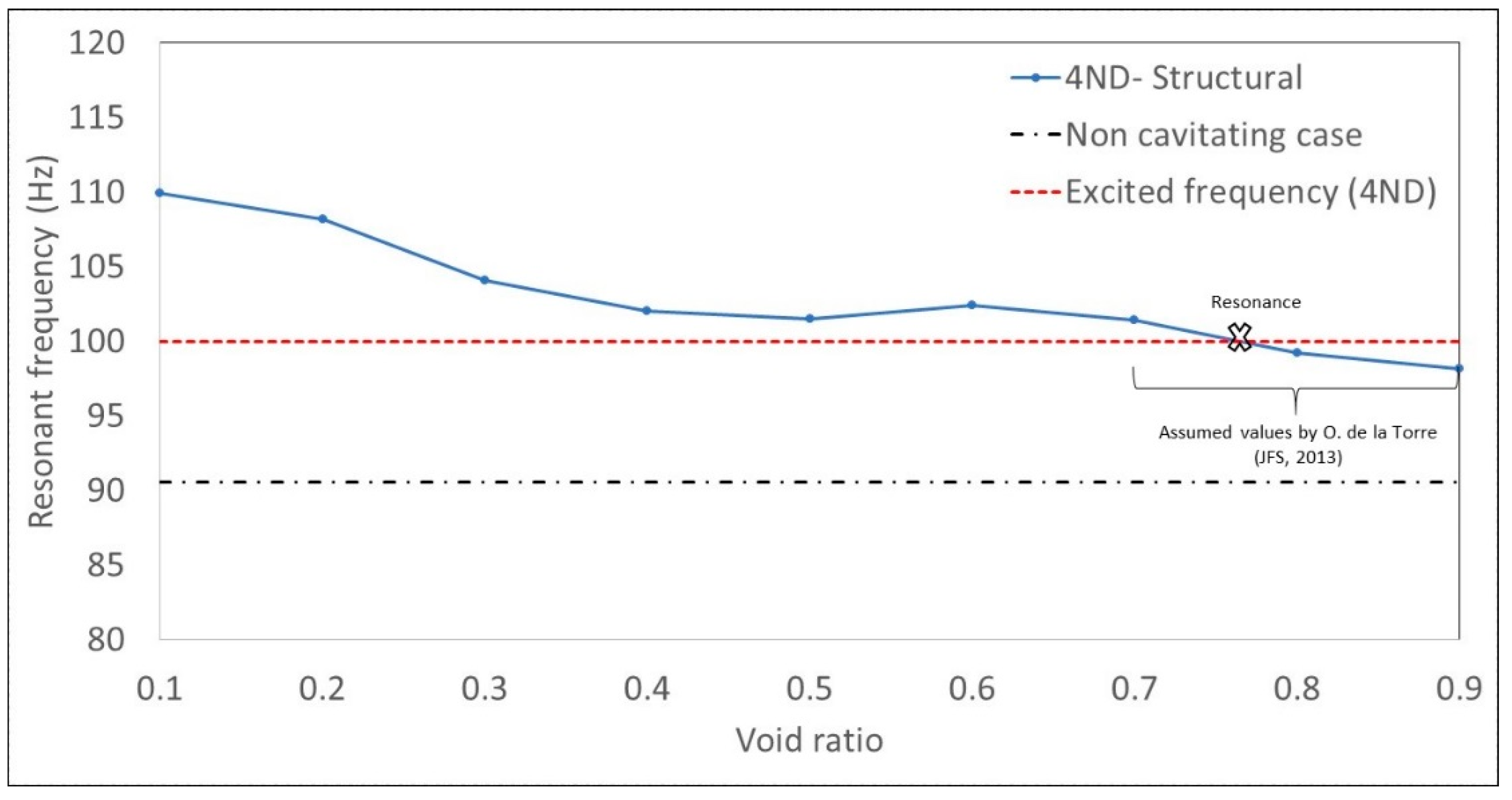
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brennen, C. A Review of Added Mass and Fluid Inertial Forces; Brennen (C.E.): Sierra Madre, CA, USA, 1982. [Google Scholar]
- Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold Co.: New York, NY, USA, 1990. [Google Scholar]
- Lamb, H. On the vibrations of an elastic plate in contact with water. Proc. R. Soc. Lond. 1921, A98, 205–216. [Google Scholar] [CrossRef]
- Amabili, M.; Kwak, M.K. Free vibrations of circular plates coupled with liquids: Revising the Lamb problem. J. Fluids Struct. 1996, 10, 743–761. [Google Scholar] [CrossRef]
- Amabili, M. Effect of finite fluid depth on the hydroelastic vibration of circular and annular plate. J. Sound Vib. 1996, 193, 909–925. [Google Scholar] [CrossRef]
- Kwak, M.K. Vibration of circular plates in contact with water. J. Appl. Mech. 1991, 58, 480–483. [Google Scholar] [CrossRef]
- Rodriguez, C.G.; Flores, P.; Pierart, F.G.; Contzen, L.R.; Egusquiza, E. Capability of structural-acoustical FSI numerical model to predict natural frequencies of submerged structures with nearby rigid surfaces. Comput. Fluids 2012, 64, 117–126. [Google Scholar] [CrossRef]
- Jeong, K.-H.; Kang, H.-S. Free vibration of multiple rectangular plates coupled with a liquid. Int. J. Mech. Sci. 2013, 74, 161–172. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Egusquiza, E.; Valero, C. Experimental study on the added mass and damping of a disk submerged in a partially fluid-filled tank with small radial confinement. J. Fluids Struct. 2014, 50, 1–17. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Influence of the rotation on the natural frequencies of a submerged-confined disk in water. J. Sound Vib. 2015, 337, 161–180. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Egusquiza, E.; Valero, C.; Egusquiza, M. Experimental Study of a Vibrating Disk Submerged in a Fluid-Filled Tank and Confined With a Nonrigid Cover. J. Vib. Acoust. 2017, 139, 021005–021011. [Google Scholar] [CrossRef]
- Bossio, M.; Valentín, D.; Presas, A.; Martin, D.R.; Egusquiza, E.; Valero, C.; Egusquiza, M. Numerical study on the influence of acoustic natural frequencies on the dynamic behaviour of submerged and confined disk-like structures. J. Fluids Struct. 2017, 73, 53–69. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Huang, X.; Jou, E.; Guardo, A.; Rodriguez, C. Failure investigation of a large pump-turbine runner. Eng. Fail. Anal. 2012, 23, 27–34. [Google Scholar] [CrossRef]
- Lais, S.; Qwenguei, L.; Henggeler, U.; Weiss, T.; Escaler Puigoriol, F.X.; Egusquiza Estévez, E. Dynamic analysis of Francis Runners-Experiment and numerical simulation. In Proceedings of the 24th IAHR Symposium on Hydraulic Machinery and Systems, Foz do Iguassu, Brazil, 27–31 October 2008. [Google Scholar]
- He, L.; Wang, Z.; Kurosawa, S.; Nakahara, Y. Resonance investigation of pump-turbine during startup process. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; p. 032024. [Google Scholar]
- Xiao, R.; Wang, Z.; Luo, Y. Dynamic Stresses in a Francis Turbine Runner Based on Fluid-Structure Interaction Analysis. Tsinghua Sci. Technol. 2008, 13, 587–592. [Google Scholar] [CrossRef]
- Liang, Q.W.; Rodríguez, C.G.; Egusquiza, E.; Escaler, X.; Farhat, M.; Avellan, F. Numerical simulation of fluid added mass effect on a francis turbine runner. Comput. Fluids 2007, 36, 1106–1118. [Google Scholar] [CrossRef]
- Dompierre, F.; Sabourin, M. Determination of turbine runner dynamic behaviour under operating condition by a two-way staggered fluid-structureinteraction method. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012085. [Google Scholar] [CrossRef]
- Hübner, B.; Seidel, U.; Roth, S. Application of fluid-structure coupling to predict the dynamic behavior of turbine components. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2010; p. 012009. [Google Scholar]
- Liu, X.; Luo, Y.; Karney, B.; Wang, Z.; Zhai, L. Virtual Testing for Modal and Damping Ratio Identification of Submerged Structures using the PolyMAX Algorithm with Two-way Fluid-Structure Interactions. J. Fluids Struct. 2015, 54, 548–565. [Google Scholar] [CrossRef]
- De La Torre, O.; Escaler, X.; Egusquiza, E.; Farhat, M. Experimental investigation of added mass effects on a hydrofoil under cavitation conditions. J. Fluids Struct. 2013, 39, 173–187. [Google Scholar] [CrossRef]
- Ducoin, A.; André Astolfi, J.; Sigrist, J.-F. An experimental analysis of fluid structure interaction on a flexible hydrofoil in various flow regimes including cavitating flow. Eur. J. Mech. B/Fluids 2012, 36, 63–74. [Google Scholar] [CrossRef]
- Benaouicha, M.; Astolfi, J.-A. Analysis of added mass in cavitating flow. J. Fluids Struct. 2012, 31, 30–48. [Google Scholar] [CrossRef]
- Lelong, A.; Guiffant, P.; Astolfi, J.A. An Experimental Analysis of the Structural Response of Flexible Lightweight Hydrofoils in Cavitating Flow. J. Fluids Eng. 2018, 140, 021116. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Theory Reference; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Junger, M.C.; Feit, D. Sound, Structures, and Their Interaction; MIT Press: Cambridge, MA, USA, 1986; p. 460. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory and Practice; Research Studies Press: Letchworth, UK, 1984; Volume 15. [Google Scholar]
- Wilhelm, W.; Florian von, L.; Philipp, C.; Jiri, K. Dynamic stresses in a Francis model turbine at deep part load. J. Phys. Conf. Ser. 2017, 813, 012014. [Google Scholar]
- Mende, C.; Weber, W.; Seidel, U. Progress in load prediction for speed-no-load operation in Francis turbines. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 062017. [Google Scholar] [CrossRef]
- Morissette, J.F.; Chamberland-Lauzon, J.; Nennemann, B.; Monette, C.; Giroux, A.M.; Coutu, A.; Nicolle, J. Stress predictions in a Francis turbine at no-load operating regime. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 072016. [Google Scholar] [CrossRef]
- Sofien Bouajila, J.B. Emmanuel Flores, Claire Segoufin, Thierry Maitre. In Advances in Hydroinformatics, 1st ed.; Gourbesville, P., Cunge, J., Caignaert, G., Eds.; Springer: Signapore, 2018. [Google Scholar]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Guide vanes embedded visualization technique for investigating Francis runner inter-blade vortices at deep part load operation. In Proceedings of the 6th IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Ljubljana, Slovania, 9–11 September 2015. [Google Scholar]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Pressure measurements and high speed visualizations of the cavitation phenomena at deep part load condition in a Francis turbine. IOP Conf. Series: Earth Environ. Sci. 2014, 22, 022011. [Google Scholar] [CrossRef]
- Huang, X.; Oram, C.; Sick, M. Static and dynamic stress analyses of the prototype high head Francis runner based on site measurement. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032052. [Google Scholar] [CrossRef]
- Seidel, U.; Mende, C.; Hübner, B.; Weber, W.; Otto, A. Dynamic loads in Francis runners and their impact on fatigue life. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032054. [Google Scholar] [CrossRef]
- Monette, C.; Marmont, H.; Chamberland-Lauzon, J.; Skagerstrand, A.; Coutu, A.; Carlevi, J. Cost of enlarged operating zone for an existing Francis runner. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 072018. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Study of the vortex-induced pressure excitation source in a Francis turbine draft tube by particle image velocimetry. Exp. Fluids 2015, 56, 215. [Google Scholar] [CrossRef]
- Duparchy, F.; Brammer, J.; Thibaud, M.; Favrel, A.; Lowys, P.; Avellan, F. Mechanical impact of dynamic phenomena in Francis turbines at off design conditions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; p. 012035. [Google Scholar]
- Bouajila, S.; De Colombel, T.; Lowys, P.; Maitre, T. Hydraulic Phenomena Frequency Signature of Francis Turbines Operating in Part Load Conditions. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016; p. 082001. [Google Scholar]
- Müller, A.; Favrel, A.; Landry, C.; Yamamoto, K.; Avellan, F. On the physical mechanisms governing self-excited pressure surge in Francis turbines. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; p. 032034. [Google Scholar]
- Valentín, D.; Presas, A.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Bossio, M. Power Swing Generated in Francis Turbines by Part Load and Overload Instabilities. Energies 2017, 10, 2124. [Google Scholar]
- Presas, A.; Valentin, D.; Egusquiza, M.; Valero, C.; Egusquiza, E. Sensor-Based Optimized Control of the Full Load Instability in Large Hydraulic Turbines. Sensors 2018, 18, 1038. [Google Scholar]
- Fisher, R.K.; Seidel, U.; Grosse, G.; Gfeller, W.; Klinger, R. A case study in resonant hydroelastic vibration: The causes of runner cracks and the solutions implemented for the Xiaolangdi hydroelectric project. In Proceedings of the XXI IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002. [Google Scholar]
- Neidhardt, T.; Jung, A.; Hyneck, S.; Gummer, J. An Alternative Approach to the Von Karman Vortex Problem in Modern Hydraulic Turbines. Available online: https://www.researchgate.net/publication/320811766 (accessed on 15 August 2018).
- Presas, A.; Egusquiza, E.; Valero, C.; Valentin, D.; Seidel, U. Feasibility of Using PZT Actuators to Study the Dynamic Behavior of a Rotating Disk due to Rotor-Stator Interaction. Sensors 2014, 14, 11919–11942. [Google Scholar] [CrossRef] [PubMed]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Coutier-Delgosha, O.; Reboud, J.L.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Avellan, F. Experimental evidence of inter-blade cavitation vortex development in Francis turbines at deep part load condition. Exp. Fluids 2017, 58. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Numerical and experimental evidence of the inter-blade cavitation vortex development at deep part load operation of a Francis turbine. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016. [Google Scholar]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. LDV survey of cavitation and resonance effect on the precessing vortex rope dynamics in the draft tube of Francis turbines. Exp. Fluids 2016, 57, 168. [Google Scholar] [CrossRef]
- Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Fluid-structure interaction mechanisms leading to dangerous power swings in Francis turbines at full load. J. Fluids Struct. 2017, 69, 56–71. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C. Detection and analysis of part load and full load instabilities in a real Francis turbine prototype. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017; p. 012038. [Google Scholar]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F.; Coussirat, M. Detection of cavitation in hydraulic turbines. Mech. Syst. Signal Process. 2006, 20, 983–1007. [Google Scholar] [CrossRef]
- De La Torre, O.; Escaler, X.; Egusquiza, E.; Farhat, M. Numerical and experimental study of a nearby solid boundary and partial submergence effects on hydrofoil added mass. Comput. Fluids 2014, 91, 1–9. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Bossio, M. Accurate Determination of the Frequency Response Function of Submerged and Confined Structures by Using PZT-Patches. Sensors 2017, 17, 660. [Google Scholar] [CrossRef] [PubMed]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Dynamic response of a rotating disk submerged and confined. Influence of the axial gap. J. Fluids Struct. 2016, 62, 332–349. [Google Scholar] [CrossRef]
- De Siervo, F.; De Leva, F. Modern trends in selecting and designing Francis turbines. Water Power Dam Constr. 1976, 28, 28–35. [Google Scholar]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. On the detection of natural frequencies and mode shapes of submerged rotating disk-like structures from the casing. Mech. Syst. Signal Process. 2015, 60, 547–570. [Google Scholar] [CrossRef]

| Condition | Operating Point with Respect to Rated Power | Head Water (m) | Rotating Speed (rpm) | Discharge (kg/s) | Torque (Nm) | Power (MW) |
|---|---|---|---|---|---|---|
| Deep part load | 36% | 102 | 250 | 21,779 | 610,371 | 16 |
| BEP | 81% | 102 | 250 | 40,595 | 1,366,638 | 35.8 |
| Harmonics m,n | (Hz) | (Hz) | Excitation Shape k |
|---|---|---|---|
| 1,2 | 100 | 116.77 | 4 |
| 2,3 | 200 | 175 | −6 |
| 2,4 | 200 | 233.33 | 8 |
| Phenomenon | Frequency (Range) | Type | Operating Points |
|---|---|---|---|
| Chaotic flow and inter-blade vortices | ≈0–5 Ω (0–20 Hz) | Stochastic | DPL |
| Vortex rope | ≈0–1 Ω (0–4 Hz) | Periodic | Between DPL and BEP (Part Load) |
| Von Karman shedding | 240–290 Hz for Deep Part Load 450–550 Hz for BEP | Periodic | Stronger at BEP |
| RSI | 100 Hz, 200 Hz | Periodic | Stronger at BEP |
| Mode | 0ND | 1ND | 2ND | 3ND | 4ND |
|---|---|---|---|---|---|
| fair | 83.67 | 117.9 | 149.81 | 228.83 | 270.52 |
| fwater | 59.87 | 62.99 | 69.03 | 84.85 | 90.51 |
| FRR | 28.4% | 46.6% | 53.9% | 62.9% | 66.5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Luo, Y.; Presas, A.; Wang, Z.; Zhou, L. Cavitation Effects on the Structural Resonance of Hydraulic Turbines: Failure Analysis in a Real Francis Turbine Runner. Energies 2018, 11, 2320. https://doi.org/10.3390/en11092320
Liu X, Luo Y, Presas A, Wang Z, Zhou L. Cavitation Effects on the Structural Resonance of Hydraulic Turbines: Failure Analysis in a Real Francis Turbine Runner. Energies. 2018; 11(9):2320. https://doi.org/10.3390/en11092320
Chicago/Turabian StyleLiu, Xin, Yongyao Luo, Alexandre Presas, Zhengwei Wang, and Lingjiu Zhou. 2018. "Cavitation Effects on the Structural Resonance of Hydraulic Turbines: Failure Analysis in a Real Francis Turbine Runner" Energies 11, no. 9: 2320. https://doi.org/10.3390/en11092320
APA StyleLiu, X., Luo, Y., Presas, A., Wang, Z., & Zhou, L. (2018). Cavitation Effects on the Structural Resonance of Hydraulic Turbines: Failure Analysis in a Real Francis Turbine Runner. Energies, 11(9), 2320. https://doi.org/10.3390/en11092320






