Characterization and Prediction of Complex Natural Fractures in the Tight Conglomerate Reservoirs: A Fractal Method
Abstract
:1. Introduction
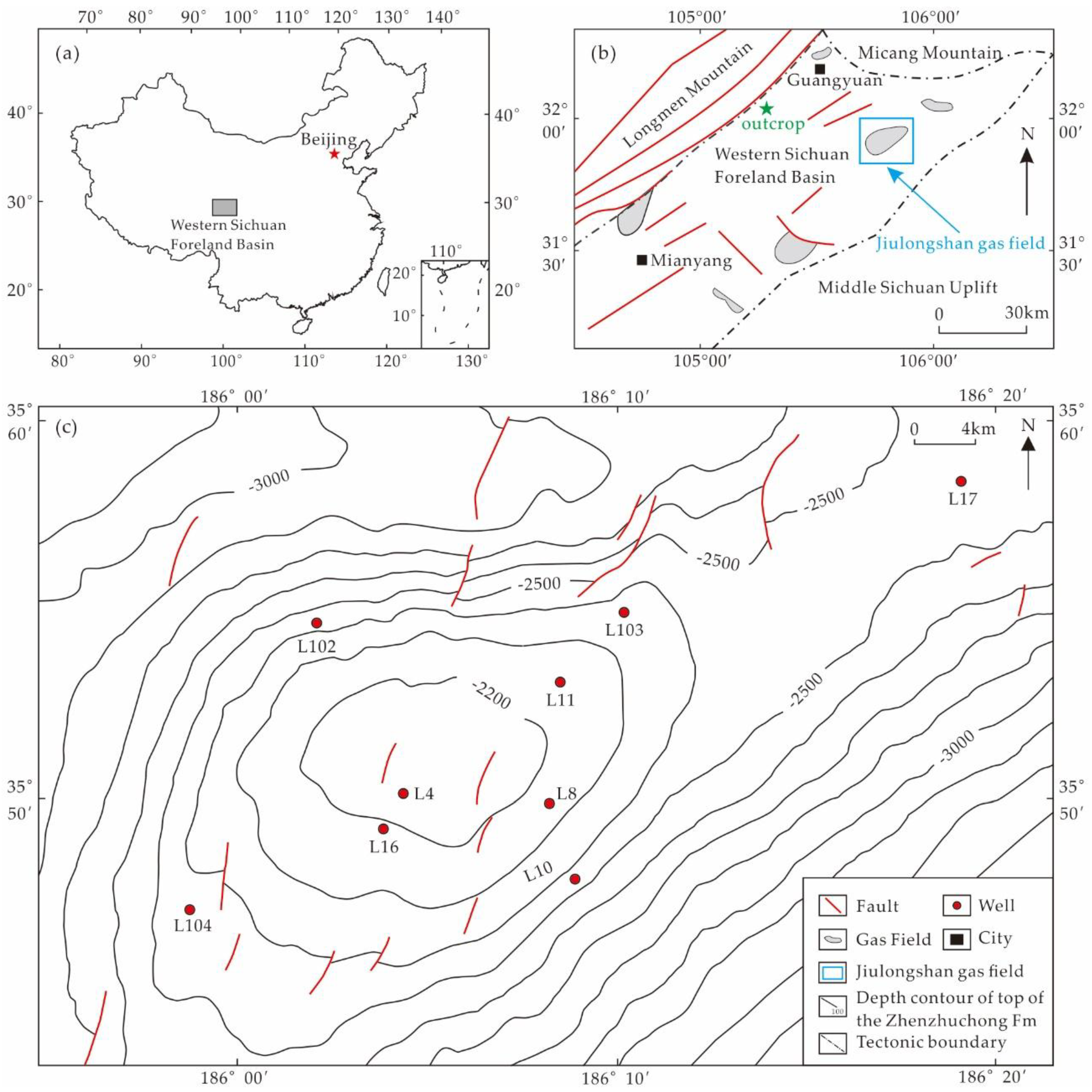
2. Geological Setting
3. Methodology
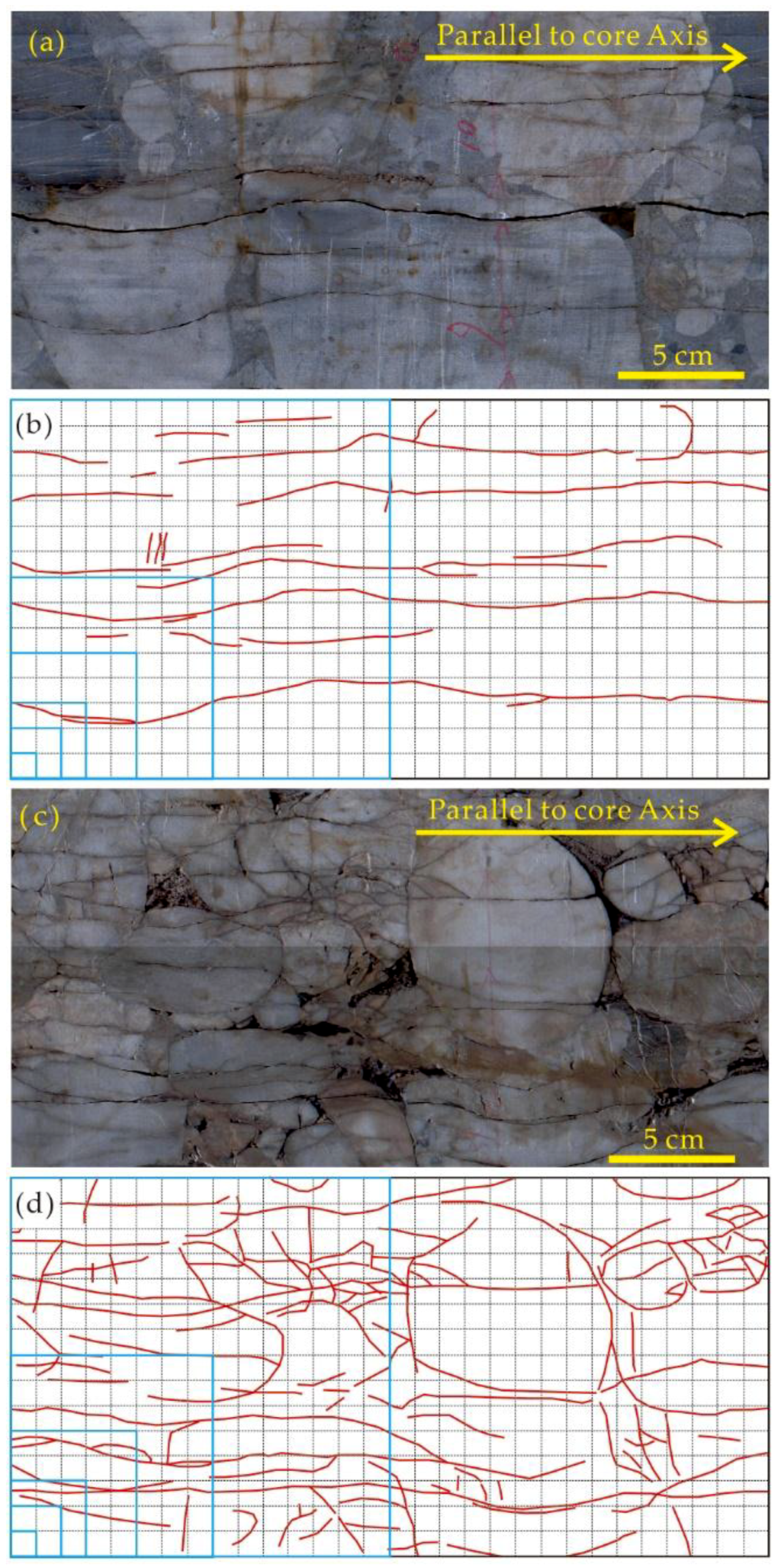
- Using a core scanner to obtain high-resolution 360° core images (Figure 2);
- Covering the image of the entire core with a mesh composed of square grids with side length of r; counting the number N(r) of boxes containing fractures;
- Gradually changing the side length r of the square grids, and repeatedly counting the corresponding N(r);
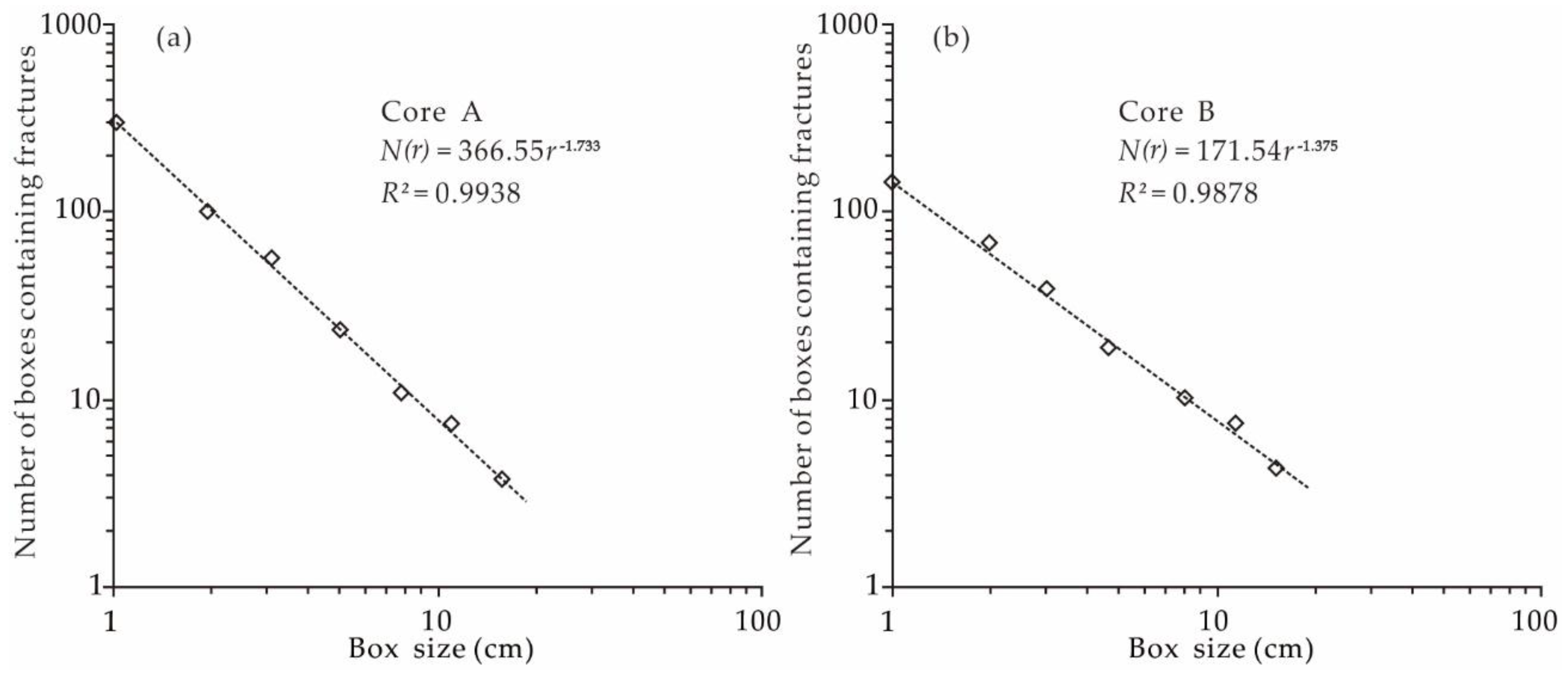
- Taking r as the abscissa and N(r) as the ordinate, using the least-square method to perform regression analysis on the statistical data in the double logarithmic coordinate system (Figure 3).
4. Fracture Characterization
4.1. Fracture Type and Characteristics
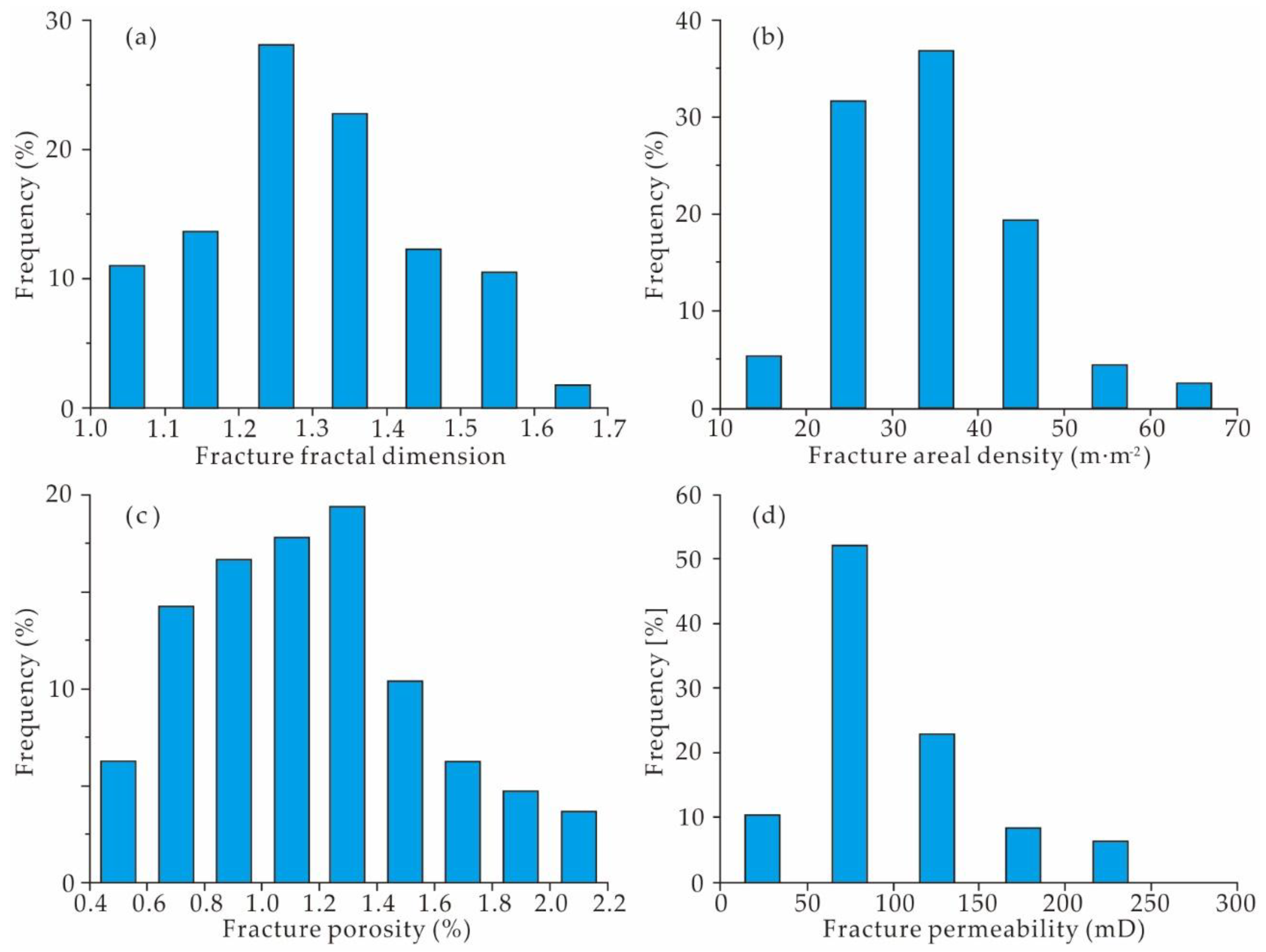
4.2. Fracture Parameters
5. Discussion
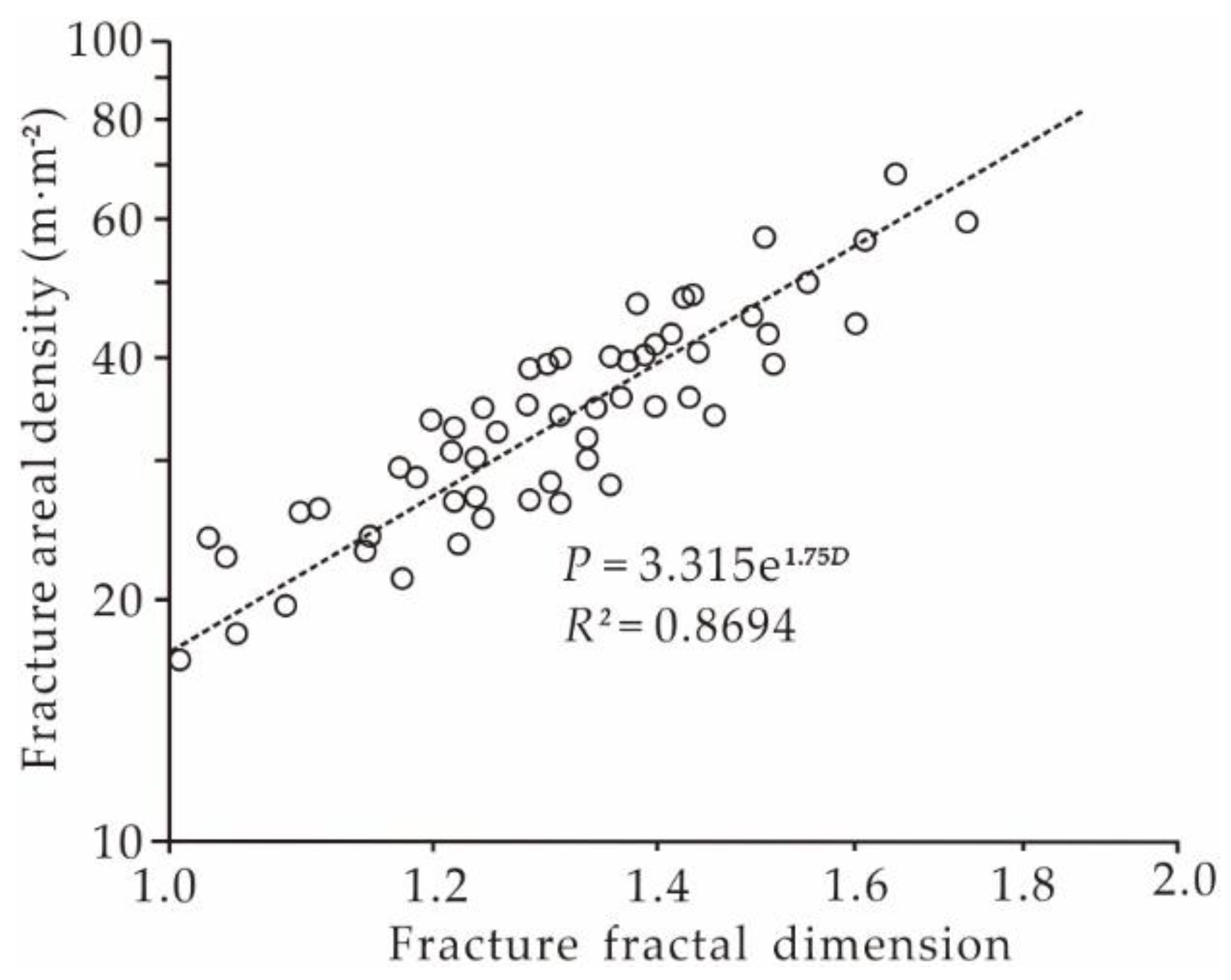
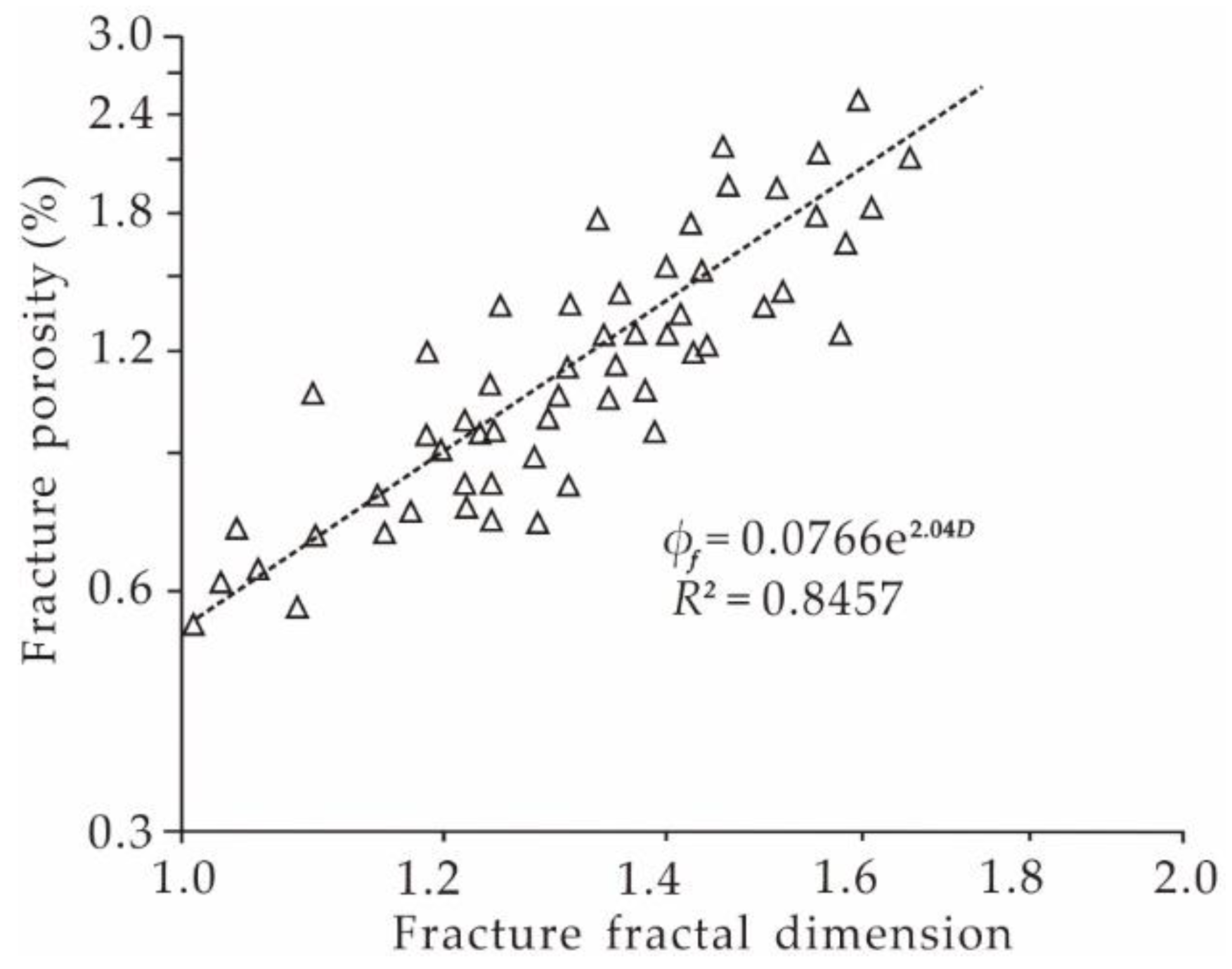
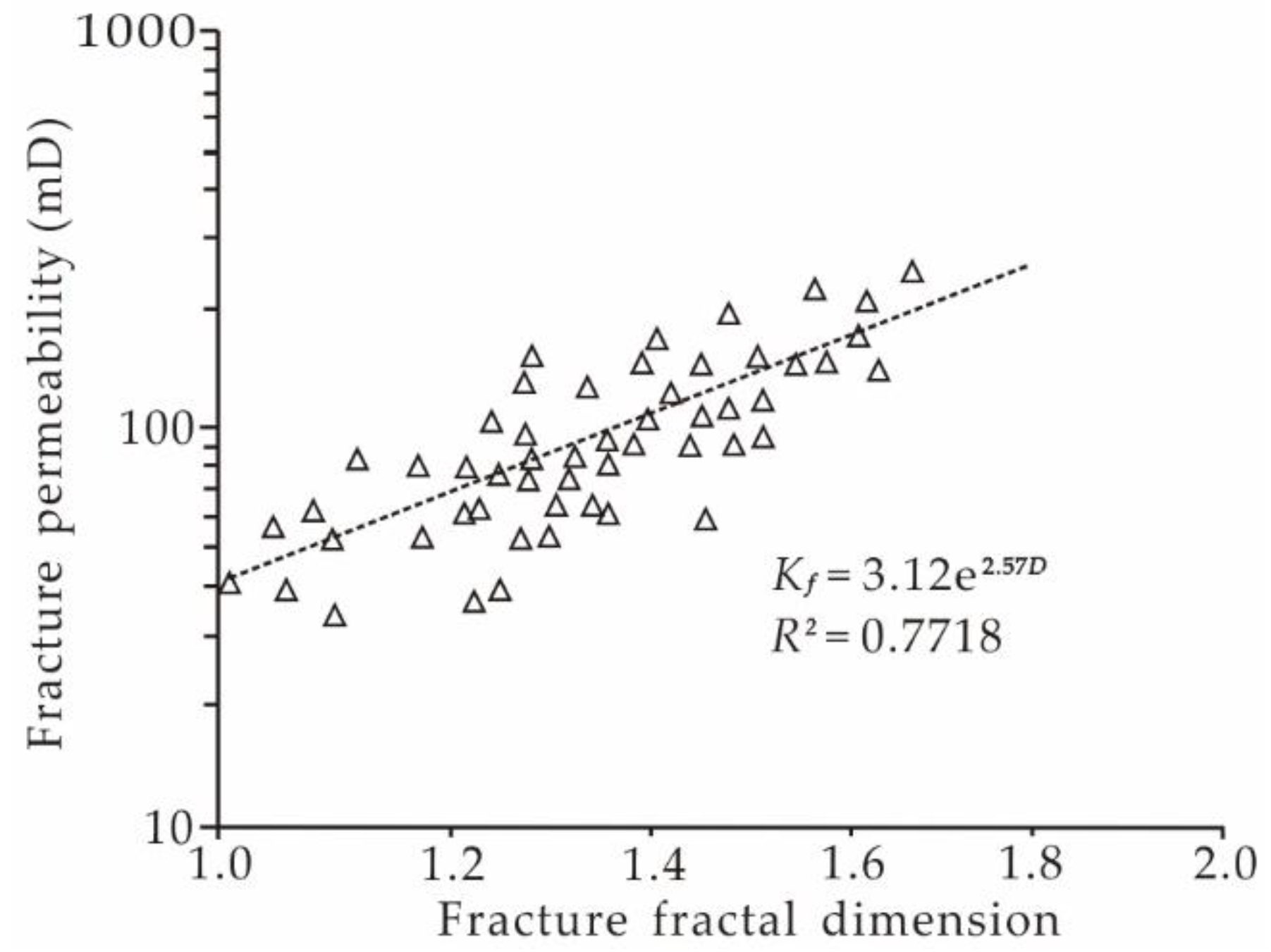
5.1. Geological Significance of Fracture Fractal Dimension
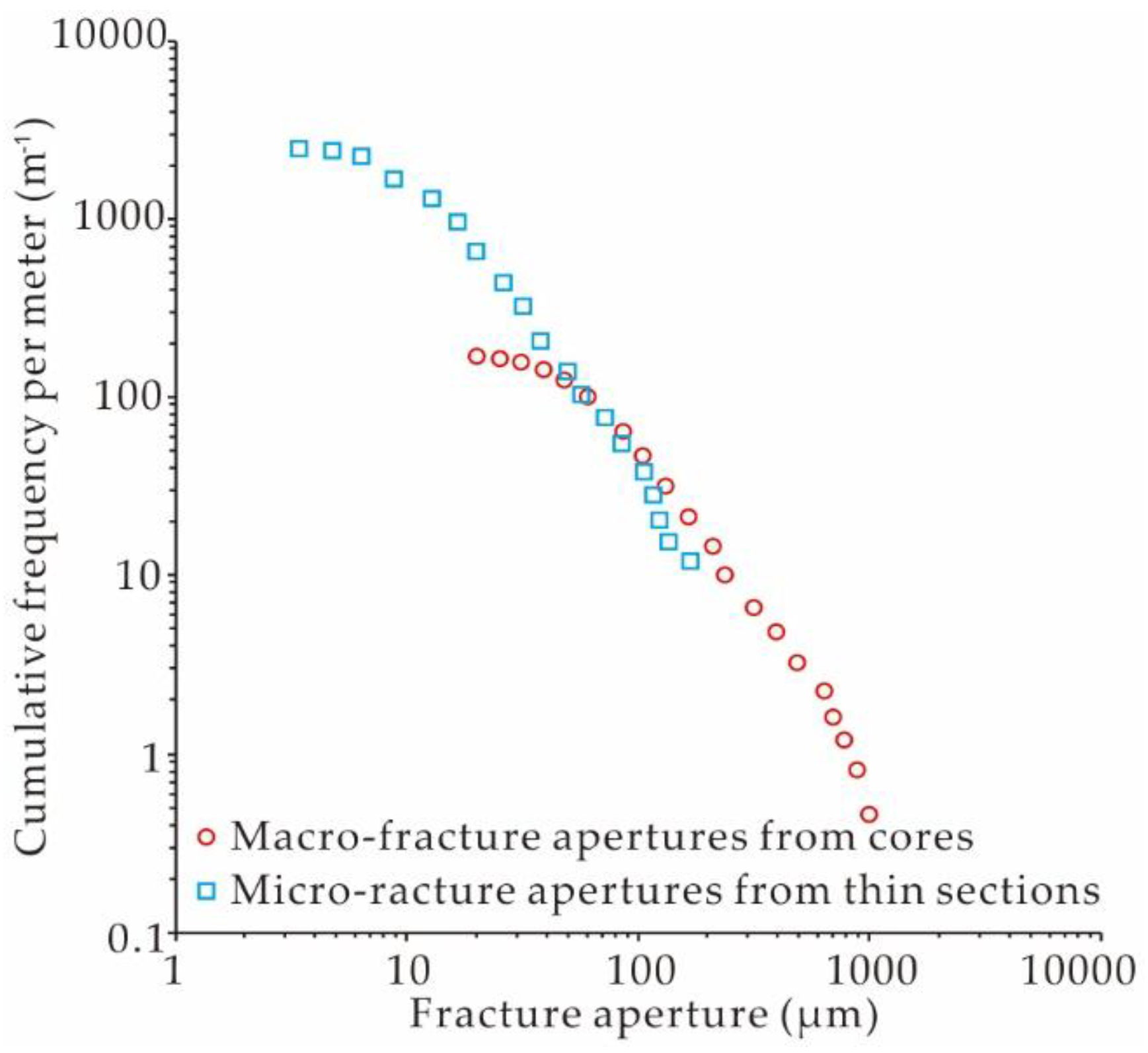
5.2. Power-Law Distribution of Fracture Parameters and Fracture Prediction
5.3. Contribution of Fractures
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zeng, L.; Su, H.; Tang, X.; Peng, Y.; Gong, L. Fractured tight sandstone oil and gas reservoirs: A new play type in the Dongpu depression, Bohai Bay Basin, China. AAPG Bull. 2013, 97, 363–377. [Google Scholar] [CrossRef]
- Laubach, S.E.; Lamarche, J.; Gauthier, B.D.M.; Dunne, W.M.; Sanderson, D.J. Spatial arrangement of faults and opening-mode fractures. J. Struct. Geol. 2018, 108, 2–15. [Google Scholar] [CrossRef] [Green Version]
- Gale, J.F.W.; Laubach, S.E.; Olson, J.E.; Eichhubl, P.; Fall, A. Natural fractures in shale: A review and new observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar] [CrossRef]
- Nelson, R.A. Geologic analysis of naturally fractured reservoirs; Elsevier: Amsterdam, Netherlands, 2001; Available online: https://www.sciencedirect.com/book/9780884153177/geologic-analysis-of-naturally-fractured-reservoirs (accessed on 17 August 2018).
- Bisdom, K.; Gauthier, B.D.M.; Bertotti, G.; Hardebol, N.J. Calibrating discrete fracture-network models with a carbonate three-dimensional outcrop fracture network: Implications for naturally fractured reservoir modeling. AAPG Bull. 2014, 98, 1351–1376. [Google Scholar] [CrossRef]
- Ghosh, K.; Mitra, S. Two-dimensional simulation of controls of fracture parameters on fracture connectivity. AAPG Bull. 2009, 93, 1517–1533. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, N.; Sima, L.Q.; Meng, F.; Guo, Y. Pore structure characterization of the tight reservoir: Systematic integration of mercury injection and nuclear magnetic resonance. Energy Fuel. 2018, 32, 7471–7484. [Google Scholar] [CrossRef]
- Strijker, G.; Bertotti, G.; Luthi, S.M. Multi-scale fracture network analysis from an outcrop analogue: A case study from the Cambro-Ordovician clastic succession in Petra, Jordan. Mar. Petrol. Geol. 2012, 38, 104–116. [Google Scholar] [CrossRef]
- Lei, Q.; Wang, X. Tectonic interpretation of the connectivity of a multiscale fracture system in limestone. Geophys. Res. Lett. 2016, 43, 1551–1558. [Google Scholar] [CrossRef] [Green Version]
- Larsen, B.; Gudmundsson, A. Linking of fractures in layered rocks: Implications for permeability. Tectonophysics 2010, 492, 108–120. [Google Scholar] [CrossRef]
- Magnusdottir, L.; Horne, R.N. Inversion of time-lapse electric potential data to estimate fracture connectivity in geothermal reservoirs. Math. Geosci. 2015, 47, 85–104. [Google Scholar] [CrossRef]
- Roques, C.; Bour, O.; Aquilina, L.; Dewandel, B.; Leray, S.; Schroetter, J.; Longuevergne, L.; Le Borgne, T.; Hochreutener, R.; Labasque, T.; et al. Hydrological behavior of a deep sub-vertical fault in crystalline basement and relationships with surrounding reservoirs. J. Hydrol. 2014, 509, 42–54. [Google Scholar] [CrossRef] [Green Version]
- Kong, L.; Ostadhassan, M.; Li, C.; Tamimi, N. Pore characterization of 3D-printed gypsum rocks: A comprehensive approach. J. Mater. Sci. 2018, 53, 5063–5078. [Google Scholar] [CrossRef]
- Ogata, K.; Senger, K.; Braathen, A.; Tveranger, J. Fracture corridors as seal-bypass systems in siliciclastic reservoir-cap rock successions: Field-based insights from the Jurassic Entrada Formation (SE Utah, USA). J. Struct. Geol. 2014, 66, 162–187. [Google Scholar] [CrossRef]
- Petrie, E.S.; Evans, J.P.; Bauer, S.J. Failure of cap-rock seals as determined from mechanical stratigraphy, stress history, and tensile-failure analysis of exhumed analogs. AAPG Bull. 2014, 98, 2365–2389. [Google Scholar] [CrossRef]
- Ingram, G.M.; Urai, J.L. Top-seal leakage through faults and fractures: The role of mudrock properties. Geol. Soc. Spec. Publ. 1999, 158, 125–135. [Google Scholar] [CrossRef]
- Jin, Z.J. A study on the distribution of oil and gas reservoirs controlled by source-cap rock assemblage in unmodified foreland region of Tarim Basin. Oil Gas Geol. 2014, 35, 763–770. [Google Scholar]
- Smith, J.; Durucan, S.; Korre, A.; Shi, J. Carbon dioxide storage risk assessment: Analysis of caprock fracture network connectivity. Int. J. Greenh. Gas Control 2011, 5, 226–240. [Google Scholar] [CrossRef]
- Alghalandis, Y.F.; Dowd, P.A.; Xu, C. Connectivity Field: a measure for characterising fracture networks. Math. Geosci. 2015, 47, 63–83. [Google Scholar] [CrossRef]
- Gong, L.; Gao, S.; Fu, X.; Chen, S.; Lyu, B.; Yao, J. Fracture characteristics and their effects on hydrocarbon migration and accumulation in tight volcanic reservoirs: A case study of the Xujiaweizi fault depression, Songliao Basin, China. Interpret. J. Sub. 2017, 5, 57–70. [Google Scholar] [CrossRef]
- Laubach, S.E.; Fall, A.; Copley, L.; Marrett, R.; Wilkins, S.J. Fracture porosity creation and persistence in a basement-involved Laramide fold, Upper Cretaceous Frontier Formation, Green River Basin, USA. Geol. Mag. 2016, 153, 887–910. [Google Scholar] [CrossRef]
- Olson, J.E.; Laubach, S.E.; Eichhubl, P. Estimating natural fracture producibility in tight gas sandstones: coupling diagenesis with geomechanical modeling. Lead. Edge 2010, 29, 1494–1499. [Google Scholar] [CrossRef]
- Peacock, D.C.P.; Sanderson, D.J.; Rotevatn, A. Relationships between fractures. J. Struct. Geol. 2018, 106, 41–53. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Nixon, C.W. The use of topology in fracture network characterization. J. Struct. Geol. 2015, 72, 55–66. [Google Scholar] [CrossRef]
- Lyu, W.Y.; Zeng, L.; Zhang, B.; Miao, F.; Lyu, P.; Dong, S. Influence of natural fractures on gas accumulation in the Upper Triassic tight gas sandstones in the northwestern Sichuan Basin, China. Mar. Petrol. Geol. 2017, 83, 60–72. [Google Scholar] [CrossRef]
- Gross, M.R.; Eyal, Y. Throughgoing fractures in layered carbonate rocks. Geol. Soc. Am. Bull. 2007, 119, 1387–1404. [Google Scholar] [CrossRef]
- Laubach, S.E.; Olson, J.E.; Gross, M.R. Mechanical and fracture stratigraphy. AAPG Bull. 2009, 93, 1413–1426. [Google Scholar] [CrossRef]
- Lyu, W.Y.; Zeng, L.B.; Liu, Z.Q.; Liu, G.P.; Zu, K.W. Fracture responses of conventional logs in tight-oil sandstones: A case study of the Upper Triassic Yanchang Formation in southwest Ordos Basin, China. AAPG Bull. 2016, 100, 1399–1417. [Google Scholar] [CrossRef]
- Luo, Q.Y.; Gong, L.; Qu, Y.S.; Zahng, K.H.; Zhang, G.L.; Wang, S.Z. The tight oil potential of the Lucaogou Formation from the southern Junggar Basin, China. Fuel 2018, 234, 858–871. [Google Scholar] [CrossRef]
- Zeng, L.B.; Tang, X.M.; Wang, T.C.; Gong, L. The influence of fracture cements in tight Paleogene saline lacustrine carbonate reservoirs, Western Qaidam Basin, Northwest China. AAPG Bull. 2012, 96, 2003–2017. [Google Scholar] [CrossRef]
- Finn, M.D.; Gross, M.R.; Eyal, Y.; Draper, G. Kinematics of throughgoing fractures in jointed rocks. Tectonophysics 2003, 376, 151–166. [Google Scholar] [CrossRef]
- Gong, L.; Zeng, L.B.; Zhang, B.J.; Zu, K.W.; Yin, H.; Ma, H.L. Control factors for fracture development in tight conglomerate reservoir of Jiulongshan structure. J. China Univ. Petrol. 2012, 36, 6–12. [Google Scholar]
- Huang, N.; Jiang, Y.J.; Liu, R.C.; Li, B.; Zhang, Z.Y. A predictive model of permeability for fractal-based rough rock fractures during shear. Fractals 2017, 25, 1750051. [Google Scholar] [CrossRef]
- Marrett, R.; Gale, J.F.W.; Gómez, L.A.; Laubach, S.E. Correlation analysis of fracture arrangement in space. J. Struct. Geol. 2018, 108, 16–33. [Google Scholar] [CrossRef]
- Casini, G.; Hunt, D.W.; Monsen, E.; Bounaim, A. Fracture characterization and modeling from virtual outcrops. AAPG Bull. 2016, 100, 41–61. [Google Scholar] [CrossRef]
- Santos, R.F.V.C.; Miranda, T.S.; Barbosa, J.A.; Gomes, I.F.; Matos, G.C.; Gale, J.F.W.; Neumann, V.H.L.M.; Guimaraes, L.J.N. Characterization of natural fracture systems: Analysis of uncertainty effects in linear scanline results. AAPG Bull. 2015, 99, 2203–2219. [Google Scholar] [CrossRef]
- Zeeb, C.; Gomez-Rivas, E.; Bons, P.D.; Blum, P. Evaluation of sampling methods for fracture network characterization using outcrops. AAPG Bull. 2013, 97, 1545–1566. [Google Scholar] [CrossRef]
- Procter, A.; Sanderson, D.J. Spatial and layer-controlled variability in fracture networks. J. Struct. Geol. 2018, 108, 52–65. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The fractal geometry of nature; W.H. Freeman and Company: New York, NY, USA, 1982; Available online: https://us.macmillan.com/books/9780716711865 (accessed on 17 August 2018).
- Cai, J.C.; Wei, W.; Hu, X.Y.; Liu, R.C.; Wang, J.J. Fractal characterization of dynamic fracture network extension in porous media. Fractals 2017, 25, 1750023. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Yu, L.; Jiang, Y.; Wang, Y.; Li, B. Recent developments on relationships between the equivalent permeability and fractal dimension of two-dimensional rock fracture networks. J. Nat. Gas Sci. Eng. 2017, 45, 771–785. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, L.; Sun, C.; Cai, C.; Wang, L. Investigation on the pore structure and multifractal characteristics of tight oil reservoirs using NMR measurements: Permian Lucaogou Formation in Jimusaer Sag, Junggar Basin. Mar. Petrol. Geol. 2017, 86, 1067–1081. [Google Scholar] [CrossRef]
- Liu, K.Q.; Ostadhassan, M.; Zhou, J.; Gentzis, T.; Rezaee, R. Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 2017, 209, 567–578. [Google Scholar] [CrossRef]
- Zhao, P.; Cai, J.; Huang, Z.; Ostadhassan, M.; Ran, F.Q. Estimating permeability of shale gas reservoirs from porosity and rock compositions. Geophysics 2018, 83, 1–36. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jing, H.; Wei, W. Analytical solutions for water–gas flow through 3D rock fracture networks subjected to triaxial stresses. Fractals 2018, 26, 1850053. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal and statistical network properties. J. Petrol. Sci. Eng. 2012, 92–93, 110–123. [Google Scholar] [CrossRef]
- Johri, M.; Zoback, M.D.; Hennings, P. A scaling law to characterize fault-damage zones at reservoir depths. AAPG Bull. 2014, 98, 2057–2079. [Google Scholar] [CrossRef]
- Maerten, L.; Gillespie, P.; Daniel, J. Three-dimensional geomechanical modeling for constraint of subseismic fault simulation. AAPG Bull. 2006, 90, 1337–1358. [Google Scholar] [CrossRef]
- Ortega, O.J.; Marrett, R.A.; Loubach, S.E. A scale-independent approach to fracture intensity and average spacing measurement. AAPG Bull. 2006, 90, 193–208. [Google Scholar] [CrossRef]
- Zhu, J.; Cheng, Y. Effective permeability of fractal fracture rocks: Significance of turbulent flow and fractal scaling. Int. J. Heat Mass Transf. 2018, 116, 549–556. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.J.; Liu, R.C.; Xia, Y.X. Size effect on the permeability and shear induced flow anisotropy of fractal rock fractures. Fractals 2018, 26, 1840001. [Google Scholar] [CrossRef]
- Li, Y.; Gong, L.; Zeng, L.; Ma, H.; Yang, H.; Zhang, B.; Zu, K. Characteristics of fractures and their contribution to the deliverability of tight conglomerate reservoirs in the Jiulongshan Structure, Sichuan Basin. Nat. Gas Ind. 2012, 32, 22–26. [Google Scholar]
- Pei, S.; Dai, H.; Yang, Y.; Li, Y.; Duan, Y. Evolutionary characteristics of T3x2 reservoir in Jiulongshan Structure, northwest Sichuan Basin. Nat. Gas Ind. 2008, 28, 51–53. [Google Scholar]
- Babadagli, T.; Develi, K. On the application of methods used to calculate the fractal dimension of fracture surfaces. Fractals 2001, 9, 105–128. [Google Scholar] [CrossRef]
- Klinkenberg, B. A review of methods used to determine the fractal dimension of linear features. Math. Geol. 1994, 26, 23–46. [Google Scholar] [CrossRef]
- Walsh, J.J.; Watterson, J. Fractal analysis of fracture patterns using the standard box-counting technique: Valid and invalid methodologies. J. Struct. Geol. 1993, 15, 1509–1512. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.M.; McKay, L.D. Fractal characterization of fracture networks: An improved box-counting technique. J. Geophys. Res. 2007, 112, B12. [Google Scholar] [CrossRef]
- Gong, L.; Zeng, L.; Miao, F.; Wang, Z.; Wei, Y.; Li, J.; Zu, K. Application of fractal geometry on the description of complex fracture systems. J. Hunan Univ. Sci. Technol. 2012, 27, 6–10. [Google Scholar]
- Mu, L.; Zhao, G.; Tian, Z.; Yuan, R.; Xu, A. Prediction of reservoir fractures; Petroleum Industry Press: Beijing, China, 2009; pp. 111–121. [Google Scholar]
- Odling, N.E. Scaling and connectivity of joint systems in sandstones from western Norway. J. Struct. Geol. 1997, 19, 1257–1271. [Google Scholar] [CrossRef]
- Gauthier, B.D.M.; Lake, S.D. Probabilistic modeling of faults below the limit of seismic resolution in Pelican Field, North Sea, offshore United Kingdom. AAPG Bull. 1993, 77, 761–777. [Google Scholar]
- Hooker, J.N.; Laubach, S.E.; Marrett, R. A universal power-law scaling exponent for fracture apertures in sandstones. Geol. Soc. Am. Bull. 2014, 126, 1340–1362. [Google Scholar] [CrossRef]



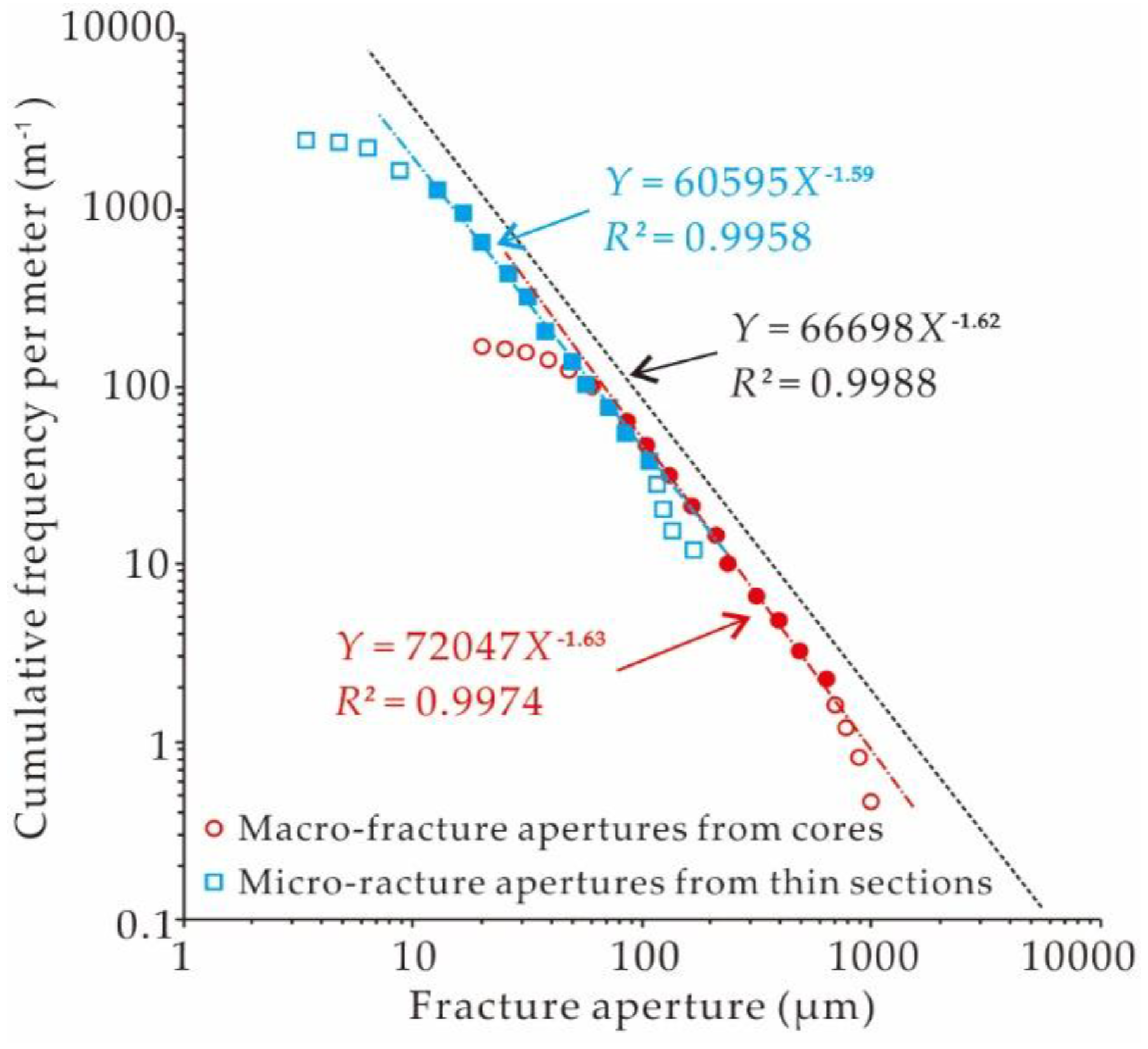
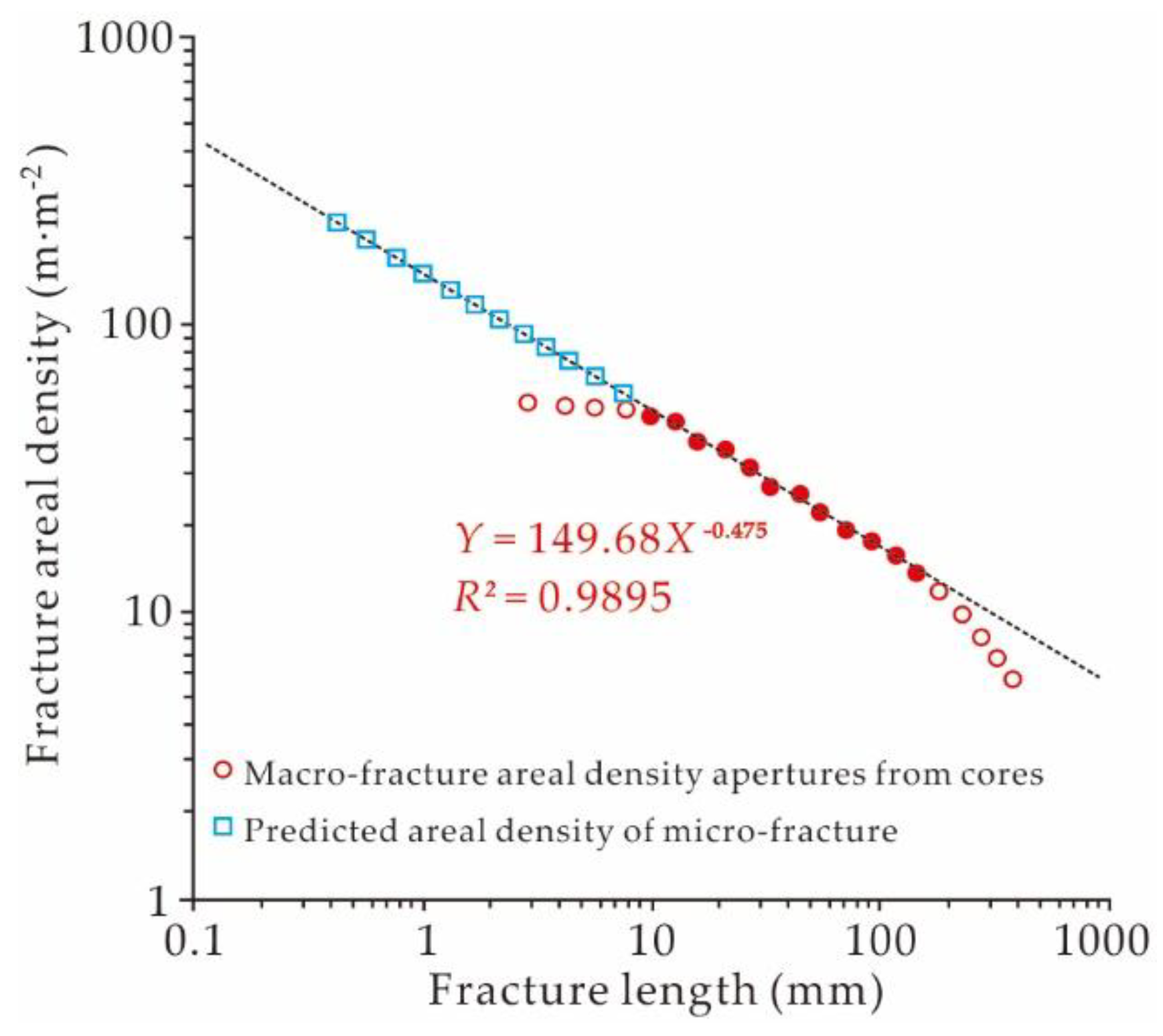
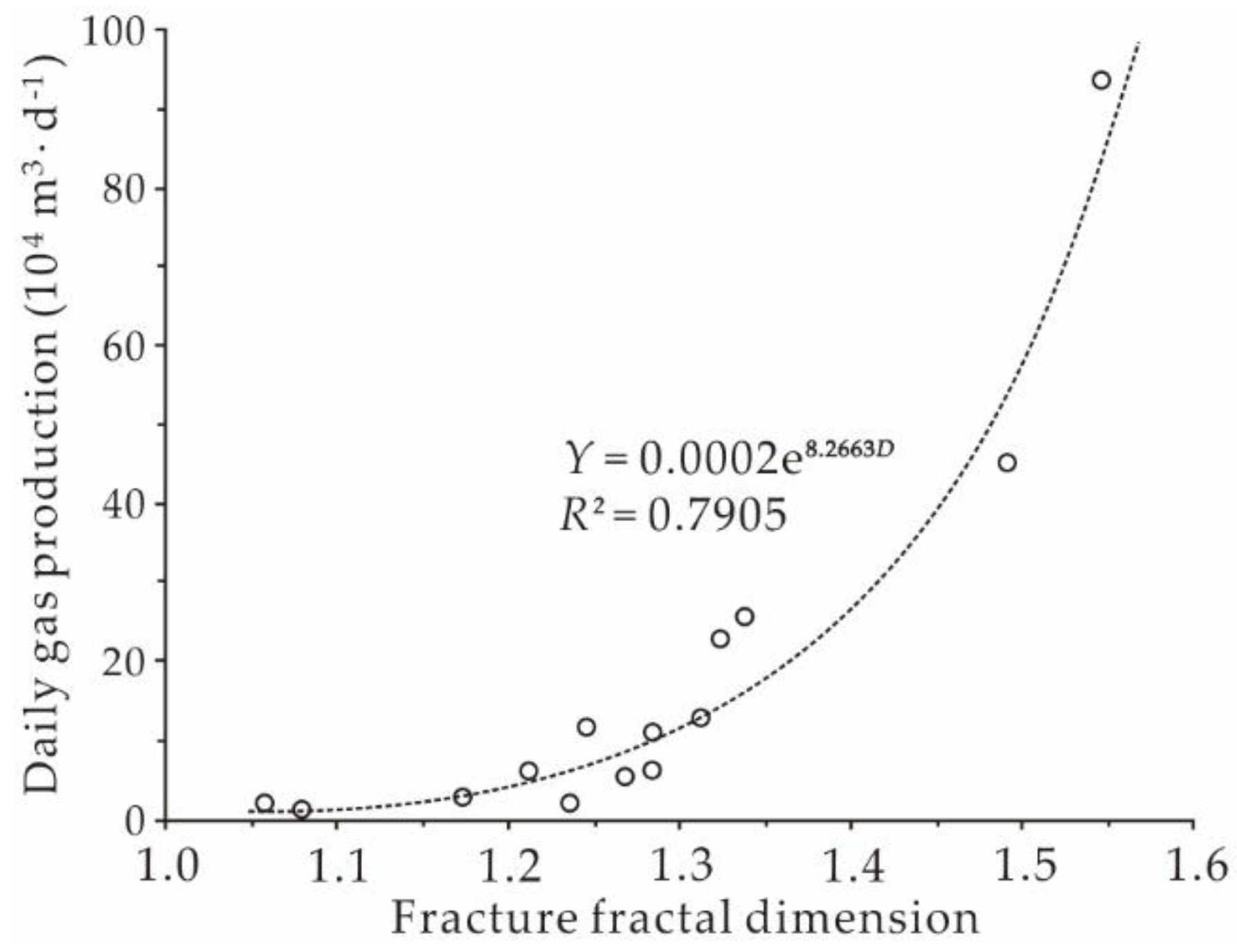
| Well Name | Interval | Fractal Dimension | Correlation Coefficient | Areal Density (m·m−2) | Porosity (%) | Permeability (mD) | |
|---|---|---|---|---|---|---|---|
| Top (m) | Bottom (m) | ||||||
| L4 | 3069.39 | 3069.55 | 1.38 | 0.9910 | 40.29 | 1.26 | 133.98 |
| L4 | 3069.64 | 3069.72 | 1.22 | 0.9891 | 26.59 | 0.99 | 38.62 |
| L4 | 3069.77 | 3069.78 | 1.22 | 0.9884 | 25.85 | 0.83 | 74.93 |
| L4 | 3069.98 | 3070.11 | 1.28 | 0.9901 | 27.87 | 1.51 | 81.98 |
| L4 | 3070.22 | 3070.29 | 1.31 | 0.9920 | 26.58 | 0.82 | 90.48 |
| L4 | 3070.49 | 3070.57 | 1.40 | 0.9908 | 40.54 | 0.96 | 106.12 |
| L4 | 3070.80 | 3070.93 | 1.43 | 0.9898 | 36.80 | 1.22 | 88.98 |
| L4 | 3071.01 | 3071.12 | 1.10 | 0.9914 | 24.98 | 0.59 | 32.00 |
| L4 | 3071.36 | 3071.56 | 1.24 | 0.9905 | 32.81 | 0.95 | 74.75 |
| L4 | 3071.71 | 3071.80 | 1.58 | 0.9897 | 39.29 | 1.27 | 138.58 |
| L4 | 3071.91 | 3072.12 | 1.17 | 0.9914 | 21.30 | 0.76 | 80.85 |
| L4 | 3072.24 | 3072.41 | 1.01 | 0.9893 | 17.95 | 0.50 | 39.93 |
| L10 | 3080.74 | 3080.91 | 1.15 | 0.9877 | 24.22 | 0.71 | 52.18 |
| L10 | 3101.61 | 3101.80 | 1.28 | 0.9927 | 26.99 | 0.74 | 67.63 |
| L10 | 3101.88 | 3102.07 | 1.03 | 0.9922 | 24.19 | 0.62 | 34.91 |
| L10 | 3102.13 | 3102.34 | 1.65 | 0.9933 | 56.49 | 1.81 | 245.25 |
| L10 | 3102.55 | 3102.71 | 1.24 | 0.9894 | 24.77 | 0.83 | 82.18 |
| L10 | 3102.81 | 3102.95 | 1.31 | 0.9896 | 40.64 | 1.15 | 79.94 |
| L10 | 3103.30 | 3103.42 | 1.24 | 0.9923 | 31.86 | 1.09 | 94.35 |
| L10 | 3103.49 | 3103.53 | 1.33 | 0.9879 | 32.42 | 1.77 | 90.54 |
| L10 | 3103.61 | 3103.79 | 1.36 | 0.9900 | 40.62 | 1.42 | 143.99 |
| L10 | 3103.88 | 3103.93 | 1.40 | 0.9876 | 35.68 | 1.54 | 58.35 |
| L10 | 3104.07 | 3104.18 | 1.37 | 0.9875 | 36.02 | 1.27 | 120.48 |
| L10 | 3104.26 | 3104.37 | 1.36 | 0.9895 | 28.56 | 1.17 | 166.58 |
| L102 | 3087.20 | 3087.34 | 1.46 | 0.9884 | 34.29 | 2.18 | 114.94 |
| L102 | 3087.51 | 3087.57 | 1.35 | 0.9887 | 30.49 | 1.05 | 103.49 |
| L102 | 3087.75 | 3087.85 | 1.50 | 0.9886 | 45.50 | 1.38 | 139.29 |
| L102 | 3087.94 | 3088.08 | 1.55 | 0.9875 | 50.57 | 1.78 | 191.51 |
| L102 | 3088.23 | 3088.33 | 1.04 | 0.9903 | 24.69 | 0.73 | 55.77 |
| L102 | 3088.60 | 3088.70 | 1.05 | 0.9886 | 18.00 | 0.69 | 55.13 |
| L102 | 3089.01 | 3089.17 | 1.51 | 0.9909 | 43.76 | 1.93 | 218.89 |
| L102 | 3089.17 | 3089.28 | 1.10 | 0.9880 | 26.70 | 1.06 | 93.28 |
| L102 | 3089.39 | 3089.55 | 1.08 | 0.9918 | 20.01 | 0.58 | 52.04 |
| L103 | 3117.23 | 3117.38 | 1.24 | 0.9889 | 30.60 | 1.11 | 128.42 |
| L103 | 3117.45 | 3117.54 | 1.43 | 0.9924 | 47.72 | 1.75 | 191.26 |
| L103 | 3117.70 | 3117.84 | 1.44 | 0.9906 | 41.50 | 1.24 | 90.64 |
| L103 | 3117.99 | 3118.05 | 1.28 | 0.9901 | 39.06 | 1.26 | 75.31 |
| L103 | 3118.15 | 3118.26 | 1.39 | 0.9895 | 47.30 | 1.08 | 88.36 |
| L103 | 3118.36 | 3118.58 | 1.19 | 0.9928 | 28.91 | 1.21 | 79.01 |
| L103 | 3118.67 | 3118.82 | 1.22 | 0.9882 | 33.35 | 0.76 | 35.99 |
| L103 | 3118.98 | 3119.03 | 1.41 | 0.9924 | 43.21 | 1.35 | 111.74 |
| L103 | 3119.09 | 3119.21 | 1.19 | 0.9894 | 28.88 | 0.95 | 60.14 |
| L103 | 3119.30 | 3119.40 | 1.56 | 0.9929 | 67.27 | 2.14 | 169.61 |
| L103 | 3119.58 | 3119.72 | 1.15 | 0.9909 | 24.14 | 0.80 | 78.47 |
| L103 | 3119.92 | 3120.16 | 1.31 | 0.9915 | 34.79 | 0.79 | 59.60 |
| L103 | 3120.32 | 3120.50 | 1.44 | 0.9930 | 48.27 | 1.53 | 90.03 |
| L103 | 3128.18 | 3128.37 | 1.52 | 0.9923 | 39.17 | 1.44 | 208.87 |
| L103 | 3128.57 | 3128.71 | 1.24 | 0.9905 | 25.29 | 1.1 | 148.97 |
| Number | Full Diameter Cores | Core Plugs | Φ1/Φ2 | K1/K3 | |||
|---|---|---|---|---|---|---|---|
| Φ1 (%) | K1 (mD) | K2 (mD) | Φ2 (%) | K3 (mD) | |||
| 1 | 3.90 | 214.50 | 0.0145 | 0.29 | 0.0021 | 13.45 | 102,142.86 |
| 2 | 3.74 | 201.69 | 0.0007 | 0.64 | 0.0084 | 5.84 | 24,010.71 |
| 3 | 3.80 | 166.57 | 0.0689 | 0.51 | 0.0056 | 7.45 | 29,744.64 |
| 4 | 3.12 | 5.75 | 0.0237 | 1.51 | 0.0105 | 2.07 | 547.62 |
| 5 | 2.61 | 83.58 | 0.0123 | 0.93 | 0.0096 | 2.81 | 8706.25 |
| 6 | 4.05 | 3.17 | 0.5917 | 1.60 | 0.0191 | 2.53 | 165.97 |
| 7 | 3.04 | 7.25 | 0.4628 | 1.26 | 0.0084 | 2.41 | 863.10 |
| 8 | 3.19 | 21.40 | 0.2450 | 1.09 | 0.0047 | 2.93 | 4553.19 |
| 9 | 3.06 | 32.30 | 0.4930 | 0.89 | 0.0079 | 3.44 | 4088.61 |
| 10 | 3.01 | 40.40 | 0.6730 | 0.95 | 0.0127 | 3.17 | 3181.10 |
| Average | 3.52 | 77.7 | 0.2586 | 0.97 | 0.0089 | 4.61 | 17,800.40 |
| Fracture Length (mm) | Fracture Areal Density | Absolute Error (m·m−2) | Relative Error (%) | |
|---|---|---|---|---|
| Measured (m·m−2) | Predicted (m·m−2) | |||
| 10 | 50.35 | 50.14 | −0.21 | 0.42 |
| 9 | 51.89 | 52.71 | 0.82 | 1.58 |
| 8 | 56.05 | 55.74 | −0.31 | 0.55 |
| 7 | 60.48 | 59.39 | –1.09 | 1.80 |
| 6 | 62.36 | 63.91 | 1.55 | 2.48 |
| 5 | 67.07 | 69.69 | 2.62 | 3.90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Fu, X.; Gao, S.; Zhao, P.; Luo, Q.; Zeng, L.; Yue, W.; Zhang, B.; Liu, B. Characterization and Prediction of Complex Natural Fractures in the Tight Conglomerate Reservoirs: A Fractal Method. Energies 2018, 11, 2311. https://doi.org/10.3390/en11092311
Gong L, Fu X, Gao S, Zhao P, Luo Q, Zeng L, Yue W, Zhang B, Liu B. Characterization and Prediction of Complex Natural Fractures in the Tight Conglomerate Reservoirs: A Fractal Method. Energies. 2018; 11(9):2311. https://doi.org/10.3390/en11092311
Chicago/Turabian StyleGong, Lei, Xiaofei Fu, Shuai Gao, Peiqiang Zhao, Qingyong Luo, Lianbo Zeng, Wenting Yue, Benjian Zhang, and Bo Liu. 2018. "Characterization and Prediction of Complex Natural Fractures in the Tight Conglomerate Reservoirs: A Fractal Method" Energies 11, no. 9: 2311. https://doi.org/10.3390/en11092311
APA StyleGong, L., Fu, X., Gao, S., Zhao, P., Luo, Q., Zeng, L., Yue, W., Zhang, B., & Liu, B. (2018). Characterization and Prediction of Complex Natural Fractures in the Tight Conglomerate Reservoirs: A Fractal Method. Energies, 11(9), 2311. https://doi.org/10.3390/en11092311






