The Interaction Stability Analysis of a Multi-Inverter System Containing Different Types of Inverters
Abstract
:1. Introduction
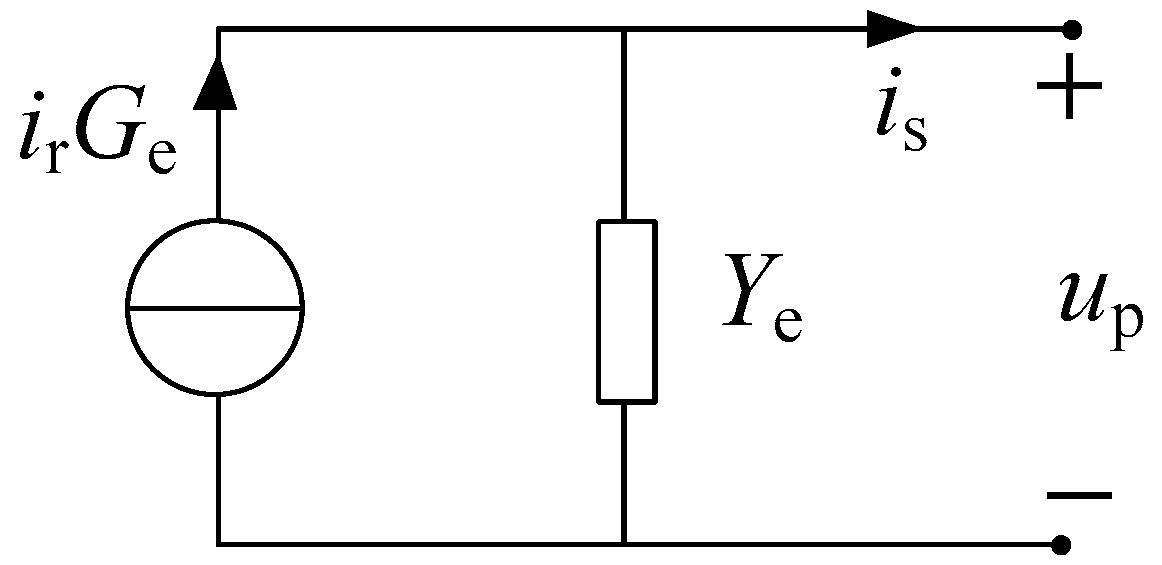
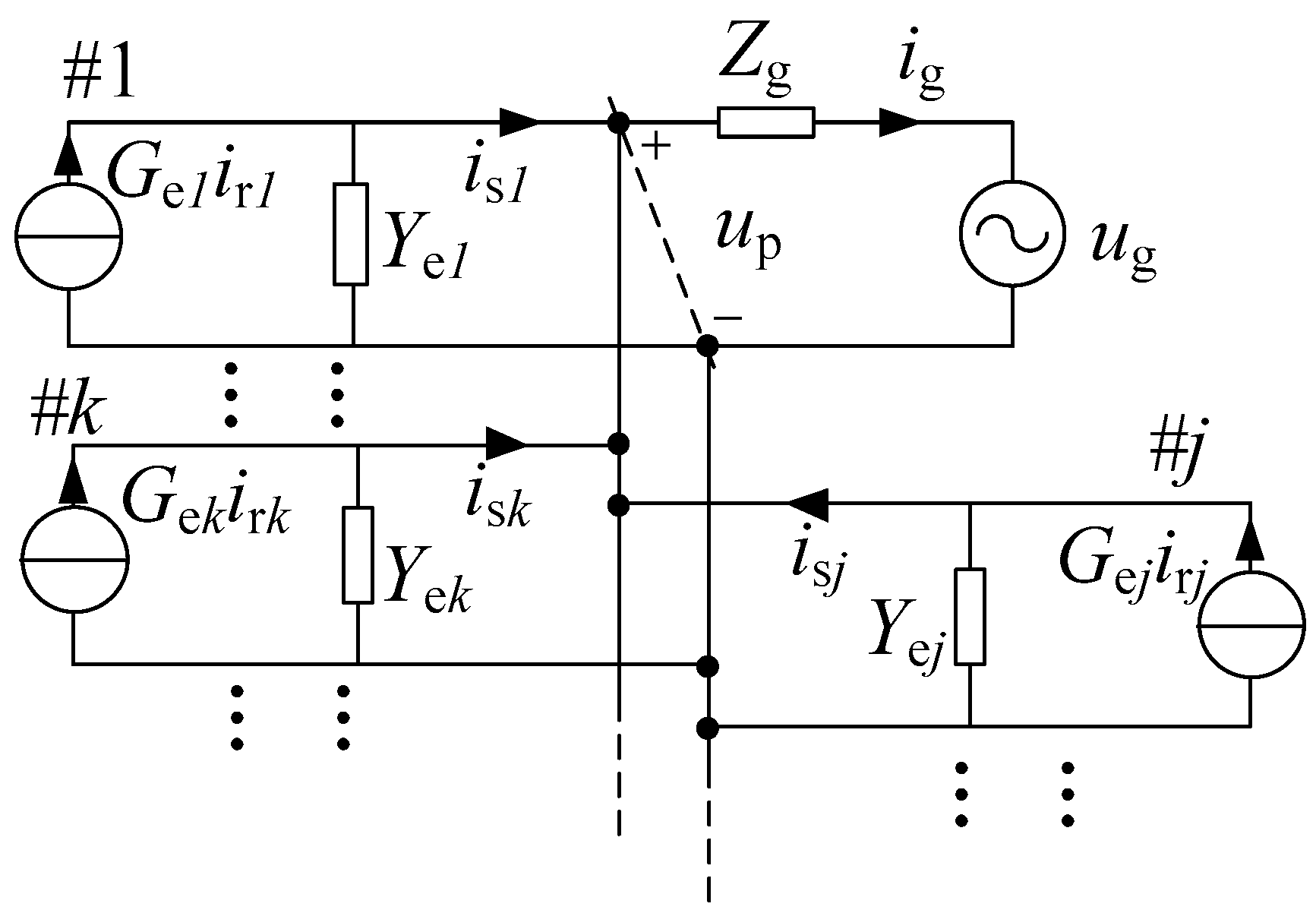
2. Multi-Inverter System Model
3. Methodology
3.1. The Set of Inverters with Some Common RHP Poles
3.2. Current of the Interaction between Inverter and Power Grid
3.3. Current of the Interaction between Different Inverters
4. Stability Criterion of Multi-Inverter System
- (a)
- Admittance network is stable.
- (b)
- Any two different inverters do not have the same RHP poles.
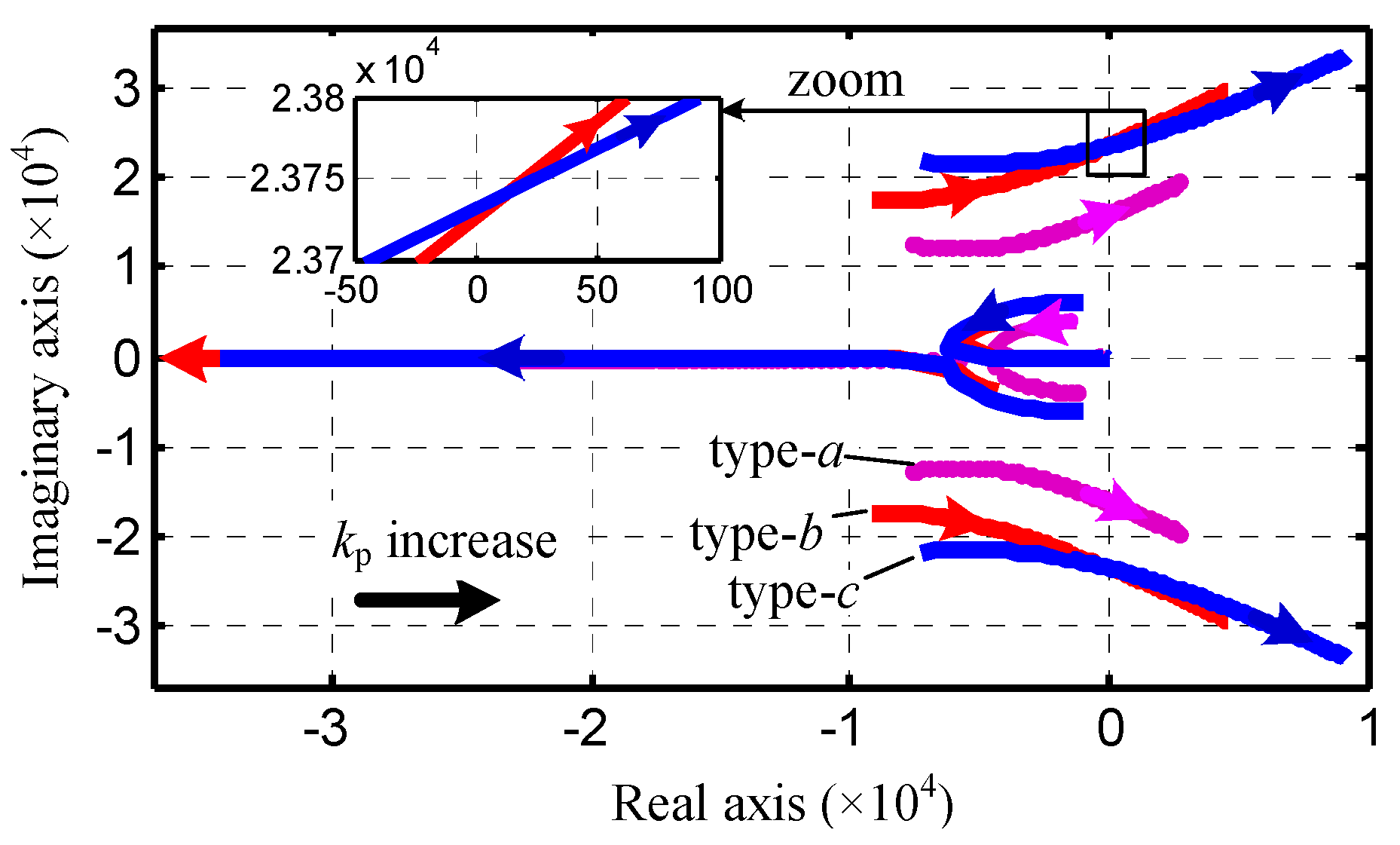
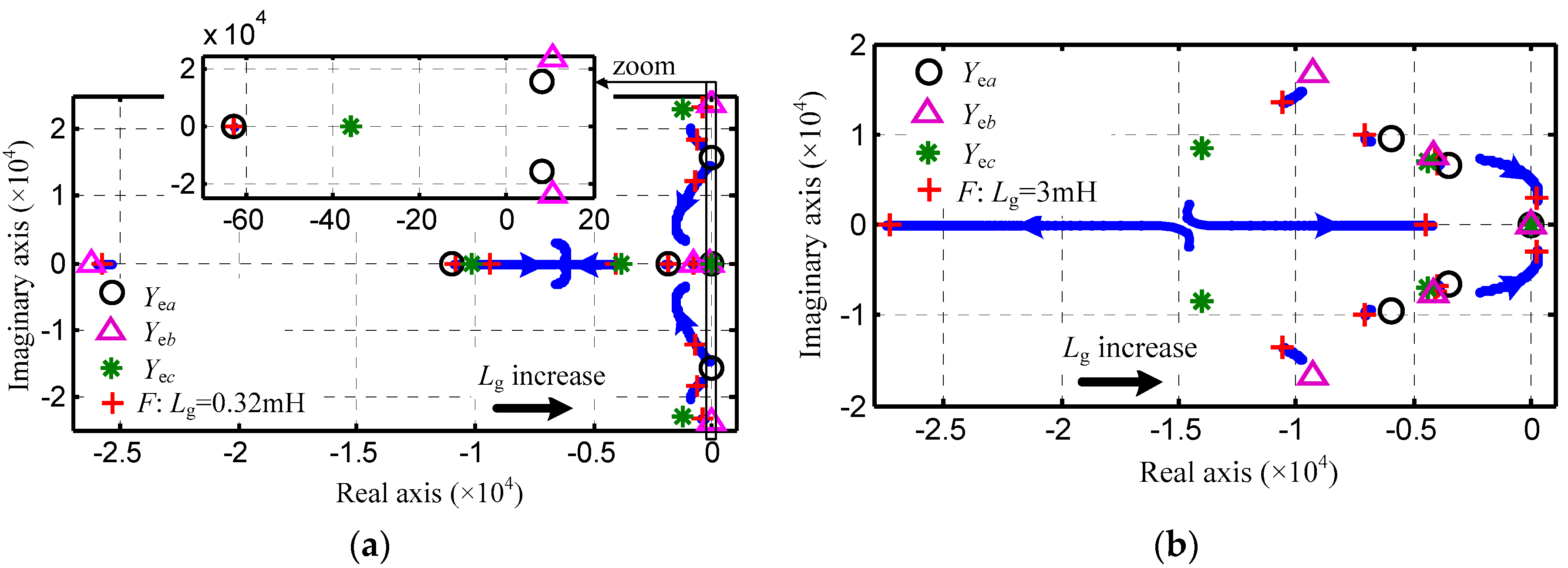
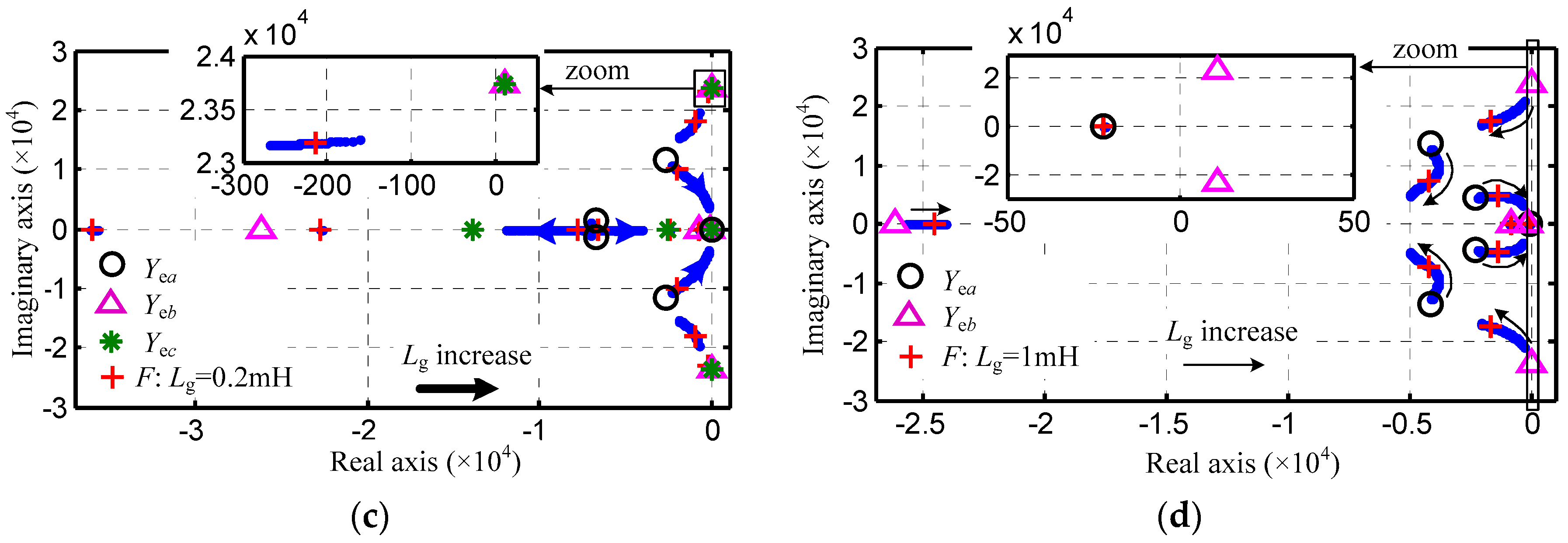
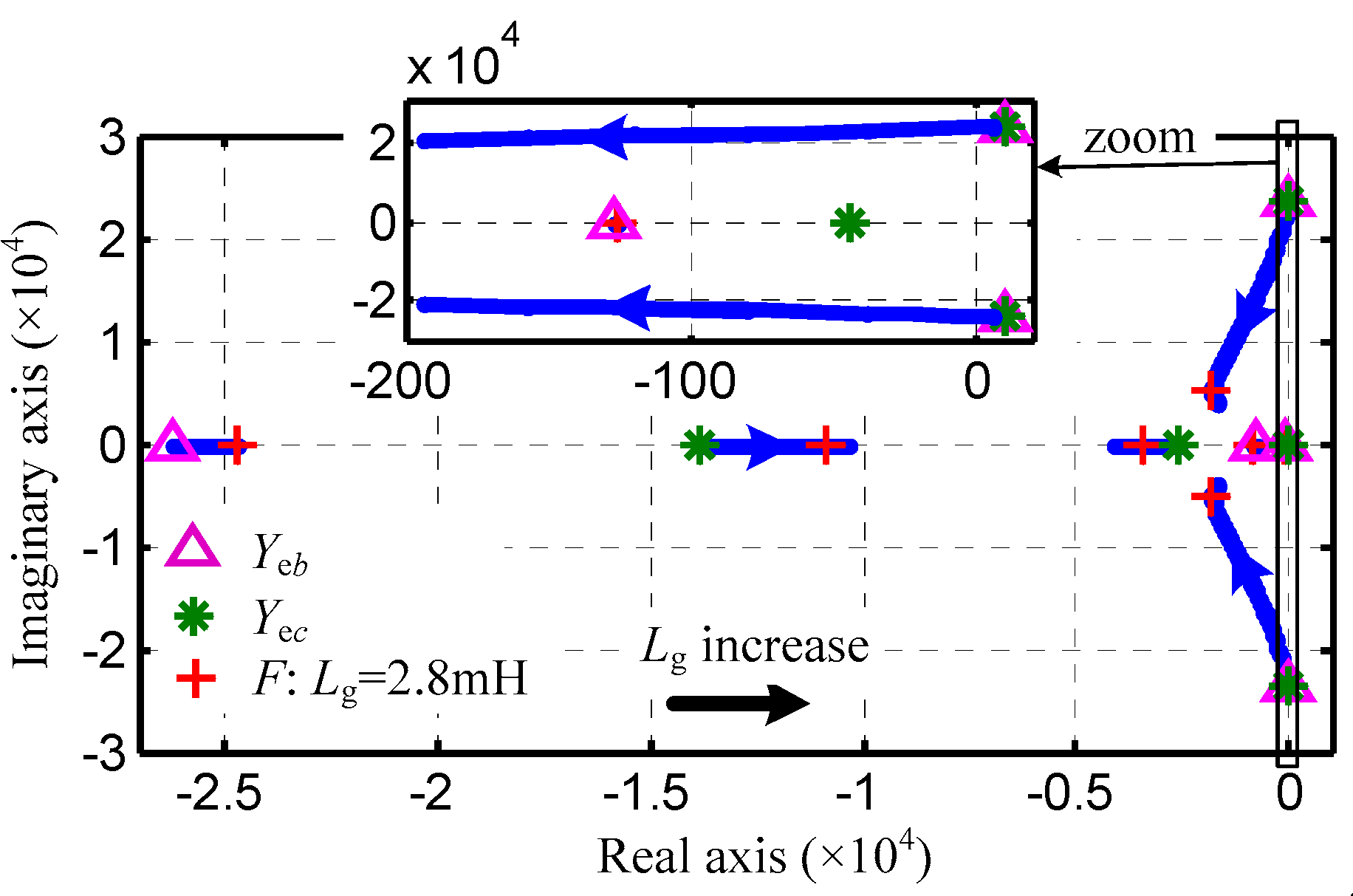
5. Case Study
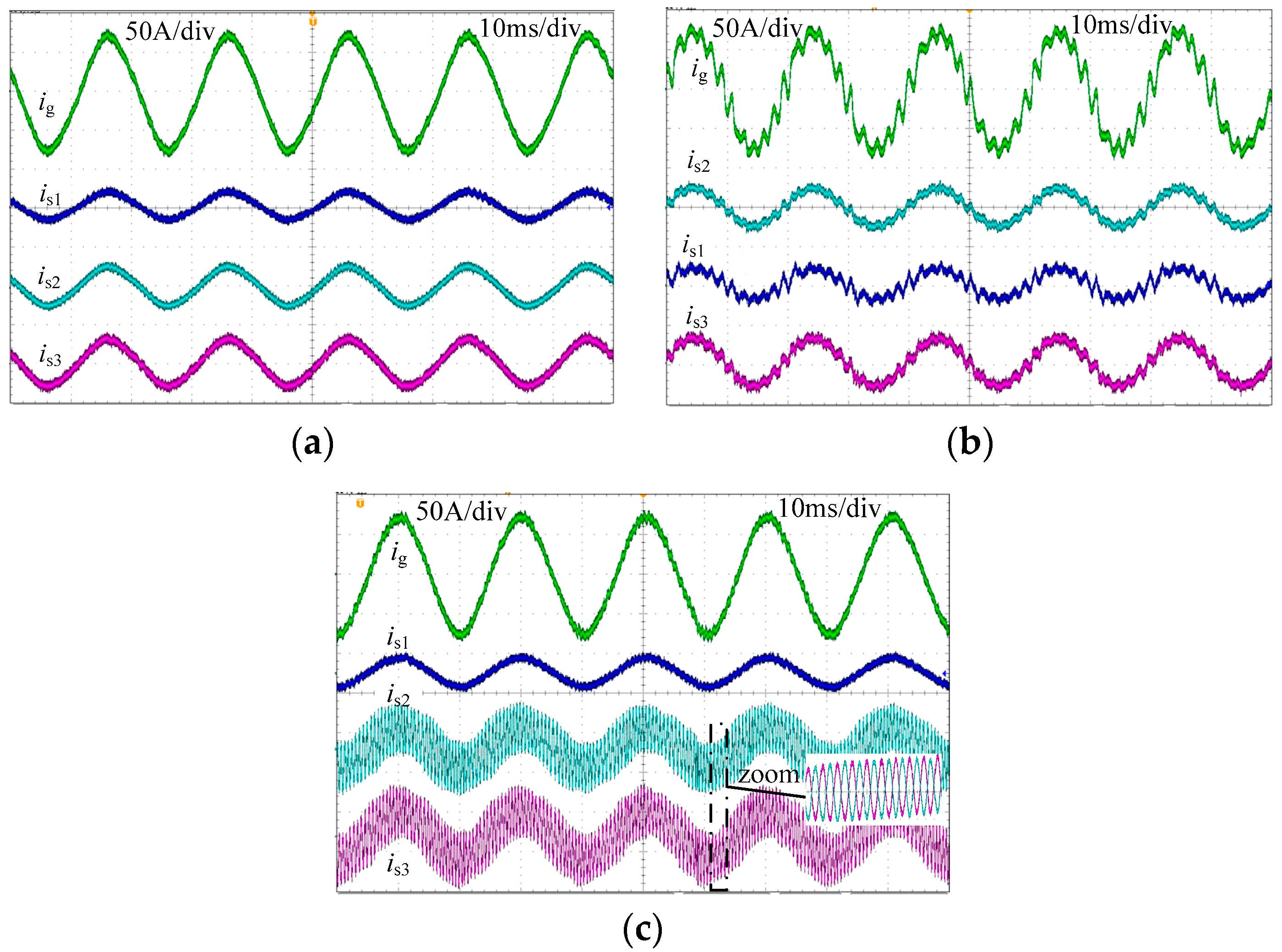
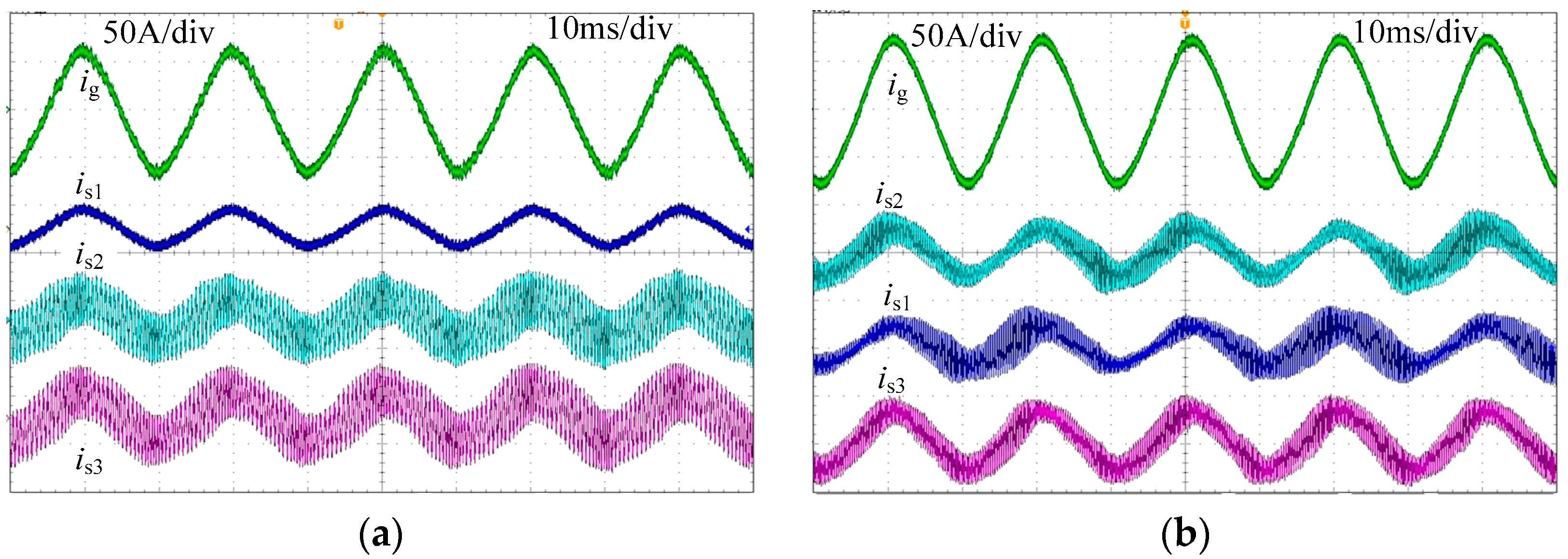
6. Simulation and Experiment Verification
6.1. Simulation Results
6.2. Experiment Results
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; PortilloGuisado, R.C.; Prats, M.A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Morjaria, M.; Anichkov, D.; Chadliev, V.; Soni, S. A grid-friendly plant: The role of utility-scale photovoltaic plants in grid stability and reliability. IEEE Power Energy Mag. 2014, 12, 87–95. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, M. Modeling and stability of large-scale PV plants due to grid impedance. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Francisco, F.D.; Rodriguez-Diaz, E.; Golsorkhi, M.S.; Vasquez, J.C.; Guerrero, J.M. A root-locus design methodology derived from the impedance/admittance stability formulation and its application for LCL grid-connected converters in wind turbines. IEEE Trans. Power Electron. 2017, 32, 8218–8228. [Google Scholar]
- Gao, L.; Wang, H.; Huang, Y. Analysis on the interaction of multi grid-connected inverters in distribution network. In Proceedings of the 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016. [Google Scholar]
- Wang, H.; Zhang, P.; Su, J.; Zhang, G. Resonant mechanism of multi grid-connected inverters in distribution power systems. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Juntunen, R.; Korhonen, J.; Musikka, T.; Smirnova, L.; Pyrhönen, O.; Silventoinen, P. Identification of resonances in parallel connected grid inverters with LC- and LCL-filters. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
- Yu, C.; Zhang, X.; Liu, F.; Li, F.; Xu, H.; Cao, R.; Ni, H. Modeling and resonance analysis of multiparallel inverters system under asynchronous carriers conditions. IEEE Trans. Power Electron. 2017, 32, 3192–3205. [Google Scholar] [CrossRef]
- Gabe, I.J.; Montagner, V.F.; Pinheiro, H. Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter. IEEE Trans. Power Electron. 2009, 24, 1444–1452. [Google Scholar] [CrossRef]
- Lorzadeh, I.; Abyaneh, H.A.; Savaghebi, M.; Bakhshai, A.; Guerrero, J.M. Capacitor current feedback-based active resonance damping strategies for digitally-controlled inductive-capacitive-inductive-filtered grid-connected inverters. Energies 2016, 9, 462. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Lin, H. Stability analysis of grid-connected converters with different implementations of adaptive PR controllers under weak grid conditions. Energies 2018, 11, 2004. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Bao, C.; Li, W.; Wang, X. Optimized controller design for LCL-type grid-connected inverter to achieve high robustness against grid-impedance variation. IEEE Trans. Ind. Electron. 2015, 62, 1537–1547. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Enslin, J.H.R.; Heskes, P.J.M. Harmonic interaction between a large number of distributed power inverters and the distributed network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Agorreta, J.L.; Borrega, M.; Lopez, J.; Marroyo, L. Modeling and control of N-paralleled grid-connected inverters with LCL filters coupled due to grid impedance in PV plants. IEEE Trans. Power Electron. 2011, 26, 770–785. [Google Scholar] [CrossRef]
- He, J.; Li, Y.; Bosnjak, D.; Harris, B. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid. IEEE Trans. Power Electron. 2013, 28, 234–246. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power-electronics-based ac systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Blaabjerg, F.; Loh, P.C. An analysis method for harmonic resonance and stability of multi-paralleled LCL-filtered inverters. In Proceedings of the 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015. [Google Scholar]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F. Interaction and aggregated modeling of multiple paralleled inverters with LCL filter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F. Resonance interaction of multiparallel grid-connected inverters with LCL filter. IEEE Trans. Power Electron. 2017, 32, 894–899. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, L.; Guo, K.; Liu, Q.; Xie, B. Stability study of large-scale photovoltaic plant containing polytype inverters. In Proceedings of the International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016. [Google Scholar]
- Yoon, C.; Bai, H.; Beres, R.N.; Wang, X.; Bak, C.L.; Blaabjerg, F. Harmonic Stability Assessment for Multiparalleled, Grid-Connected Inverters. IEEE Trans. Sustain. Energy 2016, 7, 1388–1396. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, L.; Li, B.; Liu, J.; Hao, G. Interaction resonance mechanism of the parallel-inverter system containing multiple types of inverters. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Pan, D.; Ruan, X.; Wang, X.; Yu, H.; Xing, Z. Analysis and design of current control achemes for LCL-type grid-connected inverter based on a general mathematical model. IEEE Trans. Power Electron. 2017, 32, 4395–4410. [Google Scholar] [CrossRef]
- Liberos, M.; González-Medina, R.; Garcerá, G.; Figueres, E. Modelling and control of parallel-connected transformerless inverters for large photovoltaic farms. Energies 2017, 10, 1242. [Google Scholar] [CrossRef]
- Sun, J. Small-signal methods for AC distributed power systems—A review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Yu, Y.; Li, H.; Li, Z.; Zhao, Z. Modeling and analysis of resonance in LCL-type grid-connected inverters under different control schemes. Energies 2017, 10, 104. [Google Scholar] [CrossRef]
- Jalili, K.; Bernet, S. Design of LCL filters of active-front-end twolevel voltage-source converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]





| Items | Type-a | Type-b | Type-c |
|---|---|---|---|
| P | 6 kW | 8 kW | 10 kW |
| ug | 220 V | 220 V | 220 V |
| udc | 330 V | 330 V | 330 V |
| L1 | 4.5 mH | 2.8 mH | 2 mH |
| Cf | 5 uF | 3.65 uF | 5 μF |
| L2 | 0.9 mH | 0.56 mH | 0.4 mH |
| Items | #1 | #2 | #3 |
|---|---|---|---|
| System I | type-a | type-b | type-c |
| System II | type-a | type-b | type-b |
| System III | type-b | type-b | type-c |
| System | State | #1 | #2 | #3 |
|---|---|---|---|---|
| System I | state-A | 0.388 | 0.5303 | 0.181 |
| state-B | 0.14 | 0.11 | 0.08 | |
| state-C | 0.2 | 0.5303 | 0.2257 | |
| System II | state-D | 0.2 | 0.5303 | 0.5303 |
| System III | state-E | 0.5303 | 0.5303 | 0.2257 |
| Items | Constitution and the Reference Current Ir | Lg |
|---|---|---|
| state-A | #1 inverter: 38 A; #2 inverter: 50 A; #3 inverter: 60 A | 0.32 mH |
| state-B | #1 inverter: 38 A; #2 inverter: 50 A; #3 inverter: 60 A | 3 mH |
| state-C | #1 inverter: 38 A; #2 inverter: 50 A; #3 inverter: 60 A | 0.2 mH |
| state-D | #1 inverter: 38 A; #2 inverter: 40 A; #3 inverter: 50 A | 1 mH |
| state-E | #1 inverter: 40 A; #2 inverter: 50 A; #3 inverter: 60 A | 2.8 mH |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Li, Q.; Zhou, L.; Li, B.; Mao, M. The Interaction Stability Analysis of a Multi-Inverter System Containing Different Types of Inverters. Energies 2018, 11, 2244. https://doi.org/10.3390/en11092244
Zheng C, Li Q, Zhou L, Li B, Mao M. The Interaction Stability Analysis of a Multi-Inverter System Containing Different Types of Inverters. Energies. 2018; 11(9):2244. https://doi.org/10.3390/en11092244
Chicago/Turabian StyleZheng, Chen, Qionglin Li, Lin Zhou, Bin Li, and Mingxuan Mao. 2018. "The Interaction Stability Analysis of a Multi-Inverter System Containing Different Types of Inverters" Energies 11, no. 9: 2244. https://doi.org/10.3390/en11092244
APA StyleZheng, C., Li, Q., Zhou, L., Li, B., & Mao, M. (2018). The Interaction Stability Analysis of a Multi-Inverter System Containing Different Types of Inverters. Energies, 11(9), 2244. https://doi.org/10.3390/en11092244





