Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models
Abstract
1. Introduction
1.1. Context
1.2. Literature Review on Related Problems
1.3. Contributions
2. Theoretical Background
2.1. Quantile Regression
2.2. Generalised Additive Models
2.3. The Proposed Models
2.3.1. Additive Quantile Regression Model
2.3.2. Forecast Error Measures
2.3.3. Percentage Improvement
2.3.4. Prediction Intervals
2.3.5. Evaluation of Prediction Intervals
2.3.6. Forecast Error Distribution
2.3.7. Forecast Combination
3. Description of the Case Study
4. Empirical Results
4.1. Exploratory Data Analysis
4.2. Forecasting Electricity Demand When Covariates Are Known in Advance
4.2.1. Forecasting Results
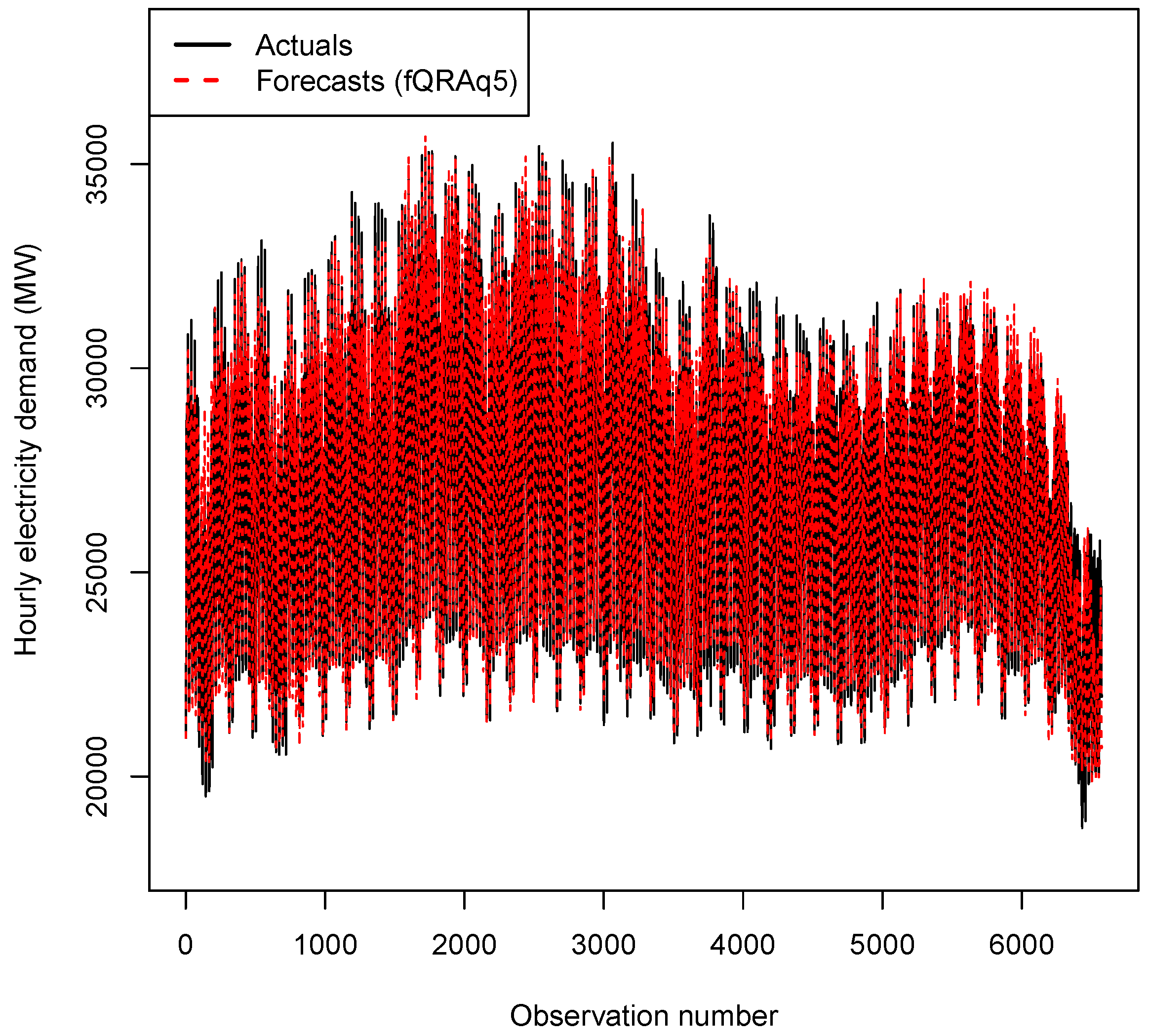
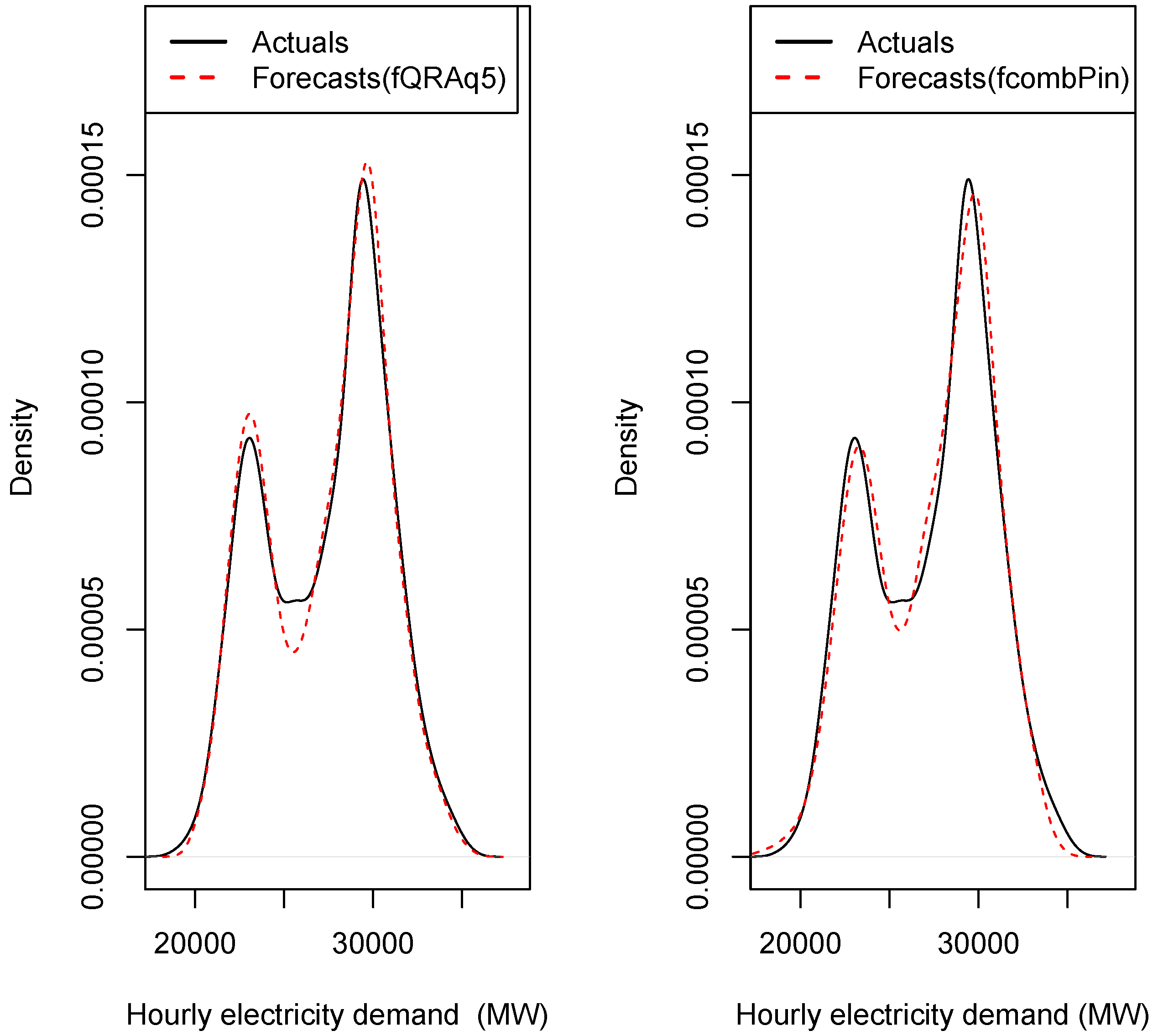
4.2.2. Out of Sample Forecasts
4.2.3. Evaluation of Prediction Intervals
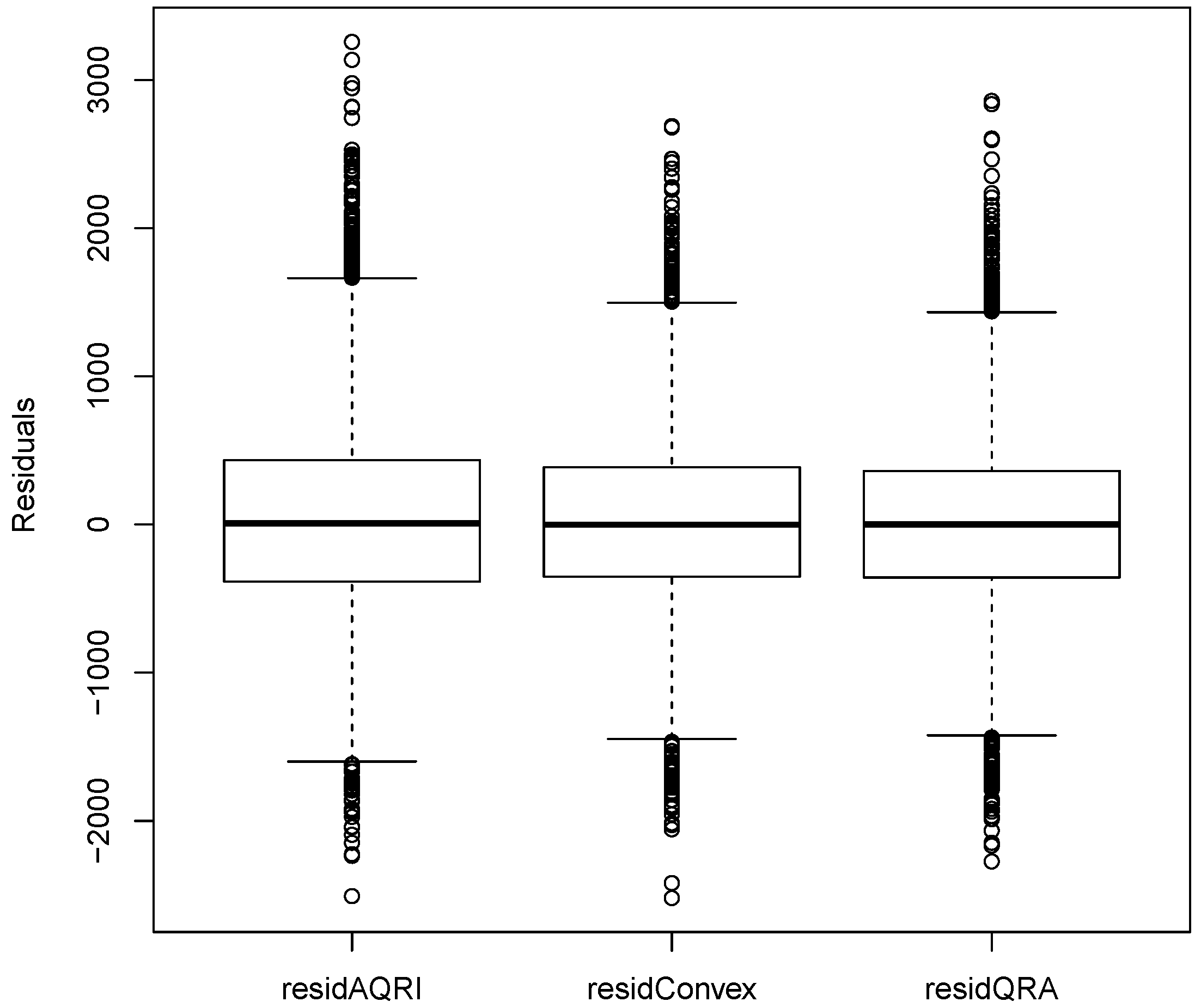
4.2.4. Residual Analysis
4.2.5. Plots of out of Sample Forecasts
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AQR | Additive Quantile Regression |
| GAM | Generalised additive model |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| PI | Prediction Interval |
| PICP | Prediction Interval Coverage Probability |
| PINAD | Prediction Interval Normalised Average Deviation |
| PINAW | Prediction Interval Normalised Average Width |
| PINC | Prediction Interval with Nominal Confidence |
| QR | Quantile Regression |
| QRA | Quantile regression averaging |
| RMSE | Root Mean Square Error |
Appendix A. Summary of the Accuracy Measures for the Months April to December 2012
| RMSE | MAE (MW) | MAPE (%) | |
|---|---|---|---|
| April | 945.5214 | 781.6429 | 3.151406 |
| May | 620.7605 | 488.6548 | 1.891559 |
| June | 665.0797 | 537.5238 | 1.898156 |
| July | 392.0611 | 329.3393 | 1.181808 |
| August | 642.6158 | 538.2321 | 1.903814 |
| September | 750.3948 | 618.5476 | 2.264714 |
| October | 345.0181 | 271.0595 | 1.010533 |
| November | 394.3301 | 302.9048 | 1.146244 |
| December | 468.6219 | 369.5595 | 1.395704 |
Appendix B. Hourly Load with Forecasts for the Months April–December 2012
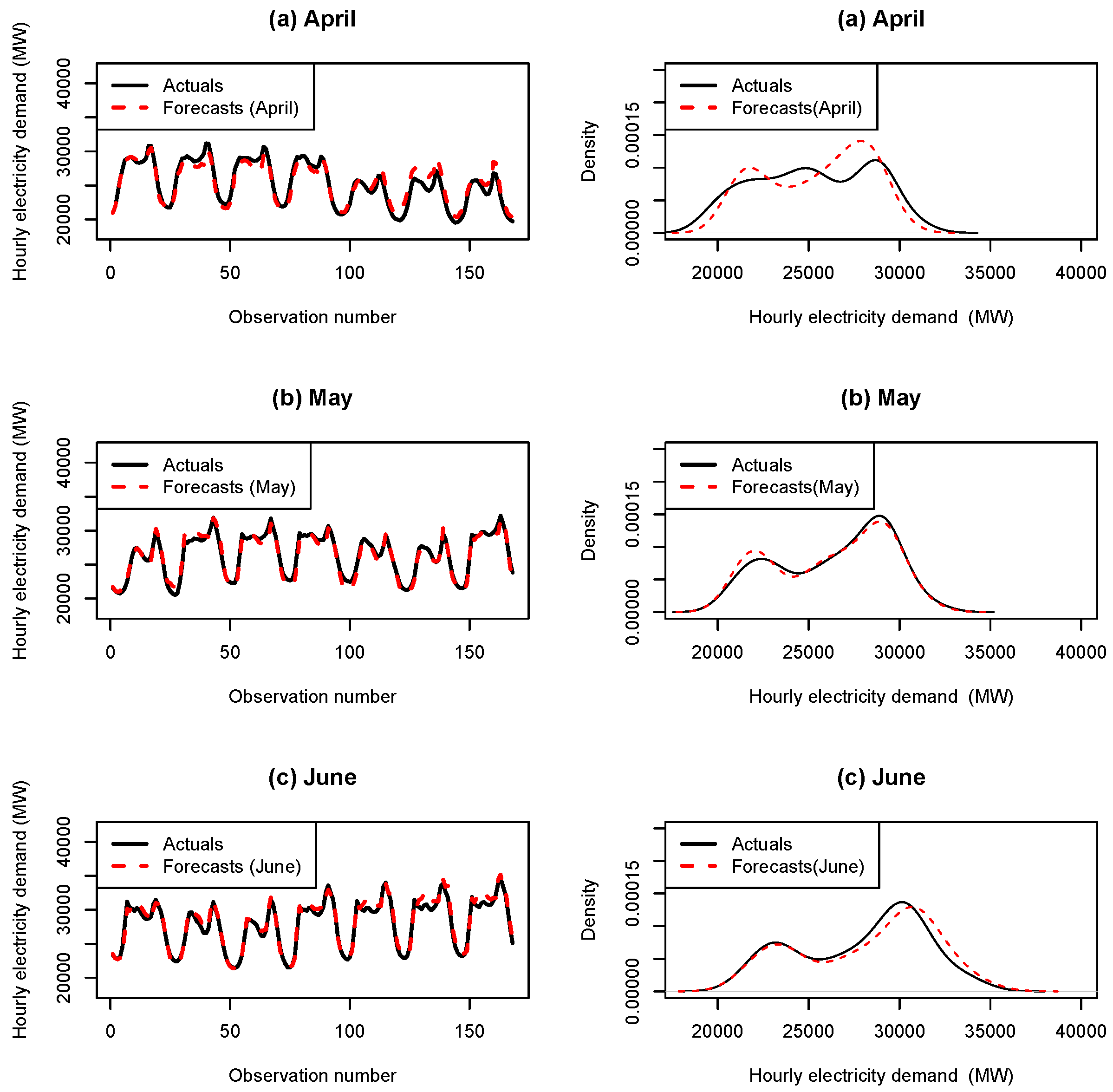
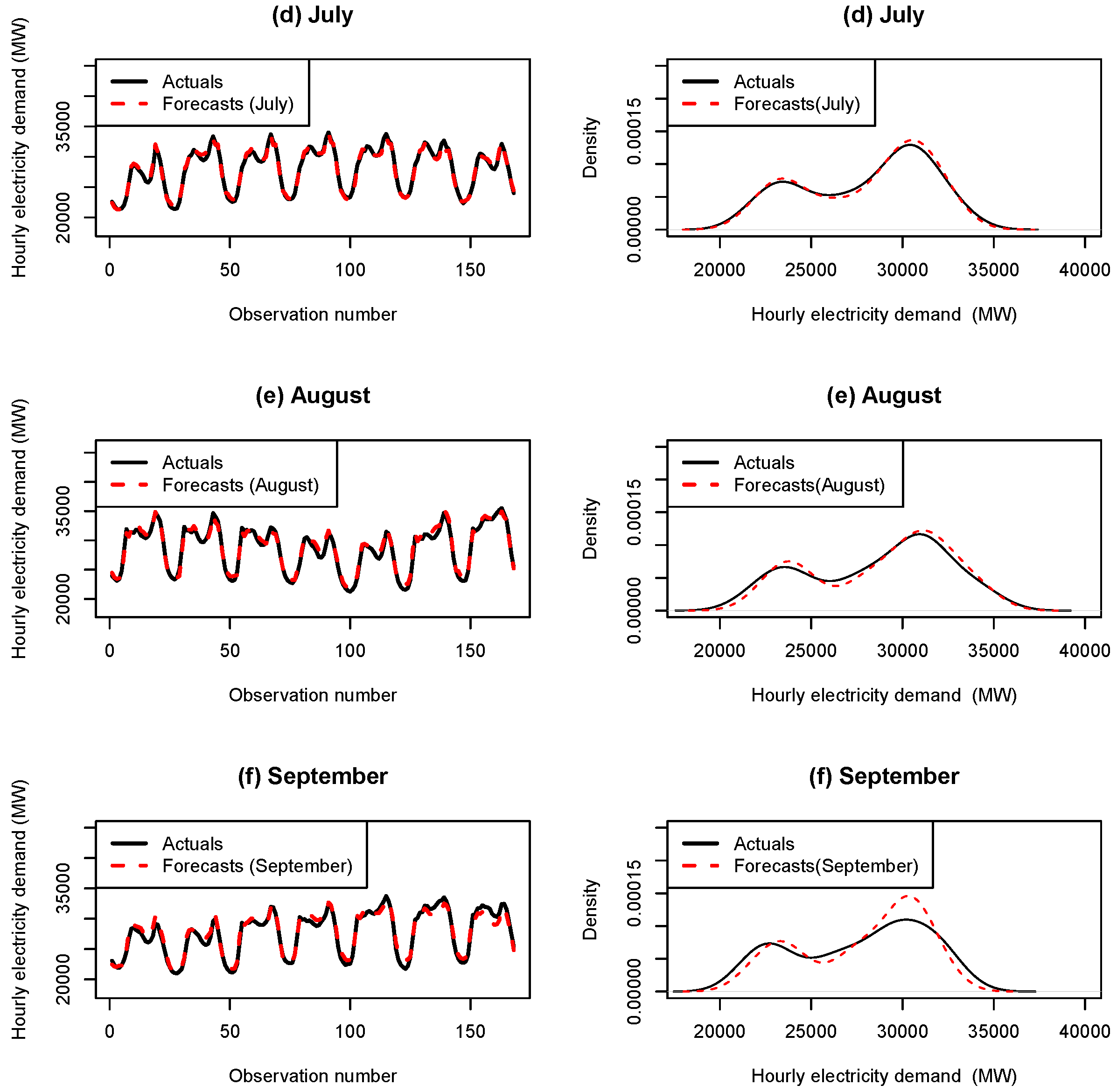
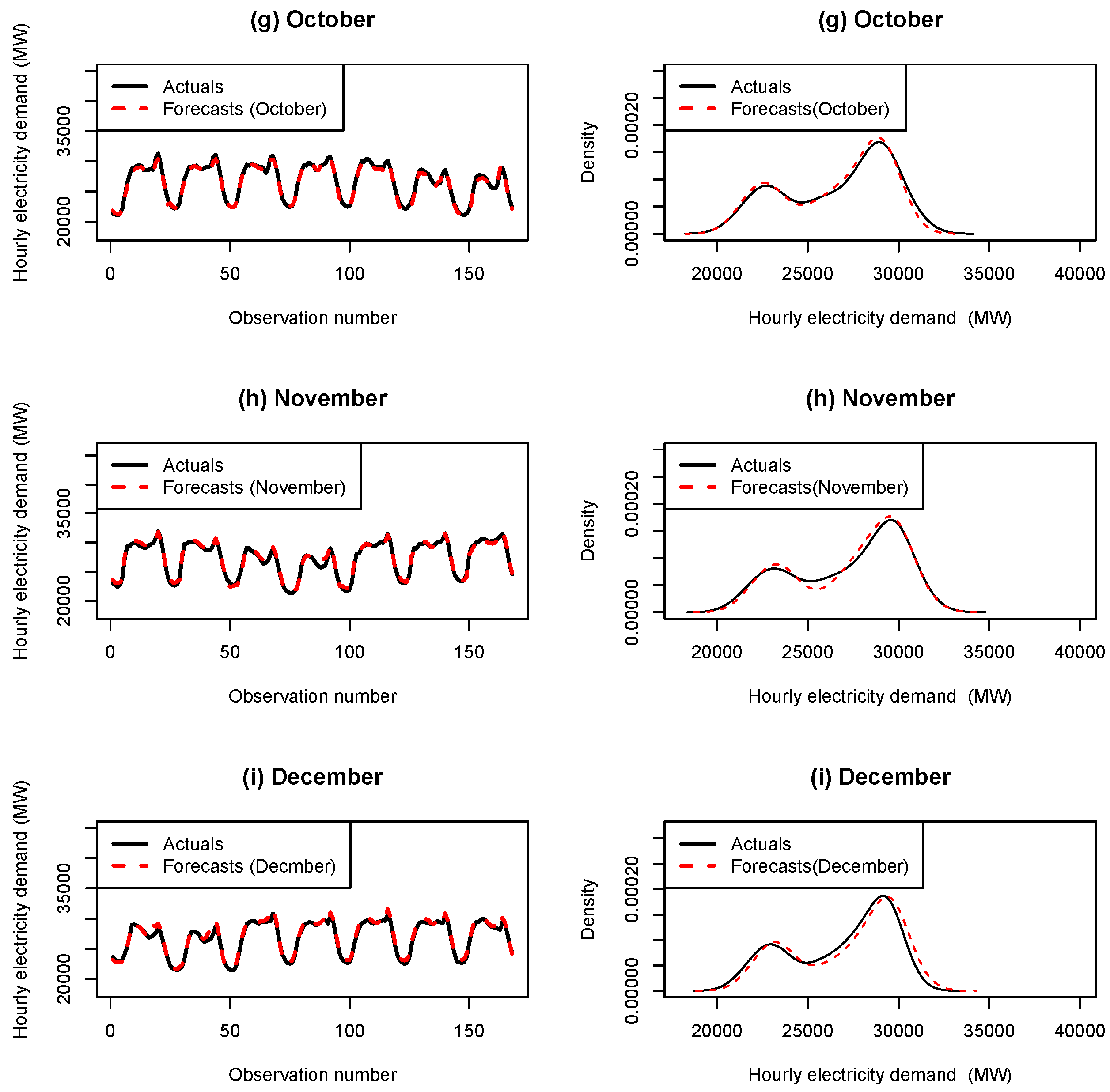
References
- Maciejowska, K.; Weron, R. Forecasting of daily electricity prices with factor models: Utilizing intra-day and inter-zone relationships. Comput. Stat. 2017, 30, 805–819. [Google Scholar] [CrossRef]
- Wood, S.N.; Goude, Y.; Shaw, S. Generalized additive models for large datasets. J. R. Stat. Soc. 2015, 64, 139–155. [Google Scholar] [CrossRef]
- Tsay, R.S. Analysis of Financial Time Series, 2nd ed.; Wiley Series in Probability and Statistics; Wiley Online Library: Hoboken, NJ, USA, 2005. [Google Scholar]
- Dordonnat, V.; Koopman, S.J.; Ooms, M. Dynamic factors in periodic time-varying regressions with an application to hourly electricity load modelling. Comput. Stat. Data Anal. 2012, 56, 3134–3152. [Google Scholar] [CrossRef]
- Soares, L.J.; Medeiros, M.C. Modeling and Forecasting Short-term Electric Load Demand: A Two-Step Methodology. 2016. Available online: https://pdfs.semanticscholar.org/734b/3f6565243912784ad7b1a7421acb7188c9ca.pdf (accessed on 28 December 2016).
- Ramanathan, R.; Engle, R.; Granger, C.W.J.; Vahid-Araghi, F.; Brace, C. Short-run forecasts of electricity loads and peaks. Int. J. Forecast. 1997, 13, 161–174. [Google Scholar] [CrossRef]
- Fan, S.; Hyndman, R.J. Short-term load forecasting based on a semi-parametric additive model. IEEE Trans. Power Syst. 2012, 27, 134–141. [Google Scholar] [CrossRef]
- Goude, Y.; Nedellec, R.; Kong, N. Local short and middle term electricity load forecasting with semi-parametric additive models. IEEE Trans. Smart Grid 2014, 5, 440–446. [Google Scholar] [CrossRef]
- Gaillard, P.; Goude, Y.; Nedellec, R. Additive models and robust aggregation for GEFcom2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 2016, 32, 1038–1050. [Google Scholar] [CrossRef]
- Fasiolo, M.; Goude, Y.; Nedellec, R.; Wood, S.N. Fast Calibrated Additive Quantile Regression. 2017. Available online: https://github.com/mfasiolo/qgam/blob/master/draftqgam.pdf (accessed on 13 March 2017).
- Laouafi, A.; Mordjaoui, M.; Haddad, S.; Boukelia, T.E.; Ganouche, A. Online electricity demand forecasting based on effective forecast combination methodology. Electr. Power Syst. Res. 2017, 148, 35–47. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
- Boroojeni, K.G.; Amini, M.H.; Bahrami, S.; Iyengar, S.S.; Sarwat, A.I.; Karabasoglu, O. A novel multi-time-scale modelling for electric power demand forecasting: From short-term to medium-term horizon. Electr. Power Syst. Res. 2017, 142, 58–73. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Zhang, X.; Anpalagan, A.; Venkatesh, B. Boosted neural networks for improved short-term electric load forecasting. Electr. Power Syst. Res. 2017, 143, 431–437. [Google Scholar] [CrossRef]
- Ekonomou, L.; Christodoulou, C.A.; Mladenov, V. A short-term load forecasting method using artificial neural networks and wavelet analysis. Int. J. Power Syst. 2016, 1, 64–68. [Google Scholar]
- Pappas, S.S.; Ekonomou, L.; Moussas, V.C.; Karampelas, P.; Katsikas, S.K. Adaptive load forecasting of the Hellenic electric grid. J. Zhejiang Univ. Sci. A 2008, 9, 1724–1730. [Google Scholar] [CrossRef]
- Gajowwniczek, K.; Zabkowski, T. Two-stage electricity demand modeling using machine learning algorithms. Energies 2017, 10, 1547. [Google Scholar] [CrossRef]
- Chapgain, K.; Kittipiyakul, S. Performance analysis of short-term electricity demand with atmospheric variables. Energies 2018, 11, 818. [Google Scholar] [CrossRef]
- Divina, F.; Gilson, A.; Goméz-Vela, F.; Torres, M.G.; Torres, J.F. Stacking ensemble learning for short-term electricity consumption forecasting. Energies 2018, 11, 949. [Google Scholar] [CrossRef]
- Nagbe, K.; Cugliari, J.; Jacques, J. Short-term electricity demand forecasting using a functional state space model. Energies 2018, 11, 1120. [Google Scholar] [CrossRef]
- Chikobvu, D.; Sigauke, C. Regression-SARIMA modelling of daily peak electricity demand in South Africa. J. Energy S. Afr. 2012, 23, 23–30. [Google Scholar]
- Sigauke, C.; Chikobvu, D. Short-term peak electricity demand in South Africa. Afr. J. Bus. Manag. 2012, 6, 9243–9249. [Google Scholar] [CrossRef]
- Sigauke, C.; Chikobvu, D. Peak electricity demand forecasting using time series regression models: An application to South African data. J. Stat. Manag. Syst. 2016, 19, 567–586. [Google Scholar] [CrossRef]
- Bien, J.; Taylor, J.; Tibshirani, R. A lasso for hierarchical interactions. Ann. Stat. 2013, 41, 1111–1141. [Google Scholar] [CrossRef] [PubMed]
- Laurinec, P. Doing Magic and Analyzing Seasonal Time Series with GAM, (Generalized Additive Model) in R. 2017. Available online: https://petolau.github.io/Analyzing-double-seasonal-time-series-with-GAM-in-R/ (accessed on 23 February 2017).
- Koenker, R.; Bassett, G. Regression quantiles. Econ. J. Econ. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized additive models (with discussion). Stat. Sci. 1986, 1, 297–318. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman & Hall: London, UK, 1990. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman & Hall: London, UK, 2006. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman & Hall: London, UK, 2017. [Google Scholar]
- Sigauke, C. Forecasting medium-term electricity demand in a South African electric power supply system. J. Energy S. Afr. 2017, 28, 54–67. [Google Scholar] [CrossRef]
- Bien, J.; Tibshirani, R. R Package “HierNet”, Version 1.6. 2015. Available online: https://cran.r-project.org/web/packages/hierNet/hierNet.pdf (accessed on 22 May 2017).
- Lim, M.; Hastie, T. Learning interactions via hierarchical group-lasso regularization. J. Comput. Graph. Stat. 2015, 24, 627–654. [Google Scholar] [CrossRef] [PubMed]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Hourly probabilistic forecasting of solar power. In Proceedings of the 49th North American Power Symposium, Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging of sister forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Z.; Hu, J. Prediction interval construction for byproduct gas flow forecasting using optimized twin extreme learning machine. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Chen, J. Wind power forecasting using multi-objective evolutionary algorithms for wavelet neural network-optimized prediction intervals. Appl. Sci. 2018, 8, 185. [Google Scholar] [CrossRef]
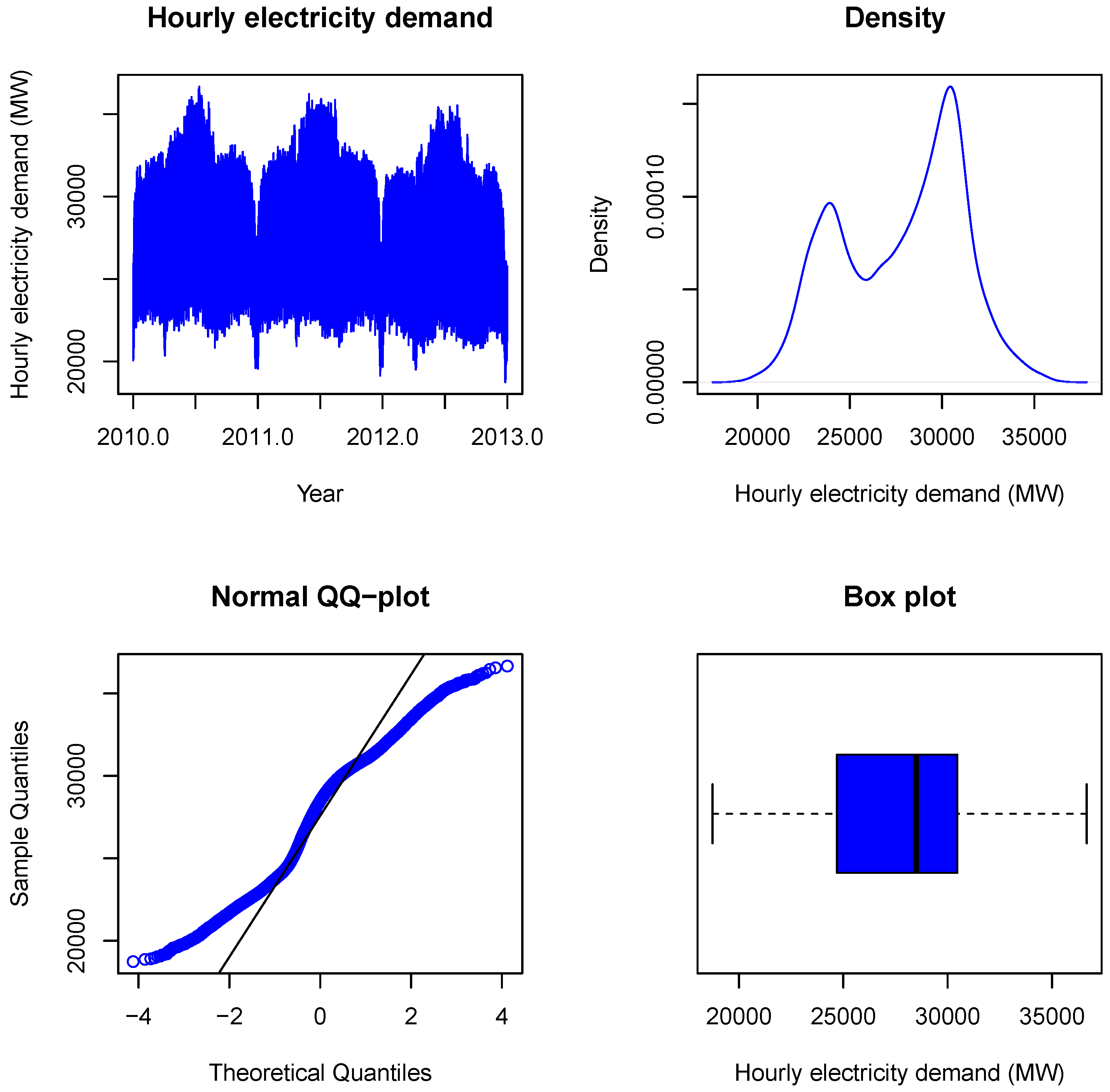
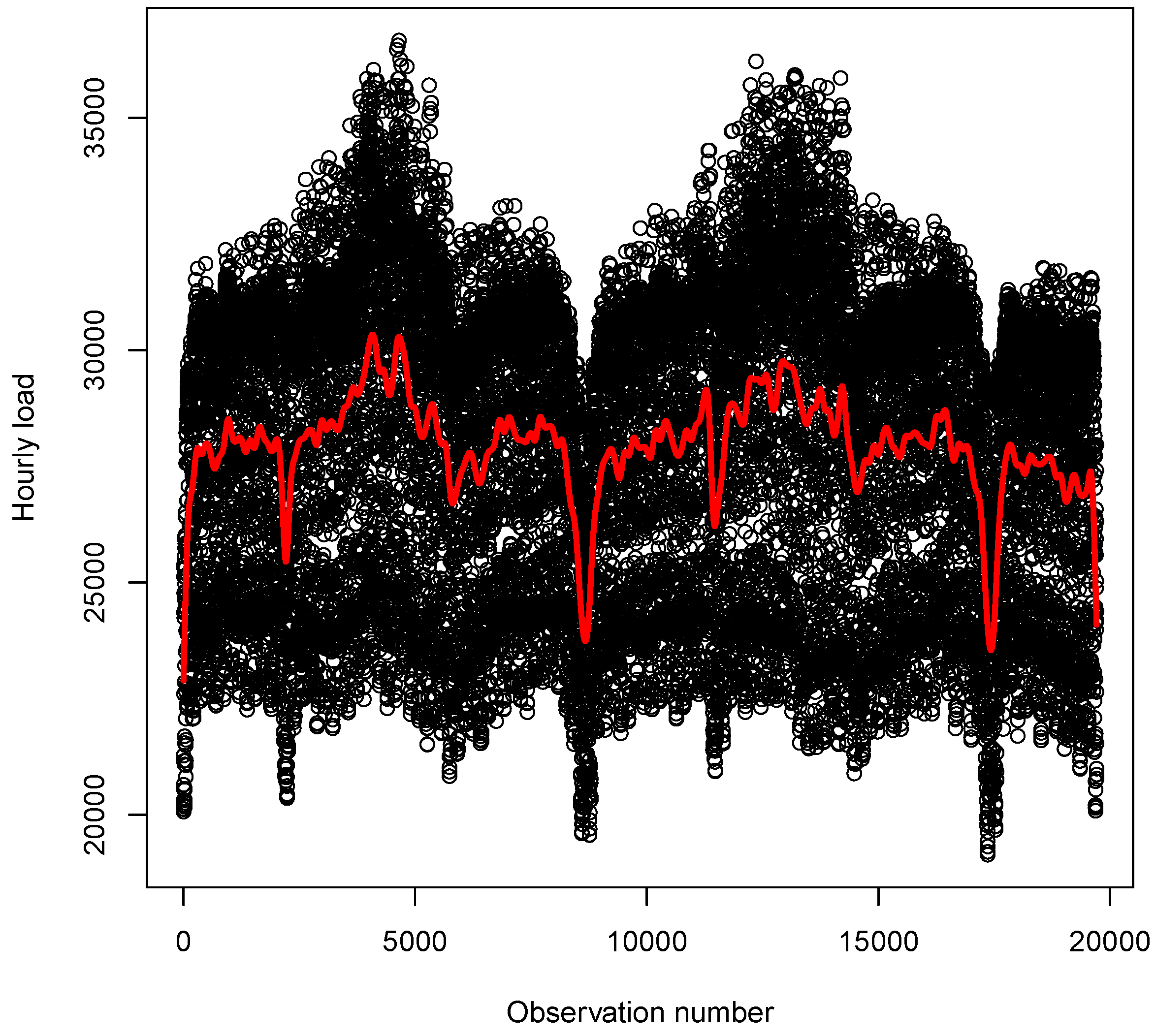


| Descriptive Statistics | Mean | Median | Max | Min | St. Dev. | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Load | 27,798 | 28,496 | 36,664 | 18,739 | 3337 | −0.2433 | 2.050 |
| RMSE | 736.2 | 662.4 | 731.5 | 648.8 | 596.1 | 577.7 |
| MAE (NW) | 568.7 | 516.2 | 549.5 | 499.7 | 459.4 | 445.2 |
| MAPE (%) | 2.15 | 1.93 | 2.04 | 1.86 | 1.70 | 1.65 |
| Under predictions | 3319 | 3279 | 3280 | |||
| Over predictions | 3251 | 3291 | 3286 |
| Average Pinball loss | 284.363 | 258.087 | 274.768 | 249.842 | 229.723 | 222.584 |
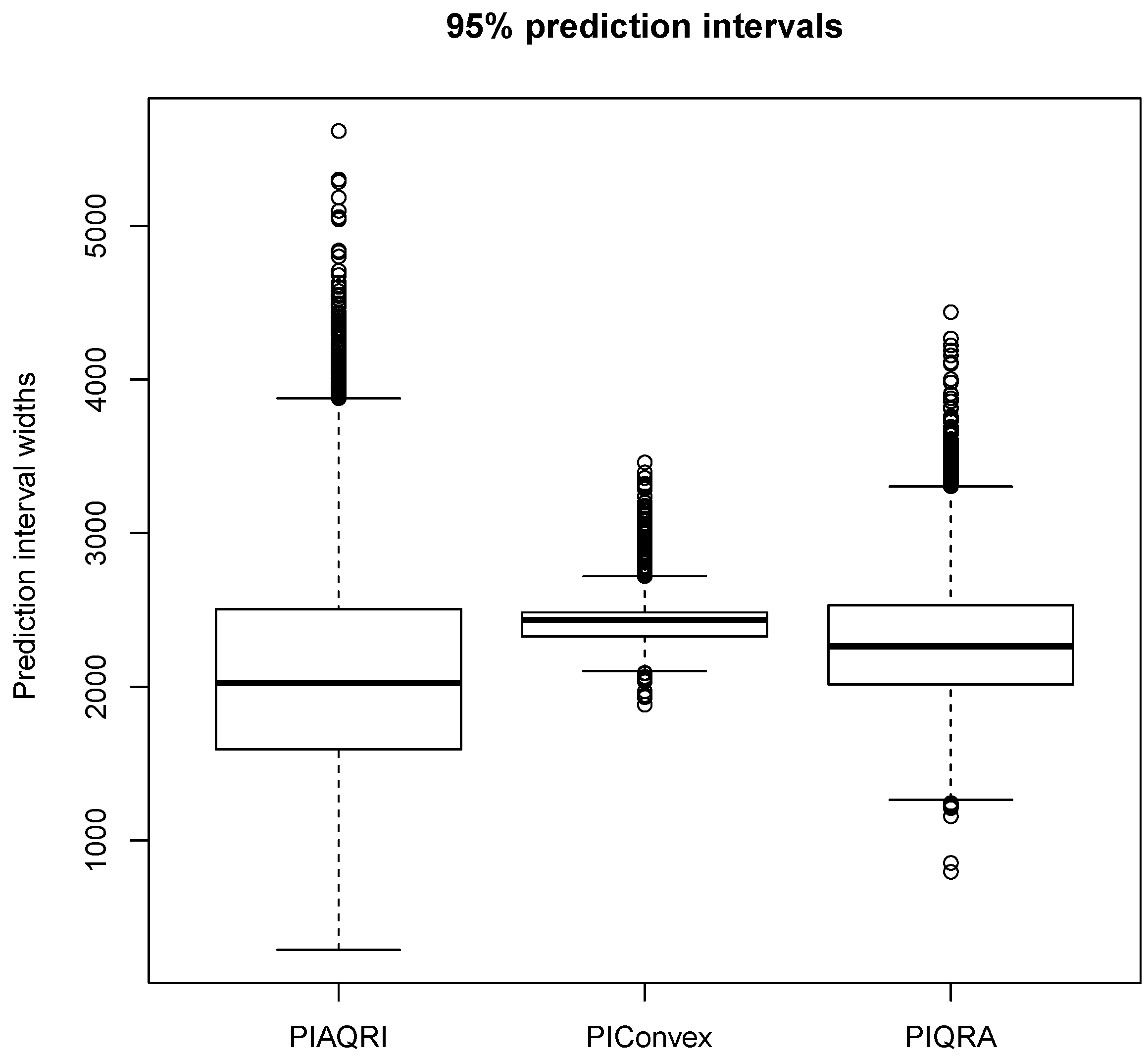
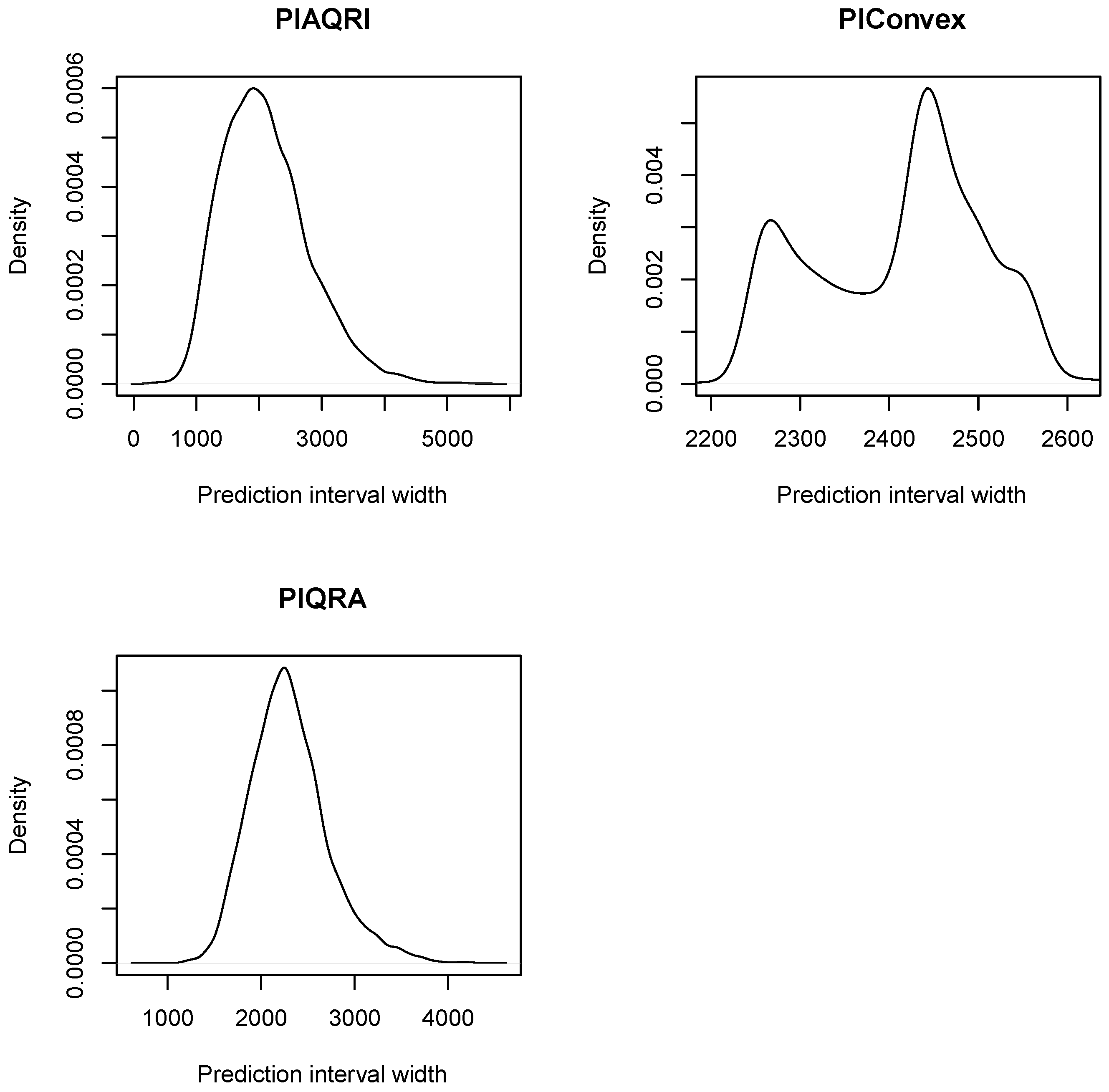
| Mean | Median | Minimum | Maximum | Standard Deviation | Skewness | Kurtosis | Range | |
|---|---|---|---|---|---|---|---|---|
| 2100.9 | 2023 | 287 | 5617 | 686.98 | 0.7256 | 3.7217 | 5330 | |
| 2419.1 | 2435 | 1883 | 3560 | 117.72 | 1.4898 | 12.3368 | 1667 | |
| 2300.0 | 2263 | 795 | 4438 | 418.11 | 0.6776 | 4.0304 | 3643 |
| PINC | Model | PICP (%) | PINAW (%) | PINAD (%) | Below LL | Above UL |
|---|---|---|---|---|---|---|
| 84.41 | 10.63 | 0.2353 | 462 | 563 | ||
| 90.46 | 11.73 | 0.1671 | 310 | 317 | ||
| 90.80 | 11.07 | 0.1347 | 301 | 304 | ||
| 91.19 | 12.52 | 0.1186 | 236 | 343 | ||
| 95.16 | 14.41 | 0.0756 | 156 | 162 | ||
| 95.31 | 13.70 | 0.0573 | 151 | 157 | ||
| 97.35 | 16.43 | 0.03127 | 36 | 138 | ||
| 99.1 | 19.87 | 0.0110 | 30 | 31 | ||
| 99.22 | 17.75 | 0.005986 | 31 | 20 |
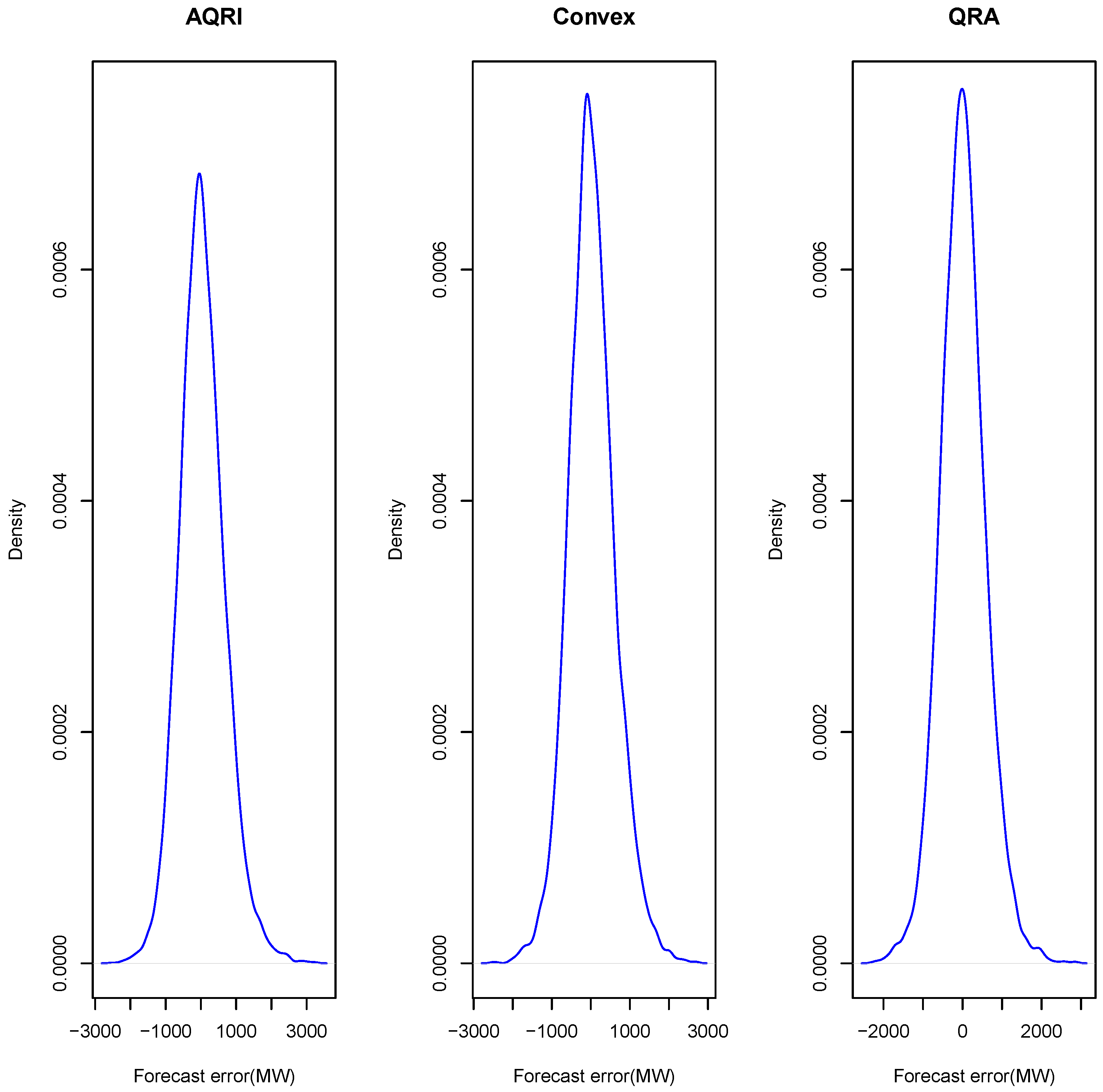
| Mean | Median | Minimum | Maximum | Standard Deviation | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|
| 44.16 | 7 | −2507 | 3258 | 647.36 | 0.3761 | 3.9266 | |
| 28.55 | −1 | −2520 | 2690 | 595.49 | 0.2442 | 3.7702 | |
| 14.98 | 0 | −2273 | 2860 | 577.56 | 0.1997 | 3.9223 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigauke, C.; Nemukula, M.M.; Maposa, D. Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models. Energies 2018, 11, 2208. https://doi.org/10.3390/en11092208
Sigauke C, Nemukula MM, Maposa D. Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models. Energies. 2018; 11(9):2208. https://doi.org/10.3390/en11092208
Chicago/Turabian StyleSigauke, Caston, Murendeni Maurel Nemukula, and Daniel Maposa. 2018. "Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models" Energies 11, no. 9: 2208. https://doi.org/10.3390/en11092208
APA StyleSigauke, C., Nemukula, M. M., & Maposa, D. (2018). Probabilistic Hourly Load Forecasting Using Additive Quantile Regression Models. Energies, 11(9), 2208. https://doi.org/10.3390/en11092208






