Low Cost Position Controller for Exhaust Gas Recirculation Valve System
Abstract
:1. Introduction
2. Mechanical Model of EGR Valve and Torque Measurement
2.1. Model Analysis of EGR Valve
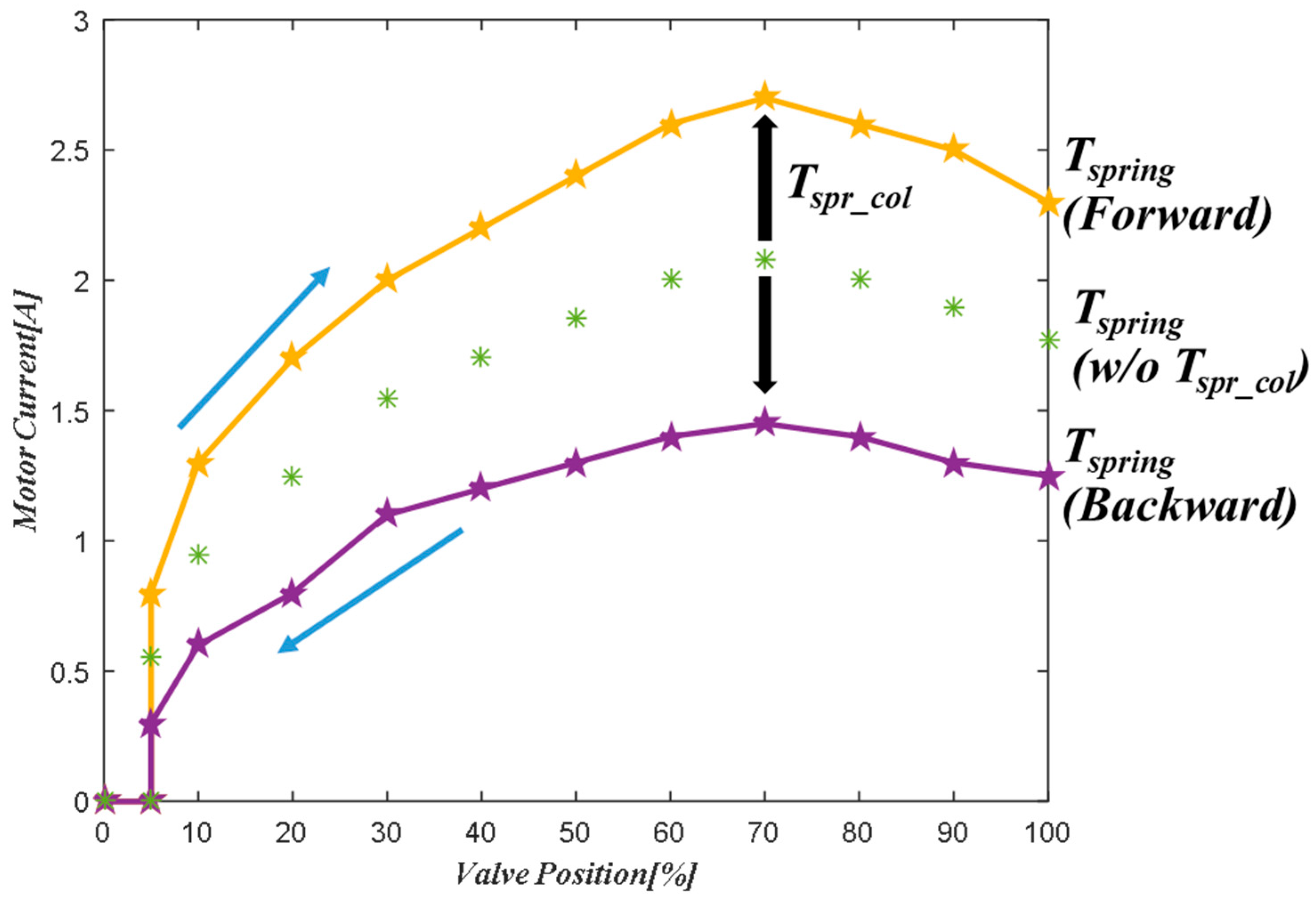
2.2. Measurement Procedures of Spring and Friction Torque
- Perform speed control on the initial EGR valve position.
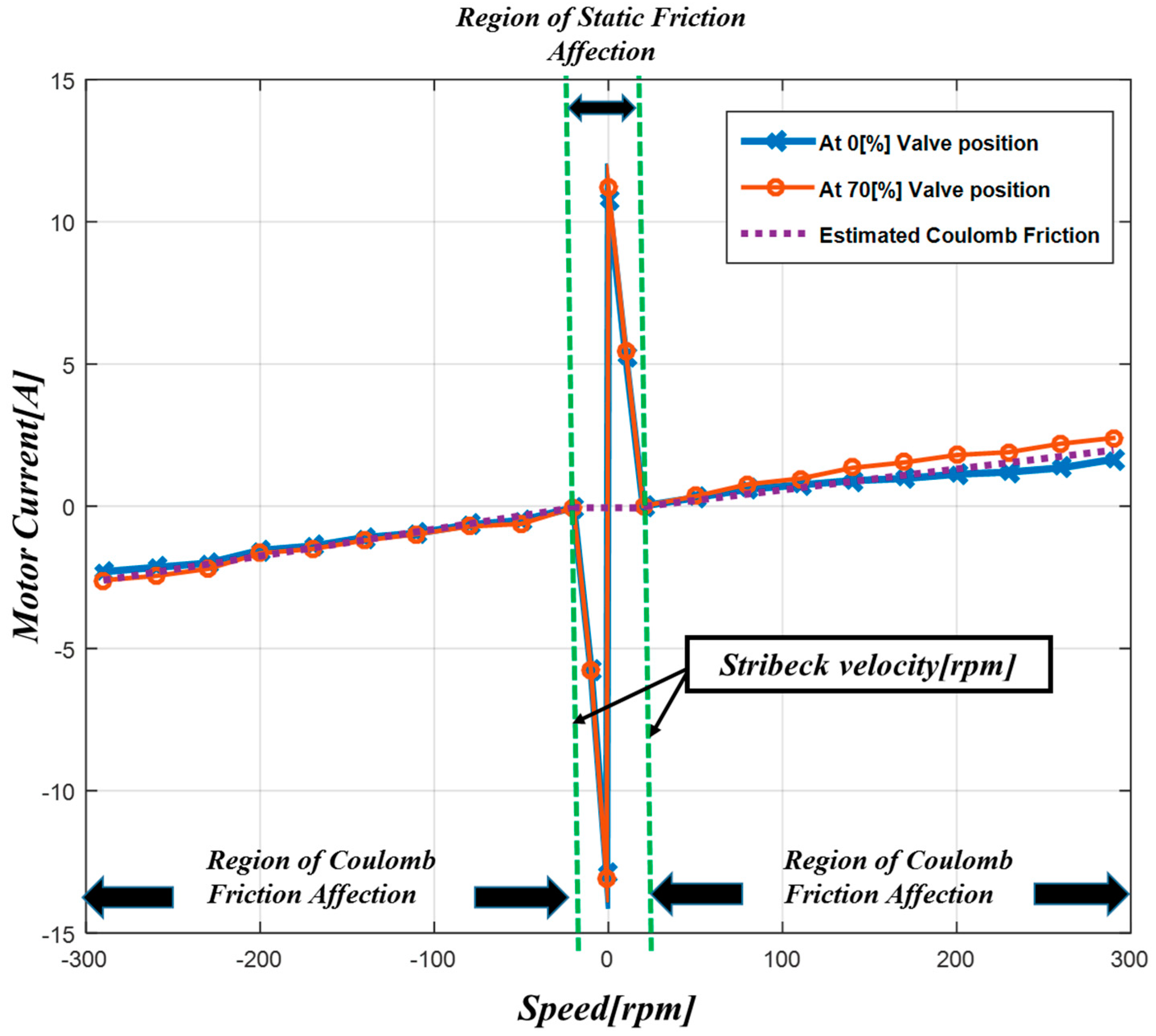
- Apply the speed reference from 10 rpm to 300 rpm.
- Measure the averaged current. The speed at which the lowest averaged current is observed is the Stribeck velocity. Repeat the experiment as necessary for gathering data.
- Control the motor using Stribeck velocity. The measured instantaneous current on steady state is the spring torque, with the assumption that the friction torque at Stribeck velocity can be ignored.
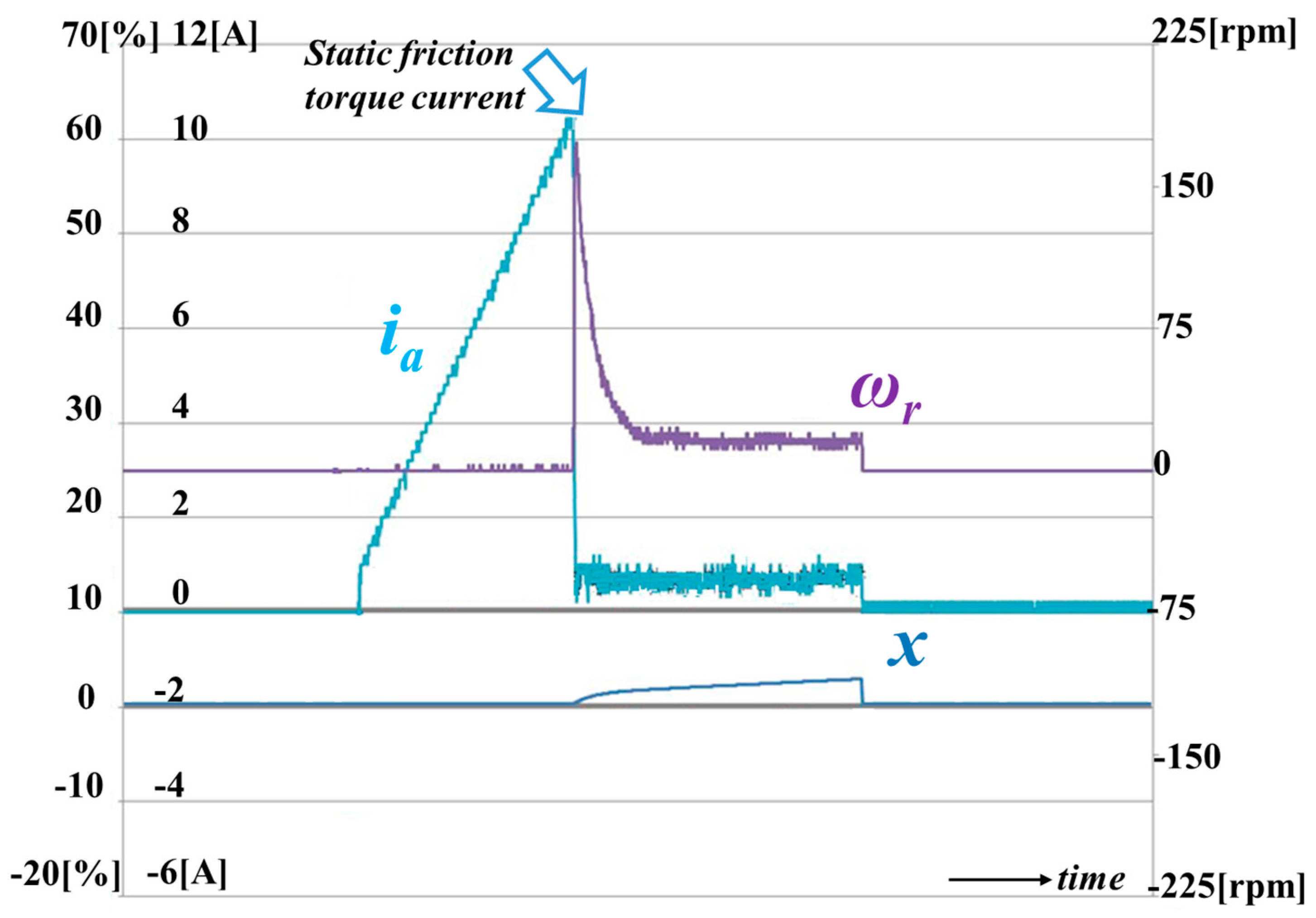
- Perform speed control started on each EGR valve position.
- Set up the small gain on the current controller in order to apply the ramp increasing current reference.
- Sudden current changes occur due to the position of the movement; measure the peak current point.
- Subtract the spring torque amount from the measurement in Step 3. The remaining value is the static friction torque.
- Perform speed control started on the initial EGR valve position.
- Apply the speed reference from 100 rpm and 300 rpm.
- Measure the instantaneous current on the steady state of each speed.
- Subtract the instantaneous current at 100 rpm from the current at 300 rpm.
- Divide 200 rpm from the result of Step 4 for removing the spring torque component.
- Multiply the speed from the result obtained in Step 5. This is the coulomb friction torque.
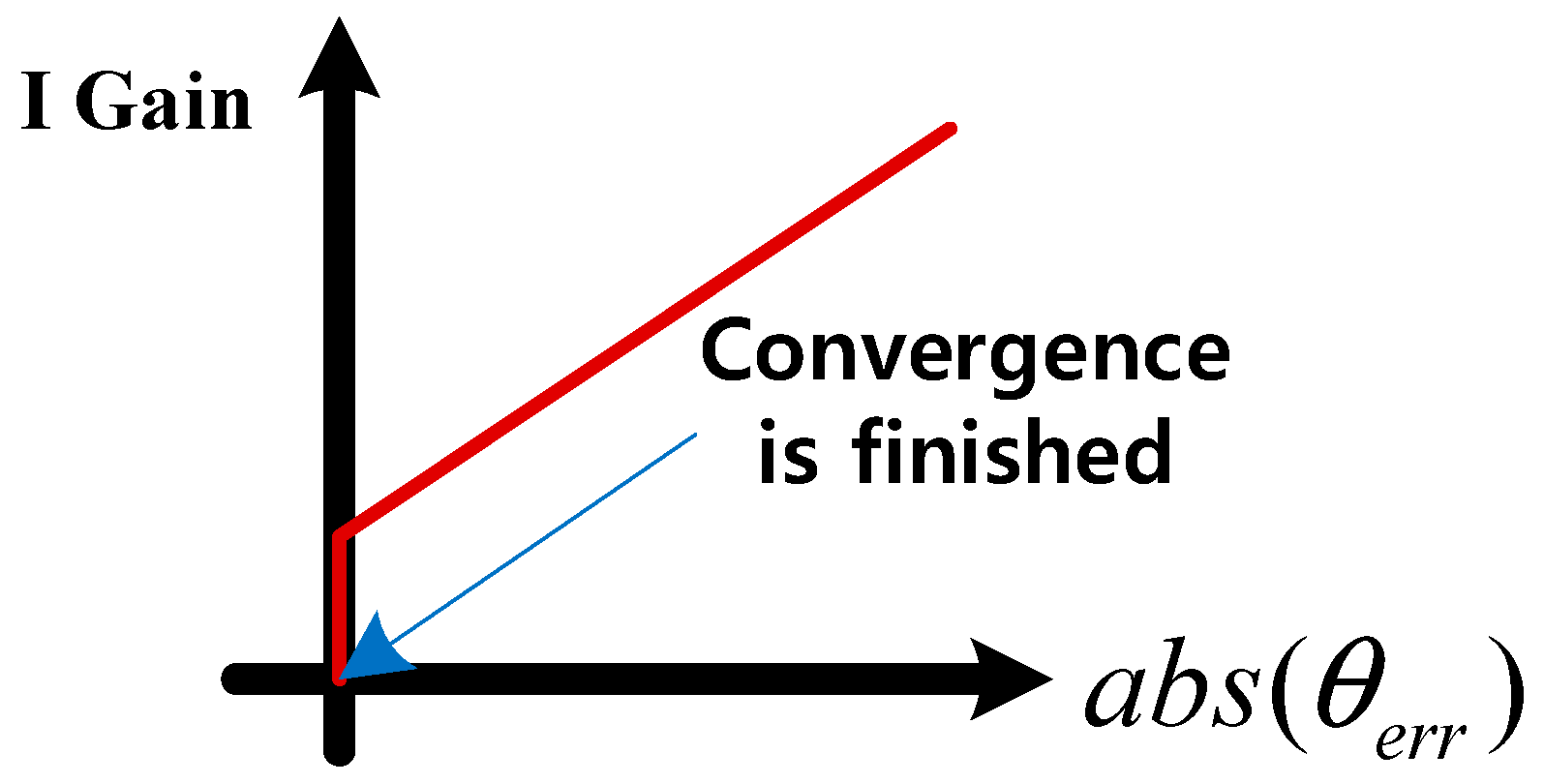
3. Proposed Position Controller
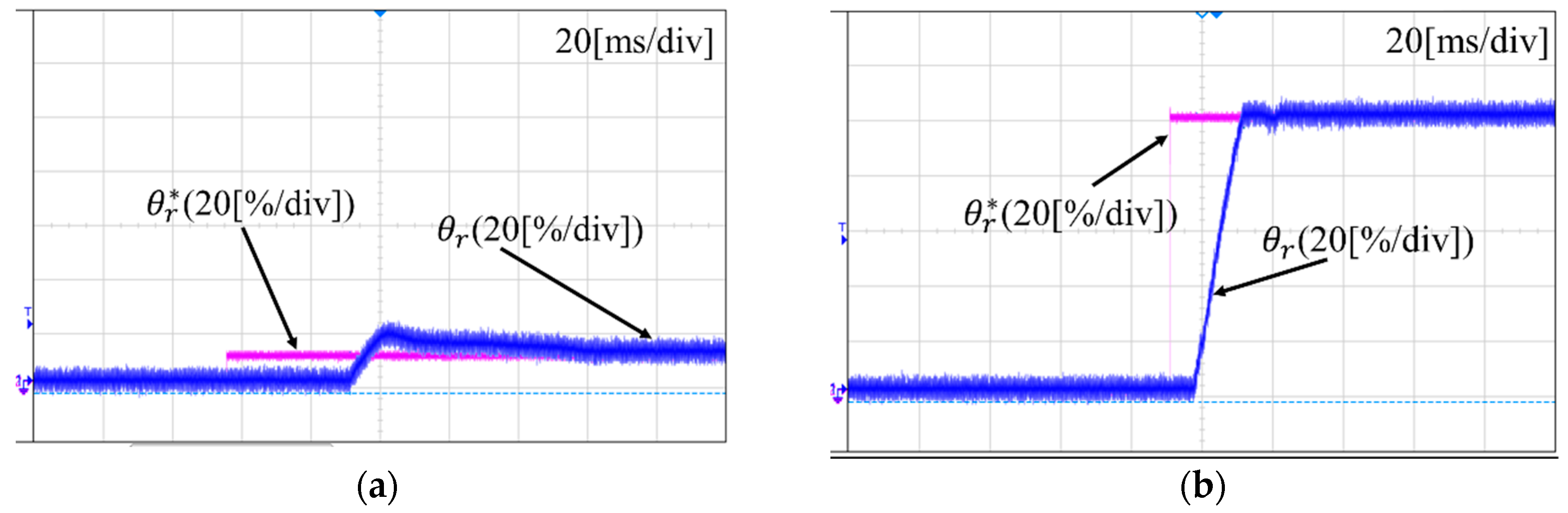
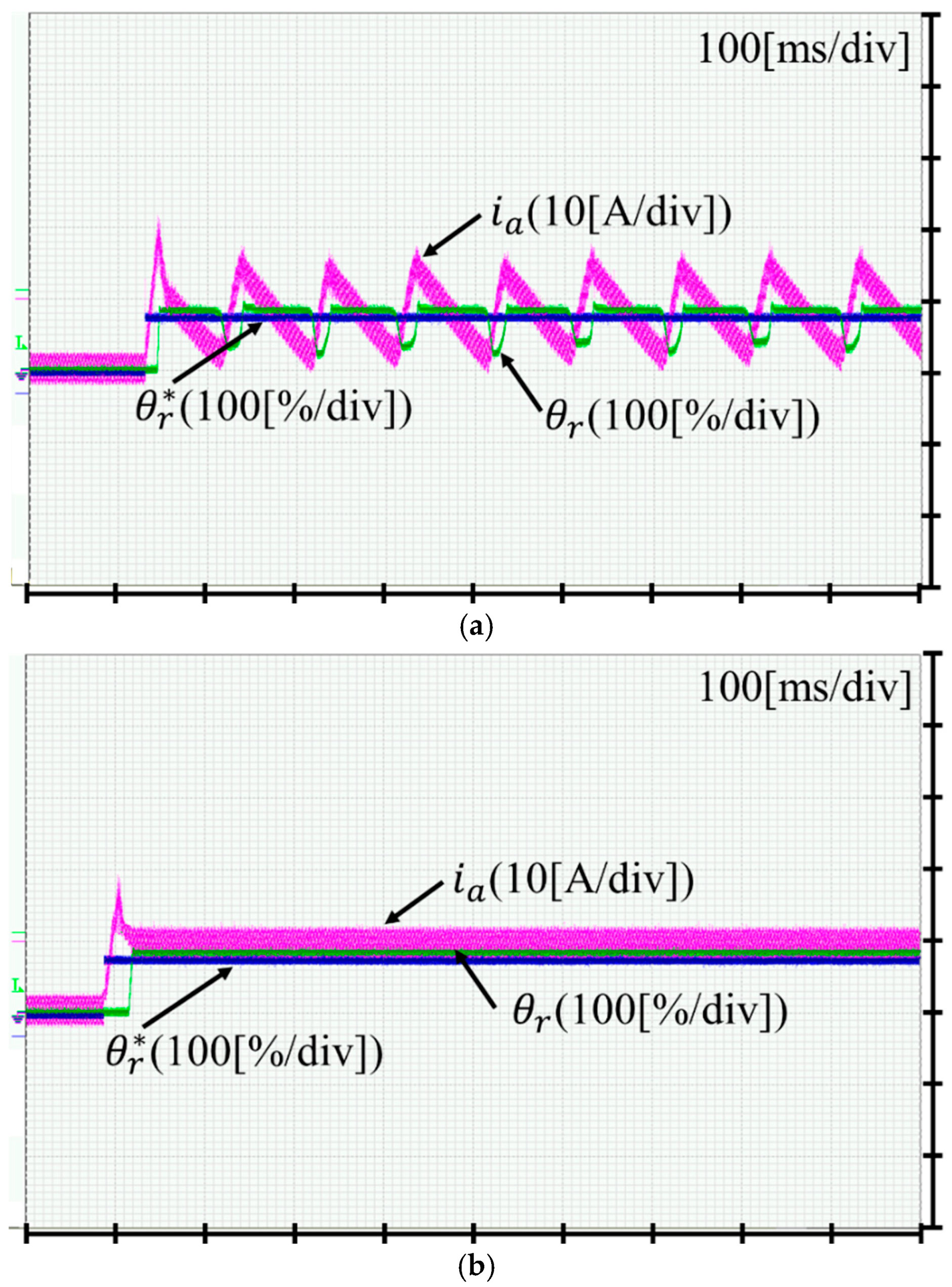
4. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Murtaza, G.; Butt, Y.A.; Bhatti, A.I. Higher Order Sliding Mode Based Control Scheme for Air Path of Diesel Engine. In Proceedings of the 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 18–19 October 2016. [Google Scholar]
- Chen, S.K.; Yanakiev, O. Transient NOx Emission Reduction Using Exhaust Oxygen Concentration Based Control for a Diesel Engine; SAE Technical Paper No. 2005-01-0372; Ford Motor Company: Dearborn, MI, USA, 2005. [Google Scholar]
- Heywood, J.B. Internal, Combustion Engine Fundamentals; McGraw-Hill Book Co.: New York, NY, USA, 1998. [Google Scholar]
- Zheng, M.; Reader, G.T.; Hawley, J.G. Diesel engine exhaust gas recirculation—A review on advanced and novel concepts. Energy Convers. Manag. 2004, 45, 883–900. [Google Scholar] [CrossRef]
- Seo, E.-S.; Shin, H.-B. Modeling of EGR Valve Actuator. Trans. KIPE 2017, 22, 390–396. [Google Scholar]
- Kim, D.T.; Zhang, Z.J. Position Control of a Pneumatic Cylinder Considering Friction Compensation. J. Drive Control 2013, 10, 1–6. [Google Scholar] [CrossRef]
- Byun, J.H. A Study on the Position Control of a Motor Cylinder with Nonlineal Friction. J. Korean Soc. Power Syst. Eng. 2008, 12, 80–86. [Google Scholar]
- Chopra, S.; Mitra, R.; Kumar, V. Reduction of Fuzzy Rules and Membership Functions and Its Application to Fuzzy PI and PD Type Controllers. Int. J. Control Autom. Syst. 2006, 4, 438–447. [Google Scholar]
- Ni, Z.; Wang, M. Research on the fuzzy neural network PID control of load simulator based on friction torque compensation. In Proceedings of the Sixth International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2014; pp. 292–295. [Google Scholar]
- Yao, J.; Deng, W.; Jiao, Z. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- Kim, H.J.; Park, H.S.; Heo, H.J.; Kim, J.M. Improvement of Position Control Performance of EGR Valve System with Low Control Frequency. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 394–399. [Google Scholar]
- Oh, B.G.; Lee, M.K.; Park, Y.S.; Lee, K.Y.; Sunwoo, M.H.; Nam, K.H.; Cho, S.H. Feedforward EGR Control of a Passenger Car Diesel Engine Equipped with a DC Motor Type EGR Valve. Trans. KSAE 2011, 19, 14–21. [Google Scholar]
- Lee, H.S.; Tomizuka, M. Robust Motion Controller Design for High Accuracy Position Systems. IEEE Trans. Ind. Electron. 1996, 43, 48–55. [Google Scholar]




| Parameter | Value | Unit |
|---|---|---|
| Rated power | 200 | W |
| Input voltage | 12 | V |
| Max. current | 20 | A |
| Rated speed | 500 | rpm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhuiyan, H.; Lee, J.-H. Low Cost Position Controller for Exhaust Gas Recirculation Valve System. Energies 2018, 11, 2171. https://doi.org/10.3390/en11082171
Bhuiyan H, Lee J-H. Low Cost Position Controller for Exhaust Gas Recirculation Valve System. Energies. 2018; 11(8):2171. https://doi.org/10.3390/en11082171
Chicago/Turabian StyleBhuiyan, Habib, and Jung-Hyo Lee. 2018. "Low Cost Position Controller for Exhaust Gas Recirculation Valve System" Energies 11, no. 8: 2171. https://doi.org/10.3390/en11082171
APA StyleBhuiyan, H., & Lee, J.-H. (2018). Low Cost Position Controller for Exhaust Gas Recirculation Valve System. Energies, 11(8), 2171. https://doi.org/10.3390/en11082171




