Abstract
This paper summarizes the results of the flow boiling heat transfer study with ethanol in a 1.8 mm deep and 2.0 mm wide horizontal, asymmetrically heated, rectangular mini-channel. The test section with the mini-channel was the main part of the experimental stand. One side of the mini-channel was closed with a transparent sight window allowing for the observation of two-phase flow structures with the use of a fast film camera. The other side of the channel was the foil insulated heater. The infrared camera recorded the 2D temperature distribution of the foil. The 2D temperature distributions in the elements of the test section with two-phase flow boiling were determined using (1) the Trefftz method and (2) the hybrid Picard–Trefftz method. These methods solved the triple inverse heat conduction problem in three consecutive elements of the test section, each with different physical properties. The values of the local heat transfer coefficients calculated on the basis of the Robin boundary condition were compared with the coefficients determined with the simplified approach, where the arrangement of elements in the test section was treated as a system of planar layers.
1. Introduction
The requirements for the efficiency of heat exchangers are increasing with the development of modern technologies thus spurring a considerable interest in enhanced compact heat exchangers [1]. In single-phase flows, maintaining efficient cooling by means of exchangers with mini-channels requires high liquid flow velocities (turbulent flow). Two-phase flow boiling ensures intensive heat transfer at low flow rates [2]. The advantage of nucleate boiling is that the value of heat transfer coefficient increases with the increase in heat flux and with an inverse dependence on the mass flux. Parallel to the experimental research, theoretical models for boiling in mini-channels have been developed. A series of experimental correlations for predicting local heat transfer coefficient values can be found in References [3,4,5,6]. Nevertheless, considering that the results published in the literature vary substantially and that the correlations proposed do not ensure satisfactory results, more research on flow boiling heat transfer in mini-channels is still required.
This study describes two-phase flow boiling experiments with ethanol in a rectangular mini-channel. The preset inlet thermal and flow parameters (fluid pressure and temperature, volumetric flow rate, the heat flux generated by the heater), outlet fluid temperature and pressure, temperature distribution on the heater external surface, and void fraction measurements provided data for numerical computations. The distribution of void fraction in the mini-channel two-phase flow was obtained from high-speed camera images. Thermograms of the external heater surface and the external surface in the adiabatic part of the mini-channel allowed producing temperature profiles along the channel length. The read out and computed parameters were then used to solve inverse heat conduction problems.
Modern research often diverges from experiments in favor of numerical simulations based mainly on commercial software, where experimental results only serve to validate numerical calculations, as in References [7,8]. The lack of generally accepted prediction techniques causes researchers to continue looking for effective methods of solving heat transfer problems in flow boiling in mini-channels. In this study, two methods based on the Trefftz functions: (1) the Trefftz method and (2) the hybrid Picard–Trefftz method were used to determine the two-dimensional temperature of three elements of a mini-channel. The Trefftz method, belonging to the class of semi-analytical methods, was originally proposed in 1926 by E. Trefftz [9] for solving linear partial differential equations. The method has been subsequently expanded by many scientist, e.g., References [10,11,12] with a focus mostly on stationary problems. The theoretical foundations and advancement of the Trefftz method are presented in References [13,14]. The Trefftz method has been used in combination with other methods such as the Finite Element Method (FEM) [15], the homotopy perturbation method [16], Beck’s method [17] and the radial basis functions method [18].
In this paper, Trefftz functions were used to solve a triple coupled inverse heat conduction problem (IHCP) in forced flow boiling in a rectangular asymmetrically heated mini-channel. The experiment aimed to describe low Reynolds number flows (for Re between 17 and 51), thus, it seemed reasonable to assume the laminarity of the flow. All data were taken under stable stationary inlet conditions. After each change of the inlet parameters, such as the volume flow rate, inlet pressure, inlet liquid temperature, and electric current supplied to the heater, new data were taken after a certain period of time necessary to observe stable values of the recorded parameters.
The temperature distributions in the boiling liquid, heating foil, and insulating foil were described with the energy equation, Poisson equation, and Laplace equation, respectively. For all these elements the boundary conditions corresponding to the observed physical process were indicated. Inverse problems in the three adjacent regions with different physical parameters were considered. The Trefftz method was used to obtain the 2D temperature distributions of the two mini-channel elements (the insulating foil and the heater). Two-dimensional fluid temperatures were calculated with the use of the hybrid Picard–Trefftz method. The heat transfer coefficient at the heater-liquid interface was determined based on the Robin boundary condition. Local values of the heat transfer coefficient calculated with Picard–Trefftz method were compared with the values obtained with a simplified 1D approach.
2. Experiment
2.1. Experimental Stand
Figure 1 shows both a photo and a schematic view of the experimental setup.
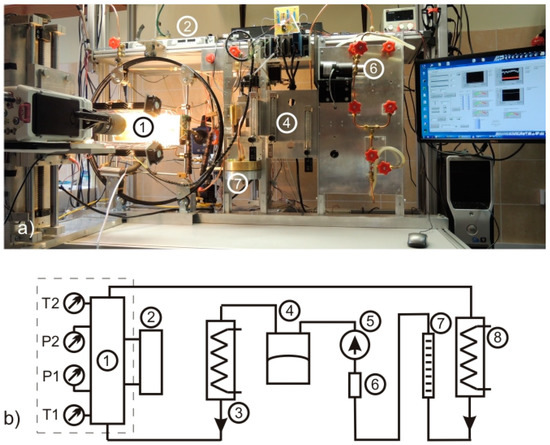
Figure 1.
(a) A view of the experimental stand; (b) Flow loop: ①: test section with the mini-channel (described in detail in Figure 2), ②: DC power supply, ③: preheater, ④: pressure control, ⑤: pump, ⑥: filter, ⑦: rotameter, and ⑧: cooler.
The main element of the system is the test section containing a milled 193 mm long, 1.8 mm deep, and 2 mm wide mini-channel with a hydraulic diameter of 1.89 mm and a cross-sectional area of 3.6 mm2 (Figure 2). The mini-channel is closed on one side with a transparent sight window for recording flow images with a high-speed camera (Phantom 711, Vision Research Company, Wayne, NJ, USA); Figure 2. The second wall of the channel is a flat DC powered Kanthal resistance strip heater, 0.1 mm thick and 93 mm long (Figure 1). The heater is insulated with a 0.18 mm thick 3M Scotch Super 33+ electrical tape, in which the two-dimensional temperature distribution was recorded using the infrared camera (Figure 2). The test section is also equipped with sensors for pressure and temperature measurements (Figure 1). The liquid of the preset temperature enters the mini-channel and is heated while flowing through the heater. Upon leaving the mini-channel it is directed to the cooler, then to the rotameter and through a filter to a precision micropump (Figure 1). The micropump pushes the liquid into a diaphragm pressure generator in which a thin rubber diaphragm separates the compressed air from the liquid (Figure 1). In order to avoid heating the flowing liquid within the candescent light, customized LED lighting was developed (Figure 2).
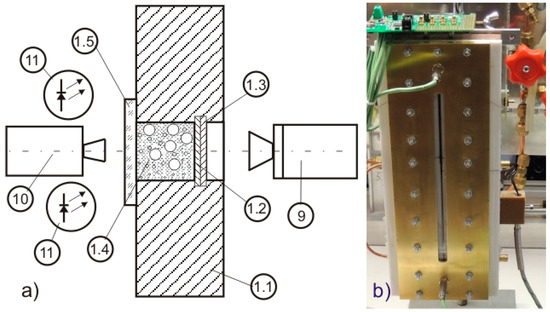
Figure 2.
(a) The cross-section of the test section with the mini-channel and the position of the infrared camera and high-speed camera and lighting.  : the hub;
: the hub;  : the heater;
: the heater;  : the insulating foil;
: the insulating foil;  : the mini-channel with flowing liquid;
: the mini-channel with flowing liquid;  : the glass lid covered the mini-channel; ⑨: an infrared camera; ⑩: a high-speed camera; ⑪: the LED lights. (b) The view of the mini-channel.
: the glass lid covered the mini-channel; ⑨: an infrared camera; ⑩: a high-speed camera; ⑪: the LED lights. (b) The view of the mini-channel.
 : the hub;
: the hub;  : the heater;
: the heater;  : the insulating foil;
: the insulating foil;  : the mini-channel with flowing liquid;
: the mini-channel with flowing liquid;  : the glass lid covered the mini-channel; ⑨: an infrared camera; ⑩: a high-speed camera; ⑪: the LED lights. (b) The view of the mini-channel.
: the glass lid covered the mini-channel; ⑨: an infrared camera; ⑩: a high-speed camera; ⑪: the LED lights. (b) The view of the mini-channel.
For the purpose of this experiment, the mini-channel was split into three domains corresponding to the heat supply method used (Figure 3). In the ΩI domain, the heat supplied to the liquid was generated by the electric heater. Due to design reasons, it was not possible to record the temperature field in the insulating foil of the ΩII domain. The ΩIII domain was quasi-adiabatic and all thermal and flow parameters were recorded there, just as in ΩI.
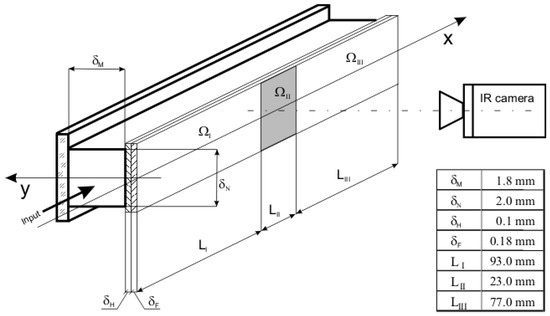
Figure 3.
The characteristic dimensions of the mini-channel.
The data were read and recorded using the measurement and control system based on the National Instruments modules (Figure 4). The main module was the NIcDAQ-9178 (National Instruments Corporation, Austin, TX, USA) in which ancillary modules were installed to measure process parameters and to control components such as a pump, lighting, a camera trigger, etc. The following modules were used:
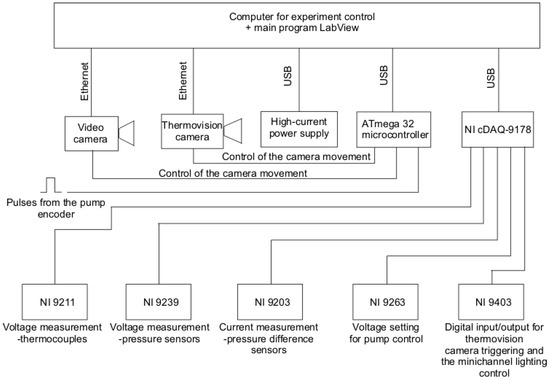
Figure 4.
The block diagram of the experimental stand control system.
- NI cDAQ-9178: main module,
- NI 9211: temperature measurement (Czaki TP-201 type K thermocouples, Czaki Thermo-Product, Pruszków, Poland),
- NI 9239: voltage measurement (Kobold pressure gauges, 0–2.5 bar measurement range),
- NI 9203: current measurement (Kobold pressure drop gauge, 0–2.5 bar),
- NI 9263: adjustment of voltage to control the pumps,
- NI 9403: digital input/output to control mini-channel lighting and to trigger the thermal imaging camera.
The main module communicated with the computer for experiment control computer via USB. The experimental stand was controlled by software developed in the LabView environment, chosen due to its versatility and full support of the control and measurement modules. The cameras were shifted using a specially constructed for this purpose module based on the ATmega 32 microprocessor (Atmel Company, San Jose, CA, USA) and controlled by dedicated software developed in the BASCOM environment (MCS Electronics, Almere, The Netherlands).
2.2. Experimental Results
The experimental setup thoroughly described in Reference [19] was designed to study the flow of the liquid at a set rate and the temperature and pressure at the inlet to the mini-channel; to heat the liquid in the mini-channel to the set temperature; to measure and record the temperature and pressure at the inlet and outlet of the mini-channel, the liquid volumetric flow rate, and the electric current supplied to the heating foil; and to record the flow structures and two-dimensional temperature distributions on the outer surface of the insulation foil. The tests included the determination of the influence of the volumetric flow rate and heat flux changes on the change in the liquid temperature along the mini-channel from the temperature at the outlet to the temperature at the mini-channel inlet. Observations of the two-phase flow structures helped determine the void fraction (Figure 5). The method of determining the void faction was described in detail in Reference [20].
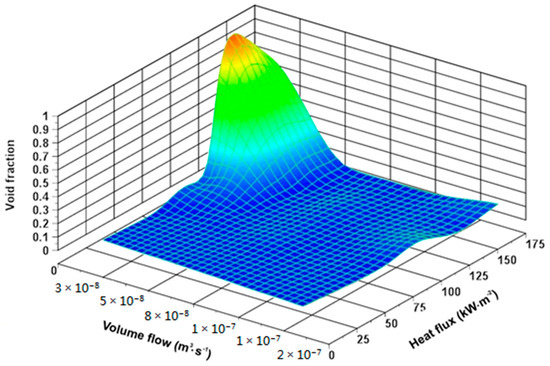
Figure 5.
The void fraction versus volumetric flow rate and heat flux.
This method is based on the script developed in a Matlab 2012 environment (MathWorks, Natick, MA, USA) that uses two toolboxes: Computer System Vision and Image Processing Toolbox 2012 (MathWorks, Natick, MA, USA). The script enables the following operations: image analysis, object segmentation, image enhancement by sharpening and noise reduction, and geometric transformations, as well as object detection and spatial dimensions determination, which subsequently lead to the designation of the void fraction in the mini-channel.
3. Mathematical Model and Methods
The 2D mathematical model included the assumption that the flow was laminar and that the physical parameters of the measurement module were time independent. Their changes in the insulating foil, heating surface, and liquid were assumed to be minor across the mini-channel width [19].
Two dimensions perpendicular to each other were factored in the model: dimension x in the direction of two-phase flow and dimension y referring to the foil thickness, to the heater and to the depth of the mini-channel (Figure 6). Further, in the article, only the central part of the test section along its length will be considered. Due to the design of the test section (Figure 6), the heat transfer mathematical model was built for the first domain, ΩI, containing the heater. The temperature of the insulating foil TF and the temperature of the heater TH were assumed to satisfy Laplace’s equation and Poisson’s equation, respectively
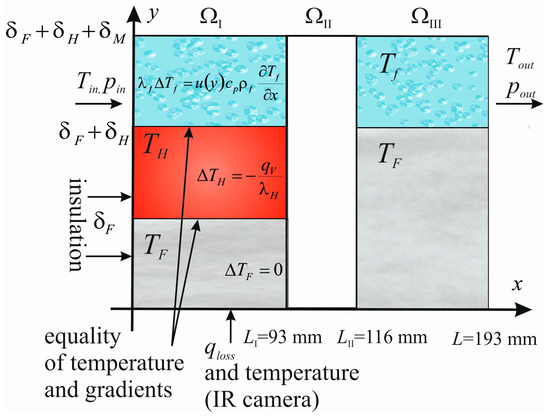
Figure 6.
The test section and its schematic, illustrating the underlying model assumptions, (pictorial view, not to scale).
For Equations (1) and (2), the following boundary conditions were adopted:
where the heat loss qloss was determined following the procedure given in Reference [15]. The insulating foil layers and the heater were considered to be in perfect thermal contact, i.e.,
The fluid temperature in the domain satisfied the energy equation
Adequate boundary conditions were adopted for Equation (9) [21]:
- A steady-state and laminar (Re < 2000) fluid flow in the mini-channel, with a constant volumetric flow rate;
- For 0 ≤ x ≤ LI, the liquid temperature in contact with the heater is equal to the saturation temperature, i.e., Tf = Tsat where the Tsat was determined by analogy to Reference [21];
- For the considered flow structures, i.e., the bubbly and bubbly-slug flow, the heat flux is transferred from the heater to the liquid phase in the proportion relative to the void fraction
- One non-zero component of the liquid velocity u(y) is parallel to the flow direction and satisfies the following condition
- The liquid temperature at the inlet of the mini-channel, Tin, is known and for x = LI, it satisfies the condition
The heat transfer coefficient at the heater-liquid interface was determined using the boundary condition of the third kind:
The reference temperature Tave was the average liquid temperature along the mini-channel depth
3.1. Hybrid Picard–Trefftz Method
Two-dimensional approximations of the insulating foil and the heater temperatures were calculated by the Trefftz method by analogy to Reference [22]. The unknown solutions of Equations (1) and (2) were approximated by a linear combination of the Trefftz functions (the harmonic polynomials in this case). The coefficients of a linear combination were to be determined so that the approximate solutions would satisfy the boundary conditions (Equations (3)–(8)) in the least-squares sense as in References [15,19,21,22,23,24].
Equation (9) was solved with a combination of the Picard and Trefftz method. This equation with the adequate boundary conditions can be written using operator notation
where differential operator N is defined as
and operator B describes the boundary conditions that are satisfied by the function Tf at the boundary ∂ΩI,f of the domain. Generally, the operator N can be non-linear and the procedure of determining the solution of Equation (9) can be applied to determining the solutions of non-linear differential equations [23].
The following procedure, supported by the Picard iterations, was used to approximate the solutions to Equation (15):
- In the first step, for k = 1:
- In subsequent steps, for k > 1:
In each consecutive step, the approximate solutions to Equations (18) and (20) were found using the Trefftz method, expressed in the following form
Function is a particular solution to the Poisson’s Equation (20), and for Equation (18), the particular solution . To find the particular solution , the Taylor series expansion of is used (expansion about point (0, 0) for simplified representation). Then the particular solution (for k = 2, 3, …) is found based on the formula
where, for the monomials in the Taylor series of the function , operator Δ−1 is defined by the formula
The coefficients of the linear combinations in Equation (22) were determined based on the adopted boundary conditions, following the method described in References [22,24].
3.2. One-Dimensional Approach
In order to verify the results of the hybrid Picard–Trefftz method, the heat transfer coefficient was determined by adopting additional simplifications. It was assumed that Equations (3), (4) and (7) and the heat flux transferred to the fluid by the heater were constant, i.e.,
Individual elements of the test section create a system of planar layers with different thicknesses and thermal conductivity. Since the thickness of the insulating foil and that of the heater are very small, it was possible to replace the partial derivatives in Equations (4) and (25) with a finite difference
Combining Equations (3), (7), (26) and (27) the following formula was obtained for the heater temperature at the boundary y = δF + δH:
Then the heat transfer coefficient at the heater-ethanol contact could be determined using the following condition
4. Results and Discussion
Numerical calculations were performed for the experimental data acquired for ethanol under two-phase flow conditions in the asymmetrically heated mini-channel. Measurements of the insulating foil temperature based on the data from the thermal imaging camera (Figure 7a) were approximated by a third-degree polynomial (Figure 7b). The void fraction determined in the manner described in Reference [20] at distances of 0 mm, 20 mm, 40 mm, 80 mm from the mini-channel inlet was also approximated by a polynomial (Figure 7c).
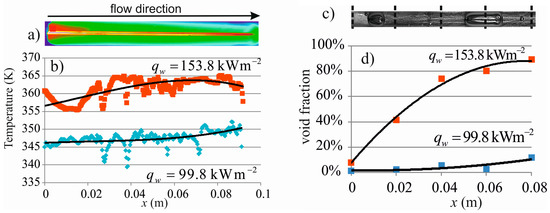
Figure 7.
(a) The thermogram example image; (b) the foil surface temperature field from the IR camera FLIR SC 7600 (FLIR Systems, Wilsonville, OR, USA) approximated using a third degree polynomial; (c) the flow structures; (d) the void fraction for qw = 99.8 kW m−2 and qw = 153.8 kW m−2.
Numerical calculations were made for the following experimental data: an inlet pressure 1.1 kPa (average), a liquid temperature at the inlet 308 K (average), a mass flow 21 kg m−2 s−1, and six heat flux densities in the range of 99.8–153.8 kW m−2. In the first place, 2D temperature distributions in the insulating foil and in the heater were determined using the Trefftz method with six Trefftz functions. In the next stage, the hybrid Picard–Trefftz method was used to determine the 2D liquid temperature distribution with four iterative steps and two harmonic polynomials at each step. The values of the local heat transfer coefficients obtained from Equation (13) based on the hybrid Picard–Trefftz method are shown in Figure 8. The heat transfer coefficients take values from 4000 Wm−2 K−1 to 6000 Wm−2 K−1 and, except one case described below, show low variability along the mini-channel length.
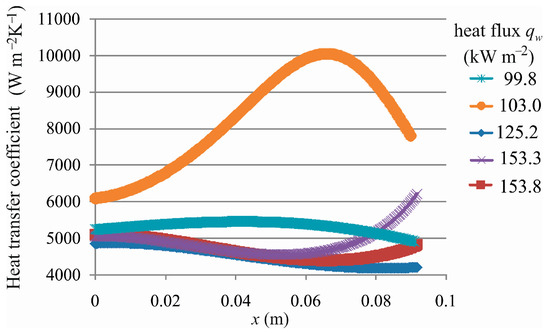
Figure 8.
The heat transfer coefficients for different heat fluxes as a function of the mini-channel length obtained using the hybrid Picard–Trefftz method.
The plot of the heat transfer coefficient variation for qw = 103 kW m−2 is different from the plots of the other functions as the result of low void fraction values. In this case, it was not more than 7% for x = LI, whereas in other cases, it was at least 12% at x = LI. A further increase in the heat flux resulted in an increased void fraction and a reduced heat transfer coefficient. The maximum relative differences (MRD) describing the difference between the heat transfer coefficients, obtained from Equations (13) and (29) were calculated from the formula
where –norm is, in this case, defined as
For all the heat fluxes considered, the maximum relative differences (MRD) ranged from 2.4% to 8.7%. The results obtained using the numerical methods were summarized, compared, and found to be similar. The mean relative error of the heat transfer coefficient α2D was determined from the formula
where, in the calculations, the following were adopted:
- The uncertainty of thermal conductivity: ∆λH = 0.1 Wm−1 K−1 (specified by the manufacturer);
- The accuracy of the foil temperature approximation: and = 10−4 m [25], and the uncertainty of temperature measurement is equal to = 0.55 K (specified by the manufacturer);
- The accuracy of the derivative of the approximate foil temperature with respect to y: ;
- The accuracy of the reference fluid temperature determination:
For the one-dimensional approach, the mean relative errors ε1D of the heat transfer coefficient α1D was calculated by analogy to ε2D. Table 1 compares the mean relative errors of the heat transfer coefficients α2D and α1D for the considered heat fluxes.

Table 1.
The values of the mean relative differences ε1D and ε2D for different heat fluxes.
The values of the mean relative errors ε1D are smaller than those for two-dimensional approach ε2D. The mean relative error ε2D does not exceed 4.54% and ε1D oscillates around 2% (maximum 2.36%). The errors decrease with the increasing heat flux supplied to the heater except for the case of qw = 103.0 kW m−2.
5. Conclusions
The application of numerical methods to the identification of temperature distribution and heat transfer coefficient in the flow boiling of ethanol in a horizontal mini-channel was proposed. The use of (1) the Trefftz method and (2) the hybrid Picard–Trefftz method allowed solving three consecutive heat conduction problems in three different elements of the test section: the insulating foil, the heating foil, and the mini-channel. In the Trefftz method, the approximate temperature of the insulating foil and the heater satisfied the governing differential equation exactly. The boundary conditions were satisfied approximately. The combination of the Picard and Trefftz methods enables finding an approximate solution to the energy equation, where the solution satisfied both the equation and the boundary conditions approximately. The hybrid Picard–Trefftz method allows solving the problems for which Trefftz functions are not known, e.g., non-linear problems. Furthermore, the method uses a small number of Trefftz functions. The mean relative error of the heat transfer coefficient does not exceed 4.54%. The values obtained from the 2D model differ by a maximum of MRD = 8.7% from the 1D approach, where the arrangement of elements in the test section was treated as a system of planar layers. For the 1D approach, the mean relative error of the heat transfer coefficient ranges from 1.24% to 2.36%. The heat transfer coefficient obtained based on the Trefftz functions and the heat transfer coefficient obtained by the simplified approach were very similar.
Author Contributions
Conceptualization, M.E.P., Methodology, S.H., Validation, S.H., A.P., Formal Analysis, M.E.P., S.H. and M.G., Investigation M.G., J.W., Writing—Original Draft Preparation, S.H., A.P., Writing—Review & Editing, S.H., M.E.P., M.G., J.W., Funding Acquisition, J.W.
Funding
The APC was funded by the Town of Płock through the Mayor’s Research Grants Programme “Collaboration with Universities”.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | approximation coefficient |
| B | boundary operator |
| cp | specific heat, J kg−1 K−1 |
| g | function |
| k | iteration number |
| L | length, m |
| M | number of Trefftz functions |
| MRD | maximum relative differences |
| N | differential operator |
| T | temperature, K |
| p | pressure, Pa |
| qw | heat flux, W m−2 |
| qV | volumetric heat flux, W m−3 |
| Re | Reynolds number |
| u | velocity, m s−1 |
| w | Trefftz function |
| x | coordinate, m |
| y | coordinate, m |
| L2-norm | |
| Greek symbols | |
| α | heat transfer coefficient, W/(m2 K) |
| Δ | Laplacian in Cartesian coordinates |
| Δ−1 | inverse Laplacian operator |
| δ | thickness; depth, m |
| ε | mean relative error |
| φ | void fraction |
| λ | thermal conductivity, W/(m K) |
| μ | dynamic viscosity, Pa s |
| ρ | density, kg m−3 |
| Ω | domain, m2 |
| ∂Ω | domain boundary, m |
| Subscripts | |
| approx | approximation |
| ave | average |
| data | measurement data |
| F | foil |
| f | fluid |
| H | heater |
| I, II, III | domain number |
| loss | heat loss |
| M | mini-channel |
| sat | saturation |
| sol | particular solution |
| 1D | one-dimensional approach |
| 2D | two-dimensional approach |
References
- Ribatski, G.; Wojtan, L.; Thome, J.R. An analysis of experimental data and prediction methods for two-phase frictional pressure drop and flow boiling heat transfer in micro-scale channels. Exp. Therm. Fluid Sci. 2006, 1, 1–19. [Google Scholar] [CrossRef]
- Karayiannis, T.G.; Mahmoud, M.M. Flow boiling in microchannels: fundamentals and applications. Appl. Them. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Kim, S.M.; Mudawar, I. Review of databases and predictive methods for heat transfer in condensing and boiling mini/micro-channel flows. Int. J. Heat Mass Transf. 2014, 77, 627–652. [Google Scholar] [CrossRef]
- Lee, H.; Park, I.; Mudawar, I.; Hasan, M.M. Micro-channel evaporator for space applications—2. Assessment of predictive tools. Int. J. Heat Mass Transf. 2014, 77, 1231–1249. [Google Scholar] [CrossRef]
- Kadam, S.T.; Kumar, R. Twenty First century cooling solution: Microchannel heat sinks. Int. J. Therm. Sci. 2014, 85, 73–92. [Google Scholar] [CrossRef]
- Asadi, M.; Xie, G.; Sunden, B. A review of heat transfer and pressure drop characteristics of single and two-phase microchannels. Int. J. Heat Mass Transf. 2014, 79, 34–53. [Google Scholar] [CrossRef]
- Guo, Z.; Haynes, B.S.; Fletcher, D.F. Numerical simulation of annular flow boiling in microchannels. J. Comput. Multiph. Flows 2016, 8, 61–82. [Google Scholar] [CrossRef]
- Yao, J.; Patel, M.K.; Yao, Y.; Mason, P.J. Numerical simulation of heat transfer in rectangular microchannel. Adv. Appl. Math. Mech. 2009, 1, 231–241. [Google Scholar]
- Trefftz, T. Ein Gegenstäuk zum Ritz‘schen Verfahren. In Proceedings of the 2nd International Congress of Applied Mechanics, Zurich, Switzerland, 12–17 September 1926. [Google Scholar]
- Jirousek, J. Basis for development of large finite elements locally satisfying all field equations. Comput. Methods Appl. Mech. Eng. 1978, 14, 65–92. [Google Scholar] [CrossRef]
- Herrera, I. Boundary Methods: An Algebraic Theory; Pitman Advanced Publishing Program: Boston, MA, USA, 1984. [Google Scholar]
- Zienkiewicz, O.C.; Kelly, D.W.; Bettes, P. The coupling of the finite element method and boundary solution procedures. Int. J. Numer. Methods Eng. 1977, 11, 355–375. [Google Scholar] [CrossRef]
- Kita, E.; Kamiya, N. Trefftz method: An overview. Adv. Eng. Softw. 1995, 24, 3–12. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, T.T.; Hu, H.Y.; Cheng, A.H.D. Trefftz and Collocation Methods; WIT Press: Boston, MA, USA, 2008; ISBN 978-1-84564-153-5. [Google Scholar]
- Piasecka, M.; Strąk, K.; Maciejewska, B. Calculations of flow boiling heat transfer in a minichannel based on liquid crystal and infrared thermography data. Heat Transf. Eng. 2016, 38, 332–346. [Google Scholar] [CrossRef]
- Hożejowska, S. Homotopy perturbation method combined with Trefftz method in numerical identification of temperature fields in flow boiling. J. Theor. Appl. Mech. 2015, 53, 969–980. [Google Scholar] [CrossRef]
- Maciejewska, B. The application of Beck’s method combined with the FEM and Trefftz functions to determine the heat transfer coefficient in minichannel. J. Theor. Appl. Mech. 2017, 55, 103–116. [Google Scholar] [CrossRef]
- Cao, L.; Qin, Q.H.; Zhao, N. A new RBF-Trefftz meshless method for partial differential equations. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10. [Google Scholar] [CrossRef]
- Hożejowska, S.; Grabowski, M. A Combined experimental-numerical approach for two-phase flow boiling in a minichannel. EPJ Web Conf. 2016, 114, 1–8. [Google Scholar] [CrossRef]
- Płaczkowski, K.; Poniewski, M.; Grabowski, M.; Alabrudziński, S. Photographic technique application to the determination of void fraction in two-phase flow boiling in mini-channels. Appl. Mech. Mater. 2015, 797, 299–306. [Google Scholar] [CrossRef]
- Hożejowska, S.; Kaniowski, R.; Poniewski, M.E. Experimental investigations and numerical modeling of 2D temperature fields in flow boiling in minichannels. Exp. Therm. Fluid Sci. 2016, 78, 18–29. [Google Scholar] [CrossRef]
- Hożejowska, S.; Piasecka, M.; Poniewski, M.E. Boiling heat transfer in vertical minichannels. Liquid crystal experiments and numerical Investigations. Int. J. Therm. Sci. 2009, 48, 1049–1059. [Google Scholar]
- Grysa, K.; Maciąg, A.; Pawińska, A. Solving nonlinear direct and inverse problems of stationary heat transfer by using Trefftz functions. Int. J. Heat Mass Transf. 2012, 55, 7336–7340. [Google Scholar] [CrossRef]
- Grysa, K.; Maciąg, A.; Adamczyk-Krasa, J. Trefftz functions applied to direct and inverse non-Fourier heat conduction problems. J. Heat Transf. Trans. ASME 2014, 139, 1–9. [Google Scholar] [CrossRef]
- Maciejewska, B.; Piasecka, M. Trefftz function-based thermal solution of inverse problem in unsteady-state flow boiling heat transfer in a minichannel. Int. J. Heat Mass Transf. 2017, 107, 925–933. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).