Abstract
A transient 3D thermal model based on the thermal quadrupole method, coupled to ray tracing analysis, is presented. This methodology can predict transient temperature maps under any time-fluctuating irradiance flux—either synthetic or experimental—providing a useful tool for the design and parametric optimization of concentration photovoltaics systems. Analytic simulations of a concentration photovoltaics system thermal response and assessment of in-plane thermal gradients induced by fast tracking point perturbations, like those induced by wind, are provided and discussed for the first time. Computation times for time-resolved temperature maps can be as short as 9 s for a full month of system operation, with stimuli inspired by real data. Such information could pave the way for more accurate studies of cell reliability under any set of worldwide irradiance conditions.
1. Introduction
Despite a constant rise in concentration photovoltaic (CPV) cell efficiency, currently more than 45% [1], CPV technologies struggle in the photovoltaic system market, as they require high precision tracking systems in order to take full advantage of direct solar radiation, and they also need appropriate cooling. Indeed, tandem solar cells endure localized high heat fluxes and high operation temperature gradients. Additionally, concentration optics deliver non-uniform irradiance profiles onto cell surfaces, due to their inherent ray tracing properties and manufacturing imperfections. Baig et al. [2] and Franklin et al. [3] found that non-uniform illumination induces efficiency losses.
Non-uniform illumination induces in-plane temperature gradients that follow complex time regimes according to ambient stimuli: slow day-night cycles, fast daytime cloud shading periodicity, and faster wind-induced tracking point perturbations. Wind influence on CPV systems performance has raised great interest in research: Chih-Kuang et al. [4] quantified how much wind induces mechanical deformation in structures supporting Fresnel lenses. Chumakov et al. [5] developed a methodology to evaluate CPV systems’ aerodynamic behavior, including wind tunnel experiments. Stafford et al. [6] performed experimental observations to assess how meteorological data correlate with tracking errors. Another factor is soiling, studied by Sanchez et al. [7] and Calvo-Parra et al. [8], which reduces CPV system performance by scattering and shading effects.
Acceptance angle is another important parameter related to receiver flux density [9]. This parameter depends on several factors such as the optical and mechanical precision in the construction of the CPV module and the quantity, type and quality of the optical elements for solar concentration. Small acceptance angles require greater precision in the tracking system, solar sensor, actuators, installation, and alignment [10]. In some systems, a secondary optical element is employed to raise the concentration ratio, increase tolerance to tracking errors or achieve a uniform flux distribution in the receptor [11,12]; however, the manufacturing cost also increases. Hence, concentrators should be designed to use the minimum amount of materials and the simplest optical scheme [11].
All these CPV-inherent factors trigger uneven and, to some extent, unpredictable thermal stress variations. They combine synergically to reduce concentration cell performance and life cycle; increasing the cost, thus restraining market penetration of CPV technology. Therefore, operation temperature predictions resolved in space and time are very valuable information and mandatory for CPV designers, issued from models that simulate and analyze the concentration, temperature and thermal stress level of the CPV cell. Hence, permitting scale concentrator apertures according to available solar radiation and CPV cell maximum operation temperatures, which range between 85–110 °C. By doing so, designers can increase the energy density and cell life-cycle, while decreasing cell cost.
Nowadays, given the complexity of CPV structures and irradiance heat fluxes spatial profiles, temperature fields are estimated by means of the finite element method (FEM) as reported in Table 1. FEM studies are costly in computing time [13] for any CPV optimization process, as they require a high number of simulations for parametric studies.

Table 1.
Literature on thermal analysis for CPV systems.
Most studies have dealt with steady-state analysis. This is not an intrinsic limitation of an FEM approach and, of course, transient simulations can also be performed, as shown by Renno et al. [14], Li et al. [15], Sweet et al. [16], Theristis et al. [22] and Oliverio et al. [23]. FEM is fundamental regarding system design since it can deal with exact complex 3D structures and also with possible nonlinearities. However, this approach can be impractical if system real-time simulation in response to fast incident flux changes (cloud shading and wind perturbations), is needed. None of the listed studies report numbers concerning computing times.
A complementary alternative for thermal modeling under such specific circumstances, conditioned to maintain an acceptable level of simplification for the 3D system structure, would be to solve the heat equation analytically; along with its inherent advantages: direct parameter estimation and optimization, straightforward parameter sensitivity studies, and fewer computing resources needed than FEM.
The thermal quadrupoles method [24] is suitable for heat transfer analysis of multilayered systems and has been extensively employed for space and time-resolved thermal simulations as varied as aircraft composite materials thermal characterization [25], ultrahigh heat flux and temperature simulations in magnetically confined plasma facilities [26], and thermal characterization of microchannel reactors in microfluidic systems [27]. The method is based on space and time integral transformations, permitting work on the transformed space [24,26,28,29] within a linear relationship between temperature and fluxes at different system layer interfaces.
In this work, the first thermal quadrupoles implementation of a 3D analytic solution for transient heat transfer in CPV systems is reported. The thermal quadrupole model is associated with ray tracing analysis which provides custom irradiance maps as an input stimulus for the thermal model. Detailed sections are organized to highlight the contributions and advantages such a combination of tools brings to CPV systems engineering.
In Section 2, Materials and Methods, the core of this work is described, starting with the procedure for irradiance profile estimation for a concentrator based on a Fresnel lens. Inspired by the specifications of a commercial Fresnel lens, simulations based on refractive surfaces generated by script are reported for the first time and preliminary comparisons between experimental and simulated irradiance spots are provided. Subsequently, a 3D analytic heat transfer model, based on the thermal quadrupole method, is introduced. A 2D time-resolved CPV temperature map can be computed from the combination of the absorbed flux map obtained from Tonatiuh and the thermal quadrupole model.
In Section 3, simulation results are presented for a typical configuration of a CPV module, i.e., a Fresnel lens to concentrate the solar radiation onto a CPV cell coupled to a passive heat sink. A parametric study is presented, revealing the best set of parameters for design optimization in order to keep operation temperatures within safe conditions. Transient thermal variations induced by tracking point dynamic perturbations are reported for the first time.
The contribution of this work is twofold: on the one hand, time-resolved surface temperature profiles in response to time-varying 2D irradiance patterns have been analytically estimated, providing a powerful tool for CPV system designers and paving the way for future thermal stress assessment, which in return would allow more accurate life-time and thermal breakdown predictions. The model covers full time regimes: transient and steady state, as shown by simulations performed with an engineering design scope. Theoretical temperature gradients induced by fast tracking point perturbations are presented for the first time and discussed. Simulation execution times are as short as 9 s for a full month of CPV system operation computed with irradiance stimulus inspired by real data.
On the other hand, Fresnel lens ray tracing implementation by means of the Tonatiuh open source software is reported for the first time. This is relevant as Fresnel lenses are extensively employed in CPV systems. A preliminary comparison between a real lens spot and the spot generated by script is discussed, indicating directions for more in-depth studies. However, this work’s focus is on the thermal quadrupole model, its capabilities, and the advantages it brings in combination with the Tonatiuh open source ray tracing software.
2. Materials and Methods
2.1. Locations, Instruments, Software and Methodology
Table 2 summarizes the resources employed for this work studies. The main purpose of this research is the development of analytic tools for CPV system thermal analysis resolved in space and time. The thermal model requires input stimuli, which is provided by a custom script representing Fresnel lens through Tonatiuh software, and delivering irradiance maps resolved in time and space; and inspired by real irradiance data and a real Fresnel lens.

Table 2.
Summary of research resources for this work.
In order to accomplish the above-mentioned objectives, a methodology has been implemented:
- (1)
- First, a Fresnel Lens model has been implemented by script, based on the software Tonatiuh (Section 2.2 and Section 2.2.1).
- (2)
- Design parameters from a commercial lens (aperture, transmissivity and prism pitch) have been introduced to the Tonatiuh model.
- (3)
- The commercial Fresnel lens has been experimentally characterized (focal length and spot spatial profile at a position below focal point, see Section 2.2.2).
- (4)
- Inspired by the commercial lens aperture, focal length and measured spot profile, the Tonatiuh Fresnel lens prisms angles were adjusted till they deliver the same focal length as the commercial lens.
- (5)
- Subsequently, both experimental and Tonatiuh spots were compared at a position below the focal point (see Section 3.1).
- (6)
- The so-obtained synthetic spots, inspired by the commercial Fresnel lens, were combined with DNI time series for the highest irradiance day of 2015, thus generating a synthetic irradiance data set, resolved in space and time, and inspired by a real Fresnel lens specifications and real irradiance data (see Section 2.2.3).
- (7)
- The irradiance data set is then introduced to the thermal quadrupole model described in Section 2.3. Temperature maps for three solar cells with different sizes are computed and a parametric study is executed (Section 3.2.1), it allows scaling the concentration ratio and preserving the operation temperature within safe ranges.
- (8)
- Finally, the possibilities of this work approach concerning the assessment of thermal gradients induced by fast tracking point perturbations are discussed in Section 3.2.3.
This work has been executed at two locations: CIO (Aguascalientes, Mexico) for the Fresnel Lens Experiments and CICY (Mérida, México) for the Tonatiuh implementation of a Fresnel lens and the thermal quadrupoles method. The following subsections describe thoroughly the methodology employed for this research.
2.2. Irradiance Map Definition
Tonatiuh is an open-source ray tracing software based on Monte Carlo analysis with an extended library of geometrical surfaces [30,32,33], allowing custom modification of available topologies and script-based design of new ones. Tonatiuh delivers irradiance flux map simulations upon custom receiver surfaces for any hour, calendar day and worldwide location; providing valuable information for designing concentrated solar power (CSP) systems, including concentrator optical properties and solar tracking systems. Unfortunately, Tonatiuh does not provide any library nor support for refraction-based optical elements, like Fresnel lenses.
2.2.1. Implementing Fresnel Lenses with Tonatiuh
Nevertheless, as stated in [34] (p. 020017-5), “…to model a refractive component on Tonatiuh one has to define two refractive surfaces with coefficients to the transmission, absorption, reflection and refractive index at each side”. This approach has been implemented successfully for this work. A custom script-based refractive object has been generated by combining a rectangular prism with a group of small prisms with triangular section and circular perimeter, concatenated on top of the rectangular base as shown in Figure 1.
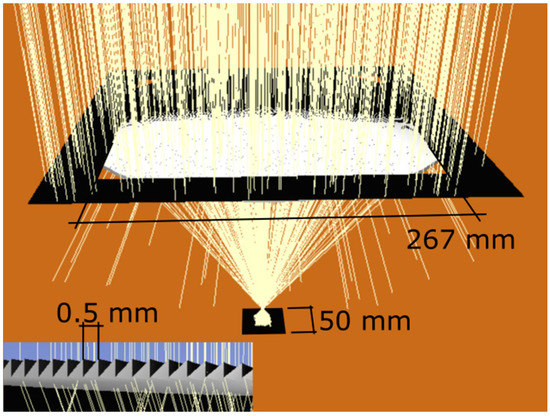
Figure 1.
Fresnel lens implemented with Tonatiuh. The 5 × 5 cm receiver is 1.5 cm below the focal point. Inset: Closer view of Fresnel lens cross-section showing periodic prisms generated by script.
The Fresnel pattern is circular, while its aperture is rectangular (represented as a dark squared mask upon a disk lens), as often found in the concentrator market. By means of the Snell law of refraction [35] (pp. 81–85), each small prism angle is adjusted so as to produce the appropriate output angle, in order to impact inside the receiver. This angle gets smaller as the prism approaches the center of the Fresnel lens as shown in Figure 1 inset (Bottom left). Such a strategy is not free of drawbacks: the diffraction patterns induced by the triangular edges cannot be represented by Tonatiuh. Nevertheless, as stated by Hornung and Nitz [36], diffraction losses are less than 1% for Fresnel lenses with pitches greater than 0.3 mm; a condition which is often met for non-imaging Fresnel lenses designed for solar concentration. Accordingly, diffraction losses at simulation stage are negligible, so ignored in this work.
The script model for the Fresnel lens has been inspired by commercial lens specifications. A summary of parameters of the real lens is shown in Table 3. Transmissivity, active area and pitch from the real lens were introduced into the Tonatiuh model. Then, the prism angles have been adjusted to deliver the same focal length as in manufacturer specifications, which is f = 22 cm. Next section describes the experimental design for the real lens irradiance maps measurements.

Table 3.
Fresnel lens specifications from manufacturer [37], also employed for Tonatiuh Model.
2.2.2. Characterising the Fresnel Lens That Inspires Tonatiuh Script: Experimental Design
An experimental design (shown in Figure 2) was conceived to compare the synthetic spot obtained with Tonatiuh, with the spot obtained by the commercial lens that inspired the script model. This design provides mechanical support for a rectangular Fresnel lenses and includes a manual solar tracking structure to ensure that the sun’s rays strike perpendicular to the plane of the Fresnel lens. In addition, an Allied Vision Technologies MAKO camera was positioned to image the receiver surface.
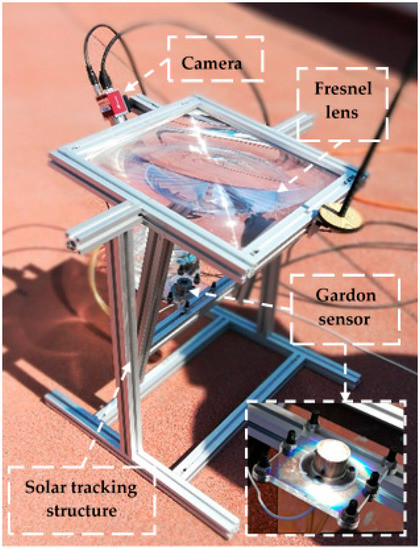
Figure 2.
Experimental setup for irradiance flux mapping.
Local Direct Normal Irradiance (DNI) data was obtained from a scientific grade solarimetric station (Solys2 + SHP1 pyrheliometer, Kipp & Zonen, Delft, The Netherlands) located at the CIO Research Institute (Aguascalientes, México). A square Fresnel lens (FL220-285, Fresnelfactory, San Jose, CA, USA) concentrator has been employed. This Fresnel lens produced a square spot of 23 mm per side on the receiver surface, the latter located at 23.5 cm below the lens, which is 1.5 cm after lens focal point. At this out-of-focal-point position, the concentration ratio was 126.9 suns. This out-of-focal-point position is still close to focal plane, and provided a bigger spot, allowing an evaluation with higher spatial resolution for the imaging system, thus a clearer comparison between spots, and a preliminary evaluation of the light cone, as the focal point was known a priori.
A Gardon-Schmidt-Boelter sensor (SBG01, Hukseflux Thermal Sensors, Delft, The Netherlands) was placed in the receptor plane 23.5 cm below the lens, 1.5 cm below the Fresnel lens focal plane, as previously mentioned (see Figure 2. Inset, bottom-right), at the center of the spot. The Gardon active area, a circle with a 1 cm diameter, generates a signal proportional to the integral of irradiance flux upon the active area. This mean flux measurement provides the calibration data for the spatially resolved flux acquired with the MAKO camera (Allied Vision, Exton, PA, USA). Indeed, the Gardon sensor delivers a signal proportional to the absorbed heat flux upon the sensor surface and measures the irradiant flux; thus obtaining the Fresnel lens optical concentration after radiation absorption, reflection and diffraction losses. The Gardon sensor was calibrated in accordance to the ISO 14934-3 standard.
Afterwards, the Gardon sensor was exchanged for a flat receiver covered in a Lambertian paint. An image of the spot generated upon the Lambertian receiver surface was then acquired by means of the MAKO camera, to gather the spatial flux distribution with the CCD matrix. Indeed, as receiver surface, CCD pixel size and magnification, and Gardon sensor surface are all known, incident fluxes can be obtained. This procedure allowed the estimation of receiver surface incident flux with spatial resolution, providing an experimental flux map. A mean DNI experimental dataset was also introduced into the Tonatiuh Fresnel lens model in order to compare model results with measured fluxes acquired by the MAKO camera.
2.2.3. Combining Flux Maps Modeled through Tonatiuh with Synthetic Ambient Irradiance Series
Tonatiuh can mimic direct solar irradiance evolution through daytime variation of zenith and azimuthal angles. Such a spatial distribution (Figure 3a) depends on the Fresnel lens geometry, focal point, aperture and DNI incidence angle. However, Tonatiuh does not represent the unpredictable amplitude variation due to atmospheric absorption, refraction and cloud shading. To overcome this limitation, a synthetic, time-resolved DNI profile is generated by combining flux maps modeled through Tonatiuh, with a set of experimental irradiance data for the highest irradiance record available (Aguascalientes, Mexico, July 2015, Figure 3b), throughout full daytime, with a sampling period of 60 s; in order to provide a synthetic flux dataset very close to real conditions. The irradiance time series of Figure 3b appears clipped at 9:00 and 17:00 to simulate a hypothetical, angular dynamic range limitation of the tracking system. The absorbed flux upon receiver surfaces is then defined as:
where is the normalized irradiance map obtained with Tonatiuh (Figure 3a) and is the synthetic solar irradiance time series (Figure 3b). This way a synthetic DNI voxel, resolved in space and time is obtained. A voxel is the 3D (x, y, t) equivalent of the well-known 2D (x,y) pixel. The so-obtained 3D voxel array will be the external stimulus for the thermal quadrupoles model described in next section.
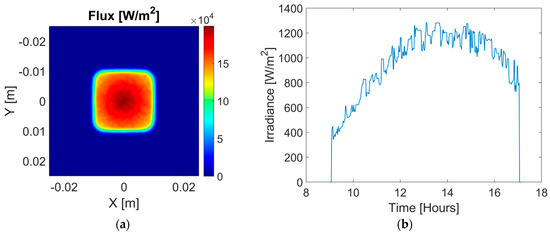
Figure 3.
Synthetic irradiance maps and time series for a high irradiance day of July 2015, Aguascalientes, Mexico. (a) Irradiance map at 12:00 computed with Tonatiuh; (b) Synthetic irradiance series.
2.3. Thermal Quadrupoles Model
Let us start, for proof of concept purposes, with a generic CPV system (Figure 4a) composed of a square aperture Fresnel lens collector (point focal) focusing light onto a CPV cell glued to an aluminum heat sink; the latter in contact with a refrigerant liquid (water) supplied in order to keep CPV cell operation temperature within a safe range as specified by the manufacturer. The refrigerant liquid is considered an isothermal heat sink. Such a simplified scheme aligns with this work’s main purpose: to highlight the capabilities and potential of this new combination of known analysis tools, rather than to focus on the details of a specific CPV system design.
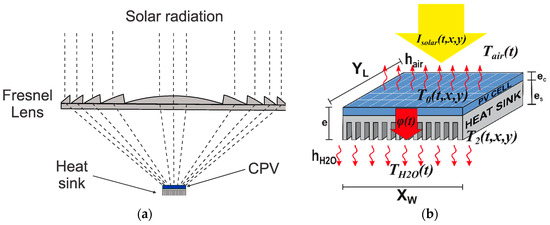
Figure 4.
(a) CPV module topology: Fresnel lens concentrator, a CPV cell + a heat sink; (b) Scheme with relevant information for thermal simulation.
Prior to heat balance, one assumption is made: CPV cell thickness (ec) is small in comparison with its in-plane dimensions Xw and YL, and heat losses upon thin lateral walls are accordingly negligible, thus ignored. The irradiance profile hitting the CPV cell has a time and space dependence. Therefore, the same is expected for the CPV cell temperature response, giving rise to a transient 3D heat transport problem, with adiabatic conditions at lateral CPV cell walls (Figure 4b). Under such a set of assumptions, heat equation and initial and boundary conditions are written as:
where a is thermal diffusivity, λ is thermal conductivity, T and t are temperature and time; and are spatial coordinates and is heat sink thickness. g accounts for internal volumetric heat sources, like Joule heating for a working CPV cell. hair and hH2O are the convection-radiation coefficients for air (CPV cell surface) and heat sink side in contact with the refrigerant fluid (water), as shown in Figure 4b. Two spatial (x → α, y → β) Fourier transforms and one time (t → p) Laplace transform are applied to the previous system of equations, and the partial differential equation (PDE) (Equation (2)) is transformed into the following ordinary differential equation (ODE):
where α, β are Fourier variables, p the Laplace variable and θ is the temperature in the transformed space (see Appendix A for details). A linear relationship between temperature and heat flux at the boundaries of each system layer emerges, allowing a representation based on quadrupoles with thermal impedances as shown in Figure 5.
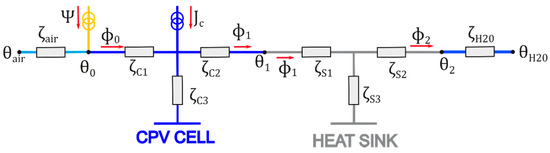
Figure 5.
Thermal quadrupoles representation of CPV system shown in Figure 4b.
Thus, heat transfer in the composite system is represented by a layer matrices product linking temperature-heat flux vectors at the boundaries of the system:
where are temperatures for CPV cell surface, air, heat sink surface and refrigerant liquid. accounts for absorbed solar radiation and and are radiation-convection losses toward air and refrigerant liquid. are quadrupole matrix coefficients, and the index j corresponds to the system layer index, 1 for CPV cell and 2 for heat sink. is the volumetric source for CPV cell Joule heating. Equation (5) can be solved algebraically for all relevant temperature and heat fluxes, which are still in the multi-transform space. To return to meaningful coordinates and time, a triple inverse transform must be applied.
Nevertheless, and are not mathematically defined, as their origin is experimental records of solar irradiance and ambient temperatures over time for a defined location. Such records exhibit unpredictable variations in time, which are hard to represent by a function in the transformed space. In such cases, a well-known strategy in linear systems analysis consists in first computing the system response to the Dirac impulse, which in this case would be spatial and time Dirac impulse, located at the center of the CPV cell. In practice, all experimental source terms and temperatures are grouped together and then replaced by the Dirac impulse transform. Then, a spatial 2D inverse Fourier transform is applied, to obtain the temperature map response to the Dirac impulse stimulus:
In practice, infinite sums in Equation (6) are truncated to 10 terms, which provides a good trade-off between precision and computing time as reported in [26]. Indeed, temperatures computed with 10 term simulations converge asymptotically, better than 99.9%, to simulations using as high as 500 terms. Temperatures calculated with 500 terms were employed as reference, as any further (>500) increase in number of terms does not produce temperature changes for double precision, floating point computations. The 10 terms figure is explained by the incident flux spatial frequency spectrum, by nature skewed toward low frequencies, and showing much less content at high spatial frequencies. Further details are provided in Section 3.3 and Appendix B.
Equation (6) remains in the Laplace space. So, a numerical inverse Laplace transform is applied by means of the Den Iseger algorithm [31], which outperforms other well-known inversion techniques such as Stehfest, and De Hoog’s [38]. Temperature response T*0(x, y, z, t) to the measured ambient variables time series and internal sources is then calculated, and consists of the sum by superposition principle of two terms.
First, the time convolution between the response to Dirac impulses without the internal Joule heating , and a time series term composed of the sum of solar irradiance Isolar and convective-radiative heat flux Tair/ζair. Second, the time convolution between the response to Dirac impulses without solar irradiance Isolar and convective-radiative heat flux Tair/ζair, and the volumetric heat source .
To obtain the system response for a custom or experimental irradiance profile covering the whole receiver surface, the CPV cell surface is split into a grid of M by N size; and a synthetic Dirac impulse “scans” each grid node, generating a set of temperature maps. This set of responses to individual scanning Dirac impulses hitting a different node in the grid each time must be added up, taking advantage of the superposition principle. The two set of M by N profiles so-obtained are added, to yield the final CPV surface temperature map:
Tair is a time series for measured ambient temperature. Isolar is the irradiance flux absorbed at the CPV surface, both space and time-resolved as defined in Section 2.2.3.
In some cases, the irradiance flux spatial function can be mathematically known, either by an analytical derivation for a Fresnel lens [39], or for a concentrator [40,41]; or by plane-fitting a measured profile with an appropriate function. Then, the analytic Fourier transform of the irradiance term can be included in system (5). In such a case, a single Dirac impulse located at the CPV cell center is enough (M = N = 1).
A more complex scenario consists in a spatial profile not known mathematically, like an experimental profile obtained from a concentrator with optical imperfections and inhomogeneities. That case requires the scanning M by N Dirac covering each grid node where the measured irradiance flux is defined. For an in-depth, full mathematical development of this section, please refer to Appendix A.
3. Coupling Ray Tracing Analysis + Thermal Quadrupoles Model: Results
3.1. Tonatiuh Fresnel Lens Model: Comparison with Commercial Lens Spot
In this section, the Tonatiuh Fresnel lens simulation is compared with experimental results from the experimental design described in Section 2.2.2. As such a Fresnel lens implementation is reported for the first time, we started from the specifications of a commercial lens, recover PMMA properties and manufacturing information.
Results for both simulated (a, top) and experimental (a, bottom) spot profiles are shown in Figure 6. They show a very similar square pattern and size. The simulated spot is ideal, and does not show inhomogeneities, whereas the experimental spot does. Indeed, the real lens combines imperfections in the sawtooth patterns, flatness variations, plastic bending and inhomogeneity in material transmittance. These aspects would explain the high spatial frequency variations within the spot area.
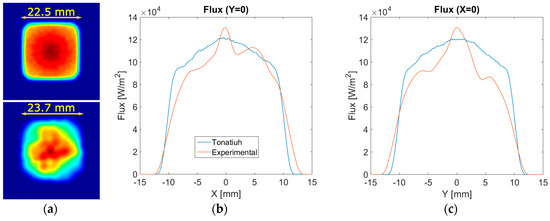
Figure 6.
Fresnel lens spots (a, top) Simulated with Tonatiuh, (a, bottom) Measured for commercial lens; Profiles along (b) x (y = 0, center of spot) and (c) y (x = 0, center of spot).
Nevertheless, it is important to mention that we are unable to claim that the teeth angles are disposed the same way in the model as in the real lens. But this procedure does provide us with a synthetic irradiant flux coming from the lens model, that mimic the real lens appropriately, delivering the same focal length and a similar spot at an out-of-focal-point position.
Indeed, it should be noted that both spots show a good agreement for total power, maximum flux and spot average flux, as summarized in Table 4. However, it is good engineering practice to employ the ideal lens figures during design, in order to take into account the maximum theoretical flux the cell would have to endure in real conditions, as if a high quality lens was employed. In any case, it is possible to use both the experimental or theoretical spots (associated to a synthetic or experimental time series) as an input stimulus for the thermal quadrupole model.

Table 4.
Comparison of Fresnel lens performance: Commercial lens and Tonatiuh model inspired by the commercial lens.
Let us insist that this comparison purpose is not to provide a demonstration of the fidelity of the simulated Fresnel lens geometry in comparison with the commercial lens. Instead, the purpose was to design a synthetic lens inspired by specifications from the commercial lens datasheet (material transmissivity, focal length, pitch and aperture), to provide the thermal quadrupole model with an irradiance spot, defined in space and time, inspired from a real lens and real irradiance data.
3.2. Time-Resolved Temperature Mapping Simulation Results
Once the flux voxel is defined in accordance with Equation (1) and the procedure described in Section 2.2.3, on a daily basis with a 1 min sampling frequency, the voxel is introduced into the thermal quadrupole model (Equation (6)) in order to compute relevant temperatures and heat fluxes at any time. Now it is straightforward to perform parametric studies in order to optimize the design and scale the CPV system. Relevant simulation parameters are summarized in Table 5.

Table 5.
Thermal Modelling Simulation Parameters and Ranges.
CPV cell thermal properties are typical values for semiconductor multijunction solar cell [42,43,44], as well as a thermal contact resistance coefficient for a thermal interface material. Design parameter ranges for concentration factor and convection coefficients are provided and discussed in next section.
3.2.1. Uneven Irradiance Profiles and High Temperature Gradients
How spatially uneven fluxes affect temperature response is an important question for CPV system performance and reliability, and accordingly, to highlight the model pertinence on this matter, let us start with the synthetic spot shown Figure 6a, top, and compute the CPV cell surface temperatures for three different CPV cell sizes (1 × 1 cm, 2 × 2 cm and 5 × 5 cm) as shown in Figure 7. It is important to note the effect of an inhomogeneous flux profile upon cell surface temperatures. Indeed, the 1 × 1 cm cell shows small spatial variations around 55 °C, whereas the 2 × 2 cm and 5 × 5 cm cells endure much higher gradients (50 °C to 55 °C, and 30 °C to 42 °C) as the bigger cells get less photons at the edges. Notice also how as the same amount of heat is distributed over a growing volume, maximum temperatures (56 °C, 53 °C, 42 °C) decreases with growing cell sizes.
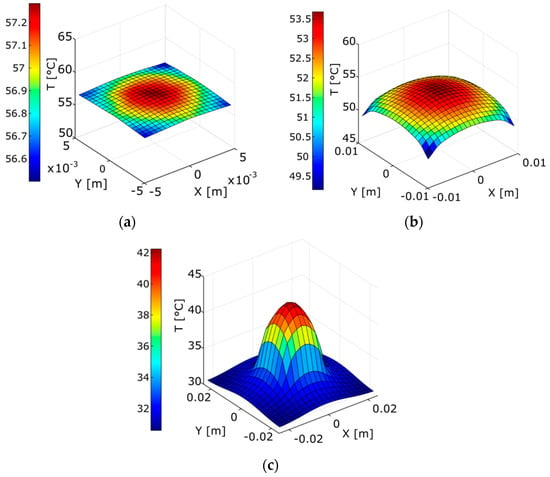
Figure 7.
Temperature maps for three CPV cell sizes (a) 1 × 1 cm (b) 2 × 2 cm (c) 5 × 5 cm in response to irradiance spot of Figure 6a, top.
Of course, for a real device, a change in position for the CPV cell would be indicated for the 2 × 2 and 5 × 5 cells, to irradiate at an out-of-focal-point position, where the spot would be bigger, and thus homogenize the temperature gradient. Such an analysis, clearly relevant for the optimization of a well-defined, specific CPV system, is beyond the scope of this work, which is centered on the thermal quadrupoles model capabilities when combined with ray-tracing analysis.
Hereafter, let us focus on the 1 × 1 cm cell, which is the most frequent size for CPV cells found in the market. Since solar cell surface temperature is strongly affected by convection on the heat sink surface (convection coefficient) and especially on concentration factor C, a parametric analysis is developed to determine an upper operation temperature according to manufacturer specifications, which is typically Tmax < 100 °C for most cells. The concentrator factor C is here defined as the ratio between Fresnel lens area and solar cell area.
3.2.2. Concentrator Scaling and Operation Temperature Optimization
Figure 8 shows a parametric study for center CPV cell temperature (b) and the CPV cell-heat sink interface, as a function of concentration factor C and heat sink convection coefficient. range was estimated in accordance with [45] in an operation range of 40–100 °C for a heat sink in natural convection. Concentration factor has been varied within the 0–500 range. For this purpose, the synthetic irradiance voxel was evaluated with the Fresnel lens model, but at closer position below the focal point (22.6 cm, which is 6 mm below focal point), thus providing a smaller spot in order to match the cell surface and the spot area. The voxel was scaled to artificially provide lower and higher irradiances, and mimic the effect a range of concentrations (0–500) would have.
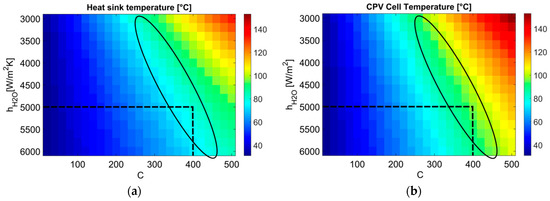
Figure 8.
CPV cell center temperatures as a function of heat sink convection coefficient and concentration factor (a) CPV cell-heat sink interface (b) CPV surface.
Safe operation temperature limits (T < 100 °C) are marked within black ellipses. As cell temperature approaches the 100 °C limit, heat sink temperature is close to 80 °C. According to reported correlations [45] and simulation results, that would correspond to a convection coefficient close to 5000. Such a set of conditions matches a concentration factor of 400, which would be the maximum allowable concentration, associated to the 5000 figure of convection exchange.
Accordingly, the simulated Fresnel lens inspired from the manufacturer specifications is found to provide the 400 suns figure at a 22.6 cm working distance, just 6 mm below focal point, conditioned to limit the aperture to a 20 × 20 cm window (20 × 20 cm/10 × 10 mm → 400 suns).
Of course, higher convection coefficients, will allow further concentration ratios, and the specific design conditions can be studied thoroughly at this design stage. Such analysis is beyond the scope of this work, whose main interest is to pinpoint the potential of the proposed methodology on this matter.
Finally, the temperature field under that set of optimal design parameters is recalculated for the highest radiation day of the year 2015 (Figure 3b), and results are shown in Figure 9, where the gradient rises to a 20 °C difference between CPV cell edges and center (Figure 9a). Heat sink top temperature and CPV cell temperature at the center are shown throughout the same day in Figure 9b. The cell temperature is kept under the safe operation range (<100 °C), as expected, thanks to the parametric study described above. Supplementary Material S1 contains a video with the time sequence of CPV surface temperature maps throughout the day in response to irradiance flux maps in Figure 3b.
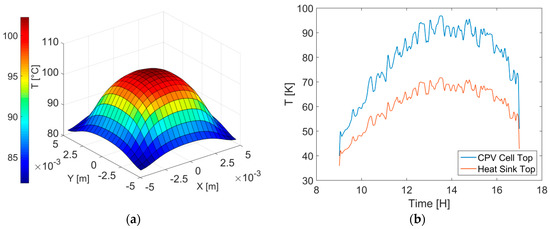
Figure 9.
Temperatures on the highest radiation day (Aguascalientes, July 2015) (a) CPV surface temperature map at 12:00; (b) Temperature at CPV cell center and heat sink-CPV cell interface temperature throughout the day.
3.2.3. Predicting Temperature Variations Due to Tracking Point Perturbations
Until now, the thermal quadrupole model has not been challenged on its transient capabilities, as the available irradiance data sampling frequency is quite low (60 s) in comparison with the CPV system dynamics. Even the fastest cloud shading observed in Figure 3b lies in the steady state regime for the CPV cell temperature. Nevertheless, wind perturbations affecting the tracking point could induce much faster flux variations and therefore unexpected temperature gradients on the CPV cell.
To assess such an effect, a periodic angular perturbation (Figure 10a, sawtooth chirp form, 0.5° amplitude, frequency starting from 5 Hz to 0.1 Hz) centered on the optimal tracking point (0°) has been introduced. This synthetic perturbation spans over 16 s and induces an absorbed flux variation (Figure 10b).
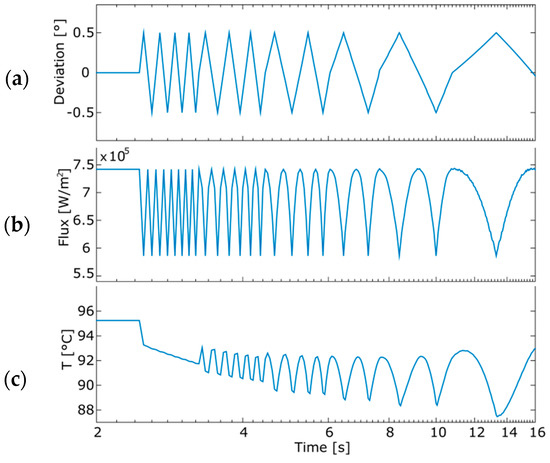
Figure 10.
System Response to Synthetic Angular Tracking Point Perturbations: (a) Degree of deviation on tracking system; (b) Flux at Cell center (c) CPV cell center temperature.
The resulting temperature variations are shown in Figure 10c, where the low pass filtering effect of heat equations is displayed. Indeed, “high frequency” perturbations (>5 Hz) do induce a mean operation temperature variation that is perceptible, but not a measurable periodic response following the perturbation periodicity. As frequency decreases down to (0.1 Hz) such a periodic component appears and grows up to variations of 6 °C, from 87 °C to 93 °C. That low pass filter behavior depends on CPV cell thermal properties and especially on cell thickness (z-axis). Greater angular perturbations will induce higher temperature variations. The assessment of the temperature variations induced by the angular perturbation effect is of great value for design purposes and a deeper investigation in future studies (beyond the scope of this work) might consider possible associated cell lifespan shortening. Indeed, as already shown in Figure 7c, an incident flux gradient induces strong temperature gradients as well. For a deeper picture of such an effect, please consult the Supplementary Material S2, where the evolution over time for the CPV cell temperature map is shown, in response to the synthetic angular perturbations of Figure 10a.
3.3. Computing Time
As stated in Section 2.2, two cases are foreseen regarding the spatial profile of an absorbed flux: a known mathematical function or a custom profile, which could be gathered from a measured flux map. The first case involves calculating a single Dirac response, whereas the second case requires M by N computations of the scanning Dirac pulses. The computing time has been estimated accordingly for time-resolved temperature maps lasting 1 day, 1 week and 1 month of CPV system operation. Results are summarized in Table 6.

Table 6.
Computing time (in seconds) for several simulation scenarios.
In practice, computation procedure starts with the calculation of one Dirac response (for a known spatial function) or M by N Dirac responses (for an unknown function spatial profile) followed by a time convolution according to the Den Iseger algorithm. When the flux spatial function is known, such an operation is very fast, lasting less than 9 s (8.2 + 0.68) for a full month of temperature map simulations. In this case, the single impulse response calculation dominates the total computation time.
Conversely, when the flux spatial function is unknown, computation time scales according to the M by N discretization. In this case the study has been performed for M by N (21 by 21) yielding a good spatial resolution for a thermal problem, whose spectral content is inherently restrained to low spatial frequencies. The computing time scales up to 29 min for a month, and down to 17 min for a day which is still a reasonable figure for a transient 3D study of thermal response. Further information on computing time optimization can be consulted in Appendix B.
4. Discussion
Script-based Fresnel lenses simulations for concentration photovoltaics were proposed. They allow the use of Tonatiuh ray tracing open source software to represent refraction objects, and obtain synthetic receiver flux maps for any worldwide date, hour and latitude. Characteristics of a commercial Fresnel lens have been introduced to the Tonatiuh script, and experimental and simulated flux distributions were compared. It should be pinpointed that commercial lens is employed in order to inspire the script-based Fresnel lens model.
For design purposes, the script-based lens was employed, as its design was inspired in the real lens, and it provides a synthetic irradiance spot similar to the real one. Additionally, it provided the maximum theoretical flux, and consequently, the highest foreseen operation temperatures.
Tonatiuh’s set of synthetic flux profiles under perfect tracking conditions throughout daytime and seasons were then combined with measured solar irradiance series, which include variations induced by cloud shading. Such a synthetic flux voxel was then introduced into the thermal quadrupole model. Indeed, an analytic model for CPV cell temperature maps estimations, based on the thermal quadrupoles method has been proposed. It accurately predicts time-lapse CPV cell surface temperature maps under any worldwide irradiance conditions, for any set of experimental or simulated irradiance fluxes. Such a thermal model, coupled with Tonatiuh ray tracing analysis, is a powerful combination of tools for CPV systems design.
Indeed, a parametric analysis to keep the system’s upper operation temperature below the maximum limit according to CPV cell specifications was developed. Computing time can be as low as a few seconds, even for a temperature map calculation spanning over a month, provided there is a known spatial function for flux. The proposed method simplifies the design of solar concentration systems and would allow studying the performance and the life cycle of concentration photovoltaic cells, through an accurate computation of thermal stress along years of operation.
The scope of the proposed methodology does not claim to replace FEM analysis. Instead, we think it provides a complementary tool that can be employed at the first stages of CPV system design to provide FEM models (more accurate for complex 3D structures representation) with narrowed and fine-tuned ranges of relevant design parameters and time regimes, minimizing computer resources usage. Furthermore, this method opens up interesting opportunities for improvement of CPV systems reliability studies.
As shown in Table 1, all prior works concerning thermal response of CPV systems consist of 3D models for average temperatures or numerical simulation by Finite Element. To our knowledge, this is the first time analytic computation of CPV cell surface temperature resolved in space and time has been proposed. The same is true for the association of the thermal quadrupole method and ray tracing analysis.
5. Conclusions and Perspectives
The thermal quadrupole model, in association with ray tracing analysis software Tonatiuh, applied to transient temperature maps, resolved in time and space was reported for the first time. Such an approach, by its analytic essence, is suitable for CPV engineering, including parametric studies, design optimization, and reliability studies. Additionally, the so-performed studies are executed in less computing time, as short as 9 s for a full month of simulated operation, with a generic laptop computer.
Nowadays these tasks are accomplished with FEM tools, which are undeniably useful and mandatory when systems structures are geometrically complex and show non-linearities. Accordingly, the claim is not replacing FEM, but rather complement it, by providing them with narrowed ranges for design parameter optimization, when working with CPV designs whose complexity cannot be properly represented by thermal quadrupole models. We would like to draw reader’s attention to another field that could benefit from this research: CPV cell reliability.
Potential for Reliability Studies
CPV cell thermal breakdown has been extensively studied and is the recognized main cause of cell failures and lifespan shortening [46,47,48,49,50,51,52,53,54]. To our knowledge all reported works employ simplified steady state models and operation condition statistics for the assessment of cyclic degradation. With FEM simulations, it is hard to foresee the implementation of transient simulations over months and years of operation with real ambient and irradiance data. Nevertheless, with the approach proposed in this work, computation times are very short and hence, it is reasonable to contemplate thermal stress simulation with real irradiance data over full years of operation. Furthermore, including higher time resolution computations which permit assessing the influence of fast angular perturbation of tracking point (wind, vibrations) is also conceivable.
The consequences on lifespan shortening induced by these temperature variations, represented with better accuracy by this work method, are still to be studied. The same is true for thermal breakdown forecasting based on full knowledge of CPV thermal response over years with high time resolution.
Finally, concerning the implementation of Fresnel lenses by refractive surfaces generated by script with Tonatiuh, which is also a novelty presented in this work: Proper validation of the script-based model by comparing real and scrip lenses, including their geometry, is worth its own research and is beyond the scope of this work, focused on the association between the thermal quadrupoles model and ray tracing analysis.
Supplementary Materials
The following are available online at https://zenodo.org/record/1340754#.W2kBabgRWUk, Video S1: Temperature throughout the highest irradiance day of the year 2015. Video S2: Incident flux and CPV surface temperature in response to synthetic angular perturbations.
Author Contributions
A.M.-C. performed the experiments, conceived and wrote Tonatiuh scripts, wrote thermal quadrupoles scripts and executed simulations. A.D.-P. and M.I.P.-C. conceived, designed and performed Fresnel lens flux estimation experiments, and contributed to Tonatiuh script optimization. J.-L.B. and C.P. contributed to the thermal quadrupole model definition. L.D.P.-L. designed and led research, and led article writing. All authors contributed to writing the final manuscript.
Funding
This research was funded by CONACYT Cátedras program through the project “3133, Desarrollo y Aprovechamiento de Energías Renovables Limpias”, also by CIO-CICY fund through the project “UER4, Diseño y Construcción de un Sistema Híbrido Fotovoltaico Concentrado + Termoeléctrico de Estado Sólido + Aprovechamiento Hídrico del Subproducto de Enfriamiento”, and by CONACYT-SENER fund through the project “Consolidación del Laboratorio de Energía Renovable del Sureste (LENERSE)” including subprojects SP2 and SP4.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Full Mathematical Development of Thermal Quadrupole Model
The heat transfer through CPV cell is:
where ac and λc are thermal diffusivity and thermal conductivity of CPV cell and T is temperature, t is time, g is internal heat source, is flux from CPV to heat sink and are spatial coordinates.
Under assumption that heat losses upon thin lateral walls are neglected, one can write:
Applying Laplace transform to system:
By taking account adiabatic conditions (A7), one can apply the Fourier cosine transform:
where the eigenvalues are:
with = 0, 1, 2, 3, … and = 0, 1, 2, 3, ….
After Laplace-Fourier transformation the differential Equation (A1) and boundaries conditions are written as:
whose solution is:
with .
By taking account boundaries Condition (A10) and using the quadrupole formalism developed in [17] one can express the transformed temperature and heat flux at z = 0 and z = , as:
where elements of matrix are defined in function of proprieties of CPV cell:
with .
And internal heat source due Joule effect [X, Y]’ are expressed as:
with:
where Rc, Ac and are resistance area and CPV cell current estimate by explicit method presented in [55] for Azur Space triple junction solar cell 3C44.
A same process is development for heat sink block with its proprieties as, λs, es, and without internal heat sours to obtain the expression:
With:
where is defines as heat sink top temperature, is the heat sink water contact temperature and is the water temperature. From (A12), (A14), (A15), (A16) one obtains (A18):
A thermal resistance is introduced between CPV cell and Heat Sink to represent thermal glue, so the full system is:
with:
whose representation with thermal impedances is shown in Figure 5, where thermal impedances are:
Since (A19) is a system of linear equations, it is possible solve for :
and subsequently one can obtain:
To keep system linearity, internal heat source is computed externally due thermal dependence. Thermal response is the sum of two external excitations ) and . As:
where:
At this point thermal response of system still in Laplace-Fourier domain, so two inverse transformation must be applied, the space transformation defined as:
with .
And inverse transformation of Laplace was made by Den Iseger algorithm to obtain thermal response due impulse response as radiation excitation and due impulse response as internal heat source.
A.1. Flux Excitation
The Den Iseger algorithm demands a defined laplace function to compute inverse transform. So one need define a function able to describe laplace transform from solar flux measurement data. Find this kind of function is not easy task due non-homogeneous distribution in space and time.
To solve this problem one can compute the response from Dirac function in time in specific area over solar cell surface and by convolution find the response from any excitation function.
Normalized Heaviside function is used to approximate Dirac function in a discrete form, in this way function is defined as:
whose Laplace-Fourier transform is find by:
Solving:
A.2. Thermal—Electric Coupling
CPV cell current is temperature dependent, yielding a no-linear problem, which has been solved by means of iterative computing as summarized in Figure A1. Starting from a an initial thermal response, the electric model is feed with first thermal estimation and delivers an estimate of the cell current, which in return is used to recalculate thermal response. This procedure is repeated until the thermal response converge according to a stop criterion (consecutive variation lower than 1%).
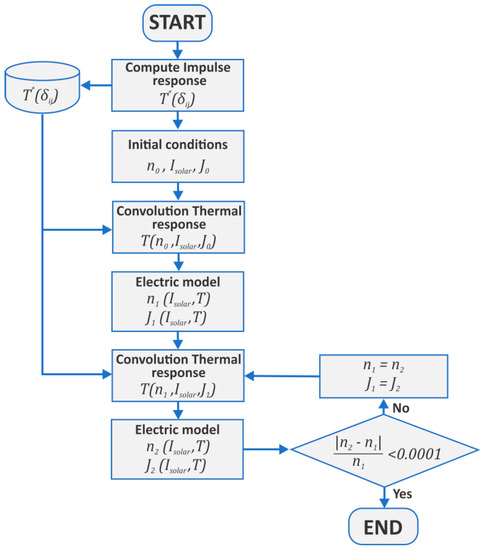
Figure A1.
Iterative procedure for estimating Joule heating contribution to CPV system temperature.
Appendix B. Truncate Inverse Fourier Transform Infinite Series and Computing Time Optimization
Simulation have been executed on a general-purpose laptop computer (Model HP Envy, processor Intel core i5-4210U, 8 GB RAM), by means of the software Matlab® (R2014b, MathWorks, Natick, MA, USA). A full day of temperature maps responses has been calculated with a 60 s sampling frequency. Global simulation time (Figure A2a), and maximum error at selected point upon CPV surface (Figure A2a), starting at the cell center and finishing on cell edges, are shown as a function of the Fourier series number of terms.
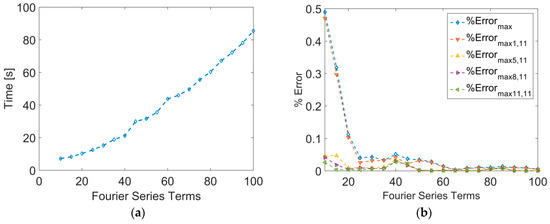
Figure A2.
Computing time (a) and Temperature convergence error (b) as a function of number of Fourier series terms during 2D inverse Fourier transformation (Equation (6)).
This error is defined as the difference in percentage with a simulation using 500 terms for the Fourier series of Equation (6). Higher number of terms (>500) did not show any further change in simulated temperature. The point with the highest error on the temperature map along the day is plotted in Figure A2b.
Afterwards, number of terms has been reduced from 100 to 10, where 10 terms implies a computing time lower than 9 s of 1 day in temperature response, as seen in Figure A2a.
Still, difference between the 10 and the 500 terms simulations is smaller than 0.05% for temperatures at center of the CPV cell and reach a maximum of 0.5% at CPV cell edges, which is an imperceptible difference for any temperature measuring device available nowadays.
Accordingly, the Fourier series term number has been set to 10. Such a figure will be specific to each case, according to the spatial frequency spectrum of the absorbed flux maps. A similar analysis each time a new problem is posed might be good engineering practices for accurate temperature simulations.
References
- Philipps, S.P.; Bett, A.W.; Horowitz, K.; Kurtz, S. Current Status of Concentrator Photovoltaic (CPV) Technology; National Renewable Energy Lab.: Golden, CO, USA, 2015. [Google Scholar]
- Baig, H.; Heasman, K.C.; Mallick, T.K. Non-uniform illumination in concentrating solar cells. Renew. Sustain. Energy Rev. 2012, 16, 5890–5909. [Google Scholar] [CrossRef]
- Franklin, E.T.; Coventry, J.S. Effects of Highly Non-uniform Illumination Distribution on Electrical Performance of Solar Cells. 2002. Available online: http://hdl.handle.net/1885/40832 (accessed on 16 July 2018).
- Lin, C.-K.; Lin, C.-Y.; Wu, J.-C.; Bett, A.W.; McConnell, R.D.; Sala, G.; Dimroth, F. Simulation Of Deformation Induced Sun Tracking Error In A High Concentrated Photovoltaic System. AIP Conf. Proc. 2010, 1277, 149–152. [Google Scholar]
- Chumakov, Y.S.; Rumyantsev, V.D.; Ascheulov, Y.V.; Chekalin, A.V. A comparative analysis of wind pressure on flat and stair-step constructions of solar plant trackers. St. Petersbg. Polytech. Univ. J. Phys. Math. 2015, 1, 299–304. [Google Scholar] [CrossRef]
- Stafford, B.; Davis, M.; Chambers, J.; Martinez, M.; Sanchez, D. Tracker accuracy: Field experience, analysis, and correlation with meteorological conditions. In Proceedings of the 2009 34th IEEE Photovoltaic Specialists Conference (PVSC), Philadelphia, PA, USA, 7–12 June 2009. [Google Scholar]
- Sanchez, D.; Trujillo, P.; Martinez, M.; Ferrer, J.P.; Rubio, F. CPV performance versus soiling effects: Cleaning policies. AIP Conf. Proc. 2012, 1477, 348–351. [Google Scholar]
- Calvo-Parra, G.; Martínez, M.; Sánchez, D.; de la Rubia, Ó.; Chatenay, P. Soiling effects comparison between CPV plants in continental and desert climates. AIP Conf. Proc. 2017, 1881, 020005. [Google Scholar]
- Luque-Heredia, I.; Moreno, J.; Magalhaes, P.; Cervantes, R.; Quemere, G.; Laurent, O. 11 Inspira’s CPV Sun Tracking. In Concentrator Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 221–251. [Google Scholar]
- Victoria, M.; Domínguez, C.; Antón, I.; Sala, G. Comparative analysis of different secondary optical elements for aspheric primary lenses. Opt. Express 2009, 17, 6487. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, G.; Bentley, R.; Weatherby, C.; Hunt, A.; Mohring, H.-D.; Klotz, F.; Keuber, P.; Miñano, J.; Alarte-Garvi, E. The development and testing of small concentrating PV systems. Sol. Energy 1999, 67, 23–34. [Google Scholar] [CrossRef]
- Leutz, R.; Suzuki, A.; Akisawa, A.; Kashiwagi, T. Nonideal concentration of nonimaging linear Fresnel lenses. Int. Soc. Opt. Photonics 2001, 4446, 100. [Google Scholar] [CrossRef]
- Lin, M.; Sumathy, K.; Dai, Y.J.; Zhao, X.K. Performance investigation on a linear Fresnel lens solar collector using cavity receiver. Sol. Energy 2014, 107, 50–62. [Google Scholar] [CrossRef]
- Renno, C.; De Giacomo, M. Dynamic Simulation of a CPV/T System Using the Finite Element Method. Energies 2014, 7, 7395–7414. [Google Scholar] [CrossRef]
- Li, Y.; Jing, D. Investigation of the performance of photovoltaic/thermal system by a coupled TRNSYS and CFD simulation. Sol. Energy 2017, 143, 100–112. [Google Scholar] [CrossRef]
- Sweet, T.K.N.; Rolley, M.H.; Li, W.; Paul, M.C.; Gao, M.; Knox, A.R. Experimental characterization and multi-physics simulation of a triple-junction cell in a novel hybrid III:V concentrator photovoltaic–thermoelectric receiver design with secondary optical element. Energy Procedia 2017, 142, 809–814. [Google Scholar] [CrossRef]
- Theristis, M.; O‘donovan, T.S. Electrical-thermal analysis of III–V triple-junction solar cells under variable spectra and ambient temperatures. Sol. Energy 2015, 118, 533–546. [Google Scholar] [CrossRef]
- Ahmad, N.; Ota, Y.; Araki, K.; Lee, K.-H.; Yamaguchi, M.; Nishioka, K. Optical and thermal simulation for wide acceptance angle CPV module. AIP Conf. Proc. 2017, 1881, 20001. [Google Scholar] [CrossRef]
- Baig, H.; Sellami, N.; Chemisana, D.; Rosell, J.; Mallick, T.K. Performance analysis of a dielectric based 3D building integrated concentrating photovoltaic system. Sol. Energy 2014, 103, 525–540. [Google Scholar] [CrossRef]
- Cotal, H.; Frost, J. Heat Transfer Modeling of Concentrator Multijunction Solar Cell Assemblies Using Finite Difference Techniques. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010. [Google Scholar]
- Min, C.; Nuo-Fu, C.; Jin-Xiang, D.; Li-Ying, L. Thermal modeling optimization and experimental validation for a single concentrator solar cell system with a heat sink. Chin. Phys. B 2013. [Google Scholar] [CrossRef]
- Theristis, M.; Fernández, E.F.; Sumner, M.; O‘donovan, T.S. Multiphysics modelling and experimental validation of high concentration photovoltaic modules. Energy Convers. Manag. 2017, 139, 122–134. [Google Scholar] [CrossRef]
- A’Oliverio, L.; Timò, G.; Minuto, A.; Groppelli, P. Thermal Simulations of A Cpv Point Focus Module Using Comsol Multiphysics. Sol. Energy Technol. 2010, 1, 55–64. [Google Scholar]
- Maillet, D.; André, S.; Batsale, J.C.; Degiovann, A.; Moyne, C. Thermal Quadrupoles: Solving the Heat Equation Through Integral Transforms; Wiley: Hoboken, NJ, USA, 2000; ISBN 0471983209. [Google Scholar]
- Bendada, A.; Erchiqui, F.; Lamontagne, M. Pulsed thermography in the evaluation of an aircraft composite using 3D thermal quadrupoles and mathematical perturbations. Inverse Probl. 2005, 21, 857–877. [Google Scholar] [CrossRef]
- Gardarein, J.-L.; Corre, Y.; Rigollet, F.; Le Niliot, C.; Reichle, R.; Andrew, P. Thermal quadrupoles approach for two-dimensional heat flux estimation using infrared and thermocouple measurements on the JET tokamak. Int. J. Therm. Sci. 2009, 48, 1–13. [Google Scholar] [CrossRef]
- Fudym, O.; Pradère, C.; Batsale, J.-C. An analytical two-temperature model for convection–diffusion in multilayered systems: Application to the thermal characterization of microchannel reactors. Chem. Eng. Sci. 2007, 62, 4054–4064. [Google Scholar] [CrossRef]
- Gerardin, J.; Aumeunier, M.-H.; Firdaouss, M.; Gardarein, J.-L.; Rigollet, F. Investigation on reduced thermal models for simulating infrared images in fusion devices. J. Phys. Conf. Ser. 2016, 745, 032019. [Google Scholar] [CrossRef]
- Pailhes, J.; Pradere, C.; Battaglia, J.-L.; Toutain, J.; Kusiak, A.; Aregba, A.W.; Batsale, J.-C. Thermal quadrupole method with internal heat sources. Int. J. Therm. Sci. 2012, 53, 49–55. [Google Scholar] [CrossRef]
- Blanco, M.J. Tonatiuh: An Object Oriented, Distributed Computing, Monte-Carlo Ray Tracer for the Design and Simulation of Solar Concentrating Systems. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.131.5087&rep=rep1&type=pdf (accessed on 16 July 2018).
- Den Iseger, P. Numerical Transform Inversion Using Gaussian Quadrature. Probab. Eng. Inform. Sc. 2006, 20, 1–44. [Google Scholar] [CrossRef]
- Blanco, M.J.; Amieva, J.M.; Mancillas, A. The Tonatiuh Software Development Project: An Open Source Approach to the Simulation of Solar Concentrating Systems. In Computers and Information in Engineering; ASME: New York, NY, USA, 2005; Volume 2005, pp. 157–164. [Google Scholar]
- Garcia, P.; Ferriere, A.; Bezian, J.-J. Codes for solar flux calculation dedicated to central receiver system applications: A comparative review. Sol. Energy 2008, 82, 189–197. [Google Scholar] [CrossRef]
- Osório, T.; Horta, P.; Larcher, M.; Pujol-Nadal, R.; Hertel, J.; Wet Van Rooyen, D.; Heimsath, A.; Schneider, S.; Benitez, D.; Frein, A.; et al. Ray-tracing software comparison for linear focusing solar collectors. AIP Conf. Proc. 2016, 1734, 020017. [Google Scholar] [CrossRef]
- Hecht, E. Optics; Addison-Wesley: Boston, MA, USA, 2002; ISBN 0805385665. [Google Scholar]
- Hornung, T.; Nitz, P. Light diffraction by concentrator Fresnel lenses. Prog. Photovolt. Res. Appl. 2013, 21, 827–837. [Google Scholar] [CrossRef] [PubMed]
- FresnelFactory.com—Fresnel Lens. Available online: http://www.fresnelfactory.com/fresnel-lens-fl220-285-f220-fresnel-magnifying-lens.html (accessed on 7 June 2018).
- Toutain, J.; Battaglia, J.-L.; Pradere, C.; Pailhes, J.; Kusiak, A.; Aregba, W.; Batsale, J.-C. Numerical Inversion of Laplace Transform for Time Resolved Thermal Characterization Experiment. J. Heat Trans. 2011, 133, 044504. [Google Scholar] [CrossRef]
- Davis, A. Fresnel lens solar concentrator derivations and simulations. In Novel Optical Systems Design and Optimization XIV; Koshel, R.J., Gregory, G.G., Eds.; International Society for Optics and Photonics: Washington, DC, USA, 2011; Volume 8129, p. 81290J. [Google Scholar]
- Parretta, A. Optics of solar concentrators Part I: Theoretical models of light collection. Int. J. Opt. Appl. 2013, 3, 27–39. [Google Scholar] [CrossRef]
- Parretta, A.; Antonini, A. Optics of solar concentrators. Part II: Models of light collection of 3D-CPCs under direct and collimated beams. Int. J. Opt. Appl. 2013, 3, 72–102. [Google Scholar] [CrossRef]
- Goodfellow Germanio. Available online: http://www.goodfellow.com/S/Germanio.html (accessed on 8 June 2018).
- Goodfellow Aluminio. Available online: http://www.goodfellow.com/S/Aluminio.html (accessed on 8 June 2018).
- Wakefield-vette Thermal Joint Compund. Available online: http://www.wakefield-vette.com/products/productlist/productdetails/tabid/341/CategoryID/153/ProductID/308/Default.aspx (accessed on 8 June 2018).
- Culham, J.R.; Yovanovich, M.M.; Lee, S. Thermal Modeling of Isothermal Cuboids and Rectangular Heat Sinks Cooled by Natural Convection. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1995, 18, 559–566. [Google Scholar] [CrossRef]
- Silverman, T.J.; Bosco, N.; Kurtz, S. Relative lifetime prediction for CPV die-attach layers. In Proceedings of the 2012 IEEE International Reliability Physics Symposium (IRPS), Anaheim, CA, USA, 15–19 April 2012. [Google Scholar]
- Bosco, N.; Silverman, T.J.; Kurtz, S. Modeling Thermal Fatigue in CPV Cell Assemblies Preprint. In Modeling Thermal Fatigue in Cpv Cell Assemblies; National Renewable Energy Lab.: Golden, CO, USA, 2011; p. 16560. [Google Scholar]
- Xu, X.; Meyers, M.M.; Sammakia, B.G.; Murray, B.T.; Chen, C. Performance and Reliability Analysis of Hybrid Concentrating Photovoltaic/Thermal Collectors with Tree-Shaped Channel Nets’ Cooling System. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 967–977. [Google Scholar] [CrossRef]
- Xu, X.; Meyers, M.M.; Sammakia, B.G.; Murray, B.T. Thermal Modeling and Life Prediction of Water-Cooled Hybrid Concentrating Photovoltaic/Thermal Collectors. J. Sol. Energy Eng. 2012, 135, 011010. [Google Scholar] [CrossRef]
- Cao, M.; Butler, S.; Benoit, J.T.; Jiang, Y.; Radhakrishnan, R.; Chen, Y.; Bendapudi, S.; Horne, S. Thermal Stress Analysis/Life Prediction of Concentrating Photovoltaic Module. J. Sol. Energy Eng. 2008, 130, 021011. [Google Scholar] [CrossRef]
- Ota, Y.; Nishioka, K. Estimation of thermal stress in concentrator cells using structural mechanics simulation. AIP Conf. Proc. 2014, 1616, 25–28. [Google Scholar] [CrossRef]
- Renno, C.; Landi, G.; Petito, F.; Neitzert, H.C. Influence of a degraded triple-junction solar cell on the CPV system performances. Energy Convers. Manag. 2018, 160, 326–340. [Google Scholar] [CrossRef]
- Bosco, N.; Kurtz, S.R. Quantifying the thermal fatigue of CPV modules. AIP Conf. Proc. 2011, 1277, 225–228. [Google Scholar]
- Peharz, G.; Ferrer Rodríguez, J.P.; Siefer, G.; Bett, A.W. Investigations on the temperature dependence of CPV modules equipped with triple-junction solar cells. Prog. Photovolt. Res. Appl. 2011, 19, 54–60. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).