In this section, the four ensemble methods that are described above are applied to the electricity consumption of a small campus university to evaluate the adequacy of each technique in this type of customers. Specifically, we will focus on 48-h-ahead predictions in order to apply them to the context of Direct Market Consumers, although different prediction horizons will be also considered for the case of XGBoost method. Some other aspects, such us predictors importance or parameter selection, for each method are also developed.
Firstly, in this section, the customer in study is introduced. Secondly, the load data, predictors, and some goodness of fit measurements are depicted. Finally, the forecasting results for the case study are shown.
3.1. Customer Description: A Campus University
The campus “Alfonso XIII” of the Technical University of Cartagena (UPCT, Spain) comprises seven buildings ranging from 2000 m2 to 6500 m2 and a meeting zone (10,000 m2). Buildings are of two kinds: naturally ventilated cellular (individual windows, local light switches, and local heating control) and naturally ventilated open-plan (office equipment, light switched in longer groups, and zonal heating control). This campus has an overall surface larger than 35,500 m2 to fulfill the needs of different Faculties for classrooms, departmental offices, administrative offices, and laboratories for 1800 students and 200 professors. Unfortunately, the age of buildings (50 years old in four cases) and architectural conditioning works are far from actual energy efficiency standards, specifically in the two main electrical end-uses of the building: air conditioning/space heating (low performance, insufficient heat insulation, and an important cluster of individual appliances for offices and small laboratories) and lighting (where conventional magnetic ballasts and fluorescent are still used at a great extend).
With respect to the share of end-uses in the “Campus Alfonso XIII” of UPCT, heating, ventilation, and air conditioning (HVAC) is the largest energy end-use (this trend is the same both in the residential and non-residential buildings in Spain and other countries, see
Table 1) with 40–50% of overall demand; lighting follows with 25–30%, electronics and office equipment 7–12% and other appliances with 8–10% (i.e., vending machines, refrigeration, water heaters WH, laboratory equipment, etc.). Notice that building type is critical in how energy end uses are distributed in each specific building.
Table 1 shows a comparative of end-uses in office buildings in three countries [
39] and in the analysed case, campus “Alfonso XIII”.
3.2. Data Description
Data used in this paper correspond to the campus Alfonso XIII of the Technical University of Cartagena, as described in the previous subsection. Hourly load data from 2011 to 2016 (both included) were analyzed, obtained from the retailer electric companies (Nexus Energía S.A. and Iberdrola S.A.). It is well known that electricity consumption is related to several exogenous factors, such as the hour of the day, the day of the week, or the month of the year, and therefore these factors must be taken into account in the design of the prediction model. Temperature is a factor that might affect the electricity consumption (cooling and heating of the university buildings). Thus, the hourly temperature was considered as an input in the forecasting model, as provided by AEMET (Agencia Española de Meteorología) for the city of Cartagena (where the campus university is located), from 2011 to 2016. Besides, depending on the end-uses of the customer in study, some other features can be relevant for the load. For example, in this case study, different types of holidays or special days have been distinguished throughout binary variables (see
Table 2 for a detailed description).
Three different measurements given in (9), (10), and (11) were used to obtain the accuracy of the forecasting models: the root mean square error (
RMSE), the
R-squared (percentage of the variability explained by the forecasting model), and the mean absolute percentage error (
MAPE). Although the
MAPE is the most used error measure, see [
1], the squared error measures might be more fitting because the loss function in Short Term Load Forecasting is not linear, see [
13]. Some descriptive measures of the errors (such as the mean, skewness, and kurtosis) were also considered to evaluate the performance of the forecasting methods.
The root mean square error is defined by:
the
R-squared is given by:
and the mean absolute percentage error is defined by:
where
is the number of data,
is the actual load at time
, and
is the forecasting load at time
.
3.3. Forecasting Results
Data from 1 January 2011 to 31 December 2015 were selected as the training period in all methods, whereas data from 1 January 2016 to 31 December 2016 constituted the test period. In this subsection, firstly a prediction horizon of 48 h is established, whose forecasting results will be used in the next section dealing with Direct Market Consumers. In this case, we consider 53 predictors (see
Table 2): 23 dummies for the hour of the day, six dummies for the day of the week, 11 dummies for the month of the year, five dummies for special days (FH1, …, FH5), two predictors of historic temperatures (lags 48 h and 72 h), and six predictors of historic loads (lags 48 h, 72 h, 96 h, 120 h, 144 h, and 168 h).
For each ensemble method, the parameter selection has been developed and measures of variable importance have been obtained (see
Table 3 for the meaning of each term). In order to have reproducible models and comparable results, the same
seed was selected in all procedures that require random sampling. In the case of bagging and random forest, we have selected an optimal number of trees (
ntree) through the OOB error estimate and we have ordered the predictors according to the node impurity importance measure, see [
28]. For bagging, the number of predictors that are considered at each split must be the total number of predictors, whereas in the case of random forest, the optimal parameter has been selected using the OOB error estimate for different values of
mtry. In the case of conditional forest, the conditional variable importance measure introduced in [
40] has been considered, which better reflects the true impact of each predictor in presence of correlated predictors.
While in bagging and random forest the OOB error was used to tune the parameters, in the case of conditional forest and XGBoost the parameters were tuned by means of cross validation with five folds (approximately one year in each fold). As for conditional forest, only two parameters need to be tuned (
ntree and
mtry), but in XGBoost, there are more parameters to tune. Although one can apply cross validation taking into account a multi-dimension grid with all of the parameters to tune (this approach would imply a high computational cost), we considered a simplification of the search selecting subsample = 0.5, max depth = 6 (appropriate in most problems) and looking for a good combination of “
eta” and “
nrounds”, see
Table 4. The rest of parameters of the method were set up by default, according to the R package [
38]. In the case of XGBoost, features have been ordered by decreasing importance while using the gain measure defined in [
36].
Table 4 shows the results of the parameter selection for the XGBoost method. Recall that a lower learning rate
eta implies a greater number of iterations
nround, but a too large
nround can lead to overfitting. Combination (
eta = 0.02,
nrounds = 3400) provided the lowest
RMSE and the highest
R-squared scores for the test data, whereas (
eta = 0.01,
nrounds = 5700) got the lowest
MAPE. However, any pair of parameters in
Table 4 could be appropriate because they lead similar accuracy.
Table 5 and
Table 6 show the results that were obtained for the best parameter selection of each ensemble method. They also include the comparison with traditional and simple forecasting models, such as naïve (prediction at hour
h is given by the real consumption at hour
h-168) and multiple linear regression (MLR) with the same predictors, as used in the ensemble methods. According to
Table 5, XGBoost method provides nearly null bias, more symmetry of the errors than the other ensemble methods and the traditional ones, as well as values of the kurtosis that are closer to zero (considered desired properties for residual in forecasting techniques).
Although bagging and random forest provide the best accuracy in the training dataset (see
Table 6), XGBoost fits better in the test dataset (in this case, gradient boosting avoid more overfitting than the others ensemble methods due to a suitable selection of the parameters). Furthermore, when comparing the results of random forest and XGBoost, we can state that the latter fits lightly better and it is twelve times faster to compute.
Table 6 also shows that all ensemble methods significantly improve the accuracy of the predictions with respect to MLR and naïve models.
It is also important to remark that, for all methods, roughly half of the predictors accumulate more that 99% of the relative importance. In the case of ensemble methods, the corresponding importance measure has been computed (for example, the node impurity for random forest and the gain for XGBoost), whereas in the case of MLR, the forward stepwise selection method and R-squared were used to evaluate the relative importance of each predictor. We can also highlight the following aspects: the electricity consumption at the same hour of the previous week (predictor LOAD_lag_168) results the most important feature in all methods, the electricity load with lags 48 h and 144 h appear among the five most important predictors in all of the ensemble methods, and finally, the presence of the features WH6, WH7, FH1, and FH3 among the five most important predictors for different methods evidences that calendar variables and types of holidays are essential for this kind of customer. However, the temperature has a reduced effect on the response because it appears between the 10th and 12th position of importance (depending on the method), with a relative importance of around 1%.
In order to compare the accuracy for the different types of day, the days of the test data (2016) were divided in two groups: special days, which include weekends, August (official academic holidays), and all days that are determined by the dummy variables FH1, …, FH5 in
Table 2; and, regular days, which include the rest of the days. Results are exposed in
Table 7. Notice that the lowest
MAPE scores are always reached for regular days.
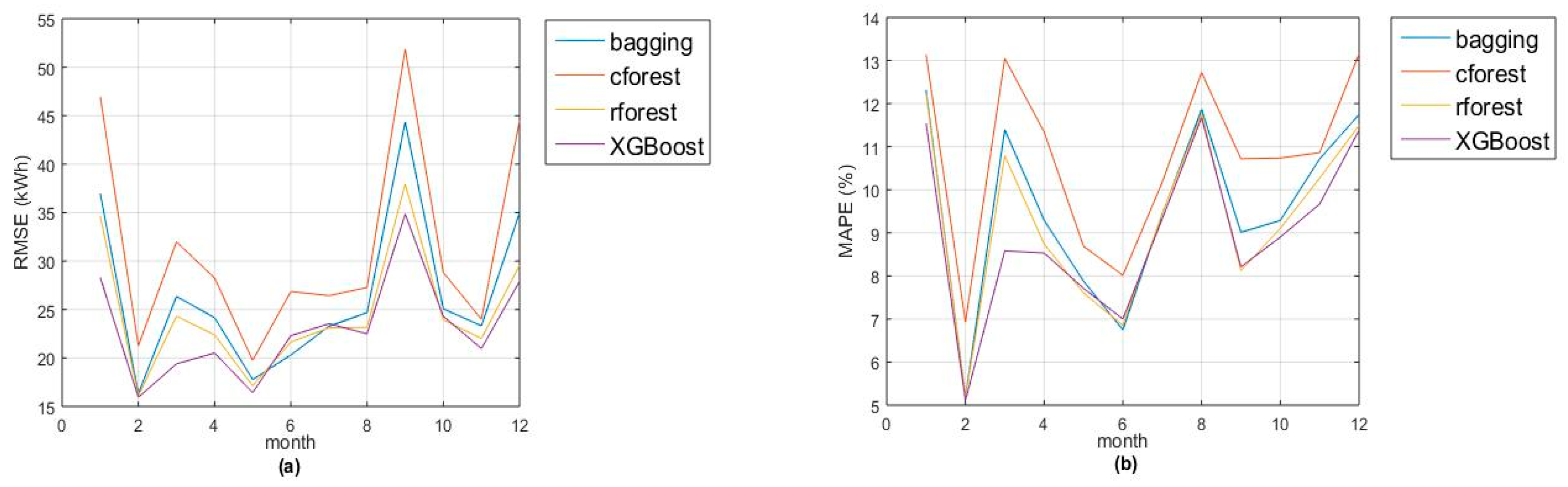
Figure 1a,b show the monthly evolution of two goodness-of-fit measures (
RMSE and
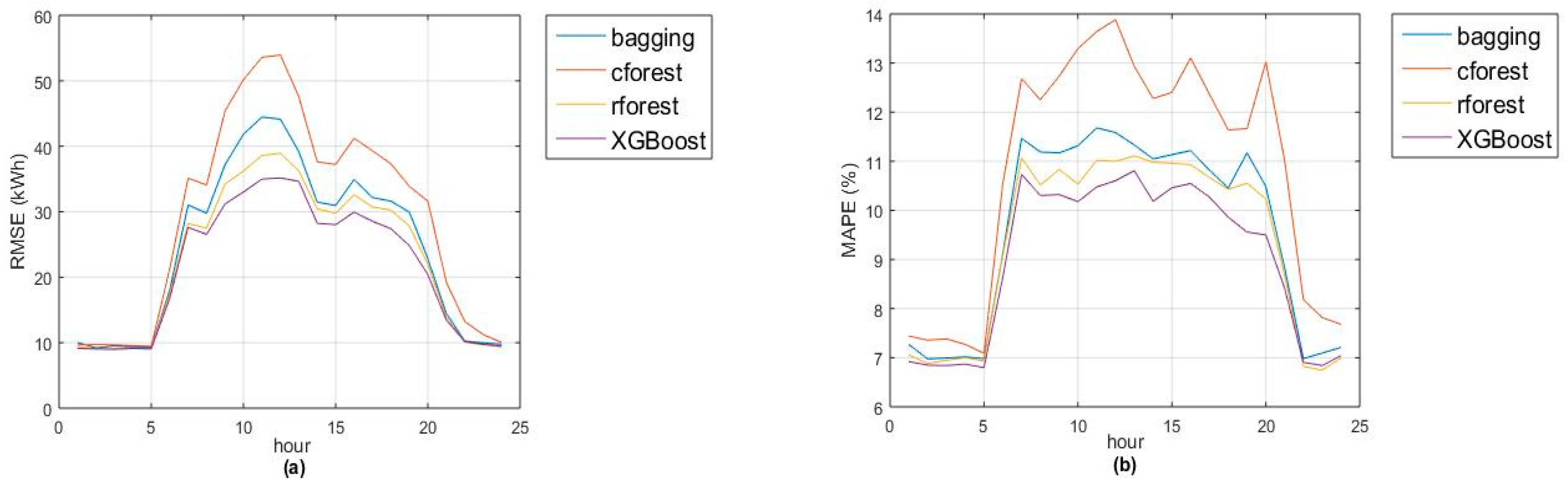
MAPE). Remark that accuracies of random forest and XGBoost are quite similar, with greatest differences in January and March (due to lack of accuracy in Christmas and Eastern days). Also, the models fit better for night hours (from 10 p.m. to 5 a.m.) due to the absence of activity during that period (see
Figure 2a,b).
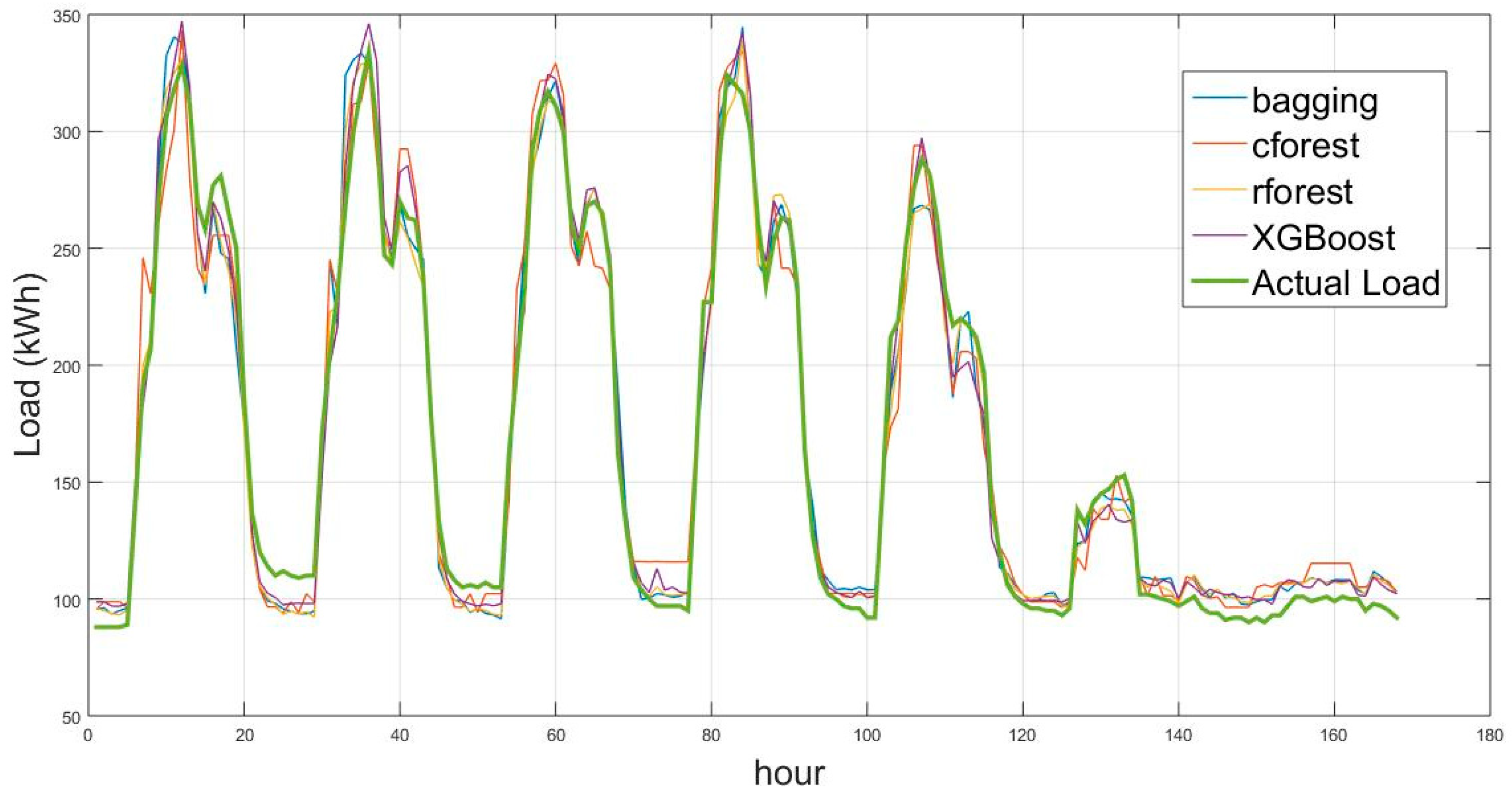
As an example,
Figure 3 shows the actual and prediction load for a complete week in May 2016.
Finally, in this section, we analyze the adecuacy of the forecasting method XGBoost for the case study when considering different prediction horizons (1 h, 2 h, 12 h, 24 h, and 48 h). In all cases, we selected the same parameters:
subsample = 0.5,
max_depth = 6,
eta = 0.05 and
nrounds = 1700. Accuracy results for the training and test datasets are given in
Table 8 as well as the most important predictors in each case.
Obviously, the best accuracies are obtained for the shortest prediction horizon (1 h), where the most important feature is the consumption at the previous hour (lag = 1) with more than 85% of relative importance. However, for the rest of prediction horizons, the most important predictor is, once again, the load with lag 168 h.