Scalable Clustering of Individual Electrical Curves for Profiling and Bottom-Up Forecasting
Abstract
1. Introduction
1.1. Industrial Context
1.2. Individual Electrical Consumption Data: A State-of-the-Art
2. Bottom-Up Forecasting from Smart Meter Data: Big Picture
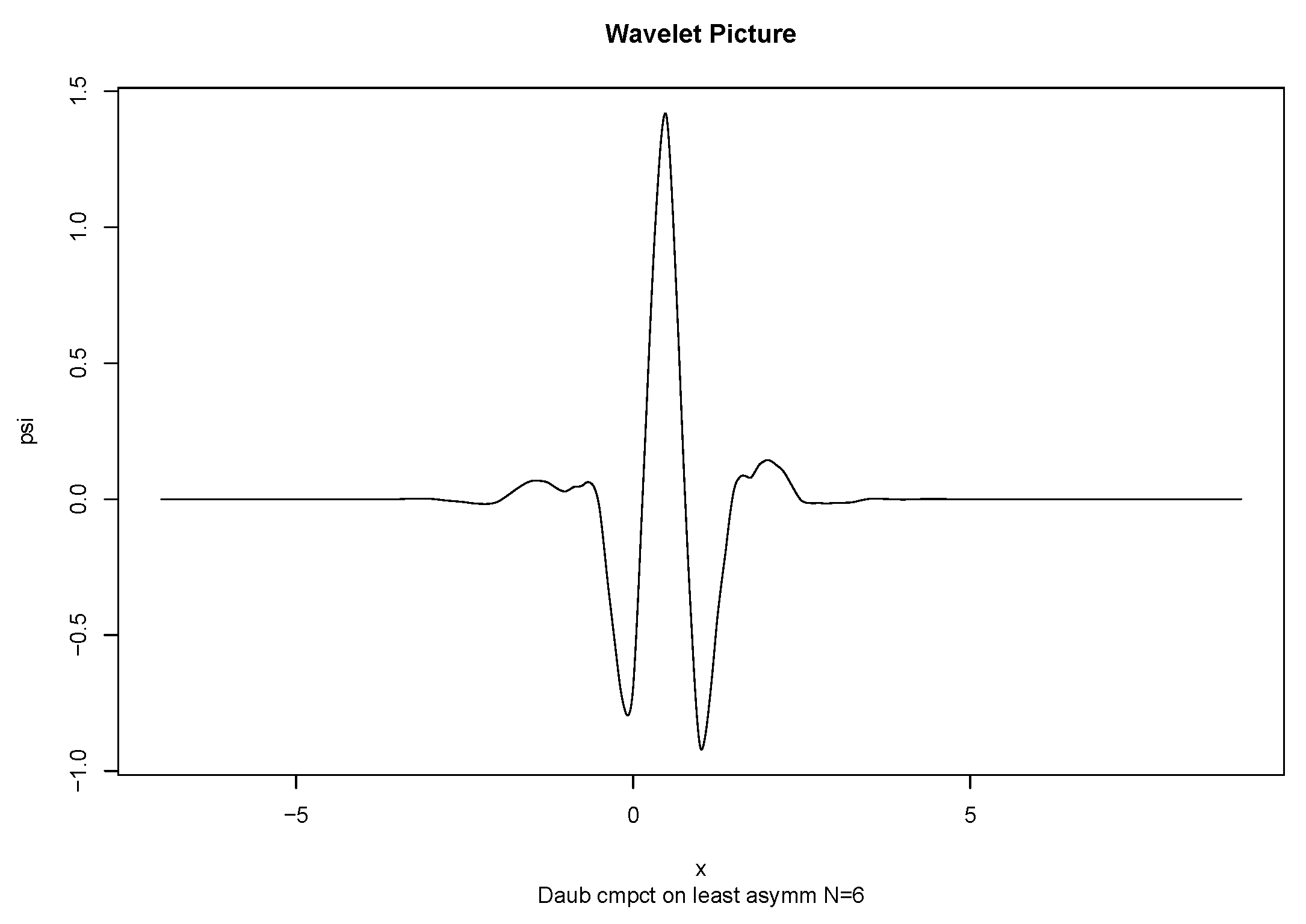
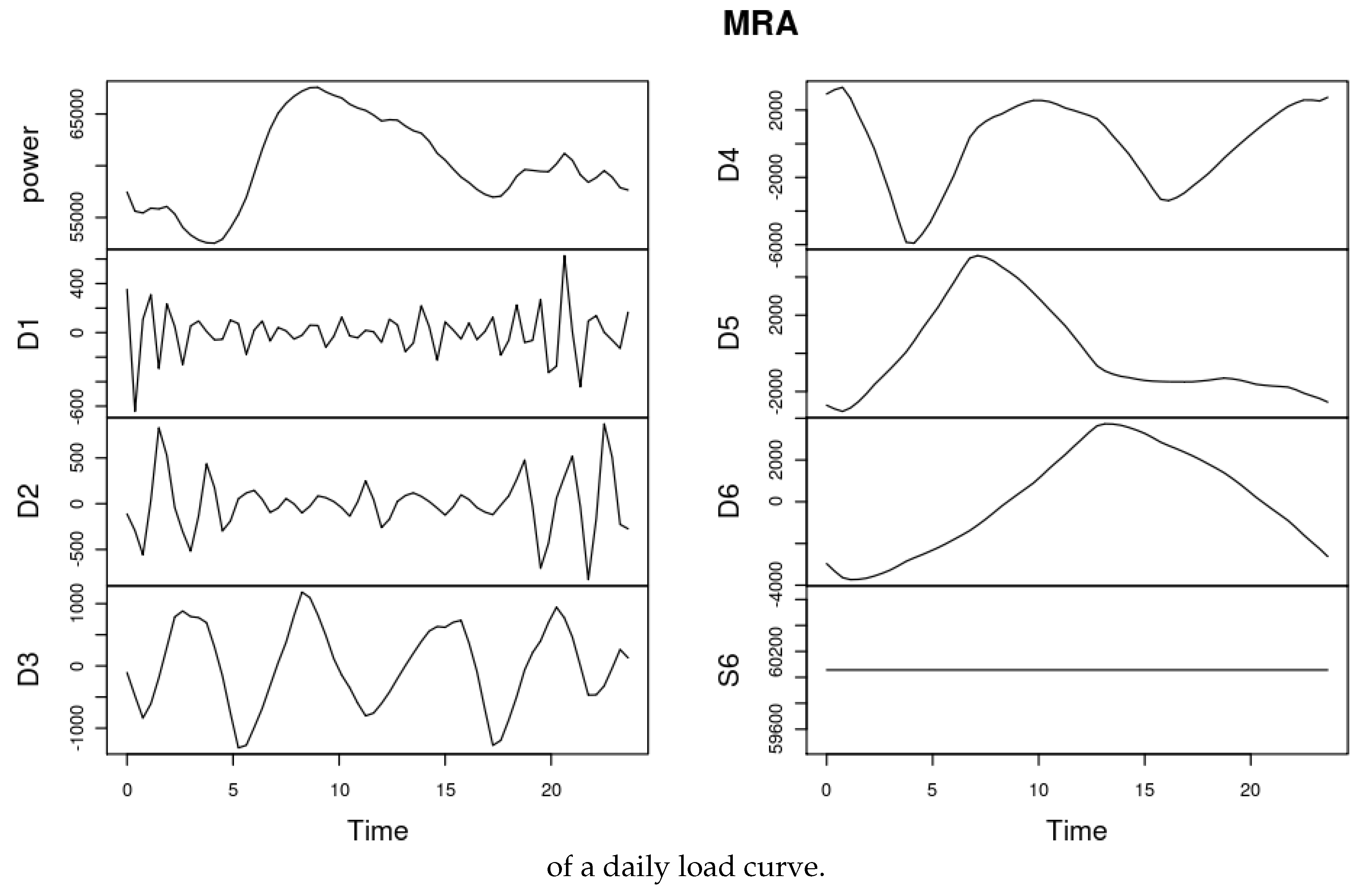
3. Wavelets
4. KWF
4.1. From Discrete to Functional Time Series
4.2. Functional Model KWF
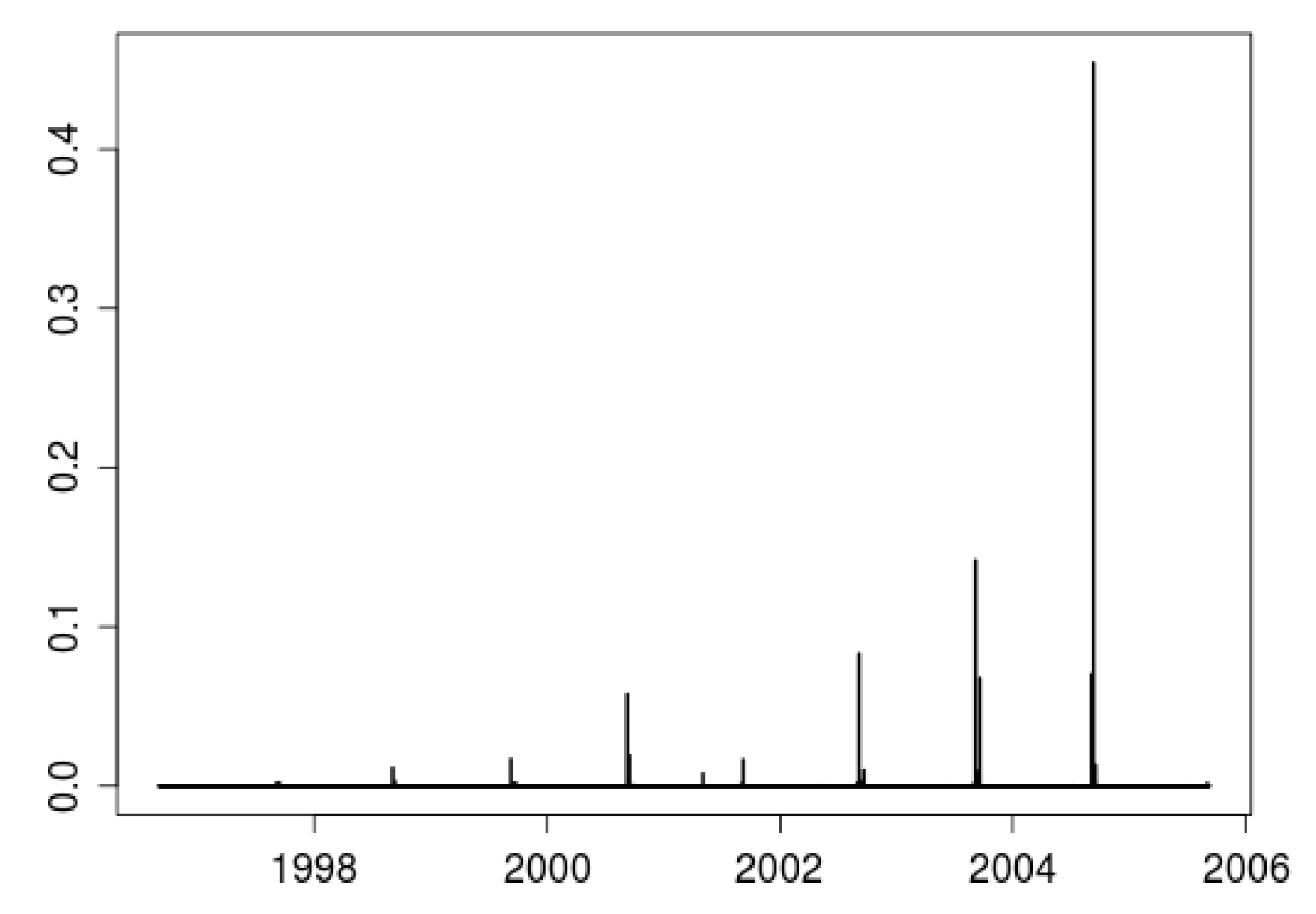
4.2.1. Stationary Case
First step.
Second step.
4.2.2. Beyond the Stationary Case
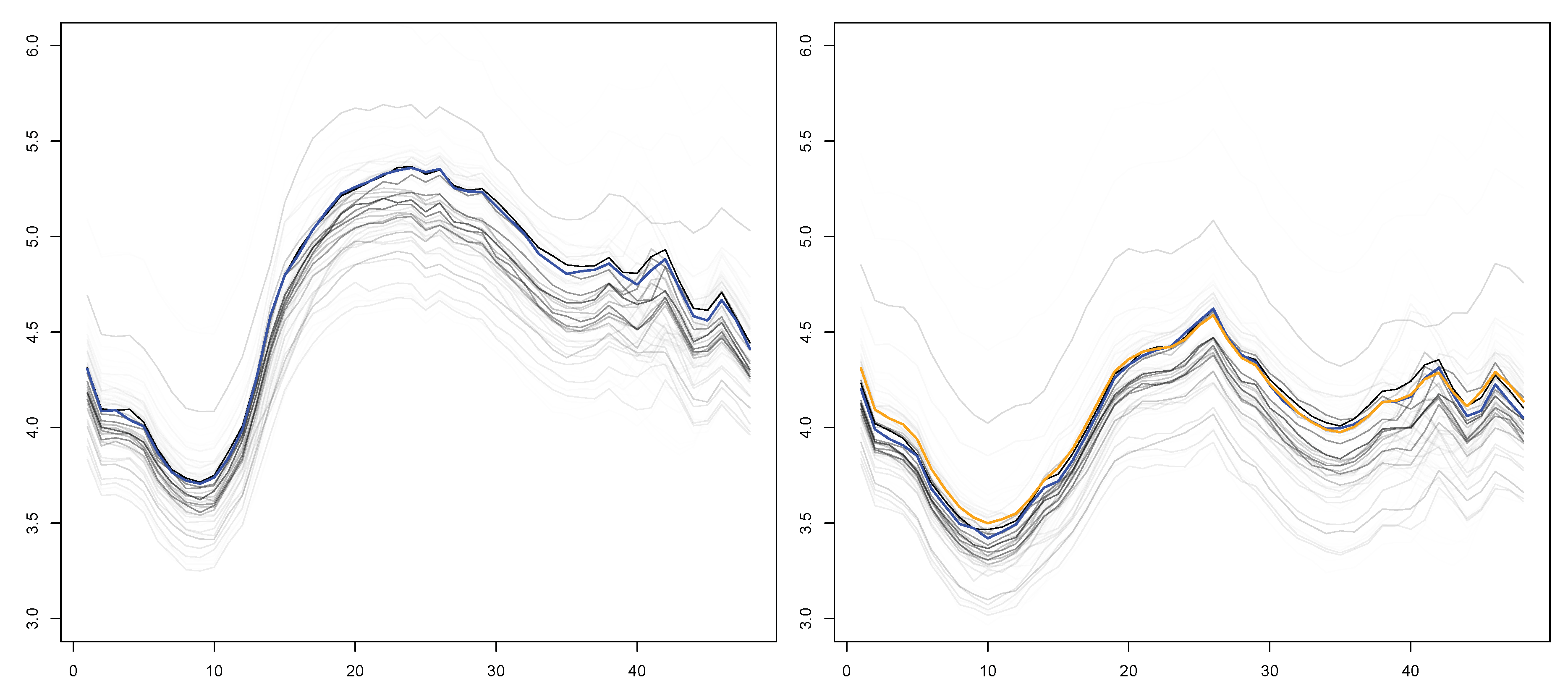
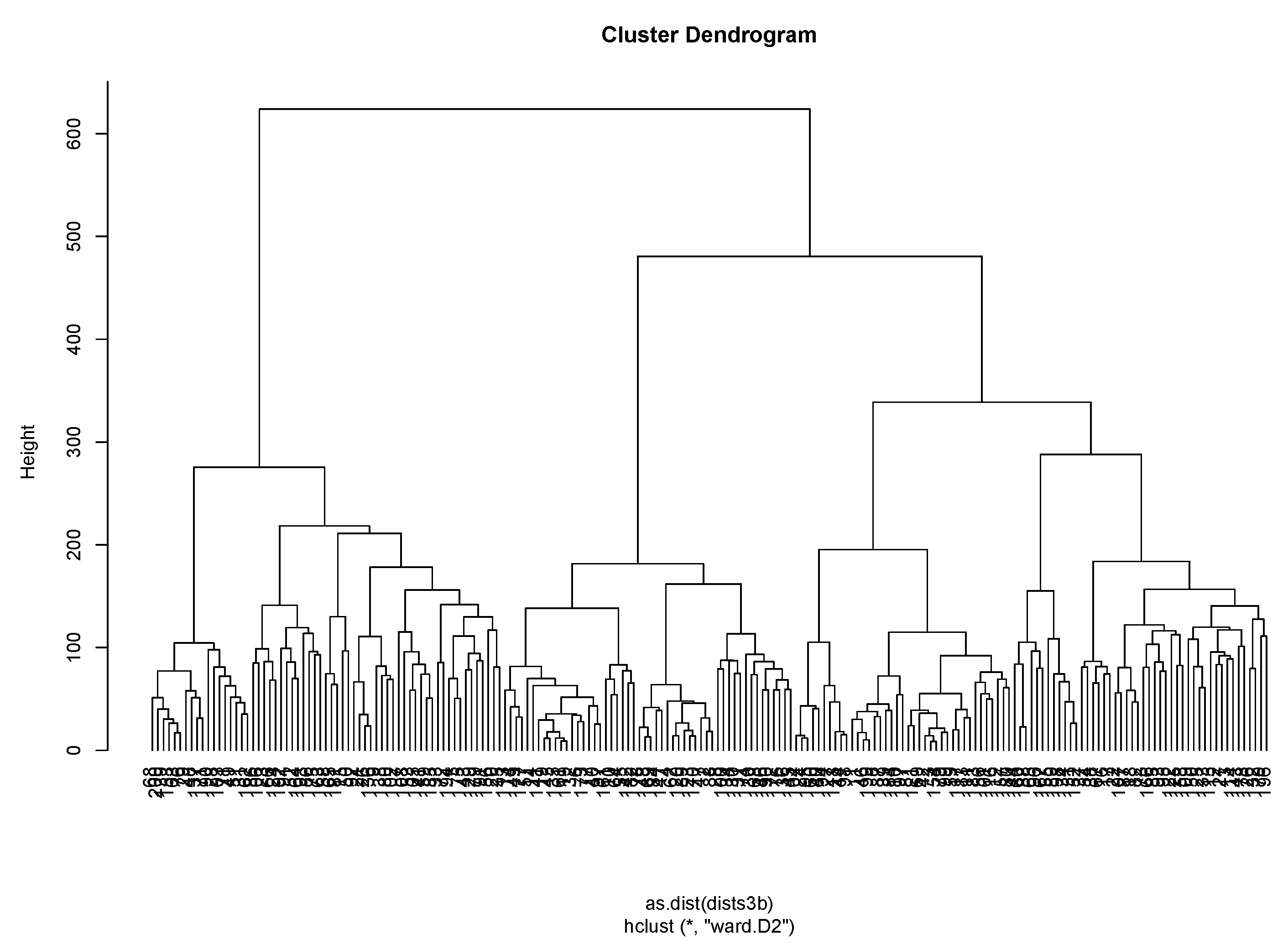
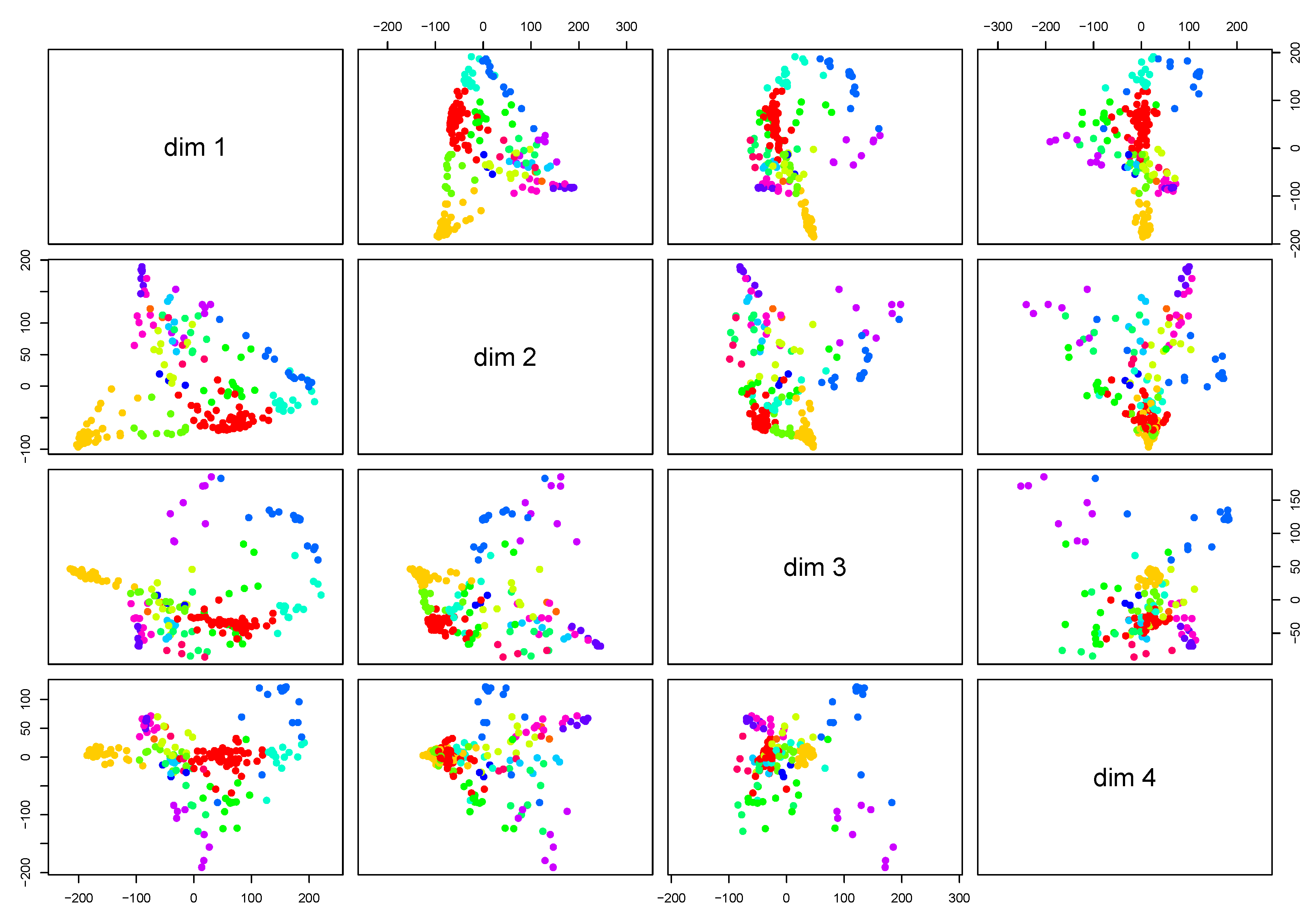
5. Clustering Electrical Load Curves
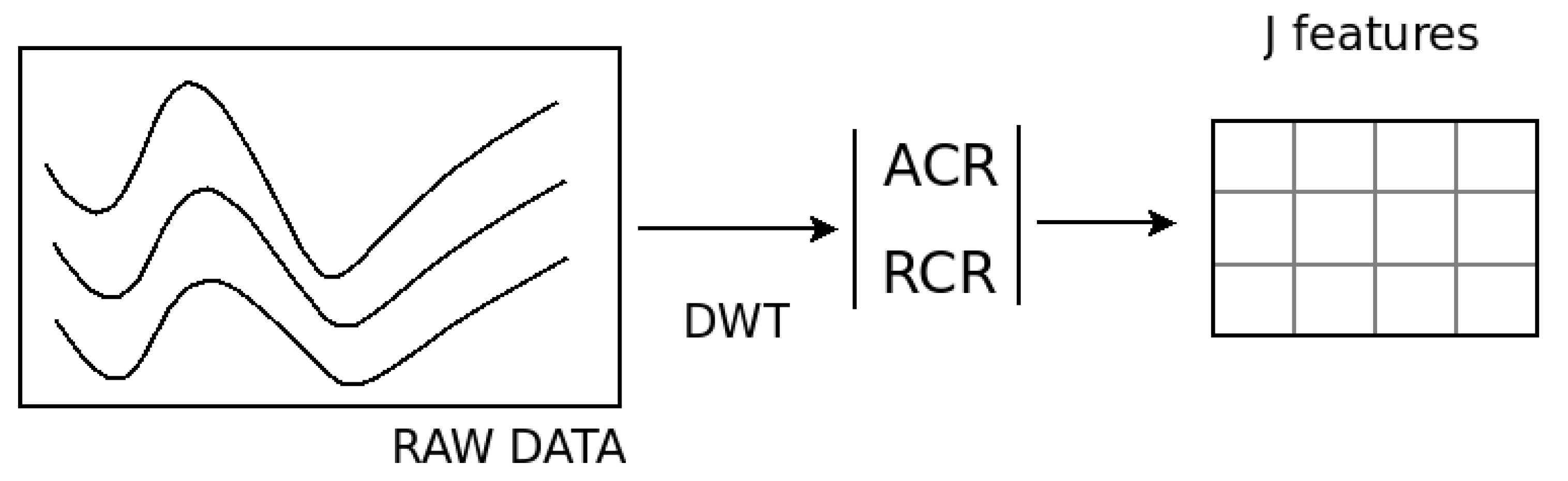
5.1. Clustering by Feature Extraction
5.2. Clustering Using a Dissimilarity Measure
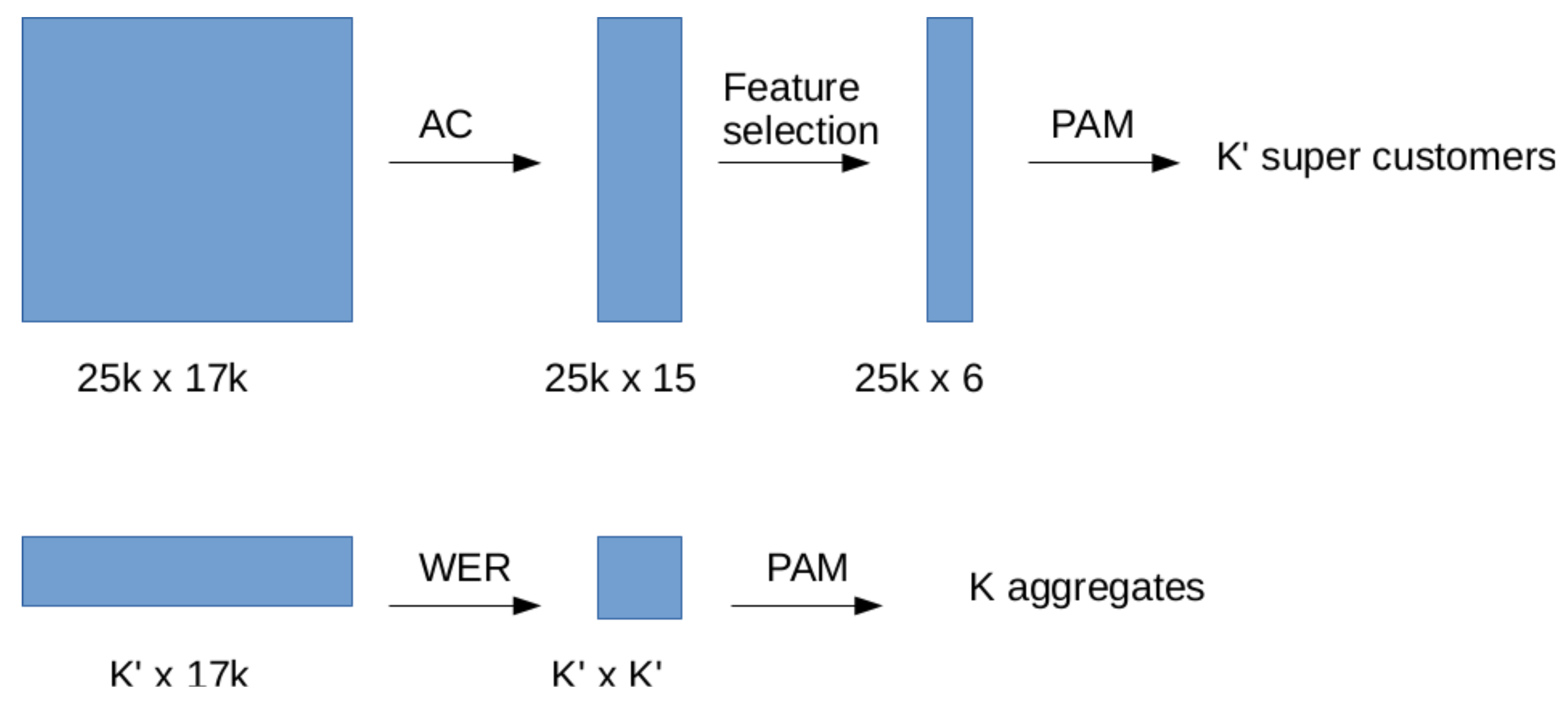
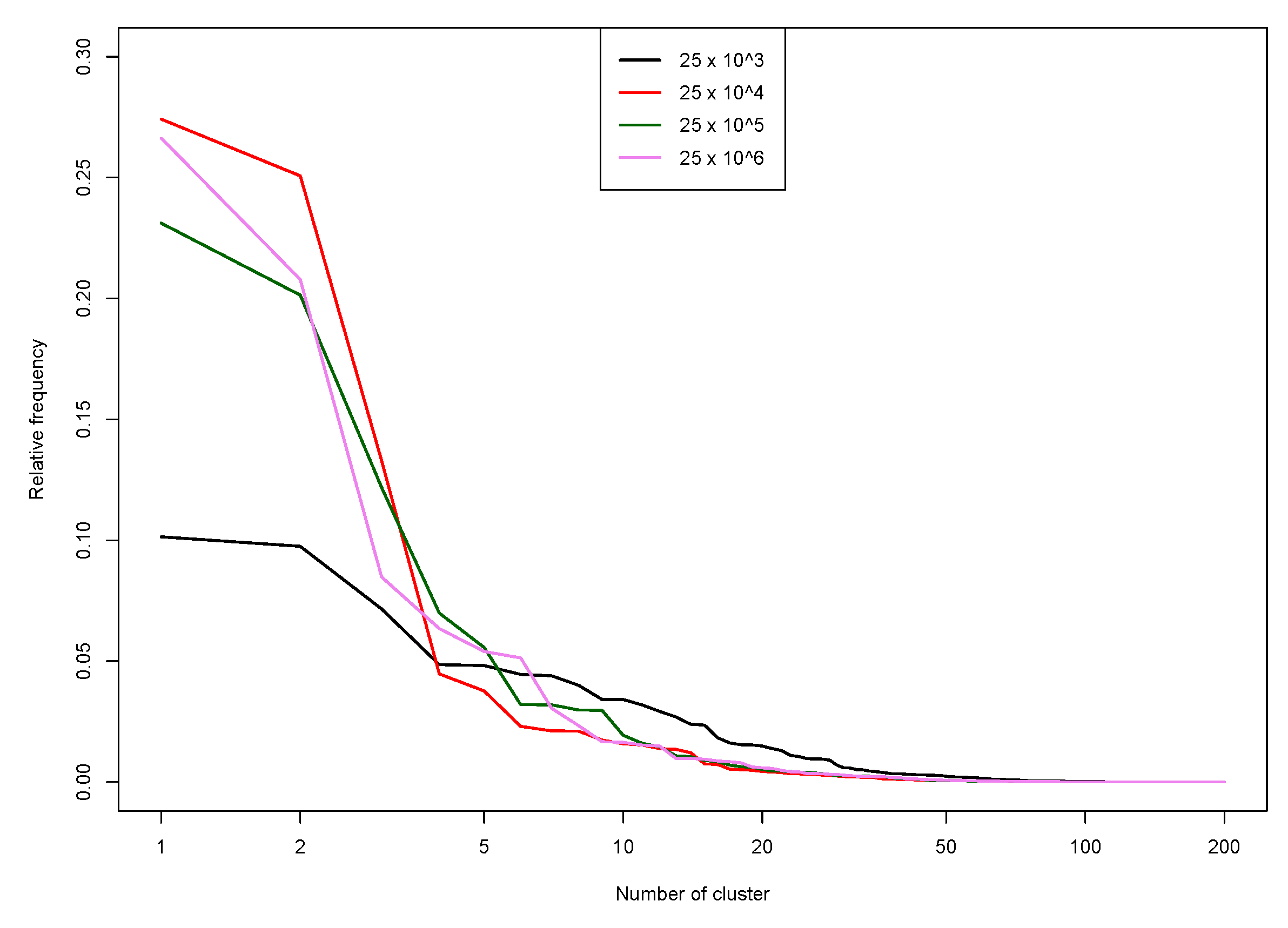
6. Upscaling
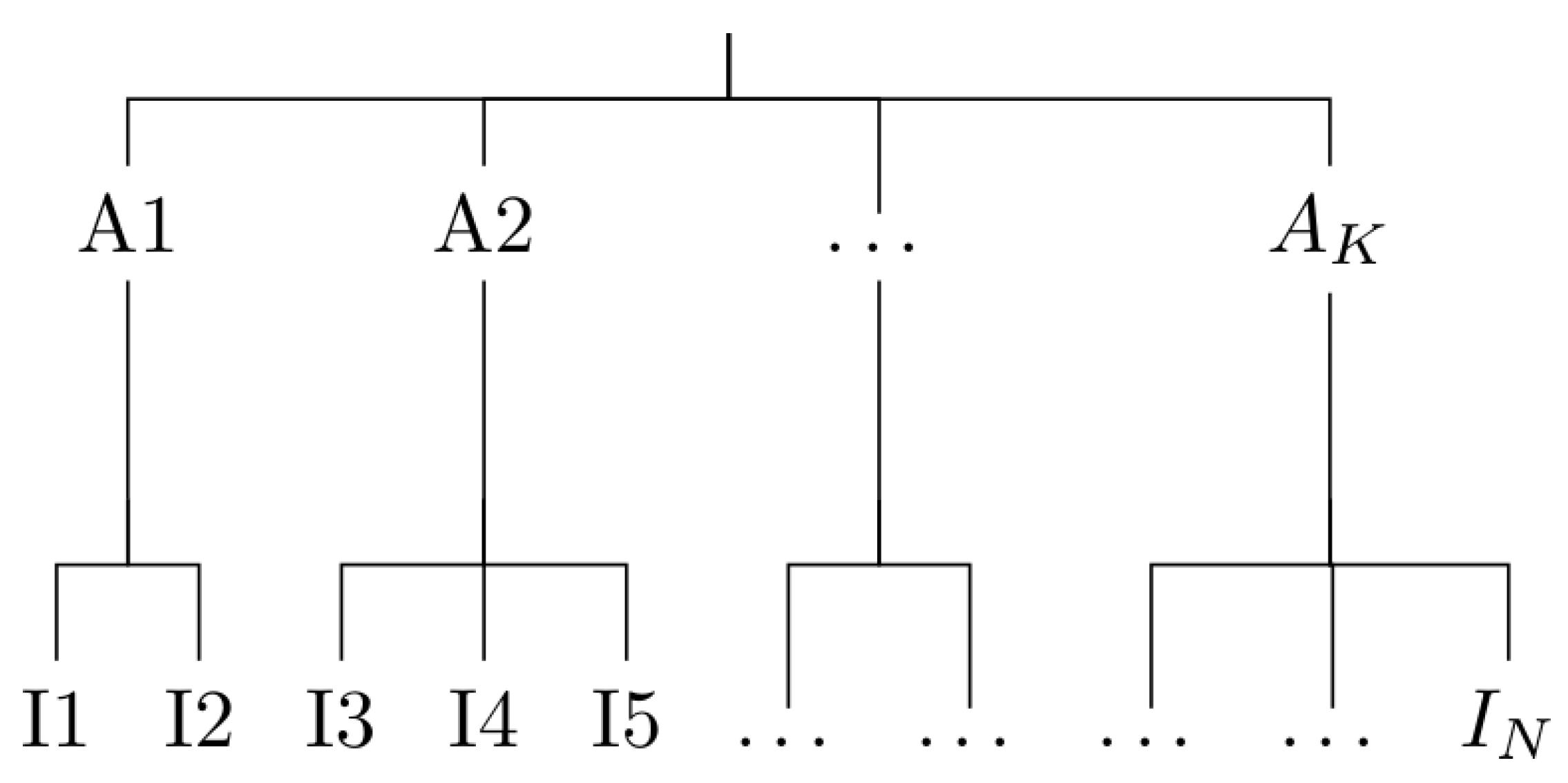
6.1. Algorithm Description
- Data serialization. Time series are given in a verbose by-column format. We re-code all of them in a binary file (if suitable), or a database.
- Dimensionality reduction. Each series of length N is replaced by the energetic coefficients defined using a wavelet basis. Eventually a feature selection step can be performed to further reduction on the number of features.
- Chunking. Data is chunked into groups of size at most , where is a user parameter (we use in the next section experiments).
- Clustering. Within each group, the PAM clustering algorithm is run to obtain clusters.
- Gathering. A final run of PAM is performed to obtain mediods, out of the mediods obtained on the chunks..
6.2. Code Profiling
6.3. Proposed Solutions
- an ASCII file, one sample per line; very fast, but data retrieval will depend on line number;
- a binary format (3 or 4 octets per value); compression is unadvised since it would increase both preprocessing time and (by a large amount) reading times;
- a database (this is the slowest option), so that retrieval can be very quick.
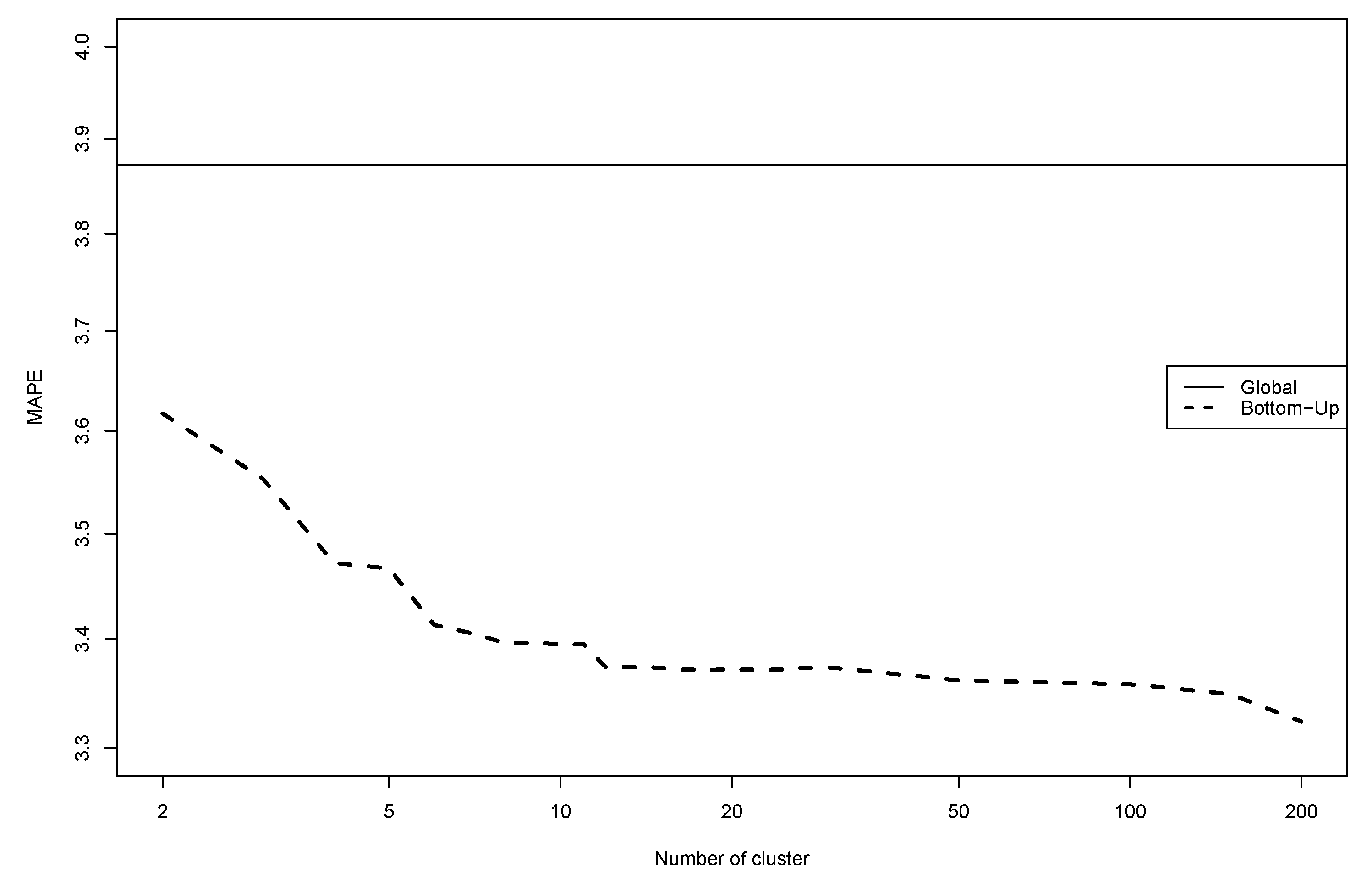
7. Forecasting French Electricity Dataset
7.1. Data Presentation
7.2. Numerical Experiments
8. Discussion
8.1. Choice of Methods
- the wavelet decomposition to represent functions and compute dissimilarities. Of course, several other choices could be interesting, such as splines for bases of functions which are independent of the data or even some data-driven bases like those coming from functional principal component analysis. With respect to these two classical alternatives, (more or less related to a monoscale strategy) the choice of wavelets allows simultaneously a parsimonious representation capturing local features of the data as well as redundant one delivering a more accurate multiscale representation. In addition, from a computational viewpoint, DWT is a very fast: of linear complexity. So to design the super-customers the discrete transform is good enough, for the final clusters, the continuous transform leads to better results. Let us remark that combining wavelets and clustering has recently been considered in [36] from a different viewpoint: details and approximations of the daily load curves are clustered separately leading to two different partitions which are then fused.
- the PAM algorithm and the hierarchical clustering to build the clusters are of very common use and well adapted to their specific role in the whole strategy. It should be noted that the use of PAM to construct the super customers must necessarily be biased towards a large number of clusters (defining the super customers) so it is useless to include sophisticated model-selection rules to choose an optimal number of clusters since the strategy is used only to define a sufficiently large number of clusters.
- the Kernel-Wavelet-Functional (KWF) method to forecast time-series. The global forecasting scheme is clearly fully modular and then, KWF could be replaced by any other time-series model forecasting. The model must be flexible and easy to automatically be tuned because the modeling and forecasting must be performed in each cluster in a rather blind way. The main difficulty with KWF is to introduce exogenous variables. We could imagine to include a single one quite easily but not a richer family in full generality. Nevertheless, it is precisely when dealing with models corresponding to some specific clusters that it could be of interest to use exogenous variables especially informative, for example describing meteo at a local level or some specific market segment. Therefore, some alternatives could be considered, such as generalized additive models (see [37] for a strategy which could be plugged into our scheme).
8.2. Multiscale Modeling and Forecasting
8.3. How to Handle Non Stationarity?
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yan, Y.; Qian, Y.; Sharif, H.; Tipper, D. A Survey on Smart Grid Communication Infrastructures: Motivations, Requirements and Challenges. IEEE Commun. Surv. Tutor. 2013, 15, 5–20. [Google Scholar] [CrossRef]
- Mallet, P.; Granstrom, P.O.; Hallberg, P.; Lorenz, G.; Mandatova, P. Power to the People!: European Perspectives on the Future of Electric Distribution. IEEE Power Energy Mag. 2014, 12, 51–64. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Hong, T.; Kang, C. Review of Smart Meter Data Analytics: Applications, Methodologies, and Challenges. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Jamme, D. Le compteur Linky: Brique essentielle des réseaux intelligents français. In Proceedings of the Office Franco-Allemand Pour La Transition énergétique, Berlin, Germany, 11 May 2017. [Google Scholar]
- Alahakoon, D.; Yu, X. Smart Electricity Meter Data Intelligence for Future Energy Systems: A Survey. IEEE Trans. Ind. Inform. 2016, 12, 425–436. [Google Scholar] [CrossRef]
- Ryberg, T. The Second Wave of Smart Meter Rollouts Begin in Italy and Sweden. 2017. Available online: https://www.metering.com/regional-news/europe-uk/second-wave-smart-meter-rollouts-begins-italy-sweden/ (accessed on 1 June 2018).
- Jiang, H.; Wang, K.; Wang, Y.; Gao, M.; Zhang, Y. Energy big data: A survey. IEEE Access 2016, 4, 3844–3861. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Liao, T.W. Clustering of time series data a survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Jacques, J.; Preda, C. Functional Data Clustering: A Survey. Adv. Data Anal. Classif. 2014, 8, 231–255. [Google Scholar] [CrossRef]
- Chicco, G. Overview and performance assessment of the clustering methods for electrical load pattern grouping. Energy 2012, 42, 68–80. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, S.; Shen, C. A review of electric load classification in smart grid environment. Renew. Sustain. Energy Rev. 2013, 24, 103–110. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Kang, C.; Zhang, M.; Wang, K.; Zhao, Y. Load profiling and its application to demand response: A review. Tsinghua Sci. Technol. 2015, 20, 117–129. [Google Scholar] [CrossRef]
- Figueiredo, V.; Rodrigues, F.; Vale, Z.; Gouveia, J.B. An electric energy consumer characterization framework based on data mining techniques. IEEE Trans. Power Syst. 2005, 20, 596–602. [Google Scholar] [CrossRef]
- Mutanen, A.; Ruska, M.; Repo, S.; Jarventausta, P. Customer Classification and Load Profiling Method for Distribution Systems. IEEE Trans. Power Deliv. 2011, 26, 1755–1763. [Google Scholar] [CrossRef]
- Rhodes, J.D.; Cole, W.J.; Upshaw, C.R.; Edgar, T.F.; Webber, M.E. Clustering analysis of residential electricity demand profiles. Appl. Energy 2014, 135, 461–471. [Google Scholar] [CrossRef]
- Kwac, J.; Flora, J.; Rajagopal, R. Household Energy Consumption Segmentation Using Hourly Data Smart Grid. IEEE Trans. 2014, 5, 420–430. [Google Scholar]
- Sun, M.; Konstantelos, I.; Strbac, G. C-Vine copula mixture model for clustering of residential electrical load pattern data. In Proceedings of the 2017 IEEE Power Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar] [CrossRef]
- Alzate, C.; Sinn, M. Improved electricity load forecasting via kernel spectral clustering of smartmeter. In Proceedings of the International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 943–948. [Google Scholar]
- Chaouch, M. Clustering-Based Improvement of Nonparametric Functional Time Series Forecasting: Application to Intra-Day Household-Level Load Curves. IEEE Trans. Smart Grid 2014, 5, 411–419. [Google Scholar] [CrossRef]
- Antoniadis, A.; Brossat, X.; Cugliari, J.; Poggi, J.M. Prévision d’un processus à valeurs fonctionnelles en présence de non stationnarités. Application à la consommation d’électricité. J. Soc. Française Stat. 2012, 153, 52–78. [Google Scholar]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.M. Optimized Clusters for Disaggregated Electricity Load Forecasting. Rev. Stat. J. 2010, 8, 105–124. [Google Scholar]
- Quilumba, F.L.; Lee, W.J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using Smart Meter Data to Improve the Accuracy of Intraday Load Forecasting Considering Customer Behavior Similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Cugliari, J.; Goude, Y.; Poggi, J.M. Disaggregated Electricity Forecasting using Wavelet-Based Clustering of Individual Consumers. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar]
- Antoniadis, A.; Brossat, X.; Cugliari, J.; Poggi, J.M. Une approche fonctionnelle pour la prévision non-paramétrique de la consommation d’électricité. J. Soc. Française Stat. 2014, 155, 202–219. [Google Scholar]
- Labeeuw, W.; Stragier, J.; Deconinck, G. Potential of active demand reduction with residential wet appliances: A case study for Belgium. Smart Grid IEEE Trans. 2015, 6, 315–323. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Bosq, D. Modelization, nonparametric estimation and prediction for continuous time processes. In Nonparametric Functional Estimation and Related Topics; Roussas, G., Ed.; NATO ASI Series, (Series C: Mathematical and Physical Sciences); Springer: Dordrecht, The Netherland, 1991; Volume 335, pp. 509–529. [Google Scholar]
- Poggi, J.M. Prévision non paramétrique de la consommation électrique. Rev. Stat. Appl. 1994, 4, 93–98. [Google Scholar]
- Antoniadis, A.; Paparoditis, E.; Sapatinas, T. A functional wavelet-kernel approach for time series prediction. J. R. Stat. Soc. Ser. B Stat. Meth. 2006, 68, 837. [Google Scholar] [CrossRef]
- Cugliari, J. Prévision Non Paramétrique De Processus à Valeurs Fonctionnelles. Application à la Consommation D’électricité. Ph.D. Thesis, Université Paris Sud, Orsay, France, 2011. [Google Scholar]
- Antoniadis, A.; Brossat, X.; Cugliari, J.; Poggi, J.M. Clustering functional data using wavelets. Int. J. Wave. Multiresolut. Inform. Proc. 2013, 11. [Google Scholar] [CrossRef]
- Steinley, D.; Brusco, A.M. new variable weighting and selection procedure for k-means cluster analysis. Multivar. Behav. Res. 2008, 43, 32. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Jiang, Z.; Lin, R.; Yang, F.; Budan, W. A Fused Load Curve Clustering Algorithm based on Wavelet Transform. IEEE Trans. Ind. Inform. 2017. [Google Scholar] [CrossRef]
- Thouvenot, V.; Pichavant, A.; Goude, Y.; Antoniadis, A.; Poggi, J.M. Electricity forecasting using multi-stage estimators of nonlinear additive models. IEEE Trans. Power Syst. 2016, 31, 3665–3673. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning; Springer: Berlin, Germany, 2012; pp. 1–34. [Google Scholar]
- Gaillard, P.; Goude, Y. Forecasting electricity consumption by aggregating experts; how to design a good set of experts. In Modeling and Stochastic Learning for Forecasting in High Dimensions; Springer: Berlin, Germany, 2015; pp. 95–115. [Google Scholar]
- Goehry, B.; Goude, Y.; Massart, P.; Poggi, J.M. Forêts aléatoires pour la prévision à plusieurs échelles de consommations électriques. In Proceedings of the 50 èmes Journées de Statistique, Paris Saclay, France, 28 May–1 June 2018. talk 112. [Google Scholar]
- Li, P.; Zhang, B.; Weng, Y.; Rajagopal, R. A sparse linear model and significance test for individual consumption prediction. IEEE Trans. Power Syst. 2017, 32, 4489–4500. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Gan, D.; Yang, J.; Kirschen, D.S.; Kang, C. Deep Learning-Based Socio-demographic Information Identification from Smart Meter Data. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Anderson, B.; Lin, S.; Newing, A.; Bahaj, A.; James, P. Electricity consumption and household characteristics: Implications for census-taking in a smart metered future. Comput. Environ. Urban Syst. 2017, 63, 58–67. [Google Scholar] [CrossRef]
- Martinez-Pabon, M.; Eveleigh, T.; Tanju, B. Smart meter data analytics for optimal customer selection in demand response programs. Energy Proc. 2017, 107, 49–59. [Google Scholar] [CrossRef]
- Maruotti, A.; Vichi, M. Time-varying clustering of multivariate longitudinal observations. Commun. Stat. Theory Meth. 2016, 45, 430–443. [Google Scholar] [CrossRef]
| Task | Time | Memory | Disk |
|---|---|---|---|
| Raw (15 Gb) to matrix | 7 min | 30 Gb | 2.7 Gb |
| Compute contributions | 7 min | <1 Gb | 7 Mb |
| 1st stage clustering | 3 min | <1 Gb | – |
| Aggregation | 1 min | 6 Gb | 30 Mb |
| Wer distance matrix | 40 min | 64 Gb | 150 Kb |
| Forecasts | 10 min | <1 Gb | – |
| Sample Size | Time (In Seconds) |
|---|---|
| 67 | |
| 513 | |
| 4420 | |
| 43,893 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auder, B.; Cugliari, J.; Goude, Y.; Poggi, J.-M. Scalable Clustering of Individual Electrical Curves for Profiling and Bottom-Up Forecasting. Energies 2018, 11, 1893. https://doi.org/10.3390/en11071893
Auder B, Cugliari J, Goude Y, Poggi J-M. Scalable Clustering of Individual Electrical Curves for Profiling and Bottom-Up Forecasting. Energies. 2018; 11(7):1893. https://doi.org/10.3390/en11071893
Chicago/Turabian StyleAuder, Benjamin, Jairo Cugliari, Yannig Goude, and Jean-Michel Poggi. 2018. "Scalable Clustering of Individual Electrical Curves for Profiling and Bottom-Up Forecasting" Energies 11, no. 7: 1893. https://doi.org/10.3390/en11071893
APA StyleAuder, B., Cugliari, J., Goude, Y., & Poggi, J.-M. (2018). Scalable Clustering of Individual Electrical Curves for Profiling and Bottom-Up Forecasting. Energies, 11(7), 1893. https://doi.org/10.3390/en11071893





