Abstract
Solar concentrator photovoltaic collectors are able to deliver energy at higher temperatures for the same irradiances, since they are related to smaller areas for which heat losses occur. However, to ensure the system reliability, adequate collector geometry and appropriate choice of the materials used in these systems will be crucial. The present work focuses on the re-design of the Concentrating Photovoltaic system (C-PV) collector reflector presently manufactured by the company Solarus, together with an analysis based on the annual assessment of the solar irradiance in the collector. An open-source ray tracing code (Soltrace) is used to accomplish the modelling of optical systems in concentrating solar power applications. Symmetric parabolic reflector configurations are seen to improve the PV system performance when compared to the conventional structures currently used by Solarus. The parabolic geometries, using either symmetrically or asymmetrically placed receivers inside the collector, accomplished both the performance and cost-effectiveness goals: for almost the same area or costs, the new proposals for the PV system may be in some cases 70% more effective as far as energy output is concerned.
1. Introduction
Modernisation plays a considerable role in the change of the people’s behaviours. People’s behaviour towards energy is not only related to the way energy is produced but also how and why it is consumed. Conventional forms of electricity generation are today still mostly based on fossil fuel, ranging from coal-based steam plants to gas boilers. In the recent years, humanity has made overwhelming advances in its capacity to improve life quality; however, in this worthy quest, mankind has created a series of new challenges that need to be tackled. Global warming is likely the most urgent of all since it threatens the continued existence of man on earth. This way, serious steps are being taken like the Paris climate agreement [1]. As mentioned, a glance at the present situation regarding the production of electricity and heat, renewable resources play a massive part in mainstream energy production and feed in the grid. By the end of 2016, 303 GW of photovoltaic system (PV) has been installed all over the world [2], 16 countries installed at least 500 MW of PV [3], Germany ranks first in solar PV per capita with 511 watts/capita [4,5].
Economics is currently mentioning it as one of a crucial aspect of sustainability, dealing mainly with the energy efficiency [6]. In 2011 (Energy Policies of International Energy Agency Countries-Sweden, 2013 Review), in Sweden, 56.7% of total electricity came from the renewable energy sources, and in the fifth place in the electricity produced from the renewable energy sources ranking. Portugal appears in the seventh position, with 47%.
The world energy consumption at the moment is 10 terawatts (TW) per year [7]. By the year 2050, the expected energy consumption would be 30 TW [8]. The conclusion is an additional 20 TW of a CO2 free energy source is required to balance the demand. One solution to stabilise CO2 might be to use photovoltaics (PV) and other renewables like for example hydro and wind for electricity (10 TW) and hydrogen for transportation (10 TW) [8]. Hence solar energy will play an essential role in the future and nowadays it is considered as the “tipping point” for the PV systems [9].
Solar energy, an inexhaustible resource, clean and non-polluting as it may have seen, however, it is not an easy task to make the most out of it [10]. Its potential lies in the method and the techniques used for the maximum efficiency possible.
Several systems have been developed to use the solar energy, for example with Flat-plate solar panels [11] or with concentrated solar power (CSP) systems [12]. These systems are some of the ways to generate power from the sun. The CSP systems could be used to extract heat from the sun, in this case, it is a thermal system [13], or it could be used to convert solar energy in electricity, and in this case, it is a concentrating photovoltaic system (C-PV) [14].
In a situation where it is necessary to reach high levels of energy conversion, C-PV technology plays an important role. Linking an optical device between the light source and the receiver/absorber, the efficiency of the collector energy conversion related to the photoelectric effect will be theoretically higher. The improvement will increase with the concentrator factor C, which represents the ratio of the total energy collected in the concentrator collector and the total energy received in the flat collector. There are three different C-PV systems:
- Low concentration (LC-PV): C between 1 and 40 suns [15];
- Medium concentration (MC-PV): C between 40 and 300 suns [16];
- High concentration (HC-PV): C between 300 and 2000 suns [16].
However, these systems also present some disadvantages that need to take into account. Namely:
- Concentration implies losses, as the reflectivity of the reflector is never 100%. A high quality reflector has 95% reflectance, which implies 5% losses. If there are multiple reflections, the reflectance losses are compounded.
- The redirection of the rays can lead to a situation in which the light does not reach the target (receiver), leading to a steep decrease in the collector efficiency. This happens when the angle is outside of the reflectors acceptance angle or due to imperfections in the shape of the concentration.
- Concentrating collectors receive 1/C of the diffuse radiation. This means that a collector with concentration factor of two will receive 50% of the diffuse solar radiation, while a high concentration collector will receiver close to 0%. This effect is particularly relevant in locations, such as Berlin or Paris, where diffuse radiation accounts for approximately 50% of the annual solar radiation.
Stationary collectors usually present C up to 5. Higher values of C can be reached but require tracking systems [17]. However, tracking systems are more complex, and they are related to higher installation and management costs. Solarus standard reflector is designed to be used in a non-tracking system.
Along with the usual partial shading effects, related to several effects (clouds, reflector boundaries, shadows, dust, or any dirtiness), the use of reflectors in stationary solar C-PV collectors usually cause non-uniform light distribution along the PV cells string. This in turn can create hot spots resulting in aging or permanent damage. When cells are entirely shaded, the hot spot evidence may prevent the triggering of the bypass (BP) diode [18], resulting in the increased temperature that will degrade the solar panel.
In mismatching operating conditions for example, due to aging, manufacturing tolerances, different orientation of the solar panels, the PV system energetic efficiency is strongly compromised. To mitigate these effects, a re-design searching for alternatives concerning the geometry of the C-PV collectors is imperative [19,20].
These systems, are classified as [21]: Parabolic trough; Central Receiver/Solar Tower; Parabolic dish; Linear Fresnel Collector; Compound Parabolic Collector (CPC), and Maximum Reflector Collector (MaReCo).
It is essential to give an overview regarding the last two, since it is the structure mostly used in the market.
The CPC system has two, parabolic reflectors with different focal points. In Figure 1, the basic shape of the collector is shown [22].
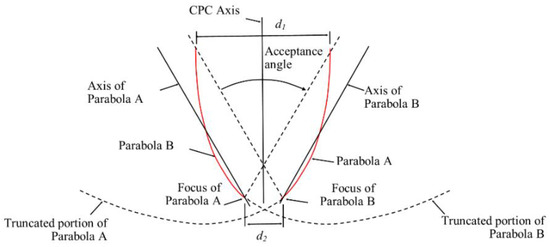
Figure 1.
Compound Parabolic Collector (CPC) [22].
The aperture d2 in the bottom of Figure 1 is the distance between the focuses of the two parabolas, A and B, and it is the receiver (solar cells) location. The two parabolas reflect the incoming solar radiation on the receiver. There is symmetry between the focal point and the axis of the compound parabolic collector. The acceptance angle between both controls the amount of light that can be reflected and finally end up on the receiver. The interesting fact is, only an incident ray that falls in the acceptance angle range will definitely be reflected by both reflectors and reach the receiver [22].
The Maximum Reflector Collector system (MaReCo) is an asymmetrical truncated trough-like CPC collector. It is mainly designed for higher latitudes [22]. It is a non-tracking collector with a bi-facial absorber. The bi-facial absorber helps to minimise the absorber area, and subsequently the production costs. It is generally used from stand-alone mounting on the ground to the roof top integration [23].
A basic structure of a CPC system is shown in Figure 2. The reflector has three parts; A: the upper parabolic reflector between points 2 and 3 with the reflection focus on the top of the absorber; B: a circular section between points 1 and 2. This part transfers the light onto the absorber and C: the lower parabolic part between points 4 and 1.
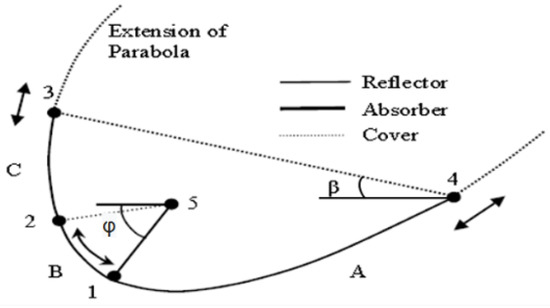
Figure 2.
Basic structure of Maximum Reflector Collector (MaReCo) [23].
In Figure 2, ϕ is the aperture tilt angle and β is the absorber inclination angle. The cover glass is attached between points 3 and 4. The position of the cover glass depends on the location of the reflector along the extended parabolas where the maximum annual irradiation onto the aperture is obtained [23].
A diagram of the stand-alone MaReCo is in Figure 3. The MaReCo structure could be dived in five different types of prototypes; the stand-alone MaReCo; the roof-integrated MaReCo; the east/west MaReCo; the spring/fall MaReCo; the wall MaReCo, and the Solarus Power Collector. The stand-alone MaReCo has a cover glass with a tilt of 30° in this cases for Stockholm conditions, concerning the horizontal. The upper and lower acceptance angle are 65° and 20°, respectively. It has a concentration area [23] of Ci = 2.2.
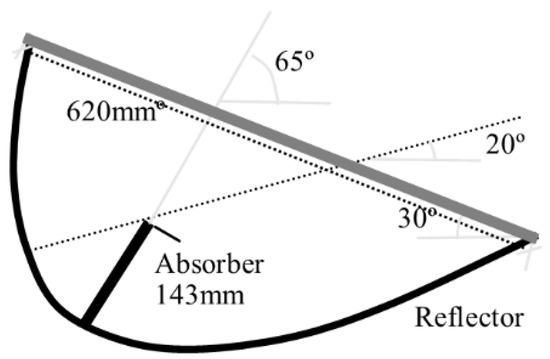
Figure 3.
Diagram of stand-alone MaReCo for Stockholm conditions with cover glass angle of 30° [15].
The roof-integrated MaReCo is specially designing for roof implementation. In this case, the cover glass starts where the circular part of MaReCo ends which means the glass is between points 2 and 4 in Figure 2. Hence, there is no upper parabolic reflector, and so the absorber is placed right under the cover. Since this collector is placed on the roof of a building, it is tilt with the roof angle. All radiations ranging from incidence angles between 0° to 60° is accepted by the reflector. The angle 60° is determined by the roof angle, and the reflector receives radiation angles from the horizon to the glass normal. The collector behaves similarly to a flat plate collector above 60° with an absorber area of one third of the aperture area which is the front side of the absorber. It has a concentration area of Ci = 1.5 when the roof is 30° tilt concerning the horizon. A diagram of roof-integrated MaReCo is in Figure 4.
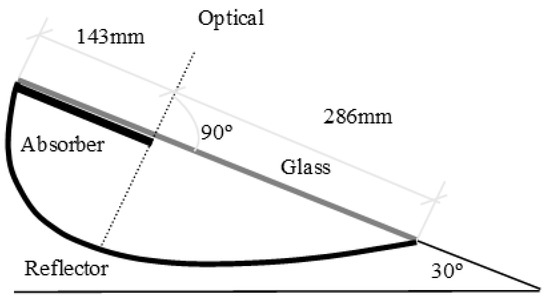
Figure 4.
Diagram of roof integrated MaReCo [23].
The east/west MaReCo with a concentration area of 2.0 is designed for exceptional cases when the roofs are not aligned in the east/west direction. In this case, the reflector axes are aligned in the east/west direction that is; it is tilted along the roof. Radiations in the range of 20° to 90° are accepted as seen in Figure 5.
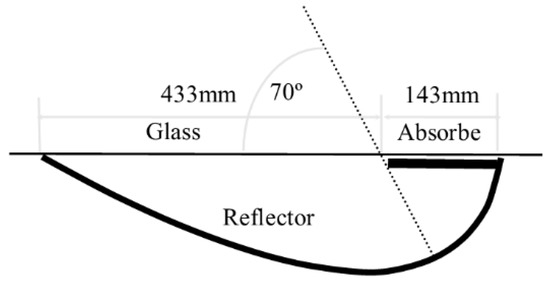
Figure 5.
Diagram of east/west MaReCo with 70° optical axis from the cover glass [23].
The spring/fall MaReCo is another prototype, is used to maximise the efficiency of the system during the spring and the fall. Radiations with angles below 15° will be reflected outside the collector. In this prototype the absorber is placed just below the cover glass. The spring/fall MaReCo has a concentration area of Ci = 1.8. Figure 6 shows a diagram of spring/fall MaReCo.
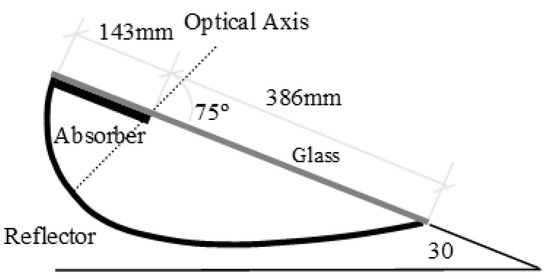
Figure 6.
Diagram of spring/fall MaReCo for roof tilt 30° [23].
An alternative to the east/west MaReCo or the spring/fall MaReCo is the wall MaReCo. It is a collector which can be installed on a wall with Ci = 2.2 for the concentration area and a range between 25° and 90° for the acceptance angle. The absorber is also placed just below the cover glass. Figure 7 shows a diagram of the wall MaReCo.
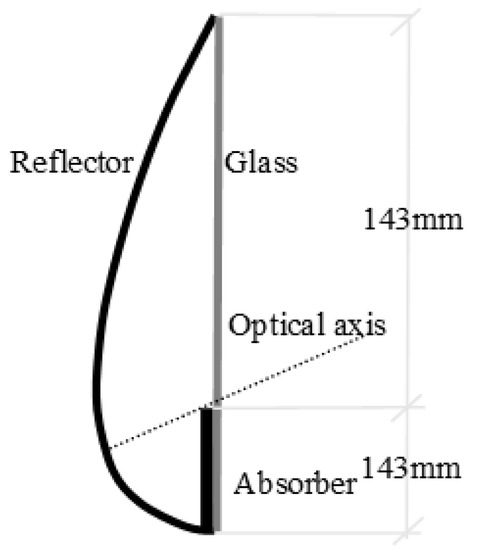
Figure 7.
Diagram of wall MaReCo designed for south facing with optical axis at 25° from the horizon [23].
A photovoltaic thermal (PVT) hybrid system is the combination of a hybrid PV and a solar-thermal system. This system is an alternative environmentally friendly way which offers both thermal, as well as electrical output from a single unit. The system allows the simultaneous acquisition of both electrical and thermal outputs while at the same time there is a reduction in the PV module electrical efficiency by preventing the temperature increase in the solar cells caused by the solar radiation. The loss reduction is achieved due to the use of coolant (water), which flows through the solar collector unit [24].
This paper is intended to expand a previous work of the authors [25] and it is organised as follows: Section 2 describes the Solarus PVT solar collector, which was used to validate the model; Section 3 describes the accomplished methodology to define the C-PV collector geometry related to the optical analysis tool designated by Soltrace; Section 4 makes a comparison, in terms of a cost-effectiveness analysis, between the conventional MaReCo Solarus configurations and the new configurations, which use symmetrical parabolic geometries for the collector-reflector. The assessment takes into account the influence of the irradiance and the receiver location inside the collector for different zones of the globe. In Section 5, some conclusions are summarised, and future trends to the next step of this work are made in Section 6.
2. Solarus Concentrating Photovoltaic (C-PV) Collector
Solarus concentrator collector is hybrid (PV plus thermal, or PVT), operates without a tracking system [26] and it is specially designed for roof applications in northern countries in Europe. The PVT Solarus collector belongs to the compound parabolic collector (CPC) type, which is commonly known as the maximum reflector concentrator (MaReCo) family [27] already described in the introduction [28,29,30]. It is formed by a reflector with two asymmetrical truncated parabolic sections separated by a circular section (compound parabolic concentrator, CPC), a flat receiver with solar cells in both sides and bi-facial absorbers. The reflector geometry is designed for high latitudes with the goal of adjusting the output of the collector to better suit the relatively flat heat demand of domestic hot water application. The electric part of each module consists of strings of 38 series-connected cells cut into 1/6 size or 19 series-connected cells cut 1/3 size (The standard cell is 0.156 × 0.156 m2). To fit the collector design, the cell is cut to 0.148 × 0.156 m2. When the larger dimension is cut into three slices, it results in a solar cell, known as 1/3 cell, whose area is 0.148 × 0.052 m2; if it is divided into six slices, a solar 1/6 is formed (0.148 × 0.026 m2). The panel has several parallel connected strings distributed over two similar troughs. For example, in Figure 8, there are 152 PV solar cells of 1/6 type. All dimensions are expressed in mm. The length of the receiver Lr is 148 mm; the aperture length Laper is 192 mm. Water connection for cooling is represented in blue; electric connections are represented in red.
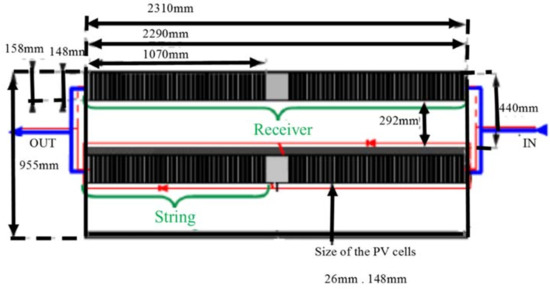
Figure 8.
Top view of the photovoltaic thermal (PVT) Solarus AB panel.
Some structural parameters that describe the collector are schematically shown in Figure 9.
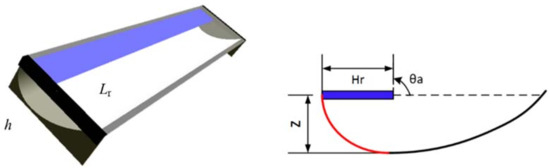
Figure 9.
Standard Solarus concentrating photovoltaic thermal (C-PVT) collector.
Other parameters related to the location and installation details of the solar panel are equally important for its complete description: the latitude (N or S), the longitude (W or E), the elevation solar angle αS, the tilt θt and the azimuthal angle γ (Figure 10).
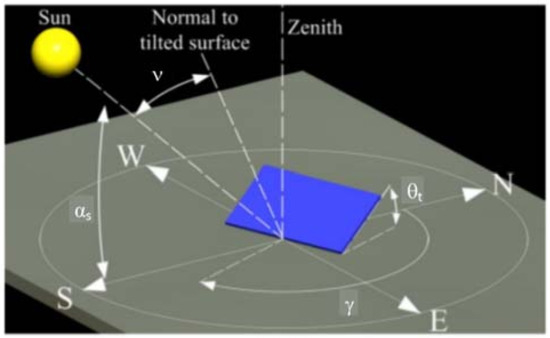
Figure 10.
Schematic representation of the azimuthal, altitude, and tilt angles for a given solar cell panel.
The aluminum reflector concentrated the sum rays into the thermal absorber. The acceptance angle for the reflector is defined by the optical axis direction related to the reflector.
The collector optical efficiency changes throughout the year. The collector tilt (the angle that the glass cover of the collector makes with ground) defines the total annual irradiation falling within the acceptance interval.
Considering anisotropic light sources, the concentrator factor related to typical MaReCo Solarus [22] structures is roughly 1.4 to 1.5 suns. In the results, this geometry will be considered as a standard geometry and it is schematically represented in Figure 8. Photos with the top and side views are shown in Figure 11.

Figure 11.
Solarus C-PVT panel: (a) the top view and (b) side view.
Some features of the standard Solarus concentrating photovoltaic thermal (C-PVT) collector can be found in [25].
A new reflector design by Solarus for lower latitudes was being designed to reach new markets and gain competitiveness against the conventional PV and thermal systems. The new reflector has the following dimensions 56 mm wide and 2310 mm long for the receiver, as shown in Figure 12.

Figure 12.
Standard Solarus collector absorber.
The solar collector is anodised aluminium reflector surface, and it is cover with a low iron glass. The optical properties of the reflector, glass and plastic gables are summarised in Table 1.

Table 1.
Summary of the properties of optical elements.
3. Efficiency Calculation Methodology and Collector Geometries
Understanding the conversion processes that are associated with solar resources requires specialised modelling tools to predict system and economic performances. One of the most important aspects concerns the collector design. For energy calculations in the receiver ray tracing software (Soltrace) are often used. In paper [27], it is possible to find an explanation of the simulation procedure adopted for the asymmetric Solarus collectors. In this paper, Soltrace software was used. Since the early 1960’s, when the first general ray-tracing procedures were described [31], a long road has been travelled, due to the need for designing and modelling solar concentrating systems. From the late 1980’s several optical specific commercial design codes have been developed by the National Renewable Energy Laboratory (NREL), but they were not general and flexible enough for a suitable analysis: a deeper insight into physical and engineering aspects was required. Based on a Monte-Carlo methodology [32], Soltrace was the answer.
The main idea is to select a given number of rays and traced his trajectory through the system when they come across various optical interactions. Some of these interactions are probabilistic while others are deterministic [32]. In each simulation, the program uses the well-known Fresnel equations.
First, in Soltrace, a solar ray could be absorbed, and if it is this the case, the program moves on to the next solar ray. If it is not absorbed, it is necessary to generate a random number between 0 and 1 to find if the solar ray is reflected or transmitted. If the reflectance defined in the program is smaller than this random number the solar ray is reflected at the specular angle, if it is not, the solar ray is transmitted. It is possible to lunch a certain number of rays for a specific sun position. At the end of the simulation, the program counts the number of rays with an associated power that reaches the receiver. In Figure 13, there is an example of a Soltrace simulation.
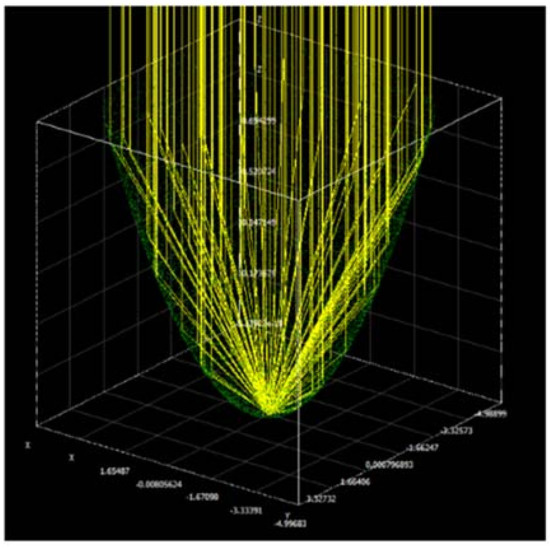
Figure 13.
Soltrace simulation. Solar ray’s interaction with a parabolic surface.
Basically Ntot solar rays are traced from the sun through the system, towards the aperture area of the collector, while encountering various optical interactions. Accuracy increases with Ntot, but the use of larger ray numbers means more processing time. A compromise shall be taken, accordingly to the desired result and the situation under analysis. For instance, relative changes in the optical efficiency for different sun angles is not as exigent (as far as Ntot is concerned) as when one needs a more accurate assessment to the flux distribution on the receiver. The particular site latitude and time (day of the year and local solar hour) shall be included in the set of data. From this information, the sun position is calculated (azimuth and elevation). The simulation analysis will allow the collected solar annual energy in each new structure to be assessed and compared to the standard C-PVT Solarus collector. The gain [32] is given by:
where Enew and Estandard are the annual flux of energy for the new CPC and the standard Solarus collector, respectively. If the gain is positive, this means a new CPC with a better performance than the standard ones. The concentration factor for 2D concentrating systems (linear: parabolic, circular, MaReCo trough collectors) is given by:
For MaReCo with acceptance angles of 90°, C = 1.414. According to [27], and using geometrical considerations, the linear concentrating factor is given by:
In (3), Aapert and Arec are the aperture and the receiver areas, respectively. Taking into account the values referred for the standard collector is concentration factor is around 1.44. Nevertheless, lower acceptance angles shall increase C. Although concentration reduces the costs, it also reduces the annual output. Due to the reflection losses, a CPC collector will always receive less energy per m2 of aperture than a flat receiver.
The CPC collector annual energy percentage ηE is given by:
The main goal is a percentage value as higher as possible. The idea is to find a new design that allows to receive as much energy as the flat collector, but at a lower cost. This will represent an upgrade. Three new geometries were proposed for lower latitudes (In the presented examples, simulations were carried out for Lisbon (Lat = 38°, 42′ N, Long = 9°, 8′ W) and Luanda (Lat = 8°, 50′ S, Long = 13°, 14′ E)). Two of them present symmetric geometries (parabolic reflector and receivers symmetrically placed) and the third has a parabolic reflector but with an asymmetrically placed receiver as standard MaReCo. For lower latitudes, the geometry symmetry increase is expected to improve the collector performance since the solar radiation difference between the winter and summer is not as large as it is in Sweden. All collectors present the same height and aperture area (Figure 14).
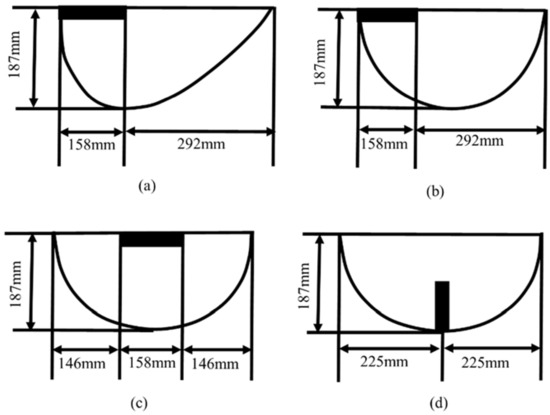
Figure 14.
Collector structures: (a) P1—standard MaReCo; (b) P2—Parabolic Reflector; Asymmetric Receiver; (c) P3—Parabolic Reflector; Symmetric Horizontal Receiver; and (d) P4—Parabolic Reflector; Symmetric Vertical Receiver.
4. Results
4.1. Structures Analysed
In this section several results were acquired for the structures previous described in Figure 14. The main idea was to redesign the reflector quipping the same area of the standard MaReCo collector and inspect who the reflector geometry affects the total energy collected. For that proposed, the performance of each collector structure was studied for three latitudes in the solstices.
The results presented in this section were obtained using Soltrace software. In the simulations, it has considered that the collector model is ideal. This means that: (i) the optical properties are ideal (no optical errors); (ii) the reflector reflectivity is 100%; (iii) the plastic side gables, the frame and the cover glass were not drawn in the 3D model; and (iv) the thickness of the absorber is negligible (2 mm), whereas the current absorber is around 11.4 mm.
4.2. The Latitude and Tilt Effects on the Studied Structures
Three latitudes were considered: Gävle in Sweden, Lisbon in Portugal, and Luanda in Angola, for two situations: winter and summer solstices for each of the four geometries: standard with two different receiver positions as well as symmetric and asymmetric parabolic. Validation of the methodology described in Section 2 was conducted by comparing the results with the simulation results concerning the current Solarus solar panels presented in [33], which uses Tonatiuh software. Results related with the solar panel efficiencies are presented in Figure 15 when the tilt of the PVT system is zero. The figure shows that, for Lisbon, the geometry that captures the most amount of solar radiation in the solstice day is P4, the symmetrical collector with a vertical receiver. In spite of being a good solution for winter solstice, geometry P3 has a poor performance during the Summer solstice in Lisbon, due to the high elevation solar angles.
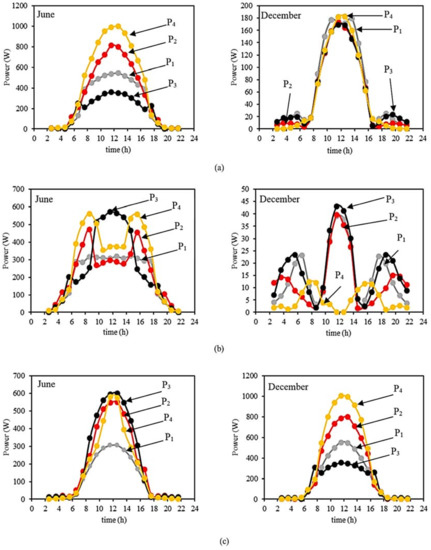
Figure 15.
Collected energy per time along the solstices for the standard and proposed structures, when tilt is zero in (a) Lisbon, (b) Gavle, and (c) Luanda. P1—standard MaReCo; P2—Parabolic Reflector; Asymmetric Receiver; P3—Parabolic Reflector; Symmetric Horizontal Receiver; P4—Parabolic Reflector; Symmetric Vertical Receiver.
The lateral collected power, which is more clearly seen during the winter solstice in Gävle and Lisbon, is associated to the transparent gambles in all existent structures (photos of Figure 11, concerning the double trough C-PVT Solarus panel).
Considering Gävle at zero tilt, the best option presented in Figure 7 is the P3 structure. It is worth noticing, that P4 is also a good solution for summertime. The distribution, along the day, in this case is more uniform, which is advantageous for the beginning and the end of the day, where the demands should be higher for grid or off-grid habitation segments or markets. However, during the winter solstice, the produced energy by P4 is negligible, due to the small elevation solar angles. Therefore, this solution should be rejected.
For the location of Luanda, and keeping in mind that this city is located in the southern hemisphere close to the equator, on the 21st of December, the Sun will be higher than on the 21st of June. This explains why, during December, P3 is not a good option, in spite of presenting a good performance in June. Some other conclusions may be highlighted, for example, the fact that: (i) P4 geometry is adequate for both solstices and (ii) standard Solarus collectors is not optimized for locations near the equator.
The collector tilt variation has a significant influence on the panel efficiency. For Gavle it has been referred that the increase of tilt angles can lead to substantial improvement, being the best performances achieved for tilts around 30° [34]. Also important to notice is that for tilts greater than 45°, due to a steep decrease of the acceptable angles during the Summer solstice, the collected energy almost vanishes, leading to a cut-off phenomenon [35]. By comparative analysis of the geometries under study, and considering the case of Gävle, it is apparent from Figure 16 that geometry P4 is the best option, presenting good performances either in summer or winter, whereas P2 is good in winter but less so in summer. For a tilt of 30°, the P4 geometry shows, according to (1), the output can increase in Gavle by 70%, being similar to the results presented in Lisbon for a more disadvantageous situation (tilt 0°), as seen in Figure 15a).
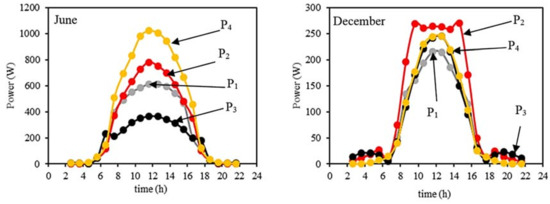
Figure 16.
Collected energy per unit time along the solstices for the standard and proposed structures, when tilt is 30° in Gävle.
4.3. Potential Choices
The simulation results have shown that for all situations, there is always at least one of the new proposals that presents better performances than the MaReCo geometry.
For example, in Lisbon with tilt 0° or in Gavle with tilt 30°, using the maximum values of energy per unit time (around midday), the proposed configuration P4 reaches gains around 70%.
Using (4), it is straightforward to show that:
As expected, an increase of 170% in the collected energy is foreseen in Gävle for the summer solstice case, when compared to a symmetric C-PVT structure with horizontal receiver and a tilt of 30° (Figure 8).
It is also worth referring, that all the proposed configurations have the same total collector area, which means that the involved costs are comparable. Costs represent an important issue for industrial applications.
Finally, it is important to highlight that although the outputs during the solstices are a useful indication, further study needs to be performed, as the annual output is, in the end, the most important result.
5. Conclusions
Alternative geometries for C-PV collectors have been studied using ray trace software Soltrace. In this paper, it has been considered three locations (Gavle, Lisbon, and Luanda) and simulation analysis have been presented for winter and summer solstices. A comparative analysis with the current MaReCo C-PVT has been assessed. In all situations, there was at least one of the new proposals that correspond to an improvement of the power production when compared to the current collector. However, the assessment should be done for the full extent of the year.
The simulation method using Soltrace is a useful tool to investigate the effect of the collector geometry on the energy output in a simpler, faster, and cheaper way than using the experimental methods. The simulation results are important input data for the electrical and thermal description of the collector [36].
These studies reveal crucial for panel manufacturers that wish to reach emerging markets. Current investments and commitments must be made to further objectives in a near future. Compromises will always be taken into account, following which the final decision will be made.
6. Future Work
The best CPV geometry optimisation procedure is a complex process since there is a large amount of parameters that need to be considered simultaneously. For instance, the sun position and the latitude of the system installation that affects the system performance. The results shown in the present paper for three different latitudes provides important insights on how the configuration of the concentrator and the position of the receiver in the concentrator affects the CPV performance. It is crucial in a future work and using the same CPV configurations, to implement an optimisation algorithm. With this algorithm, it is possible to optimise these structures regarding the several parameters that affect his performance. Several optimisation algorithms can be used to optimise these structures. We are going to focus our attention in the machine learning algorithms and the genetic algorithms. The first one, has already been used to directly predict and optimise the best collector geometries in several cases [37,38], similar to the second one [39].
Author Contributions
J.P.N.T. performed all the simulations and post-processing, analysed the results, and wrote the manuscript. C.A.F.F., J.G., B.L., G.C., O.O. and P.J.C.B. analysed the simulation results and revised the manuscript. All authors read and approved the final manuscript.
Acknowledgments
This work was supported by FCT, through IDMEC, under LAETA, project UID/EMS/50022/2013 and under IT, project UID/EEA/50008/2013.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Aapert | aperture area of the collector (m2) |
| Arcev | receiver area (m2) |
| C | concentration factor |
| Eflat | Energy produced by the flat panel (W·h) |
| Enew | Energy produced by the new geometry (W·h) |
| Estandard | Energy produced by MaRECo structure (W·h) |
| G | gain or energy ratio |
| Ntot | number of total rays in the simulation |
| Greek Symbols | |
| αs | elevation solar angle (°) |
| ν | incident angle (°) |
| ηE | electrical efficiency |
| θa | acceptance angle (°) |
| θt | tilt angle of the glass cover (°) |
| Acronyms and abbreviations | |
| BP | Bypass |
| CPC | Compound Parabolic Concentrator |
| C-PV | Concentrating Photovolaitc |
| CSP | Concentrated solar power |
| HC-PV | High Concentration Photovoltaic |
| LC-PV | Low Concentration Photovoltaic |
| MC-PV | Medium Concentration Photovoltaic |
| MaReCo | Maximum Reflector Collector |
| PV | Photovoltaic |
| PVT | Photovoltaic and Thermal |
References
- Bhor, S.J. Paris Agreement on Climate Change: A Booster to Enable Sustainable Global Development and Beyond. Int. J. Environ. Res. Public Health 2016, 13, 1134. [Google Scholar] [CrossRef] [PubMed]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Háber, I.; Pintér, G. Economic and Technical Aspects of Flexible Storage Photovoltaic Systems in Europe. Energies 2018, 11, 1445. [Google Scholar] [CrossRef]
- Baurzhan, S.; Jenkins, G.P. On-Grid Solar PV versus Diesel Electricity Generation in Sub-Saharan Africa: Economics and GHG Emissions. Sustainability 2017, 9, 372. [Google Scholar] [CrossRef]
- Gul, M.; Kotak, Y.; Muneer, T. Review on recent trend of solar photovoltaic technology. Energy Explor. Exploit. 2016, 34, 485–526. [Google Scholar] [CrossRef]
- Becker, R.; Thrän, D. Optimal Siting of Wind Farms in Wind Energy Dominated. Power Syst. Energies 2018, 11, 978. [Google Scholar]
- Koltun, P. Materials and sustainable development. Prog. Nat. Sci. Mater. Int. 2010, 20, 16–29. [Google Scholar] [CrossRef]
- Avgerinou, M.; Bertoldi, P.; Castellazzi, L. Trends in Data Centre Energy Consumption under the European Code of Conduct for Data Centre Energy Efficiency. Energies 2017, 10, 1470. [Google Scholar] [CrossRef]
- Zweibel, K. The Terawatt challenge for thin film PV. In Thin Film Solar Cells: Fabrication, Characterization and Application; Poortmans, J., Archipov, V., Eds.; John Wiley: Hoboken, NJ, USA, 2005; pp. 18–22. [Google Scholar]
- Kazmerski, L. Solar photovoltaics R&D: At the tipping point: A 2005 technology overview. J. Electron Spectrosc. Relat. Phenom. 2006, 150, 105–135. [Google Scholar]
- Aschilean, I.; Rasoi, G.; Raboaca, M.S.; Filote, C.; Culcer, M. Design and Concept of an Energy System Based on Renewable Sources for Greenhouse Sustainable Agriculture. Energies 2018, 11, 1201. [Google Scholar] [CrossRef]
- Arikan, E.G.; Glu, S.A.; Gazi, M. Experimental Performance Analysis of Flat Plate Solar Collectors Using Different Nanofluids. Sustainability 2018, 10, 1794. [Google Scholar] [CrossRef]
- Qiu, S.; Solomon, L.; Rinker, G. Development of an Integrated Thermal Energy Storage and Free-Piston Stirling Generator for a Concentrating Solar Power System. Energies 2017, 10, 1361. [Google Scholar] [CrossRef]
- Llamas, J.M.; Bullejos, D.; Adana, M.R. Techno-Economic Assessment of Heat Transfer Fluid Buffering for Thermal Energy Storage in the Solar Field of Parabolic Trough Solar Thermal Power Plants. Energies 2017, 10, 1123. [Google Scholar] [CrossRef]
- Tien, N.X.; Shin, S. A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation. Appl. Sci. 2016, 6, 251. [Google Scholar] [CrossRef]
- Famosoa, F.; Lanzafamea, R.; Maenzaa, S.; Scanduraa, P.F. Performance comparison between Low Concentration Photovoltaic and fixed angle PV systems. In Proceedings of the 69th Conference of the Italian Thermal Engineering Association (ATI 2014), Milan, Italy, 10–13 September 2014; Volume 81, pp. 516–525. [Google Scholar]
- Khamooshi, M.; Salati, H.; Egelioglu, F.; Faghiri, A.H.; Tarabishi, J.; Babadi, S. A Review of Solar Photovoltaic Concentrators. Int. J. Photoenergy 2014, 2014. [Google Scholar] [CrossRef]
- Pérez-Higueras, P.; Muñoz, E.; Almonacid, G.; Vidal, P. High-concentrator photovoltaics efficiencies: Present status and forecast. Renew. Sustain. Energy Rev. 2011, 15, 1810–1815. [Google Scholar] [CrossRef]
- Torres, J.P.N.; Nashih, S.K.; Fernandes, C.A.F.; Leite, J.C. The effect of shading on photovoltaic solar panels. Energy Syst. 2018, 9, 195–208. [Google Scholar] [CrossRef]
- Carotenuto, P.; Curcio, S.; Manganiello, P.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Algorithms and devices for the dynamical reconfiguration of PV arrays. In Proceedings of the PCIM Europe 2013, Nuremberg, Germany, 14–16 May 2013; pp. 765–772. [Google Scholar]
- Balato, M.; Constanzo, L.; Vitelli, M. Multi-Objective Optimization of PV arrays performances by means of the dynamical reconfiguration of PV modules connections. In Proceedings of the 4th International Conference on Renewable Energy Research and Applications, Palermo, Italy, 22–25 November 2015; pp. 1646–1650. [Google Scholar]
- Herrando, M.; Markides, C. Hybrid PV and solar-thermal systems for domestic heat and power provision in the UK: Techno-economic considerations. J. Appl. Energy 2016, 161, 512–532. [Google Scholar] [CrossRef]
- Tang, J.; Yu, Y.; Tang, R. A Three-Dimensional Radiation Transfer Model to Evaluate Performance of Compound Parabolic Concentrator-Based Photovoltaic Systems. Energies 2018, 11, 896. [Google Scholar] [CrossRef]
- Krishna, N.; Venkat, K.; Murugan, E. Power Analysis of non-tracking PV system with low power RTC based sensor independent solar tracking (SIST) PV system. Mater. Today Proc. 2018, 5, 1076–1081. [Google Scholar] [CrossRef]
- Barell, L.; Bidini, G.; Bonucci, F.; Castellini, L.; Castellini, S.; Ottaviano, A.; Pelosi, D.; Zuccari, A. Dynamic Analysis of a Hybrid Energy Storage System(H-ESS) Coupled to a Photovoltaic (PV) Plant. Energies 2018, 11, 396. [Google Scholar] [CrossRef]
- Gomes, J.; Luc, B.; Fernandes, C.A.F.; Torres, J.P.N.; Olsson, O.; Branco, P.J.C.; Nashih, S.K. Analysis of different C-PVT reflector geometries. In Proceedings of the IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016. [Google Scholar]
- Monika, A. Solar Thermal Collectors at High Latitudes, Design and Performance of Non-Tracking Concentrators. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2012. [Google Scholar]
- Bernanrdo, R.; Davidsson, H.; Karlsson, B. Performance Evaluation of a High Solar Fraction CPC-Collector System. Jpn. Soc. Mech. Eng. J. Environ. Eng. 2011, 6, 680–692. [Google Scholar]
- Bernardo, R.; Perers, B.; Håkansson, H.; Karlsson, B. Performance Evaluation of Low Concentrating Photovoltaic/Thermal Systems: A Case Study from Sweden. Sol. Energy 2011, 85, 1499–1510. [Google Scholar] [CrossRef]
- Bernardo, R.; Davidsson, H.; Gentile, N.; Mumba, C.; Gomes, J. Measurements of the Electrical Incidence Angle Modifiers of an Asymmetrical Photovoltaic/Thermal Compound Parabolic Concentrating–Collector. Sci. Res. Eng. 2013, 5, 37–43. [Google Scholar]
- Ngoc, T.N.; Phung, Q.N.; Tung, L.N.; Sanseverino, E.R.; Romano, P.; Viola, F. Increasing efficiency of photovoltaic systems under non-homogeneous solar irradiation using improved Dynamic Programming methods. Sol. Energy 2017, 150, 325–334. [Google Scholar] [CrossRef]
- Spence, G.; Murty, M. General ray-tracing procedure. JOSA 1962, 52, 672–676. [Google Scholar] [CrossRef]
- Wendelin, T.; Lewandowski, A.; Dobos, A. SolTrace; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Puerto, J.M. Performance Evaluation of the Solarus AB Asymmetric Concentrating Hybrid PV/T Collector. Master’s Thesis, University of Gavle, Gavle, Sweden, 2014. [Google Scholar]
- Diwan, L. Study of Optimizations in a Novel Asymmetric Photovoltaic/Thermal Hybrid Solar Collector. Master’s Thesis, Instituto Superior Técnico, Lisboa, Portugal, 2013. [Google Scholar]
- Giovinazo, C.; Bonfiglio, L.; Gomes, J.; Karlssson, B. Ray Tracing model of an Asymmetric Concentrating PVT. In Proceedings of the Eurosun 2014-International Conference on Solar Energy and Buildings, Aix-les-Bains, France, 16–19 September 2014. [Google Scholar]
- Hossain, M.; Saidur, R.; Fayaz, H.; Rahim, N.; Islam, M.; Ahamed, J.; Rahman, M. Review on solar water heater collector and thermal energy performance of circulating pipe. Renew. Sustain. Energy Rev. 2011, 15, 3801–3812. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Liu, K.; Zhang, Z. Predictive Power of Machine Learning for Optimizing Solar Water Heater Performance: The Potential Application of High-Throughput Screening. Int. J. Photoenergy 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Farooqui, S.Z. Determination of Performance Measuring Parameters of an Improved Dual Paraboloid Solar Cooker. Int. J. Photoenergy 2017, 2017. [Google Scholar] [CrossRef]
- Burhana, M.; Chuaa, K.J.E.; Ng, K.C. Sunlight to hydrogen conversion: Design optimization and energy management of concentrated photovoltaic (CPV-Hydrogen) system using micro genetic algorithm. Energy 2016, 99, 115–128. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).