Design, Analysis and Model Predictive Control of an Axial Field Switched-Flux Permanent Magnet Machine for Electric Vehicle/Hybrid Electric Vehicle Applications
Abstract
1. Introduction
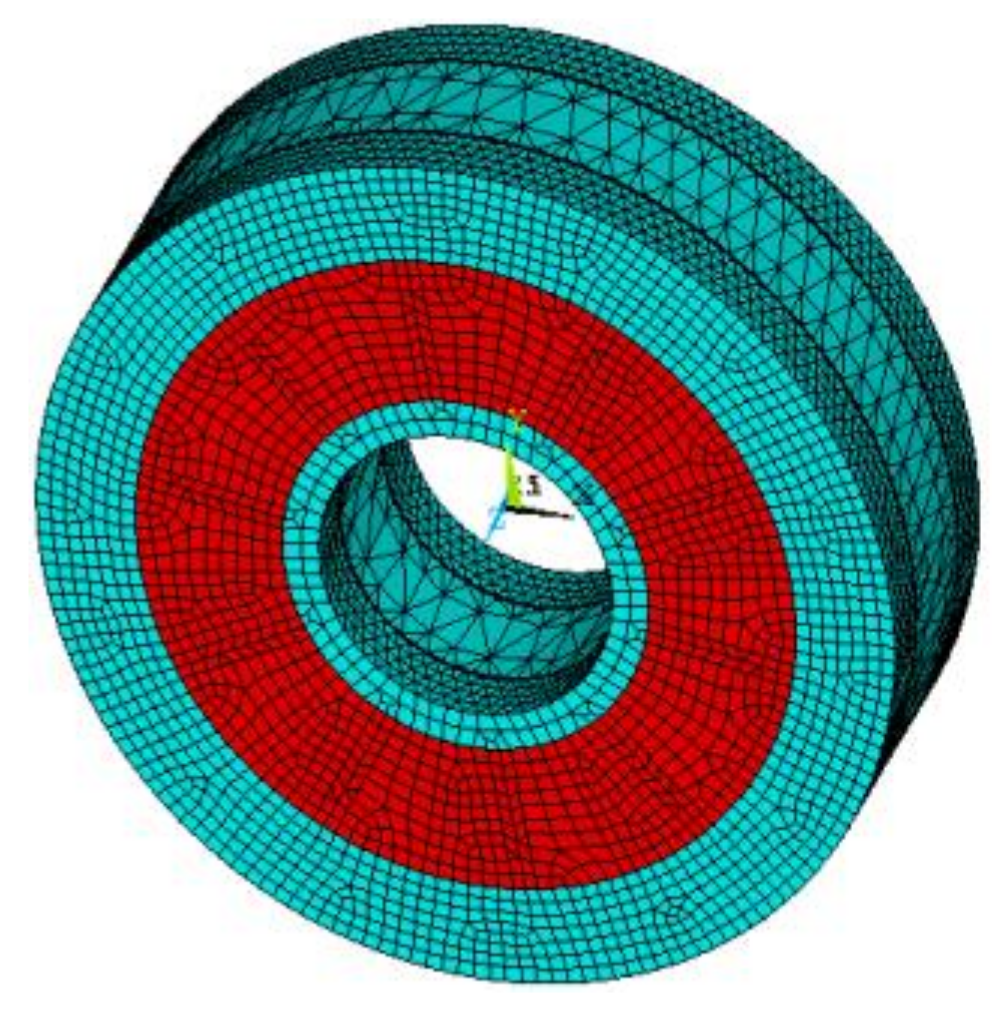
2. Machine Design
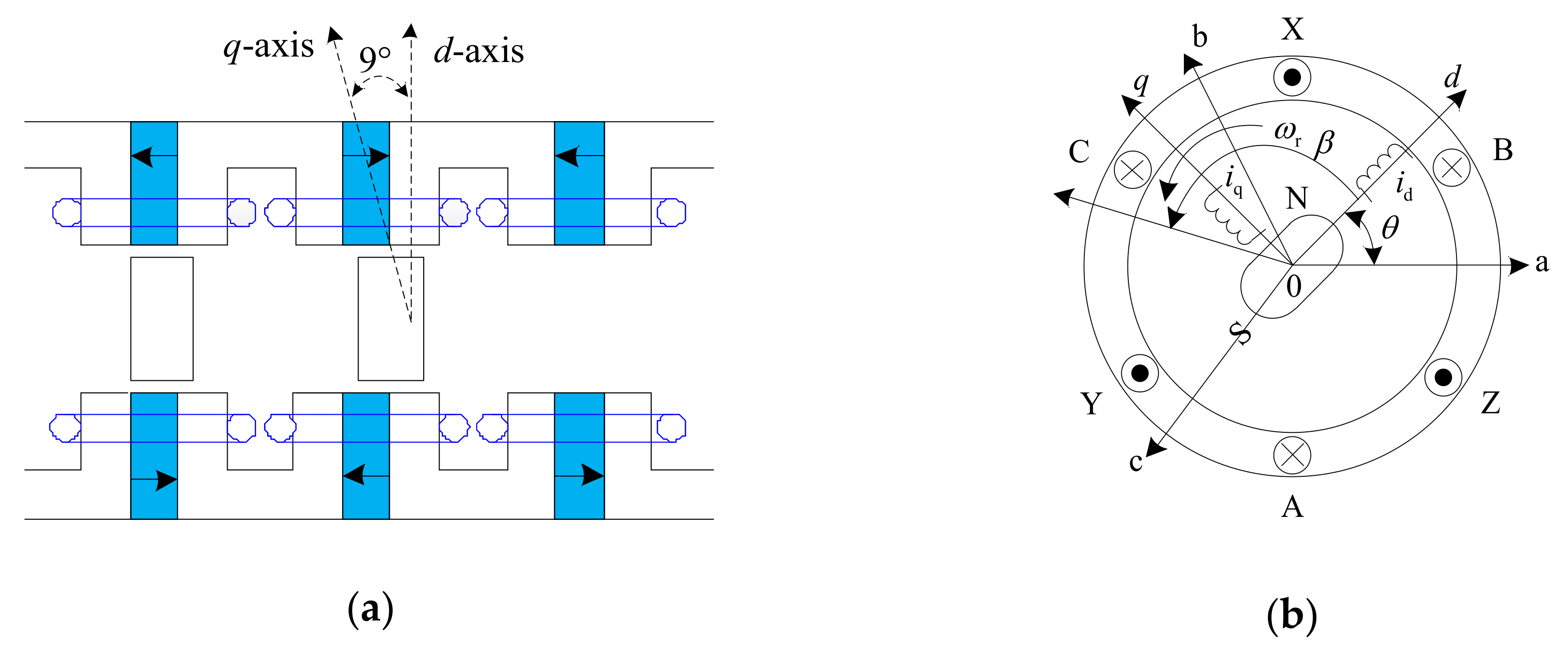
2.1. Target Machine Configuration
2.2. Operating Principle
2.3. Key Dimensions
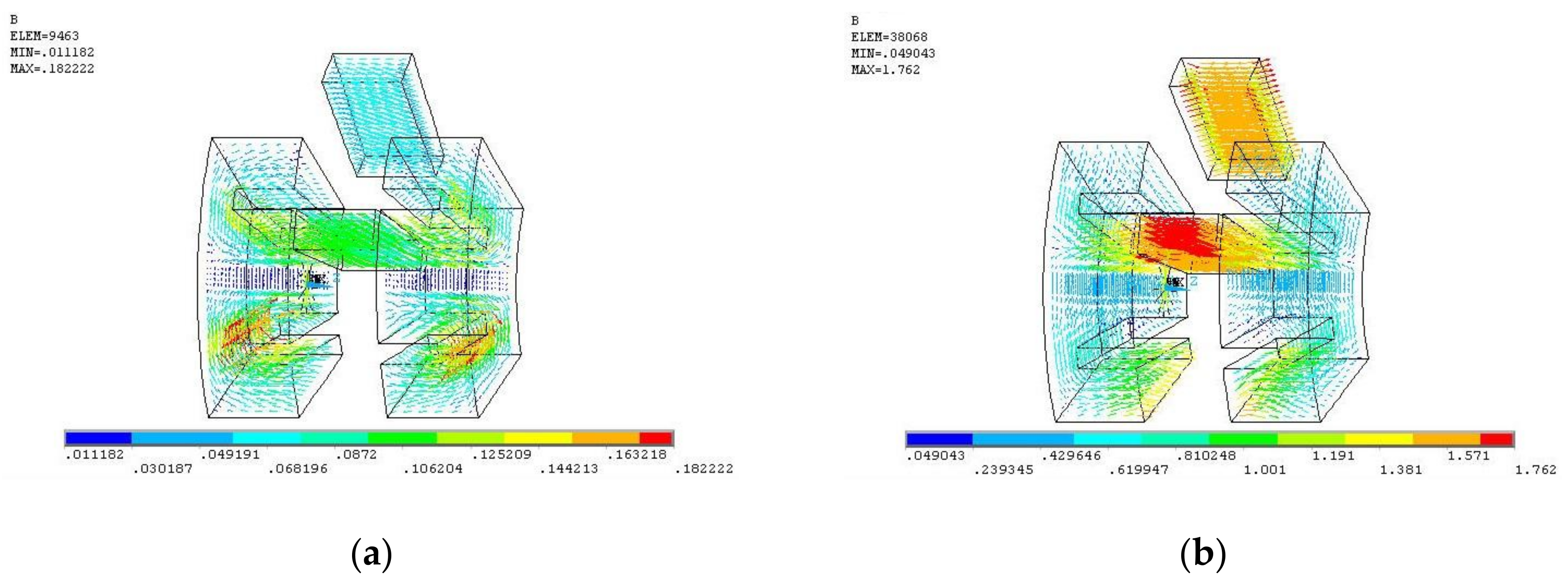
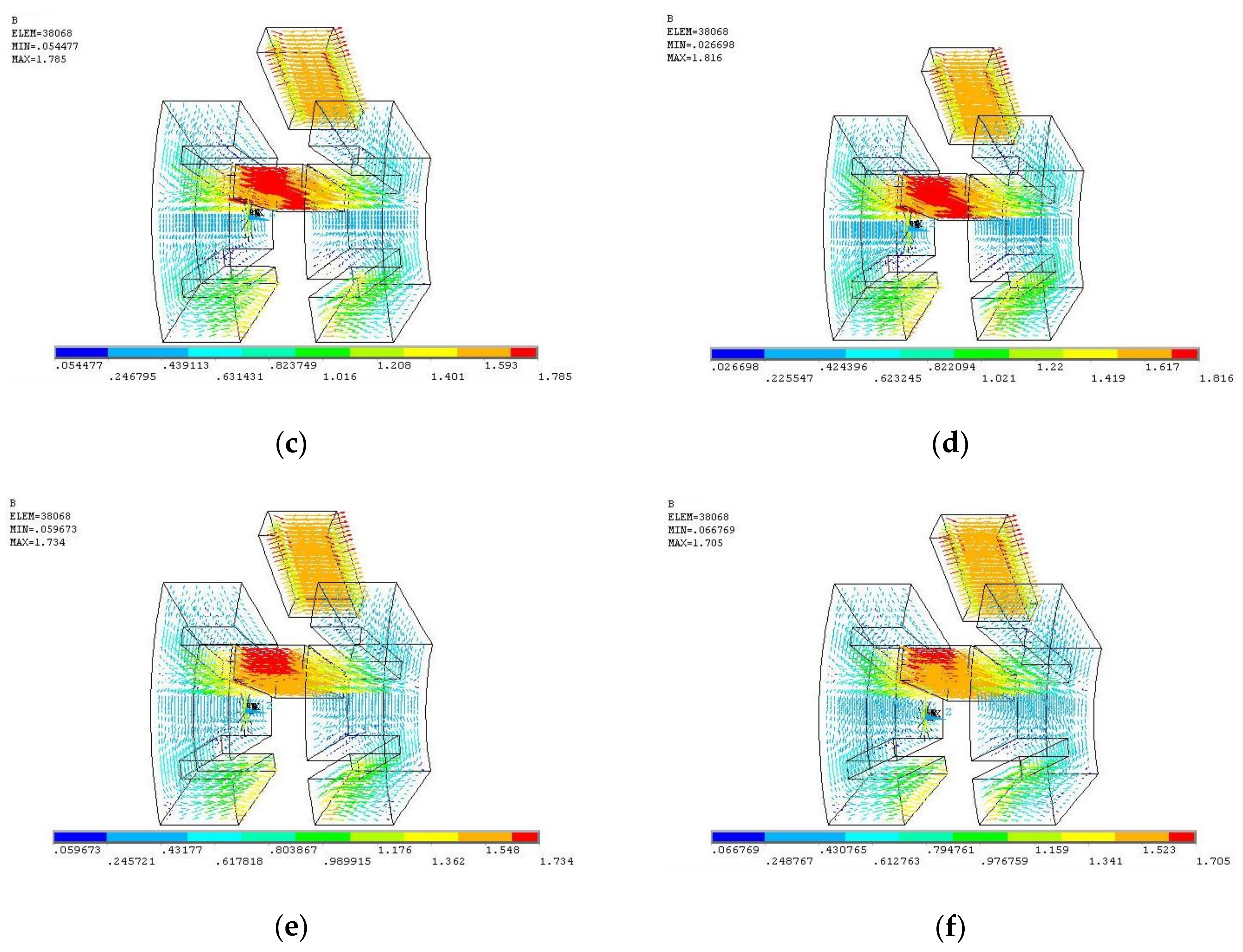
3. Electromagnetic Performance Analysis
3.1. Magnetic Field Distribution
3.2. PM Flux-Linkage, Back-EMF, Inductance and Cogging Torque
4. Model Predictive Control
4.1. Discrete Model of AFSFPM Machine
4.2. Cost Function
4.3. Current Predictive Model
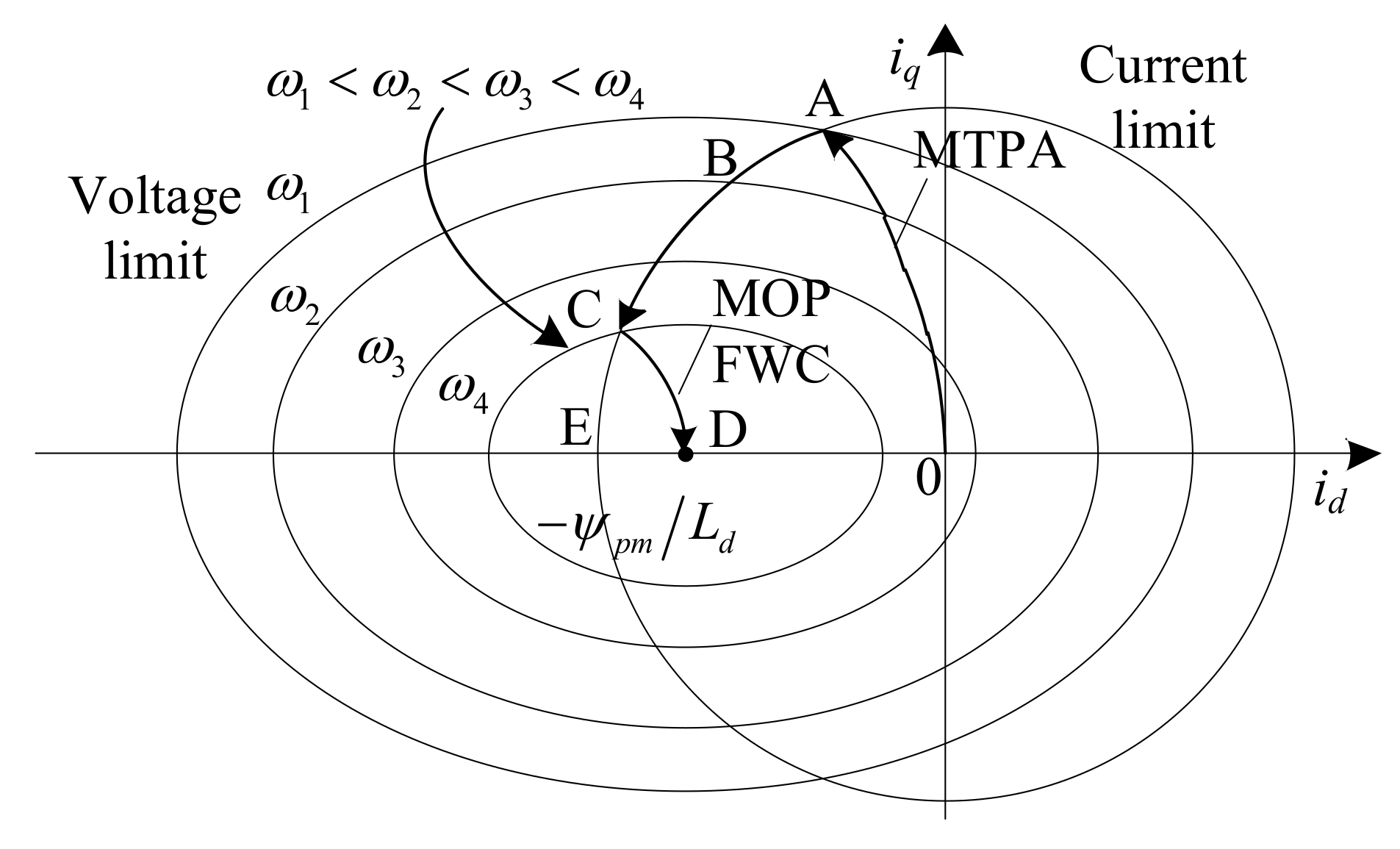
4.4. Reference Current Calculation
4.4.1. Constant Torque Region
4.4.2. Constant Power Region
5. Simulation and Experiment
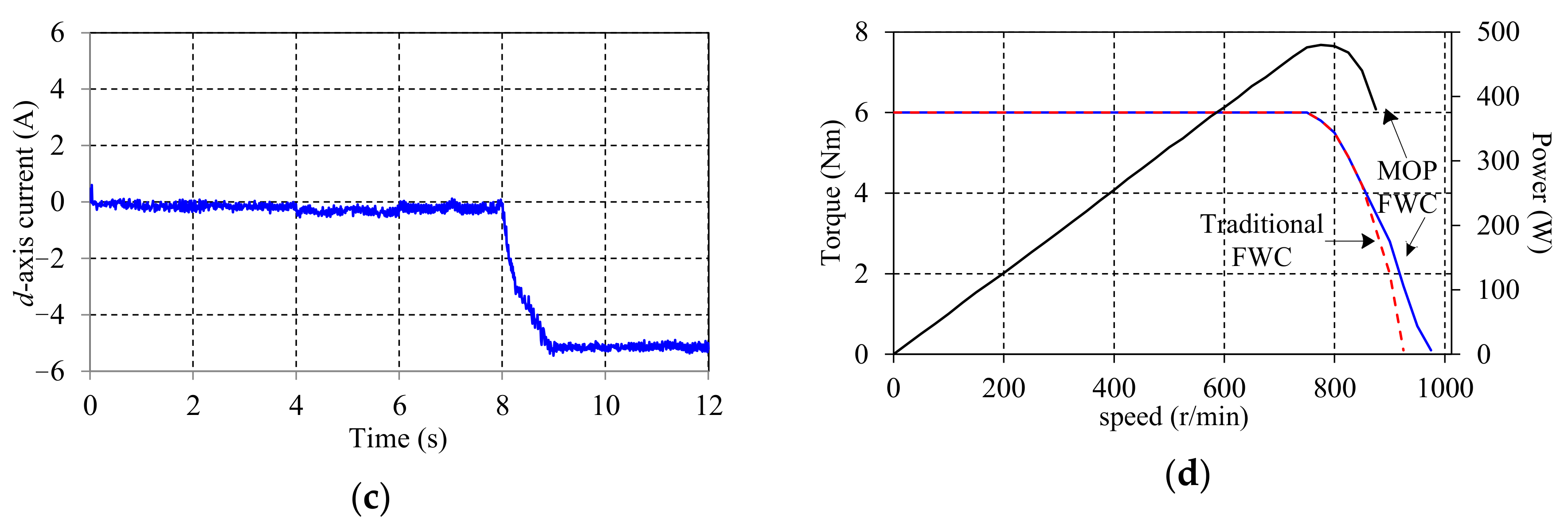
5.1. Simulation Analysis
5.2. Experimental Research
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Chan, T.F.; Lai, L.L. An axial-flux permanent-magnet synchronous generator for a direct-coupled wind-turbine system. IEEE Trans. Energy Convers. 2007, 22, 86–94. [Google Scholar] [CrossRef]
- Marignetti, F.; Colli, V.D.; Coia, Y. Design of axial flux PM synchronous machines through 3-D coupled electromagnetic thermal and fluid-dynamical finite-element analysis. IEEE Trans. Ind. Electron. 2008, 55, 3591–3601. [Google Scholar] [CrossRef]
- Capponi, F.G.; De Donato, G.; Caricchi, F. Recent advances in axial-flux permanent-magnet machine technology. IEEE Trans. Ind. Appl. 2012, 48, 2190–2205. [Google Scholar] [CrossRef]
- De Bisschop, J.; Sergeant, P.; Hemeida, A.; Vansompel, H.; Dupré, L. Analytical model for combined study of magnet demagnetization and eccentricity defects in axial flux permanent magnet synchronous machines. IEEE Trans. Magn. 2017, 53, 8107712. [Google Scholar] [CrossRef]
- Hemeida, A.; Taha, M.; Abdallh, A.A.E.; Vansompel, H.; Dupré, L.; Sergeant, P. Applicability of fractional slot axial flux permanent magnet synchronous machines in the field weakening region. IEEE Trans. Energy Convers. 2017, 32, 111–121. [Google Scholar] [CrossRef]
- Ogidi, O.O.; Barendse, P.S.; Khan, M.A. Influence of rotor topologies and cogging torque minimization techniques in the detection of static eccentricities in axial-flux permanent-magnet machine. IEEE Trans. Ind. Appl. 2017, 53, 161–170. [Google Scholar] [CrossRef]
- Kappatou, J.C.; Zalokostas, G.D.; Spyratos, D.A. 3-D FEM Analysis, Prototyping and Tests of an Axial Flux Permanent-Magnet Wind Generator. Energies 2017, 10, 1269. [Google Scholar] [CrossRef]
- Hoang, E.; Ben-Ahmed, A.H.; Lucidarme, J. Switching flux permanent magnet polyphased synchronous machines. In Proceedings of the 7th Europe Conference Power Electronics and Applications, Trondheim, Norway, 8–10 September 1997; pp. 903–908. [Google Scholar]
- Zhu, Z.Q.; Chen, J.T. Advanced switched-flux permanent magnet brushless machines. IEEE Trans. Magn. 2010, 46, 1447–1453. [Google Scholar] [CrossRef]
- Yu, F.; Cheng, M.; Chau, K.T.; Li, F. Control and Performance Evaluation of Multiphase FSPM Motor in Low-Speed Region for Hybrid Electric Vehicles. Energies 2015, 8, 10335–10353. [Google Scholar] [CrossRef]
- Dupas, A.; Hlioui, S.; Hoang, E.; Gabsi, M.; Lecrivain, M. Investigation of a new topology of hybrid-excited switched-flux machine with static global winding: experiments and modeling. IEEE Trans. Ind. Appl. 2016, 52, 1413–1421. [Google Scholar]
- Wu, Z.Z.; Zhu, Z.Q. Analysis of magnetic gearing effect in partitioned stator switched flux PM machines. IEEE Trans. Energy Convers. 2016, 31, 1239–1249. [Google Scholar] [CrossRef]
- Zhu, X.; Shu, Z.; Quan, L.; Xiang, Z.; Pan, X. Multi-objective optimization of an outer-rotor V-shaped permanent magnet flux switching motor based on multi-level design method. IEEE Trans. Magn. 2016, 52, 1–8. [Google Scholar] [CrossRef]
- Hua, W.; Zhang, H.; Cheng, M.; Meng, J.; Hou, C. An outer-rotor switched-flux permanent-magnet machine with wedge-shaped magnets for in-wheel light traction. IEEE Trans. Ind. Electron. 2017, 64, 69–80. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, Y.; Zhu, C.; Liu, X.; Li, B. A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor. Energies 2017, 10, 937. [Google Scholar] [CrossRef]
- Hao, L.; Lin, M.; Li, W.; Luo, H.; Fu, X.; Jing, P. Novel dual-rotor axial field switched-flux permanent magnet machine. IEEE Trans. Magn. 2012, 48, 4232–4235. [Google Scholar] [CrossRef]
- Hao, L.; Lin, M.; Xu, D.; Fu, X.; Zhang, W. Static Characteristics of a Novel Axial Field Switched-flux Permanent Magnet Motor with Three Stator Structures. IEEE Trans. Magn. 2014, 50, 4002604. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, M.; Xu, D.; Fu, X.; Hao, L. Novel fault-tolerant design of axial field switched-flux permanent magnet machine. IEEE Trans. Appl. Supercond. 2014, 24, 0503804. [Google Scholar]
- Zhang, W.; Liang, X.; Lin, M.; Hao, L.; Li, N. Design and analysis of novel hybrid-excited axial field switched-flux permanent magnet machines. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar]
- Zhao, W.; Lipo, T. A.; Kwon, B.I. A novel dual-rotor, axial field, fault-tolerant switched-flux permanent magnet machine with high-torque performance. IEEE Trans. Magn. 2015, 51, 7112204. [Google Scholar] [CrossRef]
- Kim, J.H.; Li, Y.; Sarlioglu, B. Novel six-slot four-pole axial switched-flux permanent magnet machine for electric vehicle. IEEE Trans. Transp. Electrification 2017, 3, 108–117. [Google Scholar] [CrossRef]
- Syed, Q.A.S.; Kurtović, H.; Hahn, I. New single-phase flux switching axial flux Permanent magnet motor. IEEE Trans. Magn. 2017, 53, 8209505. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Xu, D.; Hao, L.; Zhang, W. Vector control of a hybrid axial field switched-flux permanent magnet machine based on particle swarm optimization. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Hasanien, H.M.; Abd-Rabou, A.S.; Sakr, S.M. Design optimization of transverse flux linear motor for weight reduction and performance improvement using response surface methodology and genetic algorithms. IEEE Trans. Energy Convers. 2010, 25, 598–605. [Google Scholar] [CrossRef]
- Jędryczka, C.; Knypiński, Ł.; Demenko, A.; Sykulski, J.K. Methodology for Cage Shape Optimization of a Permanent Magnet Synchronous Motor Under Line Start Conditions. IEEE Trans. Magn. 2018, 54, 8102304. [Google Scholar] [CrossRef]
- Lei, G.; Xu, W.; Hu, J.F.; Zhu, J.G.; Guo, Y.G.; Shao, K.R. Multilevel design optimization of a FSPMM drive system by using sequential subspace optimization method. IEEE Trans. Magn. 2014, 50, 7016904. [Google Scholar] [CrossRef]
- Ma, B.; Lei, G.; Zhu, J.; Guo, Y.; Liu, C. Application-Oriented Robust Design Optimization Method for Batch Production of Permanent-Magnet Motors. IEEE Trans. Ind. Electron. 2018, 65, 1728–1739. [Google Scholar] [CrossRef]
- Lei, G.; Zhu, J.G.; Guo, Y.G.; Liu, C.C.; Ma, B. A Review of Design Optimization Methods for Electrical Machines. Energies 2017, 10, 1962. [Google Scholar] [CrossRef]
- Morel, F.; Lin-Shi, X.; Retif, J.M.; Allard, B.; Buttay, C. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive. IEEE Trans. Ind. Electron. 2009, 56, 2715–2728. [Google Scholar] [CrossRef]
- Formentini, A.; Trentin, A.; Marchesoni, M.; Zanchetta, P.; Wheeler, P. Speed finite control set model predictive control of a PMSM fed by matrix converter. IEEE Trans. Ind. Electron. 2015, 62, 6786–6796. [Google Scholar] [CrossRef]
- Siami, M.; Arab Khaburi, D.; Rodriguez, J. Simplified finite control set-model predictive control for matrix converter-fed PMSM drives. IEEE Trans. Power Electron. 2018, 33, 2438–2446. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rodríguez, J. Torque ripple reduction of predictive torque control for PMSM drives with parameter mismatch. IEEE Trans. Power Electron. 2017, 32, 7160–7168. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Cheng, M. Common model predictive control for permanent-magnet synchronous machine drives considering single-phase open-circuit fault. IEEE Trans. Power Electron. 2017, 32, 5862–5872. [Google Scholar] [CrossRef]
- Hao, L.; Lin, M.; Zhao, X.; Fu, X.; Zhu, Z.Q.; Jin, P. Static characteristics analysis and experimental study of a novel axial field switched-flux permanent magnet generator. IEEE Trans. Magn. 2012, 48, 4212–4215. [Google Scholar] [CrossRef]
- Hao, L.; Lin, M.; Xu, D.; Li, N.; Zhang, W. Cogging torque reduction of axial-field switched-flux permanent magnet machine by rotor tooth notching. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]











| Item | Original Parameter | Optimized Parameter |
|---|---|---|
| Slot/pole number | 12/10 | 12/10 |
| Rated output power (W) | 600 | 600 |
| Rated speed (r/min) | 750 | 750 |
| Rated current (A) | 3.5 | 3.5 |
| Turns per phase | 180 | 184 |
| Stator outer diameter (mm), Dso | 150 | 150 |
| Stator inner diameter (mm), Dsi | 82 | 82 |
| Stator axial length (mm), ls | 20 | 16 |
| Stator yoke thickness (mm), hys | 7 | 3 |
| Rotor axial length (mm), lr | 17.5 | 17.5 |
| Air-gap length (mm), g | 1 | 1 |
| Stator tooth width (°), βt | 7.5 | 7.5 |
| Stator slot width (°), βs | 7.5 | 7.5 |
| Stator magnet thickness (°), βPM | 7.5 | 7.5 |
| Rotor pole width (°), βr | 7.5 | 12.5 |
| Parameters | Value |
|---|---|
| Slot/pole | 12/10 |
| Rated power | 600 W |
| Rated phase voltage | 67 V |
| Rated phase current | 3.5 A |
| Rated torque | 7 N·m |
| Stator resistance Rs | 1.5 Ω |
| d-axis inductance Ld | 4 mH |
| q-axis inductance Lq | 5 mH |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Quan, X.; Jing, M.; Lin, M.; Li, N. Design, Analysis and Model Predictive Control of an Axial Field Switched-Flux Permanent Magnet Machine for Electric Vehicle/Hybrid Electric Vehicle Applications. Energies 2018, 11, 1859. https://doi.org/10.3390/en11071859
Zhao J, Quan X, Jing M, Lin M, Li N. Design, Analysis and Model Predictive Control of an Axial Field Switched-Flux Permanent Magnet Machine for Electric Vehicle/Hybrid Electric Vehicle Applications. Energies. 2018; 11(7):1859. https://doi.org/10.3390/en11071859
Chicago/Turabian StyleZhao, Jilong, Xiaowei Quan, Mengdie Jing, Mingyao Lin, and Nian Li. 2018. "Design, Analysis and Model Predictive Control of an Axial Field Switched-Flux Permanent Magnet Machine for Electric Vehicle/Hybrid Electric Vehicle Applications" Energies 11, no. 7: 1859. https://doi.org/10.3390/en11071859
APA StyleZhao, J., Quan, X., Jing, M., Lin, M., & Li, N. (2018). Design, Analysis and Model Predictive Control of an Axial Field Switched-Flux Permanent Magnet Machine for Electric Vehicle/Hybrid Electric Vehicle Applications. Energies, 11(7), 1859. https://doi.org/10.3390/en11071859





