A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contributions
- A one-class support vector classification (SVC)-based DPVS detection (DPVSD) model with the input features extracted according to the unique weather status driven characteristic of DPVS output power is proposed to distinguish customers with DPVSs from those without. This model can not only accurately detect the existence of DPVS, but also reliably distinguish load components showing similar output characteristic to DPVS, such as electric vehicles and energy storage devices, which means it is robust to the interference from those load components that are most likely misrecognized by other methods.
- A bootstrap-support vector regression (SVR) based DPVSCE model with the input features describing the difference of daily total PV power generation between DPVSs with different capacities is proposed to further estimate the specific capacity of the detected DPVS. This model can keep stable promising performance under the scenario of limited training samples and imbalance dataset.
- The effectiveness of the proposed approach is verified on a realistic dataset. Furthermore, the robustness of the model under several scenarios (e.g., the existence of storage devices, different lengths of available historical data) is analyzed and discussed.
1.4. Structure of This Paper
2. Problem Formulation
2.1. Problem Statement
2.2. Framework of the Proposed Approach
3. One-Class SVC Based DPVSD Model
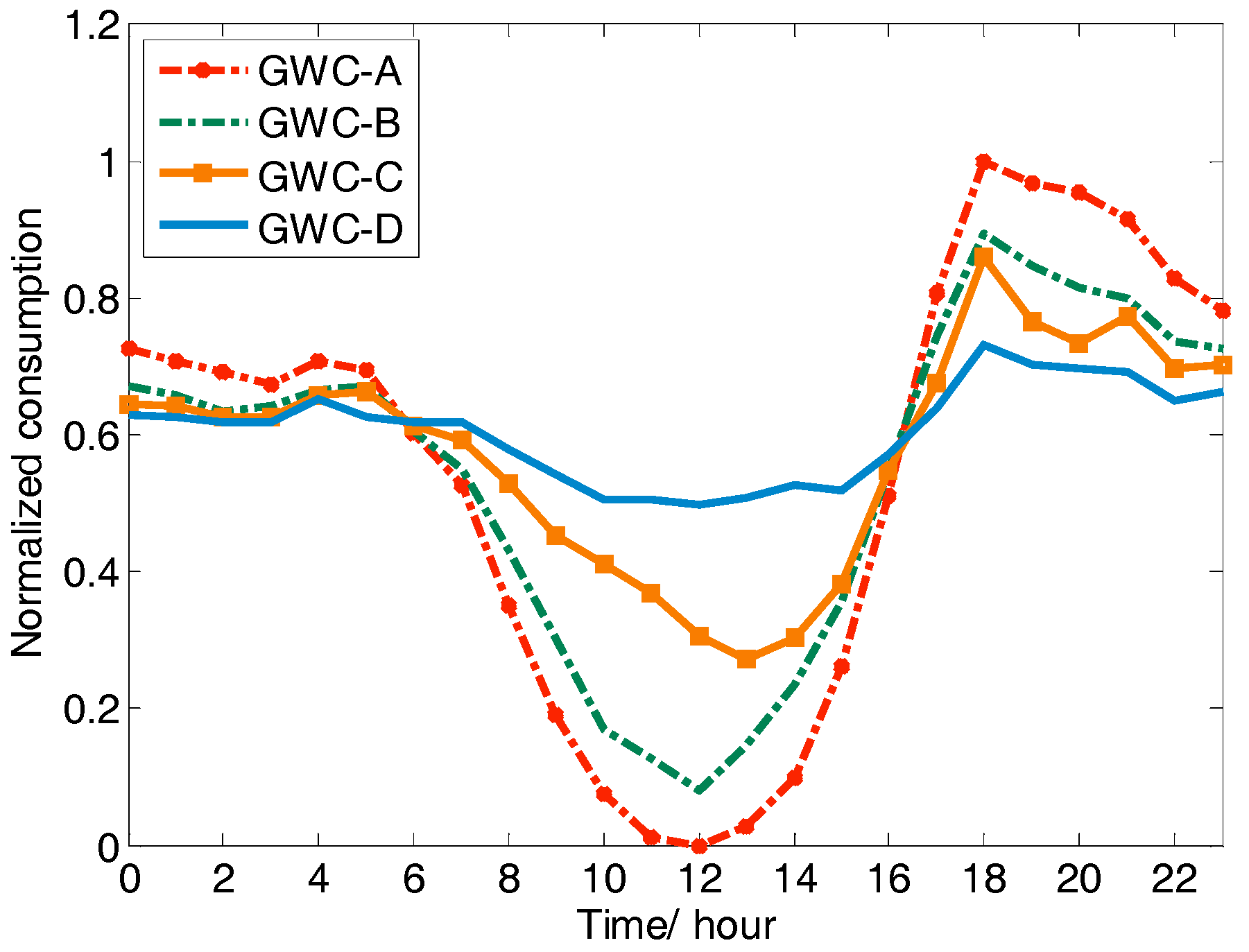
3.1. Generalized Weather Classes
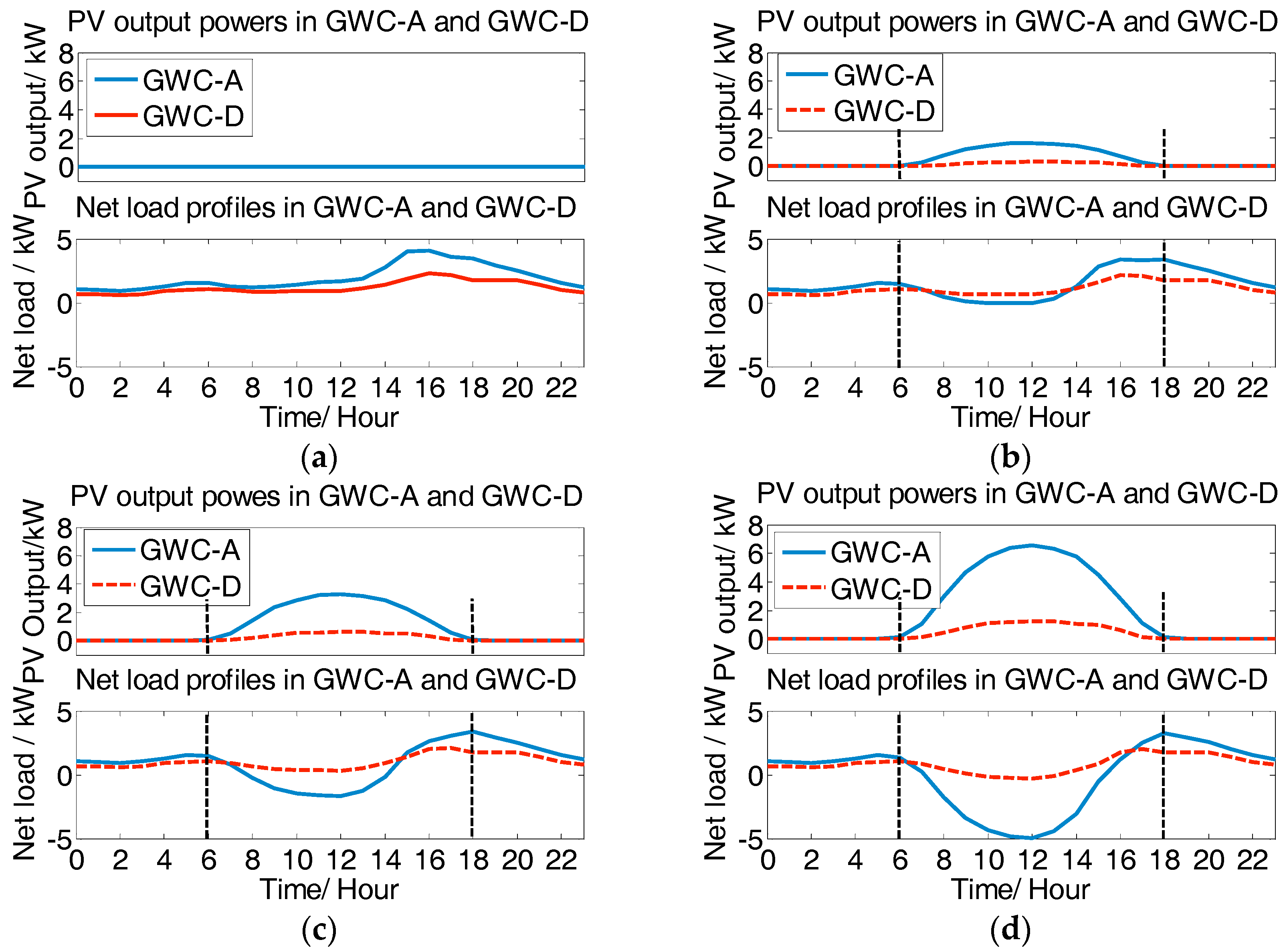
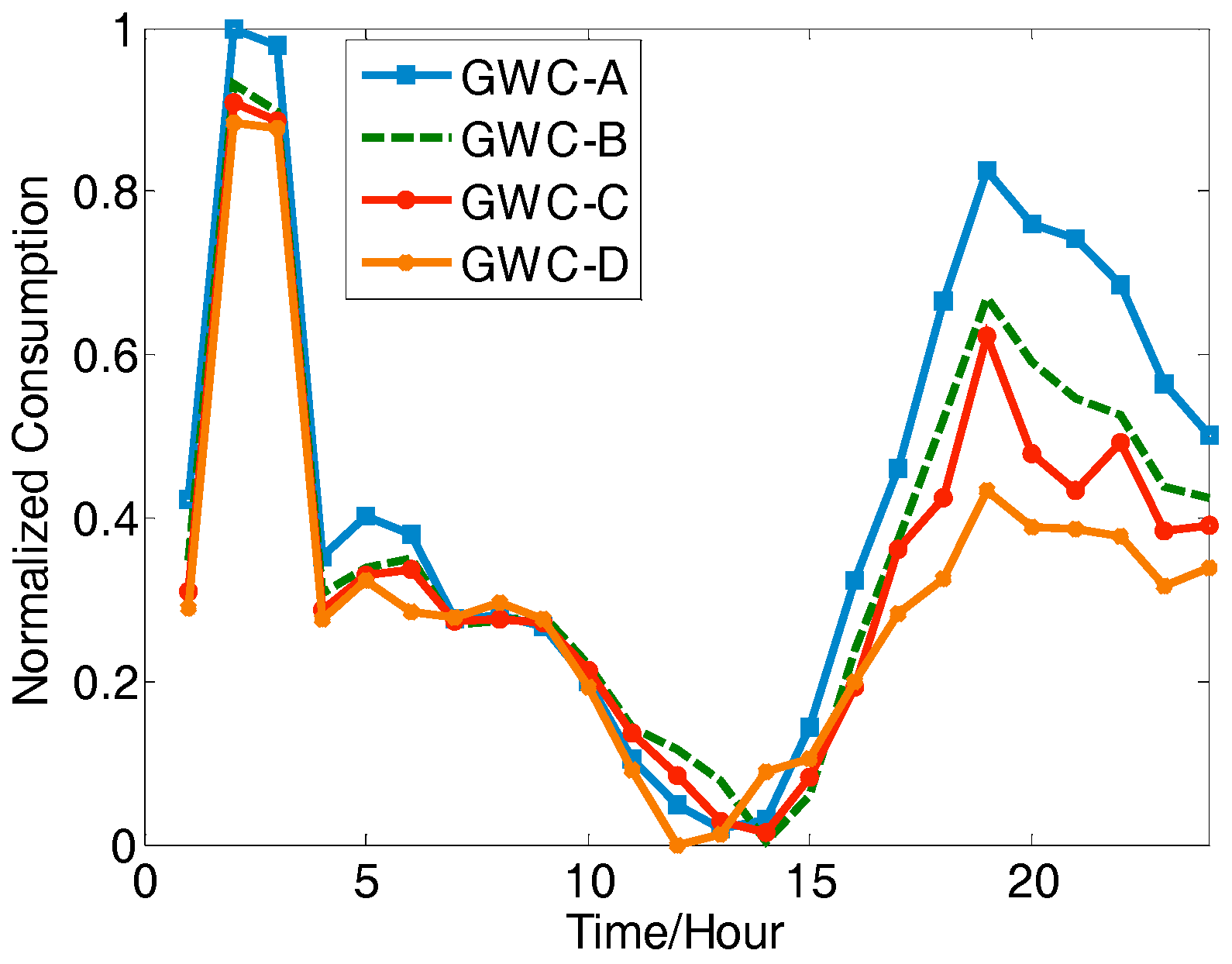
3.2. Typical Net Load Pattern
3.3. Feature Extraction
3.3.1. Ratio of Total Electricity Consumption in GWC-A to GWC-D
3.3.2. Concave Shape Index
3.3.3. Concavity Degree
3.3.4. Load Ramping Rate
3.4. One-Class SVC Based DPVSD Model
4. Bootstrap-SVR Based DPVSCE Model
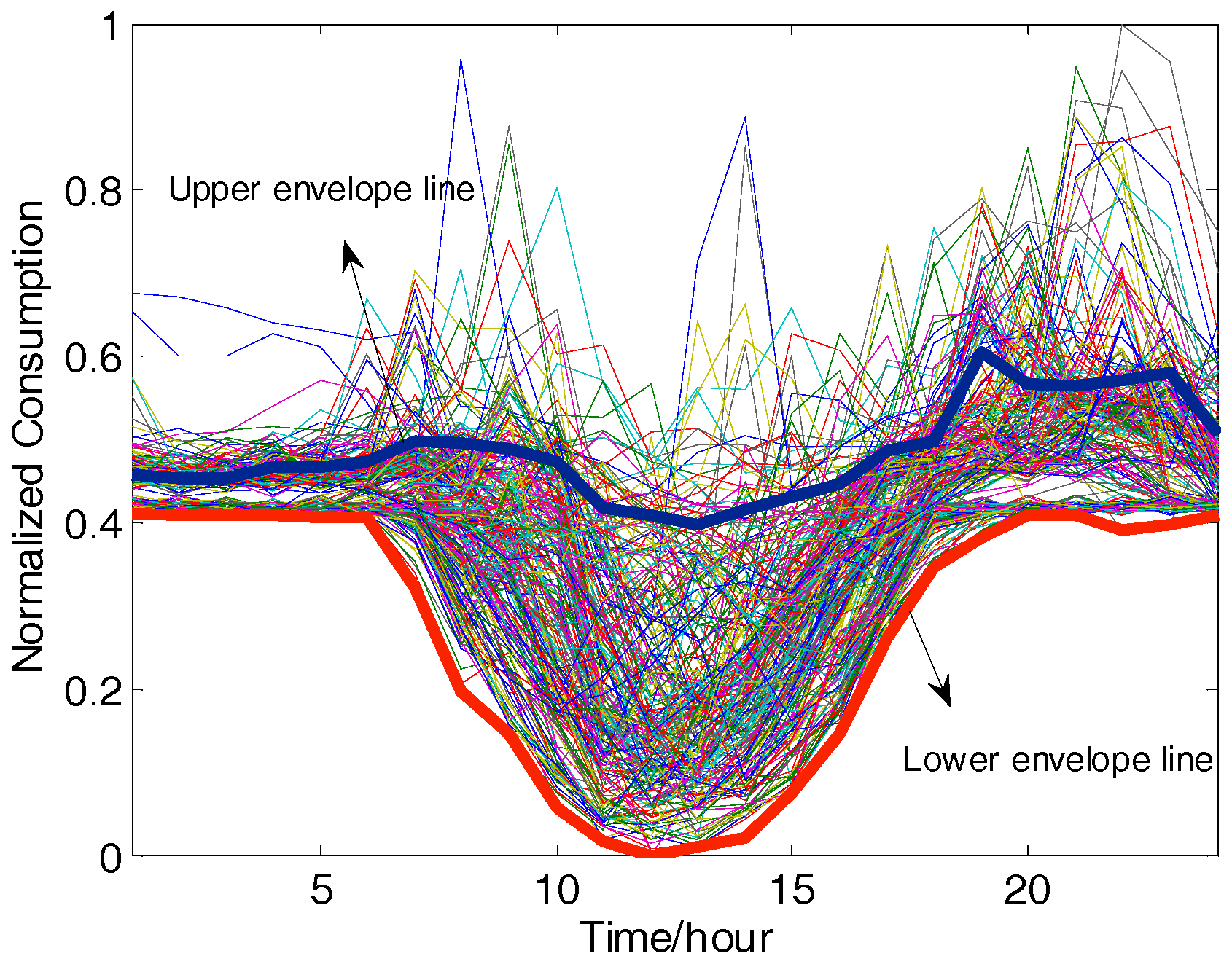
4.1. Extraction of Envelope Lines
4.1.1. Extraction of LEL
4.1.2. Extraction of UEL
4.2. Extremum Difference Based Feature Extraction
4.2.1. Minimum Net Load Power
4.2.2. Maximum Difference of PV Output Power
4.2.3. Total PV Power Generation during Time Window
4.3. Bootstrap-SVR Based DPVSCE Model
5. Case Study
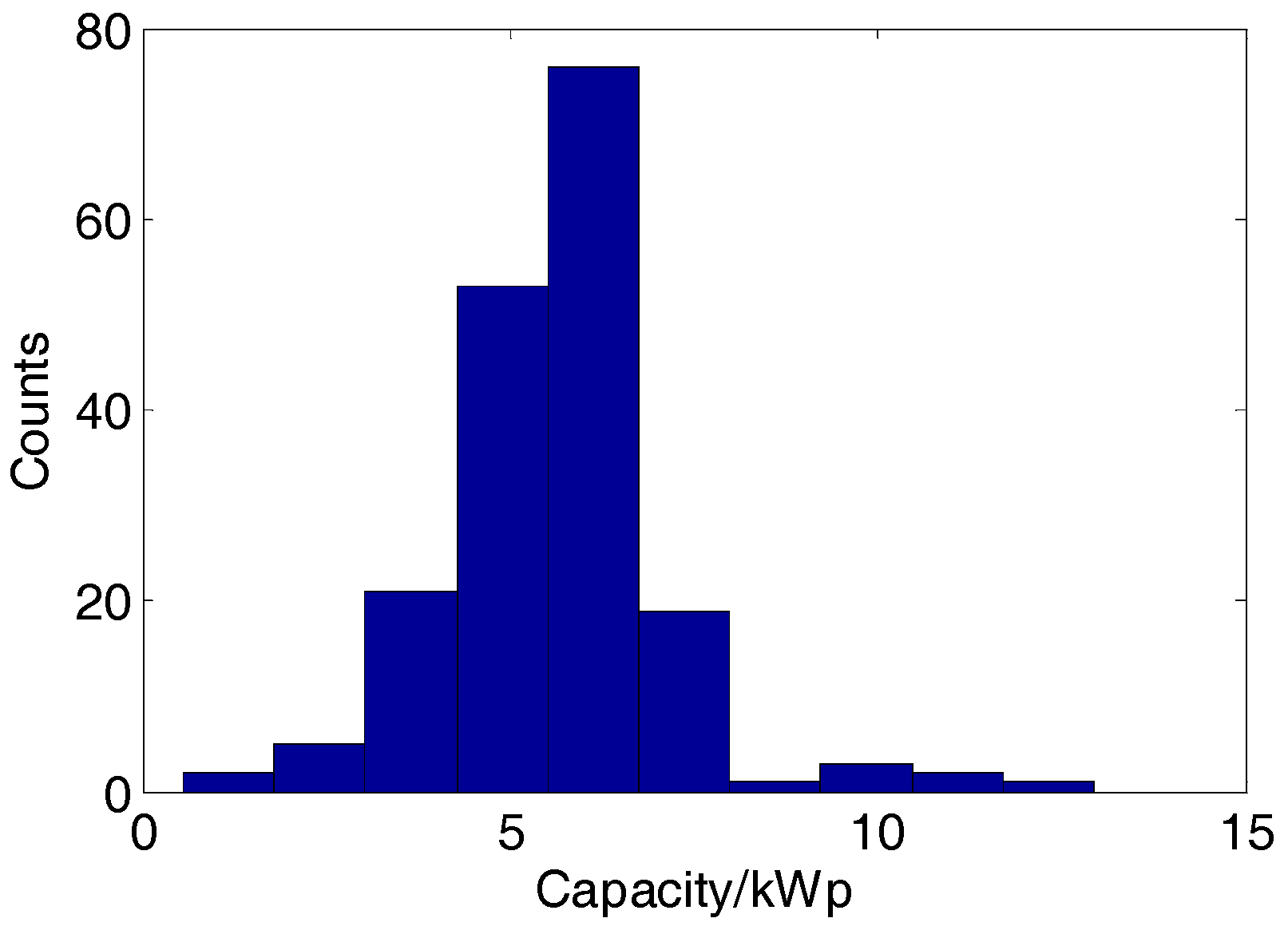
5.1. Dataset
5.2. Performance Metric
5.2.1. Performance Metric for DPVSD Model
5.2.2. Performance Metric for DPVSCE Model
5.3. Experiment Design
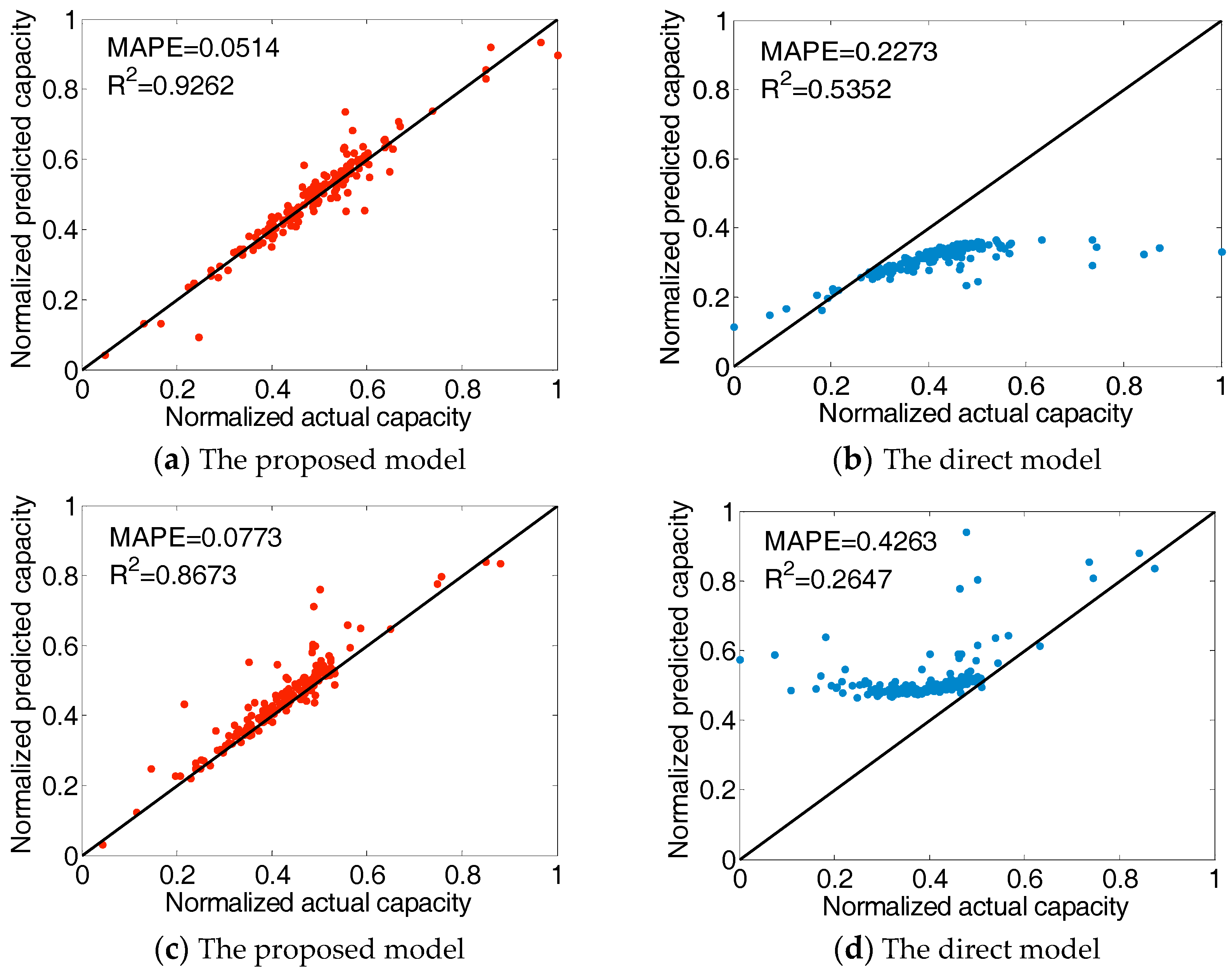
5.3.1. Experiment 1: Performance Test of the DPVSD Model
5.3.2. Experiment 2: Performance Test of the DPVSCE Model
6. Discussion
6.1. Correlation Analysis
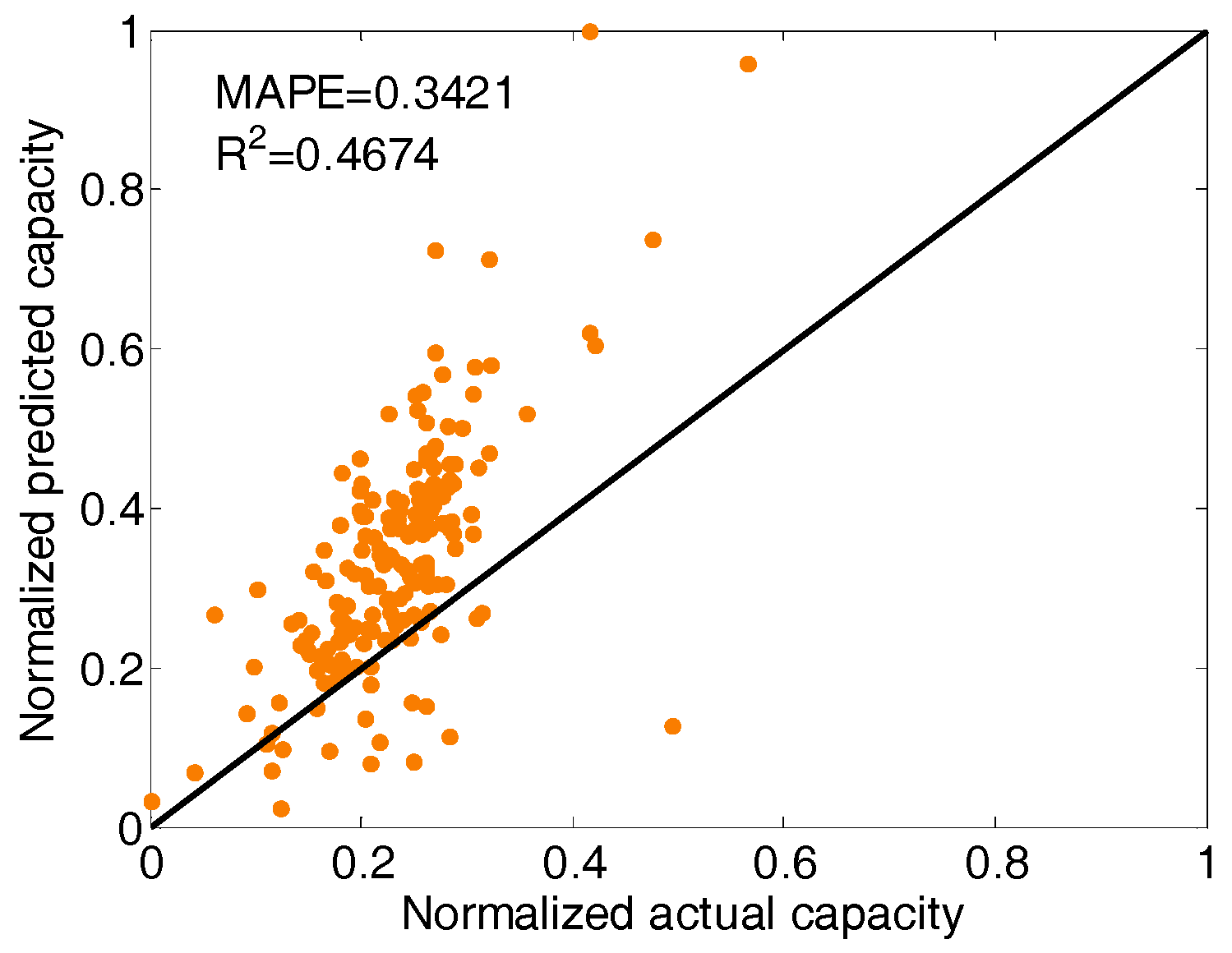
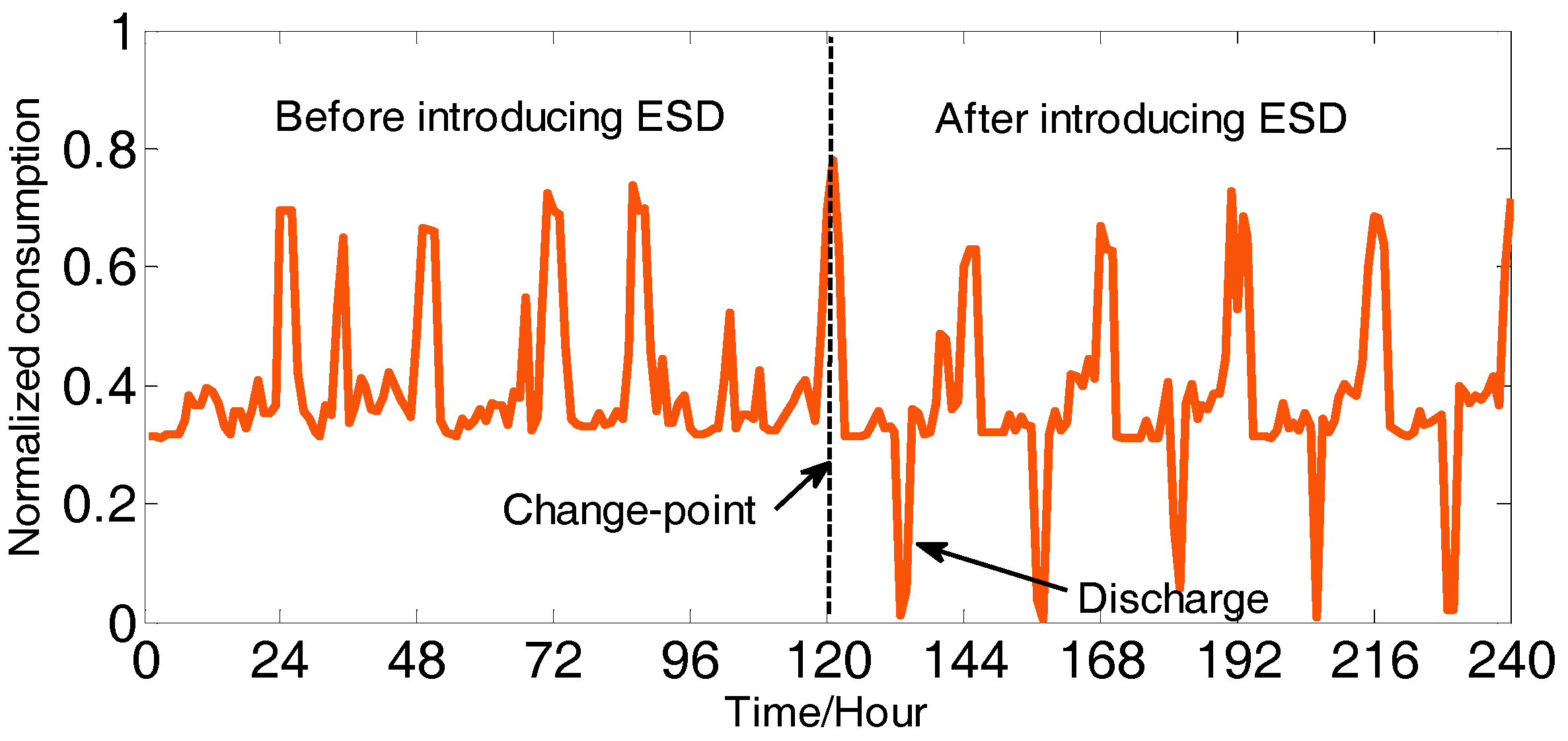
6.2. The Impact of Energy Storage on DPVSD Model
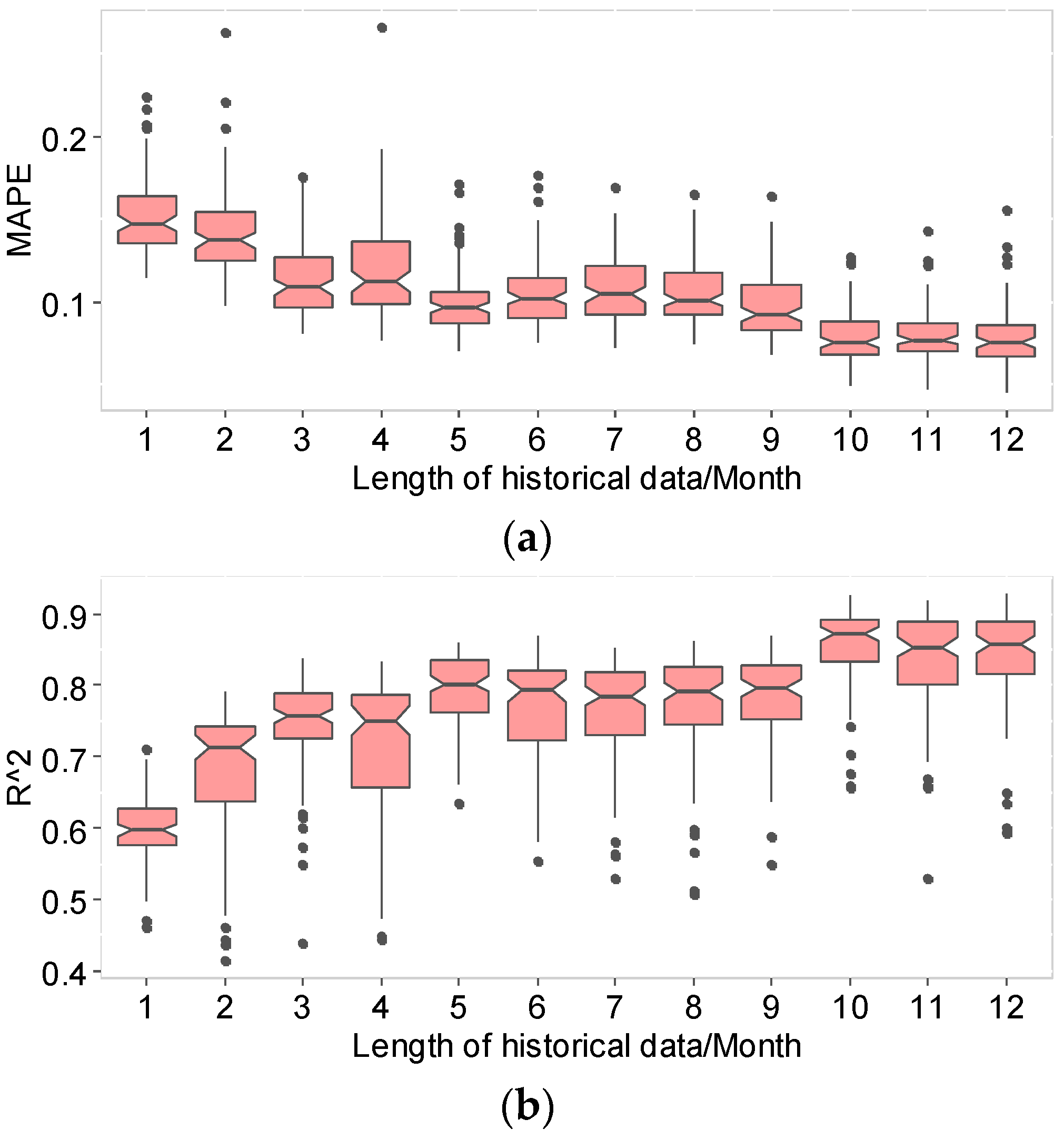
6.3. The Impact of Length of Historical Data on the DPVSCE Model
7. Conclusions
- Testing the proposed approach in other sites with different latitudes and user profiles to further verify its effectiveness.
- Explore DPVS output power simulation methods to improve the performance of the DPVSCE model in the case of limited historical data.
- Investigating the robustness of the proposed approach in the presence of DR (e.g., the TOU price DR [26]).
- Extending the proposed approach to detect the orientation of the installed PV to check whether the PV system is operating on the optimal orientation.
Author Contributions
Funding
Conflicts of Interest
References
- Preliminary Market Report. Available online: http://www.iea-pvps.org/index.php?id=266 (accessed on 21 April 2018).
- National Survey Reports, International Energy Agency Photovoltaic Power Systems Programme. Available online: http://www.iea-pvps.org/index.php?id=93 (accessed on 21 April 2018).
- Wang, F.; Xu, H.; Xu, T.; Li, K.; Shafie-khah, M.; João, P.S.; Catalão, J.P.S. The values of market-based demand response on improving power system reliability under extreme circumstances. Appl. Energy 2017, 193, 220–231. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, F.; Hodge, B.M.; Zhang, J.; Li, Z.; Shafie-Khah, M.; Catalao, J.P.S. Dynamic Price Vector Formation Model-Based Automatic Demand Response Strategy for PV-Assisted EV Charging Stations. IEEE Trans. Smart Grid 2017, 8, 2903–2915. [Google Scholar] [CrossRef]
- Wang, F.; Liu, L.; Yu, Y.; Li, G.; Li, J.; Shafie-khah, M.; Catalão, J. Impact Analysis of Customized Feedback Interventions on Residential Electricity Load Consumption Behavior for Demand Response. Energies 2018, 11, 770. [Google Scholar] [CrossRef]
- Talari, S.; Shafie-khah, M.; Wang, F.; Aghaei, J.; Catalao, J.P.S. Optimal Scheduling of Demand Response in Pre-emptive Markets based on Stochastic Bilevel Programming Method. IEEE Trans. Ind. Electron. 2017. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Liu, C.; Mi, Z.; Shafie-khah, M.; Catalao, J.P.S. Synchronous Pattern Matching Principle Based Residential Demand Response Baseline Estimation: Mechanism Analysis and Approach Description. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Wijaya, T.K.; Vasirani, M.; Aberer, K. When bias matters: An economic assessment of demand response baselines for residential customers. IEEE Trans. Smart Grid 2014, 5, 1755–1763. [Google Scholar] [CrossRef]
- Kaur, A.; Pedro, H.T.C.; Coimbra, C.F.M. Impact of onsite solar generation on system load demand forecast. Energy Convers. Manag. 2013, 75, 701–709. [Google Scholar] [CrossRef]
- Massidda, L.; Marrocu, M. Decoupling Weather Influence from User Habits for an Optimal Electric Load Forecast System. Energies 2017, 10, 2721. [Google Scholar] [CrossRef]
- Yu, Y.; Wen, X.; Zhao, J.; Xu, Z.; Li, J. Co-Planning of Demand Response and Distributed Generators in an Active Distribution Network. Energies 2018, 11, 354. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Luo, J.; Duan, J.; Gao, H.; Xiao, X. Multi-Objective Coordinated Planning of Distributed Generation and AC/DC Hybrid Distribution Networks Based on a Multi-Scenario Technique Considering Timing Characteristics. Energies 2017, 10, 2137. [Google Scholar] [CrossRef]
- EIA Electricity Data Now Include Estimated Small-Scale Solar PV Capacity and Generation. Available online: https://www.eia.gov/todayinenergy/detail.cfm?id=23972 (accessed on 1 December 2018).
- Hawaiian Electric. Hawaiian Electric Asking Customers with Unauthorized Rooftop PV Systems to Disconnect to Ensure Safety, Fairness for All. Available online: https://www.hawaiianelectric.com/hawaiian-electric-asking-customers-with-unauthorized-rooftop-pv-systems-to-disconnect-to-ensure-safety-fairness-for-all (accessed on 3 June 2018).
- Malof, J.M.; Bradbury, K.; Collins, L.M.; Newell, R.G. Automatic detection of solar photovoltaic arrays in high resolution aerial imagery. Appl. Energy 2016, 183, 229–240. [Google Scholar] [CrossRef]
- Zhang, X.; Grijalva, S. A Data-Driven Approach for Detection and Estimation of Residential PV Installations. IEEE Trans. Smart Grid 2016, 7, 2477–2485. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Mi, Z.; Sun, H.; Su, S.; Yang, G. Solar irradiance feature extraction and support vector machines based weather status pattern recognition model for short-term photovoltaic power forecasting. Energy Build. 2015, 86, 427–438. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, F.; Wang, B.; Chen, Q.; Engerer, N.; Mi, Z. Correlation Feature Selection and Mutual Information Theory Based Quantitative Research on Meteorological Impact Factors of Module Temperature for Solar Photovoltaic Systems. Energies 2017, 10, 7. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term solar irradiance forecasting model based on artificial neural network using statistical feature parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Wang, B.; Mi, Z. Comparative Study on KNN and SVM Based Weather Classification Models for Day Ahead Short Term Solar PV Power Forecasting. Appl. Sci. 2017, 8, 28. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Liu, C.; Mi, Z.; Hodge, B.M.; Shafie-khah, M.; Catalão, J.P.S. Image phase shift invariance based cloud motion displacement vector calculation method for ultra-short-term solar PV power forecasting. Energy Convers. Manag. 2018, 157, 123–135. [Google Scholar] [CrossRef]
- PECAN STREET. Available online: http://www.pecanstreet.org/what-is-pecan-street-inc/ (accessed on 15 September 2017).
- Wang, F.; Li, K.; Duić, N.; Mi, Z.; Hodge, B.M.; Shafie-khah, M.; Catalão, J.P.S. Association rule mining based quantitative analysis approach of household characteristics impacts on residential electricity consumption patterns. Energy Convers. Manag. 2018, 171, 839–854. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Powerwall. Available online: https://www.tesla.com/powerwall (accessed on 12 September 2017).
- Wang, F.; Zhou, L.; Ren, H.; Liu, X.; Shafie-khah, M. Multi-objective Optimization Model of Source-Load-Storage Synergetic Dispatch for Building Energy System Based on TOU Price Demand Response. IEEE Trans. Ind. Appl. 2018, 54, 1017–1028. [Google Scholar] [CrossRef]

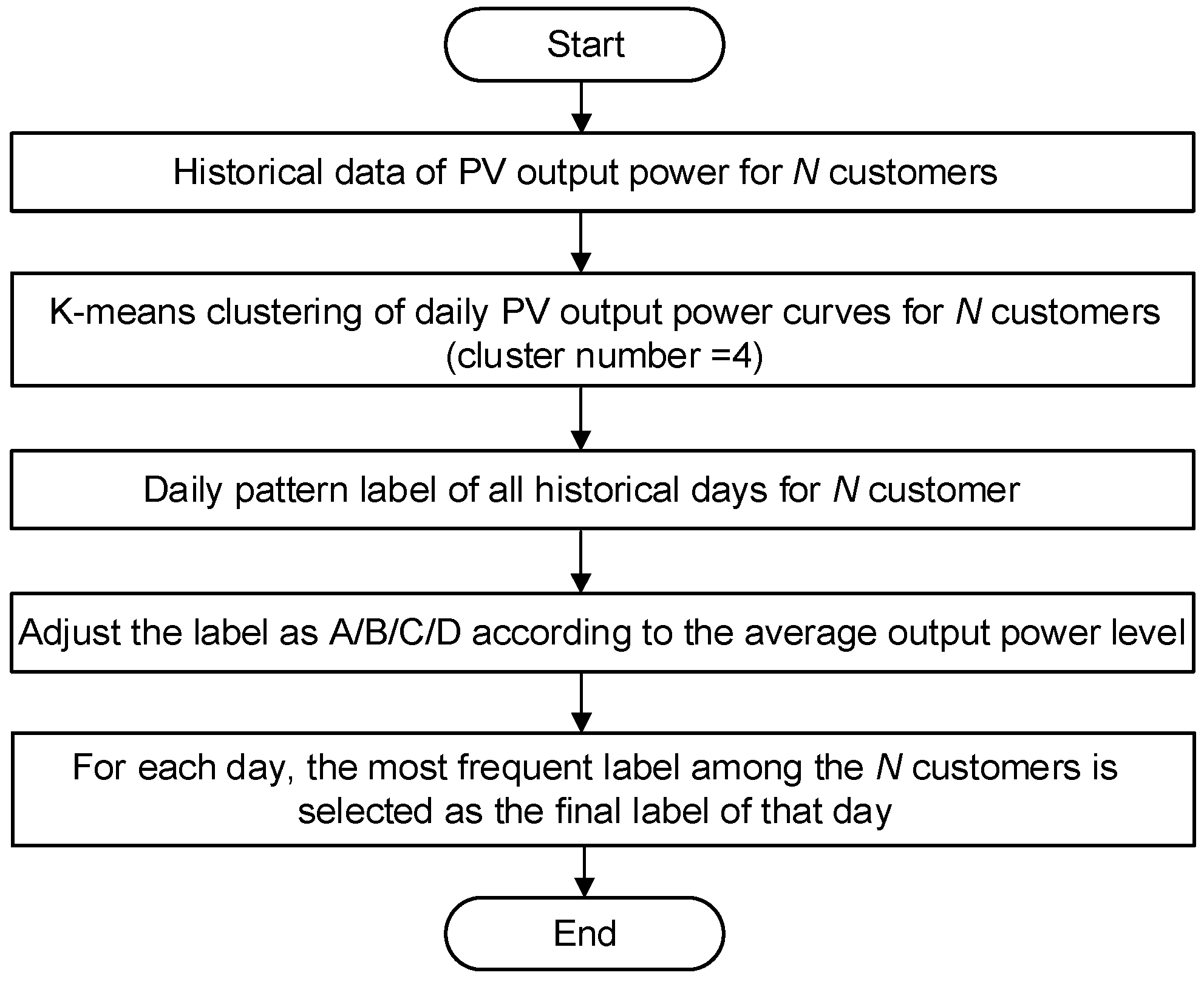


| GWC Label Generation Based on the Output Power Data from Single PV System | ||||
| Label | Performance Metrics | Best (%) | Average (%) | Worst (%) |
| Label = 1 | PA1 | 95.35 | 91.33 | 84.44 |
| UA1 | 100 | 97.25 | 95.74 | |
| Label = 0 | PA2 | 100 | 97.05 | 95.00 |
| UA2 | 96.08 | 90.76 | 86.54 | |
| OA | 97.83 | 93.73 | 90.22 | |
| GWC Label Generation Based on the Voting Method | ||||
| Label = 1 | PA1 | 100 | 92.04 | 84.44 |
| UA1 | 100 | 98.89 | 95.74 | |
| Label = 0 | PA2 | 100 | 98.96 | 95.00 |
| UA2 | 100 | 92.61 | 86.54 | |
| OA | 100 | 95.51 | 90.22 | |
| Feature | ||||
| MIC value | 0.688 | 0.445 | 0.565 | 0.367 |
| Feature | |||
| MIC value | 0.937 | 0.505 | 0.602 |
| Label | Performance Metrics | Best (%) | Average (%) | Worst (%) |
|---|---|---|---|---|
| Label = 1 | PA1 | 93.18 | 83.92 | 80.00 |
| UA1 | 95.35 | 96.20 | 97.78 | |
| Label = 0 | PA2 | 95.83 | 97.05 | 97.30 |
| UA2 | 93.88 | 85.48 | 76.60 | |
| OA | 94.57 | 90.16 | 86.96 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Li, K.; Wang, X.; Jiang, L.; Ren, J.; Mi, Z.; Shafie-khah, M.; Catalão, J.P.S. A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features. Energies 2018, 11, 1750. https://doi.org/10.3390/en11071750
Wang F, Li K, Wang X, Jiang L, Ren J, Mi Z, Shafie-khah M, Catalão JPS. A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features. Energies. 2018; 11(7):1750. https://doi.org/10.3390/en11071750
Chicago/Turabian StyleWang, Fei, Kangping Li, Xinkang Wang, Lihui Jiang, Jianguo Ren, Zengqiang Mi, Miadreza Shafie-khah, and João P. S. Catalão. 2018. "A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features" Energies 11, no. 7: 1750. https://doi.org/10.3390/en11071750
APA StyleWang, F., Li, K., Wang, X., Jiang, L., Ren, J., Mi, Z., Shafie-khah, M., & Catalão, J. P. S. (2018). A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features. Energies, 11(7), 1750. https://doi.org/10.3390/en11071750







