Game Theoretic Spectrum Allocation in Femtocell Networks for Smart Electric Distribution Grids
Abstract
1. Introduction
- Since the overall bandwidth is limited, the total bandwidth that is divided between MUs and FUs should meet bandwidth capacity limitation. To this end, at first, we formulate a game theory and convex optimization problem. Then we derive a closed form solution for the proposed formulation. To tackle this problem, authors in [33] solve a resource allocation problems in an iterative fashion whereas [34] propose a Fuzzy Logic approach to solve this problem.
- In this work, we offer an efficient, robust spectrum assignment technique, through two adjustable coefficients, the first coefficient is used to specify the allocation strategy. To this end four strategies are considered: maximizing femtocell utility, establishing fair access for all MUs, removing macro users with maximum bandwidth needs while promoting macro users with bandwidth minimum needs and vice-versa.
- The second coefficient prioritizes each MU to access more or less amount of bandwidth. The coefficient can be calculated based on the distance, signal-to-interference-plus-noise ratio (SINR) or similar index. For example, since the distance between FBS and MUs increase, FBS usually spend more power to transmit a signal. In this case, FBS prefers to assign less priority to such a user.
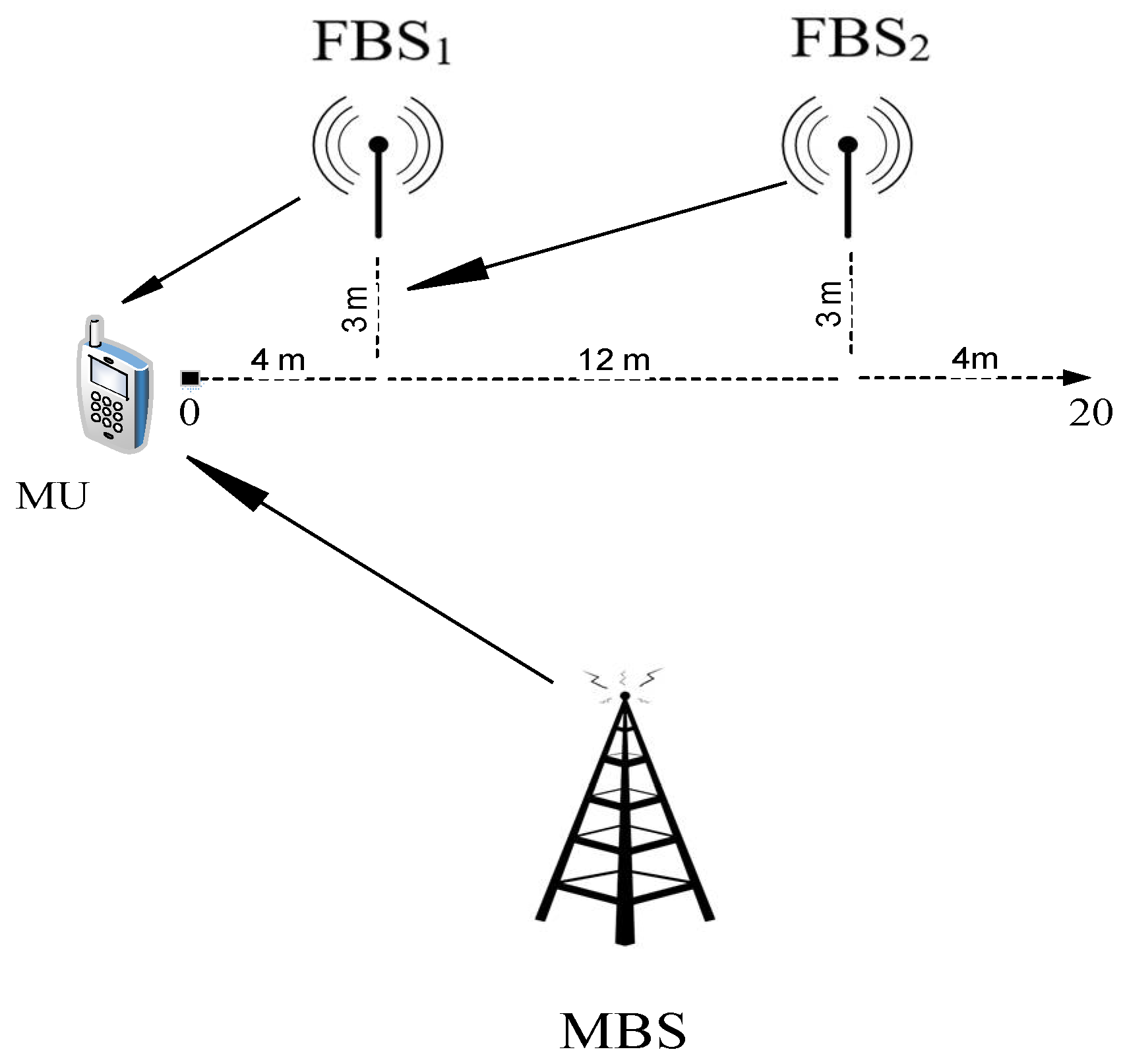
2. System Model
3. Problem Formulation
3.1. Utility Function
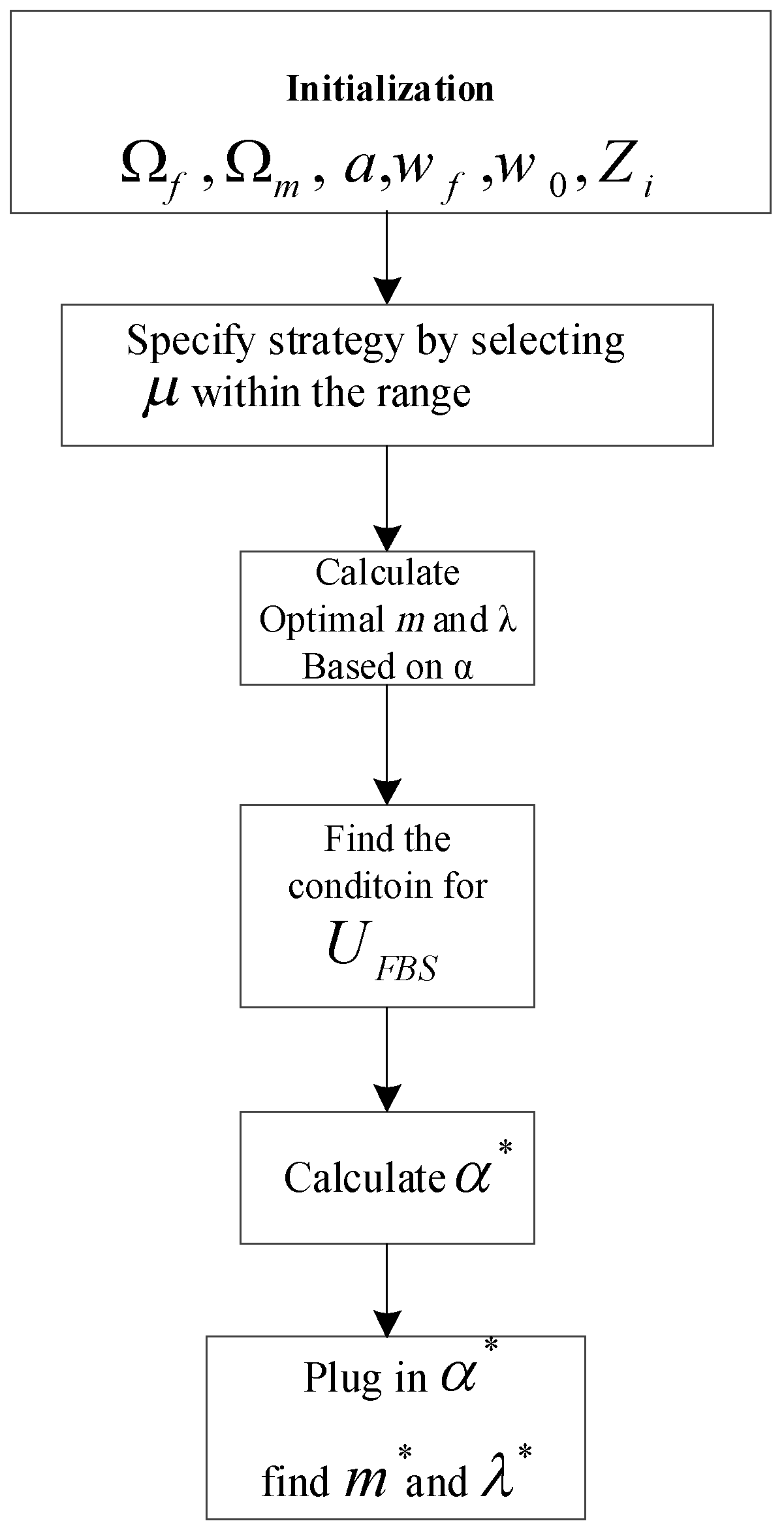
4. Game Theory Analysis
- Find the optimal value for revenue () and Lagrange multipliers based on .
- Derive the condition that can be a maximized point.
- Find an optimal value for by solving first order optimality solutions.
4.1 Macro Users’ Payment
5. Simulation Results and Discussion
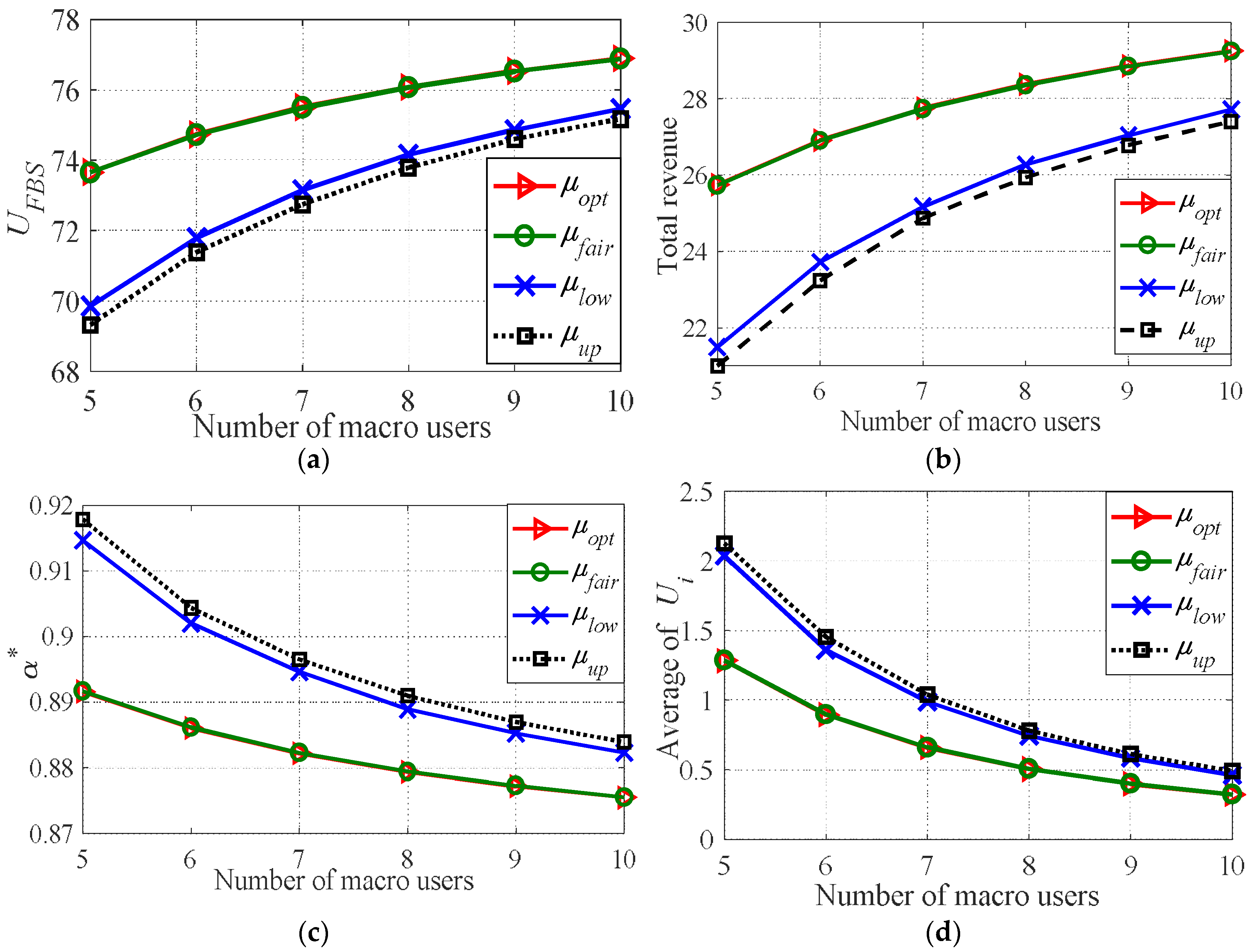
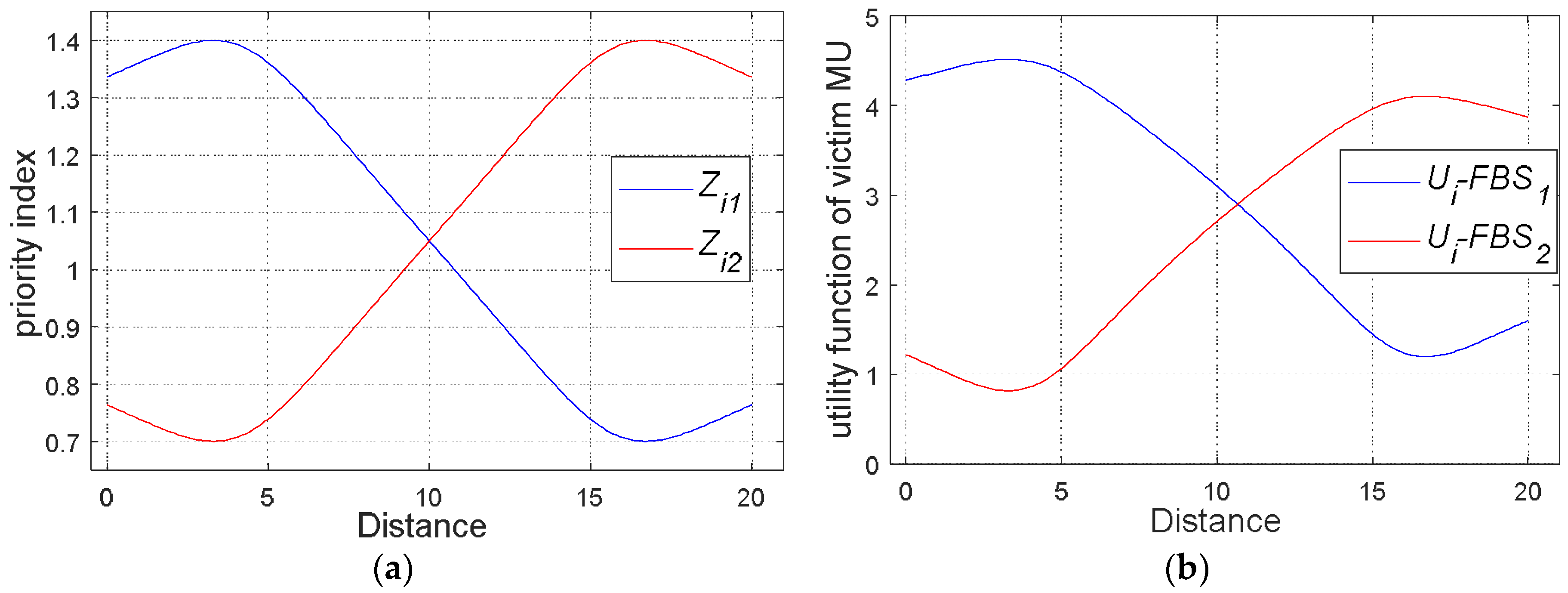
5.1. Impact Number of Macro Users on System Performance with the Same Priority
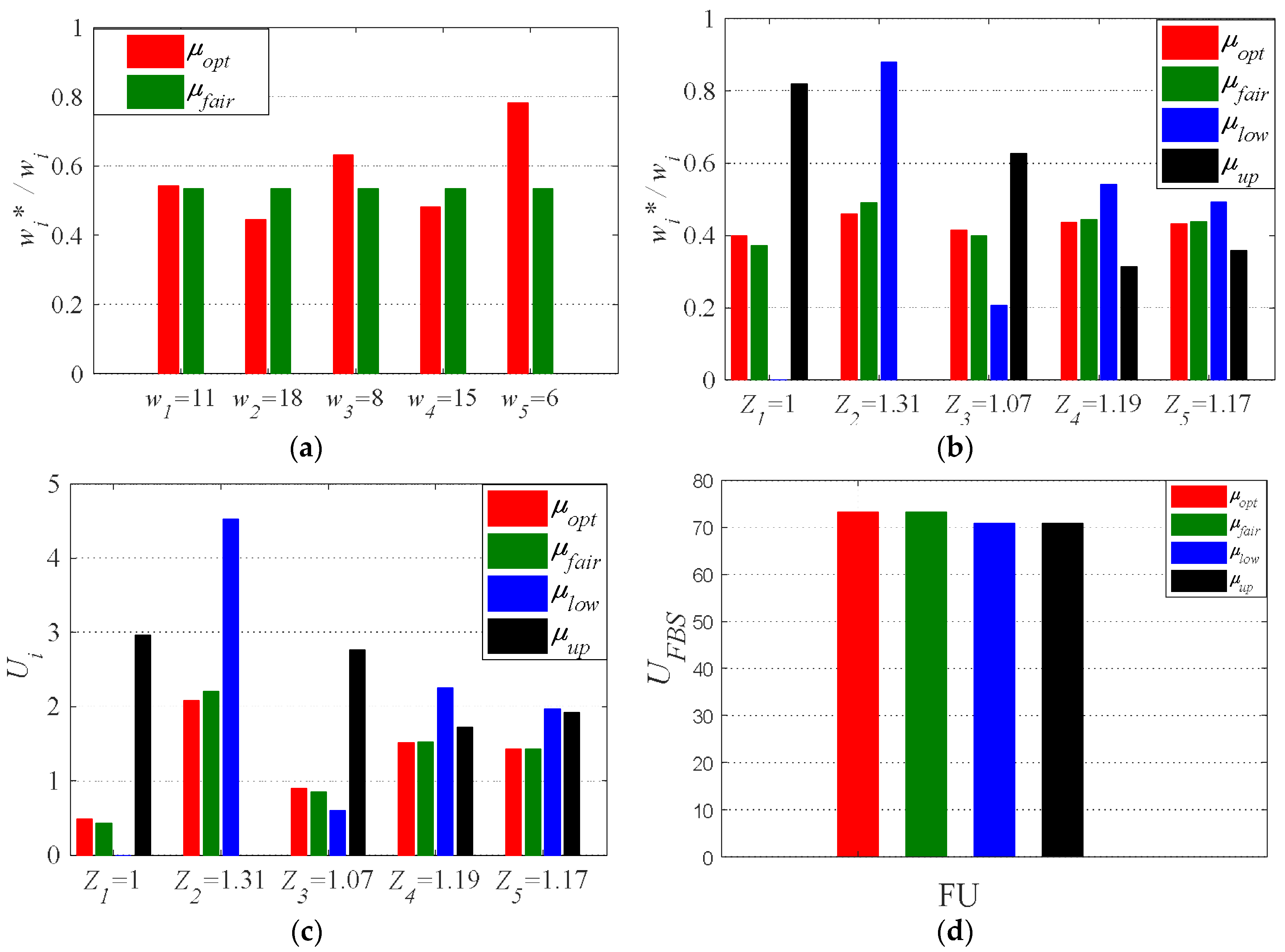
5.2. Assignment of Bandwidth Based on Different Decision Rules
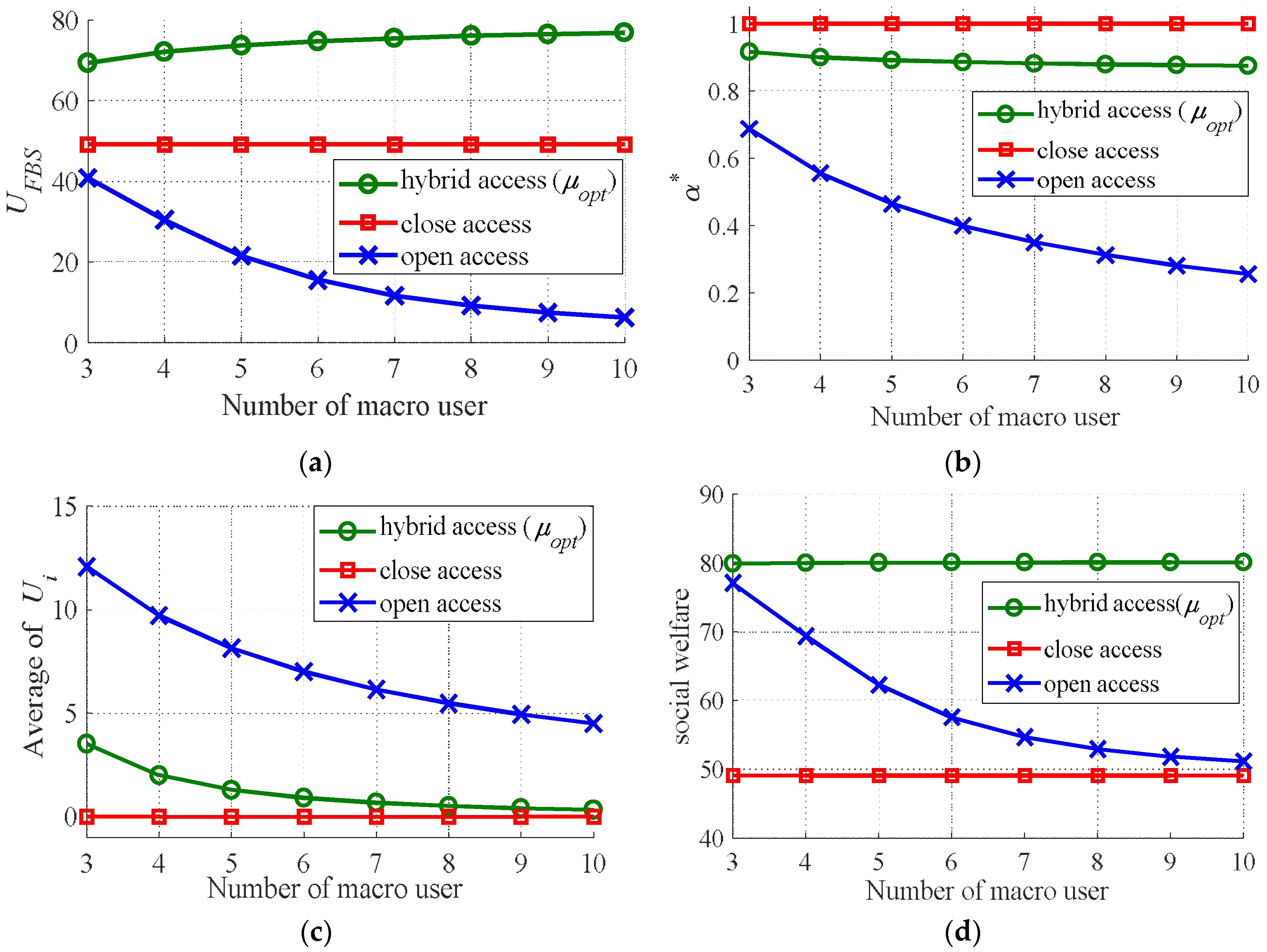
5.3. Hybrid Access Model
5.4. The Impact of Interference on Hybrid Access
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalao, J.P. A Decentralized Electricity Market Scheme Enabling Demand Response Deployment. IEEE Trans. Power Syst. 2017. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalao, J.P. A Decentralized Renewable Generation Management and Demand Response in Power Distribution Networks. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Amini, M.H.; Boroojeni, K.G.; Iyengar, S.; Pardalos, P.M.; Blaabjerg, F.; Madni, A.M. Sustainable Interdependent Networks: From Theory to Application; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Mohammadi, A.; Mehrtash, M.; Kargarian, A.; Barati, M. Tie-Line Characteristics based Partitioning for Distributed Optimization of Power Systems. arXiv, 2018; arXiv:1805.09779. [Google Scholar]
- Toulabi, M.; Bahrami, S.; Ranjbar, A.M. Application of Edge theorem for robust stability analysis of a power system with participating wind power plants in automatic generation control task. IET Renew. Power Gener. 2017, 11, 1049–1057. [Google Scholar] [CrossRef]
- Bahrami, S.; Wong, V.W. Security-constrained unit commitment for ac-dc grids with generation and load uncertainty. IEEE Trans. Power Syst. 2017, 33, 2717–2732. [Google Scholar] [CrossRef]
- Amini, M.H.; Karabasoglu, O. Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks. Energies 2018, 11, 196. [Google Scholar] [CrossRef]
- Toulabi, M.; Bahrami, S.; Ranjbar, A.M. An Input-to-State Stability Approach to Inertial Frequency Response Analysis of Doubly-Fed Induction Generator-Based Wind Turbines. IEEE Trans. Energy Convers. 2017, 32, 1418–1431. [Google Scholar] [CrossRef]
- Kar, S.; Hug, G.; Mohammadi, J.; Moura, J.M. Distributed State Estimation and Energy Management in Smart Grids: A Consensus+ Innovations Approach. IEEE J. Sel. Top. Signal Process. 2014, 8, 1022–1038. [Google Scholar] [CrossRef]
- Mohammadi, A.; Mehrtash, M.; Kargarian, A. Diagonal quadratic approximation for decentralized collaborative TSO+ DSO optimal power flow. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Mehrtash, M.; Kargarian, A.; Mohammadi, A. Partition-based bus renumbering effect on interior point-based OPF solution. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Bahrami, S.; Amini, M.H. A Decentralized Trading Algorithm for an Electricity Market with Generation Uncertainty. arXiv, 2017; arXiv:1705.02577. [Google Scholar] [CrossRef]
- Shih, Y.-Y.; Pang, A.-C.; Tsai, M.-H.; Chai, C.-H. A rewarding framework for network resource sharing in co-channel hybrid access femtocell networks. IEEE Trans. Comput. 2015, 64, 3079–3090. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, R.; Motani, M. Price-based resource allocation for spectrum-sharing femtocell networks: A stackelberg game approach. IEEE J. Sel. Areas Commun. 2012, 30, 538–549. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Andrews, J.G.; Muharemovic, T.; Shen, Z.; Gatherer, A. Power control in two-tier femtocell networks. IEEE Trans. Wirel. Commun. 2009, 8, 4316–4328. [Google Scholar] [CrossRef]
- López-Pérez, D.; Valcarce, A.; de la Roche, G.; Zhang, J. OFDMA femtocells: A roadmap on interference avoidance. IEEE Commun. Mag. 2009, 47, 41–48. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Andrews, J.G. Spectrum allocation in tiered cellular networks. IEEE Trans. Commun. 2009, 57, 3059–3068. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, Q.; Huang, J.; Tsang, D.H. Revenue sharing based resource allocation for dynamic spectrum access networks. IEEE J. Sel. Areas Commun. 2014, 32, 2280–2296. [Google Scholar] [CrossRef]
- Choi, D.; Monajemi, P.; Kang, S.; Villasenor, J. Dealing with loud neighbors: The benefits and tradeoffs of adaptive femtocell access. In Proceedings of the 2008 Global Telecommunications Conference, 2008 IEEE GLOBECOM, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Valcarce, A.; Lopez-Perez, D.; de la Roche, G.; Zhang, J. Limited access to OFDMA femtocells. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 1–5. [Google Scholar]
- Skoutas, D.N.; Makris, P.; Skianis, C. Optimized admission control scheme for coexisting femtocell, wireless and wireline networks. Telecommun. Syst. 2013, 53, 357–371. [Google Scholar] [CrossRef]
- Xie, R.; Yu, F.R.; Ji, H.; Li, Y. Energy-efficient resource allocation for heterogeneous cognitive radio networks with femtocells. IEEE Trans. Wirel. Commun. 2012, 11, 3910–3920. [Google Scholar]
- Duong, N.D.; Madhukumar, A.; Niyato, D. Stackelberg Bayesian game for power allocation in two-tier networks. IEEE Trans. Veh. Technol. 2016, 65, 2341–2354. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.S.; Sung, C.W.; Singh, C. A Game Theoretic Distributed Algorithm for FeICIC Optimization in LTE-A HetNets. IEEE/ACM Trans. Netw. 2017, 25, 3500–3513. [Google Scholar] [CrossRef]
- Yi, C.; Cai, J. Two-stage spectrum sharing with combinatorial auction and Stackelberg game in recall-based cognitive radio networks. IEEE Trans. Commun. 2014, 62, 3740–3752. [Google Scholar] [CrossRef]
- Sundaresan, K.; Rangarajan, S. Efficient resource management in OFDMA femto cells. In Proceedings of the Tenth ACM International Symposium on Mobile Ad Hoc Networking and Computing, New Orleans, LA, USA, 18–21 May 2009; pp. 33–42. [Google Scholar]
- Liang, Y.-S.; Chung, W.-H.; Ni, G.-K.; Chen, Y.; Zhang, H.; Kuo, S.-Y. Resource allocation with interference avoidance in OFDMA femtocell networks. IEEE Trans. Veh. Technol. 2012, 61, 2243–2255. [Google Scholar] [CrossRef]
- Yu, J.; Han, S.; Li, X. A Robust Game-Based Algorithm for Downlink Joint Resource Allocation in Hierarchical OFDMA Femtocell Network System. IEEE Trans. Syst. Man Cybern. Syst. 2018. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Vamvakas, P.; Papavassiliou, S. Supermodular game-based distributed joint uplink power and rate allocation in two-tier femtocell networks. IEEE Trans. Mob. Comput. 2017, 16, 2656–2667. [Google Scholar] [CrossRef]
- Zhu, K.; Hossain, E.; Anpalagan, A. Downlink power control in two-tier cellular OFDMA networks under uncertainties: A robust Stackelberg game. IEEE Trans. Commun. 2015, 63, 520–535. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Liu, K.R. Game theory for cognitive radio networks: An overview. Comput. Netw. 2010, 54, 2537–2561. [Google Scholar] [CrossRef]
- Zhang, N.; Cheng, N.; Lu, N.; Zhou, H.; Mark, J.W.; Shen, X. Risk-aware cooperative spectrum access for multi-channel cognitive radio networks. IEEE J. Sel. Areas Commun. 2014, 32, 516–527. [Google Scholar] [CrossRef]
- Hamouda, S.; Zitoun, M.; Tabbane, S. Win-win relationship between macrocell and femtocells for spectrum sharing in LTE-A. IET Commun. 2014, 8, 1109–1116. [Google Scholar] [CrossRef]
- Mohammadi, A.; Dehghani, M.J. Spectrum allocation using fuzzy logic with optimal power in wireless network. In Proceedings of the 2014 4th International eConference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2014; pp. 532–536. [Google Scholar]
- Chen, Y.; Zhang, J.; Zhang, Q. Utility-aware refunding framework for hybrid access femtocell network. IEEE Trans. Wirel. Commun. 2012, 11, 1688–1697. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q. Stackelberg game for utility-based cooperative cognitiveradio networks. In Proceedings of the Tenth ACM International Symposium on Mobile Ad Hoc Networking and Computing, New Orleans, LA, USA, 18–21 May 2009; pp. 23–32. [Google Scholar]
| Parameter | Value |
|---|---|
| Total amount of power for both FBS, MHz | 50 |
| for victim MUs | 18 |
| for MUs of | 10 |
| for MUs of | [10, 12, 15, 8] |
| for MUs of | [1.1, 1, 1.2, 1.4] |
| for MUs of | 15 |
| for MUs of | [13, 13, 12, 9] |
| for MUs of | [1.1, 1.2, 1.3, 1.2] |
| Distance from MBS, m | 700 |
| Path Loss , dB | ; d in Km |
| Path Loss , dB | ; d in m |
| 50 | |
| 1 | |
| Thermal noise power dBm/Hz | −174 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, A.; Dehghani, M.J.; Ghazizadeh, E. Game Theoretic Spectrum Allocation in Femtocell Networks for Smart Electric Distribution Grids. Energies 2018, 11, 1635. https://doi.org/10.3390/en11071635
Mohammadi A, Dehghani MJ, Ghazizadeh E. Game Theoretic Spectrum Allocation in Femtocell Networks for Smart Electric Distribution Grids. Energies. 2018; 11(7):1635. https://doi.org/10.3390/en11071635
Chicago/Turabian StyleMohammadi, Ali, Mohammad Javad Dehghani, and Elham Ghazizadeh. 2018. "Game Theoretic Spectrum Allocation in Femtocell Networks for Smart Electric Distribution Grids" Energies 11, no. 7: 1635. https://doi.org/10.3390/en11071635
APA StyleMohammadi, A., Dehghani, M. J., & Ghazizadeh, E. (2018). Game Theoretic Spectrum Allocation in Femtocell Networks for Smart Electric Distribution Grids. Energies, 11(7), 1635. https://doi.org/10.3390/en11071635





