Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Background of the Spectral Wave Models
2.2. Description of the Wave Prediction System
2.3. Model System Validations and Data Assimilation
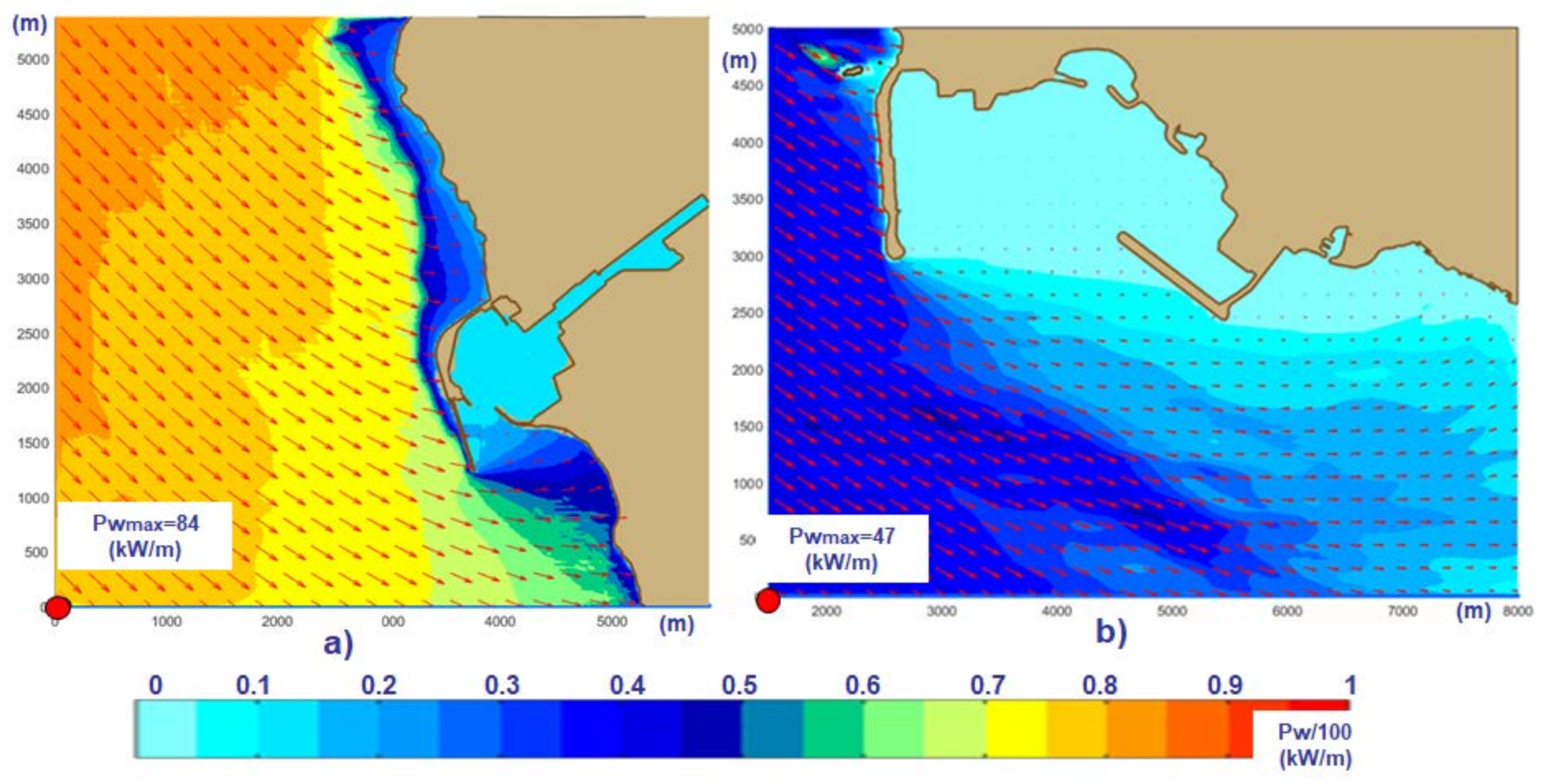
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
Nomenclature
| CAPEX | Capital Expenditure |
| DA | Data Assimilation |
| GFS | Global Forecast System |
| LCOE | Levelized Cost of Energy |
| EU | European Union |
| Hs | Significant Wave Height |
| MM5 | Fifth-Generation Mesoscale Model |
| NCAR | US National Center for Atmospheric Research |
| NOAA | US National Oceanic and Atmospheric Administration Model |
| OI | Optimal Interpolation |
| OPEX | Operational Expenditure |
| Pw | Wave power |
| PTO | Power take-off |
| SCM | Successive Correction Method |
| SET | Strategic Energy Technology |
| SWAN | Simulating Waves Nearshore |
| WAM | Wave Modeling |
| WEC | Wave Energy Converter |
| WT | Wind Turbines |
| WW3 | Wave Watch 3 |
References
- European Commission. Strategic Energy Technology Plan; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- JRC. JRC Wind Energy Status Report 2016 Edition. 2016. Available online: http://publications.jrc.ec.europa.eu/repository/bitstream/JRC105720/kjna28530enn.pdf (accessed on 22 February 2018).
- Jensen, P.H.; Chaviaropoulos, T.; Natarajan, A. LCOE Reduction for the Next Generation Offshore Wind Turbines; Outcomes from the INNWIND.EU Project. 2017. Available online: file:///C:/Users/user/Downloads/Innwind-final-printing-version.pdf (accessed on 24 February 2018).
- SET Plan—Declaration of Intent on Strategic Targets in the Context of an Initiative for Global Leadership in Ocean Energy. 2016. Available online: https://setis.ec.europa.eu/system/files/integrated_set-plan/declaration_of_intent_ocean_0.pdf (accessed on 24 February 2018).
- Zhang, X.; Yang, J. Power capture performance of an oscillating-body WEC with nonlinear snap through PTO systems in irregular waves. Appl. Ocean Res. 2015, 52, 261–273. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, D.; Guo, F.; Gao, Y.; Sun, Y. The maximum wave energy conversion by two interconnected floaters: Effects of structural flexibility. Appl. Ocean Res. 2018, 71, 34–47. [Google Scholar] [CrossRef]
- Rezanejad, K.; Soares, C.G.; Lópezb, I.; Carballo, R. Experimental and numerical investigation of the hydrodynamic performance of an oscillating water column wave energy converter. Renew. Energy 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Liu, Z.; Han, Z.; Shi, H.; Yang, W. Experimental study on multi-level overtopping wave energy convertor under regular wave conditions. Int. J. Nav. Archit. Ocean Eng. 2017, in press. [Google Scholar] [CrossRef]
- Rusu, L.; Onea, F. The performance of some state-of-the-art wave energy converters in locations with the worldwide highest wave power. Renew. Sustain. Energy Rev. 2017, 75, 1348–1362. [Google Scholar] [CrossRef]
- Veigas, M.; López, M.; Iglesias, G. Assessing the optimal location for a shoreline wave energy converter. Appl. Energy 2014, 132, 404–411. [Google Scholar] [CrossRef]
- Bernardino, M.; Guedes Soares, C. Evaluating marine climate change in the Portuguese coast during the 20th century. In Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2018; pp. 1089–1095. [Google Scholar]
- Iglesias, G.; Carballo, R. Wave energy and nearshore hot spots: The case of the SE Bay of Biscay. Renew. Energy 2010, 35, 2490–2500. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Offshore and inshore wave energy assessment: Asturias (N Spain). Energy 2010, 35, 1964–1972. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the death coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy resource in the Estaca de Bares area (Spain). Renew. Energy 2010, 35, 1574–8154. [Google Scholar] [CrossRef]
- Rusu, E.; Soares, C.G. Wave energy assessments in the coastal environment of Portugal continental. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 6, pp. 761–772. [Google Scholar]
- Rusu, L.; Pilar, P.; Soares, C.G. Reanalysis of the wave conditions on the approaches to the Portuguese port of Sines. In Maritime Transportation and Exploitation of Ocean and Coastal Resources; Taylor & Francis Group: London, UK, 2005; Volume 1, pp. 1137–1142. [Google Scholar]
- Silva, D.; Rusu, E.; Soares, C.G. Evaluation of Various Technologies for Wave Energy Conversion in the Portuguese Nearshore. Energies 2013, 6, 1344–1364. [Google Scholar] [CrossRef]
- Silva, D.; Martinho, P.; Soares, C.G. Wave power resources at Portuguese test sites from 11-year hindcast data. In Renewable Energies Offshore; Taylor & Francis Group: London, UK, 2015; pp. 113–121. [Google Scholar]
- Carballo, R.; Sánchez, M.; Ramos, V.; Taveira-Pinto, F.; Iglesias, G. A high resolution geospatial database for wave energy exploitation. Energy 2014, 68, 572–583. [Google Scholar] [CrossRef]
- Rusu, E.; Silva, D.; Soares, C.G. Efficiency assessments for different WEC types operating in the Portuguese coastal environment. In Developments in Maritime Transportation and Exploitation of Sea Resources; Taylor & Francis Group: London, UK, 2014; pp. 961–972. [Google Scholar]
- Silva, D.; Rusu, E.; Soares, C.G. Evaluation of the expected power output of wave energy converters in the north of the Portuguese nearshore. In Progress in Renewable Energies Offshore; Taylor & Francis Group: London, UK, 2016; pp. 875–882. [Google Scholar]
- Iuppa, C.; Cavallaro, L.; Vicinanza, D.; Foti, E. Investigation of suitable sites for Wave Energy Converters around Sicily (Italy). Ocean Sci. 2015, 11, 543–557. [Google Scholar] [CrossRef]
- Iuppa, C.; Cavallaro, L.; Foti, E.; Vicinanza, D. Potential wave energy production by different wave energy converters around sicily. J. Renew. Sustain. Energy 2015, 7. [Google Scholar] [CrossRef]
- Vicinanza, D.; Contestabile, P.; Ferrante, V. Wave energy potential in the north-west of sardinia (Italy). Renew. Energy 2013, 50, 506–521. [Google Scholar] [CrossRef]
- Holthuijsen, H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007; p. 387. [Google Scholar]
- Rusu, E. Strategies in using numerical wave models in ocean/coastal applications. J. Mar. Sci. Technol. 2011, 19, 58–75. [Google Scholar]
- Bretherton, F.P.; Garrett, C.J.R. Wave trains in inhomogeneous moving media. Proc. R. Soc. Lond. Ser. A 1968, 302, 529–554. [Google Scholar] [CrossRef]
- SWAN Team. Scientific and Technical Documentation; SWAN Cycle III; Department of Civil Engineering, Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Gómez Lahoz, M.; Carretero Albiach, J.C. A two-way nesting procedure for the WAM model: Application to the Spanish Coast. J. Offshore Mech. Arctic Eng. 1997, 119, 20–24. [Google Scholar] [CrossRef]
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Silva, D.; Martinho, P.; Guedes Soares, C. Modeling wave energy for the Portuguese coast. In Maritime Engineering and Technology; Guedes Soares, C., Garbatov, Y., Sutulo, S., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2012; pp. 647–653. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third generation wave model for coastal regions. Part 1: Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Rusu, E.; Soares, C.V.; Rusu, L. Computational strategies and visualisation techniques for the wave modelling in the Portuguese nearshore. In Maritime Transportation and Exploitation of Ocean and Coastal Resources; Taylor & Francis: London, UK, 2005; Volume 1, pp. 1129–1136. [Google Scholar]
- Soares, C.G.; Rusu, L.; Bernardino, M. An operational wave forecasting system for the Portuguese continental coastal area. J. Oper. Oceanogr. 2011, 4, 17–27. [Google Scholar] [CrossRef]
- Dudhia, J. A nonhydrostatic version of the Penn State–NCAR mesoscale model: Validation tests and simulation of an Atlantic cyclone and cold front. Mon. Weather Rev. 1993, 121, 1493–1513. [Google Scholar] [CrossRef]
- Rusu, L.; Soares, C.G. Evaluation of a high-resolution wave forecasting system for the approaches to ports. Ocean Eng. 2013, 58, 224–238. [Google Scholar] [CrossRef]
- Rusu, L.; Soares, C.G. Impact of assimilating altimeter data on wave predictions in the western Iberian coast. Ocean Model. 2015, 96, 126–135. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003; p. 341. [Google Scholar]
- Lionello, P.; Günther, H.; Janssen, P.A.E.M. Assimilation of altimeter data in a global third-generation wave model. J. Geophys. Res. 1992, 97, 14453–14474. [Google Scholar] [CrossRef]
- Silva, D.; Rusu, E.; Soares, C.G. High-resolution wave energy assessment in shallow water accounting for tides. Energies 2016, 9, 761. [Google Scholar] [CrossRef]
- Rusu, E.; Guedes Soares, C. Numerical modeling to estimate the spatial distribution of the wave energy in the Portuguese nearshore. Renew. Energy 2009, 34, 1501–1516. [Google Scholar] [CrossRef]
- Soares, C.G.; Bento, A.R.; Goncalves, M.; Silva, D.; Martinho, P. Numerical evaluation of the wave energy resource along the Atlantic European coast. Comput. Geosci. 2014, 71, 37–49. [Google Scholar] [CrossRef]
- Silva, D.; Bento, A.R.; Martinho, P.; Soares, C.G. High resolution local wave energy modelling for the Iberian Peninsula. Energy 2015, 91, 1099–1112. [Google Scholar] [CrossRef]
- Bento, A.R.; Martinho, P.; Soares, C.G. Wave energy resource assessment for Northern Spain from a 13-year hindcast. In Renewable Energies Offshore; Taylor & Francis Group: London, UK, 2015; pp. 63–69. [Google Scholar]
- Silva, D.; Martinho, P.; Soares, C.G. Trends in the available wave power at the Portuguese pilot zone. In Progress in Renewable Energies Offshore; Taylor & Francis Group: London, UK, 2016; pp. 53–59. [Google Scholar]
- Onea, F.; Rusu, E. The expected efficiency and coastal impact of a hybrid energy farm operating in the Portuguese nearshore. Energy 2016, 97, 411–423. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. Study on the influence of the distance to shore for a wave energy farm operating in the central part of the Portuguese nearshore. Energy Convers. Manag. 2016, 114, 209–223. [Google Scholar] [CrossRef]
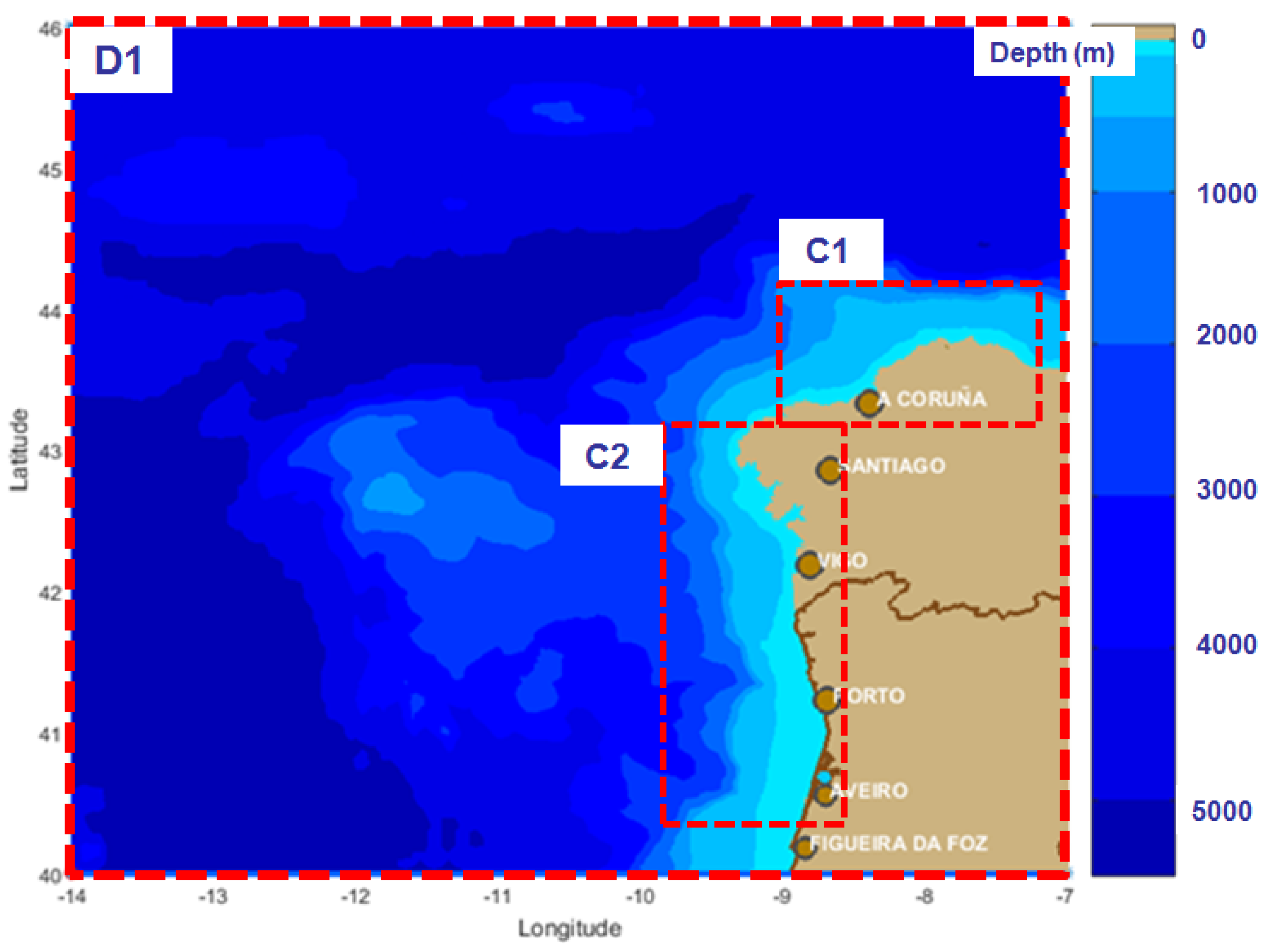
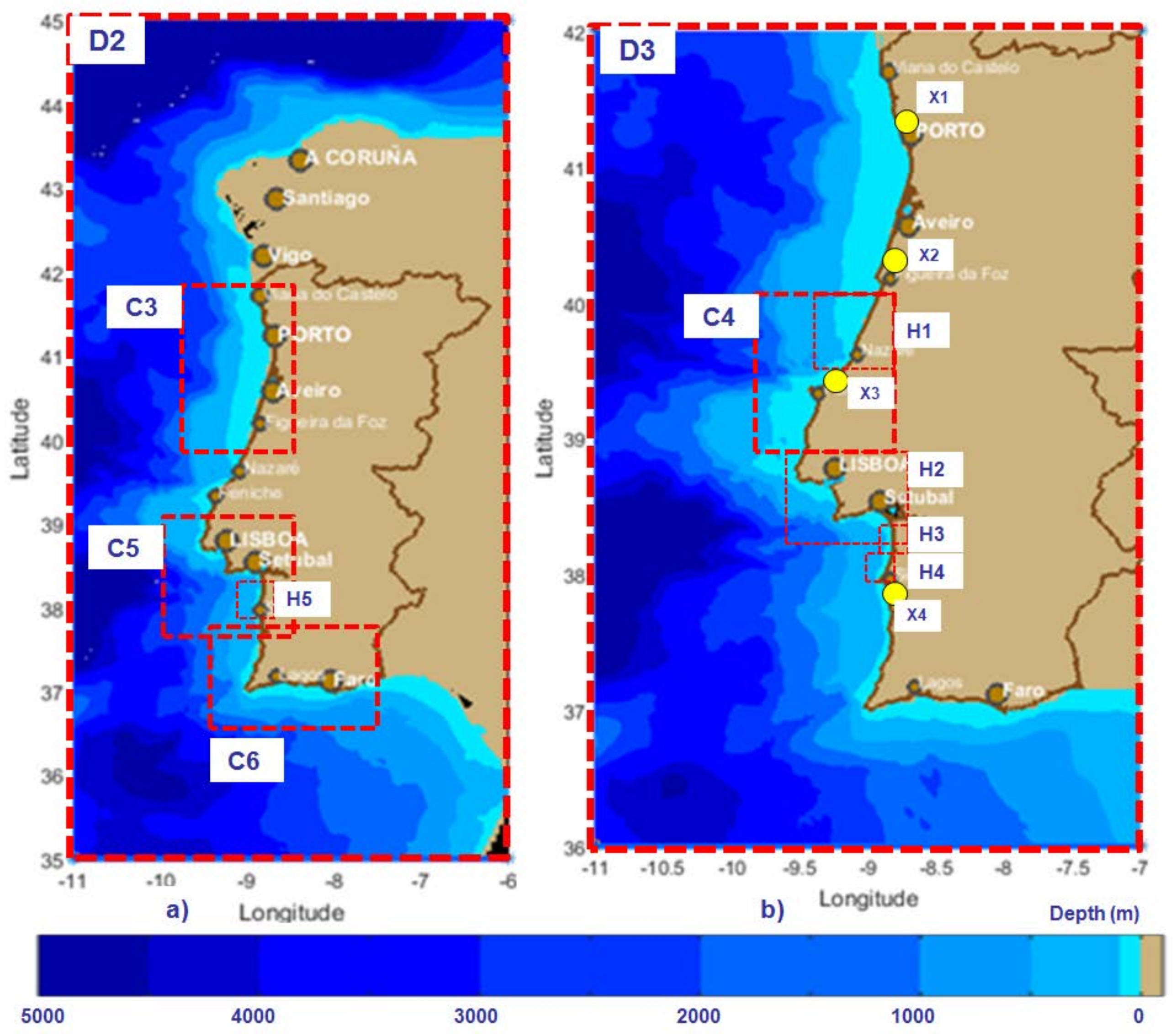
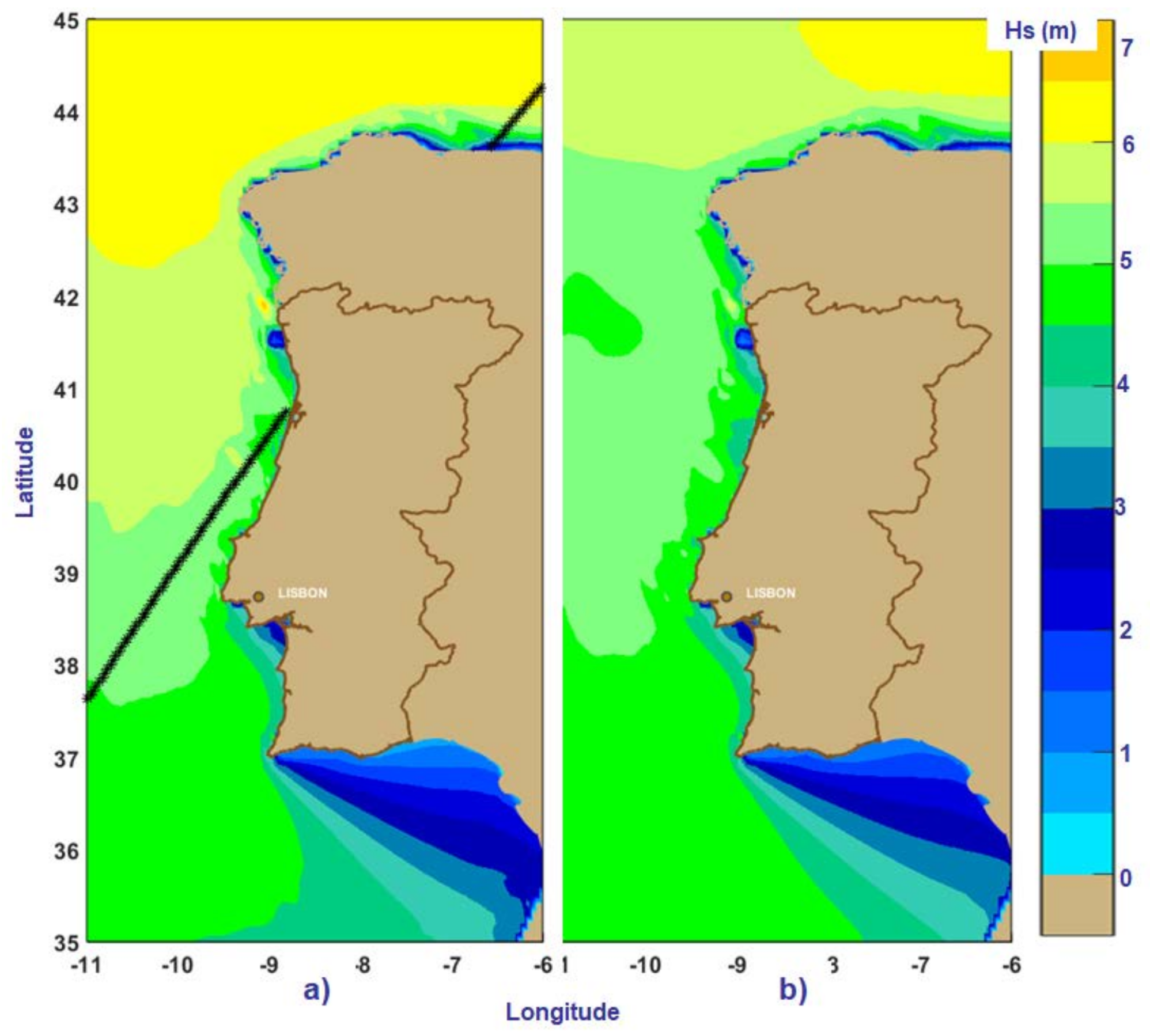
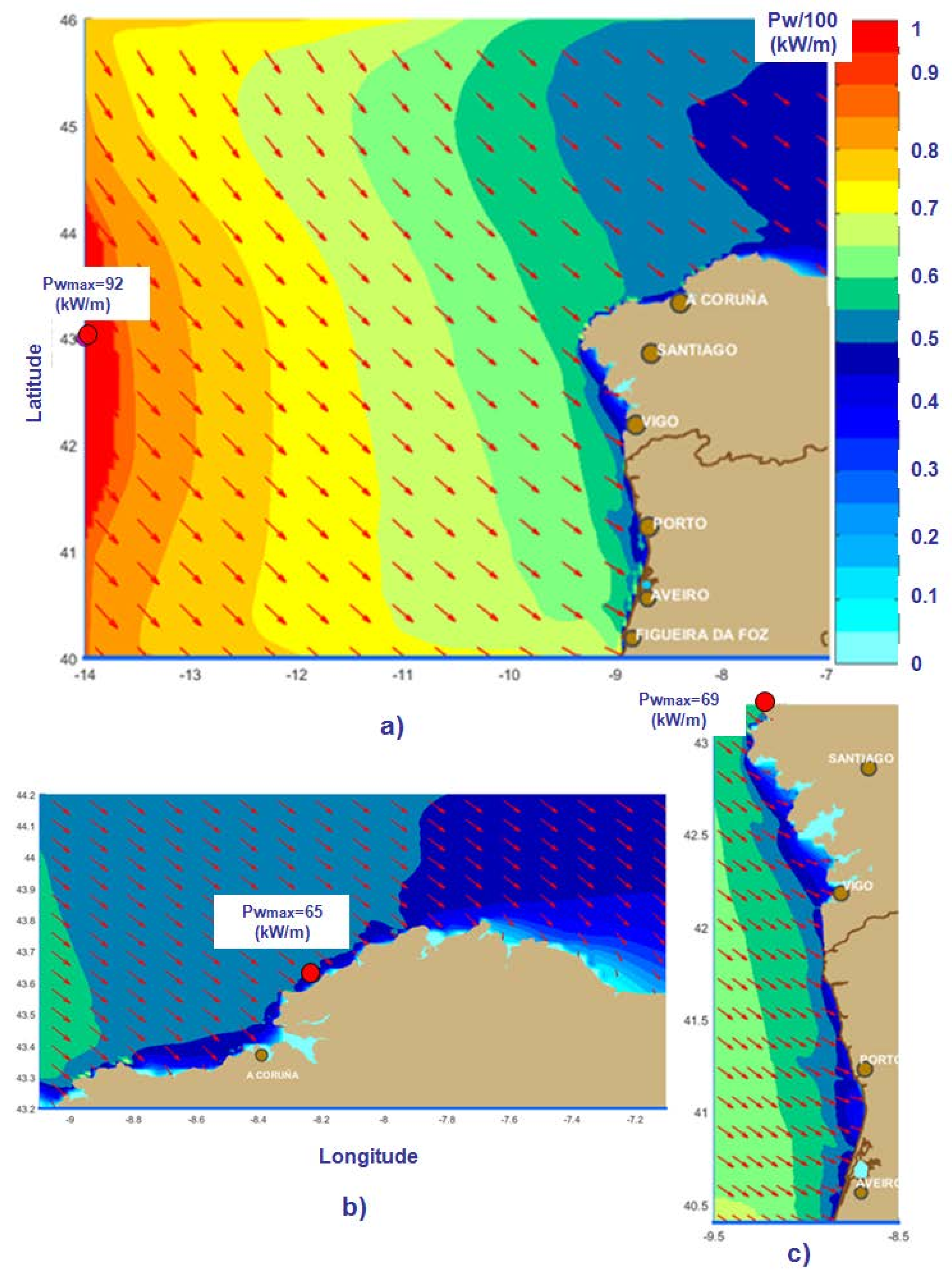
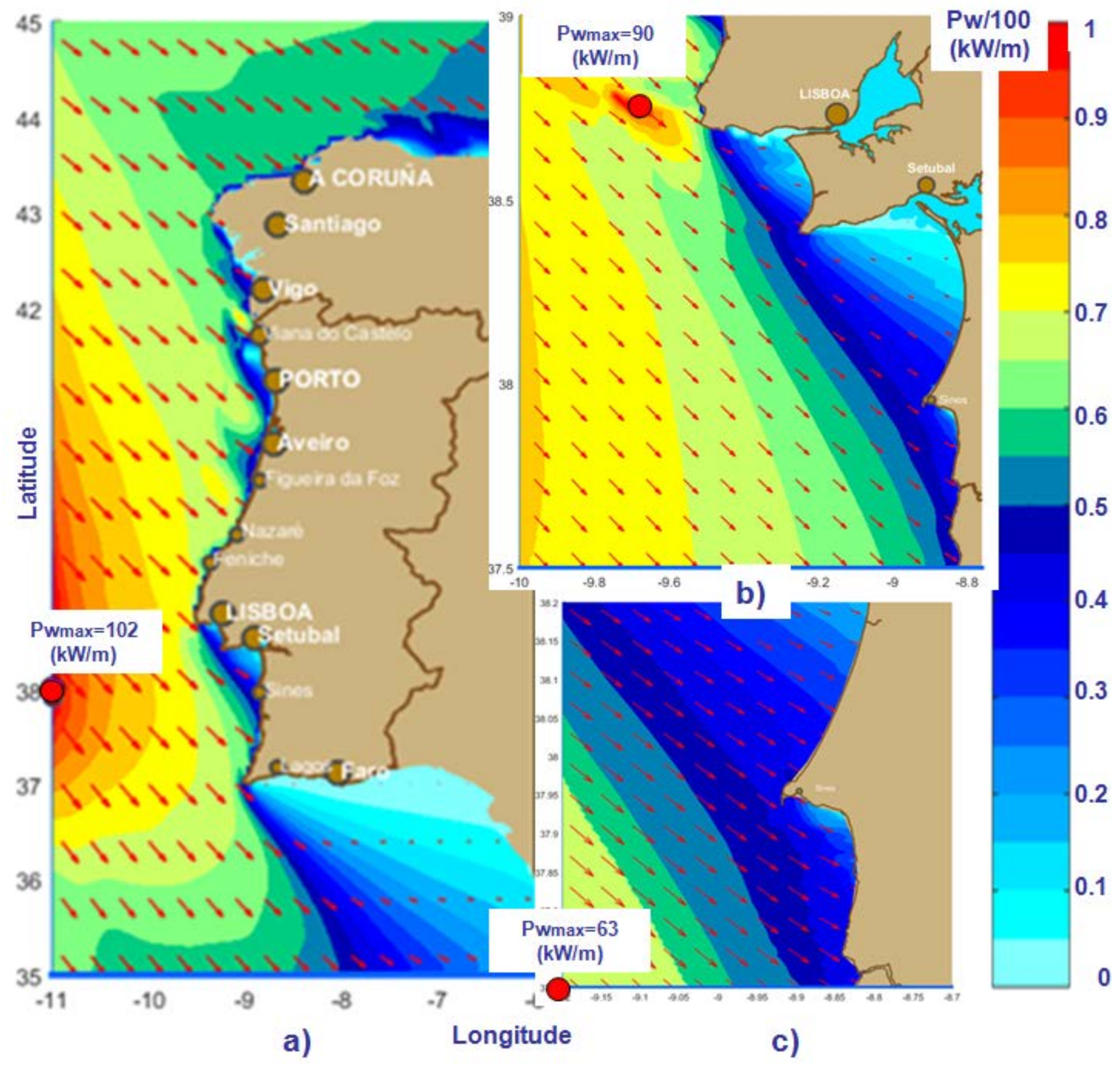
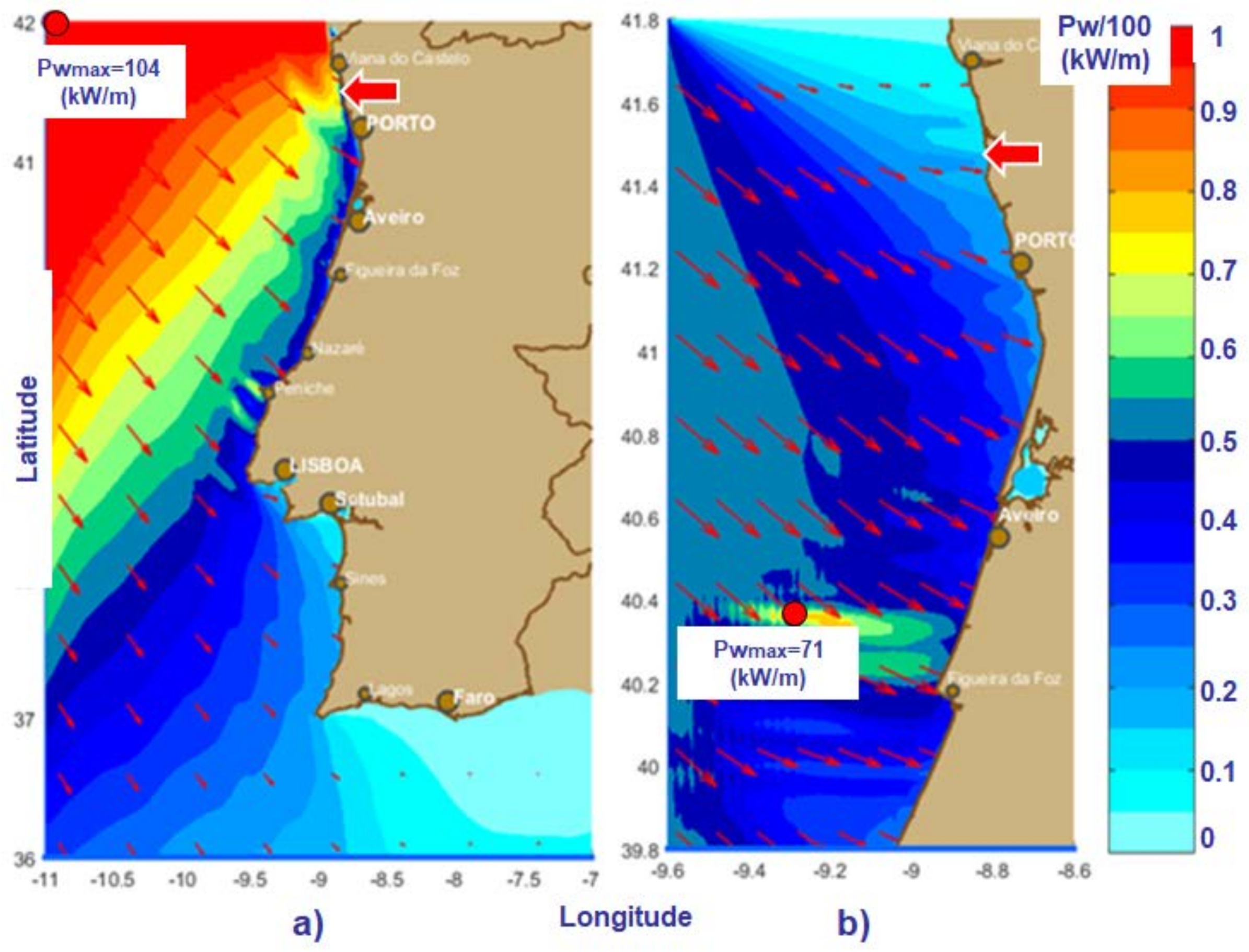
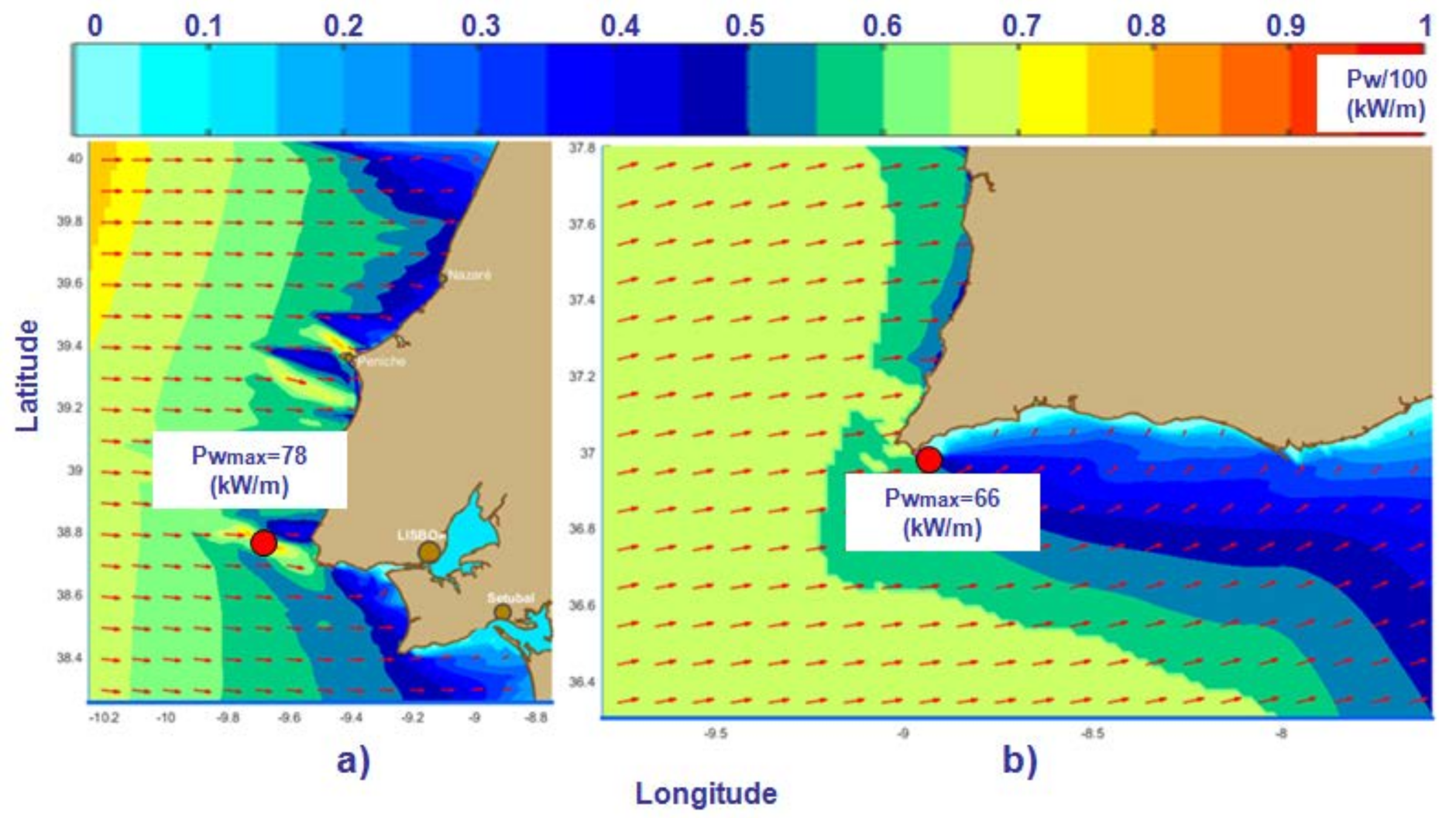

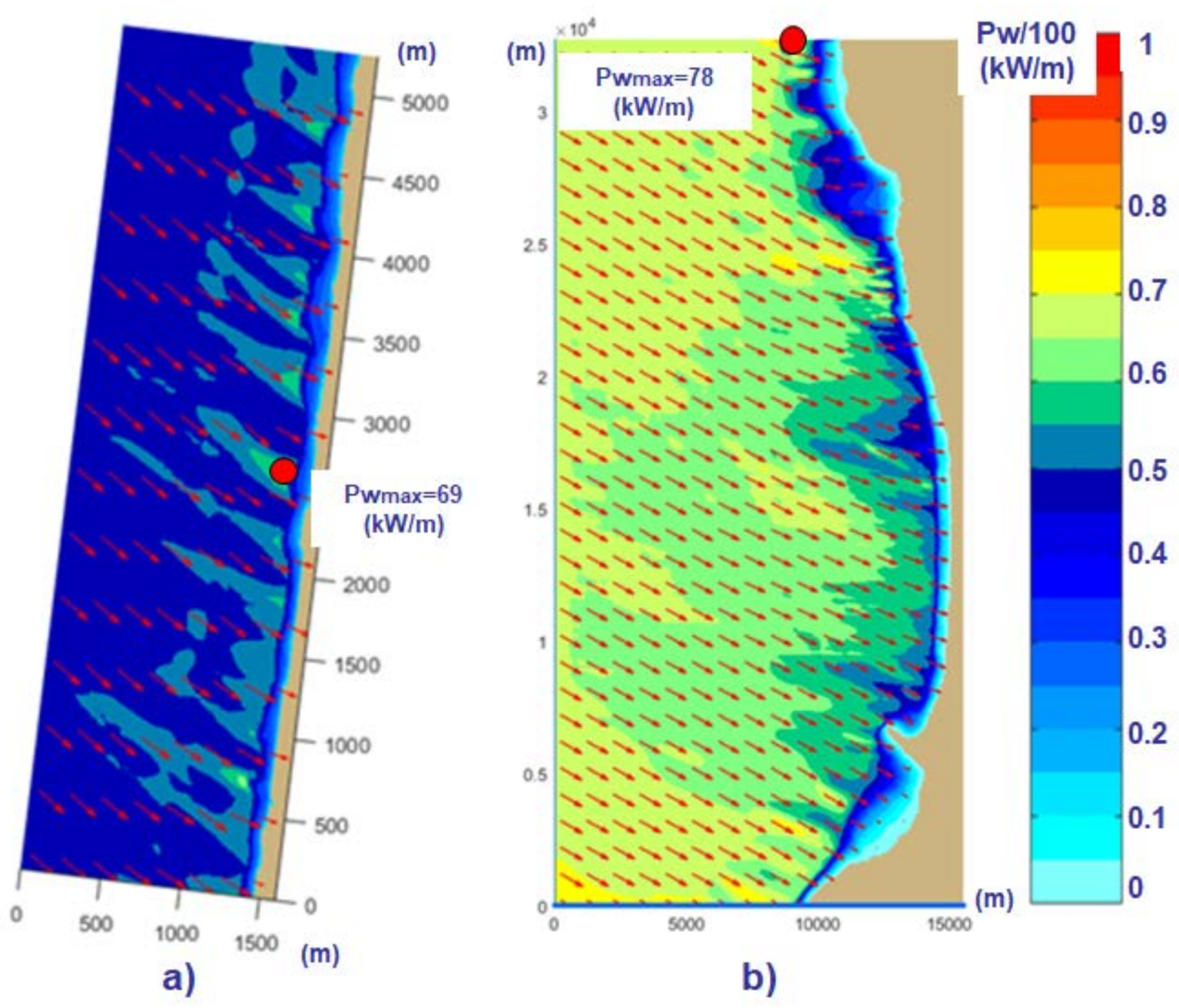
| Driver Domains | Δλ × Δφ | Δt (min) | nf | nθ | ngλ × ngφ = np |
|---|---|---|---|---|---|
| D1-Northern | 0.05° × 0.05° | 10 non-stat | 24 | 24 | 141 × 121 = 17,061 |
| D2-Western | 0.05° × 0.1° | 10 non-stat | 24 | 24 | 101 × 101 = 10,201 |
| D3-Portuguese | 0.05° × 0.05° | 10 non-stat | 24 | 24 | 81 × 121 = 9801 |
| Coastal Domains | Δλ × Δφ | Δt (min) | nf | nθ | ngλ × ngφ = np |
|---|---|---|---|---|---|
| C1-Northern | 0.02° × 0.01° | 10 non-stat | 24 | 36 | 101 × 101 = 10,201 |
| C2-North Western 01 | 0.01° × 0.02° | 10 non-stat | 24 | 36 | 101 × 141 = 14,241 |
| C3-North Western 02 | 0.01° × 0.02° | 10 non-stat | 24 | 36 | 101 × 101 = 10,201 |
| C4-Central 01 | 0.02° × 0.02° | 10 non-stat | 24 | 36 | 76 × 91 = 6916 |
| C5-Central 02 | 0.02° × 0.02° | 10 non-stat | 24 | 36 | 63 × 76 = 4788 |
| C6-Southern | 0.02° × 0.02° | 10 non-stat | 24 | 36 | 111 × 76 = 8436 |
| High Resolution Domains | Δλ × Δφ | Δt (min) | nf | nθ | ngλ × ngφ = np |
|---|---|---|---|---|---|
| H1-Peniche | 0.01° × 0.01° | 10 non-stat | 30 | 36 | 91 × 81 = 7371 |
| H2-Lisbon | 0.005° × 0.01° | 10 non-stat | 30 | 36 | 91 × 81 = 7371 |
| H3-Pinheiro da Cruz | 0.001° × 0.0025° | 10 non-stat | 30 | 36 | 91 × 81 = 7371 |
| H4- Sines North | 0.002° × 0.003° | 10 non-stat | 30 | 36 | 91 × 81 = 7371 |
| H5-Sines | 0.005° × 0.005° | 10 non-stat | 30 | 36 | 101 × 101 = 10,201 |
| Cartesian Domains | Δx × Δy (m) | Δt (min) | nf | nθ | ngx × ngy = np |
|---|---|---|---|---|---|
| X1-Leixoes harbor | 25 × 25 | 60 stat | 30 | 36 | 236 × 216 = 50,976 |
| X2-Figueira da Foz | 25 × 50 | 60 stat | 30 | 36 | 65 × 106 = 6890 |
| X3-Obidos | 100 × 100 | 60 stat | 30 | 36 | 156 × 328 = 51,168 |
| X4-Sines harbor | 25 × 25 | 60 stat | 30 | 36 | 261 × 201 = 52,461 |
| Parameter | Grid | Bias | RMSE | SI | R | S | Buoy |
|---|---|---|---|---|---|---|---|
| Hs (m) | D2 | 0.09 | 0.47 | 0.22 | 0.92 | 1.02 | Leixoes N = 1374 |
| C3 | 0.12 | 0.40 | 0.18 | 0.95 | 1.04 | ||
| Tm02 (s) | D2 | −0.47 | 1.29 | 0.18 | 0.80 | 0.95 | |
| C3 | −0.55 | 1.06 | 0.15 | 0.86 | 0.93 | ||
| Hs (m) | D2 | 0.25 | 0.44 | 0.25 | 0.92 | 1.13 | Sines N = 1087 |
| C5 | 0.15 | 0.35 | 0.20 | 0.93 | 1.07 | ||
| H5 | 0.14 | 0.35 | 0.20 | 0.93 | 1.06 | ||
| Tm02 (s) | D2 | −0.37 | 1.26 | 0.18 | 0.81 | 0.96 | |
| C5 | −0.55 | 1.09 | 0.15 | 0.86 | 0.93 | ||
| H5 | −0.57 | 1.07 | 0.15 | 0.87 | 0.93 |
| Parameter | MeanMes (m) | MeanSim (m) | Bias (m) | RMSE (m) | SI | R | S | Buoy |
|---|---|---|---|---|---|---|---|---|
| Hs-WDA | 2.15 | 2.23 | 0.08 | 0.47 | 0.22 | 0.91 | 1.03 | Leixoes (N = 1374) |
| Hs-DA | 2.21 | 0.06 | 0.42 | 0.20 | 0.92 | 1.01 | ||
| Hs-WDA | 1.72 | 1.98 | 0.26 | 0.44 | 0.25 | 0.92 | 1.13 | Sines (N = 1087) |
| Hs-DA | 1.95 | 0.23 | 0.39 | 0.23 | 0.93 | 1.12 |
| Input/Process | Wave | Wind | Tide | Curr | Gen | Wcap | Quad | Triad | Diff | Bfric | Set up | Br |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Domains | ||||||||||||
| Driver | X | X | 0 | 0 | X | X | X | 0 | 0 | X | 0 | X |
| Coastal | X | X | 0 | 0 | X | X | X | X | 0 | X | 0 | X |
| High Resolution | X | X | X | 0 | X | X | X | X | X | X | 0 | X |
| Cartesian | X | X | X | 0 | X | X | X | X | X | X | X | X |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusu, E. Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore. Energies 2018, 11, 980. https://doi.org/10.3390/en11040980
Rusu E. Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore. Energies. 2018; 11(4):980. https://doi.org/10.3390/en11040980
Chicago/Turabian StyleRusu, Eugen. 2018. "Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore" Energies 11, no. 4: 980. https://doi.org/10.3390/en11040980
APA StyleRusu, E. (2018). Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore. Energies, 11(4), 980. https://doi.org/10.3390/en11040980





