Next Article in Journal
Value of Residential Investment in Photovoltaics and Batteries in Networks: A Techno-Economic Analysis
Previous Article in Journal
Investigation of Pumped Storage Hydropower Power-Off Transient Process Using 3D Numerical Simulation Based on SP-VOF Hybrid Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 11
Issue 4
10.3390/en11041021
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems

by
Edison Banguero
1,*,
Antonio Correcher
1,
Ángel Pérez-Navarro
2,
Francisco Morant
1 and
Andrés Aristizabal
3
1
Instituto de Automática e Informática Industrial, Universitat Politècnica de València, Camino de Vera, s/n, 46022 Valencia, Spain
2
Instituto Universitario de Ingeniería Energética, Universitat Politècnica de València; Camino de Vera, s/n, 46022 Valencia, Spain
3
Engineering Department, Universidad de Bogotá Jorge Tadeo Lozano, Carrera 4 # 22-61, 34185 Bogotá D.C., Colombia
*
Author to whom correspondence should be addressed.
Energies 2018, 11(4), 1021; https://doi.org/10.3390/en11041021
Submission received: 23 March 2018 / Revised: 17 April 2018 / Accepted: 18 April 2018 / Published: 23 April 2018
Browse Figures
Versions Notes

Abstract

:
Energy storage has become a fundamental component in renewable energy systems, especially those including batteries. However, in charging and discharging processes, some of the parameters are not controlled by the battery’s user. That uncontrolled working leads to aging of the batteries and a reduction of their life cycle. Therefore, it causes an early replacement. Development of control methods seeks battery protection and a longer life expectancy, thus the constant-current–constant-voltage method is mostly used. However, several studies show that charging time can be reduced by using fuzzy logic control or model predictive control. Another benefit is temperature control. This paper reviews the existing control methods used to control charging and discharging processes, focusing on their impacts on battery life. Classical and modern methods are studied together in order to find the best approach to real systems.

1. Introduction

Electrification of remote and rural isolated areas with the national grid is not always possible, being cost-prohibitive. Therefore, many off-the-grid communities have been using diesel engines as their main power source. To meet the energy needs, governments have opted to install independent renewables sets with battery energy storage systems (BESS) [1]. However, energy storage is one of the greatest challenges for renewable energy systems, especially in stand-alone photovoltaic system and wind farms, where they have proven to be very reliable due to their efficiency and high response time [2,3]. As if it were not enough, the energy storage system (ESS) in a photovoltaic system represents 40% of the total cost [4,5].
Storage technologies are classified according to the time needed to store energy in the applications; such categories are instantaneous (less than a few seconds), short-term (less than a few minutes), mid-term (less than a few hours), and long-term (days) [1,6]. Moreover, of the BESS, there are different types of energy storage technologies [6,7,8,9,10,11,12,13,14]: pumped hydro energy storage (PHES), compressed air energy storage (CAES), flywheel energy storage (FES), the hydrogen-based energy storage system (HES), flow battery energy storage (FBES), superconducting magnetic energy storage (SME), and supercapacitor energy storage (SES). However, because of its localization flexibility, efficiency, scalability, and other appealing features [15], the BESS is the preferred technology [16] (see Figure 1).
At present, there are numerous commercial batteries used in renewable energy systems (RES), such as lead-acid, lithium ion (Li-Ion), nickel cadmium (Ni–Cd), and sodium sulfur (Na–S) batteries, among others. Table 1 shows the main features of these types of batteries [7,9,10,11,12,13,17,18,19,20,21,22].
Regarding BESS used in photovoltaic systems, lead-acid is the most used technology [11,18], due to its low cost, maturity, high reliability, fast response, and low self-discharge rate [11,23]. However, the charging process is nonlinear [24].
Due to the high economic cost generated by the replacement of a BESS, a charge control method and control strategy is required to protect the battery from overcharging and overdischarging [25,26].
The charge control method’s efficiency will depend on the amount of current used for the charging process, the level of the oscillations in the charging current, the charging voltage levels, the charging time, and the fluctuations in the temperature during the charging [27]. Moreover, there are battery parameters that due to their complexity, cannot be obtained by using conventional control methods.
New research trends in energy storage include Li-ion batteries, especially those of lithium iron phosphate (LiFePO4) batteries. This technology has greater advantages in energy density, voltage, useful life, and speed in loading and unloading compared to lead-acid technology. However, nowadays, most renewable facilities include lead-acid batteries and they demand new control methods to improve the useful life of the system. This paper will focus only on control methods applied to lead-acid batteries.
Regarding battery management systems, the research was focused on fuzzy logic control (FLC) and model predictive control (MPC), due to their leading roles in battery control (Figure 2). Where the power input can be supplied by the grid, a photovoltaic system or wind power system is not required.
Fuzzy logic control (FLC) and model predictive control (MPC) have been proven to have higher performance than traditional charging control methods in terms of energy management, thus improving charging time, charging efficiency, states of charge (SOC), and battery life expectancy. The strategies used, goals, and results reached with these controls are detailed and useful. In general terms, the input variables used in an FLC and MPC are battery voltage and temperature, SOC, energy prices, photovoltaic system power, and weather forecast, among others. The current, ESS power, and grid power are used as output variables.
The paper is structured as follows: Section 2 describes traditional methods used to control the charging and discharging of batteries, and the time and state of charge reached. In Section 3, the strategies and fields where the FLC and MPC controls have been applied are described. The obtained results are presented and discussed in Section 4. Section 5 concludes by stating possible paths for future research while summarizing the paper’s main contributions.

2. Traditional Charging Control Methods

The main goal of charging control methods is to increase the SOC. However, specifications such as battery performance, charging time, battery protection from overcharging or overdischarging, and increase of life are very important too.
As the battery charging process is nonlinear [24], different methods have been developed to effectively control battery charging. Control methods commonly used in battery charging are: constant current (CC), constant voltage (CV), two-step charging (i.e., CC–CV), pulse charging (PC), reflex charging or negative pulse charging (NPC), trickle charge or taper-current (TC), and float charge (FC) [28,29,30,31].

2.1. Constant Current (CC)

This method consists of charging the battery with a constant current. This method limits the current to prevent over-current of the initial charge [32]. The voltage value will depend on the charging current, and one advantage is easy calculation of the charging time and the SOC [33]. As voltage is not usually controlled, this can cause battery overcharging and a temperature rise, resulting in battery life degradation [28,30].

2.2. Constant Voltage (CV)

This method is commonly used to charge the battery by applying a constant voltage on its terminals. During the initial stage of charging, the charge current is high. As the battery voltage reaches the charger’s voltage set limit, the charge current decreases [30]. This type of control is used in applications that require extended charging periods to reach full charge. As it requires a long charging time, it can cause temperature rises and degradation of the battery life.

2.3. Constant Current–Constant Voltage (CC–CV)

This charging method is also known as the two-step method, because it combines both CC and CV. CC is applied at the initial charging stage until the battery voltage reaches an overcharged stage or a predefined voltage [34].
At a second stage, the charging method switches to CV to maintain the battery voltage, so that it avoids overvoltage [28,33].
Previous research has shown that the CC–CV charging method is the most efficient for battery charging, regardless of the battery type [26,35], and also that it is the most used control method [26,36,37]. However, its charging speed and efficiency are very low [38]. Moreover, the CC–CV is not suitable for rapid charging, because the CV charging stage prolongs the charging time, causing battery temperature rises and battery lifecycle reductions [39,40,41].

2.4. Pulse Charging (PC)

This charging method consists of periodically applying a pulsed current to the battery. Batteries are completely discharged and recharged periodically in what is called an equalizing charge [42]. This will allow the battery voltage to become more stable. In this charging method, is important to take into account the charging frequency, the pulse peak, and pulse width, because they are related to the capacity and the charging time. This method can reduce the polarization to prevent the battery temperature rise [32]. The weak point of this charging method is its complexity.

2.5. Reflex Charging or Negative Pulse Charging (NPC)

This is an improvement of the PC. The concept of applying reflex charging started with the patents by W. Burkett & J. Bigbee and W. Burkett & R. Jackson [33,43] in 1971. NPC follows this charging sequence: a positive charging pulse, a rest period (not charging), and a discharge pulse (burp) [43]. This method could eliminate polarization so that the temperature rise is decreased [44]. However, it also may reduce the charge efficiency [44,45].

2.6. Trickle Charge or Taper-Current (TC)

This method consists of providing the battery with a continuous CC charge at a low (about C/100) rate [46]. It is designed to compensate for the self-discharge of the battery [42]. This method can charge the battery up to 100% by using a very small charge current. This is typically used for starting, lighting, or ignition (SLI) battery applications, but it is not suitable for batteries that are susceptible to being damaged by overcharging.

2.7. Float Charge (FC)

This method involves a CV charge set to a value just sufficient to finish the battery charge or to maintain the full charge of the battery [47,48]. This method is used for stationary batteries, mainly lead-acid batteries [42].
These traditional charging control methods have been incorporated in commercial inverters such as Victron Energy and the Sunny Island solar technology, among others. The latter controls the charge of the battery in three phases: CC (I phase/bulk phase), CV phase (absorption phase/Vo phase), and float charge/V phase (Figure 3).

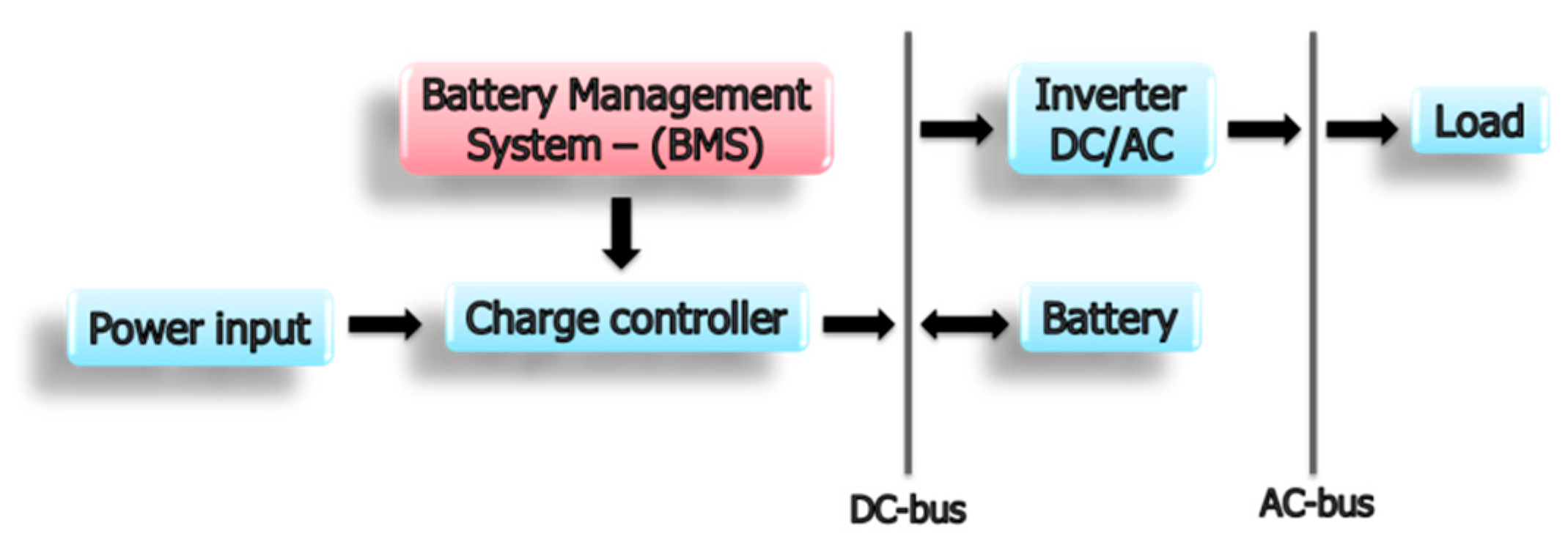
3. Battery Management Systems

Because the process of battery charging and discharging is complex, it required the design of a robust supervisory control over the classic controller, presented in Section 2.
FLC and MPC are especially suitable for battery charging management because they do not require a precise knowledge of mathematical system models and they have high flexibility. Additional information is found in Appendix A.

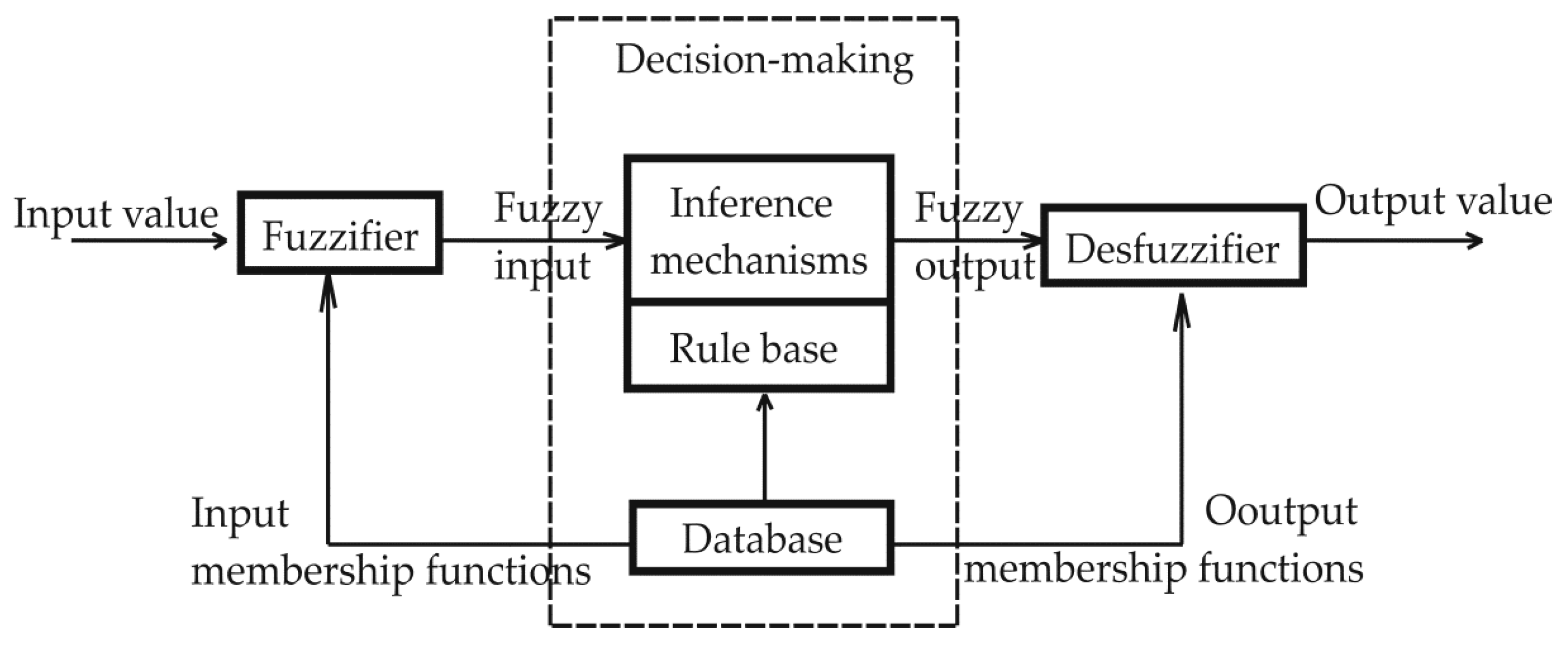
3.1. Fuzzy Logic Control (FLC)

In 1965, Lotfi Zadeh first proposed fuzzy theory [50]. Between the applications of fuzzy logic, fuzzy control (FC) has been one of the fields where fuzzy techniques have obtained a greater amount of successful results working with complex nonlinear systems or even nonanalytic ones [51,52]. FLC is composed by a knowledge base where its parameters can be determined without an exact model of the system [53,54,55].

3.1.1. Fuzzy Logic Control of Energy Storage Systems in Stand-Alone Applications

A FLC method was developed by Bandara et al. [27] to charge a lead-acid battery. The FLC charges the battery at two stages. At the first stage, they use a high current that allows them to reach 70% of their total battery capacity [27]. At the second stage, the voltage of the battery is maintained at a constant value, while the current decreases exponentially [27]. Rahim et al. [56] described a battery charger with a digital signal processor which included FLC as a control algorithm. This approach produced a higher charging current and it supported higher input supplies [56]. Thus, the charging time could be reduced.
Huang et al. [57] used a single crystal processor as the basic controller and a digital signal processor (DSP) to get the voltages, current, and temperature of the batteries [58]. This approach allowed them to lower the battery temperature by about four degrees. Kim et al. [59] proposed a fuzzy proportional integral derivate (PID) controller to improve performance of the frequency control of an islanded microgrid. The control strategy consisted of first, controlling the BESS, and secondly, controlling the energy management system [60]. The control is composed of FLC and a conventional proportional integral (PI) controller, connected in series [59]. The gains of the conventional PI controller and fuzzy PID controller were determined by the particle swarm optimization (PSO) algorithm. The simulation showed that using the proposed controller, the performance was improved compared to a conventional PI.
Welch et al. [61] showed that using particle swarm optimization (PSO), the optimized FLC performed with 26.13% decreased energy usage compared to unoptimized FLC. The charge strategy was improved about 5.22% in relation to a previous study [62]. Fu-shun et al. [63] observed that using a PIC6014 microcontroller as the control core in the design of the FLC, the battery charge time is reduced by two hours compared to the three-stage control method. According to Swathika et al. [64], using an FLC, the battery voltage can be controlled more efficiently than with a traditional controller. Also, the integral square error (ISE), integral absolute error (IAE), and settling time can be reduced considerably in comparison to a PI control. Safari et al. [65] developed an optimized FLC based on the particle swarm optimization (PSO) algorithm. In the control design, they took into account the operation and maintenance costs and the loss of power supply probability [65]. The results of the simulation showed that optimized FLC reduces fluctuations in batteries’ SOC, extending battery life expectancy. Moreover, it can lower operational and maintenance costs and loss of power supply probability by 57% and 33%, respectively, and average SOC can be increased by 6.18% [65]. Also, it reduces the capacity investment cost by up to 18% of autonomous hybrid green power system (HGPS) equipment. Improving what was presented in [61]. Berrazouane et al. [66] adopt the idea of an optimized FLC, but contrary to [61,65], use cuckoo search (CS) to adjust the shape of the FLC system membership functions to achieve a better performance, instead of using a conventional FLC or an optimized FLC based on the PSO algorithm. Compared to the FLC based on PSO, the proposed control reduced the loss of power supply probability, excess energy, and levelized cost of energy [66].

3.1.2. Fuzzy Logic Control of Energy Storage Systems in Grid-Connected Applications

Yin et al. [24] divided the charging process into two stages. At the first stage, they implemented a FLC to determine the start charging time and to prevent overcharging or insufficient battery charging. At the second stage, they used the normal charging method. However, during the simulation, the temperature was not taken into account in the inner loop of the control unit.
Contrary to [59], Haoran et al. [60] took into account the SOC of the BESS as an input to the FLC, where FLC adjusts the active power output of the BESS and the microgrid active power flow. Arcos-Aviles et al. [67] divided their strategy into two stages: at the first stage, minimizing the power peaks and fluctuations in the grid’s power profile and maintaining the lead-acid battery SOC above 70%; at the second stage, performing an offline optimization process based on a set of evaluation quality criteria [67]. With that strategy, the proposed control reduced the maximum and minimum grid power by 61% and 15%, respectively; and 53% and 4%, respectively, if compared to the FLC based on the microgrid’s net power trend. The strategy proposed by Derrouazin et al. [68] led to optimal use of available energy resources beyond a threshold to withstand the load demand, giving priority to the highest power source, while enough of the available energy was routed directly to the battery through a charging/discharging regulator system. This allowed them improve energy efficiency by about 7% compared with the classical FLC. Paliwal et al. [69] revealed that incorporating battery charging efficiency as a battery SOC function offers a more practical approach to system planning. In this research, the authors go on to conclude that assuming a constant value of efficiency may lead to an impediment that allows them to ensure optimal system performance, because the charging efficiency obtained will be greater or less than the constant assumed value affecting the charging power drawn by the energy storage system [69]. Teo et al. [70] designed a control based on the fuzzy inference system (FIS) to determine the charging/discharging rate and current SOC of an energy storage system where power quality (PQ), power variation range (PVR), and battery dynamic range (BDR) were used as quality indices [60]. The maximum and minimum power of the grid was reduced. Hussain et al. [71] proposed a control strategy where the controller decides the mode of BESS operation: subservient mode, resilient mode, or emergency mode. In subservient mode, the battery energy storage system is controlled by the energy management system, and the resilient mode minimizes the operational cost of the microgrid [71]. The goal of the emergency mode operation was to reduce the load shedding during the emergency period. Regarding the latter, load shedding can be reduced by 92%.

3.2. Model Predictive Control (MPC)

Model predictive control (MPC) is a control method which provides the sequence of optimal control variables over a finite time horizon by solving an optimization problem [72,73]. Therefore, it is widely used in many fields [74,75,76,77,78,79,80].

3.2.1. Model Predictive Control of Energy Storage Systems in Stand-Alone Applications

Perez et al. [81] designed a control that anticipates the future saturations of the ESS. The MPC allowed the system to reduce its power production during the first hours [81]. To obtain the optimal performance of the battery, Pezeshki et al. [82] focused on two goals: energy operational cost and smooth charging.
Based on a nonlinear model predictive control (NMPC), Dizqah et al. [83] developed an energy management strategy that commands the energy flow through a standalone direct current (DC) microgrid. The NMPC solves an optimal control problem, finding the optimum values for the pitch angle [83]. The control had three main goals: voltage level regulation, battery management system (BMS), and proportional reactive power sharing [83]. While Morstyn et al. [84] used a convex formulation of the DC microgrid dynamic optimal power flow problem, the proposal was based on a constant voltage-current model and linear power flow approximations. Simulations were made on a real-time digital simulator (RTDS) which used nonlinear battery models and switching converter models. The convex MPC provides an environment for generating reasonable approximated values based on the microgrid operating state, allowing reduction of the computation time by a factor of 1000 [85]. Including additional constraints to the MPC to keep the battery voltage below the upper threshold voltage level provided by the manufacturer leads to the MPC decreasing the charging current [86]. However, this generates a slower charging in comparison with the traditional MPC. Zeng et al. [87] proposed to combine a MPC and a hierarchical optimization to increase output of the renewable energy system generation and to decrease fluctuations between the intraday schedules and day-ahead schedule [87]. Li et al. [88] presented a MPC to mitigate wind power intermittency. The proposed control took into account two features: the smoothness in wind power scheduling and the efficiency loss of the BESS [88].

3.2.2. Model Predictive Control of Energy Storage Systems in Grid-Connected Applications

A control system based on MPC was proposed by Khalid et al. [89] for primary frequency regulation of the BESS to keep a reliable operation. Through a frequency predictor, they optimized the performance of the controller using multi-step-ahead predictions [90]. They presented two scenarios: the first scenario where the BESS operation was adjusted between 40% and 80%; and a second one where the BESS was adjusted between 10% and 50%. In the first case, the maximum battery SOC was reached at ~17 min, while the minimum battery SOC was reached at ~70 min. In the second case, the maximum battery SOC was reached at ~80 min, while the minimum battery SOC was reached at ~12 min.
Ferrarini et al. [73] developed a MPC to store the energy necessary for a building, delivering it when the building load requires it instead of buying from the grid. They designed two MPC controls: the building MPC and the battery MPC. The goal of the building MPC was to optimize the temperature control [73]. Additionally, the battery MPC had the main goal of minimizing the power flow at the point of common coupling (PCC). The PCC power flow was successfully maintained at around 50% until the battery reached a SOC of 90%. Wang et al. [91] used a MPC to optimize and distribute the prosperity energy storage project in New Mexico (PNM). The storage system was divided into two BESS units: a large and slow-moving unit for energy shifting and arbitrage and a small rapid-charging unit for smoothing [91]. The first goal was to provide energy arbitrage and to smooth the intermittent output from the photovoltaic (PV) array [91]. The second goal was to reduce the excessive charge/discharge cycles of the BESS units [91]. A MPC and an EMS based on optimal generation scheduling (OGS) were combined to optimize the short-term operation of the microgrid [92]. The OGS was used to compare the expected power produced by the renewable generators with the expected load demanded over a period of days [92]. Also, it defined the scheduling and evolution of the SOC of the ESSs for a few hours, minimizing the operating cost of the overall microgrid. The MPC aims for real-time control in order to guarantee the microgrid stability [92]. A stochastic approach was implemented to forecast weather and load uncertainties. OGS and MPC working simultaneously can reduce computational load, as achieved in [85].
Matthiss et al. [93] used a MPC to maintain high levels of self-consumption, reduce the peak feed-in power to improve grid compatibility, and to minimize energy costs. In this case, four battery charge algorithms were implemented: charge at the earliest opportunity, linear delayed charging, peak shaving, and a model predictive control (MPC). Additionally, energy pricing was used as an additional parameter of the optimization process. The results show that using a MPC, wind energy is improved by 35% and the energy costs could be reduced about 25%.

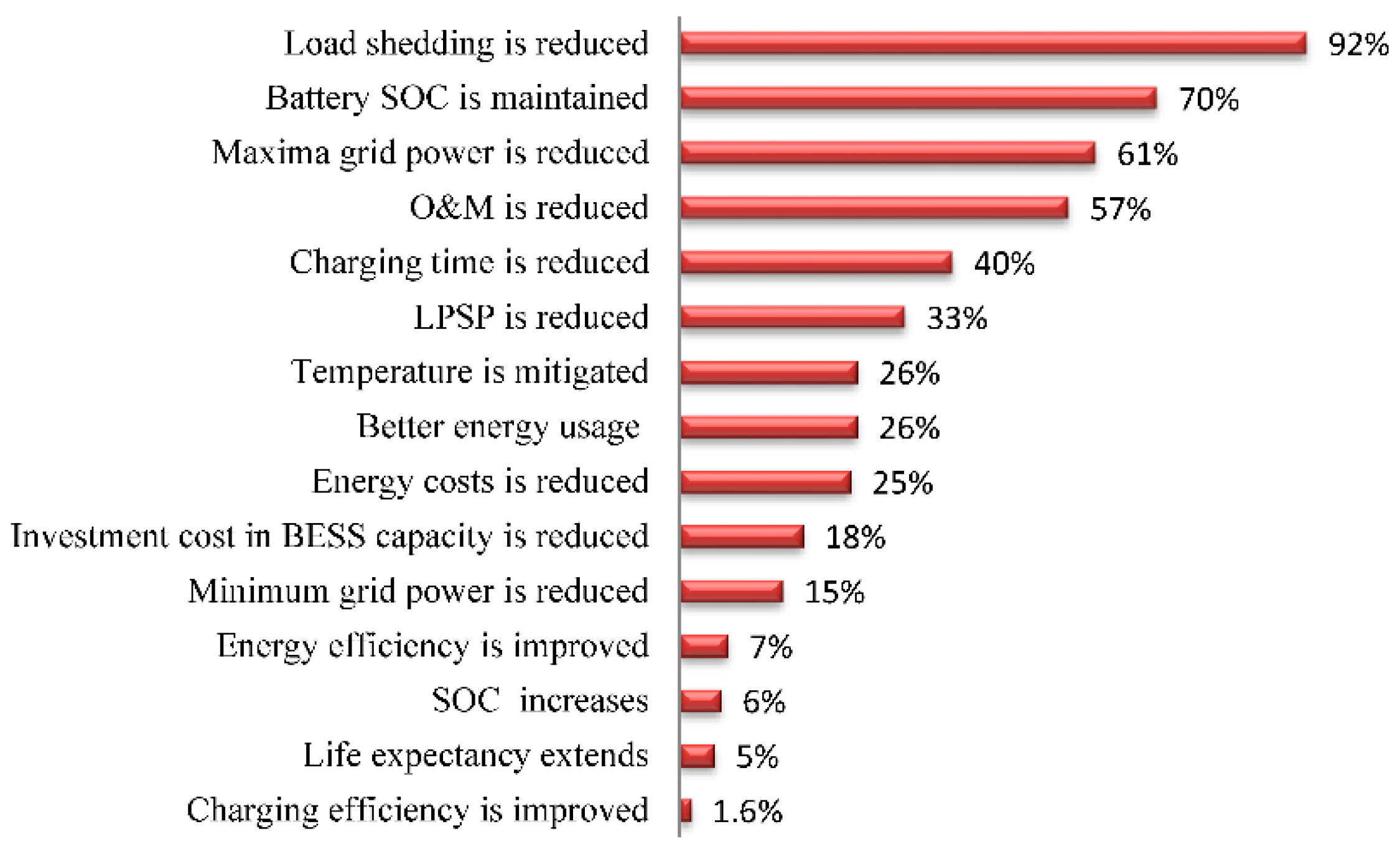
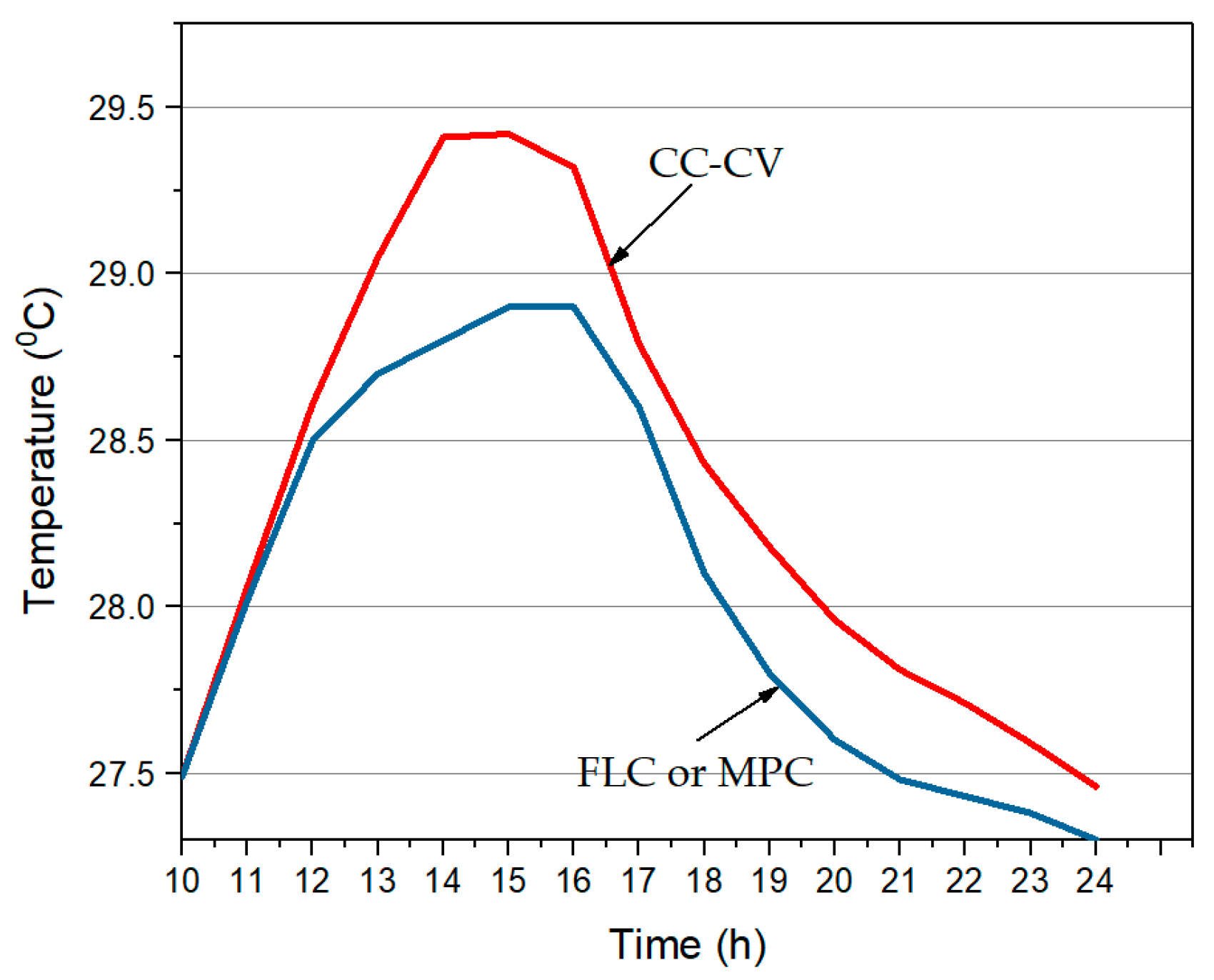
4. Results and Discussion

This research shows that the most used control method for charging and discharging lead-acid batteries in renewable energy systems with battery energy storage is that of CC–CV. However, this control method requires a long time to charge the battery. This prolongation in the charging time generates battery temperature rises, so it produces irreversible battery damage. Moreover, during the process of battery charging and discharging, traditional controls leave some aspects uncontrolled.
In order to solve these events, simulations and in some cases, experimental tests with FLC and MPC are being carried out. Generally, these controls are being used in the energy management of stand-alone microgrids and grid-connected microgrids. These controls have been proven to be more efficient than a traditional control. Figure 4 shows some results achieved using FLC or MPC in renewable energy systems with battery energy storage. When comparing these results with a traditional control, some advantages are found: The load shedding can be reduced up to 92%; also, the implementation of these controls allows maintenance of the SOC above 50%, thus deep discharges are avoided, protecting the battery from wear and tear. Through optimum use of energy, the maximum and minimum power of the grid can be reduced by 61% and 15%, respectively. This rational and efficient use of energy allows reduction of microgrid energy costs by 25%. Also, the operating and maintenance and loss of power supply probability can be lowered by around 57% and 33%, respectively. Regarding the energy storage systems in batteries, the charging time is reduced about 40%, which leads to a decrease in temperature of about 26% and a reduction of the investment cost in energy storage capacity of about 18%; thus, it allowed some approaches to extend the life expectancy by around 5%.
Despite the advantages of FLC and MPC controllers compared to traditional controls, their implementation is required in real environments with large-scale energy storage systems, because many of the results have been achieved through simulation; for example, Figure 5.
Moreover, parameters such as the dynamic selection of battery SOC limits and the influence of ambient variables such as relative humidity or state of health (SOH) prediction were not studied. Finally, these controls are also being implemented to control the charging of lithium iron phosphate (LiFePO4) batteries, as shown in [94,95,96].

5. Conclusions and Future Work

Renewable energy systems have been a short-term solution in the mitigation of energy needs in isolated areas where there is no on-grid energy service. Many of these systems have battery energy storage to give energy in those hours where natural resources such as sun or wind are not present. In a connected microgrid, the BESS is used to reduce active power exchange at the PCC of the microgrid.
A control method and control strategy are required to optimize the energy management and to avoid overcharging and overdischarging of the energy storage system. Despite the fact that constant-current–constant-voltage (CC–CV) is the most used control method for battery charging and discharging, other methods such as FLC or MPC have shown better performances. The main benefits are: reduced charging time, improved charging efficiency, mitigation of the temperature rises, and keeping the battery SOC within secure limits. Moreover, the reduction of the investment cost in energy storage capacity and the life expectancy increase.
Most of the papers consulted based their results on simulations and in some cases, on experimental tests with valve regulated lead acid (VRLA) batteries. Therefore, many more real-world experiments are needed to extend the conclusion to real systems.
The extension to other types of batteries such as OPzS lead-acid batteries and lithium iron phosphate (LiFePO4) batteries is also a hot research topic. However, the high cost of LiFePO4 batteries becomes a constraint for large-scale implementations in RES.
Future work will focus on the experimental application of FLC and MPC in the energy management of a grid-connected system located in the Chocó Department, Colombia (in Spanish).

Acknowledgments

The authors would like to acknowledge the research project “Implementación de un programa de desarrollo e investigación de energías renovables en el departamento del Chocó, BPIN 2013000100285 (in Spanish)” and the Universidad Tecnológica del Chocó (in Spanish). The authors would like to thank the anonymous reviewers as well as the editor for their valuable comments that have greatly improved the final version of the paper.

Author Contributions

All authors have worked on this manuscript together and all authors have read and approved the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Appendix A.1. FLC Applied to PV Systems with BESS

The basic structure of a FLC is shown in Figure A1, and mainly consists of four parts: a fuzzifier or fuzzification where the input data is converted into suitable linguistic values [97]; a knowledge base, conformed by a database with the necessary linguistic definitions and the control rule set which provide the knowledge that helps to control the system in the best possible manner [64,97]; a decision-making which, simulate a human decision process, infer the fuzzy control action from the knowledge of the control rules and linguistic variable definitions [97]; a defuzzification which yields non fuzzy control action from an inferred fuzzy control action [97,98].
Energies 11 01021 g0a1 550
Figure A1. Structure of a FLC [99].
Figure A1. Structure of a FLC [99].
Energies 11 01021 g0a1

Appendix A.2. MPC Applied to PV Systems with BESS

Figure A2 shows the general principle of MPC.
Energies 11 01021 g0a2 550
Figure A2. Principle of a MPC [100].
Figure A2. Principle of a MPC [100].
Energies 11 01021 g0a2
The cost function or objective function is given as [81,101]:
J N = ∑ k = 0 N λ ( k ) c ( t + k ) T [ P g r i d ( t + k ) − P r e f ( t + k ) ] + c s o c ( t + N + 1 ) E E S ( t + N + 1 )
where λ ( k ) is a weighting sequence, c ( t + k ) is the imbalance cost at instant ( t + k ) , T is the sampling period of the MPC, P g r i d ( t + k ) is the power fed to the grid at ( t + k ) , P r e f ( t + k ) is the future constant by hours power production committed by the photovoltaic system, c s o c ( t + N + 1 ) is the value of the energy stored in the battery energy storage system (BESS) at instant ( t + N + 1 ) , and E E S ( t + N + 1 ) is the energy stored in the BESS at instant ( t + N + 1 ) . The energy stored in the BESS at any future instant E E S ( t + k ) can be calculated as: E E S ( t + k ) = E E S ( t + k − 1 ) − T P E S ( t + K − 1 ) .

References

  1. Khalilpour, R.; Vassallo, A. Planning and operation scheduling of PV-battery systems: A novel methodology. Renew. Sustain. Energy Rev. 2016, 53, 194–208. [Google Scholar] [CrossRef]
  2. Yang, Z.; Zhang, J.; Kintner-Meyer, M.C.; Lu, X.; Choi, D.; Lemmon, J.P.; Liu, J. Electrochemical energy storage for green grid. Chem. Rev. 2011, 111, 3577–3613. [Google Scholar] [CrossRef] [PubMed]
  3. Bamgbopa, M.O.; Almheiri, S.; Sun, H. Prospects of recently developed membraneless cell designs for redox flow batteries. Renew. Sustain. Energy Rev. 2017, 70, 506–518. [Google Scholar] [CrossRef]
  4. Sayigh, A. (Ed.) Renewable Energy in the Service of Mankind Vol I: Selected Topics from the World Renewable Energy Congress WREC 2014; Springer: Berlin, Germany, 2015. [Google Scholar]
  5. Armstrong, S.; Glavin, M.E.; Hurley, W.G. Comparison of battery charging algorithms for stand-alone photovoltaic systems. In Proceedings of the 2008 Power Electronics Specialists Conference (PESC 2008), Rhodes, Greece, 15–19 June 2008; pp. 1469–1475. [Google Scholar]
  6. Koohi-Kamali, S.; Tyagi, V.V.; Rahim, N.A.; Panwar, N.L.; Mokhlis, H. Emergence of energy storage technologies as the solution for reliable operation of smart power systems: A review. Renew. Sustain. Energy Rev. 2013, 25, 135–165. [Google Scholar] [CrossRef]
  7. Kousksou, T.; Bruel, P.; Jamil, A.; El Rhafiki, T.; Zeraouli, Y. Energy storage: Applications and challenges. Sol. Energy Mater. Sol. Cells 2014, 120, 59–80. [Google Scholar] [CrossRef]
  8. Akinyele, D.; Belikov, J.; Levron, Y. Battery Storage Technologies for Electrical Applications: Impact in Stand-Alone Photovoltaic Systems. Energies 2017, 10, 1760. [Google Scholar] [CrossRef]
  9. Kaldellis, J.K.; Zafirakis, D.; Kavadias, K. Techno-economic comparison of energy storage systems for island autonomous electrical networks. Renew. Sustain. Energy Rev. 2009, 13, 378–392. [Google Scholar] [CrossRef]
  10. Ferreira, H.L.; Garde, R.; Fulli, G.; Kling, W.; Lopes, J.P. Characterization of electrical energy storage technologies. Energy 2013, 53, 288–298. [Google Scholar] [CrossRef]
  11. Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
  12. Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
  13. Evans, A.; Strezov, V.; Evans, T.J. Assessment of utility energy storage options for increased renewable energy penetration. Renew. Sustain. Energy Rev. 2012, 16, 4141–4147. [Google Scholar] [CrossRef]
  14. Sedighnejad, H.; IqbaL, T.; Quaicoe, J. Compressed air energy storage system control and performance assessment using energy harvested index. Electronics 2014, 3, 1–21. [Google Scholar] [CrossRef]
  15. Alotto, P.; Guarnieri, M.; Moro, F. Redox flow batteries for the storage of renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 29, 325–335. [Google Scholar] [CrossRef]
  16. Nikdel, M. Various battery models for various simulation studies and applications. Renew. Sustain. Energy Rev. 2014, 32, 477–485. [Google Scholar]
  17. Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems—A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar] [CrossRef]
  18. Hesse, H.C.; Martins, R.; Musilek, P.; Naumann, M.; Truong, C.N.; Jossen, A. Economic optimization of component sizing for residential battery storage systems. Energies 2017, 10, 835. [Google Scholar] [CrossRef]
  19. Fathima, H.; Palanisamy, K. Optimized sizing, selection, and economic analysis of battery energy storage for grid-connected wind-PV hybrid system. Model. Simul. Eng. 2015, 2015, 16. [Google Scholar] [CrossRef]
  20. Battke, B.; Schmidt, T.S.; Grosspietsch, D.; Hoffmann, V.H. A review and probabilistic model of lifecycle costs of stationary batteries in multiple applications. Renew. Sustain. Energy Rev. 2013, 25, 240–250. [Google Scholar] [CrossRef]
  21. Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
  22. Dekka, A.; Ghaffari, R.; Venkatesh, B.; Wu, B. A survey on energy storage technologies in power systems. In Proceedings of the Electrical Power and Energy Conference (EPEC), London, ON, Canada, 26–28 October 2015; pp. 105–111. [Google Scholar]
  23. Hsieh, H.-I.; Tsai, C.-Y.; Hsieh, G.-C. Photovoltaic burp charge system on energy-saving configuration by smart charge management. IEEE Trans. Power Electron. 2014, 29, 1777–1790. [Google Scholar] [CrossRef]
  24. Yin, Y.; Luo, X.; Guo, S.; Zhou, Z.; Wang, J. A battery charging control strategy for renewable energy generation systems. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2008; pp. 2–4. [Google Scholar]
  25. Dakkak, M.; Hasan, A. A charge controller based on microcontroller in stand-alone photovoltaic systems. Energy Procedia 2012, 19, 87–90. [Google Scholar] [CrossRef]
  26. Eldahab, Y.E.A.; Saad, N.H.; Zekry, A. Enhancing the design of battery charging controllers for photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 58, 646–655. [Google Scholar] [CrossRef]
  27. Bandara, G.; Ivanov, R.; Gishin, S. Intelligent fuzzy controller for a lead-acid battery charger. In Proceedings of the 1999 IEEE International Conference on Systems, Man, and Cybernetics (SMC’99), Tokyo, Japan, 12–15 October 1999; pp. 185–189. [Google Scholar]
  28. Hua, C.-C.; Lin, M.-Y. A study of charging control of lead-acid battery for electric vehicles. In Proceedings of the 2000 IEEE International Symposium on Industrial Electronics (ISIE 2000), Cholula, Puebla, Mexico, 4–8 December 2000; pp. 135–140. [Google Scholar]
  29. Ayoub, E.; Karami, N. Review on the charging techniques of a li-ion battery. In Proceedings of the Third International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Beirut, Lebanon, 29 April–1 May 2015; pp. 50–55. [Google Scholar]
  30. Rand, D.A.J.; Moseley, P.T.; Rand, D.A.J.; Moseley, P.T.; Garche, J.; Parker, C.D. Valve Regulated Lead Acid Batteries; Elsevier: New York, NY, USA, 2004; ISBN 0-4445-0746-9. [Google Scholar]
  31. Lin, F.J.; Huang, M.S.; Yeh, P.Y.; Tsai, H.C.; Kuan, C.H. DSP-based probabilistic fuzzy neural network control for Li-ion battery charger. IEEE Trans. Power Electron. 2012, 27, 3782–3794. [Google Scholar] [CrossRef]
  32. Hua, A.C.-C.; Syue, B.Z.-W. Charge and discharge characteristics of lead-acid battery and LiFePO4 battery. In Proceedings of the IEEE 2010 International Power Electronics Conference (IPEC), Sapporo, Japan, 21–24 June 2010; pp. 1478–1483. [Google Scholar]
  33. Lee, C.S.; Lin, H.C.; Lai, S.-Y. Development of fast large lead-acid battery charging system using multi-state strategy. Int. J. Comput. Consum. Control 2013, 2, 56–65. [Google Scholar]
  34. Lin, H.C.; He, Y.J.; Liu, C.W. Design of an Efficient Battery Charging System Based on Ideal Multi-State Strategy. In Proceedings of the IEEE 2016 International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 956–959. [Google Scholar]
  35. Yan, J.; Xu, G.; Qian, H.; Xu, Y.; Song, Z. Model predictive control-based fast charging for vehicular batteries. Energies 2011, 4, 1178–1196. [Google Scholar] [CrossRef]
  36. Wong, Y.S.; Hurley, W.G.; Wölfle, W.H. Charge regimes for valve-regulated lead-acid batteries: Performance overview inclusive of temperature compensation. J. Power Sources 2008, 183, 783–791. [Google Scholar] [CrossRef]
  37. Rossinot, E.; Lefrou, C.; Dalard, F.; Cun, J.P. Batteries in standby applications: Comparison of alternate mode versus floating. J. Power Sources 2001, 101, 27–34. [Google Scholar] [CrossRef]
  38. Chen, L.-R. Design of duty-varied voltage pulse charger for improving Li-ion battery-charging response. IEEE Trans. Ind. Electron. 2009, 56, 480–487. [Google Scholar] [CrossRef]
  39. Liu, C.L.; Chiu, Y.S.; Liu, Y.H.; Ho, Y.H.; Huang, S.S. Optimization of a fuzzy-logic-control-based five-stage battery charger using a fuzzy-based taguchi method. Energies 2013, 6, 3528–3547. [Google Scholar] [CrossRef]
  40. Huang, S.-J.; Huang, B.-G.; Pai, F.-S. Fast Charge Strategy Based on the Characterization and Evaluation of LiFePO4 Batteries. IEEE Trans. Power Electron. 2013, 28, 1555–1562. [Google Scholar] [CrossRef]
  41. Liu, Y.-H.; Teng, J.-H. Design and implementation of a fully-digital Lithium-Ion battery charger. In Proceedings of the 2006 IEEE Region 10 Conference (TENCON 2006), Hongkong, China, 14–17 November 2006; pp. 1–4. [Google Scholar]
  42. Linden, D.; Reddy, T.B. Handbook of Batteries, 3rd ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
  43. Nasser, K. Negative Pulse Charging: Myths and Facts. Available online: http://www.batterypoweronline.com/images/PDFs_articles_whitepaper_appros/powerdesigners.pdf (accessed on 3 May 2017).
  44. Li, S.; Zhang, C.; Xie, S. Research on fast charge method for lead-acid electric vehicle batteries. In Proceedings of the IEEE International Workshop on Intelligent Systems and Applications ISA 2009, Wuhan, China, 23–24 May 2009; pp. 1–5. [Google Scholar]
  45. James, M.; Grummett, J.; Rowan, M.; Newman, J. Application of pulse charging techniques to submarine lead-acid batteries. J. Power Sources 2006, 162, 878–883. [Google Scholar] [CrossRef]
  46. Battery Application & Technology. Available online: https://www.engineersedge.com/battery/trickle_charging.htm (accessed on 5 April 2018).
  47. Chuang, Y.C.; Ke, Y.L.; Chuang, H.S.; Chang, S.Y. Battery float charge technique using parallel-loaded resonant converter for discontinuous conduction operation. IEEE Trans. Ind. Appl. 2012, 48, 1070–1078. [Google Scholar] [CrossRef]
  48. Battery Charging Methods. Available online: http://www1.labvolt.com/publications/Exercises/86351-00_4.pdf (accessed on 5 April 2018).
  49. Battery Management of the SunnyIsland. Available online: http://files.sma.de/dl/7910/SI_Batteriemanagement-TI-en-21.pdf (accessed on 22 June 2017).
  50. Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
  51. Hsieh, G.-C.; Chen, L.-R.; Huang, K.-S. Fuzzy-controlled Li-ion battery charge system with active state-of-charge controller. IEEE Trans. Ind. Electron. 2001, 48, 585–593. [Google Scholar] [CrossRef]
  52. Precup, R.-E.; Hellendoorn, H. A survey on industrial applications of fuzzy control. Comput. Ind. 2011, 62, 213–226. [Google Scholar] [CrossRef]
  53. Liu, C.-L.; Chen, J.-H.; Liu, Y.H.; Yang, Z.-Z. An asymmetrical fuzzy-logic-control-based MPPT algorithm for photovoltaic systems. Energies 2014, 7, 2177–2193. [Google Scholar] [CrossRef]
  54. Gdaim, S.; Mtibaa, A.; Mimouni, M.F. Design and experimental implementation of DTC of an induction machine based on fuzzy logic control on FPGA. IEEE Trans. Fuzzy Syst. 2015, 23, 644–655. [Google Scholar] [CrossRef]
  55. Bago, J.C.; Galán, S.G.; Aguilera, J.; Velasco, J.R.; Magdalena, L. Fuzzy controller applications in stand-alone photovoltaic systems. Mathw. Soft Comput. 2008, 9, 85–105. [Google Scholar]
  56. Rahim, N.A.; Mekhilef, S.; Chan, E.L.; Ping, H.W. Fuzzy-controlled battery charger state-of-charge controller. Int. J. Model. Simul. 2006, 26, 106–111. [Google Scholar] [CrossRef]
  57. Huang, C.H.; Huang, C.C.; Ou, T.C.; Lu, K.H.; Hong, C.M. Intelligent fuzzy logic controller for a solar charging system. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2009), Singapore, 14–17 July 2009; pp. 1412–1417. [Google Scholar]
  58. Yarn, K.F.; Wu, K.K.; Chung, L.Y. Fuzzy logic control of Photovoltaic Lead-Acid Charging System. Adv. Mater. Res. 2011, 219–220, 941–944. [Google Scholar] [CrossRef]
  59. Kim, J.Y.; Kim, H.M.; Kim, S.K.; Jeon, J.H.; Choi, H.K. Designing an energy storage system fuzzy PID controller for microgrid islanded operation. Energies 2011, 4, 1443–1460. [Google Scholar] [CrossRef]
  60. Zhao, H.; Wu, Q.; Wang, C.; Cheng, L.; Rasmussen, C.N. Fuzzy logic based coordinated control of battery energy storage system and dispatchable distributed generation for microgrid. J. Mod. Power Syst. Clean Energy 2015, 3, 422–428. [Google Scholar] [CrossRef]
  61. Welch, R.L.; Venayagamoorthy, G.K. Energy dispatch fuzzy controller for a grid-independent photovoltaic system. Energy Convers. Manag. 2010, 51, 928–937. [Google Scholar] [CrossRef]
  62. Welch, R.L.; Venayagamoorthy, G.K. Comparison of two optimal control strategies for a grid independent photovoltaic system. In Proceedings of the Conference Record of the 2006 IEEE 41st IAS Annual Meeting Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 1120–1127. [Google Scholar]
  63. Wang, F.-S.; Suo, X.-S. Research on Batterys charging system based on the Fuzzy control. In Proceedings of the 2nd International Conference on Computer Science and E-lectronics Engineering, Hangzhou, China, 22–23 March 2013. [Google Scholar]
  64. Swathika, R.; Ram, R.G.; Kalaichelvi, V.; Karthikeyan, R. Application of fuzzy logic for charging control of lead-acid battery in stand-alone solar photovoltaic system. In Proceedings of the 2013 International Conference on Green Computing, Communication and Conservation of Energy (ICGCE), Chennai, India, 12–14 December 2013; pp. 377–381. [Google Scholar]
  65. Safari, S.; Ardehali, M.M.; Sirizi, M.J. Particle swarm optimization based fuzzy logic controller for autonomous green power energy system with hydrogen storage. Energy Convers. Manag. 2013, 65, 41–49. [Google Scholar] [CrossRef]
  66. Berrazouane, S.; Mohammedi, K. Parameter optimization via cuckoo optimization algorithm of fuzzy controller for energy management of a hybrid power system. Energy Convers. Manag. 2014, 78, 652–660. [Google Scholar] [CrossRef]
  67. Arcos-Aviles, D.; Pascual, J.; Marroyo, L.; Sanchis, P.; Guinjoan, F. Fuzzy logic-based energy management system design for residential grid-connected microgrids. IEEE Trans. Smart Grid 2016, 9, 530–543. [Google Scholar] [CrossRef]
  68. Derrouazin, A.; Aillerie, M.; Mekkakia-Maaza, N.; Charles, J.P. Fuzzy logic controller versus classical logic controller for residential hybrid solar-wind-storage energy system. AIP Conf. Proc. 2016, 1758, 030055. [Google Scholar]
  69. Paliwal, P.; Patidar, N.P.; Nema, R.K. Fuzzy logic based determination of battery charging efficiency applied to hybrid power system. J. World Acad. Eng. Sci. Technol. 2012, 71, 1164–1168. [Google Scholar]
  70. Teo, T.T.; Logenthiran, T.; Woo, W.L.; Abidi, K. Fuzzy logic control of energy storage system in microgrid operation. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 65–70. [Google Scholar]
  71. Hussain, A.; Bui, V.H.; Kim, H.-M. Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids. Energies 2017, 10, 271. [Google Scholar] [CrossRef]
  72. Maciejowski, J.M. Predictive Control: With Constraints; Pearson Education: Upper Saddle River, NJ, USA, 2002; ISBN 0 201 39823 0. [Google Scholar]
  73. Ferrarini, L.; Mantovani, G.; Costanzo, G.T. A Distributed Model predictive control approach for the integration of flexible loads, storage and renewables. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1700–1705. [Google Scholar]
  74. Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
  75. Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
  76. Geyer, T.; Papafotiou, G.; Morari, M. Hybrid model predictive control of the step-down DC–DC converter. IEEE Trans. Control Syst. Technol. 2008, 16, 1112–1124. [Google Scholar] [CrossRef]
  77. Cortes, P.; Rodriguez, J.; Antoniewicz, P.; Kazmierkowski, M. Direct power control of an AFE using predictive control. IEEE Trans. Power Electron. 2008, 23, 2516–2523. [Google Scholar] [CrossRef]
  78. Xie, Y.H.; Ghaemi, R.; Sun, J.; Freudenberg, J.S. Implicit model predictive control of a full bridge DC–DC converter. IEEE Trans. Power Electron. 2009, 24, 2704–2713. [Google Scholar]
  79. Quevedo, D.E.; Aguilera, R.P.; Perez, M.A.; Cortés, P.; Lizana, R. Model predictive control of an AFE rectifier with dynamic references. IEEE Trans. Power Electron. 2012, 27, 3128–3136. [Google Scholar] [CrossRef]
  80. Townsend, C.D.; Summers, T.J.; Betz, R.E. Multigoal heuristic model predictive control technique applied to a cascaded H-bridge StatCom. IEEE Trans. Power Electron. 2012, 27, 1191–1200. [Google Scholar] [CrossRef]
  81. Perez, E.; Beltran, H.; Aparicio, N.; Rodriguez, P. Predictive power control for PV plants with energy storage. IEEE Trans. Sustain. Energy 2013, 4, 482–490. [Google Scholar] [CrossRef]
  82. Pezeshki, H.; Wolfs, P.; Ledwich, G. A model predictive approach for community battery energy storage system optimization. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
  83. Dizqah, A.M.; Maheri, A.; Busawon, K.; Kamjoo, A. A multivariable optimal energy management strategy for standalone dc microgrids. IEEE Trans. Power Syst. 2015, 30, 2278–2287. [Google Scholar] [CrossRef]
  84. Morstyn, T.; Hredzak, B.; Agelidis, V.G. Dynamic optimal power flow for DC microgrids with distributed battery energy storage systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
  85. Morstyn, T.; Hredzak, B.; Aguilera, R.P.; Agelidis, V.G. Model predictive control for Distributed Microgrid Battery Energy Storage Systems. IEEE Trans. Control Syst. Technol. 2018, 26, 1107–1114. [Google Scholar] [CrossRef]
  86. Kujundžić, G.; Ileš, Š.; Matuško, J.; Vašak, M. Optimal charging of valve-regulated lead-acid batteries based on model predictive control. Appl. Energy 2017, 187, 189–202. [Google Scholar] [CrossRef]
  87. Zeng, P.P.; Wu, Z.; Zhang, X.P.; Liang, C.; Zhang, Y. Model predictive control for energy storage systems in a network with high penetration of renewable energy and limited export capacity. In Proceedings of the 2014 IEEE Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
  88. Li, C.-T.; Peng, H.; Sun, J. Predictive control and sizing of energy storage to mitigate wind power intermittency. Wind Energy 2016, 19, 437–451. [Google Scholar] [CrossRef]
  89. Khalid, M.; Savkin, A.V. Model predictive control based efficient operation of battery energy storage system for primary frequency control. In Proceedings of the 2010 IEEE 11th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 7–10 December 2010; pp. 2248–2252. [Google Scholar]
  90. Khalid, M.; Savkin, A.V. An optimal operation of wind energy storage system for frequency control based on model predictive control. Renew. Energy 2012, 48, 127–132. [Google Scholar] [CrossRef]
  91. Wang, T.; Kamath, H.; Willard, S. Control and optimization of grid-tied photovoltaic storage systems using model predictive control. IEEE Trans. Smart Grid 2014, 5, 1010–1017. [Google Scholar] [CrossRef]
  92. Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerra, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
  93. Matthiss, B.; Müller, D.; Binder, J.; Pietruschka, D. Model Predicitive Control Schemes for PV-Storage Systems to Increase Grid Compatibility and Optimise Energy Costs. In Proceedings of the 29th European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 22–26 September 2014; pp. 3581–3586. [Google Scholar]
  94. Kim, J.; Nikitenkov, D. Fuzzy logic-controlled online state-of-health (SOH) prediction in large format LiMn2O4 cell for energy storage system (ESS) applications. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, South Korea, 26 February–1 March 2014; pp. 474–479. [Google Scholar]
  95. Li, X.; Yan, H. Fuzzy logic-based coordinated control method for multi-type battery energy storage systems. Artif. Intell. Rev. 2018, 49, 227–243. [Google Scholar] [CrossRef]
  96. Li, X.; Li, N.; Jia, X.; Hui, D. Fuzzy logic based smoothing control of wind/PV generation output fluctuations with battery energy storage system. In Proceedings of the 2011 International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar]
  97. Nik IsmaiL, N.F.; Musirin, I.; Baharom, R.; Johari, D. Fuzzy logic controller on DC/DC boost converter. In Proceedings of the 2010 IEEE International Conference on Power and Energy (PECon), Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 661–666. [Google Scholar]
  98. Mattavelli, P.; Rossetto, L.; Spiazzi, G.; Tenti, P. General-purpose fuzzy controller for dc/dc converters. In Proceedings of the Tenth Annual 1995 IEEE Applied Power Electronics Conference and Exposition (APEC’95), Dallas, TX, USA, 5–9 March 1995; pp. 723–730. [Google Scholar]
  99. Eker, I.; Torun, Y. Fuzzy logic control to be conventional method. Energy Convers. Manag. 2006, 47, 377–394. [Google Scholar] [CrossRef]
  100. Chen, H.; Allgöwer, F. Nonlinear model predictive control schemes with guaranteed stability. In Nonlinear Model Based Process Control; Springer: Dordrecht, The Netherland, 1998; pp. 465–494. [Google Scholar]
  101. Sultana, W.R.; Sahoo, S.K.; Sukchai, S.; Yamuna, S.; Venkatesh, D. A review on state of art development of model predictive control for renewable energy applications. Renew. Sustain. Energy Rev. 2017, 76, 391–406. [Google Scholar] [CrossRef]
Energies 11 01021 g001 550
Figure 1. Energy storage systems (ESS). HES: hydrogen-based energy storage system; FBES: flow battery energy storage; SES: supercapacitor energy storage; PHES: pumped hydro energy storage; SMES: superconducting magnetic energy storage system; CAES: compressed air energy storage; FES: flywheel energy storage and BESS: battery energy storage systems.
Figure 1. Energy storage systems (ESS). HES: hydrogen-based energy storage system; FBES: flow battery energy storage; SES: supercapacitor energy storage; PHES: pumped hydro energy storage; SMES: superconducting magnetic energy storage system; CAES: compressed air energy storage; FES: flywheel energy storage and BESS: battery energy storage systems.
Energies 11 01021 g001
Energies 11 01021 g002 550
Figure 2. Battery control scheme.
Figure 2. Battery control scheme.
Energies 11 01021 g002
Energies 11 01021 g003 550
Figure 3. Sunny Island charging phases with sample values for an absorbent glass mat (AGM) battery [49]. AptTmBoost: Absorption time of the boost charge in minutes; ChrgVtgBoost: Setpoint of the cell voltage at boost charge in V; AptTmFul: Absorption time for full charge in hours; ChrgVtgFul: Cell voltage setpoint for full charge in V; AptTmEqu: Absorption time for equalization charge in hours; ChrgVtgEqu: Cell voltage setpoint for equalization charge in V; SilentTmFlo: Time until switchover to energy-saving mode; ChrgVtgFlo: Cell voltage setpoint for float charge in V and SilentTmMax: Maximum duration of energy-saving mode.
Figure 3. Sunny Island charging phases with sample values for an absorbent glass mat (AGM) battery [49]. AptTmBoost: Absorption time of the boost charge in minutes; ChrgVtgBoost: Setpoint of the cell voltage at boost charge in V; AptTmFul: Absorption time for full charge in hours; ChrgVtgFul: Cell voltage setpoint for full charge in V; AptTmEqu: Absorption time for equalization charge in hours; ChrgVtgEqu: Cell voltage setpoint for equalization charge in V; SilentTmFlo: Time until switchover to energy-saving mode; ChrgVtgFlo: Cell voltage setpoint for float charge in V and SilentTmMax: Maximum duration of energy-saving mode.
Energies 11 01021 g003
Energies 11 01021 g004 550
Figure 4. Main advantages of fuzzy logic control (FLC) or model predictive control (MPC) with respect to traditional control methods. SOC: state of charge; O&M: The operating and maintenance costs of a battery energy storage system (BESS) and LPSP: loss possibility to supply power.
Figure 4. Main advantages of fuzzy logic control (FLC) or model predictive control (MPC) with respect to traditional control methods. SOC: state of charge; O&M: The operating and maintenance costs of a battery energy storage system (BESS) and LPSP: loss possibility to supply power.
Energies 11 01021 g004
Energies 11 01021 g005 550
Figure 5. Simulation of battery temperature.
Figure 5. Simulation of battery temperature.
Energies 11 01021 g005
Table
Table 1. Battery technologies in renewable energy systems (RES). Pb-Acid: lead-acid; Li-Ion: lithium-ion; Ni–Cd: nickel-cadmium; Na–S: sodium-sulfur; PSB: Polysulphide–bromide flow battery; VRB: vanadium redox flow battery.
Table 1. Battery technologies in renewable energy systems (RES). Pb-Acid: lead-acid; Li-Ion: lithium-ion; Ni–Cd: nickel-cadmium; Na–S: sodium-sulfur; PSB: Polysulphide–bromide flow battery; VRB: vanadium redox flow battery.
TechnologyPb-AcidLi-IonNi–CdNa–SPSBVRB
Capital cost ($/kWh)50–400600–2500400–2400200–600150–1000150–1000
Efficiency (%)70–9075–9560–7071–9060–7565–85
Operating temperature (°C)−5 to 40−30 to 60−40 to 503250 to 400 to 40
Depth of discharge (DOD, %)60–708010060–1007575
Energy density (Wh/kg)30–5075–25050–75100–240>40010–75
Life cycles (cycles)500–20001000–10,0001000–35002000–5000100–13,00012,000+
Lifetime (years)3–155–205–205–2010–155–20
Availability (%)99.9997+99+Up to 99.98*****96–99
Technological maturity level (1: lower to 5: higher)5444*****3
Response time (ms)FastFastFastFast**********
Capacity (MW)0.001–500.001–500–500.05–300.005–1200.005–1.5
Note: *****: there are no data available.

Share and Cite

MDPI and ACS Style

Banguero, E.; Correcher, A.; Pérez-Navarro, Á.; Morant, F.; Aristizabal, A. A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems. Energies 2018, 11, 1021. https://doi.org/10.3390/en11041021

AMA Style

Banguero E, Correcher A, Pérez-Navarro Á, Morant F, Aristizabal A. A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems. Energies. 2018; 11(4):1021. https://doi.org/10.3390/en11041021

Chicago/Turabian Style

Banguero, Edison, Antonio Correcher, Ángel Pérez-Navarro, Francisco Morant, and Andrés Aristizabal. 2018. "A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems" Energies 11, no. 4: 1021. https://doi.org/10.3390/en11041021

APA Style

Banguero, E., Correcher, A., Pérez-Navarro, Á., Morant, F., & Aristizabal, A. (2018). A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems. Energies, 11(4), 1021. https://doi.org/10.3390/en11041021

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop