Advanced One-Dimensional Entrained-Flow Gasifier Model Considering Melting Phenomenon of Ash
Abstract
:1. Introduction
2. EFG Model
2.1. Basic Assumptions
- The inside of the gasifier is cylindrical; this assumption is suitable for modeling the Texaco EFG [17].
- Coal and gas mass flow rates are constant.
- Temperature and gas concentration are uniform in the radial direction.
- Each cell is perfectly mixed.
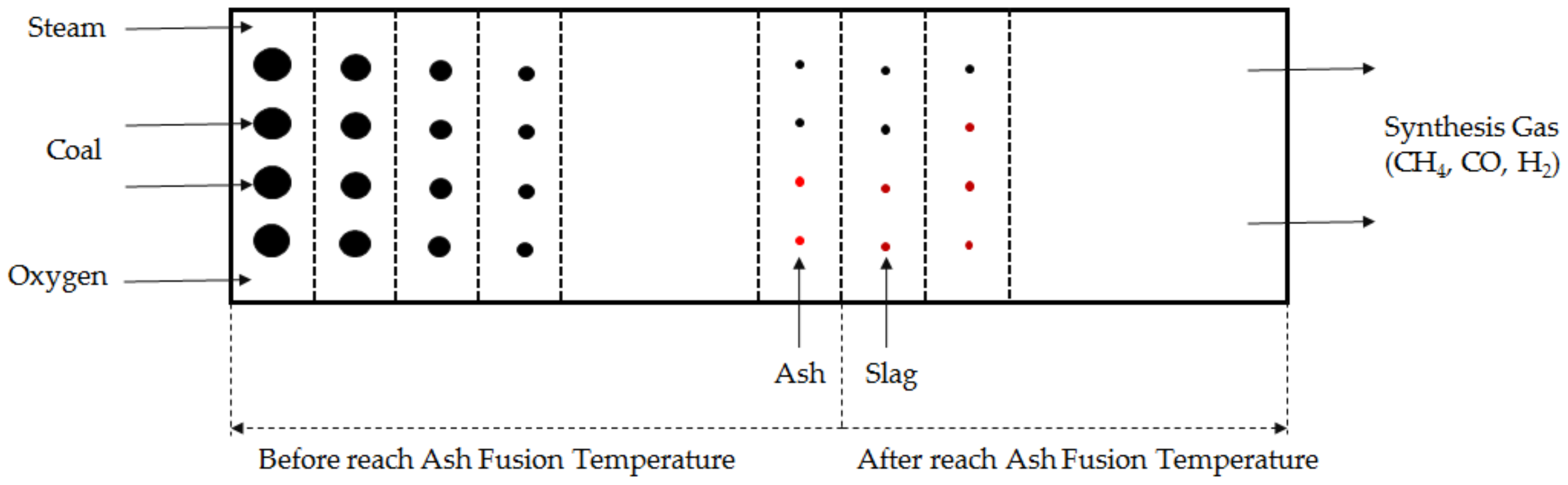
- The reactor consists of equally divided cells (Figure 1). The reaction rate depends on each cell’s conditions.
- Spherical coal particles react from the outer surface while moving through the cell from front to end. As the reaction of the coal progresses, the size of the particles decreases.
- All of the coal grains in the same cell are uniform.
- Ash changes to slag after temperature exceed an AFT.
- Ashes are inert.
2.2. Reaction Kinetics
3. Solving Procedure
3.1. Mass Balance
3.2. Energy Balance
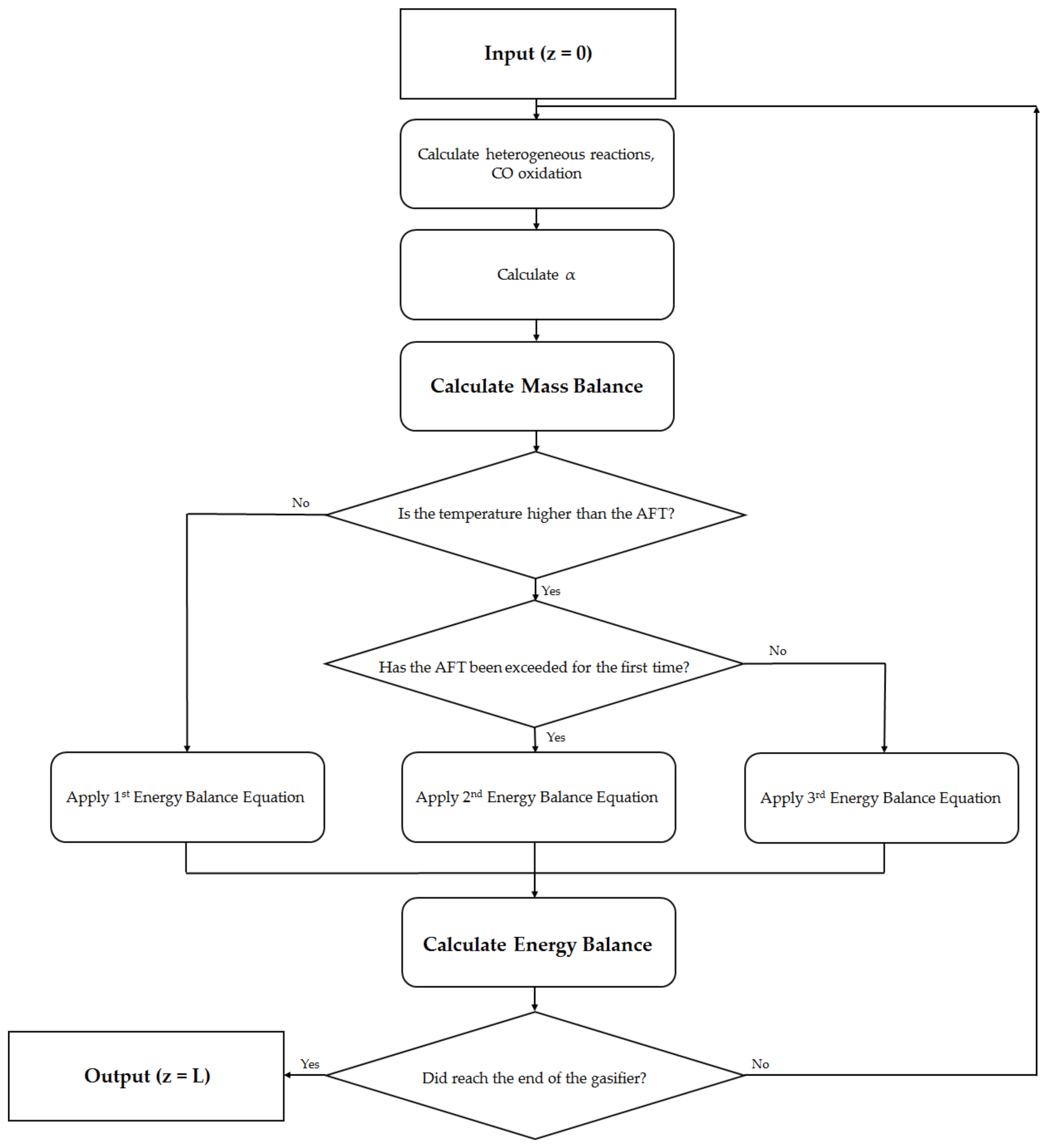
3.3. Solving Algorithm
- Information about coal: coal conversion, coal mass flow rate.
- Molar flow rate of product gas.
- Temperature profile.
4. Required Information for Simulation
4.1. Operating Variables and Reactor Size
4.2. Coal Properties
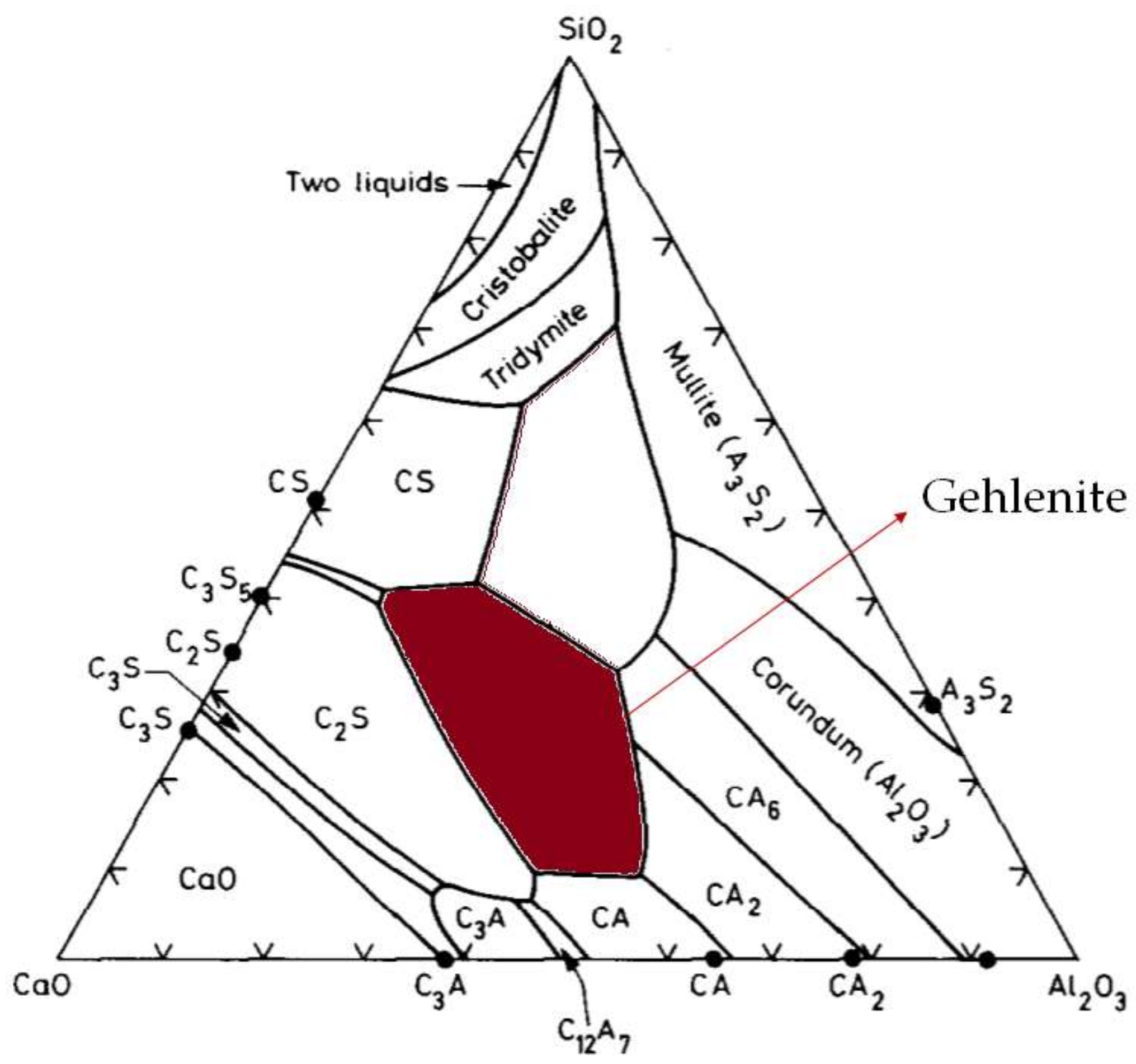
4.3. Ash and Slag Properties
5. Results and Discussion
5.1. Model Valdation
5.2. Simulation Results
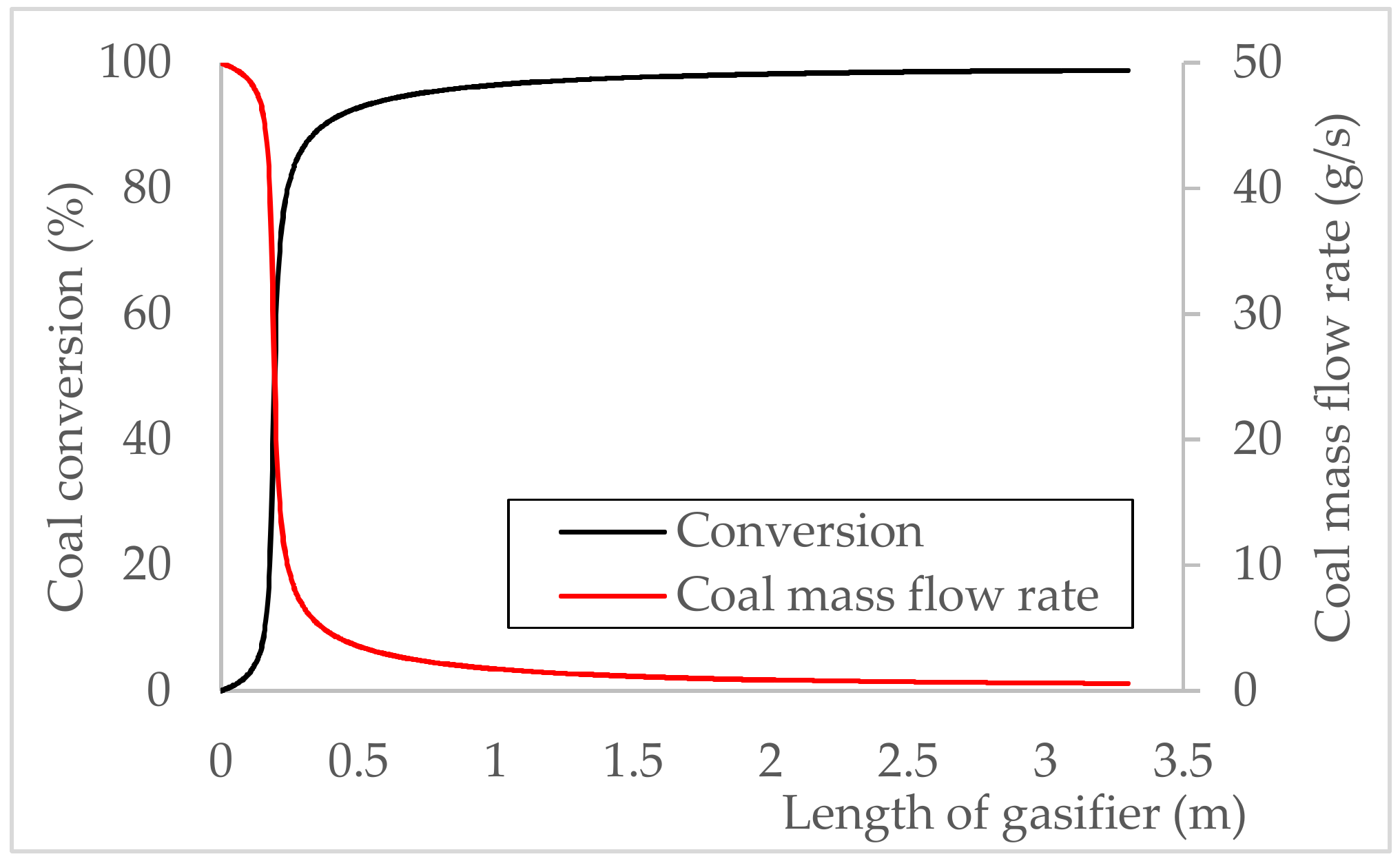
5.2.1. Coal Conversion
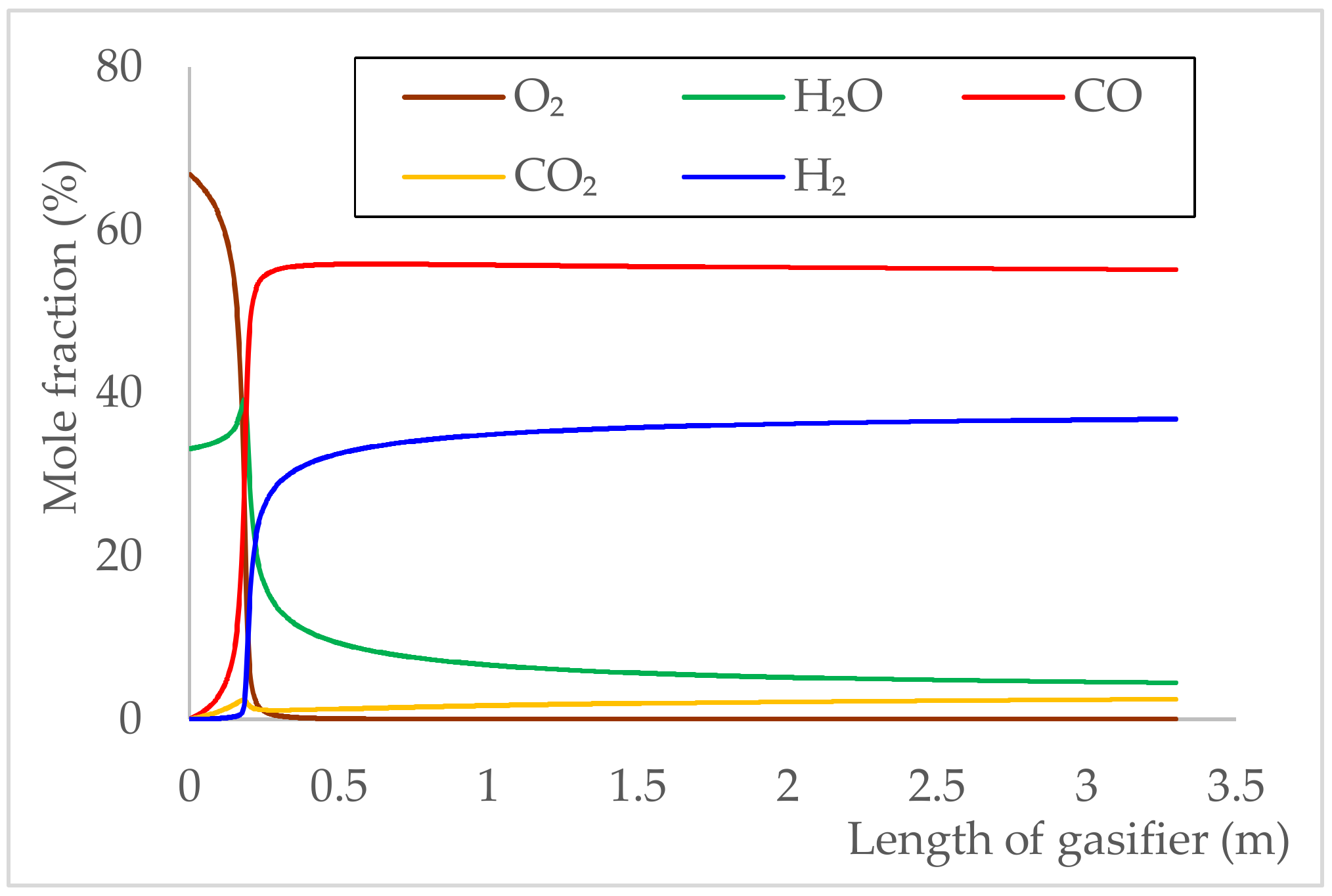
5.2.2. Gas Composition
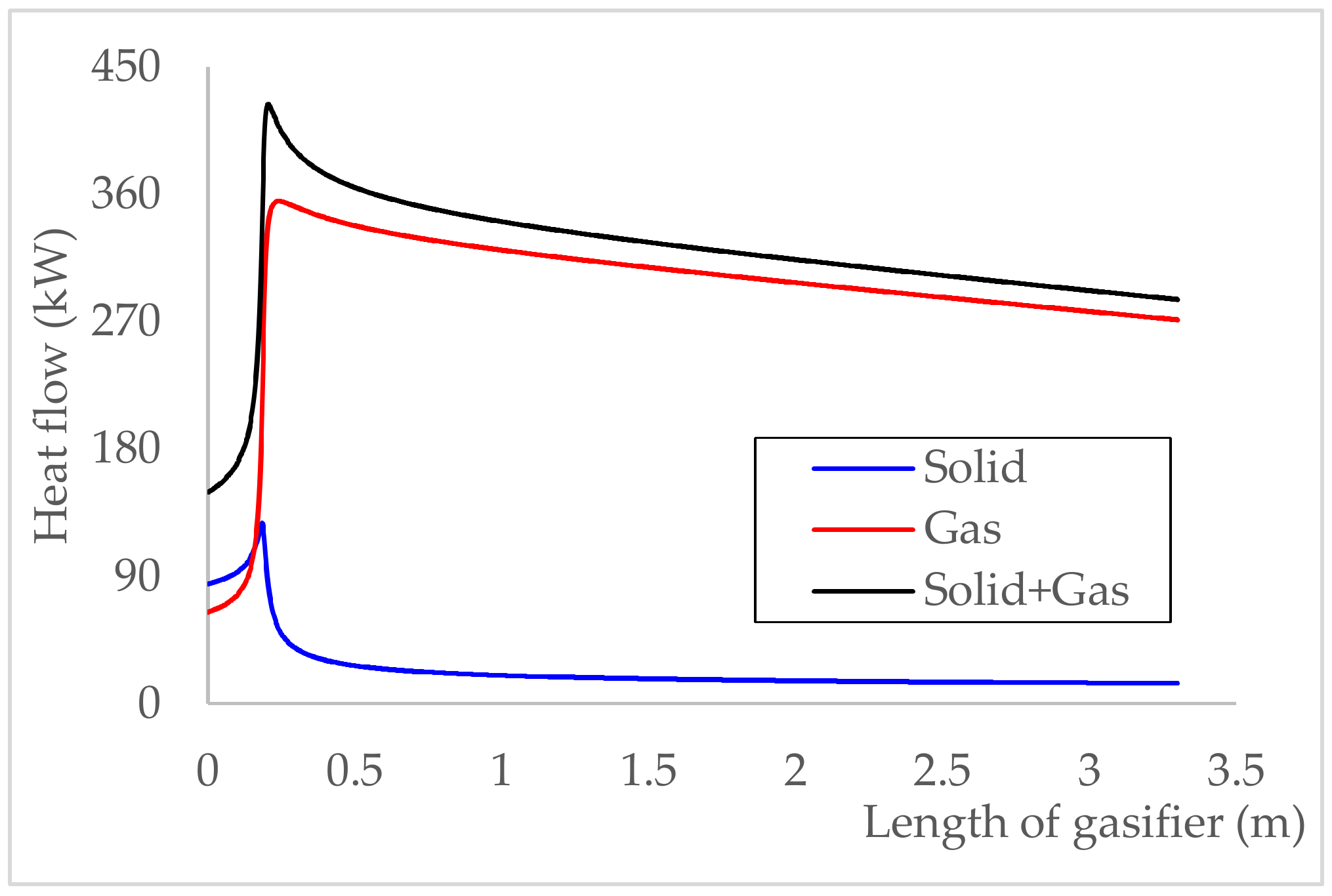
5.2.3. Temperature and Heat Flow
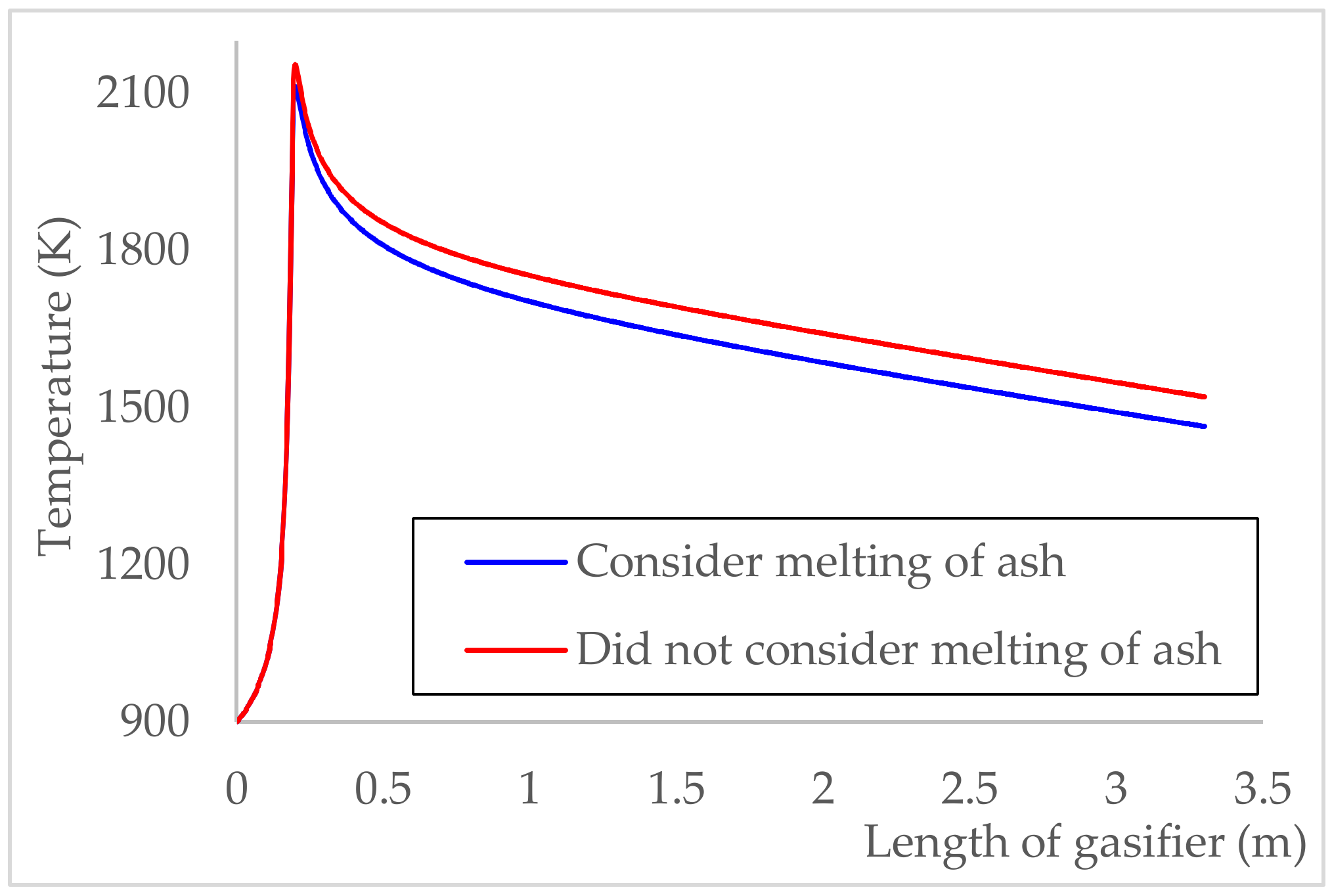
5.3. Consideration of Ash Melting Effect
5.4. Applicability of High Ash Content Coal and Limitations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | cross section area of gasifier (m2) |
| C | molar concentration (mole/m3) |
| cp | specific heat capacity (J/g·K for solid, J/mole·K for gas) |
| dc | coal particle size (m) |
| F | molar flow rate of gas (mole/s) |
| H | enthalpy (J) |
| Hloss | heat loss to outer wall (J/s) |
| HHV | high heating value of coal (J/g) |
| K | equilibrium constant of water gas shift reaction (-) |
| ki | rate constant of ith reaction |
| L | reactor length (m) |
| mc | mass of one coal particle (g/#) |
| MW | molecular weight (g/gmole) |
| Nv | number of particles contained in coal (#/m3) |
| Pi | partial pressure of gas i (atm) |
| Rj | reaction rate of j (g/s for heterogeneous reaction, mole/s for homogeneous reaction) |
| T | temperature (K) |
| vc | coal velocity (m/s) |
| Wa | ash mass flow rate (g/s) |
| Wc | coal mass flow rate (g/s) |
| Ws | slag mass flow rate (g/s) |
| w | phi control function according to temperature (-) |
| X | Coal conversion (-) |
| Z | the coordinates of the axis of the gasifier in the previous model (m) |
| z | the coordinates of the axis of the gasifier in this model (m) |
| Greek Characters | |
| α | degree of deviation from equilibrium (mole/s) |
| φ | the stoichiometric coefficient to adjust the complete, incomplete combustion |
| ξ | stoichiometric coefficient |
| Subscripts | |
| a | the weight of C contained in 1 g of coal |
| b | the weight of H contained in 1 g of coal |
| c | the weight of O contained in 1 g of coal |
| d | the weight of N contained in 1 g of coal |
| e | the weight of S contained in 1 g of coal |
| f | the weight of ash contained in 1 g of coal |
| i | gas species |
| j | reaction |
| L | value at the reactor exit |
| 0 | value at the reactor inlet |
References
- Phillips, J. Different types of gasifiers and their integration with gas turbines. In The Gas Turbine Handbook; 2006; Volume 1. Available online: https://www.netl.doe.gov/File%20Library/Research/Coal/energy%20systems/turbines/handbook/1-2-1.pdf (accessed on 2 January 2018).
- Guo, X.; Dai, Z.; Gong, X.; Chen, X.; Liu, H.; Wang, F.; Yu, Z. Performance of an entrained-flow gasification technology of pulverized coal in pilot-scale plant. Fuel Process. Technol. 2007, 88, 451–459. [Google Scholar] [CrossRef]
- Wang, T.; Stiegel, G.J. Integrated Gasification Combined Cycle (IGCC) Technologies; Woodhead Publishing: Cambridge, UK, 2016; ISBN 978-0-08-100185-1. [Google Scholar]
- Vamvuka, D.; Woodburn, E.T.; Senior, P.R. Modelling of an entrained flow coal gasifier. 2. Effect of operating conditions on reactor performance. Fuel 1995, 74, 1461–1465. [Google Scholar] [CrossRef]
- Vamvuka, D.; Woodburn, E.T.; Senior, P.R. Modelling of an entrained flow coal gasifier. 1. Development of the model and general predictions. Fuel 1995, 74, 1452–1460. [Google Scholar] [CrossRef]
- Hwang, M.; Song, E.; Song, J. One-Dimensional Modeling of an Entrained Coal Gasification Process Using Kinetic Parameters. Energies 2016, 9, 99. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Perlmutter, D.D. A random pore model for fluid-solid reactions: II. Diffusion and transport effects. AIChE J. 1981, 27, 247–254. [Google Scholar] [CrossRef]
- Ishida, M.; Wen, C.Y. Comparison of kinetic and diffusional models for solid-gas reactions. AIChE J. 1968, 14, 311–317. [Google Scholar] [CrossRef]
- Sadhukhan, A.K.; Gupta, P.; Saha, R.K. Modelling of combustion characteristics of high ash coal char particles at high pressure: Shrinking reactive core model. Fuel 2010, 89, 162–169. [Google Scholar] [CrossRef]
- Gupta, P.; Sadhukhan, A.K.; Saha, R.K. Analysis of the combustion reaction of carbon and lignite char with ignition and extinction phenomena: Shrinking sphere model. Int. J. Chem. Kinet. 2007, 39, 307–319. [Google Scholar] [CrossRef]
- Kong, X.; Zhong, W.; Du, W.; Qian, F. Three Stage Equilibrium Model for Coal Gasification in Entrained Flow Gasifiers Based on Aspen Plus. Chin. J. Chem. Eng. 2013, 21, 79–84. [Google Scholar] [CrossRef]
- Biagini, E.; Bardi, A.; Pannocchia, G.; Tognotti, L. Development of an Entrained Flow Gasifier Model for Process Optimization Study. Ind. Eng. Chem. Res. 2009, 48, 9028–9033. [Google Scholar] [CrossRef]
- Chen, C.; Horio, M.; Kojima, T. Numerical simulation of entrained flow coal gasifiers. Part I: Modeling of coal gasification in an entrained flow gasifier. Chem. Eng. Sci. 2000, 55, 3861–3874. [Google Scholar] [CrossRef]
- Eri, Q.; Wu, W.; Zhao, X. Numerical Investigation of the Air-Steam Biomass Gasification Process Based on Thermodynamic Equilibrium Model. Energies 2017, 10, 2163. [Google Scholar] [CrossRef]
- Liu, X.; Wei, J.; Huo, W.; Yu, G. Gasification under CO2–Steam Mixture: Kinetic Model Study Based on Shared Active Sites. Energies 2017, 10, 1890. [Google Scholar] [CrossRef]
- Wen, C.Y.; Chaung, T.Z. Entrainment Coal Gasification Modeling. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 684–695. [Google Scholar] [CrossRef]
- Govind, R.; Shah, J. Modeling and simulation of an entrained flow coal gasifier. AIChE J. 1984, 30, 79–92. [Google Scholar] [CrossRef]
- Robin, A.M. Hydrogen Production from Coal Liquefaction Residues; Final Report; Montebello Research Lab, Texaco, Inc.: Montebello, CA, USA, 1976. [Google Scholar]
- Basu, P. Biomass Gasification and Pyrolysis: Practical Design and Theory; Academic Press: New York, NY, USA, 2010; ISBN 978-0-08-096162-0. [Google Scholar]
- Callaghan, C.A. Kinetics and Catalysis of the Water-Gas-Shift Reaction: A Microkinetic and Graph Theoretic Approach. Ph.D Dissertation, Worcester Polytechnic Institute, Worcester, MA, USA, 2006. [Google Scholar]
- Deng, Z.; Xiao, R.; Jin, B.; Huang, H.; Shen, L.; Song, Q.; Li, Q. Computational Fluid Dynamics Modeling of Coal Gasification in a Pressurized Spout-Fluid Bed. Energy Fuels 2008, 22, 1560–1569. [Google Scholar] [CrossRef]
- Breault, R.W. Gasification Processes Old and New: A Basic Review of the Major Technologies. Energies 2010, 3, 216–240. [Google Scholar] [CrossRef]
- Gazzani, M.; Manzolini, G.; Macchi, E.; Ghoniem, A.F. Reduced order modeling of the Shell–Prenflo entrained flow gasifier. Fuel 2013, 104, 822–837. [Google Scholar] [CrossRef]
- Tremel, A.; Becherer, D.; Fendt, S.; Gaderer, M.; Spliethoff, H. Performance of entrained flow and fluidised bed biomass gasifiers on different scales. Energy Convers. Manag. 2013, 69, 95–106. [Google Scholar] [CrossRef]
- Krishnamoorthy, V.; Pisupati, S.V. A Critical Review of Mineral Matter Related Issues during Gasification of Coal in Fixed, Fluidized, and Entrained Flow Gasifiers. Energies 2015, 8, 10430–10463. [Google Scholar] [CrossRef]
- Richardson, M.J. The specific heats of coals, cokes and their ashes. Fuel 1993, 72, 1047–1053. [Google Scholar] [CrossRef]
- Rezaei, H.R.; Gupta, R.P.; Bryant, G.W.; Hart, J.T.; Liu, G.S.; Bailey, C.W.; Wall, T.F.; Miyamae, S.; Makino, K.; Endo, Y. Thermal conductivity of coal ash and slags and models used. Fuel 2000, 79, 1697–1710. [Google Scholar] [CrossRef]
- Mills, K.C.; Rhine, J.M. The measurement and estimation of the physical properties of slags formed during coal gasification: 1. Properties relevant to fluid flow. Fuel 1989, 68, 193–200. [Google Scholar] [CrossRef]
- Blissett, R.S.; Rowson, N.A. A review of the multi-component utilisation of coal fly ash. Fuel 2012, 97, 1–23. [Google Scholar] [CrossRef]
- Žigo, O.; Adamkovičová, K.; Kosa, L.; Nerád, I.; Proks, I. Determination of the heat of fusion of 2CaOAl2O3 SiO2 (gehlenite). Chem. Pap. 1987, 41, 171–181. [Google Scholar]
- Richet, P.; Fiquet, G. High-Temperature Heat Capacity and Premelting of Minerals in the System MgO-CaO-Al2O3-SiO2. J. Geophys. Res. 1991, 96, 445–456. [Google Scholar] [CrossRef]
- Berman, R.G.; Brown, T.H. Heat capacity of minerals in the system Na2O-K2O-CaO-MgO-FeO-Fe2O3-Al2O3SiO2-TiO2-H2O-CO2: Representation, estimation, and high temperature extrapolation. Contrib. Mineral. Petrol. 1985, 89, 168–183. [Google Scholar] [CrossRef]
| Researcher | Kinetics | Momentum | Energy Balance |
|---|---|---|---|
| Wen et al. | 3 reaction zones | Stokes’ law approximation | Thermal |
| Govind and Shah | 3 reaction zones | Not considered | Thermal |
| Vamvuka et al. | Parameter based on thermogravimetric analysis | Not considered | Thermal |
| Hwang et al. | 2 reaction zones | Stokes’ law approximation | Thermal |
| Reaction Type | Reaction | Description |
|---|---|---|
| Heterogeneous | Coal↔O2 | |
| Coal↔CO2 | ||
| Coal↔H2O | ||
| Coal↔H2 | ||
| Homogeneous | WGS | |
| CO oxidation |
| action Type | Reaction Rate (g/s) | k (g/(m2·atm·s)) | Reference |
| Heterogeneous | [5,6] | ||
| Homogeneous | Equilibrium | Equilibrium Constant | Reference |
| [20] | |||
| Reaction Rate (mole/s) | k (m3/(moles)) | Reference | |
| [21] |
| Operating Variables | This Work | Wen | Govind |
| Coal feed rate (g/s) | 50 | 75 | 77 |
| Steam to coal ratio (-) | 0.24 | 0.24 | 0.241 |
| Oxygen to coal ratio (-) | 0.86 | 0.86 | 0.86 |
| Feed coal temperature (K) | 900 | 900 | 505 |
| Feed gas temperature (K) | 900 | 900 | 697(H2O), 298(O2) |
| Gasifier pressure (MPa) | 2.0 | 2.0 | 2.4 |
| Gasifier wall temperature (K) | Not considered | 2100–600(Z/L) | 2100–600(Z/L) |
| Gasifier Size | This Work | Wen | Govind |
| Gasifier length (cm) | 330 | 330 | 330 |
| Inner diameter (cm) | 152 | 152 | 152 |
| Element | Measurement |
| C | 74.05 |
| H | 6.25 |
| O | 1.32 |
| N | 0.71 |
| S | 1.77 |
| Ash | 15.33 |
| Coal Properties | Assumed |
| Density (g/cm3) | 1.80 |
| Specific heat capacity (cal/(g·K)) | 0.45 |
| Feed Conditions | Set |
| Feed particle size (. ) | 41 |
| Velocity (cm/s) | 50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Oh, H.; Lee, S.; Yoon, Y.-S. Advanced One-Dimensional Entrained-Flow Gasifier Model Considering Melting Phenomenon of Ash. Energies 2018, 11, 1015. https://doi.org/10.3390/en11041015
Kim J, Oh H, Lee S, Yoon Y-S. Advanced One-Dimensional Entrained-Flow Gasifier Model Considering Melting Phenomenon of Ash. Energies. 2018; 11(4):1015. https://doi.org/10.3390/en11041015
Chicago/Turabian StyleKim, Jinsu, Hyunmin Oh, Seokyoung Lee, and Young-Seek Yoon. 2018. "Advanced One-Dimensional Entrained-Flow Gasifier Model Considering Melting Phenomenon of Ash" Energies 11, no. 4: 1015. https://doi.org/10.3390/en11041015
APA StyleKim, J., Oh, H., Lee, S., & Yoon, Y.-S. (2018). Advanced One-Dimensional Entrained-Flow Gasifier Model Considering Melting Phenomenon of Ash. Energies, 11(4), 1015. https://doi.org/10.3390/en11041015




