Load Disaggregation via Pattern Recognition: A Feasibility Study of a Novel Method in Residential Building
Abstract
:1. Introduction
2. Related Works
2.1. Algorithms
2.2. Signatures
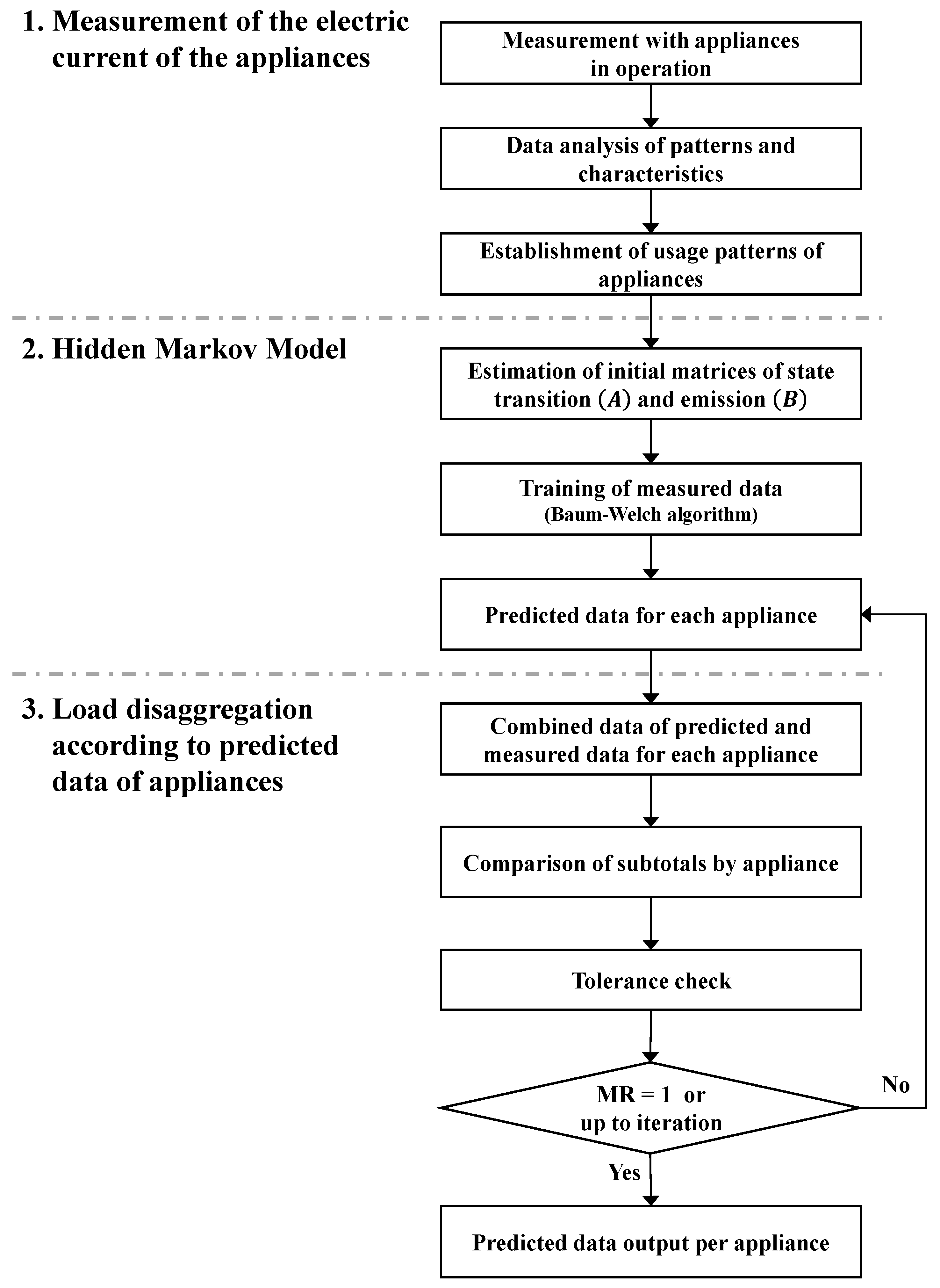
3. Method
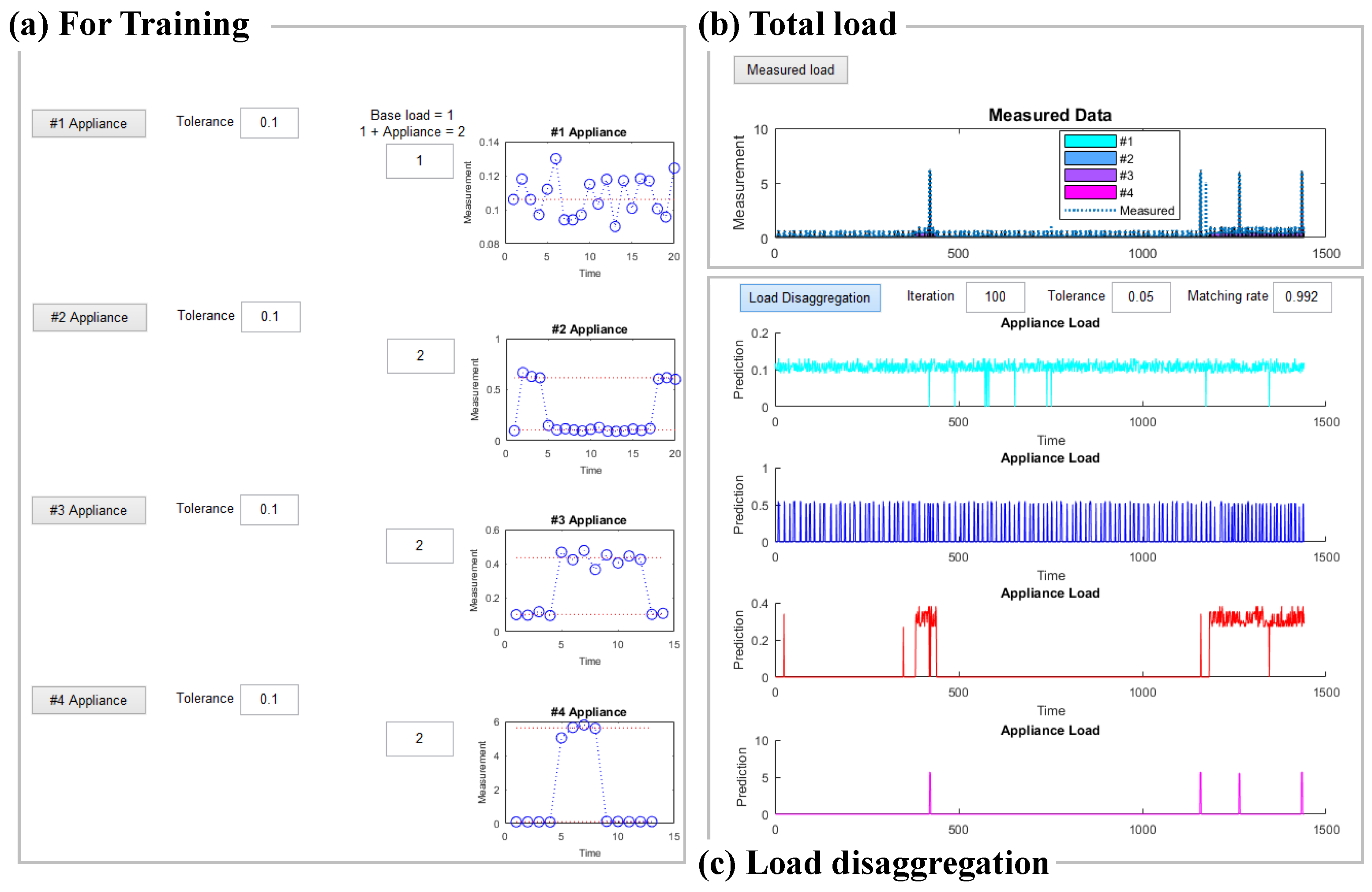
- Data were measured when the appliances were in operation. The electric current of the four types of appliances was measured using a device, and their patterns and characteristics were analyzed, classified, and determined for entry into a HMM.
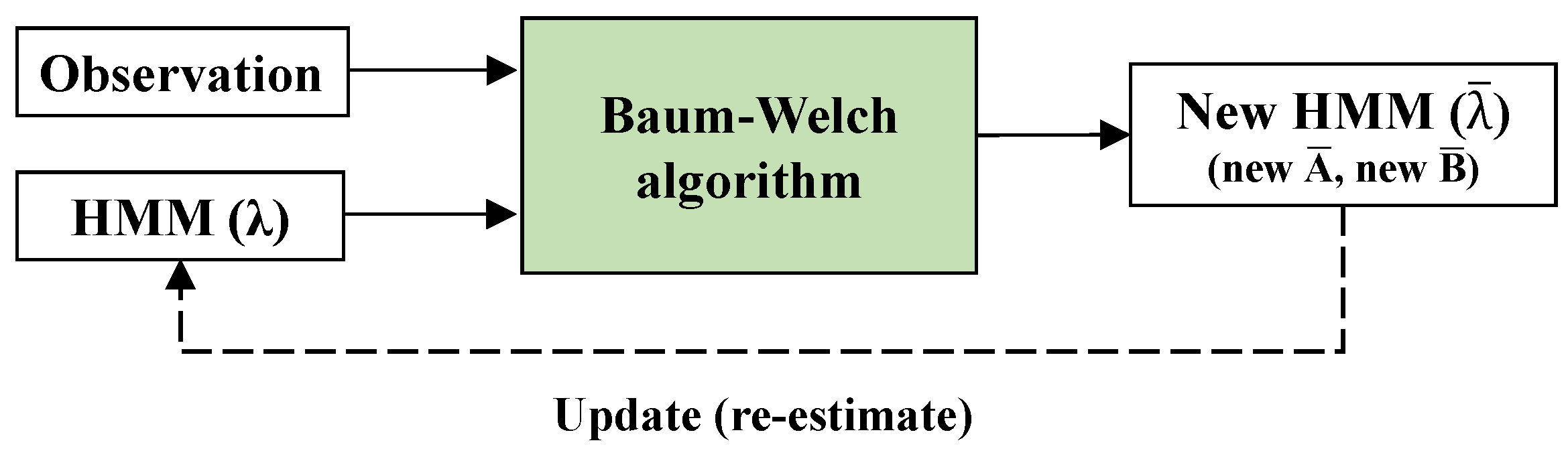
- The determined pattern data for each appliance, which estimated the initial values of matrices of state transition probabilities and emission probabilities , were used as HMM input variables. The HMM was completed by being trained with the Baum–Welch algorithm, and the electric current was predicted in the completed HMM for each appliance.
- All predicted electric current data for each appliance were combined, the sum of which was compared with that of data measured for the appliance used over the course of a day. A matching rate that met the tolerance level of the measured and predicted data was calculated for all times. If the matching rate was less than one, then values within tolerance was used repeatedly for prediction; if the matching rate equaled one or repeated up to the set number of repetitions, then the process was terminated, even if the matching rate was less than one. If the error between the measured and predicted data was within the tolerance, then the load of each appliance in the measured data was considered to have disaggregated, and the predicted data for each appliance were recorded.
3.1. Measurement of Usage Data of Major Appliances
3.1.1. Measuring Equipment
3.1.2. Measurement Plan
3.2. Data Measurement
3.2.1. Measurement Data of Major Appliances for Training
3.2.2. Measurement for Load Disaggregation Verification Data
3.3. Hidden Markov Model (HMM)
3.4. Load Disaggregation by Predicting the Electric Current of Appliances
3.5. Algorithm Platform Development Environment
4. Case Study and Results
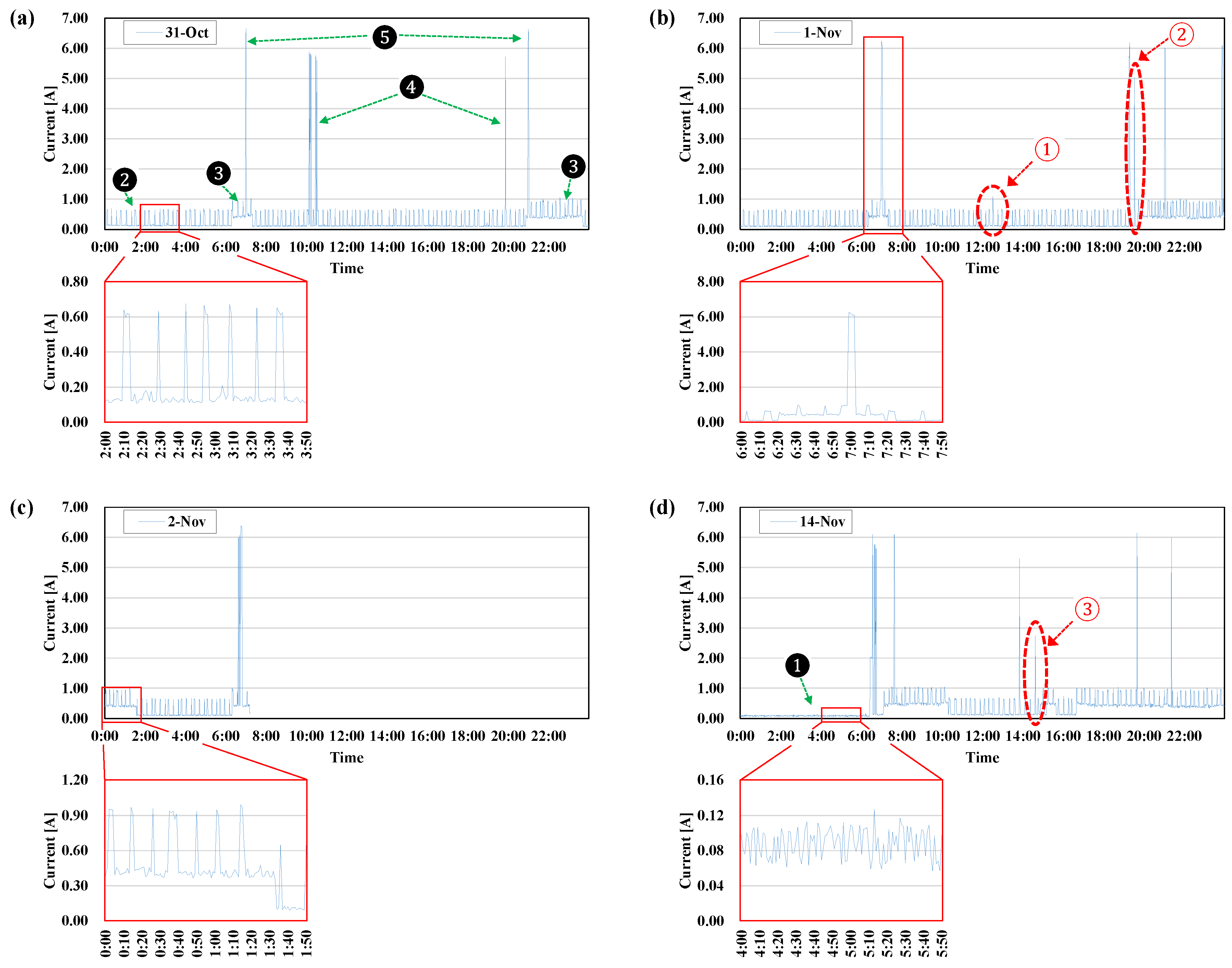
4.1. Case 1: 31 October (0:00–23:59)
4.2. Case 2: 1 November (0:00–23:59)
4.3. Case 3: 2 November (0:00–7:13)
4.4. Case 4: 14 November (0:00–23:59)
4.5. Performance Metrics
5. Discussion
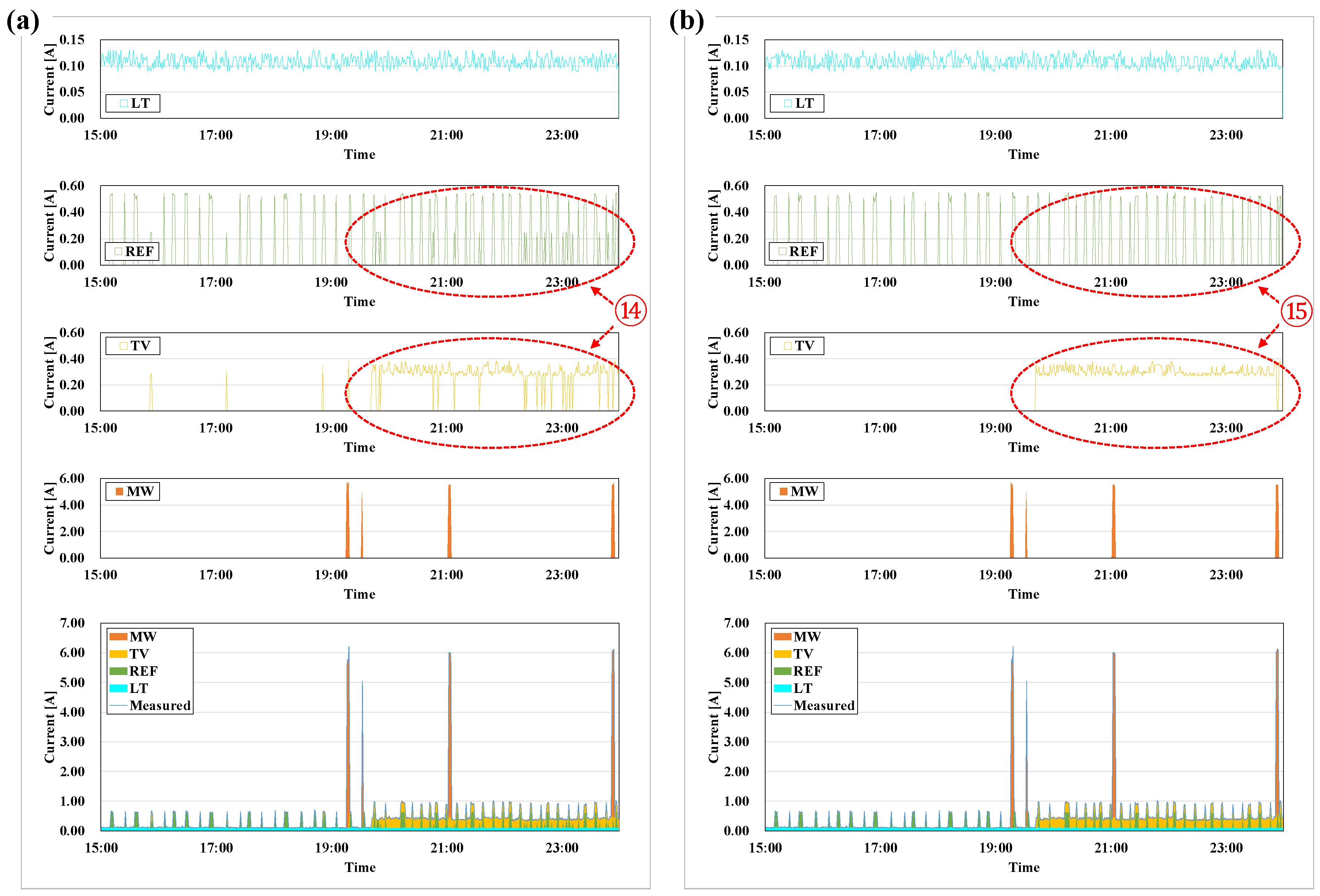
5.1. Conditions of Training Data
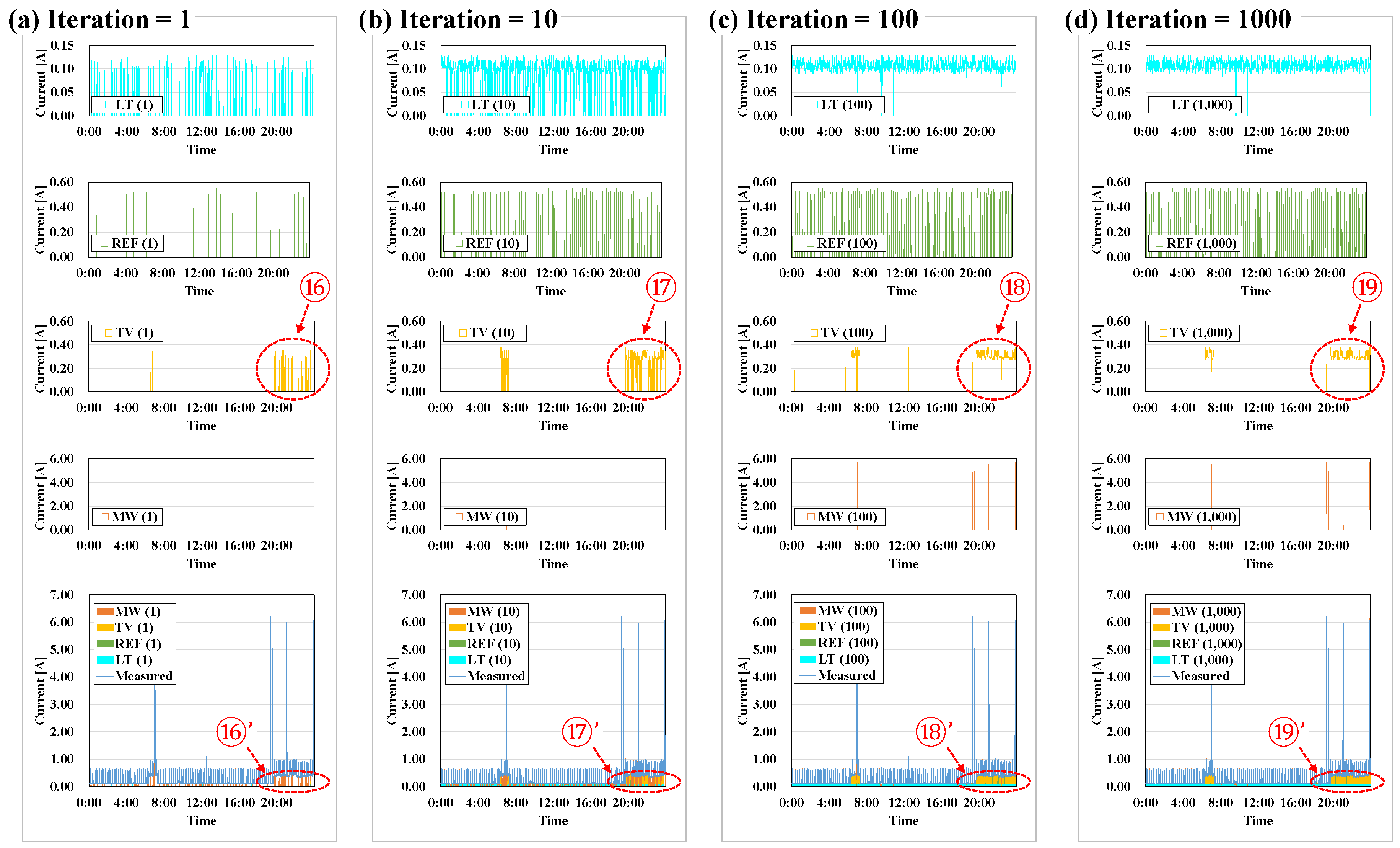
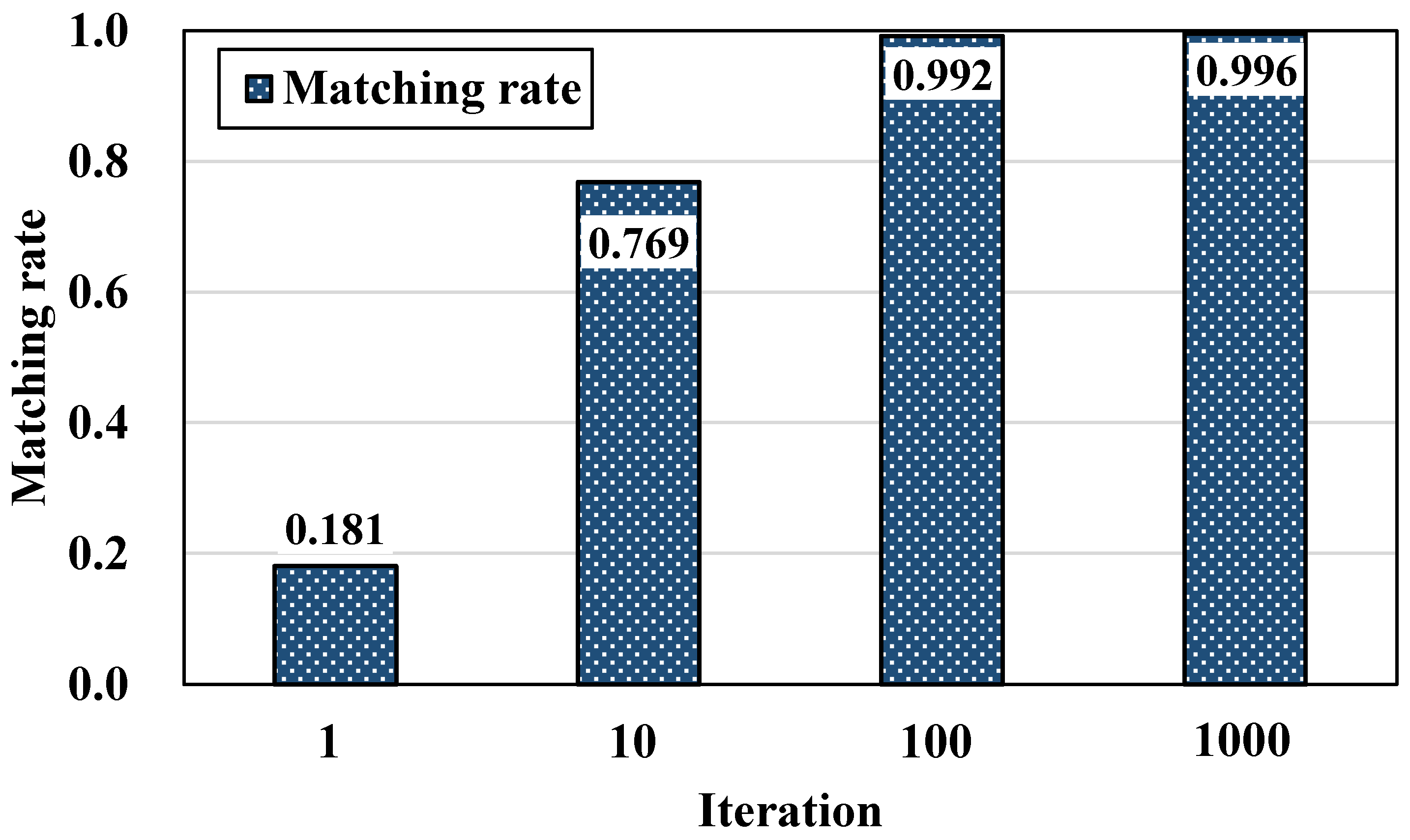
5.2. Iteration
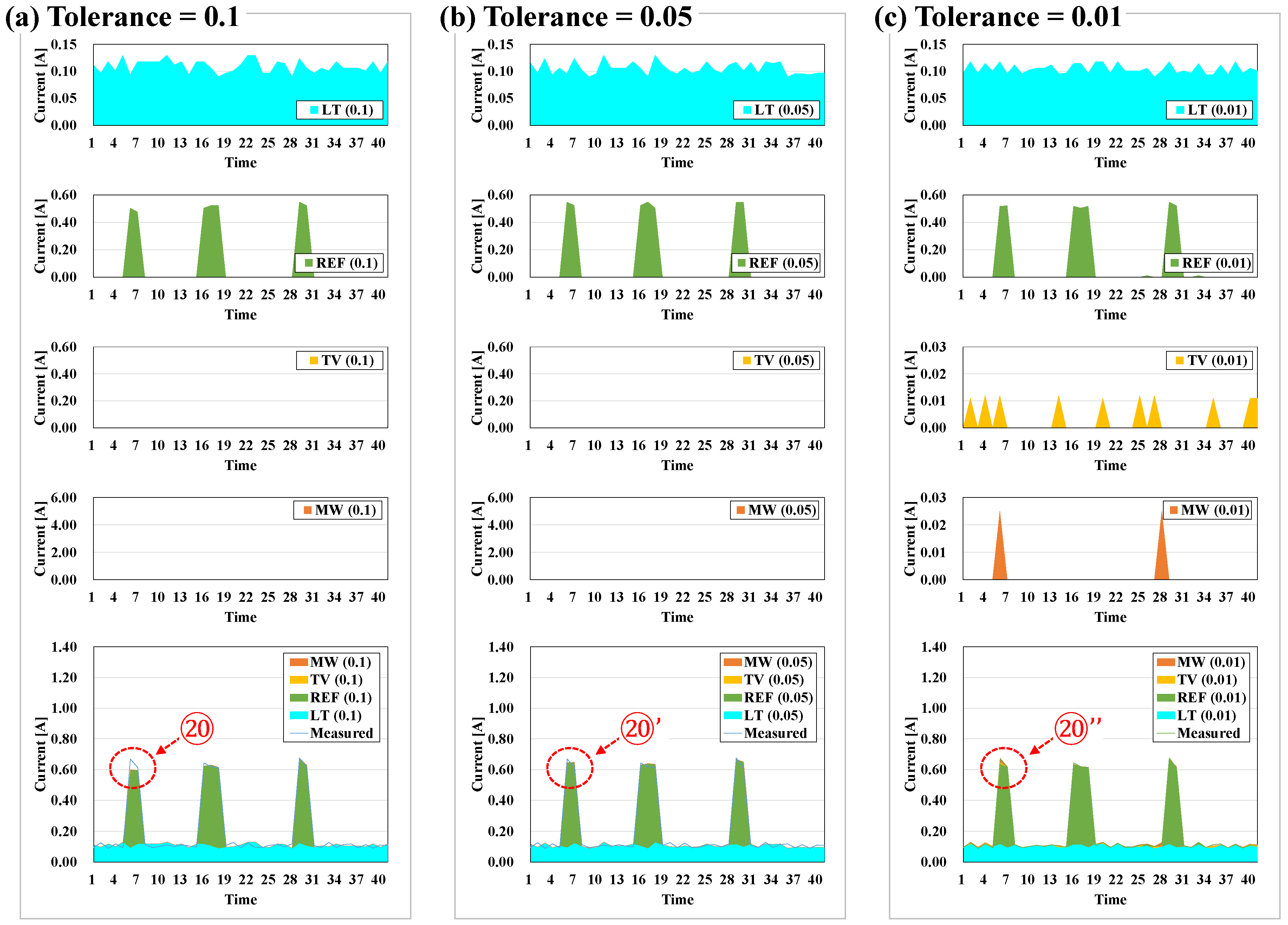
5.3. Tolerance
5.4. Applicability Review
- The current algorithm should measure the training data so that the characteristics of the load are clearly classified. It is necessary to compensate for the data with intermediate values so that the characteristics of the training data can be discriminated by varying the measurement interval.
- The greater the number of iterations, the fewer the errors and the higher the matching rates, but the execution time of the algorithm becomes longer. Therefore, an additional algorithm for determining the optimal number of iterations is necessary.
- The tolerance should be set to fall within the load disaggregation but not be too limited. When disaggregating the load for major appliances other than the ones examined in the study, however, it is necessary to check the scale of the measurement data. Among the appliances examined, all but MW had tolerance of less than 1 A, and tolerance was therefore set at 0.05 A. However, for appliances whose data were measured to be greater than 1 A, tolerance should be greater than the presently set tolerance because a minimal tolerance that remains within the tolerance is pivotal to increasing the performance of load disaggregation.
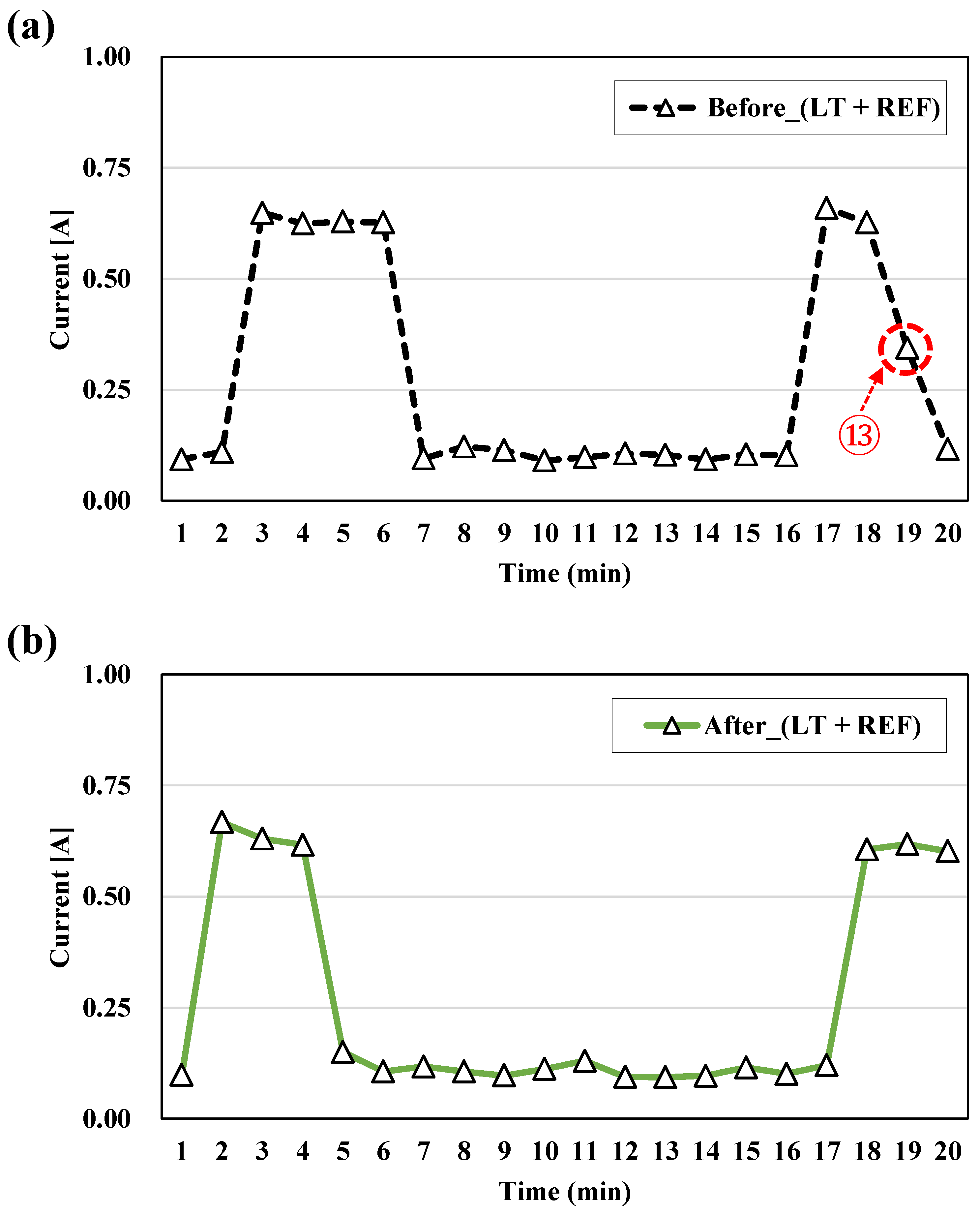
- If untrained patterns or outliers are detected, then response measures require greater flexibility.
5.5. Contribution and Limitation
6. Conclusions
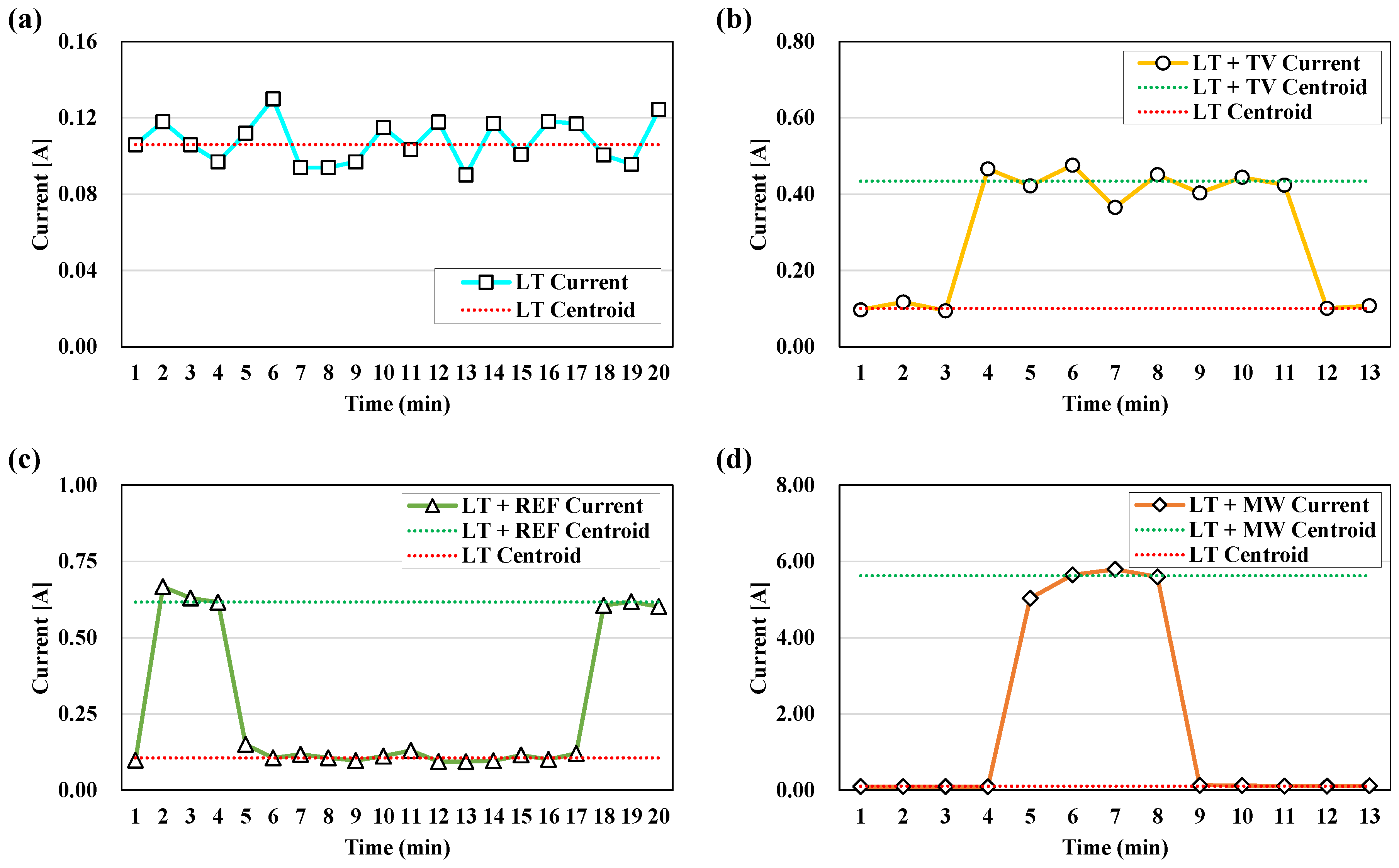
- The electric current of four types of major appliances was measured in a residential building currently inhabited. Data were measured when an appliance was in operation. For LT, the base load or normal operating load of a general residential building was assumed, and measurement was performed for combinations of LT, LT + REF, LT + TV, and LT + MW. Measured data were used as training data of load disaggregation.
- Measured data were updated (i.e., re-estimated) by using the Baum–Welch algorithm, and the current data of the appliances were predicted using the HMM. Errors in predicted and measured data were checked for whether they fell within the tolerance. That process was repeated to obtain predicted data whose values were approximate to those of the measured data.
- The results were examined and reviewed for 4 days: 31 October and 1, 2, and 14 November. Respective matching rates of 0.994, 0.992, 0.982, and 0.988 were achieved.
- The applicability of the load disaggregation method developed in the study was examined, and results revealed that additional research is needed to improve the measurement method for training data, to add an algorithm to determine optimal iteration, and to determine a tolerance. Flexible measures should also be secured in the case that unexplored patterns or outliers are detected.
Acknowledgments
Author Contributions
Conflicts of Interest
Acronyms and Abbreviations
| DTW | Dynamic time warping |
| FHMM | Factorial Hidden Markov Model |
| FN | False negative |
| FP | False positive |
| GP | Generic programming |
| GUI | Graphic user interface |
| HMM | Hidden Markov Model |
| K-NN | K-nearest neighbors |
| k-NNR | k-nearest neighbors rule |
| LT | Laptop |
| MR | Matching rate |
| MW | Microwave |
| NILM | Non-intrusive load monitoring |
| NN | Neural network |
| REDD | Reference energy disaggregation dataset |
| REF | Refrigerator |
| SVM | Support vector machine |
| TC | Temporal correlation |
| TP | True positive |
| TV | Television |
| TN | True negative |
| WLS | Weighted least squares |
References
- Ministry of Land, Infrastructure, and Transport. Building Statistics Book; Ministry of Land, Infrastructure, and Transport: Sejong, Korea, 2016. [Google Scholar]
- Farinaccio, L.; Zmeureanu, R. Using a pattern recognition approach to disaggregate the total electricity consumption in a house into the major end-uses. Energy Build. 1999, 30, 245–259. [Google Scholar] [CrossRef]
- De Baets, L.; Ruyssinck, J.; Develder, C.; Dhaene, T.; Deschrijver, D. On the Bayesian optimization and robustness of event detection methods in NILM. Energy Build. 2017, 145, 57–66. [Google Scholar] [CrossRef]
- Marceau, M.L.; Zmeureanu, R. Nonintrusive load disaggregation computer program to estimate the energy consumption of major end uses in residential buildings. Energy Convers. Manag. 2000, 41, 1389–1403. [Google Scholar] [CrossRef]
- Ehrhardt-Martinez, K.; Donnelly, K.A.; John, A. Advanced Metering Initiatives and Residential Feedback Programs: A Meta-Review for Household Electricity-Saving Opportunities; American Council for an Energy-Efficient Economy: Washington, DC, USA, 2010. [Google Scholar]
- Lin, S.; Zhao, L.; Li, F.; Liu, Q.; Li, D.; Fu, Y. A noninstrusive load identification method for residential applications based on quadratic programming. Electr. Power Syst. Res. 2016, 133, 241–248. [Google Scholar] [CrossRef]
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Chang, H.-H. Non-intrusive demand monitoring and load identification for energy management systems based on transient feature analyses. Energies 2012, 5, 4569–4589. [Google Scholar] [CrossRef]
- Bouhouras, A.S.; Gkidatzis, P.A.; Chatzisavvas, K.C.; Panagiotou, E.; Poulakis, N.; Christoforidis, G.C. Load signature formulation for non-intrusive load monitoring based on current measurements. Energies 2017, 10, 538. [Google Scholar] [CrossRef]
- Aiad, M.; Lee, P.H. Unsupervised approach for load disaggregation with devices interactions. Energy Build. 2016, 116, 96–113. [Google Scholar] [CrossRef]
- Parson, O.; Ghosh, S.; Weal, M.; Rogers, A. An unsupervised training method for non-intrusive appliance load monitoring. Artif. Intell. 2014, 217, 1–19. [Google Scholar] [CrossRef]
- Zeifman, M.; Roth, K. Nonintrusive appliance load monitoring: Review and outlook. IEEE Trans. Consum. Electron. 2011, 57, 76–84. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Agbossou, K.; Kelouwani, S.; Cardenasa, A. Non-intrusive load monitoring through home energy management systems: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 1266–1274. [Google Scholar] [CrossRef]
- Kamilaris, A.; Kalluri, B.; Kondepudi, S.; Wai, T.K. A literature survey on measuring energy usage for miscellaneous electric loads in offices and commercial buildings. Renew. Sustain. Energy Rev. 2014, 34, 536–550. [Google Scholar] [CrossRef]
- Zoha, A.; Gluhak, A.; Imran, M.A.; Rajasegarar, S. Non-Intrusive Load Monitoring Approaches for Disaggregated Energy Sensing: A Survey. Sensors 2012, 12, 16838–16866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abubakar, I.; Khalid, S.N.; Mustafa, M.W.; Shareef, H.; Mustapha, M. Application of load monitoring in appliances’ energy management—A review. Renew. Sustain. Energy Rev. 2017, 67, 235–245. [Google Scholar] [CrossRef]
- Basu, K.; Debusschere, V.; Ahlame Douzal-Chouakria, A.; Bacha, S. Time series distance-based methods for non-intrusive load monitoring in residential buildings. Energy Build. 2015, 96, 109–117. [Google Scholar] [CrossRef]
- Liu, B.; Luan, W.; Yu, X. Dynamic time warping based non-intrusive load transient identification. Appl. Energy 2017, 195, 634–645. [Google Scholar] [CrossRef]
- Aiad, M.; Lee, P.H. Non-intrusive load disaggregation with adaptive estimations of devices main power effects and two-way interactions. Energy Build. 2016, 130, 131–139. [Google Scholar] [CrossRef]
- Zoha, A.; Gluhak, A.; Nati, M.; Imran, M.A. Low-power appliance monitoring using Factorial Hidden Markov Models. In Proceedings of the 2013 IEEE Eighth International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, VIC, Australia, 2–5 April 2013; pp. 527–532. [Google Scholar]
- Parson, O.; Ghosh, S.; Weal, M.; Rogers, A. Using Hidden Markov Models for Iterative Non-Intrusive Appliance Monitoring. Available online: http://nips.cc/Conferences/2011 (accessed on 18 April 2018).
- Figueiredo, M.; de Almeida, A.; Ribeiro, B. Home electrical signal disaggregation for non-intrusive load monitoring (NILM) systems. Neurocomputing 2012, 96, 66–73. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.G.; Farhangi, H.; Palizban, A. Data mining of smart meters for load category based disaggregation of residential power consumption. Sustain. Energy Grids Netw. 2017, 10, 92–103. [Google Scholar] [CrossRef]
- Basu, K.; Debusschere, V.; Bacha, S.; Hably, A.; Delft, D.V.; Dirven, G.J. A generic data driven approach for low sampling load disaggregation. Sustain. Energy Grids Netw. 2017, 9, 118–127. [Google Scholar] [CrossRef]
- Bonfigli, R.; Principi, E.; Fagiani, M.; Severini, M.; Squartini, S.; Piazza, F. Non-intrusive load monitoring by using active and reactive power in additive Factorial Hidden Markov Models. Appl. Energy 2017, 208, 1590–1607. [Google Scholar] [CrossRef]
- Korea Institute of Civil Engineering and Building Technology. Development of the Building Energy Analysis Algorithm Using Measured Data; Korea Institute of Civil Engineering and Building Technology: Goyang, Korea, 2017. (In Korean) [Google Scholar]
- ROOTECT. ACCURA 2300/2350 Distribution Panel Digital Power Mater/Power Measuring Module. (In Korean). Available online: www.rootech.com (accessed on 18 April 2018).
- Rabiner, L.R.; Juang, B.H. An Introduction to Hidden Markov Models. Available online: https://ieeexplore.ieee.org/document/1165342/ (accessed on 18 April 2018).
- Tang, G.; Ling, Z.; Li, F.; Tang, D.; Tang, J. Occupancy-aided energy disaggregation. Comput. Netw. 2017, 117, 42–51. [Google Scholar] [CrossRef]
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A.E. A Hybrid Signature-based Iterative Disaggregation algorithm for Non-Intrusive Load Monitoring. Appl. Energy 2017, 185, 331–344. [Google Scholar] [CrossRef]
- Liang, J.; Ng, S.K.; Kendall, G.; Cheng, J.W. Load signature study—Part II: Disaggregation framework, simulation, and applications. IEEE Trans Power Deliv. 2010, 25, 561–569. [Google Scholar] [CrossRef]



| Algorithms | Authors | Accuracy (%) | Average Accuracy (%) |
|---|---|---|---|
| Bayesian | Zoha et al. [15] * | 80–99 | 89.5 |
| DTW (KNN) | Basu et al. [17] | 84.8 | 87.7 |
| Liu et al. [18] | 90.5 | ||
| Euclidean (KNN) | Basu et al. [17] | 83.5 | 83.5 |
| FHMM | Abubakar et al. [16] * | 1% error | 84.2 |
| Aiad and Lee [19] | 68.5 | ||
| Zoha et al. [20] | 85.0 | ||
| HMM | Zoha et al. [15] * | 75–95 | 81.1 |
| Basu et al. [17] | 75.3 | ||
| Parson et al. [21] | 83.0 | ||
| Hybrid SVM/GMM | Abubakar et al. [16] * | more than 90 | 90.0 |
| K-NN | Zoha et al. [15] * | 70–90 | 80.0 |
| k-NNR & ANN | Abubakar et al. [16] * | more than 95 | 95.0 |
| NN | Zoha et al. [15] * | 80–97 | 91.6 |
| Abubakar et al. [16] * | 94.6 | ||
| NN & GP | Abubakar et al. [16] * | 100 | 100.0 |
| Optimization | Zoha et al. [15] * | 60–97 | 78.5 |
| SVM | Zoha et al. [15] * | 75–98 | 84.0 |
| Figueiredo et al. [22] | 81.5 | ||
| TC (KNN) | Basu et al. [17] | 69.5 | 69.5 |
| WLS | Zhang et al. [23] | over 80 | 80.0 |
| Signatures | Average Accuracy (%) |
|---|---|
| Current (I) | 93.0 |
| Harmonic (H) | 92.2 |
| Real and reactive power (PQ) | 95.5 |
| Geometrical properties of the V-I curve (V-I) | 92.4 |
| Instantaneous power (p) | 91.3 |
| Division | Specification |
|---|---|
| Device name | Accura2350-1P-30A-35 |
| Measurement | RMS Current [A] |
| Resolution | |
| Sampling rate | 1 min |
| Usage Pattern Numbers | Usage Patterns of Appliances |
|---|---|
| ❶ | LT |
| ❷ | LT + REF |
| ❸ | LT + REF + TV |
| ❹ | LT + REF + MW |
| ❺ | LT + REF + TV + MW |
| Date | Accuracy | Precision | Recall | F-Measure | Matching Rate |
|---|---|---|---|---|---|
| 31 October | 0.994 | 1.000 | 0.994 | 0.997 | 0.994 |
| 1 November | 0.992 | 1.000 | 0.992 | 0.996 | 0.992 |
| 2 November | 0.982 | 1.000 | 0.982 | 0.991 | 0.982 |
| 14 November | 0.988 | 1.000 | 0.988 | 0.994 | 0.988 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, Y.; Hwang, J.; Lee, T. Load Disaggregation via Pattern Recognition: A Feasibility Study of a Novel Method in Residential Building. Energies 2018, 11, 1008. https://doi.org/10.3390/en11041008
Kwak Y, Hwang J, Lee T. Load Disaggregation via Pattern Recognition: A Feasibility Study of a Novel Method in Residential Building. Energies. 2018; 11(4):1008. https://doi.org/10.3390/en11041008
Chicago/Turabian StyleKwak, Younghoon, Jihyun Hwang, and Taewon Lee. 2018. "Load Disaggregation via Pattern Recognition: A Feasibility Study of a Novel Method in Residential Building" Energies 11, no. 4: 1008. https://doi.org/10.3390/en11041008
APA StyleKwak, Y., Hwang, J., & Lee, T. (2018). Load Disaggregation via Pattern Recognition: A Feasibility Study of a Novel Method in Residential Building. Energies, 11(4), 1008. https://doi.org/10.3390/en11041008




