A Domestic Microgrid with Optimized Home Energy Management System
Abstract
:1. Introduction
- We proposed three hybrid schemes: WDGA, WDGWO and WBPSO.
- This work considered the grid-connected microgrid system with multiple appliances.
- Our proposed work minimized the electricity cost and PAR.
- By implementing our proposed schemes, user can enjoy maximum comfort.
- Imported electricity was also reduced by integrating microgrid.
2. Literature Review
3. Motivation and Problem Description
4. Formulation of the Problem Statement
4.1. PV Generation
4.2. Wind Generation
4.3. BBS
4.4. Energy Consumption
4.5. Energy Pricing and Electricity Cost
4.6. PAR
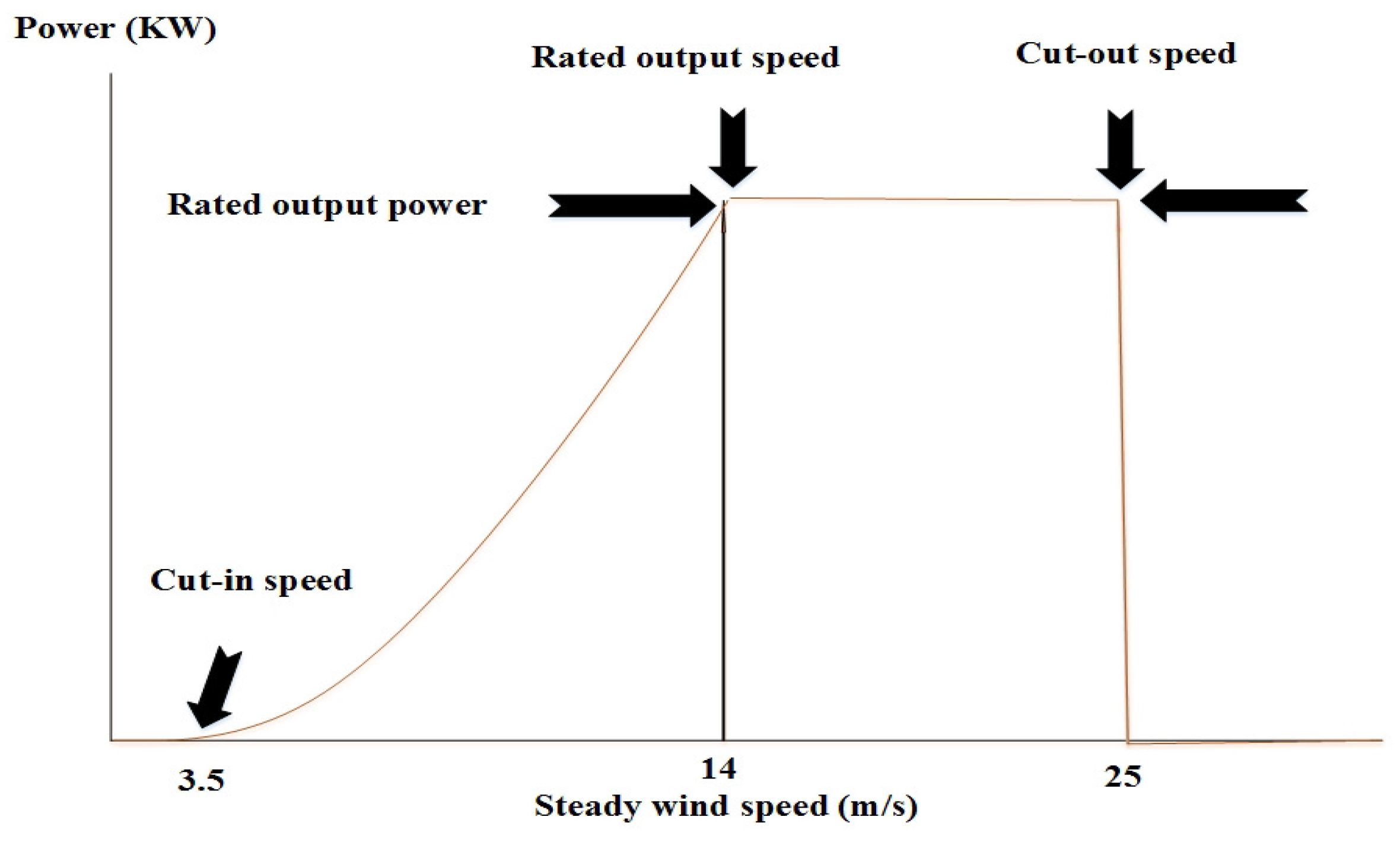
4.7. AWT
4.8. Objective Function
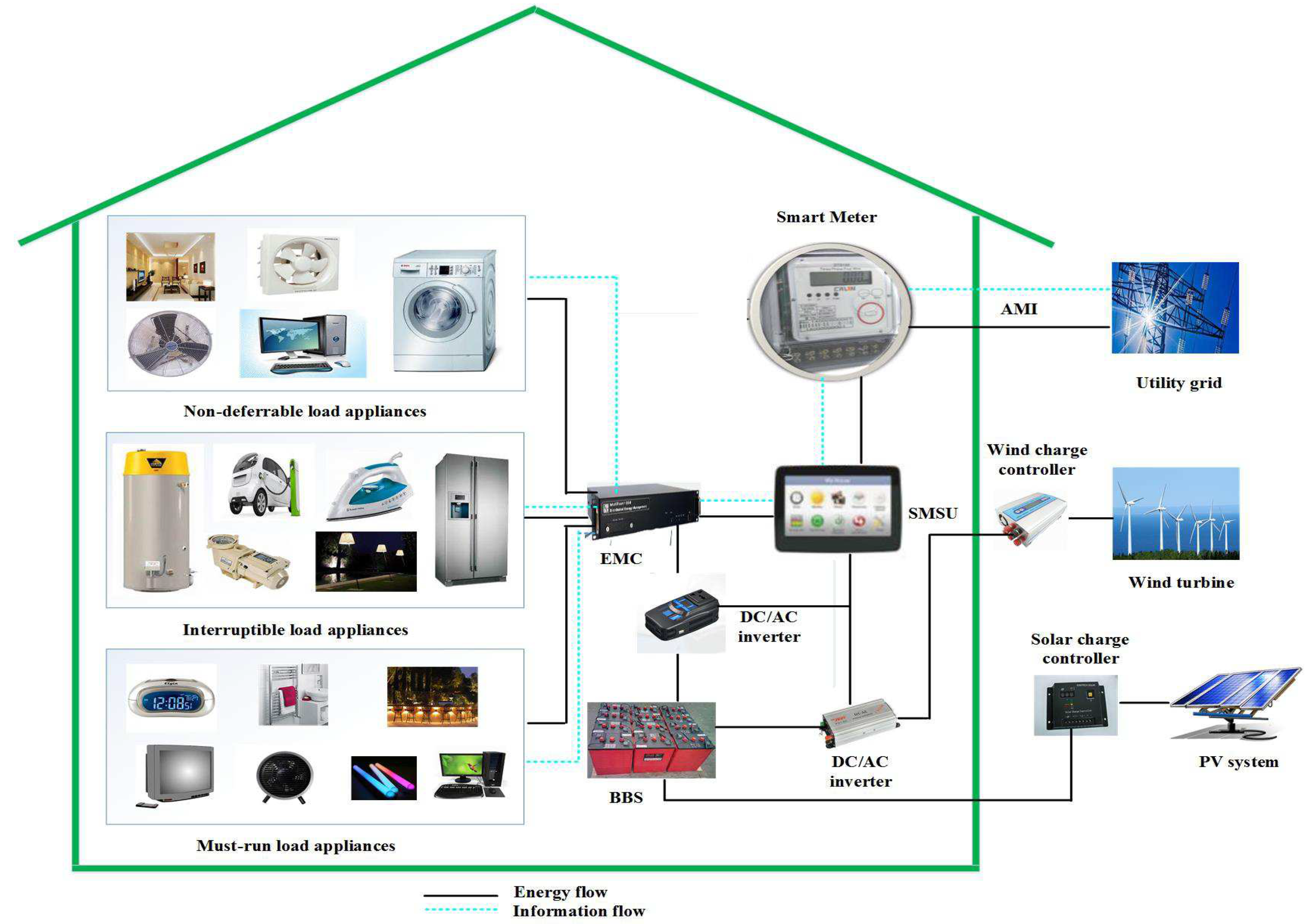
5. System Model
6. Optimization Techniques
6.1. GWO
6.2. GA
6.3. BPSO
6.4. WDO
6.5. WDGA
6.6. WDGWO
6.7. WBPSO
| Algorithm 1 WDGA | |
| Input: set of appliances or population; | |
| Initialization genetic parameters: peak hour, off peak hour, t = 0, H, vmax, vmin, no of iteration; Initialization wind driven parameters: dimMin, dimMax, dim, param.rt, param.g, param.alp, param.c; | |
| 1: | fordo |
| 2: | for do |
| 3: | Generate population randomly; |
| 4: | for do |
| 5: | Fitness calculation; Select best population, pop save in pop1; Status check of appliance using peak hour and off peak hour; |
| 6: | if t == peak hour then |
| 7: | Shift on RESs and BBS; |
| 8: | OR wait for off peak hour; |
| 9: | if Consumption == high then |
| 10: | Check remaining t of all App and check LOT until it is 0; |
| 11: | end if |
| 12: | end if |
| 13: | end for |
| 14: | Generate new population; |
| 15: | Replace the genetic operators by particles pressure; |
| 16: | Evaluate and find air parcels (population) pressure; |
| 17: | for do |
| 18: | for do |
| 19: | x(K,h) = (dimMax - dimMin) * ((x(K,h)+1)./2) + dimMin; |
| 20: | Pres(K,h) = sum ; |
| 21: | end for |
| 22: | end for |
| 23: | Save air parcels value in pop2; |
| 24: | Check and find air parcels velocity; |
| 25: | Vel = min(vel, maxV); and vel = max(vel, -maxV); |
| 26: | Find and update air parcel positions; |
| 27: | x = x + vel; and x = min(x, 1.0); and x = max (x, -1.0); |
| 28: | Finding best particle in population |
| 29: | Globalpres, indx = min (pres); and globalx = x (indx, :); |
| 30: | Find min location for this iteration |
| 31: | Minpres, indx = min (pres); and minpos = x (indx, :); |
| 32: | Rank the air parcels: sortedpres rankind = sort (pres); |
| 33: | Sort the air parcels position, velocity and pressure: |
| 34: | Pres = sortedpres; |
| 35: | Updating the global best: |
| 36: | Better = minpres < globalpres; |
| 37: | if Solution = better then |
| 38: | Globalpres = minpres; |
| 39: | Globalpos = minpos; |
| 40: | end if |
| 41: | Save the velocity and position value in pop3; |
| 42: | Select from pop2 and pop3; |
| 43: | New velocity and position of air parcels; |
| 44: | if Solution == infeasible then |
| 45: | Update solution; |
| 46: | Update with sol in pop2 and pop3; |
| 47: | end if |
| 48: | Update pop best solution; |
| 49: | Update t = t+1 till 24 h; |
| 50: | Terminate when t = 24 h or iter = Max; |
| 51: | end for |
| 52: | end for |
| Algorithm 2 WDGWO | |
| Input: set of appliances or population; | |
| Initialization grey wolf parameters: Max iter, Np, D, alpha, beta, delta, search agents; | |
| Initialization wind driven parameters: dimMin, dimMax, dim, param.rt, param.g, param.alp, param.c; | |
| 1: | Randomly initialize the position of search agents i.e., positions = rand (Np, D); |
| 2: | Evaluate the position of search agents |
| 3: | whiledo |
| 4: | for do |
| 5: | Calculate objective function for each search agent Fitness = sum (electricity cost * positionsx); Update alpha, beta and delta |
| 6: | if then |
| 7: | |
| 8: | |
| 9: | end if |
| 10: | if then |
| 11: | |
| 12: | |
| 13: | end if |
| 14: | if then |
| 15: | |
| 16: | |
| 17: | end if |
| 18: | end for |
| 19: | ; a value linearly from 2 to 0 |
| 20: | for do |
| 21: | for do |
| 22: | r1, r2 randomly initialize the value between 0 to 1 |
| 23: | Vel = maxV * 2 * (rand (Np, D)-0.5) |
| 24: | for do |
| 25: | for do |
| 26: | Velot (i, j) = vel (i, j); |
| 27: | Vel (i, j) = ( 1 - alp ) * vel (i, j) - ( g * positions (i, j)) + abs (1 - 1/i) * (((positions (i, j) - positions (i, j))).* RT ) + ( c * velot (i, j) / i) |
| 28: | if ((vel (i, j) < vmax) and (vel (i, j) > vmin)) then |
| 29: | Velot (i, j) = vel (i, j); |
| 30: | else if ( vel (i, j) < vmin ) then |
| 31: | Vel (i, j) = vmin |
| 32: | else if (vel (i, j) > vmax) then |
| 33: | Vel (i, j) = vmax; |
| 34: | end if |
| 35: | Position updating |
| 36: | Sig (i, j) = 1/(1+exp (-vel (i, j))); |
| 37: | if rand (1) < sig (i, j) then |
| 38: | Positions (i, j) = 1; |
| 39: | else |
| 40: | Positions (i, j) = 0; |
| 41: | end if |
| 42: | end for |
| 43: | end for |
| 44: | end for |
| 45: | end for |
| 46: | end while |
| Algorithm 3 WBPSO | |
| Require: Number of particles, swarm size, , electricity price, LOT and appliance power consumption rating | |
| Require: vmax, vmin, no of iter, c1, c2, param.RT, param.g, param.alp, param.c, dimMin, dimMax, dim | |
| 1: | Randomly generate the particles’ positions and velocities |
| 2: | |
| 3: | fortodo |
| 4: | Initialize (swarmsize, tbits) |
| 5: | |
| 6: | |
| 7: | |
| 8: | end for |
| 9: | for h = 1 to 24 do |
| 10: | Validate constraints |
| 11: | for to M do |
| 12: | if then |
| 13: | |
| 14: | end if |
| 15: | if then |
| 16: | |
| 17: | else |
| 18: | |
| 19: | end if |
| 20: | Decrement one from the TOT of the working appliance |
| 21: | if > then |
| 22: | if then |
| 23: | Switch the load to RESs and BBS |
| 24: | else |
| 25: | Consume the grid energy |
| 26: | end if |
| 27: | end if |
| 28: | Return |
| 29: | Vel = maxV * 2 * (rand (swarm, n)-0.5); |
| 30: | for i = 1 : swarm do |
| 31: | for j = 1 : n do |
| 32: | Velot (i, j) = vel (i, j); |
| 33: | Vel (i, j) = ( 1 - param.alp ) * vel (i, j) - ( param.g * pres (i, j)) + abs (1 - 1/i) * (((pres (i, j) - pres (i, j))).*param.RT) + (param.c * velot (i, j) /i); |
| 34: | if ((vel (i, j) < = vmax) and (vel (i, j) >= vmin)) then |
| 35: | vel (i, j) = vel (i, j); |
| 36: | elseif ( vel (i, j) < vmin); vel (i, j) = vmin; elseif ( vel (i, j) > vmax); vel (i, j) = vmax; |
| 37: | end if |
| 38: | Sig (i, j) = 1 / ( 1 + exp ( -vel (i, j))); |
| 39: | if rand (1) < sig (i, j) then |
| 40: | x (i, j) = 1; |
| 41: | else |
| 42: | x (i, j) = 0; |
| 43: | end if |
| 44: | end for |
| 45: | end for |
| 46: | Check velocity: vel = min (vel, maxV); vel = max (vel, -maxV); |
| 47: | Update air parcel positions: x = x + vel; x = min (x, 1.0); x = max (x, -1.0); |
| 48: | Evaluate population: (pressure) |
| 49: | Finding best particle in population |
| 50: | Globalpres, indx = min (pres); globalx = x (indx, :); |
| 51: | Min location for this iteration |
| 52: | Minpres, indx = min (pres); minpos = x (indx, :); |
| 53: | Rank the air parcels; |
| 54: | Sorted-pres rank-ind = sort (pres); |
| 55: | Sort the air parcels position, velocity and pressure; |
| 56: | Pres = sorted-pres; |
| 57: | Updating the global best; |
| 58: | Better = minpres < globalpres; |
| 59: | if Better then |
| 60: | Globalpres = minpres; globalpos = minpos; |
| 61: | end if |
| 62: | end for |
| 63: | end for |
7. Simulation Results and Discussion
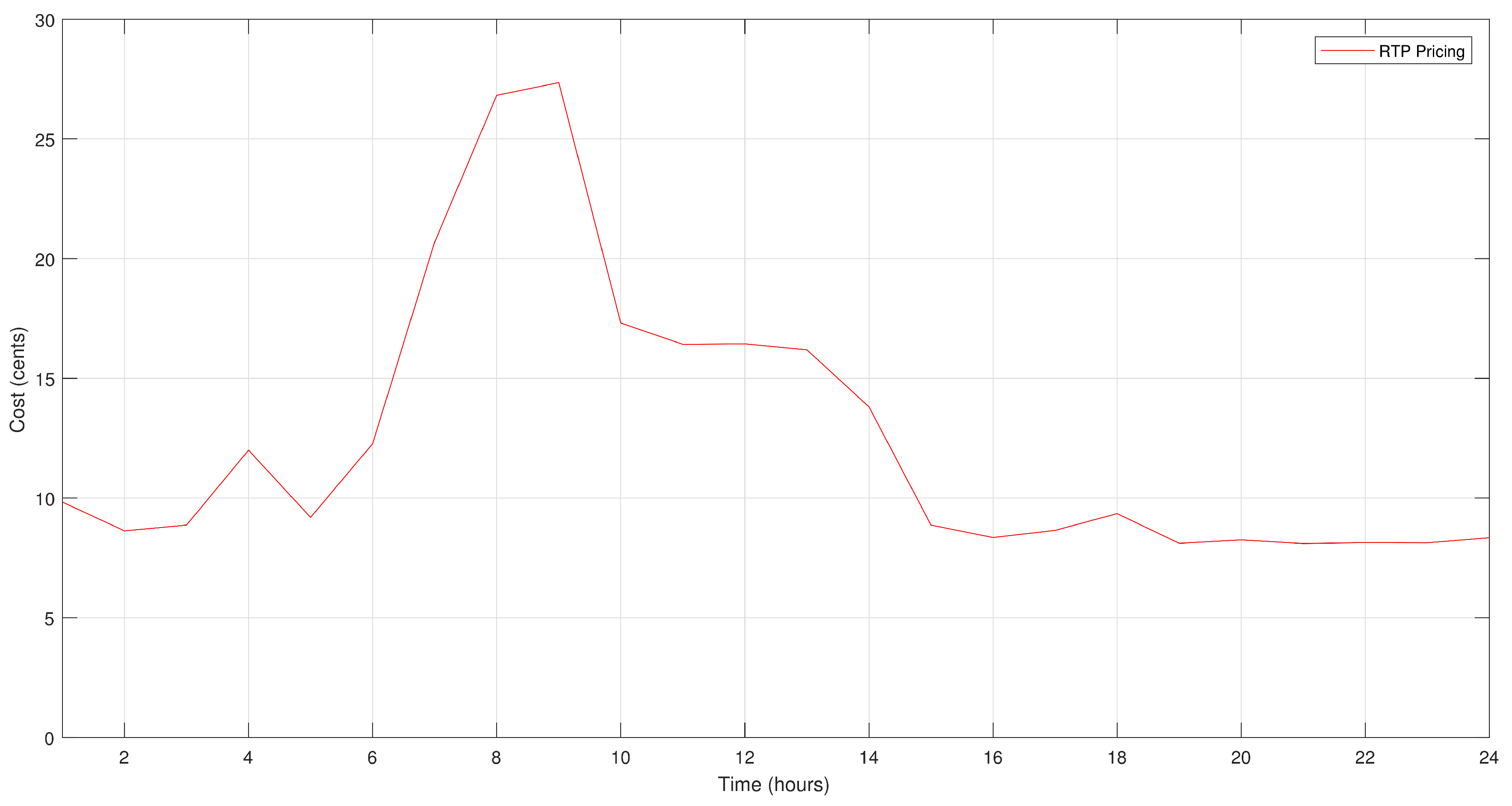
7.1. RTP Scheme
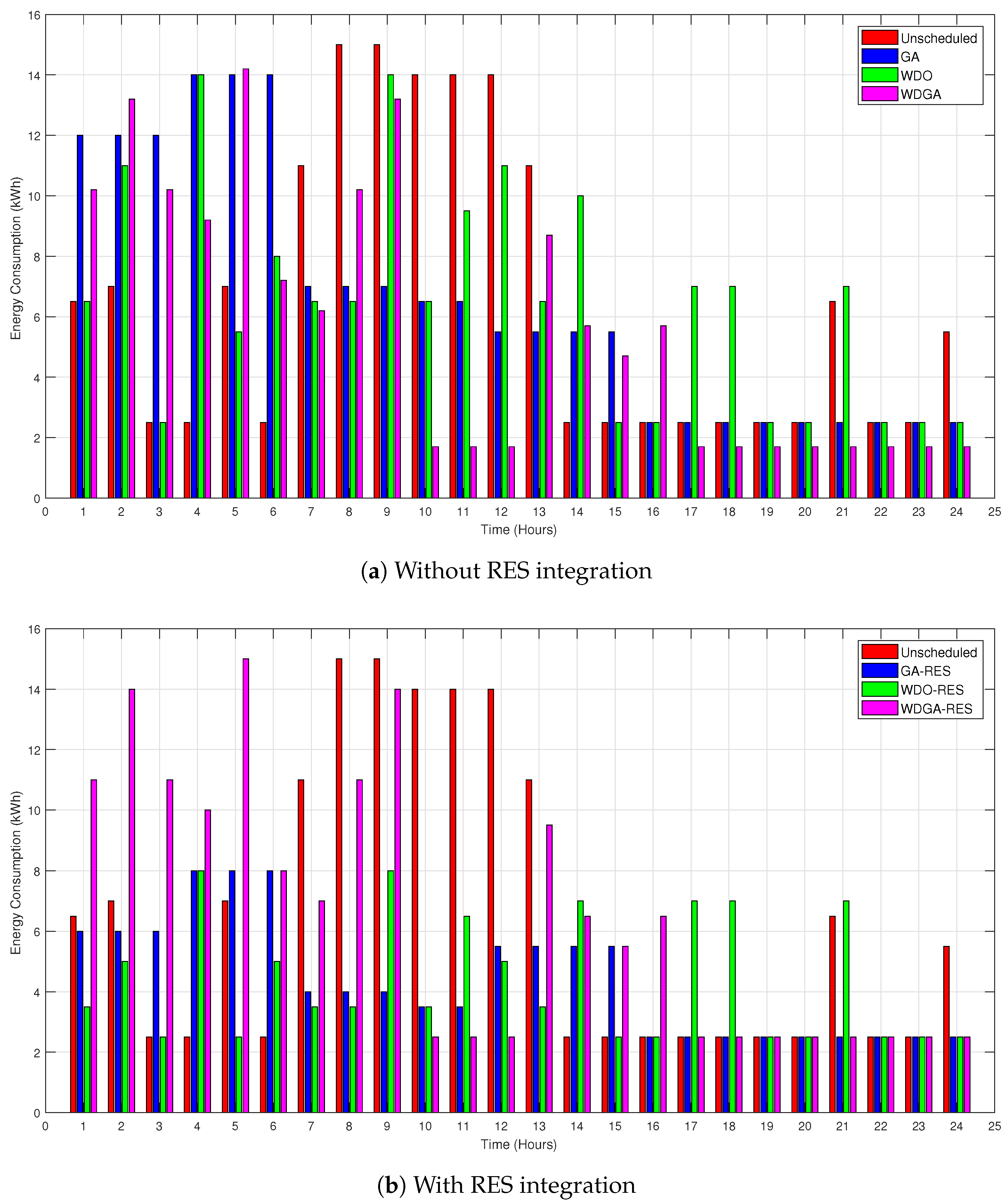
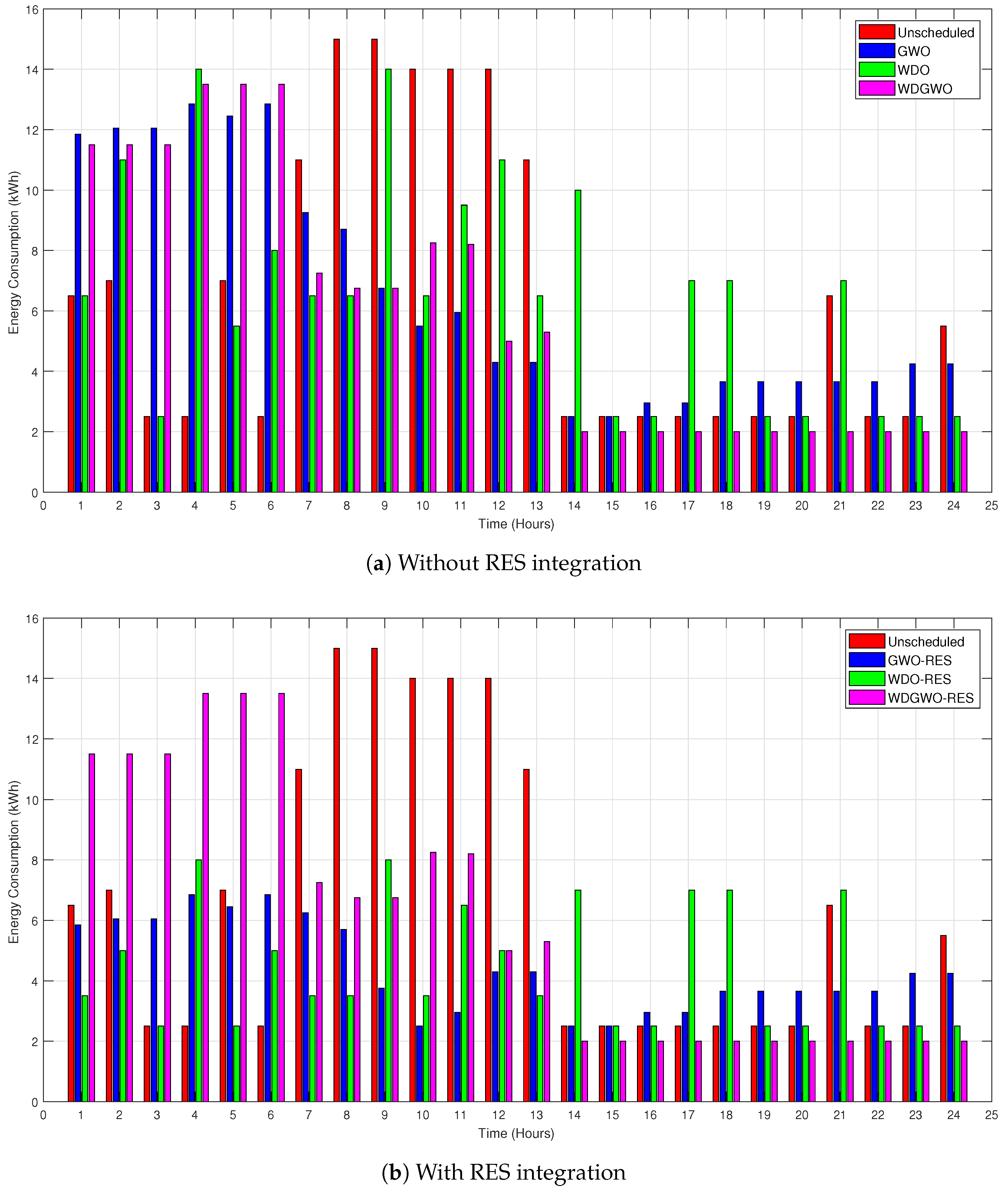
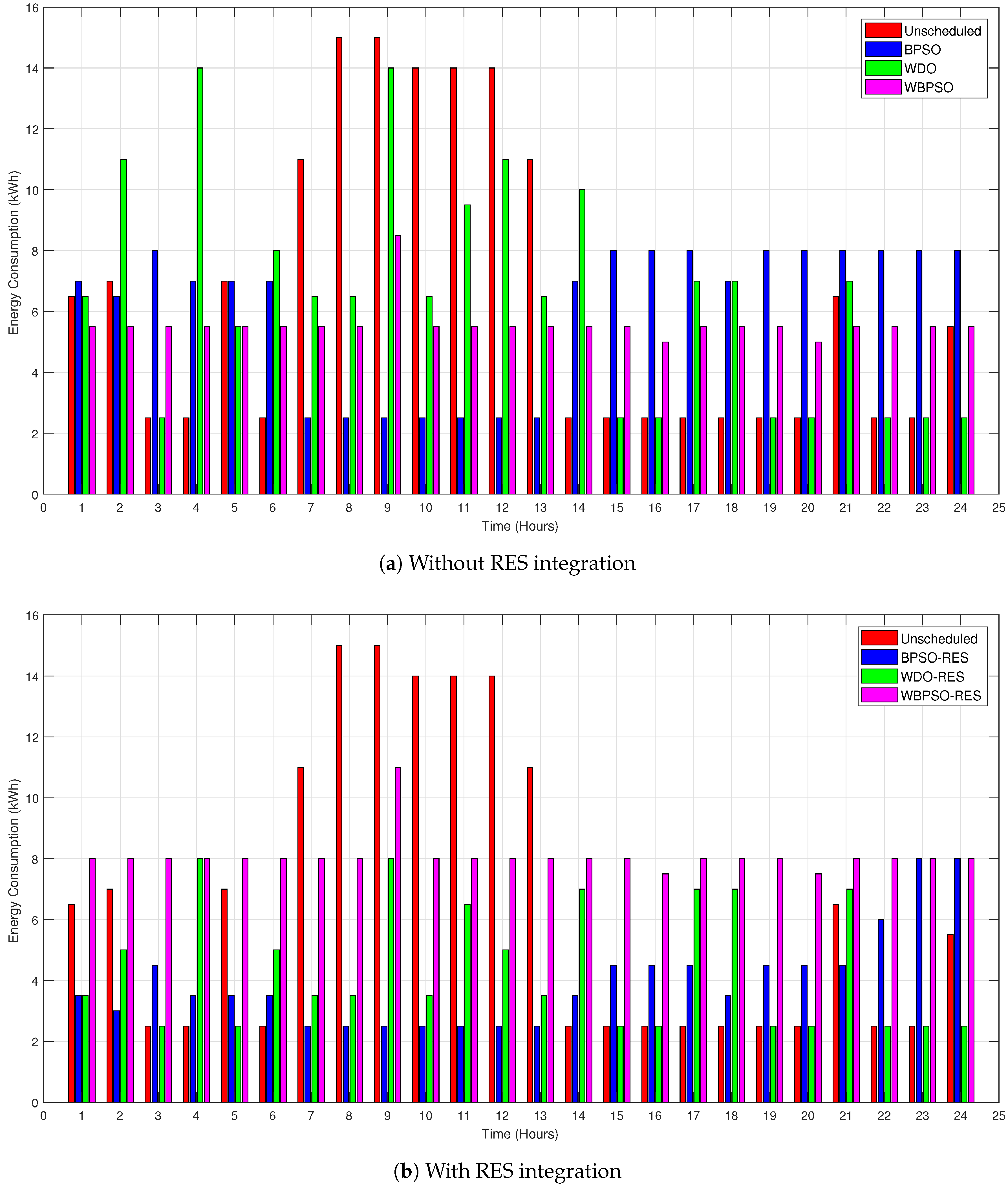
7.2. Energy Consumption Profile
7.2.1. Energy Consumption with and without RESs
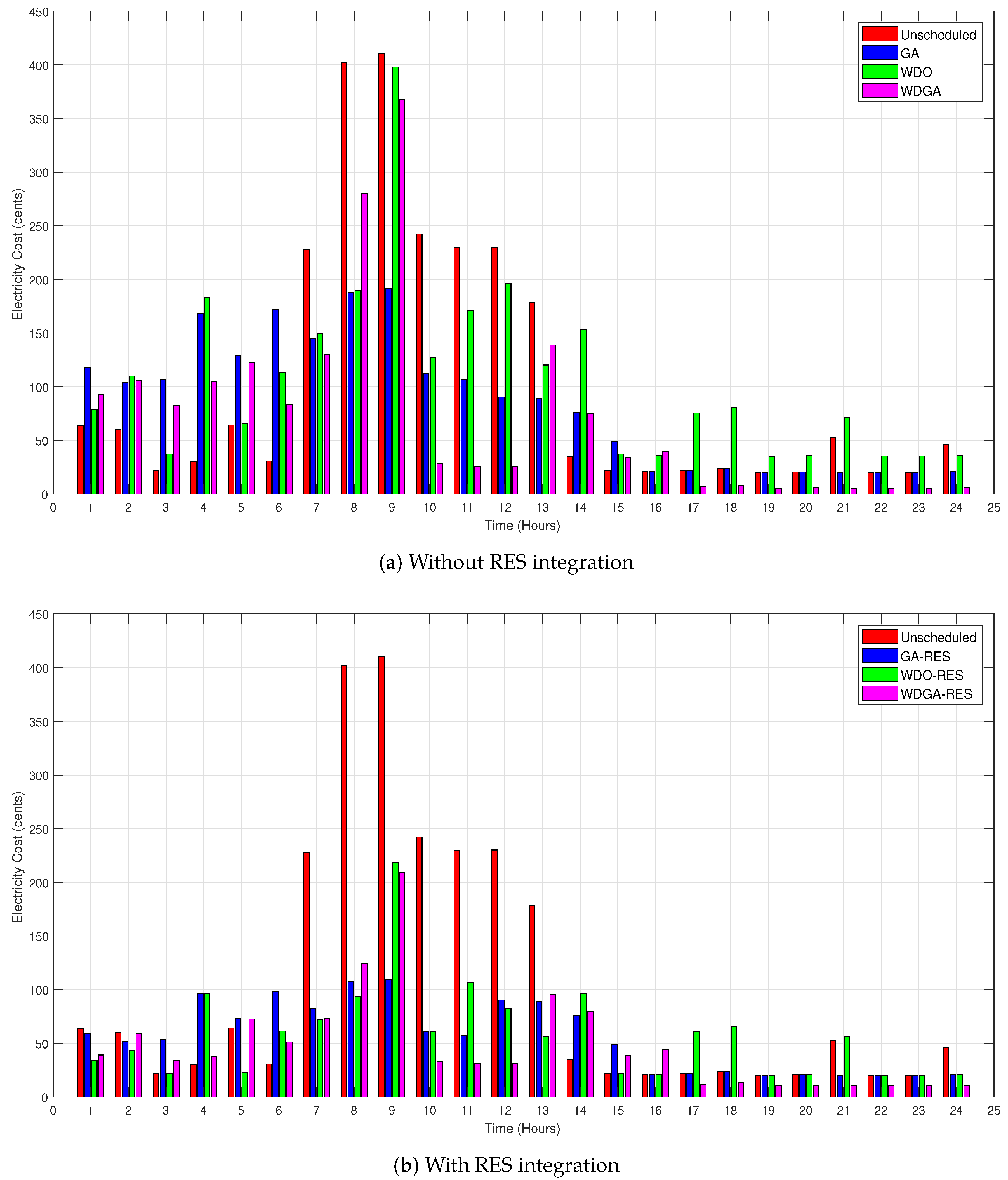
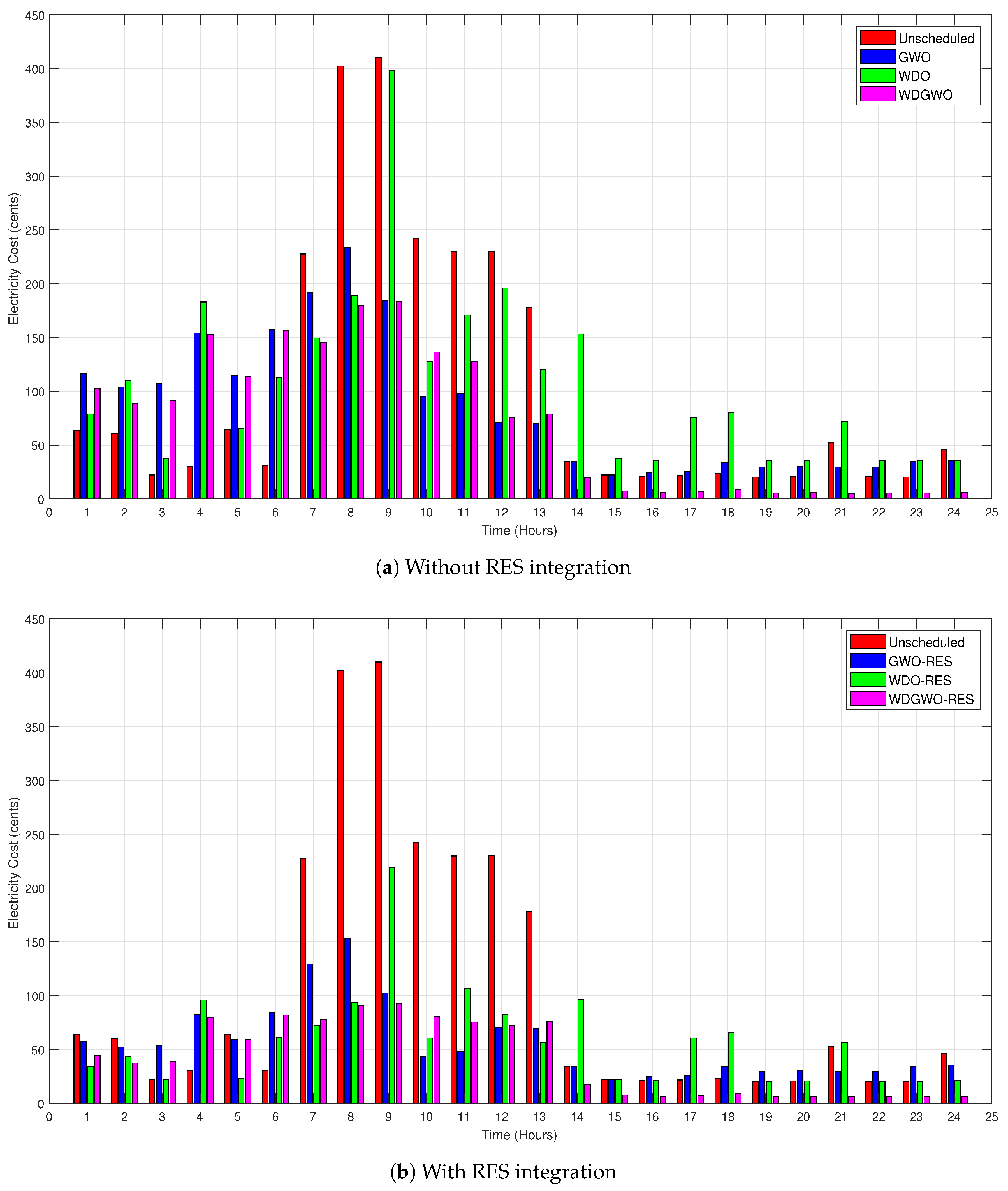
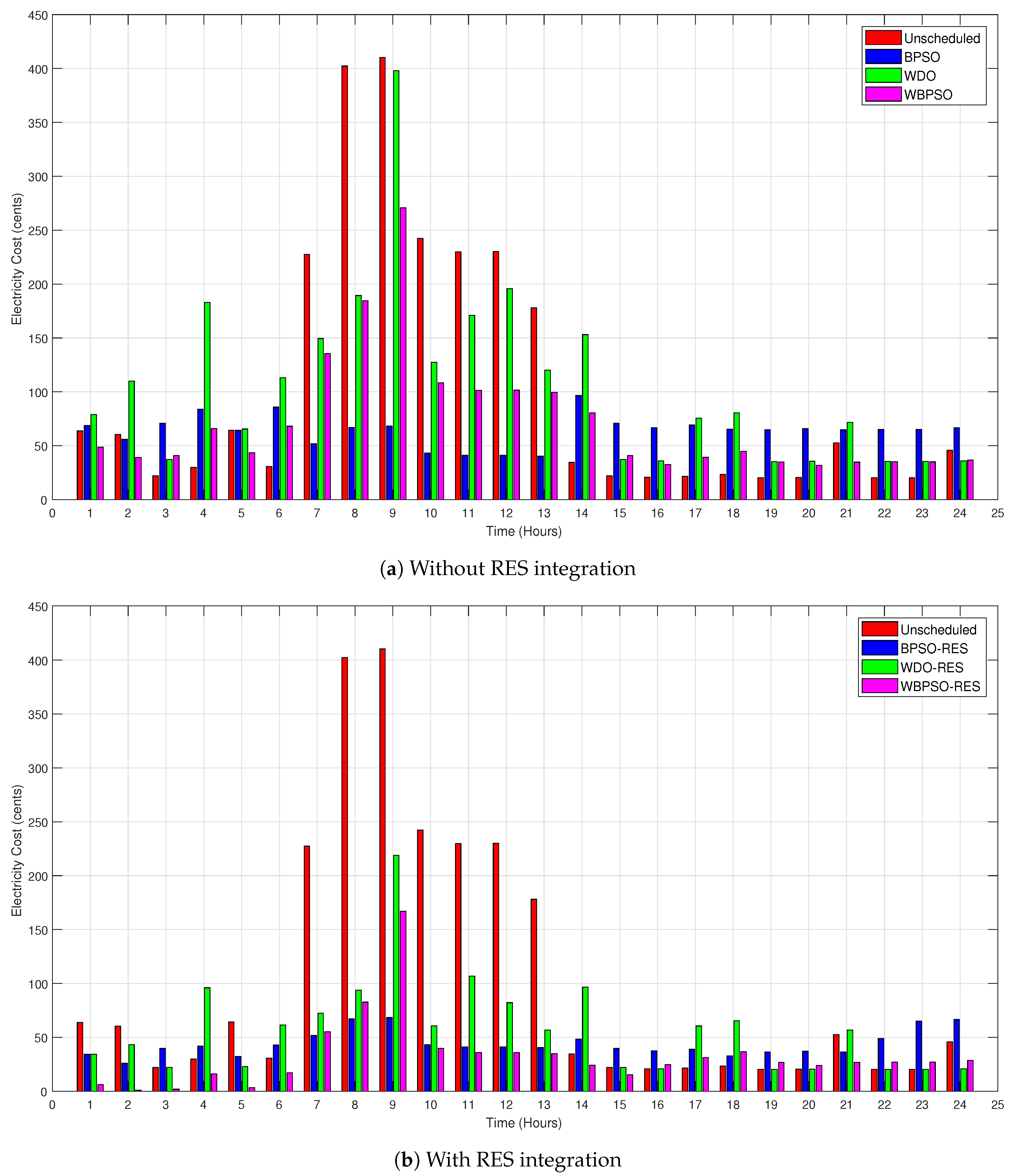
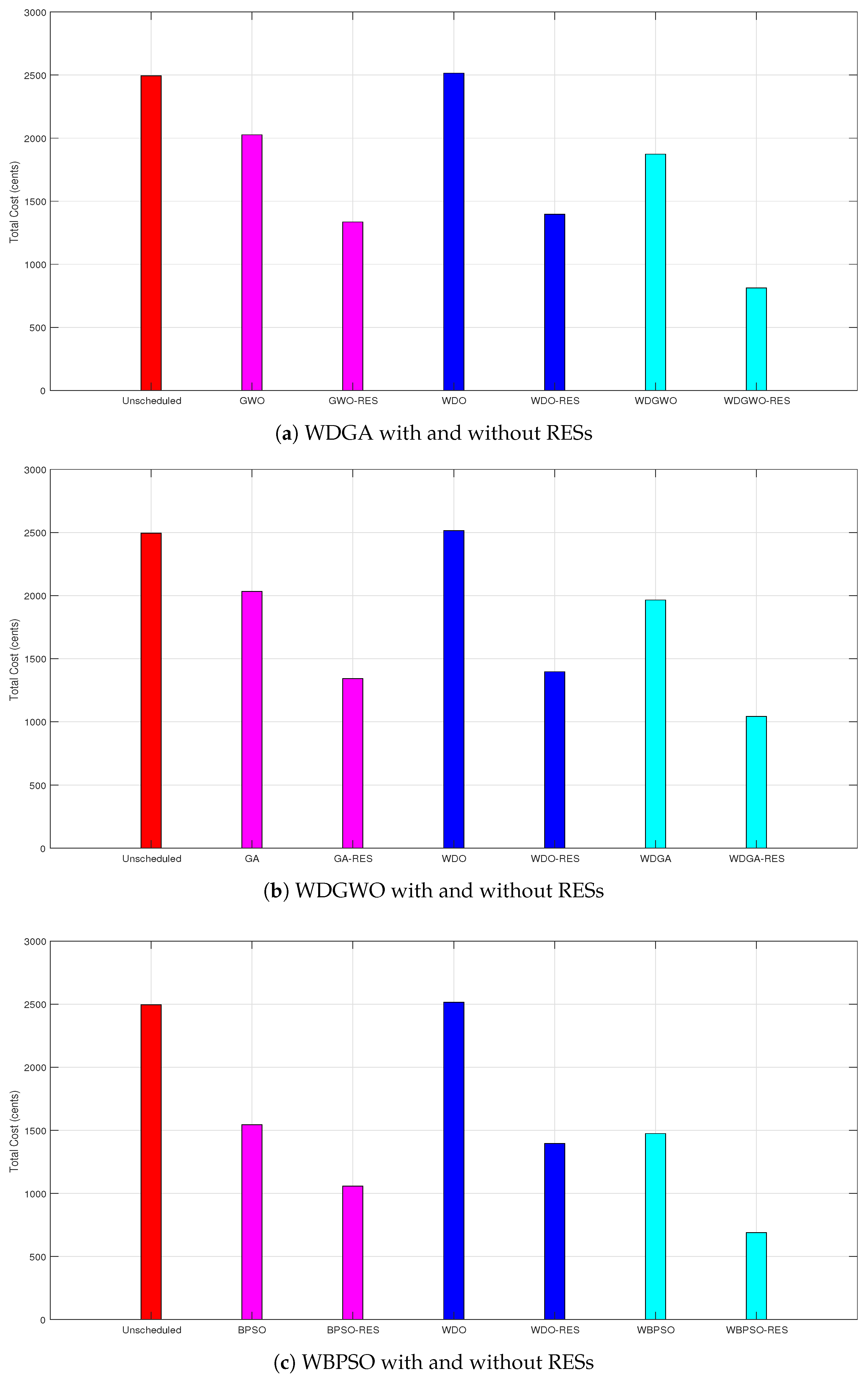
7.3. Electricity Cost
Electricity Cost Profile with and without RESs
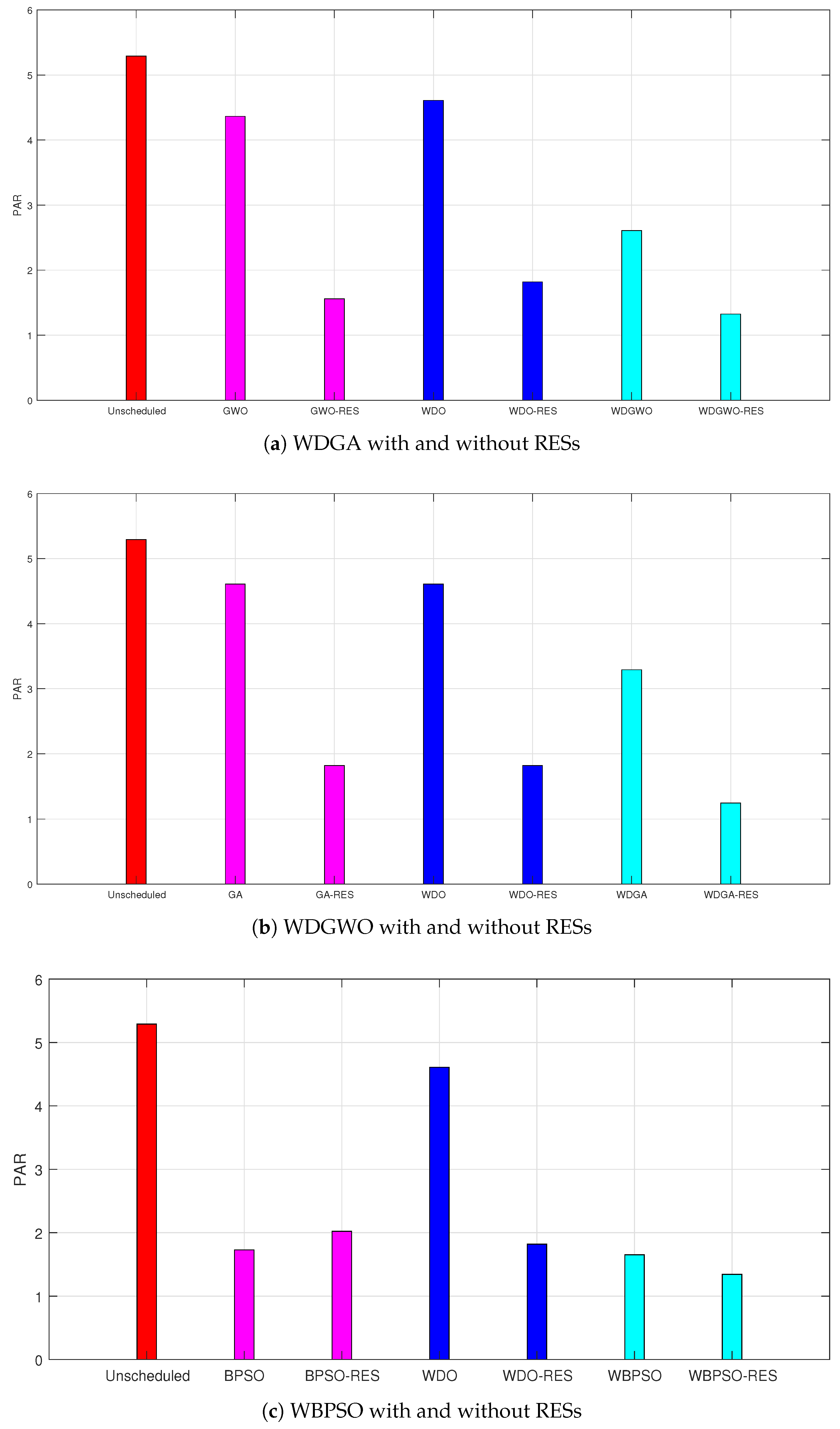
7.4. PAR
PAR with and without RESs
7.5. AWT
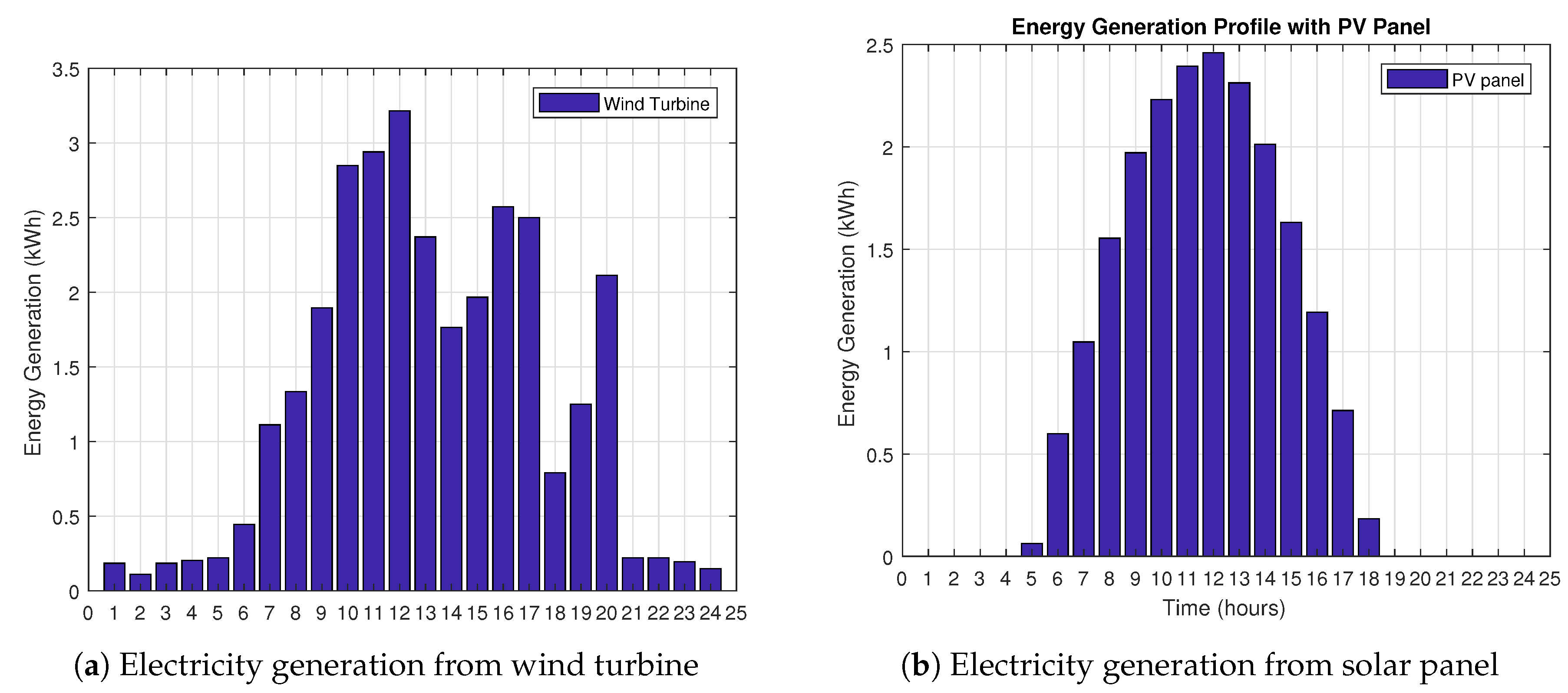
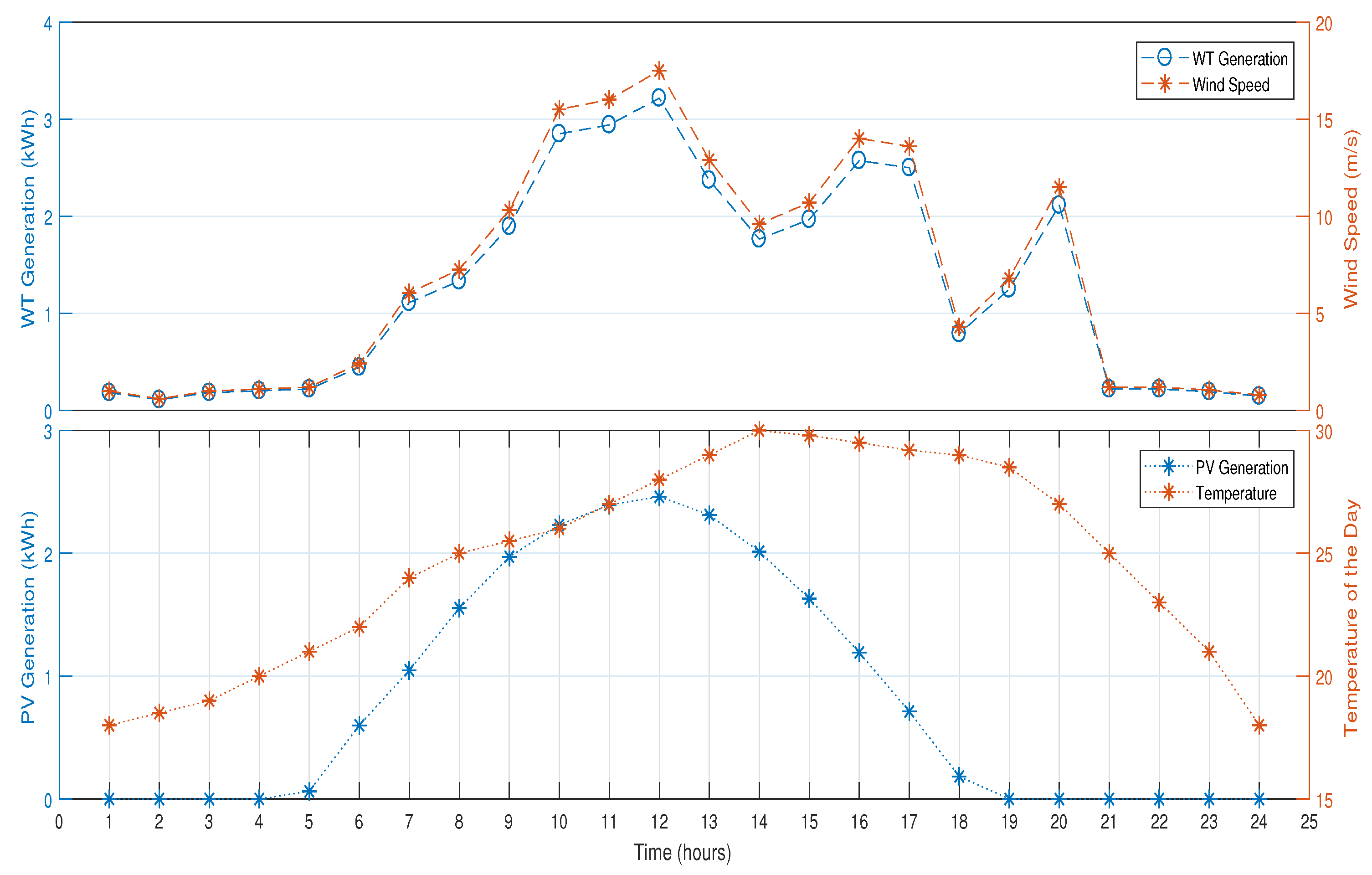
7.6. Energy Generation Profile of Microgrid
7.6.1. Energy Generation with Wind Turbine and Solar Panel
8. Conclusion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Acronyms | Description |
| Alternate current | |
| Autonomy days | |
| Advanced Information Networking and Applications | |
| Advanced metering infrastructure | |
| Appliances waiting time | |
| Battery bank storage | |
| Battery electric vehicle | |
| Bacterial foraging algorithm | |
| Binary particle swarm optimization | |
| Chaos BPSO | |
| Convex programming | |
| Critical peak pricing | |
| Critical peak price with rebate | |
| Day-ahead pricing | |
| Direct current | |
| Distributed energy management strategy | |
| Distributed energy resources | |
| Distributed generation | |
| Depth of discharge | |
| Dynamic programming | |
| Demand response | |
| Demand side management | |
| Energy consumption | |
| Energy consumption and generation | |
| Energy management controller | |
| Energy management system | |
| Electricity price | |
| Energy storage system | |
| Electric vehicle | |
| Genetic algorithm | |
| Grey wolf optimization | |
| Hourly pricing | |
| Hybrid power system | |
| Home energy management system | |
| Information and communication technologies | |
| Interruptible load | |
| Interruptible load appliances | |
| Integer linear programming | |
| Improved PSO | |
| Kilowatt | |
| Kilowatt hour | |
| Locational marginal pricing | |
| Length of operation time | |
| Linear programming | |
| Mixed integer programming | |
| Mixed-integer linear programming | |
| Mixed integer nonlinear programming | |
| Multiple knapsack problem | |
| Model predictive control | |
| Multi-parametric programming | |
| Must-run load | |
| MRLA | Must run load appliances |
| Multi-team PSO | |
| Non-critical peak | |
| Non-deferrable load | |
| Non-deferrable load appliances | |
| Optimal control method | |
| Peak-to-average ratio | |
| Plug-in electric vehicle | |
| Personal computer | |
| Predictor corrector proximal multiplier | |
| Plug-in hybrid electric vehicle | |
| Phaser measurement unit | |
| Power management unit | |
| Peak pricing | |
| Price signal | |
| Particle swarm optimization | |
| Photovoltaic | |
| Autonomy days | |
| Hourly pricing | |
| Price signal | |
| Renewable energy | |
| Renewable energy sources | |
| Real-time market pricing | |
| RTP | Real time pricing |
| SCADA | Supervisory control and data acquisition |
| SI | Set of IL appliances |
| SM | Smart meter |
| SM | Set of must-run appliances |
| SMSU | Smart schedular unit |
| SN | Set of NDL appliances |
| T | Temperature |
| TOU | Time of use |
| UC | User comfort |
| USA | United States of America |
| WBPSO | Wind driven BPSO |
| WDGA | Wind driven genetic algorithm |
| WDGWO | Wind driven GWO algorithm |
| WDO | Wind driven optimization |
| Symbol | Description |
| PV panel output power | |
| Solar radiation at reference conditions | |
| Temperature coefficient of the PV panel | |
| Air density | |
| Wind turbine power coefficient | |
| S | Set of appliances |
| Cut-in wind speed | |
| BBS storage capacity | |
| BBS voltage | |
| Available power from BBS at time slot t | |
| BBS self-discharge rate | |
| Minimum allowable energy level remain in the BBS | |
| Appliance | |
| Real time PS in time slot t | |
| ON/OFF state of IL appliances | |
| EP of NDL appliances in time slot t | |
| EP of MRL appliances in time slot t | |
| Represents NDL appliances | |
| Represents MRL appliances | |
| SI represents the number of appliances of IL | |
| PAR of the demanded load | |
| Waiting time of appliance | |
| Appliance start time | |
| Appliance maximum waiting time | |
| EC of IL appliances in time slot t | |
| Available energy from PV in time slot t | |
| Available energy from battery in time slot t | |
| Available energy from utility grid in time slot t | |
| Lower limit of scheduling horizon | |
| Scheduling time of appliance | |
| Position of particle i in the d dimension at time slots t | |
| Velocity of particle i in the d dimension at time slots t-1 | |
| Best positions obtained by particle i and swarm in d dimension in time slot t-1 | |
| c | Coriolis force |
| r | Variable value for the rank of air parcels |
| Coriolis force | |
| Wind velocity | |
| Air density | |
| g | Acceleration of gravity |
| Pressure gradient | |
| Friction coefficient | |
| Current and new velocity of the air parcels | |
| Global best position | |
| Rated or nominal power of PV cell at reference conditions | |
| Energy consumption by NDL appliances | |
| Energy consumption by MRL appliances | |
| Average load | |
| In , t is current iteration | |
| Prey position vector | |
| Best search agent | |
| Third best search agent | |
| G | Solar radiation |
| Cell temperature at reference conditions | |
| Rotor swept area | |
| Average wind velocity | |
| Rated wind speed | |
| Cut-out wind speed | |
| Wind turbine rated output power | |
| Daily EC | |
| BBS efficiency | |
| Available power from BBS at time slot (t-1) hour | |
| BBS power in time slot t | |
| Maximum allowable energy level remain in the BBS | |
| Energy consumed by appliance in time slot t | |
| ON/OFF state of NDL appliances | |
| ON/OFF state of MRL appliances | |
| EP of IL appliances in time slot t | |
| ps | Price signal |
| Represents the set of IL appliances | |
| SN represents the set of NDL appliances | |
| SM represents the set of MRL appliances | |
| Total load of all consumers | |
| Appliance ON time | |
| Appliance Length of operation time | |
| EC of NDL appliances in time slot t | |
| EC of MRL appliances in time slot t | |
| Available energy from wind in time slot t | |
| Total EC of NDL, IL and MRL appliances in time slot t | |
| Minimum amount of EC in unscheduled case | |
| Upper limit of scheduling horizon | |
| Position of particle i in the d dimension at time slots t | |
| Velocity of particle i in the d dimension at time slots t | |
| Best positions obtained by particle i and swarm in d dimension in time slot t-1 | |
| and | Acceleration coefficients |
| and | Random numbers between 0 and 1 |
| Velocity of particle in particular time slot | |
| Earth rotation | |
| Gravitational force | |
| Air finite volume | |
| Pressure gradient force | |
| Friction force | |
| Current and new velocity of the air parcels | |
| Current and new positions of the air parcels | |
| R | Universal gas constant |
| Temperature of PV cell C | |
| Energy consumption by IL appliances | |
| Peak load | |
| A term used for AWT | |
| Coefficient vectors | |
| Position vector of grey wolf | |
| Second best search agent | |
| D | Encircling of prey |
References
- Guo, Y.; Pan, M.; Fang, Y. Optimal power management of residential customers in the smart grid. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1593–1606. [Google Scholar] [CrossRef]
- Agnetis, A.; de Pascale, G.; Detti, P.; Vicino, A. Load scheduling for household energy consumption optimization. IEEE Trans. Smart Grid 2013, 4, 2364–2373. [Google Scholar] [CrossRef]
- Hossain, E.; Kabalci, E.; Bayindir, R.; Perez, R. Microgrid testbeds around the world: State of art. Energy Convers. Manag. 2014, 86, 132–153. [Google Scholar] [CrossRef]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Dizqah, A.M.; Maheri, A.; Busawon, K.; Fritzson, P. Standalone DC microgrids as complementarity dynamical systems: Modeling and applications. Control Eng. Pract. 2015, 35, 102–112. [Google Scholar] [CrossRef]
- Tsui, K.M.; Chan, S.C. Demand response optimization for smart home scheduling under real-time pricing. IEEE Trans. Smart Grid 2012, 3, 1812–1821. [Google Scholar] [CrossRef]
- Oberdieck, R.; Pistikopoulos, E.N. Multi-objective optimization with convex quadratic cost functions: A multi-parametric programming approach. Comput. Chem. Eng. 2016, 85, 36–39. [Google Scholar] [CrossRef]
- Hubert, T.; Grijalva, S. Realizing smart grid benefits requires energy optimization algorithms at residential level. In Proceedings of the IEEE PES Innovative Smart Grid Technologies (ISGT), Anaheim, CA, USA, 17–19 January 2011; pp. 1–8. [Google Scholar]
- Corchero, C.; Cruz-Zambrano, M.; Heredia, F.J. Optimal energy management for a residential microgrid including a vehicle-to-grid system. IEEE Trans. Smart Grid 2014, 5, 2163–2172. [Google Scholar]
- Graditi, G.; Ippolito, M.G.; Telaretti, E.; Zizzo, G. Technical and economical assessment of distributed electrochemical storages for load shifting applications: An Italian case study. Renew. Sustain. Energy Rev. 2016, 57, 515–523. [Google Scholar] [CrossRef]
- Ippolito, M.G.; Telaretti, E.; Zizzo, G.; Graditi, G. A new device for the control and the connection to the grid of combined RES-based generators and electric storage systems. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 262–267. [Google Scholar]
- Molderink, A.; Bakker, V.; Bosman, M.G.; Hurink, J.L.; Smit, G.J. Management and control of domestic smart grid technology. IEEE Trans. Smart Grid 2010, 1, 109–119. [Google Scholar] [CrossRef]
- Siano, P.; Graditi, G.; Atrigna, M.; Piccolo, A. Designing and testing decision support and energy management systems for smart homes. J. Ambient Intell. Hum. Comput. 2013, 4, 651–661. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S. An algorithm for intelligent home energy management and demand response analysis. IEEE Trans. Smart Grid 2012, 3, 2166–2173. [Google Scholar] [CrossRef]
- Iqbal, Z.; Javaid, N.; Khan, M.R.; Khan, F.A.; Khan, Z.A.; Qasim, U. A Smart Home Energy Management Strategy Based on Demand Side Management. In Proceedings of the 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA), Crans-Montana, Switzerland, 23–25 March 2016; pp. 858–862. [Google Scholar]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Heydarian-Forushani, E.; Shafie-Khah, M.; Siano, P. Stochastic optimal scheduling of distributed energy resources with renewables considering economic and environmental aspects. Renew. Energy 2018, 116, 272–287. [Google Scholar] [CrossRef]
- Deconinck, G.; Decroix, B. Smart metering tariff schemes combined with distributed energy resources. In Proceedings of the 2009 Fourth International Conference on Critical Infrastructures, Linkoping, Sweden, 27 March–30 April 2009; pp. 1–8. [Google Scholar]
- Yoo, J.; Park, B.; An, K.; Al-Ammar, E.A.; Khan, Y.; Hur, K.; Kim, J.H. Look-ahead energy management of a grid-connected residential PV system with energy storage under time-based rate programs. Energies 2012, 5, 1116–1134. [Google Scholar] [CrossRef]
- Wu, Z.; Tazvinga, H.; Xia, X. Demand-side management of photovoltaic-battery hybrid system. Appl. Energy 2015, 148, 294–304. [Google Scholar] [CrossRef]
- Isikman, A.O.; Yildirim, S.A.; Altun, C.; Uludag, S.; Tavli, B. Optimized scheduling of power in an islanded microgrid with renewables and stored energy. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 855–860. [Google Scholar]
- Boopathy, C.P.; Sivakumar, L. Implementation of a real-time supervisory controller for an isolated hybrid (wind/solar/diesel) power system. Int. J. Eng. Technol. 2014, 6, 745–753. [Google Scholar]
- Erdinc, O.; Paterakis, N.G.; Pappi, I.N.; Bakirtzis, A.G.; Catalão, J.P. A new perspective for sizing of distributed generation and energy storage for smart households under demand response. Appl. Energy 2015, 143, 26–37. [Google Scholar] [CrossRef]
- Peyvandi, M.; Zafarani, M.; Nasr, E. Comparison of particle swarm optimization and the genetic algorithm in the improvement of power system stability by an SSSC-based controller. J. Electr. Eng. Technol. 2011, 6, 182–191. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S. Energy and reserve scheduling of microgrid using multi-objective optimization. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar]
- Shi, W.; Xie, X.; Chu, C.C.; Gadh, R. A distributed optimal energy management strategy for microgrids. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 200–205. [Google Scholar]
- Liu, Z.; Chen, C.; Yuan, J. Hybrid Energy Scheduling in a Renewable Micro Grid. Appl. Sci. 2015, 5, 516–531. [Google Scholar] [CrossRef]
- Yang, H.T.; Yang, C.T.; Tsai, C.C.; Chen, G.J.; Chen, S.Y. Improved PSO based home energy management systems integrated with demand response in a smart grid. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 275–282. [Google Scholar]
- Inam, W.; Strawser, D.; Afridi, K.K.; Ram, R.J.; Perreault, D.J. Architecture and system analysis of microgrids with peer-to-peer electricity sharing to create a marketplace which enables energy access. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 464–469. [Google Scholar]
- Aslam, S.; Iqbal, Z.; Javaid, N.; Khan, Z.A.; Aurangzeb, K.; Haider, S.I. Towards Efficient Energy Management of Smart Buildings Exploiting Heuristic Optimization with Real Time and Critical Peak Pricing Schemes. Energies 2017, 10, 2065. [Google Scholar] [CrossRef]
- Sheraz, A.; Nadeem, J.; Muhammad, A.; Zafar, I.; Mian, A.; Mohsin, G. A mixed integer linear programming based optimal home energy management scheme considering grid-connected microgrids. In Proceedings of the 14th IEEE International Wireless Communications and Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018. [Google Scholar]
- Lior, N. Sustainable energy development: The present (2009) situation and possible paths to the future. Energy 2010, 35, 3976–3994. [Google Scholar] [CrossRef]
- Javaid, N.; Ullah, I.; Akbar, M.; Iqbal, Z.; Khan, F.A.; Alrajeh, N.; Alabed, M.S. An intelligent load management system with renewable energy integration for smart homes. IEEE Access 2017, 5, 13587–13600. [Google Scholar] [CrossRef]
- Yu, T.; Kim, D.S.; Son, S.Y. Optimization of Scheduling for Home Appliances in Conjunction with Renewable and Energy Storage Resources. Int. J. Smart Home 2013, 7, 261–271. [Google Scholar]
- Moon, S.; Lee, J.W. Multi-residential demand response scheduling with multi-class appliances in smart grid. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Sou, K.C.; Weimer, J.; Sandberg, H.; Johansson, K.H. Scheduling smart home appliances using mixed integer linear programming. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 December 2011; pp. 5144–5149. [Google Scholar]
- Tischer, H.; Verbic, G. Towards a smart home energy management system-a dynamic programming approach. In Proceedings of the Innovative Smart Grid Technologies Asia (ISGT), Jeddah, Saudi Arabia, 17–20 December 2011; pp. 1–7. [Google Scholar]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R. Optimal and autonomous incentive-based energy consumption scheduling algorithm for smart grid. In Proceedings of the Innovative Smart Grid Technologies (ISGT), Gaithersburg, MD, USA, 19–21 January 2010; pp. 1–6. [Google Scholar]
- Üçtuğ, F.G.; Yükseltan, E. A linear programming approach to household energy conservation: Efficient allocation of budget. Energy Build. 2012, 49, 200–208. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, J.; Lambotharan, S.; Chin, W.H.; Fan, Z. An integer linear programming based optimization for home demand-side management in smart grid. In Proceedings of the Innovative Smart Grid Technologies (ISGT), Columbia, SC, USA, 16–20 January 2012; pp. 1–5. [Google Scholar]
- Ali, E.S.; Abd-Elazim, S.M. Bacteria foraging optimization algorithm based load frequency controller for interconnected power system. Int. J. Electr. Power Energy Syst. 2011, 33, 633–638. [Google Scholar] [CrossRef]
- Fernandes, F.; Sousa, T.; Silva, M.; Morais, H.; Vale, Z.; Faria, P. Genetic algorithm methodology applied to intelligent house control. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Paris, France, 10–16 April 2011; pp. 1–8. [Google Scholar]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the Antennas and Propagation Society International Symposium (APS/URSI), Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Solar Energy. Available online: https://en.wikipedia.org/wiki/Solar_energy (accessed on 25 June 2017).
- Lotfi, S.; Tarazouei, F.L.; Ghiamy, M. Optimal Design of a Hybrid Solar-Wind-Diesel Power System for Rural Electrification Using Imperialist Competitive Algorithm. Int. J. Renew. Energy Res. 2013, 3, 403–411. [Google Scholar]
- Ismail, M.S.; Moghavvemi, M.; Mahlia, T.M.I. Design of a PV/diesel stand alone hybrid system for a remote community in Palestine. J. Asian Sci. Res. 2012, 2, 599. [Google Scholar]
- Daud, A.K.; Ismail, M.S. Design of isolated hybrid systems minimizing costs and pollutant emissions. Renew. Energy 2012, 44, 215–224. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic-wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Liu, L.; Kong, F.; Liu, X.; Peng, Y.; Wang, Q. A review on electric vehicles interacting with renewable energy in smart grid. Renew. Sustain. Energy Rev. 2015, 51, 648–661. [Google Scholar] [CrossRef]
- Wang, X.; Palazoglu, A.; El-Farra, N.H. Operational optimization and demand response of hybrid renewable energy systems. Appl. Energy 2015, 143, 324–335. [Google Scholar] [CrossRef]
- The WindPower Program and the UK NOABL Wind Speed Database. Available online: http://www.wind-power-program.com/index.htm (accessed on 29 March 2018).
- Khatib, T.; Mohamed, A.; Sopian, K.; Mahmoud, M. Optimal sizing of building integrated hybrid PV/diesel generator system for zero load rejection for Malaysia. Energy Build. 2011, 43, 3430–3435. [Google Scholar] [CrossRef]
- Suryoatmojo, H.; Elbaset, A.A.; Pamuji, F.A.; Riawan, D.C.; Abdillah, M. Optimal Sizing and Control Strategy of Hybrid PV-Diesel-Battery Systems for Isolated Island. In Proceedings of the 5th International Symposium on Advanced Control of Industrial Processes (ADCONIP 2014), Hiroshima, Japan, 28–30 May 2014. [Google Scholar]
- Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Azim Niaz, I. An Optimized Home Energy Management System with Integrated Renewable Energy and Storage Resources. Energies 2017, 10, 549. [Google Scholar] [CrossRef]
- Javaid, N.; Khan, I.; Ullah, M.N.; Mahmood, A.; Farooq, M.U. A survey of home energy management systems in future smartgrid communications. In Proceedings of the 2013 Eighth International Conference on Broadband and Wireless Computing, Communication and Applications, Compiegne, France, 28–30 October 2013; pp. 459–464. [Google Scholar]
- Wolak, F.A. Increasing the IQ of the Smart Grid Through Active Customer Participation in Wholesale Electricity Markets. Available online: http://www.stanford.edu/~wolak (accessed on 29 March 2018).
- Liu, Y.; Yuen, C.; Huang, S.; Hassan, N.U.; Wang, X.; Xie, S. Peak-to-average ratio constrained demand-side management with consumer’s preference in residential smart grid. IEEE J. Sel. Top. Signal Process. 2014, 8, 1084–1097. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Gherboudj, A.; Chikhi, S. BPSO Algorithms for Knapsack Problem. In Recent Trends in Wireless and Mobile Networks; Springer: Berlin/Heidelberg, Germany, 2011; Volume 162, pp. 217–227. [Google Scholar]
- Soares, J.; Silva, M.; Sousa, T.; Vale, Z.; Morais, H. Distributed energy resource short-term scheduling using Signaled Particle Swarm Optimization. Energy 2012, 42, 466–476. [Google Scholar] [CrossRef]
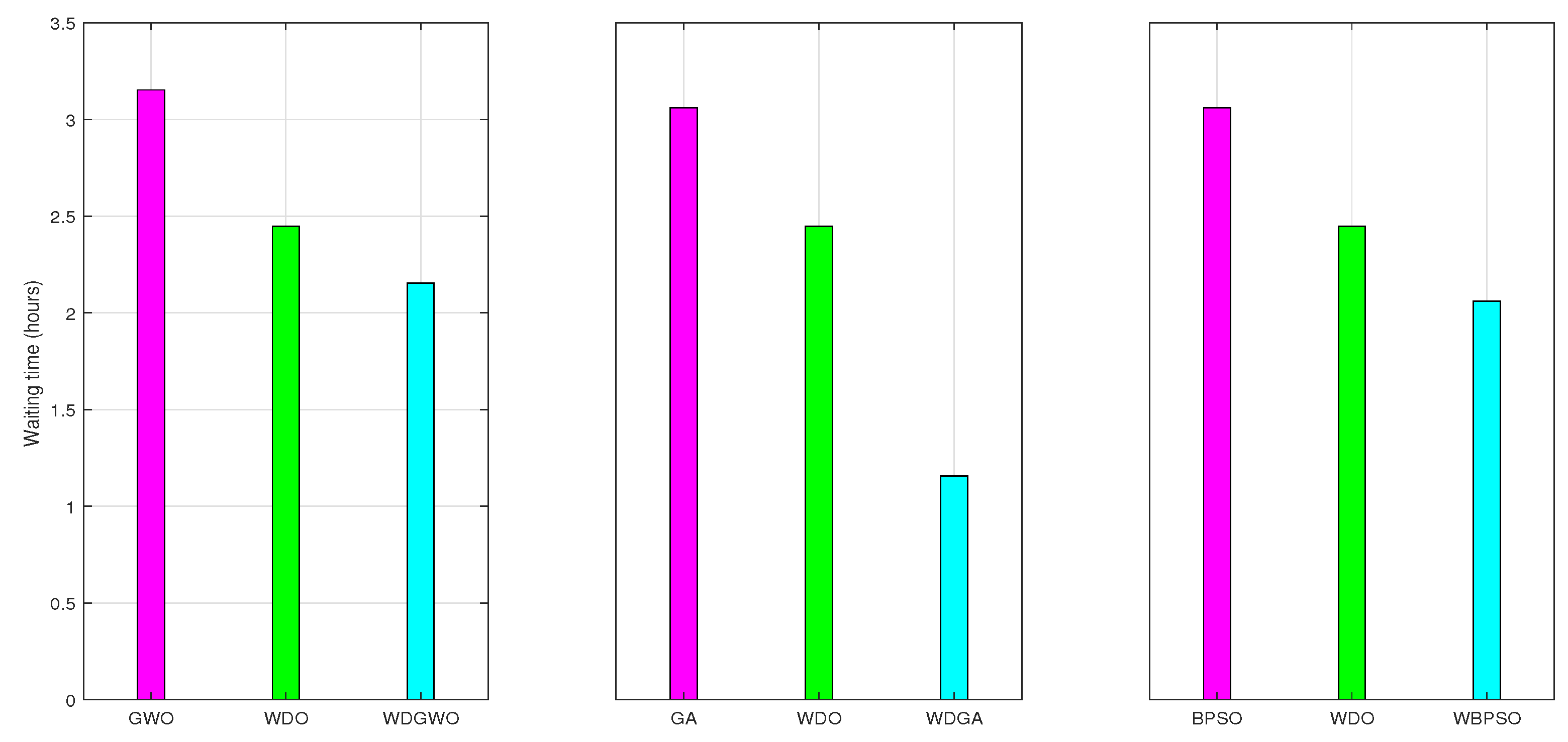
| Technique(s) | Objective(s) | Finding(s) | Limitation(s) |
|---|---|---|---|
| GA [18] | Electricity cost and PAR reduction | Cost and PAR is reduced using RTP and TOU | UC is not considered |
| MILP [19] | PAR and cost reduction with RESs integration | Cost is reduced | Expensive for small scale residential users |
| OCM and MPC [20] | Electricity bill reduction | Optimal energy management solution and cost saving | AWT for UC is not taken into account |
| MIP [21] | Optimal scheduling of energy resources among users | Maximizes energy utilization | UC is not considered |
| SCADA [22] | A hybrid power generation model | Design of hybrid power system | UC is not considered |
| MILP [23] | HEMS modeling and techno-economic sizing | Used single step methodology to size additional PV and ESS | UC and cost reduction are ignored |
| PSO and GA [24] | To minimize electricity cost | Cost is reduced using PSO and GA | To reduce cost UC is compromised |
| MILP [25] | Reduction of emission and cost | emission and cost minimization | UC and PAR are not considered |
| PCPM [26] | Design of a distributed EMS | EMS is designed using optimal operation of microgrids | PAR and UC are not addressed |
| MTPSO [27] | Cost reduction | Cost reduction achieved | UC is not discussed |
| IPSO [28] | Peak load reduction | They achieve desired objectives | UC is compromised and only passive appliances is considered. |
| PMU [29] | To reduce electricity cost | Cost is reduced by peer-to-peer electricity sharing | UC is decreased |
| Component | Rating |
|---|---|
| Battery | 1.2 kWh |
| Wind turbine | 10 kW |
| Solar panel | 230 W |
| Non-Deferrable Loads | Interruptible Loads | Must-Run Loads |
|---|---|---|
| Home lightings | Water heater | Fans |
| Fan | PEV | Optional lightings |
| Exhaust fan | Iron | Heated towel rails |
| Desktop PC | Pool Pump | Personal computer |
| ESS | Refrigerator | Television |
| Washing machine | Out-door lightings | Electric clock |
| Parameters | Value |
|---|---|
| Total iterations | 50 |
| Population size | 200 |
| 2 to 0 | |
| Random vectors r1, r2 | 0, 1 |
| n | 18 |
| Parameters | Value |
|---|---|
| Number of iterations | 50 |
| Population size | 200 |
| Probability of mutation | 0.1 |
| Probability of crossover | 0.9 |
| n | 18 |
| Parameters | Values |
|---|---|
| Number of iterations | 50 |
| Swarm size | 200 |
| Maximum velocity | 4 |
| Minimum velocity | −4 |
| Initial weight constant | 2 |
| Final weight constant | 0.4 |
| Local pull | 2 |
| Global pull | 2 |
| n | 18 |
| Parameters | Values |
|---|---|
| Total iterations | 50 |
| Population size | 200 |
| dimMin | −5 |
| dimMax | 5 |
| vmin | −0.3 |
| vmax | 0.3 |
| Universal gas constant | 3 |
| n | 18 |
| Gravity | 0.2 |
| Coefficient of friction | 0.4 |
| Parameters | Values |
|---|---|
| Number of iterations | 50 |
| Parcels size | 200 |
| Dimensions | [−1, +1] |
| Maximum velocity | 0.4 |
| Universal gas constant | 3.0 |
| Gravity | 0.2 |
| Coefficient of friction | 0.4 |
| Crossover rate | 0.9 |
| Mutation rate | 0.1 |
| Parameters | Values |
|---|---|
| Number of iterations | 50 |
| Population size | 200 |
| Dimensions | [−1, +1] |
| Maximum velocity | 0.4 |
| Universal gas constant | 3.0 |
| Gravity | 0.2 |
| Coefficient of friction | 0.4 |
| 2 to 0 | |
| Random vectors r1, r2 | 0, 1 |
| n | 18 |
| Parameters | Values |
|---|---|
| Number of iterations | 50 |
| Population size | 200 |
| Dimensions | [−1, +1] |
| Maximum velocity | 0.4 |
| Minimum velocity | −4 |
| Initial weight constant | 2 |
| Final weight constant | 0.4 |
| Local pull | 2 |
| Global pull | 2 |
| Gravity | 0.2 |
| Coefficient of friction | 0.4 |
| n | 18 |
| Technique | Total Energy Demand(kW) | Imported Energy from Utility (kW) | Difference (kW) | Reduction (%) |
|---|---|---|---|---|
| Unscheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| GA scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| BPSO scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| WDO scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| GWO scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| WDGA scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| WDGWO scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| WBPSO scheduled | 156.5000 | 156.5000 | 0.0000 | 0.0000% |
| Unscheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| GA scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| BPSO scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| WDO scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| GWO scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| WDGA scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| WDGWO scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| WBPSO scheduled + RESs | 156.5000 | 103.5+53 | 53.0000 | 33.860% |
| Technique | Cost (Cents/hour) | Difference (Cents/hour) | Reduction (%) |
|---|---|---|---|
| Unscheduled | 103.9500 | 0.0000 | 0.0000% |
| GA scheduled | 84.6842 | 0.0000 | 0.0000% |
| BPSO scheduled | 64.3556 | 0.0000 | 0.0000% |
| WDO scheduled | 96.3625 | 0.0000 | 0.0000% |
| GWO scheduled | 77.9125 | 0.0000 | 0.0000% |
| WDGA scheduled | 83.1125 | 0.0000 | 0.0000% |
| WDGWO scheduled | 71.2750 | 0.0000 | 0.0000% |
| WBPSO scheduled | 73.1100 | 0.0000 | 0.0000% |
| Unscheduled + RESs | 72.8857 | 31.0643 | 42.6205% |
| GA scheduled + RESs | 55.9129 | 28.7713 | 33.9700% |
| BPSO scheduled + RESs | 44.0948 | 20.2608 | 31.4800% |
| WDO scheduled + RESs | 51.5500 | 44.8125 | 46.0500% |
| GWO scheduled + RESs | 53.6400 | 24.2725 | 31.1500% |
| WDGA scheduled + RESs | 54.0355 | 29.0770 | 34.9800% |
| WDGWO scheduled + RESs | 41.2500 | 30.0250 | 42.1200% |
| WBPSO scheduled + RESs | 32.8900 | 40.2200 | 55.0100% |
| Technique | Cost (Cents/day) | Difference (Cents/day) | Reduction (%) |
|---|---|---|---|
| Unscheduled | 2494.8000 | 0.0000 | 0.0000% |
| GA scheduled | 2032.4000 | 0.0000 | 0.0000% |
| BPSO scheduled | 1544.5000 | 0.0000 | 0.0000% |
| WDO scheduled | 2257.7000 | 0.0000 | 0.0000% |
| GWO scheduled | 1869.9000 | 0.0000 | 0.0000% |
| WDGA scheduled | 2174.7000 | 0.0000 | 0.0000% |
| WDGWO scheduled | 1870.6000 | 0.0000 | 0.0000% |
| WBPSO scheduled | 1474.7000 | 0.0000 | 0.0000% |
| Unscheduled + RESs | 1781.0814 | 713.7186 | 40.0722% |
| GA scheduled + RESs | 1341.9000 | 690.5000 | 33.9700% |
| BPSO scheduled + RESs | 1058.3000 | 486.2000 | 31.4700% |
| WDO scheduled + RESs | 1237.4000 | 1020.3000 | 45.1900% |
| GWO scheduled + RESs | 1287.4000 | 582.5000 | 31.1500% |
| WDGA scheduled + RESs | 1196.9000 | 977.8000 | 44.9600% |
| WDGWO scheduled + RESs | 810.0805 | 664.6195 | 35.5200% |
| WBPSO scheduled + RESs | 900.5800 | 574.12000 | 38.9300% |
| Technique | PAR | Difference | Reduction (%) |
|---|---|---|---|
| Unscheduled | 5.2915 | 0.0000 | 0.0000% |
| GA scheduled | 4.6095 | 0.0000 | 0.0000% |
| BPSO scheduled | 2.7294 | 0.0000 | 0.0000% |
| WDO scheduled | 5.2915 | 0.0000 | 0.0000% |
| GWO scheduled | 4.2426 | 0.0000 | 0.0000% |
| WDGA scheduled | 3.2915 | 0.0000 | 0.0000% |
| WDGWO scheduled | 2.6095 | 0.0000 | 0.0000% |
| WBPSO scheduled | 1.6518 | 0.0000 | 0.0000% |
| Unscheduled + RESs | 5.2915 | 0.0000 | 0.0000% |
| GA scheduled + RESs | 1.8199 | 2.7896 | 60.5100% |
| BPSO scheduled + RESs | 2.0211 | 0.7083 | 74.0400% |
| WDO scheduled + RESs | 2.5024 | 2.7891 | 47.2900% |
| GWO scheduled + RESs | 1.6265 | 2.6161 | 38.3300% |
| WDGA scheduled + RESs | 1.2474 | 2.0441 | 62.1000% |
| WDGWO scheduled + RESs | 1.3251 | 1.2844 | 49.2200% |
| WBPSO scheduled + RESs | 1.3427 | 0.3091 | 81.2800% |
| Wind Generation (kWh) | Wind Speed (m/s) | PV Generation (kWh) | Temperature (C) |
|---|---|---|---|
| 0.1838 | 1.0000 | 0 | 18.0000 |
| 0.1103 | 0.6000 | 0 | 18.5000 |
| 0.1838 | 1.0000 | 0 | 19.0000 |
| 0.2021 | 1.1000 | 0 | 20.0000 |
| 0.2205 | 1.2000 | 0.0622 | 21.0000 |
| 0.4447 | 2.4200 | 0.5988 | 22.0000 |
| 1.1111 | 6.0470 | 1.0475 | 24.0000 |
| 1.3331 | 7.2550 | 1.5535 | 25.0000 |
| 1.8945 | 10.3100 | 1.9714 | 25.5000 |
| 2.8481 | 15.5000 | 2.2306 | 26.0000 |
| 2.9400 | 16.0000 | 2.3946 | 27.0000 |
| 3.2156 | 17.5000 | 2.4600 | 28.0000 |
| 2.3704 | 12.9000 | 2.3126 | 29.0000 |
| 1.7640 | 9.6000 | 2.0132 | 30.0000 |
| 1.9661 | 10.7000 | 1.6314 | 29.8000 |
| 2.5725 | 14.0000 | 1.1918 | 29.5000 |
| 2.4990 | 13.6000 | 0.7123 | 29.2000 |
| 0.7901 | 4.3000 | 0.1831 | 29.0000 |
| 1.2495 | 6.8000 | 0 | 28.5000 |
| 2.1131 | 11.5000 | 0 | 27.0000 |
| 0.2205 | 1.2000 | 0 | 25.0000 |
| 0.2205 | 1.2000 | 0 | 23.0000 |
| 0.1929 | 1.0500 | 0 | 21.0000 |
| 0.1470 | 0.8000 | 0 | 18.0000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, Z.; Javaid, N.; Iqbal, S.; Aslam, S.; Khan, Z.A.; Abdul, W.; Almogren, A.; Alamri, A. A Domestic Microgrid with Optimized Home Energy Management System. Energies 2018, 11, 1002. https://doi.org/10.3390/en11041002
Iqbal Z, Javaid N, Iqbal S, Aslam S, Khan ZA, Abdul W, Almogren A, Alamri A. A Domestic Microgrid with Optimized Home Energy Management System. Energies. 2018; 11(4):1002. https://doi.org/10.3390/en11041002
Chicago/Turabian StyleIqbal, Zafar, Nadeem Javaid, Saleem Iqbal, Sheraz Aslam, Zahoor Ali Khan, Wadood Abdul, Ahmad Almogren, and Atif Alamri. 2018. "A Domestic Microgrid with Optimized Home Energy Management System" Energies 11, no. 4: 1002. https://doi.org/10.3390/en11041002
APA StyleIqbal, Z., Javaid, N., Iqbal, S., Aslam, S., Khan, Z. A., Abdul, W., Almogren, A., & Alamri, A. (2018). A Domestic Microgrid with Optimized Home Energy Management System. Energies, 11(4), 1002. https://doi.org/10.3390/en11041002