Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines
Abstract
:1. Introduction
1.1. Motivation
1.2. Dual Fuel Technology
1.3. State-of-the-Art Simulation of Dual Fuel Combustion
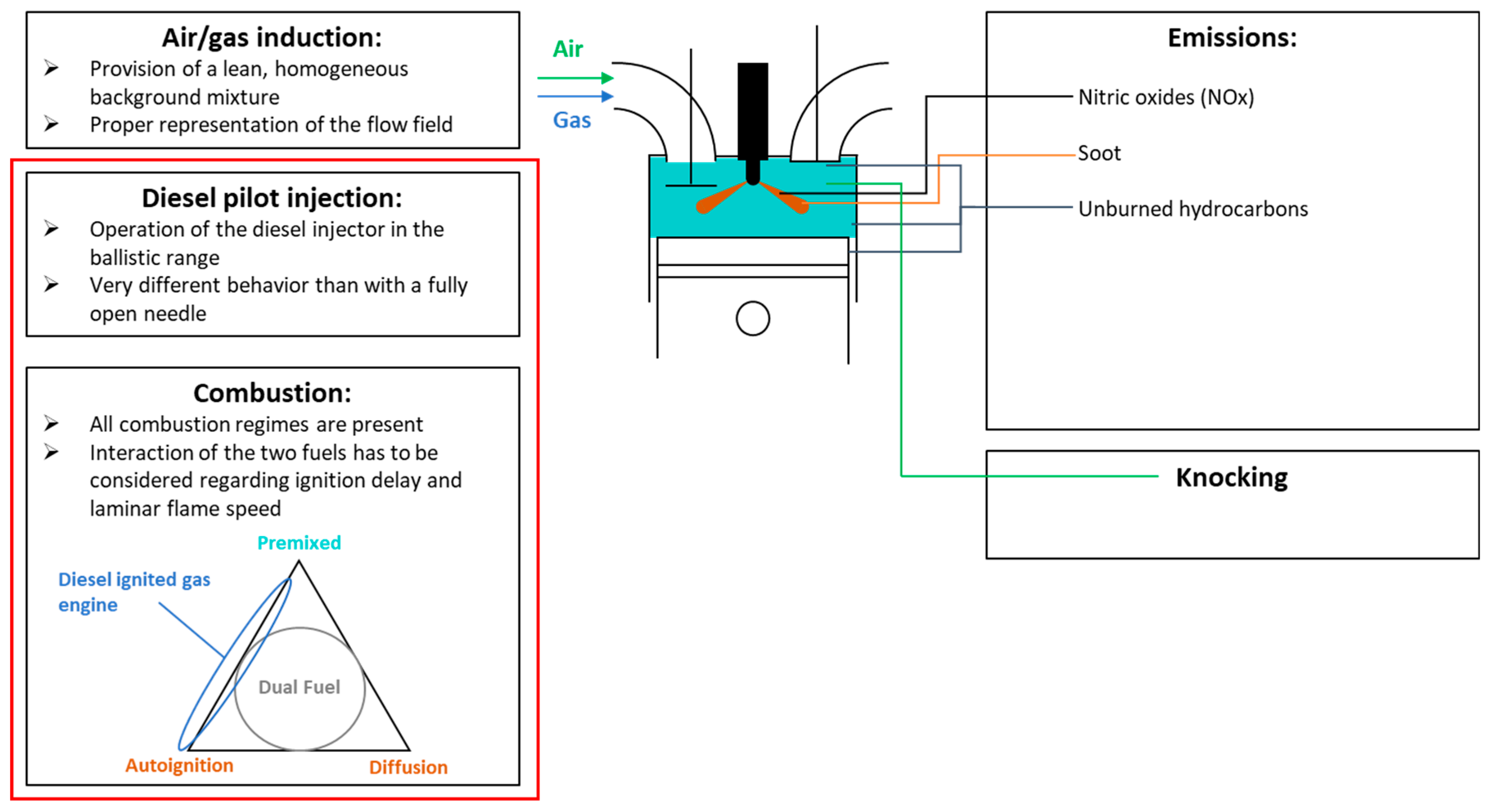
2. Challenges of Dual Fuel Combustion Modeling
2.1. Injection Modeling
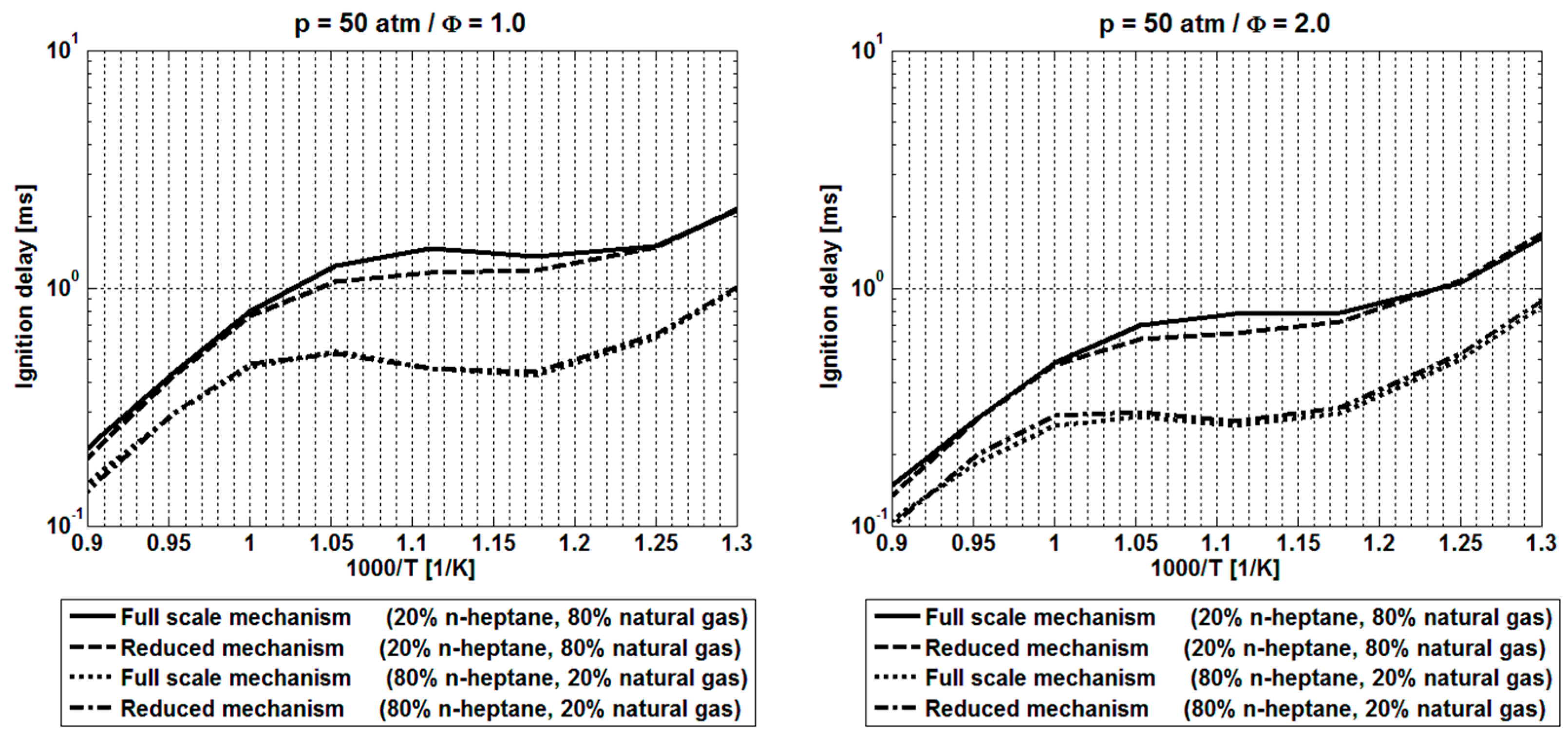
2.2. Ignition Delay Modeling
2.3. Two-Stage Ignition with an Interpolation Function
2.4. Two-Stage Ignition with a Specific Dual Fuel Mechanism
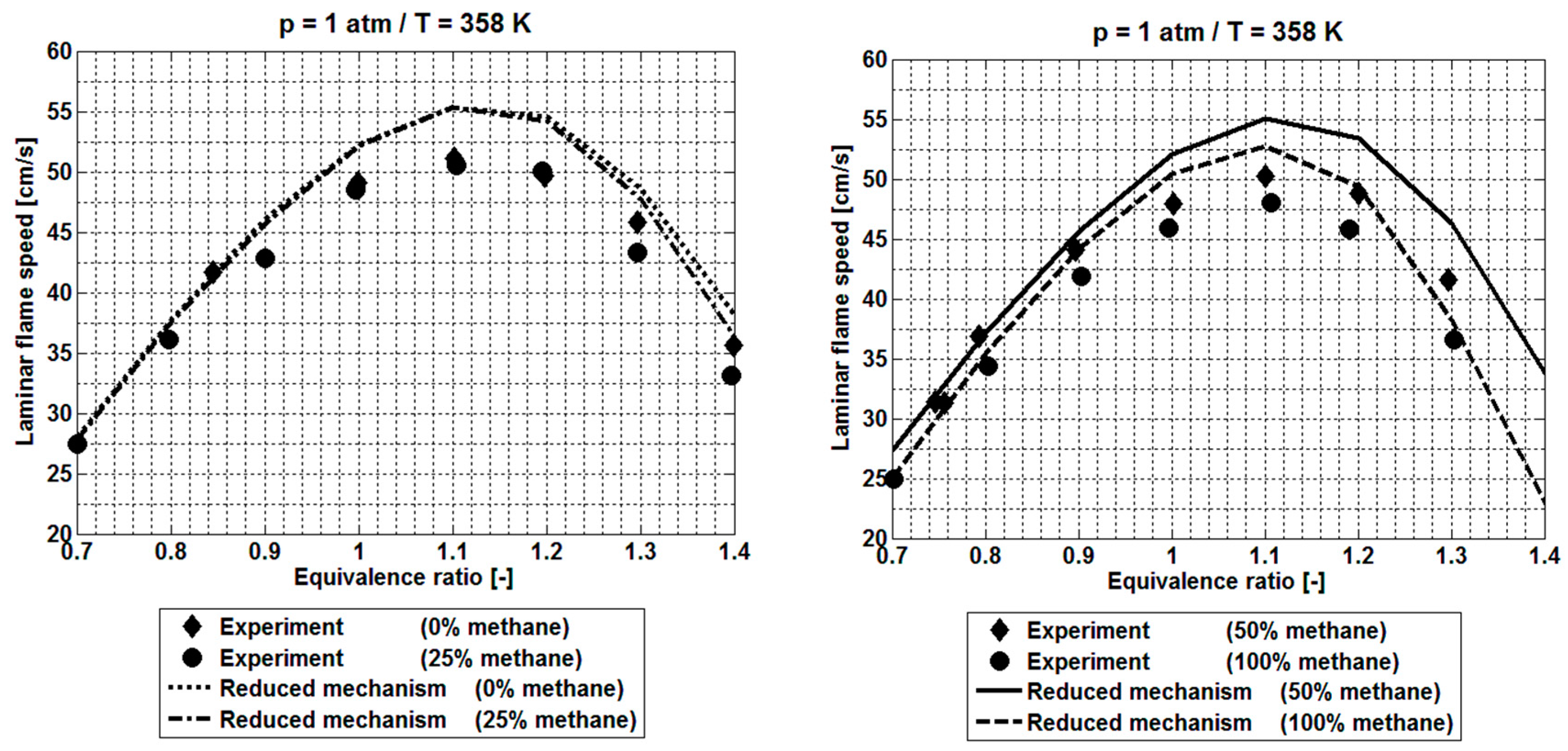
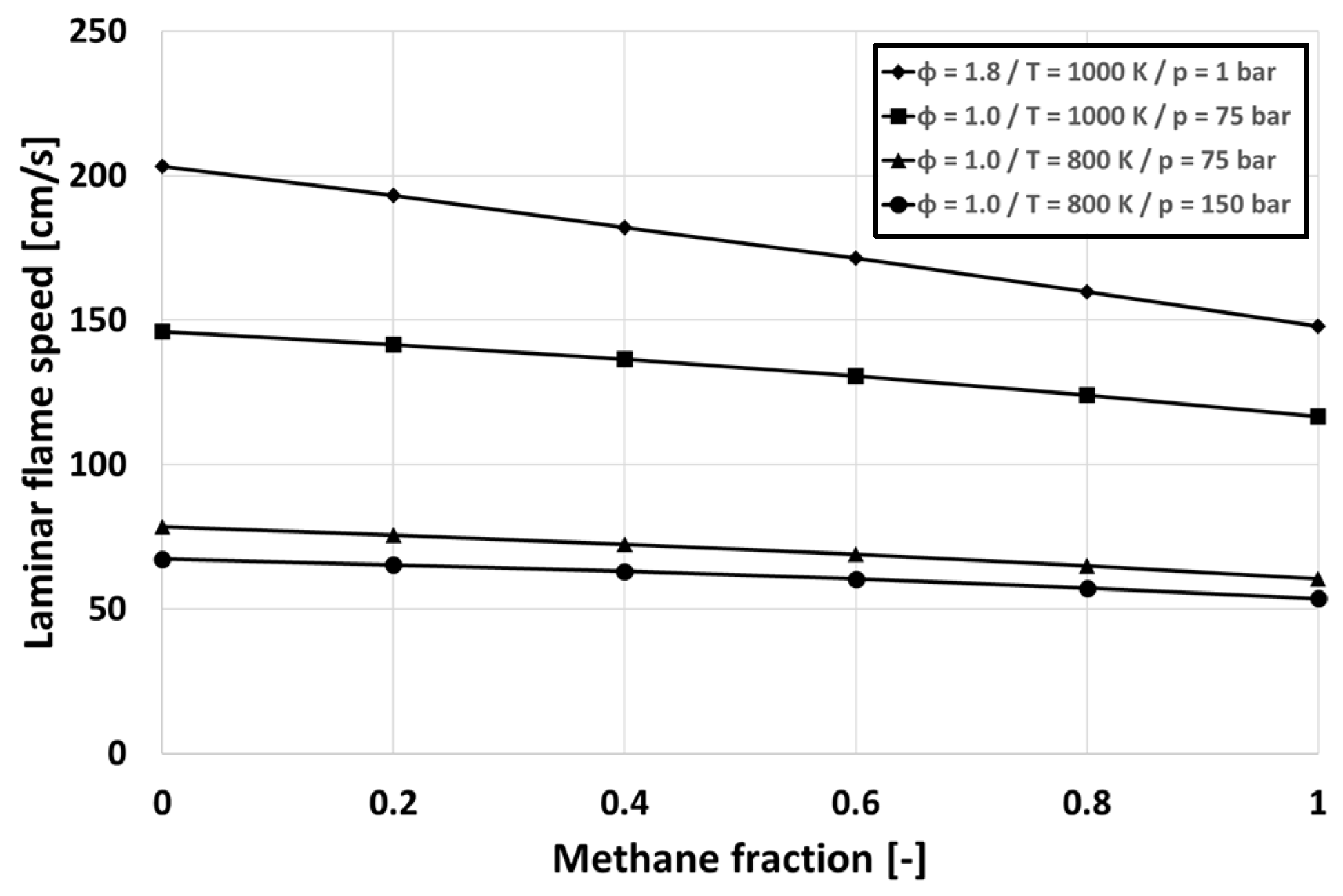
2.5. Premixed Flame Propagation Modeling
3. Validation of Injection Modeling
3.1. Experimental Setup
3.2. Numerical Setup
3.3. Validation Cases
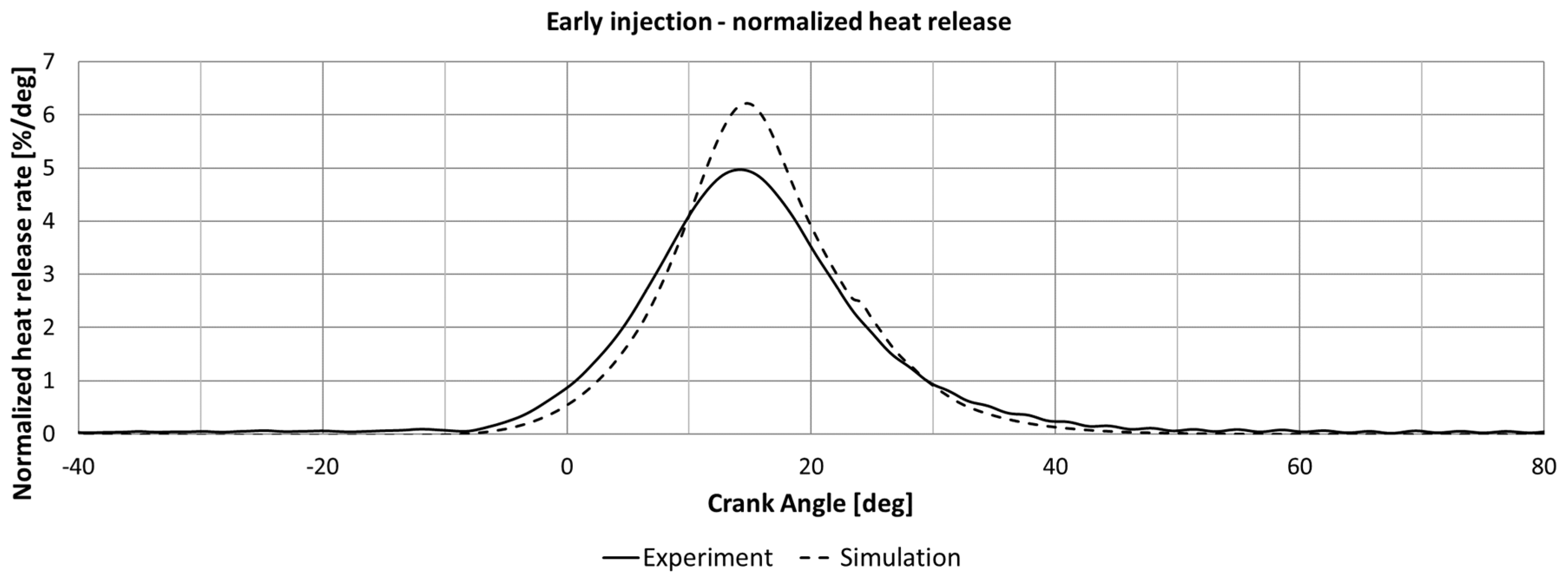
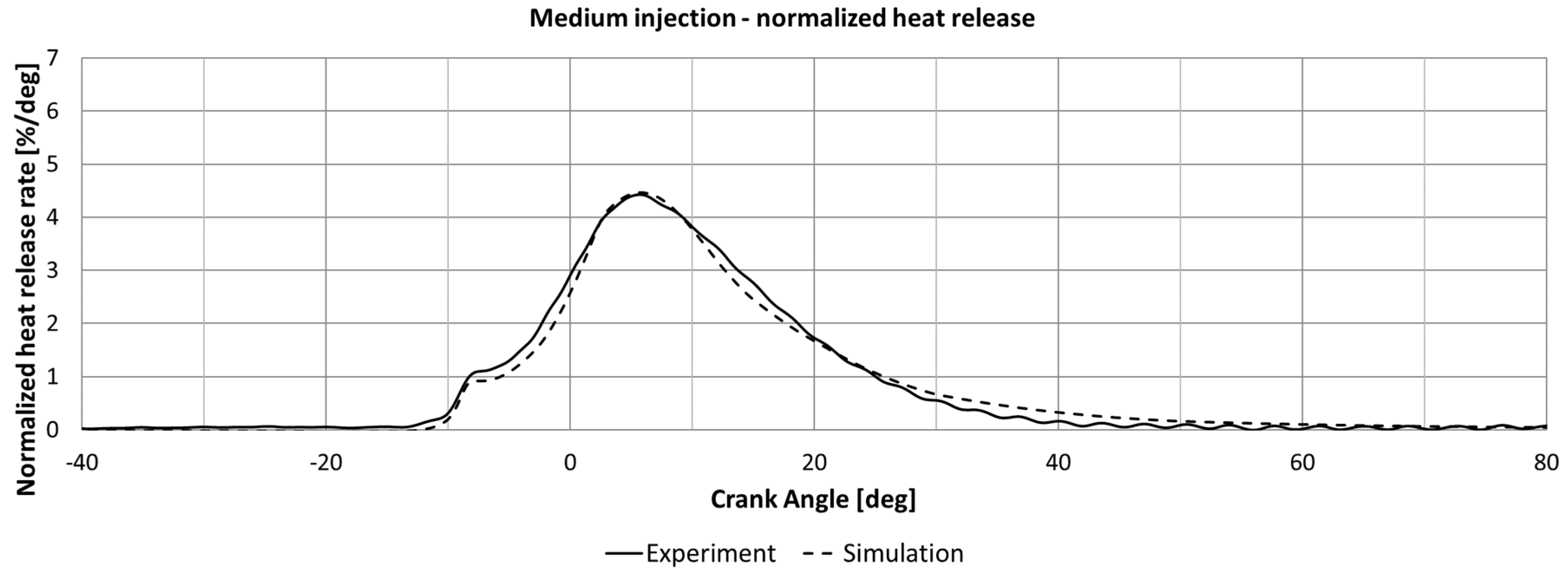
4. Validation of Combustion Modeling
4.1. Experimental Setup
4.2. Numerical Setup
4.3. Validation Cases
5. Discussion of Results
5.1. Injection and Ignition Delay Modeling
5.2. Combustion Modeling
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Verdolini, E.; Vona, F.; Popp, D. Bridging the Gap: Do Fast Reacting Fossil Technologies Facilitate Renewable Energy Diffusion; National Bureau of Economic Research (NBER): Cambridge, MA, USA, 2016.
- International Transport Forum. ITF Transport Outlook 2015; International Transport Forum: Paris, France, 2015. [Google Scholar]
- Pirker, G.; Wimmer, A. Sustainable power generation with large gas engines. Energy Convers. Manag. 2017, 149, 1048–1065. [Google Scholar] [CrossRef]
- International Maritime Organization. Nitrogen Oxides (NOx)—Regulation 13, 2015. Available online: http://www.imo.org/en/OurWork/Environment/PollutionPrevention/AirPollution/Pages/Nitrogen-oxides-(NOx)-–-Regulation-13.aspx (accessed on 12 September 2016).
- Buchholz, B. Saubere Großmotoren für die Zukunft—Herausforderung für die Forschung. In Rostock Large Engine Symposium; FVTR: Rostock, Germany, 2014. [Google Scholar]
- Zelenka, J.; Kammel, G. The Quality of Gaseous Fuels and Consequences for Gas Engines. In Proceedings of the 10th Internationale Energiewirtschaftstagung (IEWT 2017), Vienna, Austria, 15–17 February 2017; pp. 1–16. [Google Scholar]
- Aaltonen, P.; Järvi, A.; Vaahtera, P.; Widell, K. Paper No. 251: New DF Engine Portfolio (Wärtsilä 4-Stroke). In Proceedings of the 28th CIMAC World Congress, Helsinki, Finland, 6–10 June 2016. [Google Scholar]
- Dillen, E.; Yearce, D.; Trask, L.; Klingbeil, A. Paper No. 214: GE Transportation Dual Fuel Locomotive Development. In Proceedings of the 28th CIMAC World Congress, Helsinki, Finland, 6–10 June 2016. [Google Scholar]
- Issei, O.; Nishida, K.; Hirose, K. Paper No. 049: New marine gas engine development in YANMAR. In Proceedings of the 28th CIMAC World Congress, Helsinki, Finland, 6–10 June 2016. [Google Scholar]
- Yoon, W. Paper No. 201: Development of HiMSEN Dual Fuel Engine Line-up. In Proceedings of the 28th CIMAC World Congress, Helsinki, Finland, 6–10 June 2016. [Google Scholar]
- Energy Information Administration (EIA). Available online: https://www.eia.gov/dnav/ng/NG_PRI_FUT_S1_M.htm (accessed on 2 February 2018).
- Mooser, D. Brenngase und Gasmotoren. In Handbuch Dieselmotoren, 3rd ed.; Aufl, K., Mollenhauer, K., Tschöke, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Redtenbacher, C.; Kiesling, C.; Wimmer, A.; Sprenger, F.; Fasching, P.; Eichelseder, H. Dual Fuel Brennverfahren—Ein zukunftsweisendes Konzept vom PKW-bis zum Großmotorenbereich? In Proceedings of the 37th International Vienna Motor Symposium, Vienna, Austria, 28–29 April 2016; pp. 403–428. [Google Scholar]
- Krenn, M.; Redtenbacher, C.; Pirker, G.; Wimmer, A. A new approach for combustion modeling of large dual-fuel engines. In Proceedings of the Heavy-Duty, On- und Off-Highway Engines 2015—10th International MTZ Conference, Speyer, Germany, 24–25 November 2015; pp. 1–19. [Google Scholar]
- Königsson, F. On Combustion in the CNG—Diesel Dual Fuel Engine. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Manns, H.J.; Brauer, M.; Dyja, H.; Beier, H.; Lasch, A. Diesel CNG—The Potential of a Dual Fuel Combustion Concept for Lower CO2 and Emissions; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Redtenbacher, C.; Kiesling, C.; Malin, M.; Wimmer, A.; Pastor, J.V.; Pinotti, M. Potential and Limitations of Dual Fuel Operation of High Speed Large Engines. In Proceedings of the ASME 2016 Internal Combustion Fall Technical Conference, San Diego, CA, USA, 4–7 November 2018. [Google Scholar]
- Hanenkamp, A.; Böckhoff, N. The 51/60 DF and V32/40 PGI—Modern Gas engines from MAN Diesel SE. Their way from development to serial application. In Proceedings of the 6th Dessauer Gasmotoren-Konferenz, Dessau-Roßlau, Germany, 26–27 March 2009; pp. 129–142. [Google Scholar]
- Troberg, M.; Portin, K.; Jarvi, A. Paper No. 406: Update on Wärtsilä 4-stroke Gas Product Development. In Proceedings of the 27th CIMAC World Congress, Shanghai, China, 13–16 May 2013. [Google Scholar]
- Böckhoff, N.; Mondrzyk, D.; Terbeck, S. Continuous Development of the 51/60G to the 51/60G TS of the MAN Diesel and Turbo SE. In Proceedings of the 10th Dessauer Gasmotoren-Konferenz, Dessau-Roßlau, Germany, 6–7 April 2017; pp. 61–71. [Google Scholar]
- Donateo, T.; Carlucci, A.P.; Strafella, L.; Laforgia, D. Experimental Validation of a CFD Model and an Optimization Procedure for Dual Fuel Engines; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Hockett, A.; Hampson, G.; Marchese, A.J. Development and Validation of a Reduced Chemical Kinetic Mechanism for Computational Fluid Dynamics Simulations of Natural Gas/Diesel Dual-Fuel Engines. Energy Fuels 2016, 30, 2414–2427. [Google Scholar] [CrossRef]
- Maghbouli, A.; Saray, R.K.; Shafee, S.; Ghafouri, J. Numerical study of combustion and emission characteristics of dual-fuel engines using 3D-CFD models coupled with chemical kinetics. Fuel 2013, 106, 98–105. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Saray, R.K.; Poorghasemi, K.; Maghbouli, A. A numerical investigation on combustion and emission characteristics of a dual fuel engine at part load condition. Fuel 2016, 166, 309–319. [Google Scholar] [CrossRef]
- Li, Y.; Guo, H.; Li, H. Evaluation of Kinetics Process in CFD Model and Its Application in Ignition Process Analysis of a Natural Gas-Diesel Dual Fuel Engine; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Maurya, R.K.; Mishra, P. Parametric investigation on combustion and emissions characteristics of a dual fuel (natural gas port injection and diesel pilot injection) engine using 0-D SRM and 3D CFD approach. Fuel 2017, 210, 900–913. [Google Scholar] [CrossRef]
- Colin, O.; Benkenida, A. The 3-Zones Extended Coherent Flame Model (ECFM3Z) for Computing Premixed/Diffusion Combustion. Oil Gas Sci. Technol. 2004, 59, 593–609. [Google Scholar] [CrossRef]
- Colin, O.; da Cruz, A.P.; Jay, S. Detailed chemistry-based auto-ignition model including low temperature phenomena applied to 3-D engine calculations. Proc. Combust. Inst. 2005, 30, 2649–2656. [Google Scholar] [CrossRef]
- Subramanian, G.; da Cruz, A.P.; Colin, O.; Vervisch, L. Modeling Engine Turbulent Auto-Ignition Using Tabulated Detailed Chemistry; SAE International: Warrendale, PA, USA, 2007; pp. 776–790. [Google Scholar]
- Subramanian, G.; Vervisch, L.; Ravet, F. New Developments in Turbulent Combustion Modeling for Engine Design: ECFM-CLEH Combustion Model; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Belaid-Saleh, H.; Jay, S.; Kashdan, J.; Ternel, C.; Mounaim-Rousselle, C. Numerical and Experimental Investigation of Combustion Regimes in a Dual Fuel Engine; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Colin, O.; Benkenida, A.; Angelberger, C. 3D Modeling of Mixing, Ignition and Combustion Phenomena in Highly Stratified Gasoline Engines. Oil Gas Sci. Technol. 2003, 58, 47–62. [Google Scholar] [CrossRef]
- Pastor, J.V.; Payri, R.; Garcia-Oliver, J. Analysis of Transient Liquid and Vapor Phase Penetration for Diesel Sprays under Variable Injection Conditions. At. Sprays 2011, 21, 503–520. [Google Scholar] [CrossRef]
- Malalasekera, W.; Versteeg, H.K. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Pearson Education Limited: London, UK, 1995. [Google Scholar]
- Merker, G.P.; Schwarz, C. Grundlagen Verbrennungsmotoren; Vieweg Teubner: Wiesbaden, Germany, 2009. [Google Scholar]
- Mastorakos, E. Ignition of turbulent non-premixed flames. Prog. Energy Combust. Sci. 2009, 35, 57–97. [Google Scholar] [CrossRef]
- Kuo, K.K.; Acharya, R. Fundamentals of Turbulent Multi-Phase Combustion; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Schlatter, S.; Schneider, B.; Wright, Y.; Boulouchos, K. Experimental Study of Ignition and Combustion Characteristics of a Diesel Pilot Spray in a Lean Premixed Methane/Air Charge Using a Rapid Compression Expansion Machine; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Schlatter, S.; Schneider, B.; Wright, Y.M.; Boulouchos, K. N-heptane micro pilot assisted methane combustion in a Rapid Compression Expansion Machine. Fuel 2016, 179, 339–352. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; Awomolo, O.; Akber, K. Ignition characteristics of heptane–hydrogen and heptane–methane fuel blends at elevated pressures. Int. J. Hydrogen Energy 2011, 36, 15392–15402. [Google Scholar] [CrossRef]
- Ban, M.; Vujanovic, M. Investigation of Dual-fuel Combustion Properties for CFD Simulation Purposes. In Proceedings of the 11th Conference on Sustainable Development of Energy, Water and Environment Systems, Lisbon, Portugal, 4–9 September 2016. [Google Scholar]
- Demosthenous, E.; Borghesi, G.; Mastorakos, E.; Cant, R.S. Direct Numerical Simulations of premixed methane flame initiation by pilot n-heptane spray autoignition. Combust. Flame 2016, 163, 122–137. [Google Scholar] [CrossRef]
- Wang, Z.; Abraham, J. Fundamental physics of flame development in an autoigniting dual fuel mixture. Proc. Combust. Inst. 2015, 35, 1041–1048. [Google Scholar] [CrossRef]
- Li, G.; Liang, J.; Zhang, Z.; Tian, L.; Cai, Y.; Tian, L. Experimental investigation on laminar burning velocities and Markstein lengths of premixed methane-n-heptane-air mixtures. Energy Fuels 2015, 29, 4549–4556. [Google Scholar] [CrossRef]
- Eder, L.; Kiesling, C.; Pirker, G.; Wimmer, A. Development and Validation of a Reduced Reaction Mechanism for CFD Simulation of Diesel Ignited Gas Engines. SAE Int. J. Fuels Lubr. 2009, 1, 675–702. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundementals; McGraw-Hill Education: New York, NY, USA, 1988. [Google Scholar]
- Donateo, T.; Strafella, L.; Laforgia, D. Effect of the Shape of the Combustion Chamber on Dual Fuel Combustion; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Kuppa, K.; Butzbach, G.; Ratzke, A.; Dinkelacker, F. A Numerical Approach for the Prediction of Unburned Hydrocarbon Emissions in Gas Engines. In Proceedings of the 8th International Seminar on Flame Structure: Flame Structure, Berlin, Germany, 21–24 September 2014. [Google Scholar]
- Chevillard, S.; Colin, O.; Bohbot, J.; Wang, M.; Pomraning, E.; Senecal, P.K. Advanced Methodology to Investigate Knock for Downsized Gasoline Direct Injection Engine Using 3D RANS Simulations; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Reitz, R.D. Modeling Atomization Processes in High-Pressure Vaporizing Sprays. At. Sprays Technol. 1987, 3, 309–337. [Google Scholar]
- AVL. AVL FIRE Spray Module—Version Manual 2014.1; AVL: Graz, Austria, 2014. [Google Scholar]
- Dukowicz, J.K. Quasi-Steady Droplet Phase Change in the Presence of Convection; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1979.
- Roth, H.; Giannadakis, E.; Gavaises, M.; Arcoumanis, C.; Omae, K.; Sakata, I.; Nakamura, M.; Yanagihara, H. Effect of Multi-Injection Strategy on Cavitation Development in Diesel Injector Nozzle Holes. SAE Trans. 2005, 114, 1029–1045. [Google Scholar]
- Arcoumanis, C.; Flora, H.; Gavaises, M.; Badami, M. Cavitation in Real-Size Multi-Hole Diesel Injector Nozzle; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Curran, H.J. Rate constant estimation for C1 to C4 alkyl and alkoxyl radical decomposition. Int. J. Chem. Kinet. 2006, 38, 250–275. [Google Scholar] [CrossRef]
- Conaire, M.Ó.; Curran, H.J.; Simmie, J.M.; Pitz, W.J.; Westbrook, C.K. A comprehensive modeling study of hydrogen oxidation. Int. J. Chem. Kinet. 2004, 36, 603–622. [Google Scholar] [CrossRef]
- Mehl, M.; Pitz, W.J.; Westbrook, C.K.; Curran, H.J. Kinetic modeling of gasoline surrogate components and mixtures under engine conditions. Proc. Combust. Inst. 2011, 33, 193–200. [Google Scholar] [CrossRef]
- Smith, G.; Bowman, T.; Frenklach, M. “GRI 3.0 Mechanism”, Gas Research Institutue—GRI, 2000. Available online: http://combustion.berkeley.edu/gri-mech/index.html (accessed on 18 November 2016).
- Mehl, M.; Chen, J.Y.; Pitz, W.J.; Sarathy, S.M.; Westbrook, C.K. An Approach for Formulating Surrogates for Gasoline with Application toward a Reduced Surrogate Mechanism for CFD Engine Modeling. Energy Fuels 2011, 25, 5215–5223. [Google Scholar] [CrossRef]
- Petersen, E.L.; Kalitan, D.M.; Simmons, S.; Bourque, G.; Curran, H.J.; Simmie, J.M. Methane/propane oxidation at high pressures: Experimental and detailed chemical kinetic modeling. Proc. Combust. Inst. 2007, 31, 447–454. [Google Scholar] [CrossRef]
- Niemeyer, K.E.; Sung, C.J.; Raju, M.P. Skeletal mechanism generation for surrogate fuels using directed relation graph with error propagation and sensitivity analysis. Combust. Flame 2010, 157, 1760–1770. [Google Scholar] [CrossRef]
- Bosch, W. Der Einspritzgesetz-Indikator, ein neues Meßgerät zur direkten Bestimmung des Einspritzgesetzes von Einzeleinspritzungen. Mot. Z. 1964, 25, 268–282. (In German) [Google Scholar]
- Kiesling, C.; Redtenbacher, C.; Kirsten, M.; Andreas, W.; Imhof, D.; Berger, J.M. IngmarGarcía-oliver, Detailed Assessment of an Advanced Wide Range Diesel Injector for Dual Fuel Operation of Large Engines. In Proceedings of the CIMAC Congress 2016, Helsinki, Finland, 6–10 June 2016. [Google Scholar]
- Eder, L.; Kiesling, C.; Pirker, G.; Priesching, P.; Wimmer, A. Multidimensional Modeling of Injection and Combustion Phenomena in a Diesel Ignited Gas Engine; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]






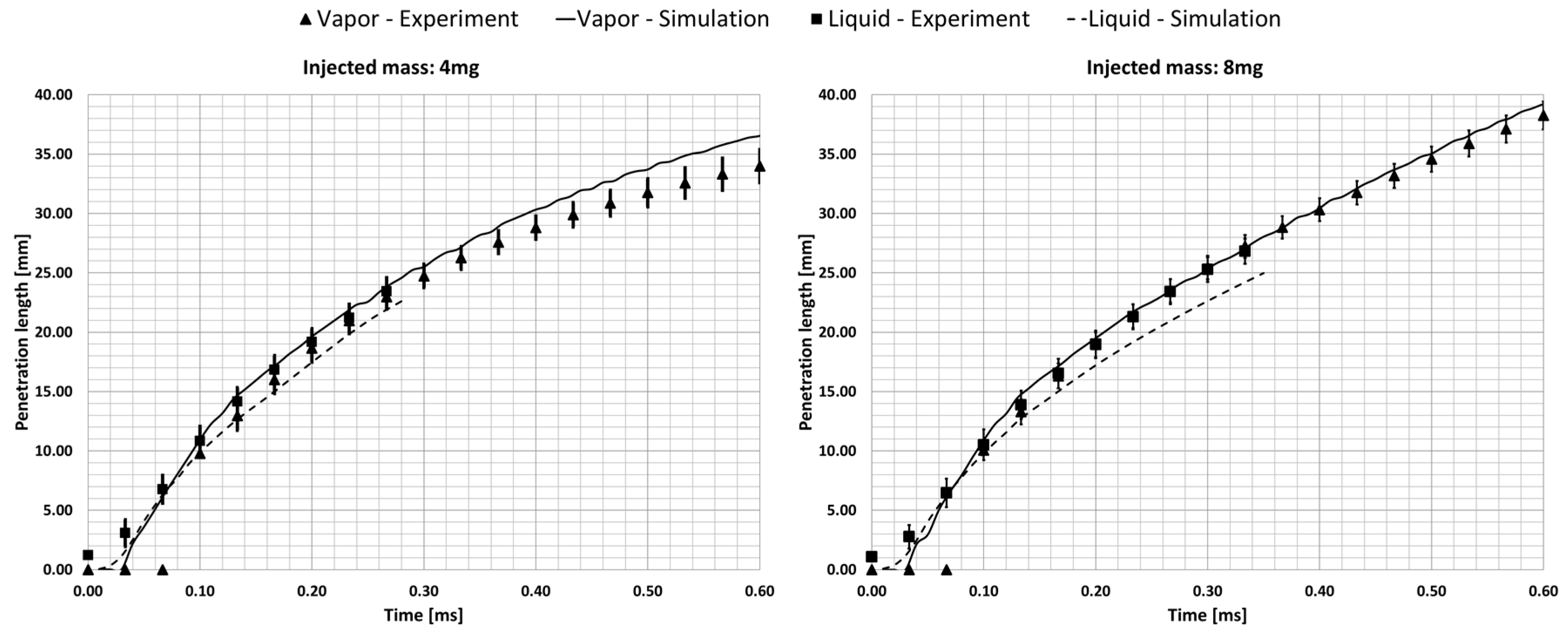
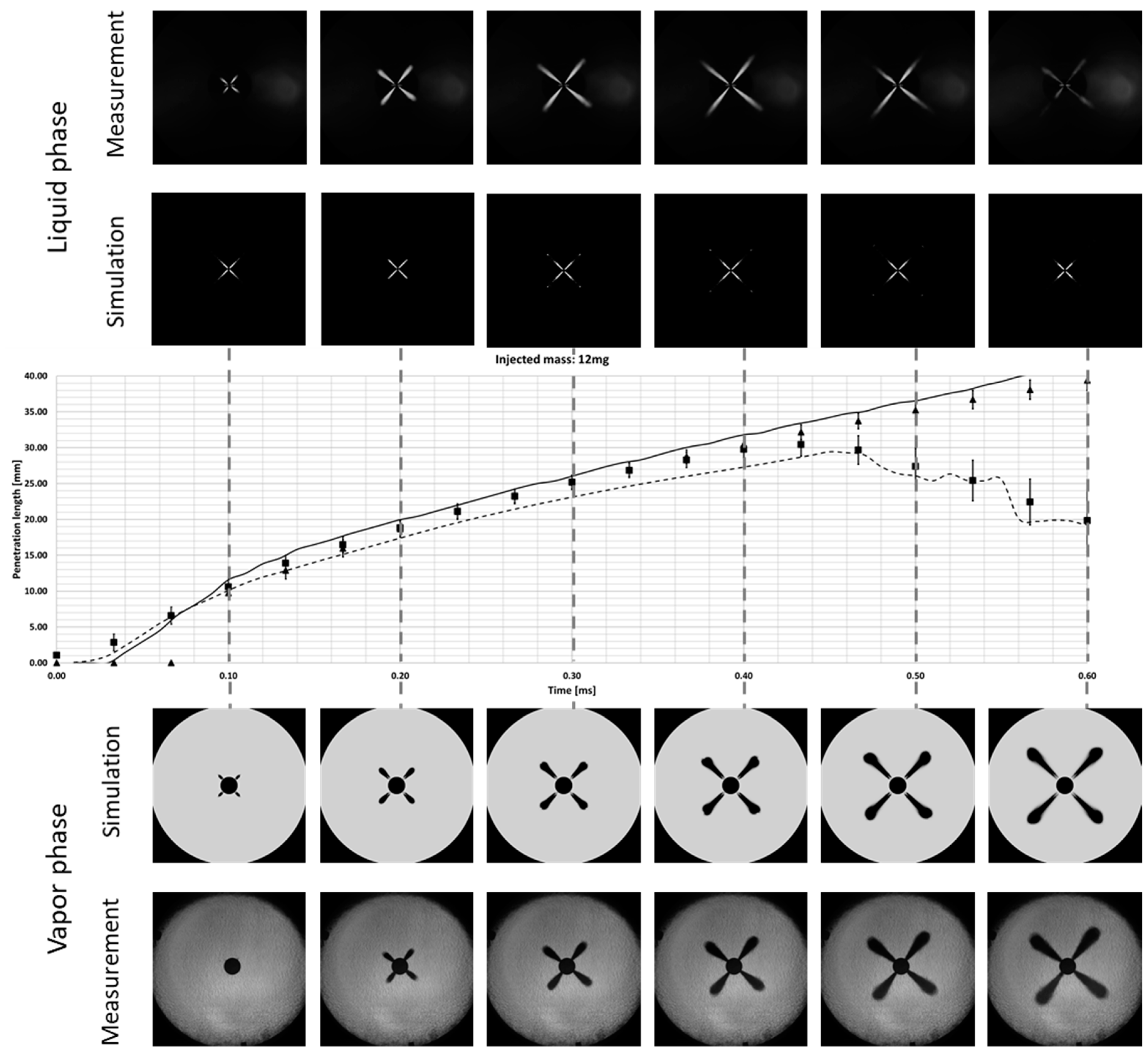
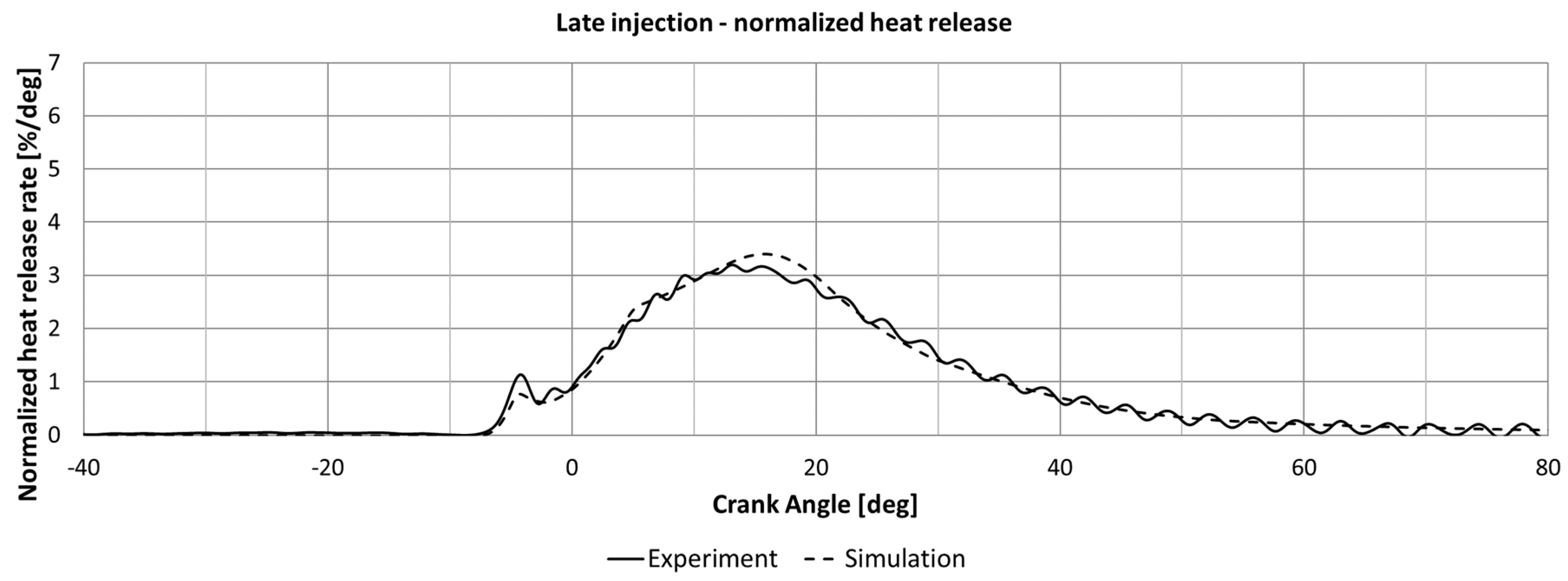
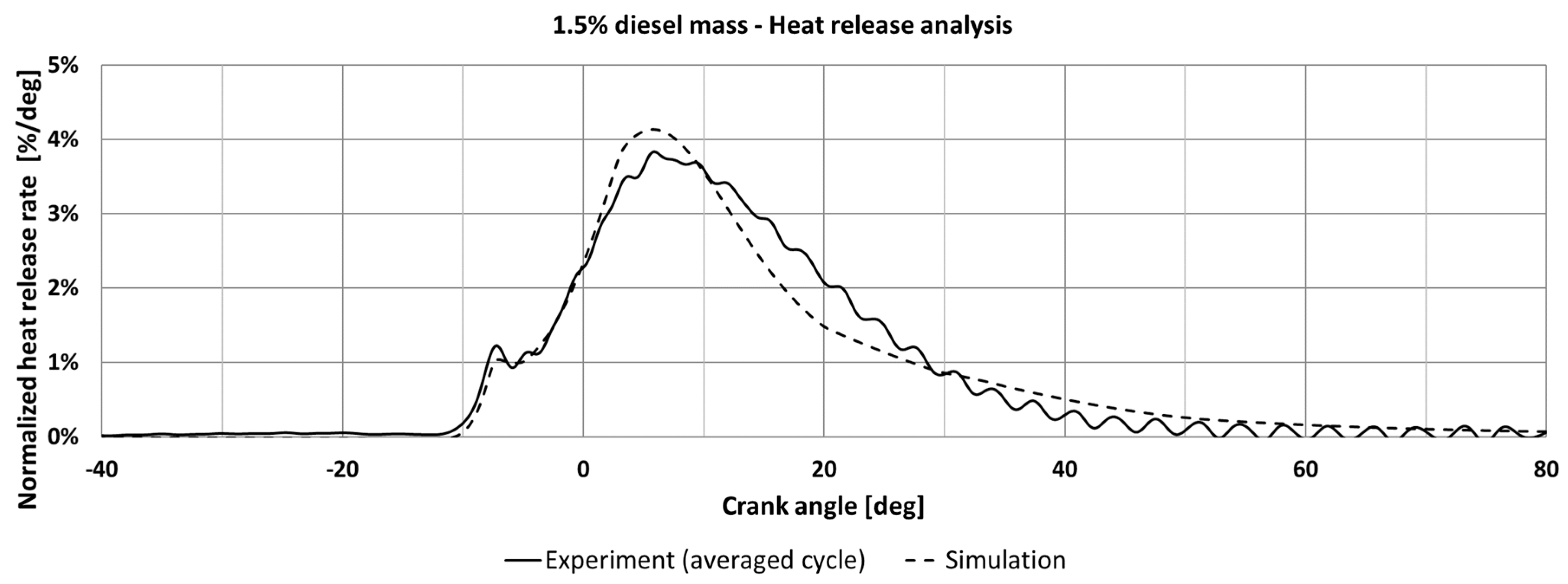


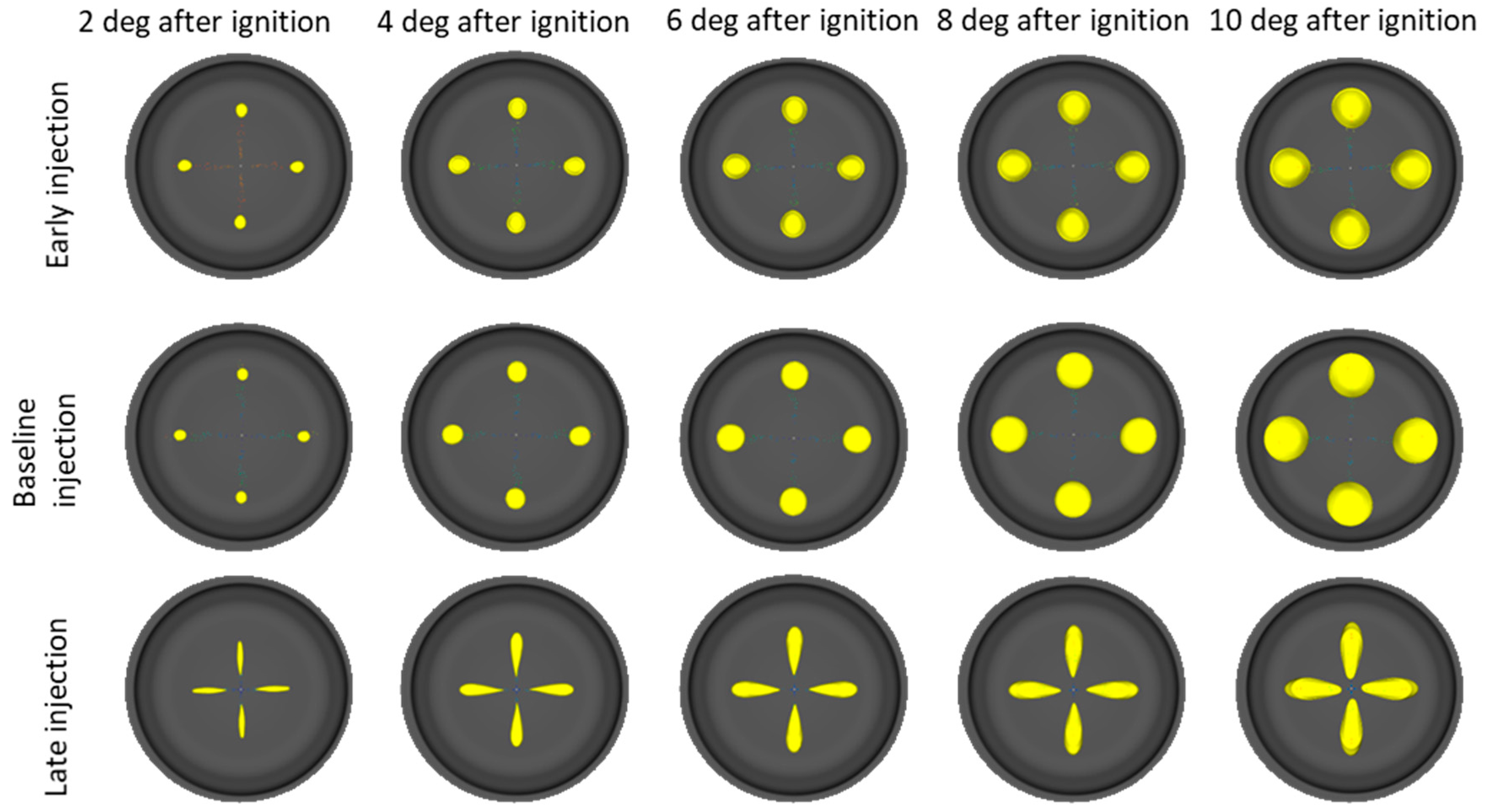
| Hardware Summary |  | |||
| Chamber | Constant volume flow | |||
| Conditions | Preconditioned pressure and temperature | |||
| Fluid | Nitrogen (N2) | |||
| Turbulence | Low | |||
| Selected Test Conditions | ||||
| Rail Pressure (bar) | Injected Mass (mg) | Chamber Pressure (bar) | Chamber Temperature (K) | |
| 1600 | 12 | 60 | 780 | |
| 8 | ||||
| 4 | ||||
| Meshing |  | |
| Type | Sector mesh | |
| Cell size | 0.6 mm (average) | |
| Dimensions | 200 mm in a radial direction | |
| General Setup | ||
| Temporal discretization | 10 μs | |
| Turbulence modeling | RANS approach, k-ζ-f model | |
| Spray submodels | WAVE breakup | |
| Dukowicz evaporation | ||
| O’Rourke turbulent dispersion | ||
| Single Cylinder Engine—Technical Specifications |  | |
| Rated speed | 1500 rpm | |
| Displacement | ≈6 dm3 | |
| Swirl/tumble | ≈0/0 | |
| Charge air | Provided by external compressors with up to 10 bar boost pressure | |
| Gas fuel supply | External mixture formation via Venturi mixer | |
| Diesel fuel supply | Common rail system with up to 1600 bar rail pressure | |
| Simulation Setup |  | |
| Turbulence modeling | RANS approach, k-ζ-f model | |
| Spray | Lagrangian particle tracking | |
| Dukowicz evaporation model | ||
| WAVE breakup model | ||
| Combustion model | ECFM-3Z | |
| Two-stage ignition tabulation | ||
| Initial flame surface density modeling | ||
| Laminar flame speed interpolation from values | ||
| Engine Parameter Variations | |||
|---|---|---|---|
| Variation | Diesel Share (Energetic) (%) | Global Lambda (–) | SOC |
| Start of Current (SoC) | 1.5 | 1.7 | Early |
| 1.5 | 1.7 | Middle | |
| 1.5 | 1.7 | Late | |
| Injected diesel mass | 1.5 | 1.7 | Late |
| 1.0 | 1.7 | Late | |
| 0.5 | 1.7 | Late | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eder, L.; Ban, M.; Pirker, G.; Vujanovic, M.; Priesching, P.; Wimmer, A. Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines. Energies 2018, 11, 643. https://doi.org/10.3390/en11030643
Eder L, Ban M, Pirker G, Vujanovic M, Priesching P, Wimmer A. Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines. Energies. 2018; 11(3):643. https://doi.org/10.3390/en11030643
Chicago/Turabian StyleEder, Lucas, Marko Ban, Gerhard Pirker, Milan Vujanovic, Peter Priesching, and Andreas Wimmer. 2018. "Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines" Energies 11, no. 3: 643. https://doi.org/10.3390/en11030643
APA StyleEder, L., Ban, M., Pirker, G., Vujanovic, M., Priesching, P., & Wimmer, A. (2018). Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines. Energies, 11(3), 643. https://doi.org/10.3390/en11030643





