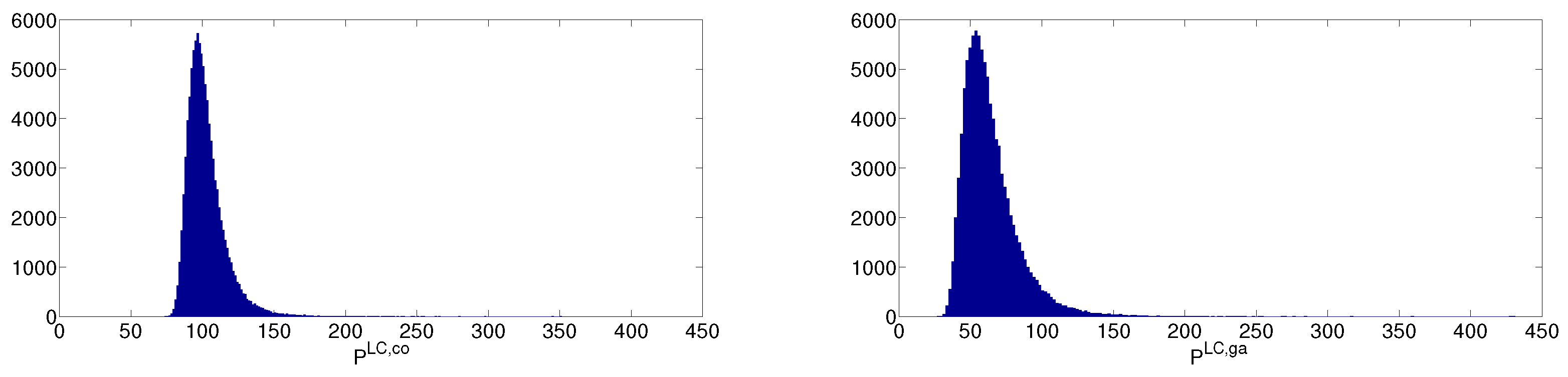
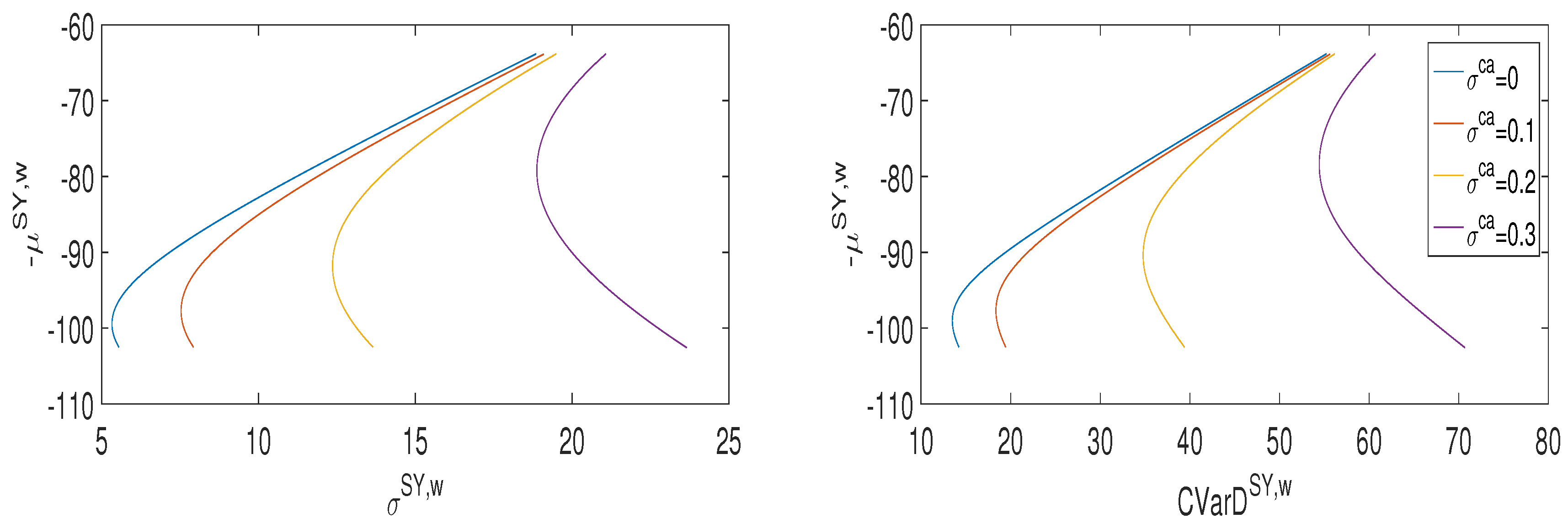In this Section, we will use the stochastic system LCOE theory for investigating the problem of the optimal integration of intermittent sources into the power system. In particular, we will provide the optimal integration solution for any initial configuration of the power system, i.e., for any dispatchable generation sources composition. The main results will be illustrated in the framework of system frontier analysis which offers a global view of the power system in terms of the cost-risk trade-off. To better discuss the impact of optimal integration strategies on the power system, we first determine system frontiers in the case of fully dispatchable (coal and gas) sources. Then, the wind technology will be included using the system LCOE approach. Finally, we will show that frontier analysis is also an important tool for investigating the effects produced on the power system by well defined renewable energy and environmental policies.
3.1. Efficient System Portfolio Frontiers: The Dispatchable Case
One of the main implications of the stochastic LCOE theory is that the joint effect of fossil fuel prices volatility and the CO
price volatility can induce rational electricity producers to diversify their generation portfolios in order to minimize the impact of such factors on the risk of electricity production [
14]. The rationale is that, since LCOE estimates always include uncertainty because of fluctuating fuel and carbon prices, instead of getting rid of this uncertainty by hiding it under the carpet, it is wiser to diversify the investment in such a way to control risk in the best possible way. Since the power system portfolio can be viewed as the generation portfolio obtained by aggregating individual producer’s portfolio choices, such diversification effects have an important impact also on the risk of the overall power system. This risk-reducing diversification is not trivial because the stochastic LCOE of the two fossil fuel components of the portfolio, i.e., coal and gas, are coupled through the CO
price process.
Table A4 shows correlation values between coal and gas stochastic LCOEs for the sequence of the CO
scenarios characterized by
= 0, 0.10, 0.20, 0.30. As
increases, the coupling between
and
strengthen, thus showing that the CO
price volatility parameter
plays an important role in the risk reduction process.
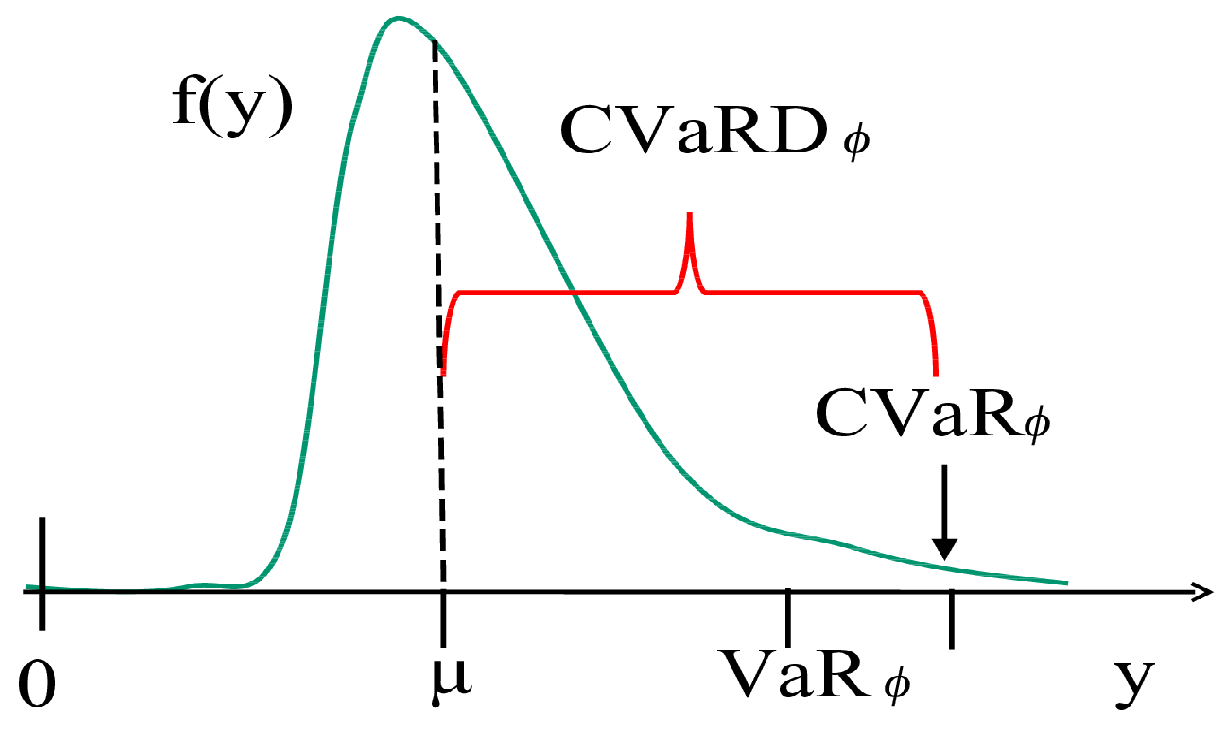
The risk assessment can be performed by determining power system portfolio frontiers. We recall that a power system portfolio belongs to the portfolio frontier if it is at minimum risk (as measured by the standard deviation or by the CVaR deviation of the stochastic system LCOE) among all system portfolios with the same LCOE mean. By using Equation (
12) for the fully dispatchable case (i.e., in the case
), it is possible to draw system portfolio frontiers by plotting for each portfolio composition (i.e., for each value of
and of
with
) the mean against standard deviation of the system LCOE, or the mean against CVaR deviation of the system LCOE. Equation (
12) shows that in the case
, the individual producer’s frontier coincides with the system frontier. In this way, we can investigate the cost-risk trade off of power system portfolios. We will show that a policy maker can use the information contained in the system portfolio frontier to value the impact on the power system of environmental and renewable energy policies.
Figure 1 depicts system portfolio frontiers in the
plane (left panel), and in the
plane (right panel) for each CO
price volatility scenario (in this paper the confidence level for the CVaRD risk measure has been taken equal to
).
By using this approach it is thus possible to determine the composition of that fully dispatchable portfolio which minimizes generation risk, i.e., the portfolio that minimizes the standard deviation or the CVaR deviation of the stochastic LCOE. In this way, optimization can be introduced in the stochastic LCOE problem, picking up portfolios of assets which have minimum dispersion about the expected LCOE as measured by standard deviation, or minimum tail risk as measured by CVaRD.
Table 2 reports respectively the composition of minimum variance portfolios (mvp) and the composition of minimum CVaRD portfolios (mcp) for all considered CO
price volatility scenarios.
We notice that in each scenario the composition of the mvp-portfolio is very similar to the composition of the mcp-portfolio. This means that a variance-risk averse investor (and a variance-risk averse policy maker) and a tail-risk averse investor (and a tail-risk averse policy maker) would select very similar portfolios.
The “efficient power system frontier” is defined as the locus of efficient power system portfolios, i.e., the locus of system portfolios that have minimum cost among all system portfolios with the same level of risk. The efficient power system frontier is represented in each graph by the upward sloping part of the curves, starting from the mvp (or the mcp) portfolio and ending with the full gas, single asset system portfolio. Efficient frontiers provide well defined trade-offs between global cost and risk and between risk an CO
emissions of the power system as a whole. As we move along the efficient frontier from left to right, the gas component increases thus reducing both costs and CO
emissions and increasing the portfolio risk. Among efficient portfolios, minimum risk portfolios (mvp or mcp) are therefore the most costly and the most emitting portfolios.
Table 2 shows that as the volatility of carbon prices increases, the weight of the coal component of such optimal portfolios decreases. As a consequence, the set of efficient portfolios is reduced (see
Figure 1). Increasing values of the CO
price volatility, in fact, make inefficient the most emitting portfolios. This is due to the fact that increasing carbon volatility makes coal generation riskier than natural gas generation, thus increasing the weight of the gas technology within individual producer’s efficient portfolios. This leads to a reduction of both generating costs and CO
emissions but increases risk. From this point of view, frontier analysis is an important tool for jointly investigating diversification and CO
emissions reduction effects on the whole power system due to individual producer’s portfolio choices. In this sense, frontier analysis is an important tool for evaluating market reactions to environmental and renewable energy policies.
3.2. Efficient System Portfolio Frontiers: Including the Wind Asset into the Power System
The first important difference with respect to the fully dispatchable case is that when the wind asset is included in the power system, the individual producer’s portfolio frontiers differs from the system portfolio frontier. This is due to the fact that individual producers can select generation portfolios with any weights of wind and fossil fuel components. In contrast, at system level the wind source has a limited availability. In fact, the fraction of the wind energy in the power system portfolio is constant and is equal to the wind penetration . Nevertheless, an analytical characterization of efficient system portfolios can be given. We will show that a policy maker can use the information contained in the system portfolio frontier to value the impact on the power system of environmental and renewable energy policies.
Looking back to Equation (
12), we notice that the composition of a system portfolio depends on the interplay between two parameters,
and
, defining the coal component of the portfolio
. In fact, if we set a given value of the coal component,
and
can be combined in many (infinite) ways to produce different system portfolios with the same value of the coal component. Since
and
, the values of
and
determine uniquely the gas component too. All these portfolios bear the same risk (as measured by the standard deviation or by the CVaR deviation, see
Appendix D) but have different generation costs (as measured by the mean of their stochastic LCOE). This is due to the fact that the last term in the r.h.s of Equation (
12)
is non stochastic and does not affect risk but it influences the LCOE mean of different system portfolio with the same coal component. In fact
depends on the integration strategy
and by capacity values, but is independent of
. Two main results then follow.
The first result regards the composition of minimum risk portfolios. Such optimal portfolios can be obtained for
and
satisfying the relationship
where “mrp” stands for mvp in the case of standard deviation, and for mcp in the case of CVaR deviation. The gas component is, of course,
and the wind component is
. The proof can be found in
Appendix D.
With respect to the dispatchable case, the weights of both fossil fuels components of minimum risk portfolios are reduced by the factor
. The same factor reduces also the overall risk of such optimal portfolios.
Table 3 and
Table 4 report, respectively, the composition of minimum variance and minimum CVaRD power system portfolios in the wind integrated case.
As a second result, a complete characterization of power system frontier portfolios can be obtained. In fact, in each set of system portfolios with the same coal component (and, consequently, the same gas and wind components, and the same risk) we can find a system portfolio characterized by the minimum expected system LCOE. By definition, such a portfolio is a frontier portfolio. It can be obtained for
, i.e., in the case of a fully gas reduction strategy (
). In fact, Equation (
12) and data reported in
Table 1 show that
is the minimum cost integration strategy for any composition of the system portfolio, i.e., for any level of risk. System frontiers can be then obtained by plotting for each frontier portfolio, i.e., for each value
, the mean against the standard deviation and the mean against the CVaR deviation of the system LCOE. In this manner, the system LCOE theory is able to produce the optimal integration strategy of intermittent generation in an endogenous way.
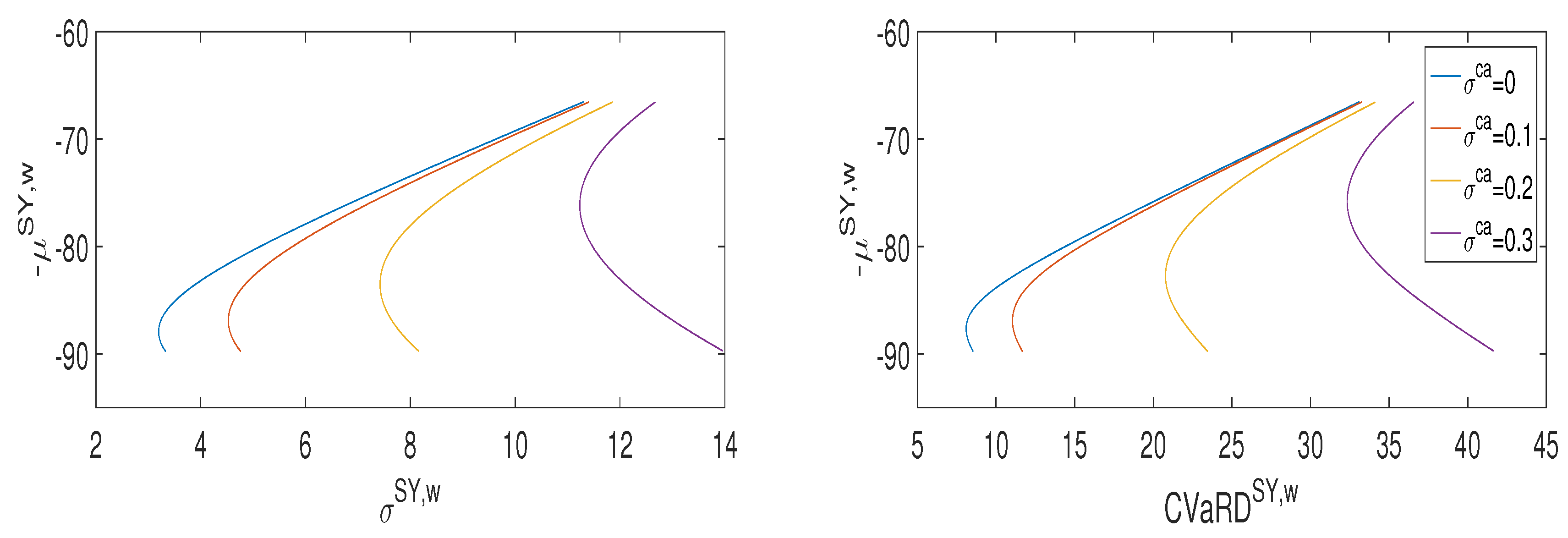
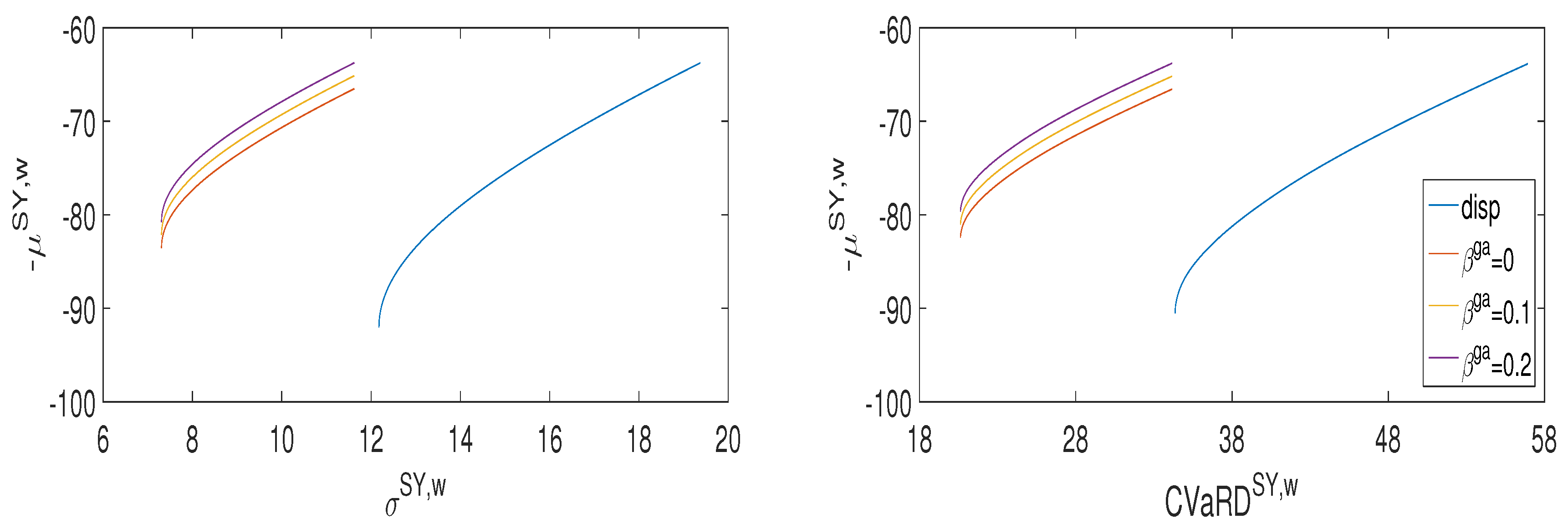
Figure 2 shows system frontiers for both risk measures in the four CO
volatility scenarios for a wind penetration
= 40% and
= 0.
Efficient system frontiers are represented by the upward sloping part of the curves, starting from the mrp portfolio and ending with the two asset, gas and wind, system portfolio. Efficient portfolios are characterized by a coal component , a gas component and a wind component equal to . As in the fully dispatchable case, efficient frontiers provide a well defined trade-off between global cost and risk of the power system. As we move along the efficient frontier from left to right, we note that cost cannot be reduced without increasing risk.
As a further result, we will show that the fully gas reduction strategy
= 0 represents also the minimum risk integration strategy for efficient system portfolios. The minimum risk integration strategy is defined for each fully dispatchable power system portfolio by the value
that minimizes the overall system portfolio risk after the wind inclusion. It can be obtained in a closed form for both risk measures. Limiting our analysis to efficient dispatchable power system portfolios (
) in which a wind component is included, the minimum risk strategy
is given by
and
. The proof can be found in
Appendix D.
Equation (
19) clearly shows that for efficient system portfolios the wind integration is performed also at minimum risk. From this point of view, a renewable energy policy characterized by a well defined penetration target for the intermittent generation and by a fully gas reduction integration strategy, generates efficient power system portfolios in which the intermittent production is integrated at minimum risk. This is an important indication for policy makers aiming at conciliating energy policies with market logics.
Figure 3 illustrates the impact on the overall power system of a renewable energy policy characterized by a given wind penetration target
. Each graph plots 3 system portfolio frontiers, namely for
= 0, 0.1, 0.2, and the dispatchable system frontier for the
= 0.2 scenario. The wind penetration target is
= 40%.
The wind inclusion sensibly reduces the risk of system portfolios. The entity of the risk reduction does not depend on the capacity value
. Referring, in fact, to Equation (
12), we note that the capacity value enters only in the last term
which is non stochastic and does not affect risk. However, the capacity value influences the LCOE mean. Increasing capacity values reduce costs. However, the entity of such a cost reduction is quite low, and as the capacity value increases the portfolio frontier moves slightly north. In
Figure 3 can be observed a reduction of the expected stochastic system LCOE due to the wind integration. This reduction is not obvious as it could seem, because of the extra costs imposed by wind integration, and depends on the specific cost data of the power technologies we used in the empirical analysis.
Efficient system frontiers also show a well defined trade-off between risk and CO
emissions. Let us recall that the CO
emissions rate of a power generation portfolio can be computed as a linear combination of single technology emissions rates, using as weights the fraction of energy generated by each single CO
emitting technology in the portfolio [
14]. Denoting by
the CO
emissions rate due to technology
x measured in tCO
/MWh, the efficient system portfolio emissions rate
is given by
Table 5 shows emission rates computed for optimal standard deviation and optimal CVaRD portfolios in both the fully dispatchable and in the wind integrated case. Emissions are computed using an emissions rate of
tCO
/MWh for coal fired plants and
tCO
/MWh for gas fired plants (see
Table A1).
The inclusion of the wind asset reduces both the risk and the CO
emission rate. The percentage abatement of CO
emissions is exactly equal to the wind penetration in the power system, i.e.,
. The entity of emissions abatement is independent from the capacity values of the power system. Equation (
12) shows, in fact, that capacity values influence generation costs but have no effect on both the risk of the system portfolio and the emissions reduction.
Among efficient system portfolios, minimum risk portfolios are characterized by the maximum CO
emission rate. As we move along the efficient system frontier starting from the minimum risk system portfolio, the risk monotonically increases and the CO
emission rate monotonically decreases. CO
emissions cannot be reduced without increasing risk. Moreover, the abatement of CO
emissions of minimum risk portfolios increases as the CO
price volatility increases (see
Table 5). As in the fully dispatchable case discussed in the previous subsection,
Figure 2 shows that increasing values of the CO
price volatility make inefficient the most emitting portfolios, thus reducing the set of efficient system portfolios. The volatility of carbon market prices plays a crucial role in the emission reduction process also in this wind integrated case because, as in fully dispatchable case, it leads rational investors to efficiently reduce the coal fraction of power generation portfolios for purely risk aversion reasons. CO
price volatility can induces therefore individual producers to modify their portfolio choices to automatically regulate the CO
emissions at a level which is lower, or at lest equal, to the CO
emission level of minimum risk system portfolios (mvp or mcp, depending on the chosen risk measure). From this point of view, the stochastic system LCOE theory is an important tool for investigating jointly diversification and CO
emissions reduction effects on the whole power system due to the reaction of individual producers to environmental and renewable energy policies. Introducing volatility, market-based mechanisms for CO
pricing can produce more significant effects on controlling CO
emissions with respect to non volatile carbon tax schemes. On one side, they contribute to reduce CO
emissions in the power system. On the other side they increase the risk of individual producer’s portfolios, and consequently, the risk of the power system portfolio. This is an important indication for a policy maker concerned with environmental issues coordinated with economic issues.