This section presents the results in terms of power production, device movements, and mooring forces, focusing on the effects of different mooring pre-tension levels.
The results are relative to ordinary and/or extreme WSs. In the latter case, no information on power production is available, and the PTO is considered to be in safe mode.
The WSs are here described by three main variables:
PW, θ, and l/L
P, where
PW is the incident wave power per unit width, θ is the main wave direction and l/L
P is the ratio between the device length and the peak wave length.
PW is selected as it is very relevant for power production and summarizes the effect of wave height and period. The choice of l/L
P was suggested by previous studies ([
14,
23]) showing that the parameter l/L
P affects the overall device behavior, in terms of hydrodynamics, power production, moorings. In fact, the device design length l should be tuned to the local wave climate.
3.1. Power Performance Optimization
The purpose of this subsection is to select the PTO resistance r and the mooring pre-tension level LC that maximize the average power production PPTO under regular wave conditions. This investigation is a very common step for R&D of WECs.
Figure 4 shows the wave averaged power production at prototype scale
PPTO (obtained using Equation 1), vs the tested values of l/L
P, for waves given in
Table 1. Since the 10 RWs are characterized by variable height and constant steepness, the higher and more energetic waves are longer, so that
PW decreases with l/L
P. The three sub-plots of
Figure 4 refer to the three different
LC and include the tests carried out for all the PTO settings (r1 up to r6).
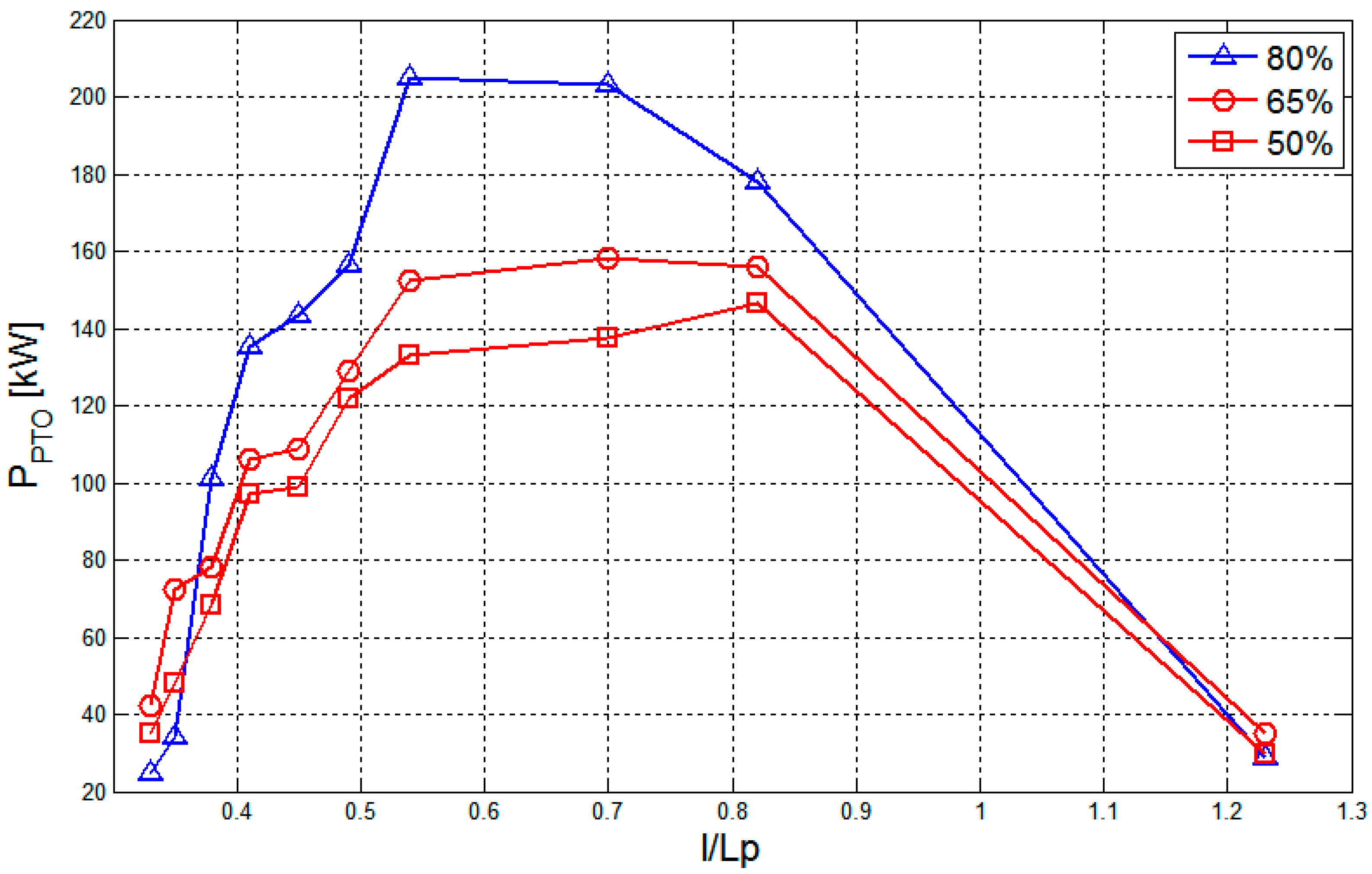
PPTO increases rather monotonically by increasing the PTO resistance up to a certain resistance value, either r4 or r5, somewhat lower than the maximum, and then decreases. More precisely, the best PTO configurations correspond to r4 for LC = 80% (i.e., vertical distance of 0.13 m), and to the r5 (i.e., vertical distance of 0.15 m) for both LC = 65% and LC = 50%. For the slack configuration (LC = 80%) the overall PPTO increases of 2.4 times from the lower to the best resistance.
Figure 5 compares the trends of the
PPTO for each value of
LC (80%, 65%, and 50%) associated to the optimal r-value (r4, r5, and r5, respectively). The figure shows that
PPTO is mooring dependent, being the highest
PPTO values relative to the slack configuration (i.e.,
LC = 80%) for the more energetic RWs. The mooring pre-tension level significantly affects the power production.
3.2. Power Production under Irregular Waves
The main goal of this subsection is to evaluate if the conclusions on the optimal value of r and
Lc, drawn under regular waves, can be extended to ordinary irregular (IR) waves. This type of investigation is not common for the R&D of WECs, since it is very time consuming. In order to reduce the number of tests, and since under extremes the PTO is usually set in safe mode, only ordinary WSs (see
Table 2) are considered in this analysis.
Figure 6 shows the
PPTO at prototype scale as function of l/L
P (as in
Figure 5). It may be observed that the slack configuration leads to the highest power production performance. The production decreases for waves longer than approximately 100 m (i.e., periods larger than 8 s), which suggests that the designed device is suited to mild wave climates. Note that all irregular waves have a steepness in the range 2.5% to 4%.
The highest value of
PPTO around 167 kW may appear too small to justify even the costs of the electrical connections from the device to the shore. Economically feasible installations for DEXA are array schemes [
24], or possibly installations in combination with wind turbines ([
25,
26]) or co-location with other economic activities ([
9]).
By assuming—for sake of simplicity—the same probability of occurrence of each WS, the power production decreases—by increasing the mooring pre-tension level—of 6% for LC = 65% and of 16% for LC = 50% compared to LC = 80%. Regardless of LC, the sets of PPTO show high values when l/LP < 0.70.
In order to find the optimal range of operation, the efficiency η instead of the total power production is investigated. The values of η are derived as the ratio between
PPTO and the value of the available wave power
PW, based on the expressions
where ρ is the water density; g is the gravity acceleration; c
g is the wave group celerity, function of the depth h equal (at full scale) to 27 m and of the energetic wave period T
e ≈ 0.9 T
p; b is the device width, equal to 22.8 m. The values of H
S and T
p were derived—for each WG—through a zero-down crossing analysis. In Equation (2), the average values of H
S and T
P recorded at the first seven WGs were considered (see
Figure 3).
The efficiency can be described by a different non-dimensional quantity, given by the product of k and C
W, where k is the wave number and C
W is the capture width (also termed capture length, [
27]), i.e., the ratio between the power output and the density of power flux of the incident wave front.
Table 3 synthesizes the values of
PPTO,
PW, and η for the three values of
LC. The dependence of η on l/L
P for the three
LC shows pretty well marked peaks around l/L
P = 0.80 or greater (see
Table 3). This result highlights the correlation between the device dimensions and the climate at the site of installation, hence the device length l should be approximately equal to the typical wave length L
P to maximize η. Due to the negative correlation with L
P, this device seems ideal for areas with short fetch rather than oceanic wave climates.
For
LC = 80%, the trends of η under oblique WSs are similar to the case of perpendicular waves, i.e., with peaks around l/L
P = 0.80. The effects of different wave obliquities seem to be limited, however η tends to decrease for the largest value of β, confirming the need to design the mooring system to allow an easy device re-orientation to the incoming waves (see
Table 3).
The results under regular WSs are confirmed, i.e., the most efficient mooring condition corresponds to LC = 80% and the best PTO setting is r4.
3.3. Device Movements
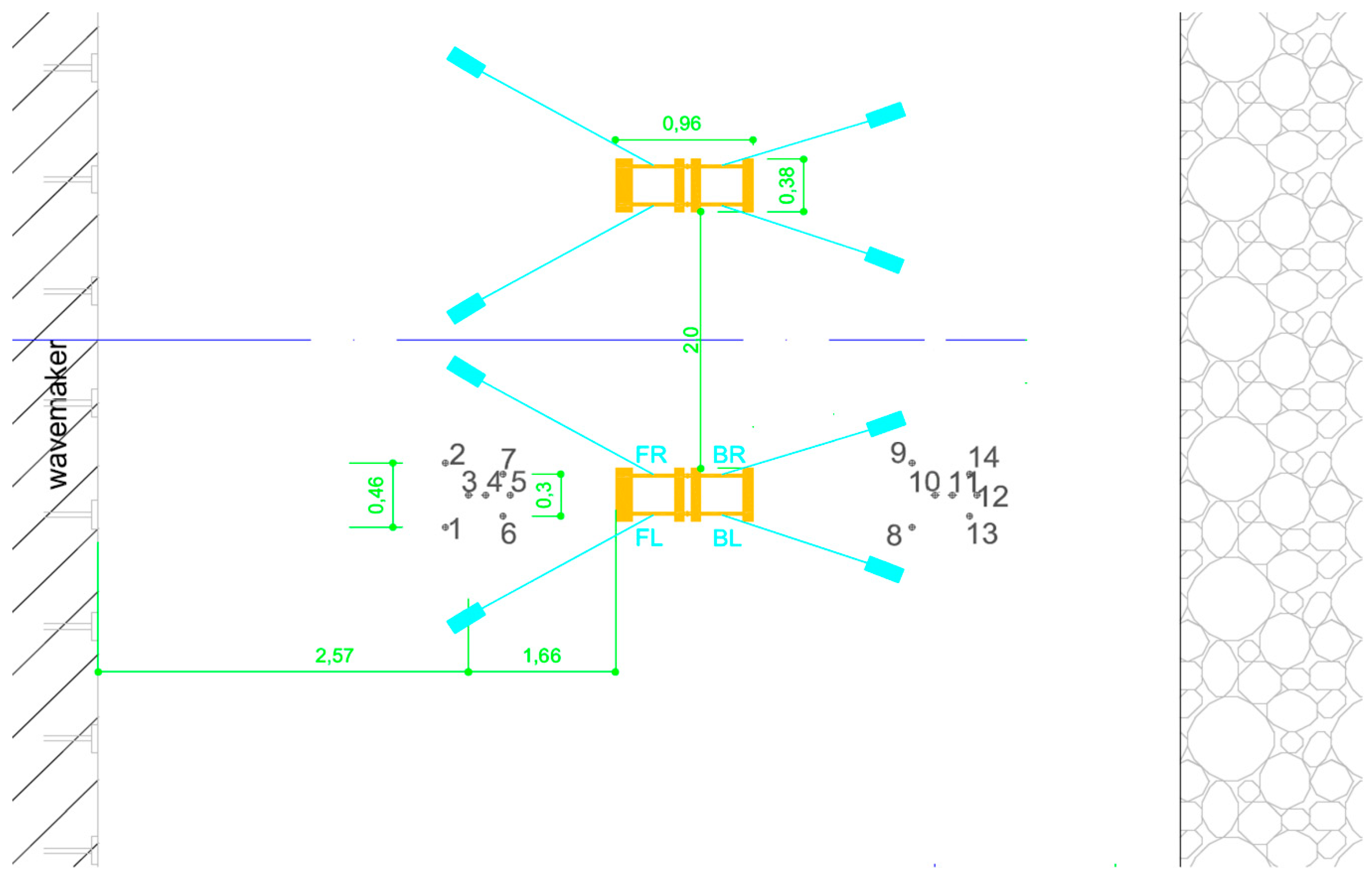
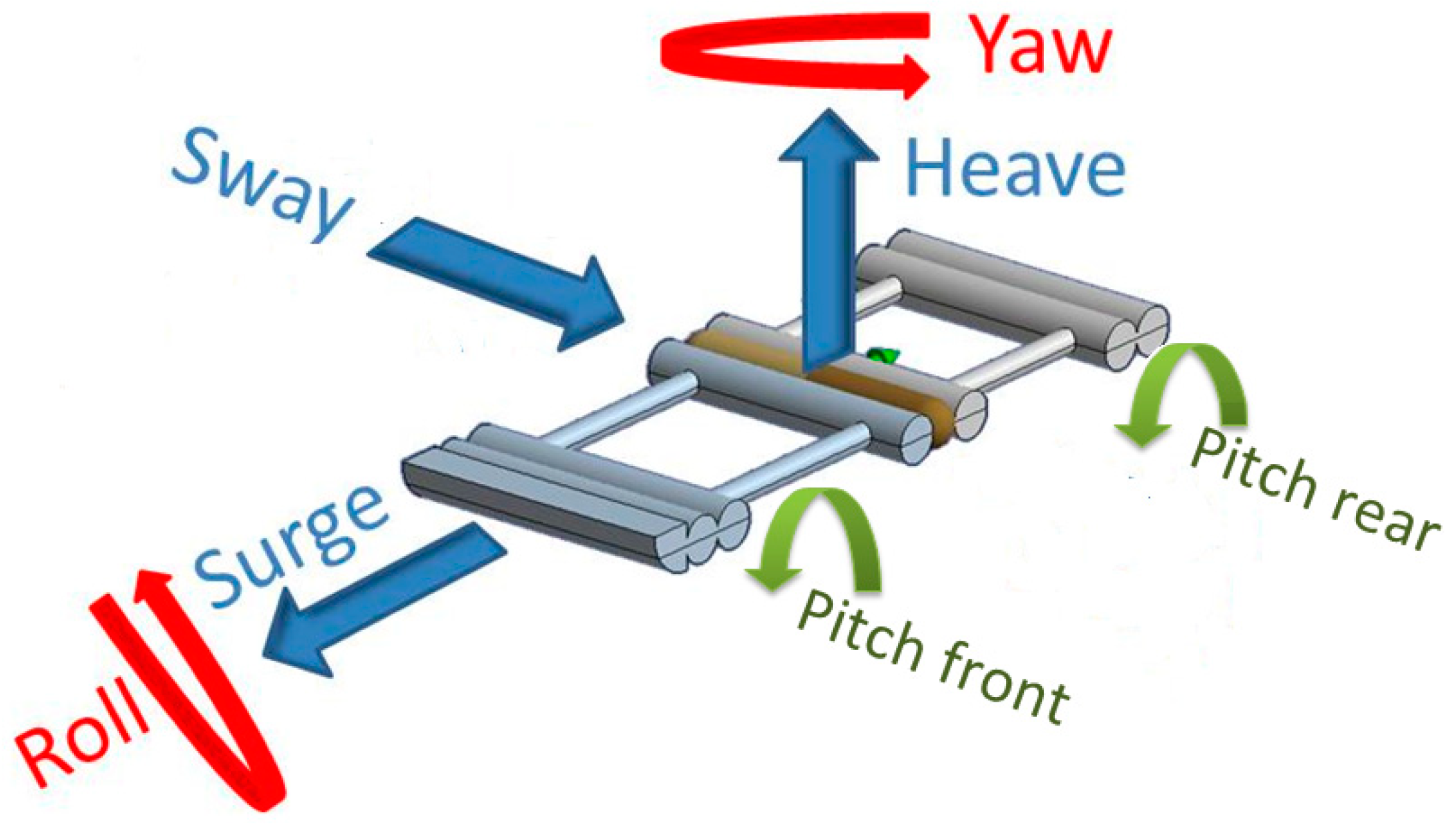
The possible degrees of freedom (DoF) of the device under analysis are 7 (see
Figure 7), i.e., one more than the 6 canonical DoF of a rigid body, since the two pontoons have a separate pitch motion (that activates the PTO system). In order to give a physically relevant information, the pitch of the front and rear pontoons are described through their average and their difference (named relative pitch in the following).
In order to derive the device movements, the following steps were undertaken:
double integration of the MTi signals to obtain positions from accelerations;
high-pass filter of the obtained position signals, to remove the linear and eventually second order terms caused by the double integration procedure;
transposition of the signal from the local to a fixed coordinate system (centered at the hinge position);
analysis of the LVDT placed on the PTO, in order to derive the time series of the relative pitch angle between the pontoons. Actually, the same information can be obtained as the instantaneous difference between the pitch signals of the two MTi placed on the two pontoons of the same device (see
Figure 2). The obtained relative pitch was not as accurate as the LVDT output and therefore the latter was preferred.
The amplitudes of the oscillations were derived from a zero-down crossing analysis of the MTi signals. The two MTi signals (front and rear pontoons) were averaged.
Table 4 shows the amplitude statistics for 5 degrees of freedom in terms of the mean of the 10% higher values, for each perpendicular ordinary WS and for the three
LC.
The amplitudes in general tend to increase with increasing HS and to decrease with increasing l/LP. For l/LP = 1.21 both translations and rotations have the minimum value and appear to be substantially independent from LC.
The amplitude of the movements (surge, sway, heave) depend on LC and on l/LP. In particular, the pretension level LC has a large influence on the movements for small wavelength, i.e., l/LP < 0.70.
For large l/LP < 0.70, and when the mooring is slack, the device easily rides the waves and it has a significant vertical motion (i.e., high heave values), whereas if the mooring is taut the horizontal component is more relevant (i.e., high surge values).
The sway oscillations are significantly limited compared to the heave and surge movements, proving that the mooring system is effective in keeping the device position. This result is important for marine spatial planning issues and/or possible collisions between closer devices, because it leads to higher device density, i.e., lower marine occupied space for the same number of devices.
The rotations are also mooring dependent (see
Table 4). In particular, yaw movements tend to decrease with decreasing
LC, whereas the roll movements are larger for the intermediate pretension level
LC.
All the movements tend to decrease by decreasing HS, i.e., increasing l/LP, with the exception of the roll that is almost constant. Roll appears to depend on the plan layout of the chains and on the rigidity to this degree of freedom.
Table 5 summarizes the translations by varying the wave obliquity β for the same
LC = 80%. All the translations tend to increase by increasing β especially for higher WSs (i.e., l/L
P < 0.5). The effects of β are more evident for the sway motion, i.e., the greater β the greater the motion, regardless of the l/L
P values.
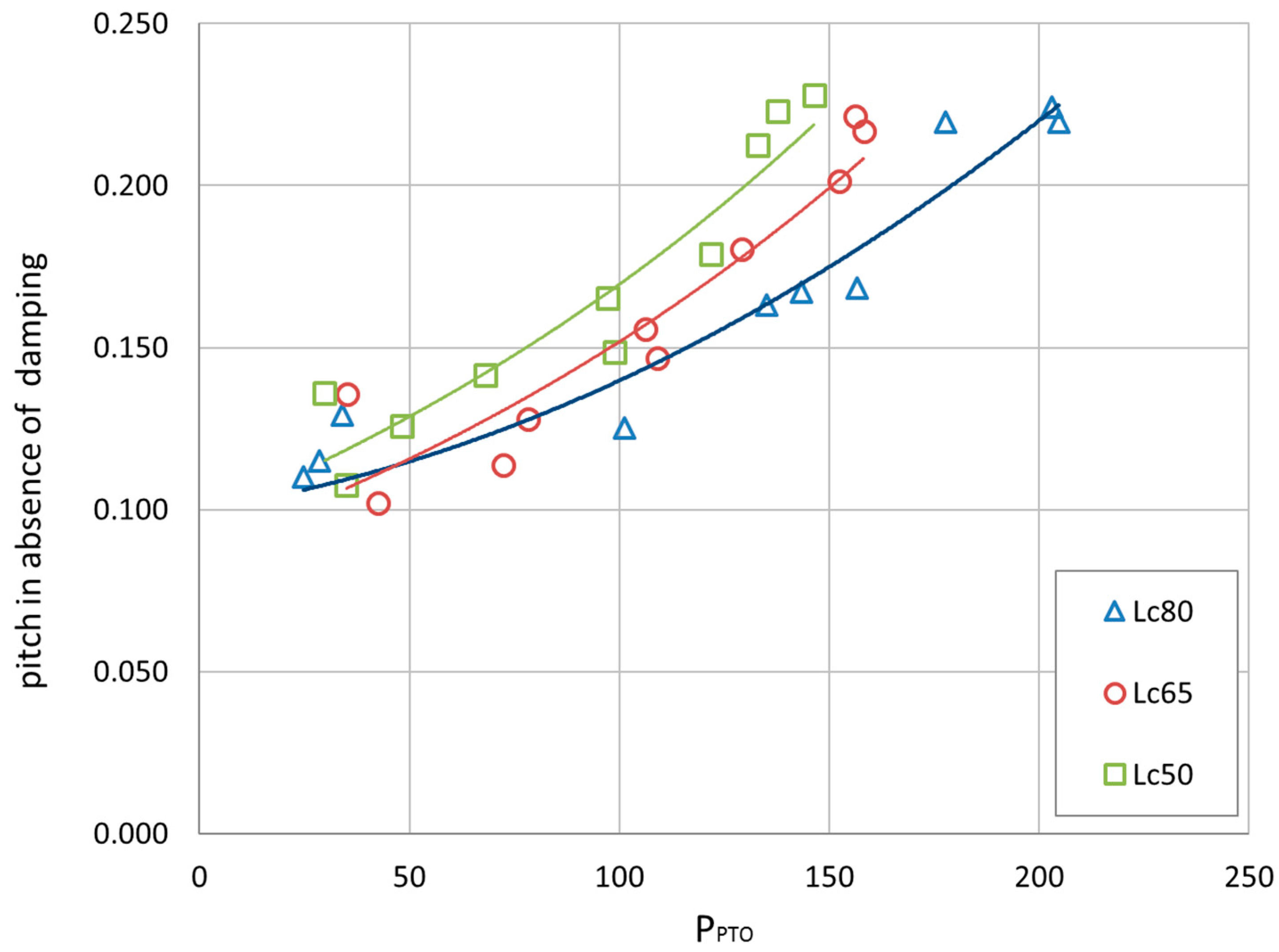
The pitch movements are extremely affected by the PTO setting. For very loose PTO resistance, the device is very mobile, and the opposite occurs for stiff resistances.
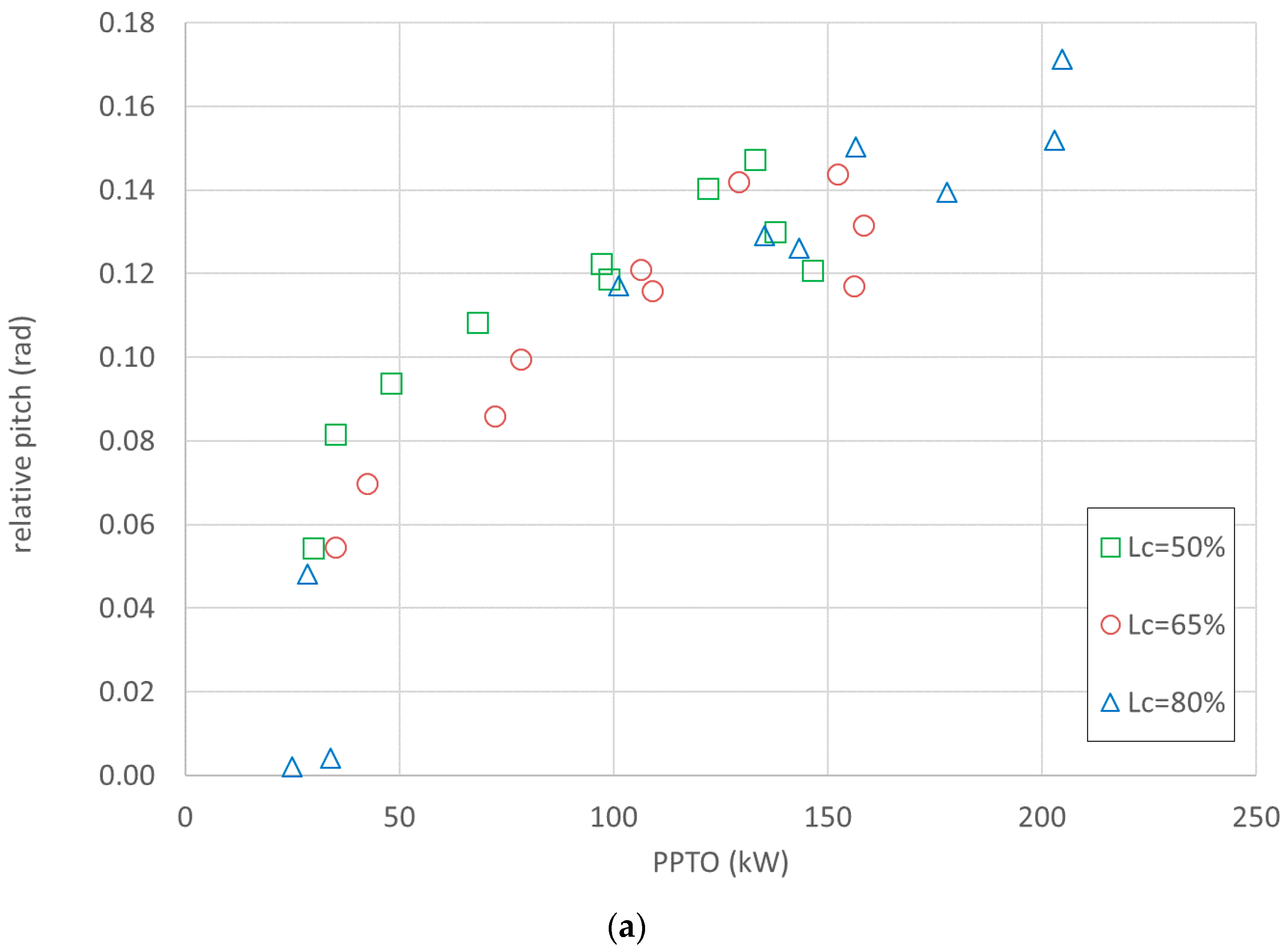
Figure 8 shows the effects in terms of relative pitch and the corresponding
PPTO for the different r settings (from 1 to 5), under the same irregular WS3. The datasets are grouped by the value of the pretension level. The relative pitch ranges from 0.11 to 0.23 rad (i.e., between 6° and 13°) and the
PPTO from 90 kW to 200 kW. Large data scatter can be observed for all WSs, showing that that the value of r and partially the mooring configuration affect the movements and the efficiency.
However, a homogeneous response characterises the tests carried out under the same PTO resistance setting. In particular, only the tests carried out under optimal PTO setting are selected in the following analysis, i.e., r4, r5, r5 for LC = 80, 65, and 50% respectively.
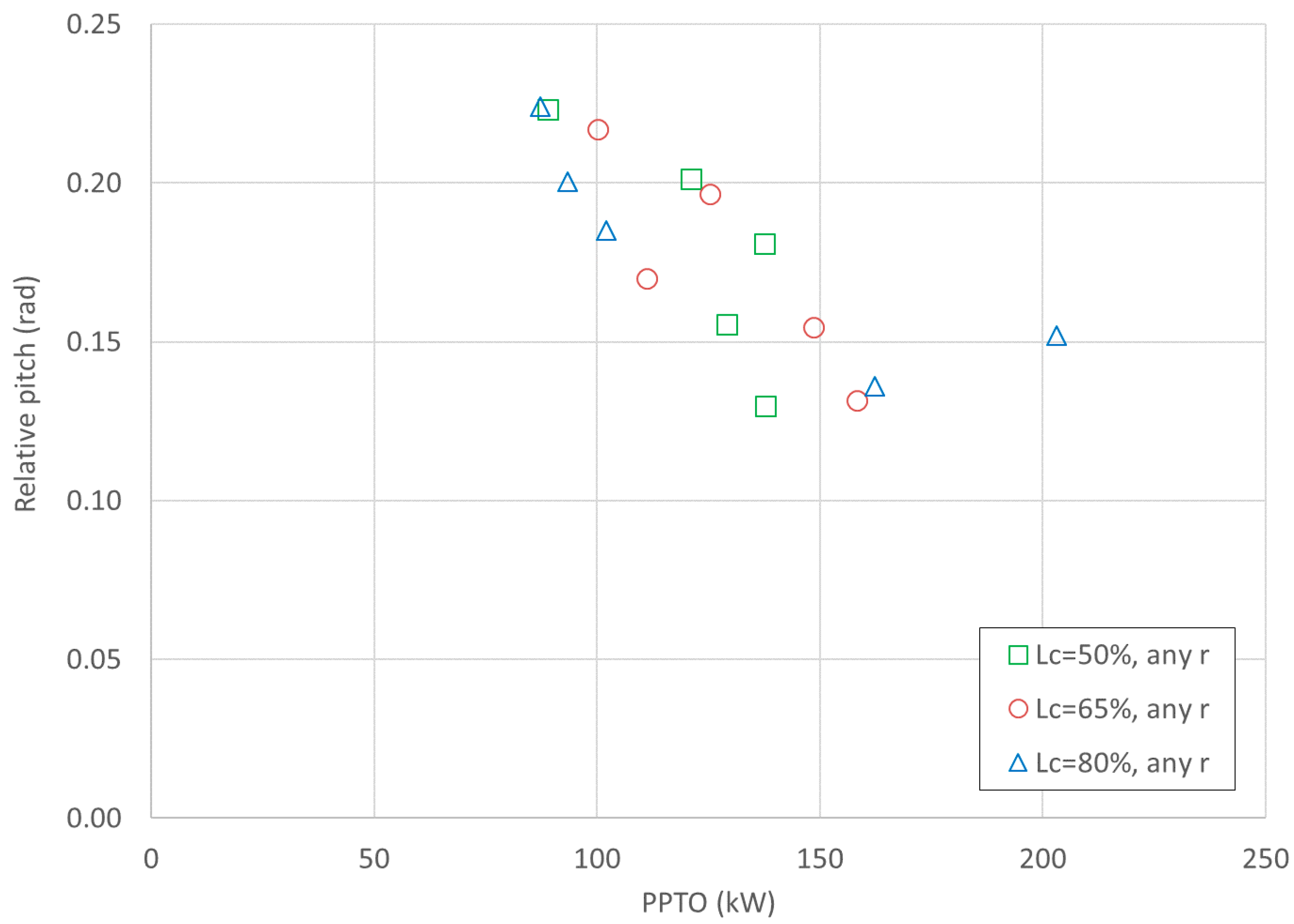
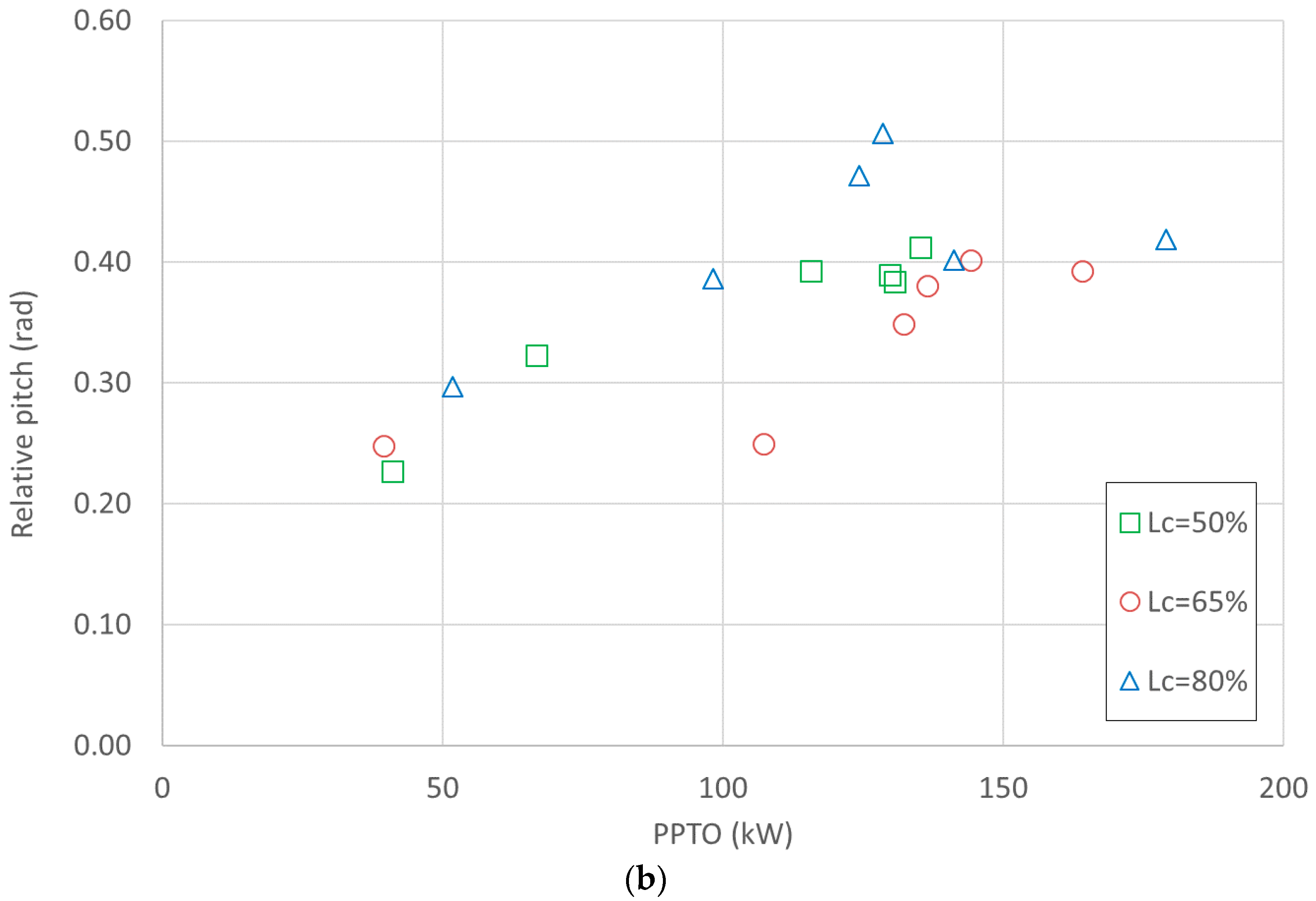
Figure 9 shows the experimental correlation between the upper 10% quantile of the relative pitch and the device power production, for the different mooring configurations, under regular and irregular WSs. The produced
PPTO is proportional to the relative pitch motion for a given PTO setting, as it may be argued by observing Equation (1). The proportionality depends also on the wave characteristics, and particularly on the frequency. The larger production is found for
LC = 80% (r = 4), coherently with
Figure 5. Under regular waves, the maximum value of the relative pitch is approximately 0.18 rad (10°) whereas the maximum is of order 0.5 rad (28°) under irregular waves.
The relative and absolute pitch are also well correlated to the incident wave power
PW. This is a consequence of the correlation between the available wave power and the produced power, for the same PTO setting.
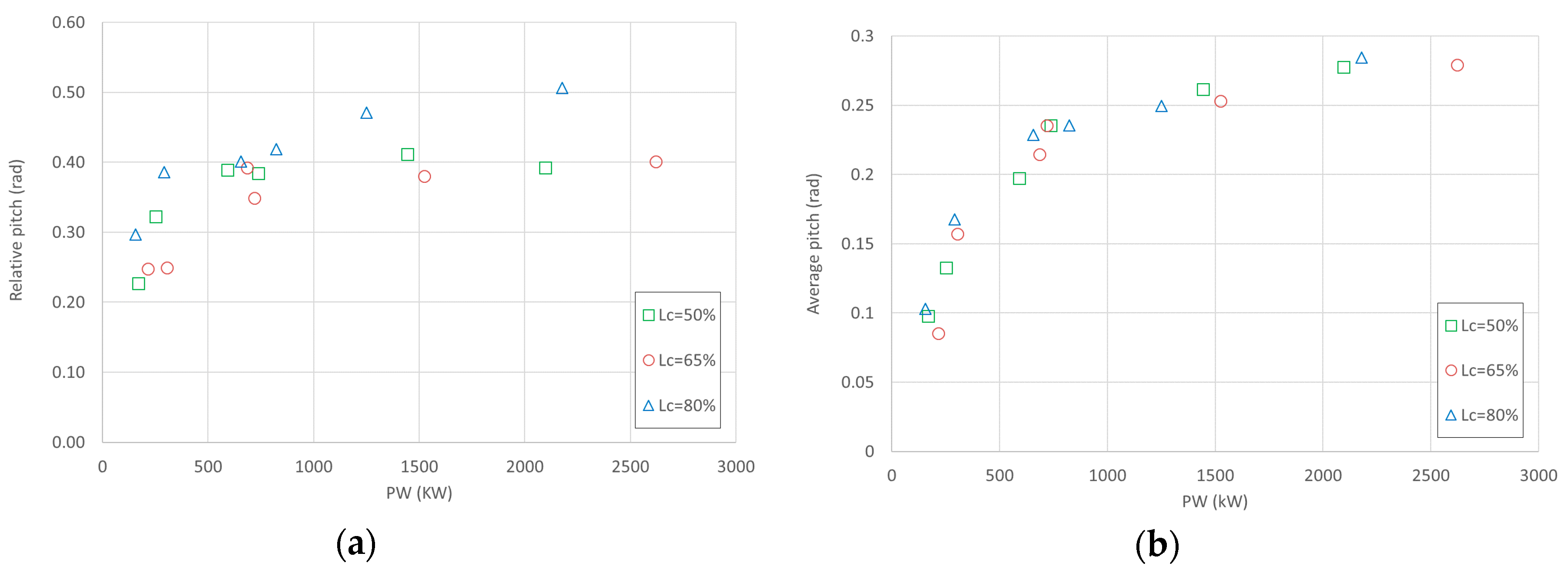
Figure 10 shows the almost monotonic trend of the relative pitch (top panel) and of the mean pitch (bottom panel) as a function of
PW. The combination of
LC = 80% and r = 4 gives the larger relative pitch for all conditions. However, the average pitch is the same for the three
LC values. It should be noted that the relative pitch is quite variable, being strongly related to power harvesting. Actually, the relative pitch is larger than the average pitch in case of large production.
From the information gathered above, it is clear that also the average pitch is strongly correlated to PPTO and to the PTO setting. It therefore becomes interesting to experimentally relate the motion of the structure under optimal PTO setting to the motion obtained in the absence of the PTO, under the same incident wave conditions.
For this purpose, only the regular WSs are considered and the setting r=1 is assumed to represent the ‘absence of PTO’ (or undamped case), since it corresponds to a very loose resistance in the air cylinder.
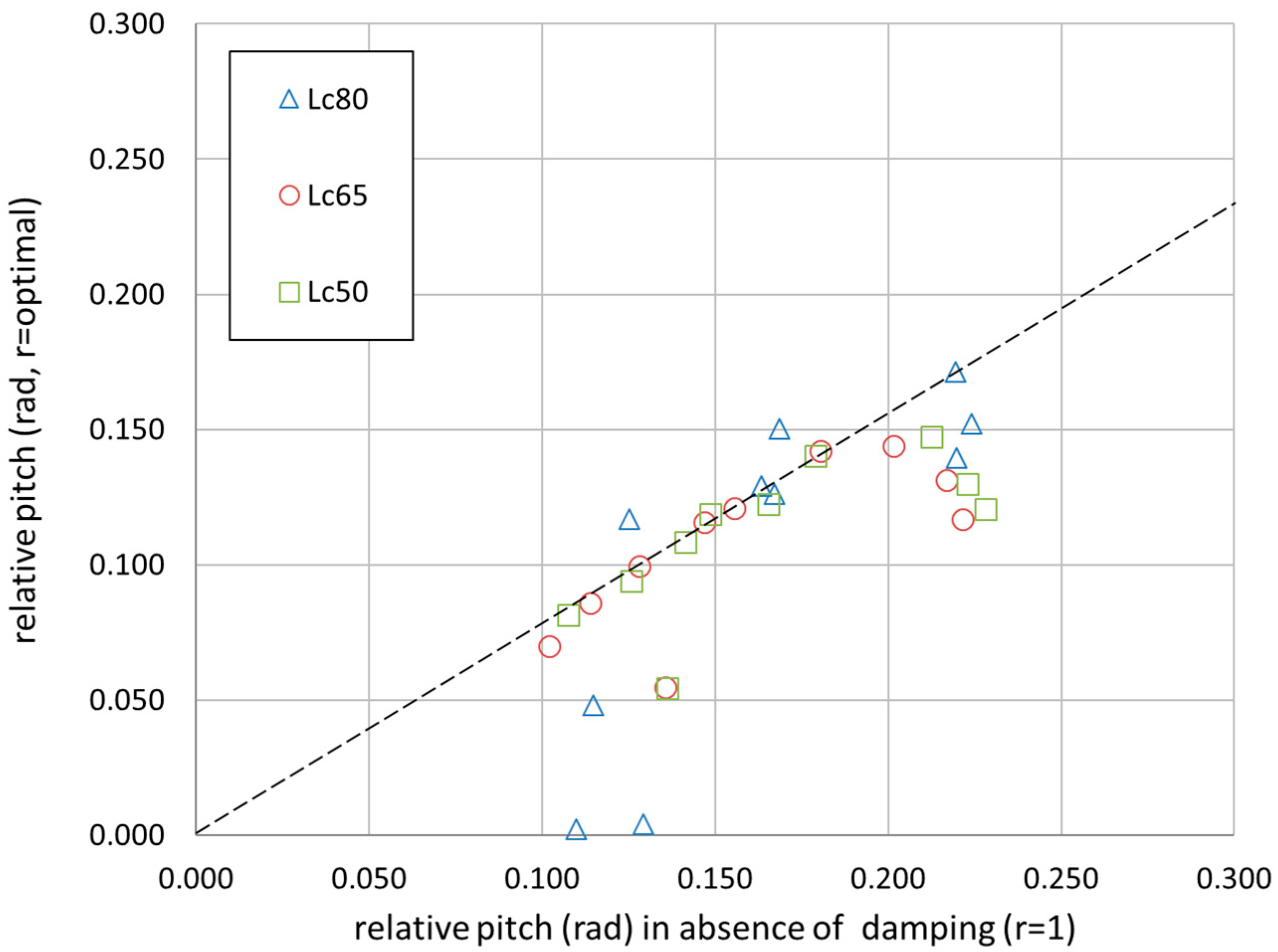
Figure 11 shows the relative pitch for r = 1, compared to the relative pitch obtained for optimal r. The correlation is significant and is almost unaffected by
Lc. Although the relation is not strictly linear in the whole range of tested conditions, most of the relative pitch values are 80% smaller for optimal setting compared to the undamped case.
Similarly,
Figure 12 shows the experimental relation between the relative pitch for r = 1 and the produced power. The data appear to be aligned along different lines (obtained by an exponential trend fitting), depending on
Lc.
The combination of
Figure 11 and
Figure 12 is very useful to anticipate the potential
PPTO of the DEXA on the basis of simple experiments, carried out in the absence of the PTO. For example, for
LC = 65%, a relative pitch of 0.16 rad is measured or predicted in absence of PTO. Then, if ones assumes that an optimal PTO is installed, the actual relative pitch would be 80% lower (
Figure 11) and the produced power would be just larger than 100 kW (
Figure 12).
3.4. Mooring Forces
The measured mooring loads are important to prove that the design is sound. The data recorded from the load cells, under ordinary and extreme WSs, were elaborated in the time domain. The characteristic value F1/50 (i.e., the mean value of the 2% of the highest points) was selected to statistically describe the largest forces during the wave attack.
The forces F1/50 are given as a function of PW.
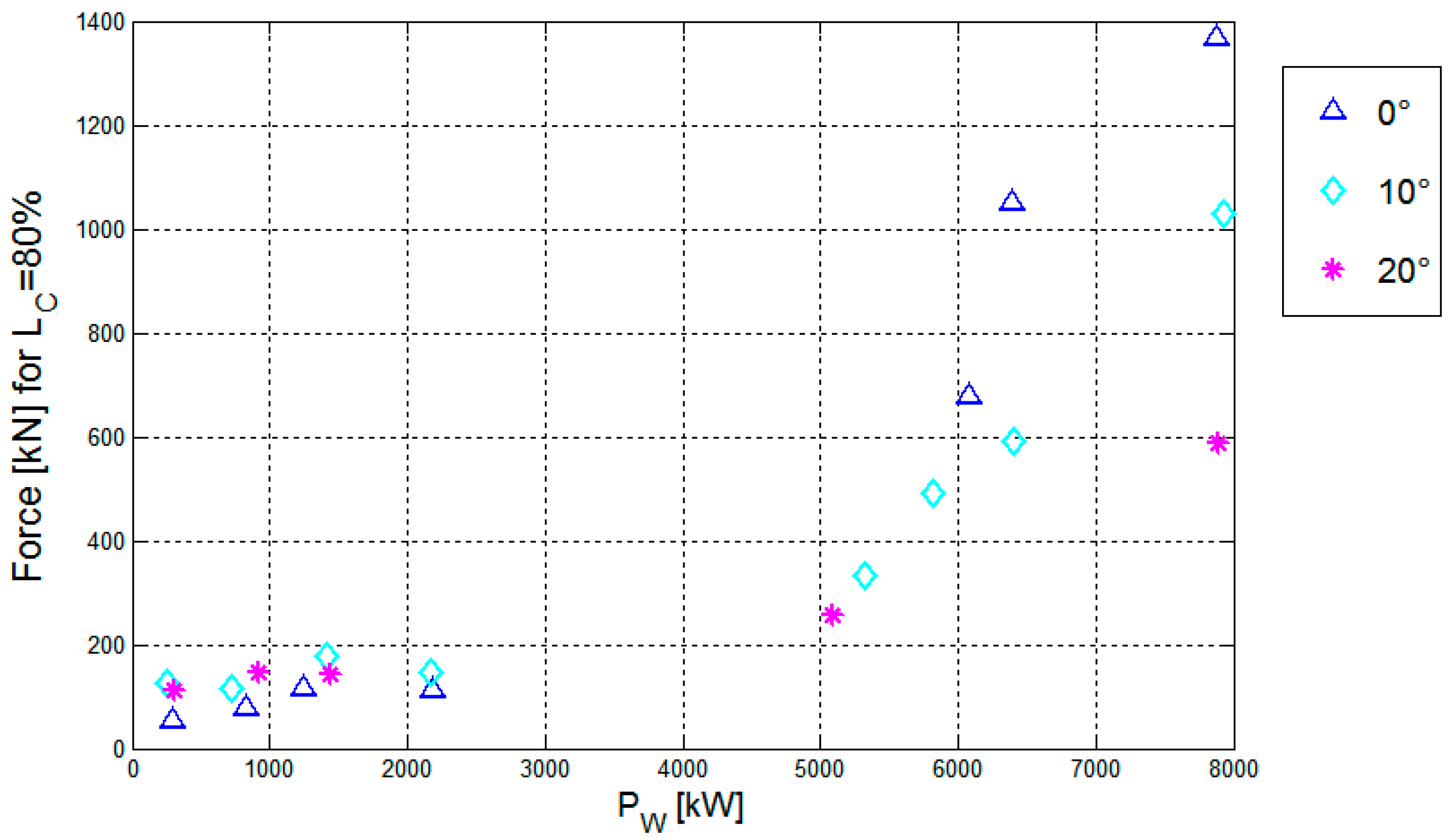
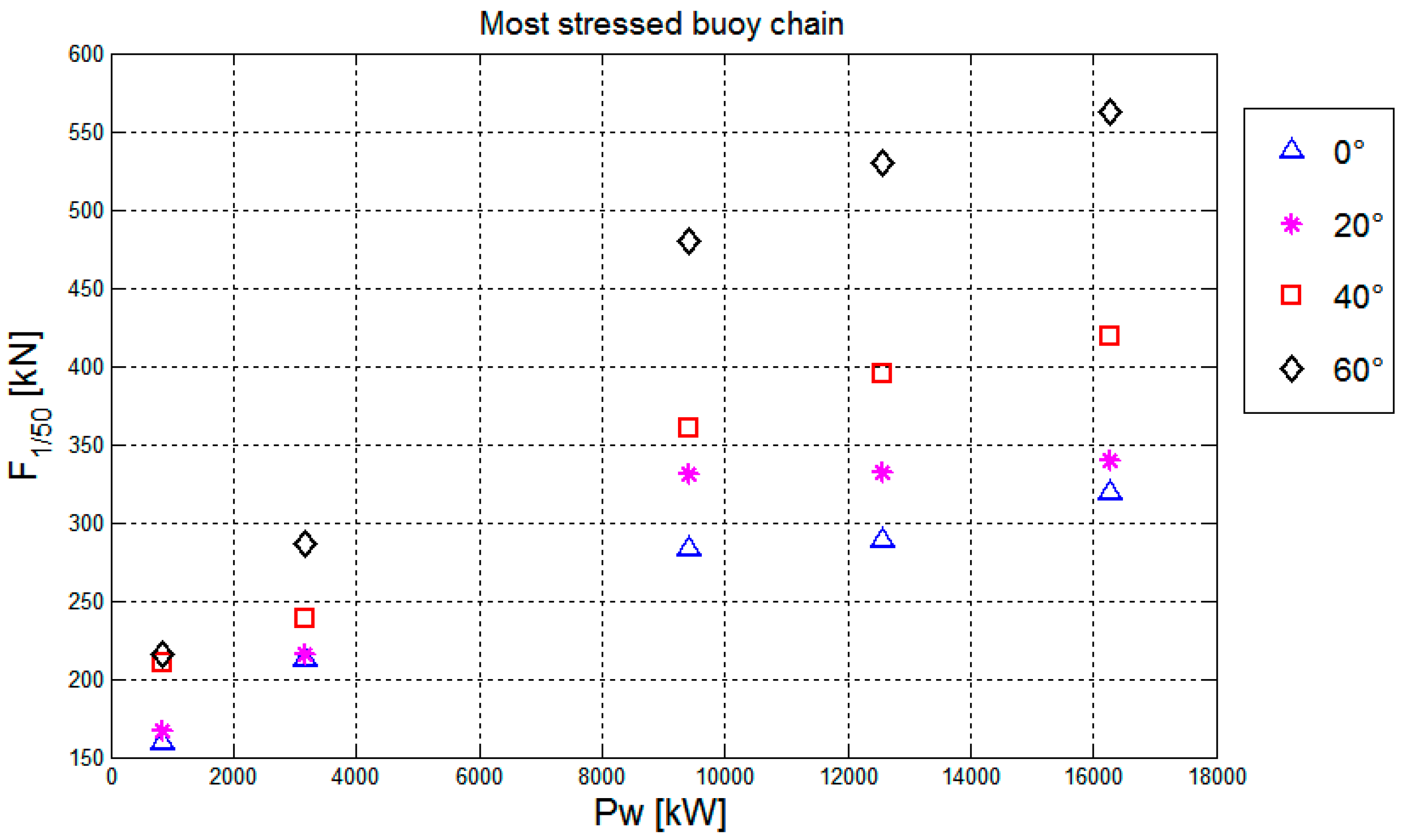
Figure 13 shows the maximum values of F
1/50 among the four chains, under perpendicular and oblique wave attacks, for
LC = 80%. The maximum loads are within an acceptable limit. For the ordinary WSs the values of F
1/50 slightly vary for different wave obliquities β, being slightly lower for perpendicular wave attacks. The lines are mainly slack and the loads are proportional to their elongation, usually very limited. Under oblique waves, yaw rotations induce a greater elongation of the chains with respect to pure surge, therefore larger loads are observed.
Conversely, in case of extreme WSs, F1/50 increases up to 3.5 times when the waves hit the device perpendicularly to its axis. The larger loads occur when the device reaches its maximum offset and the lines are fully stretched, and the load is proportional to the device deceleration. When the device is forced to yaw before reaching the maximum offset, the device deceleration is slower and the loads are smaller than in case of pure surge.
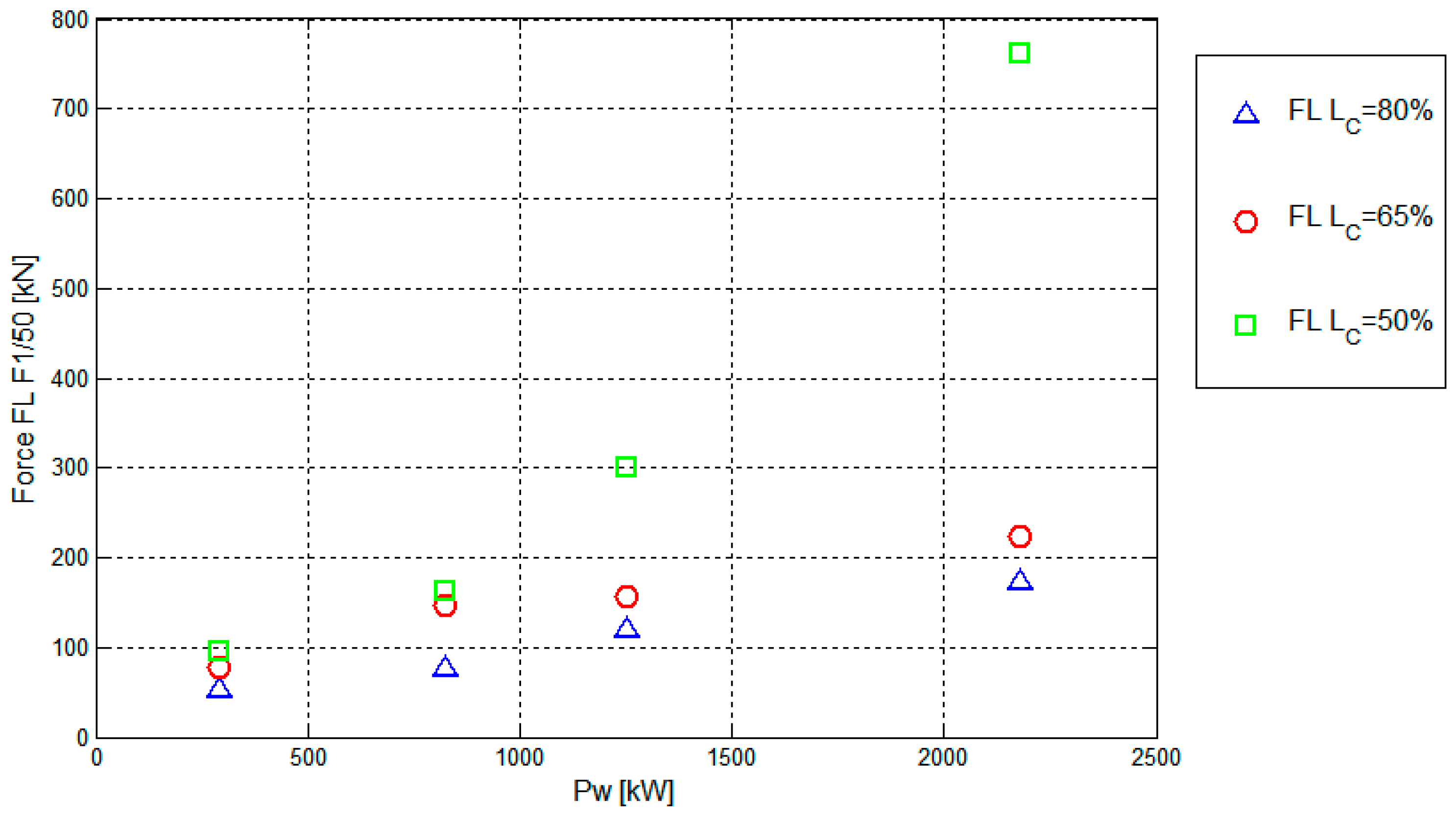
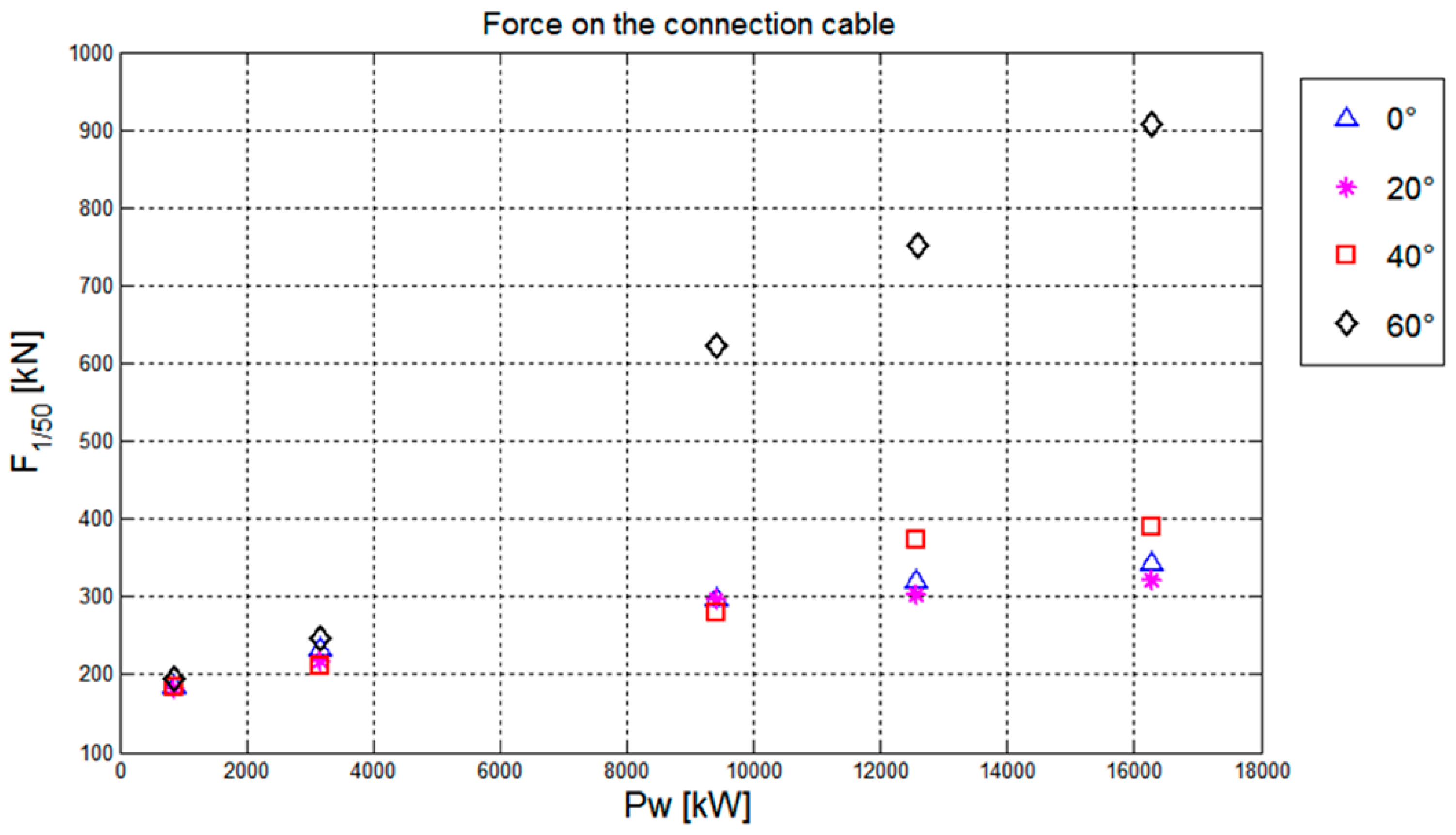
Figure 14 shows the values of F
1/50 for different
LC on the same chain as functions of
PW, only available for ordinary WSs. The increase of F
1/50 with
PW looks pretty linear for
LC = 80%, indicating a slack reaction. The trend of F
1/50 is quadratic for
LC = 50%, while the case with
LC = 65% follows an intermediate trend. Only for
LC = 80%, the load is available also for extreme WSs (see
Figure 13, perpendicular case) and it is evident that the linear trend is abandoned.