Deep Highway Networks and Tree-Based Ensemble for Predicting Short-Term Building Energy Consumption
Abstract
1. Introduction
1.1. Context and Objectives
1.2. Related Work
- The use of tree-based ensemble techniques and deep highway networks for predicting HVAC energy consumption from contextual data;
- Studying the impact of networks’ depth on prediction performance of DHN models;
- Demonstrate a prediction error of nearly 6% (normalised root mean square error)on hourly data for two of the best currently known machine learning algorithms (tree-based ensembles and deep learning).
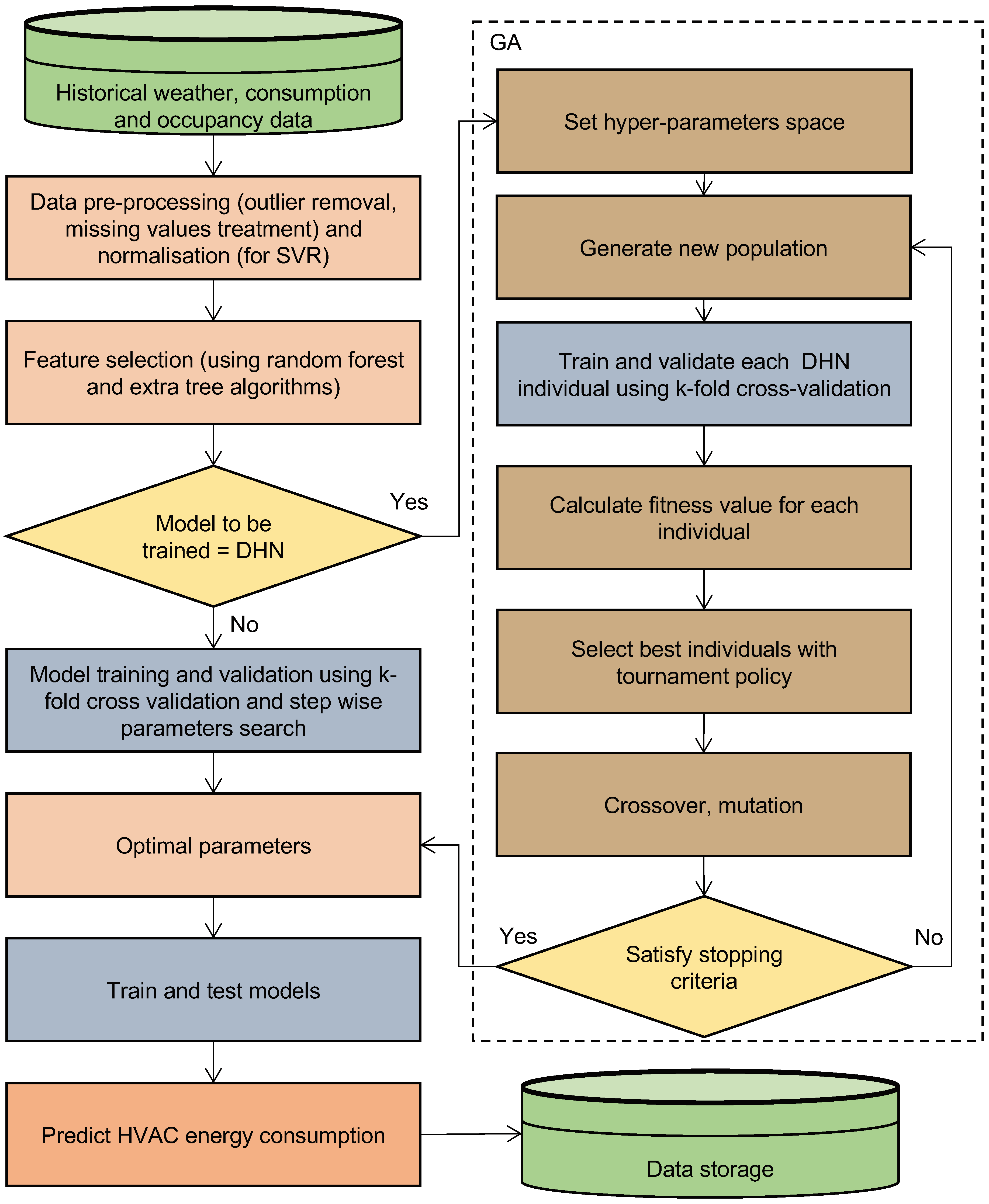
2. Materials and Methods
2.1. Machine Learning Algorithms
2.1.1. Support Vector Regression
2.1.2. Deep Highway Networks
2.1.3. Extremely Randomized Trees
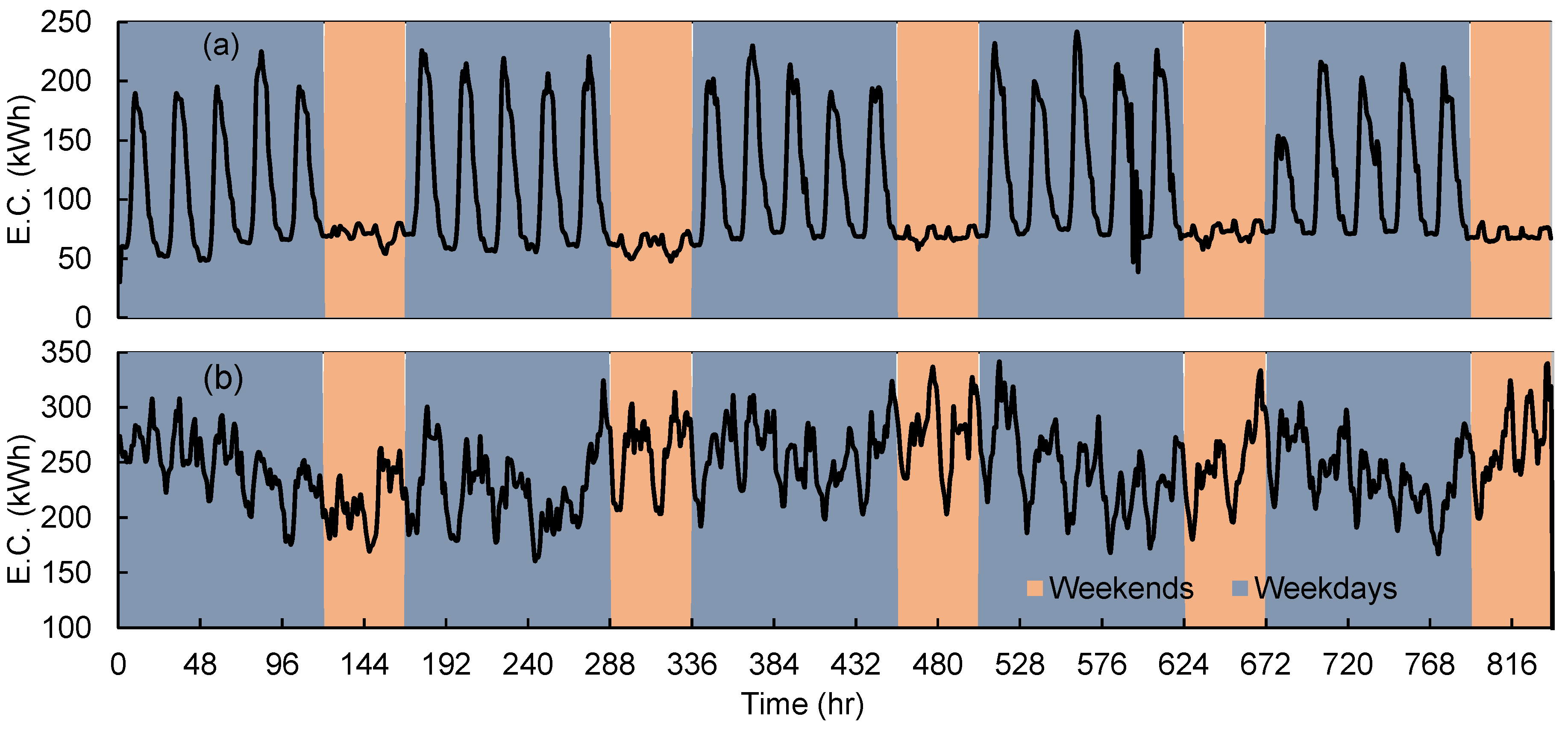
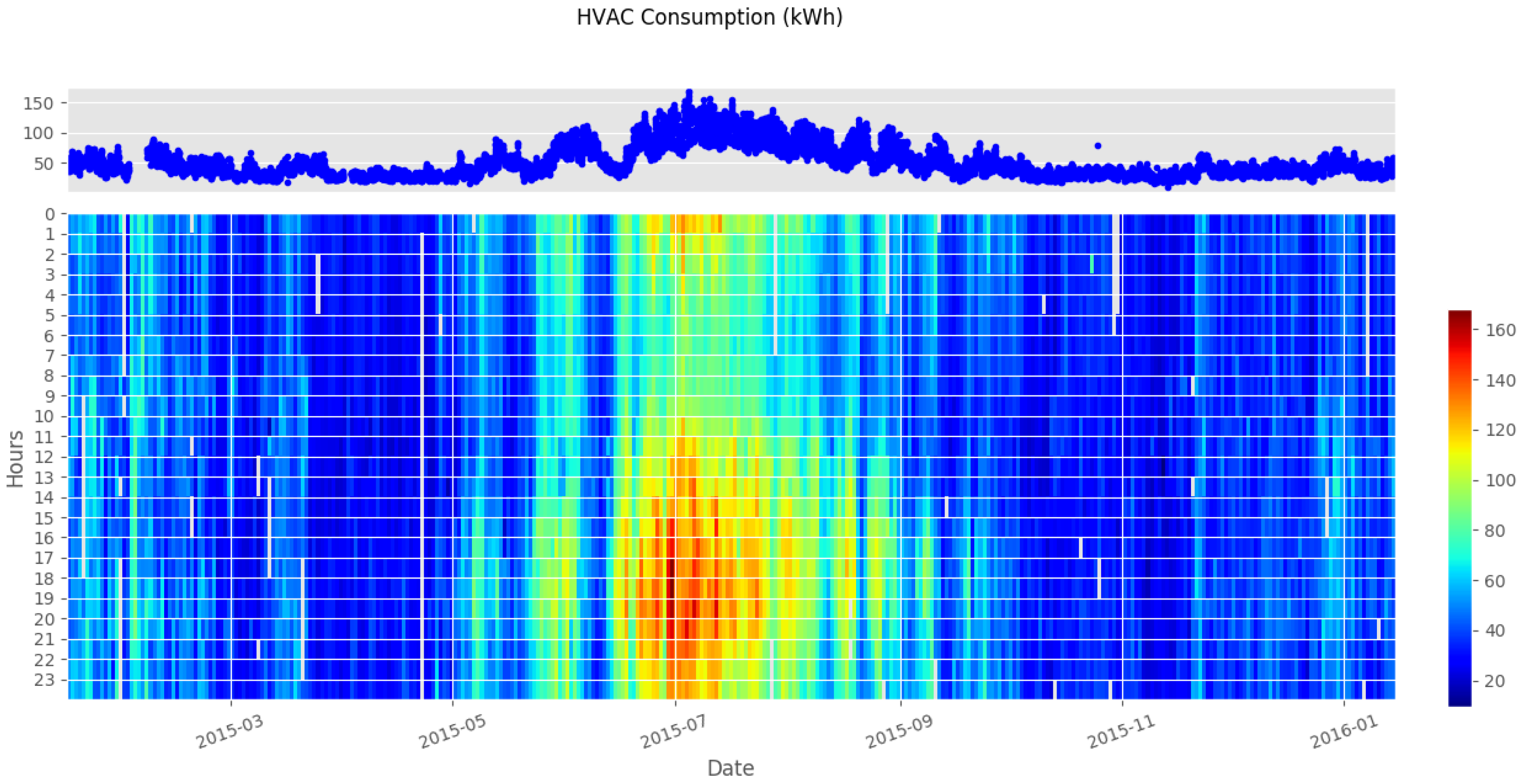
2.2. Data Description
2.3. Model Evaluation Metrics
3. Results
3.1. DHN Hyper-Parametric Tuning
3.2. SVR Hyper-Parametric Tuning
3.3. ET Hyper-Parametric Tuning
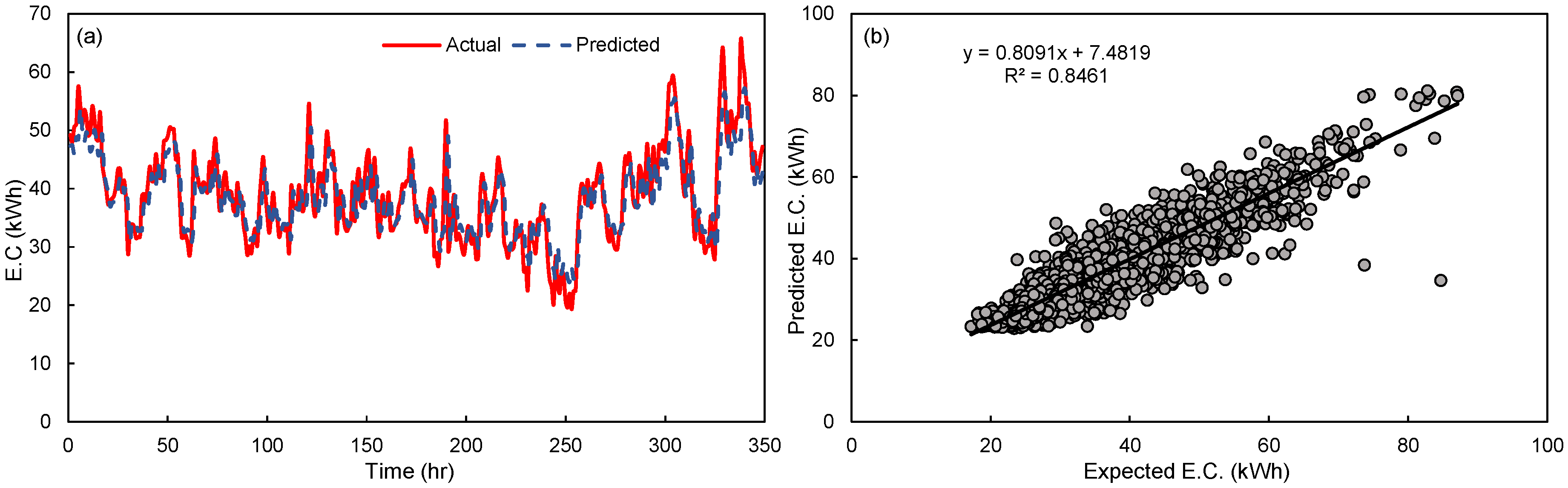
4. Comparison and Discussion
- The obtained performance is optimal and no further improvement could be achieved;
- The complexity may not have been increased enough to show significant changes in the performance of the model;
- Some variables of interest may not have been taken into account;
- The historical data used in this study is not sufficient to ensure the reliable training of a deep learning models’ deep highway network in our case.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahmad, M.W.; Mourshed, M.; Mundow, D.; Sisinni, M.; Rezgui, Y. Building energy metering and environmental monitoring— A state-of-the-art review and directions for future research. Energy Build. 2016, 120, 85–102. [Google Scholar] [CrossRef]
- Ponta, L.; Raberto, M.; Teglio, A.; Cincotti, S. An Agent-based Stock-flow Consistent Model of the Sustainable Transition in the Energy Sector. Ecol. Econ. 2018, 145, 274–300. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Dascalaki, E.; Balaras, C.A. XENIOS—A methodology for assessing refurbishment scenarios and the potential of application of RES and RUE in hotels. Energy Build. 2004, 36, 1091–1105. [Google Scholar] [CrossRef]
- Sloan, P.; Legrand, W.; Chen, J.S. (Eds.) Chapter 2—Energy Efficiency. In Sustainability in the Hospitality Industry; Butterworth-Heinemann: Boston, MA, USA, 2009; pp. 13–26. [Google Scholar]
- de Wilde, P. The gap between predicted and measured energy performance of buildings: A framework for investigation. Autom. Constr. 2014, 41, 40–49. [Google Scholar] [CrossRef]
- Meyers, R.J.; Williams, E.D.; Matthews, H.S. Scoping the potential of monitoring and control technologies to reduce energy use in homes. Energy Build. 2010, 42, 563–569. [Google Scholar] [CrossRef]
- Reddy, T.A. Literature Review on Calibration of Building Energy Simulation Programs: Uses, Problems, Procedures, Uncertainty, and Tools. ASHRAE Trans. 2006, 112, 226. [Google Scholar]
- Raftery, P.; Keane, M.; O’Donnell, J. Calibrating whole building energy models: An evidence-based methodology. Energy Build. 2011, 43, 2356–2364. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398. [Google Scholar] [CrossRef]
- Manfren, M.; Aste, N.; Moshksar, R. Calibration and uncertainty analysis for computer models—A meta-model based approach for integrated building energy simulation. Appl. Energy 2013, 103, 627–641. [Google Scholar] [CrossRef]
- Brea, J.; Senn, W.; Pfister, J.P. Matching Recall and Storage in Sequence Learning with Spiking Neural Networks. J. Neurosci. 2013, 33, 9565–9575. [Google Scholar] [CrossRef] [PubMed]
- Diehl, P.U.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Proceedings of the 2015 IEEE International Joint Conference on Neural Networks (IJCNN), Killarney, UK, 12–16 July 2015; pp. 1–8. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. arXiv, 2015; arXiv:1502.01852. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F.A. Learning to forget: Continual prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks (ICANN ’99), Edinburgh, UK, 7–10 September 1999. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv, 2015; arXiv:1506.04214. [Google Scholar]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115. [Google Scholar] [CrossRef] [PubMed]
- McCann, B.; Keskar, N.S.; Xiong, C.; Socher, R. The natural language decathlon: Multitask learning as question answering. arXiv, 2018; arXiv:1806.08730. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529. [Google Scholar] [CrossRef] [PubMed]
- Yıldırım, Ö.; Pławiak, P.; Tan, R.S.; Acharya, U.R. Arrhythmia detection using deep convolutional neural network with long duration ECG signals. Comput. Biol. Med. 2018, 102, 411–420. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv, 2015; arXiv:1512.03385. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. arXiv, 2017; arXiv:1610.02357. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway Networks. arXiv, 2015; arXiv:1505.00387. [Google Scholar]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building Energy Load Forecasting using Deep Neural Networks. In Proceedings of the 42nd IEEE Annual Conference of the IEEE Industrial Electronics Society (IECON), Florence, Italy, 24–27 October 2016. [Google Scholar]
- Li, C.; Ding, Z.; Zhao, D.; Zhang, J.Y.G. Building Energy Consumption Prediction: An Extreme Deep Learning Approach. Erngies 2017, 10, 1525. [Google Scholar] [CrossRef]
- Mouraud, A. Innovative time series forecasting: auto regressive moving average vs deep networks. Entrep. Sustain. Issues 2017, 4, 282–293. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J. On-Line Building Energy Optimization using Deep Reinforcement Learning. arXiv, 2017; arXiv:1707.05878. [Google Scholar]
- Fan, C.; Xiao, F.; Zha, Y. A short-term building cooling load prediction method using deep learning algorithms. Appl. Energy 2017, 195, 222–233. [Google Scholar] [CrossRef]
- Liang, J.; Du, R. Model-based Fault Detection and Diagnosis of HVAC systems using Support Vector Machine method. Int. J. Refrig. 2007, 30, 1104–1114. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Sengur, A.; Esen, M. Modeling a ground-coupled heat pump system by a support vector machine. Renew. Energy 2008, 33, 1814–1823. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networks. Energy Convers. Manag. 2009, 50, 90–96. [Google Scholar] [CrossRef]
- Li, X.; Deng, Y.; Ding, L.; Jiang, L. Building cooling load forecasting using fuzzy support vector machine and fuzzy C-mean clustering. In Proceedings of the 2010 International Conference On Computer and Communication Technologies in Agriculture Engineering (CCTAE), Chengdu, China, 12–13 June 2010; Volume 1, pp. 438–441. [Google Scholar]
- Yu, Z.; Haghighat, F.; Fung, B.C.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Hong, T.; Koo, C.; Jeong, K. A decision support model for reducing electric energy consumption in elementary school facilities. Appl. Energy 2012, 95, 253–266. [Google Scholar] [CrossRef]
- Hong, T.; Koo, C.; Park, S. A decision support model for improving a multi-family housing complex based on CO2 emission from gas energy consumption. Build. Environ. 2012, 52, 142–151. [Google Scholar] [CrossRef]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive modelling for solar thermal energy systems: A comparison of support vector regression, random forest, extra trees and regression trees. J. Clean. Prod. 2018, 203, 810–821. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Tree-based ensemble methods for predicting PV power generation and their comparison with support vector regression. Energy 2018, 164, 465–474. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 630–645. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Scalzo, F.; Xu, P.; Asgari, S.; Bergsneider, M.; Hu, X. Regression analysis for peak designation in pulsatile pressure signals. Med. Biol. Eng. Comput. 2009, 47, 967–977. [Google Scholar] [CrossRef] [PubMed]
- Nattee, C.; Khamsemanan, N.; Lawtrakul, L.; Toochinda, P.; Hannongbua, S. A novel prediction approach for antimalarial activities of Trimethoprim, Pyrimethamine, and Cycloguanil analogues using extremely randomized trees. J. Mol. Gr. Model. 2017, 71, 13–27. [Google Scholar] [CrossRef] [PubMed]
- John, V.; Liu, Z.; Guo, C.; Mita, S.; Kidono, K. Real-Time Lane Estimation Using Deep Features and Extra Trees Regression. In Image and Video Technology: 7th Pacific-Rim Symposium, PSIVT 2015, Auckland, New Zealand, November 25–27 2015, Revised Selected Papers; Bräunl, T., McCane, B., Rivera, M., Yu, X., Eds.; Springer: Cham, Switzerland, 2016; pp. 721–733. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Dieleman, S. Highway Networks. Available online: https://github.com/Lasagne/Lasagne/blob/highway_example/examples/Highway%20Networks.ipynb (accessed on 5 November 2018).
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 1139–1147. [Google Scholar]
- Carstens, H.; Xia, X.; Yadavalli, S. Low-cost energy meter calibration method for measurement and verification. Appl. Energy 2017, 188, 563–575. [Google Scholar] [CrossRef]
| Input/Output Variables | Min | Max | Mean | Median |
|---|---|---|---|---|
| Outdoor air temperature (°C) | −5.5 | 40.5 | 14.65 | 13 |
| Dew point air temperature (°C) | −12 | 20 | 4.84 | 5 |
| Outdoor air Relative Humidity (%) | 7.95 | 100 | 58.69 | 58.53 |
| Wind speed (mph) | 0 | 33.65 | 6.35 | 4.6 |
| No. of rooms booked (-) | 23 | 111 | 79.50 | 83 |
| No of guests (-) | 40 | 201 | 124.71 | 127 |
| HVAC hourly energy consumption (kWh) | 9.3 | 167.8 | 47.78 | 40.2 |
| Decision Variable | Possible Values |
|---|---|
| Number of hidden layer neurons | [5, 10, 20, 30] |
| Number of hidden layers | [1, 5, 10, 20, 50] |
| Epochs | [150, 200, 500, 1000, 2000] |
| Learning Rate | [0.005, 0.05, 0.01] |
| Momentum | [0.95, 0.99, 0.995] |
| Activation function | [’VlReLu’, ’Sigmoid’, ’Linear’, ’ReLu’] |
| Bias | [−4.0, −3.0, −2.0, −1.0, 0.0, 1.0] |
| Model Inputs | [[ 1, 1, 1, 2], [1, 1, 1, 24], [24, 24, 1, 24]] |
| Model Inputs | Number of Neurons | Activation Function | Number of Layers | Training Epochs | Bias | Learning Rate | Momentum | R2 | NRMSE (%) |
|---|---|---|---|---|---|---|---|---|---|
| ReLu | 1 | 150 | 0.84 | ||||||
| VlReLu | 1 | 500 | 0.8492 | ||||||
| Linear | 1 | 500 | 0.8490 | ||||||
| Linear | 1 | 500 | 0.8490 | ||||||
| Linear | 1 | 500 | 0.8489 | ||||||
| VlReLu | 50 | 1000 | 0.8484 | ||||||
| VlReLu | 1 | 1000 | 0.8482 | ||||||
| Linear | 50 | 1000 | 0.8482 | ||||||
| Linear | 20 | 500 | 0.8481 | ||||||
| VlReLu | 1 | 1000 | 0.8481 | ||||||
| VlReLu | 50 | 2000 | 0.8481 |
| Model Inputs | Number of Neurons | Activation Function | Number of Layers | Training Epochs | Bias | Learning Rate | Momentum | R2 | NRMSE (%) |
|---|---|---|---|---|---|---|---|---|---|
| 10 | VlReLu | 1 | 1000 | ||||||
| 10 | ReLu | 1 | 150 | ||||||
| 30 | VlReLu | 1 | 200 | ||||||
| 5 | Linear | 1 | 500 | ||||||
| 5 | Linear | 1 | 200 | ||||||
| 5 | ReLu | 1 | 1000 |
| C | R2 (–) | RMSE (kWh) | MAE (kWh) |
|---|---|---|---|
| −0.336 | 12.501 | 10.601 | |
| −0.307 | 12.362 | 10.448 | |
| −0.259 | 12.132 | 10.188 | |
| −0.176 | 11.726 | 9.752 | |
| 0.021 | 10.700 | 8.795 | |
| 0.380 | 8.518 | 6.912 | |
| 0.670 | 5.926 | 4.658 | |
| 0.801 | 4.821 | 3.644 | |
| 0.829 | 4.472 | 3.316 | |
| 0.839 | 4.343 | 3.188 | |
| 0.843 | 4.288 | 3.123 | |
| 0.844 | 4.274 | 3.102 | |
| 0.844 | 4.269 | 3.091 | |
| 0.844 | 4.268 | 3.088 | |
| 0.844 | 4.269 | 3.087 |
| R2 (–) | RMSE (kWh) | MAE (kWh) | |
|---|---|---|---|
| 0.84427 | 4.2675 | 3.0924 | |
| 0.84428 | 4.2673 | 3.0922 | |
| 0.84429 | 4.2671 | 3.0920 | |
| 0.84427 | 4.2674 | 3.0922 | |
| 0.84421 | 4.2682 | 3.0928 | |
| 0.84416 | 4.2690 | 3.0927 | |
| 0.84418 | 4.2686 | 3.0916 | |
| 0.84426 | 4.2675 | 3.0903 | |
| 0.84453 | 4.2639 | 3.0881 | |
| 0.84467 | 4.2619 | 3.0849 | |
| 0.84477 | 4.2606 | 3.0877 | |
| 0.84536 | 4.2525 | 3.0896 | |
| 0.84027 | 4.3219 | 3.2041 | |
| 0.79878 | 4.8508 | 3.8013 | |
| 0.55341 | 7.2267 | 6.1642 | |
| −0.44957 | 13.0200 | 11.2723 |
| R2 (–) | RMSE (kWh) | MAE (kWh) | |
|---|---|---|---|
| 2 | 0.819 | 4.601 | 3.405 |
| 3 | 0.822 | 4.564 | 3.377 |
| 5 | 0.828 | 4.485 | 3.312 |
| 7 | 0.832 | 4.427 | 3.266 |
| 10 | 0.837 | 4.372 | 3.223 |
| K | R2 (–) | RMSE (kWh) | MAE (kWh) |
|---|---|---|---|
| 1 | 0.7485 | 5.423 | 4.200 |
| 2 | 0.8091 | 4.724 | 3.555 |
| 3 | 0.8226 | 4.555 | 3.385 |
| 4 | 0.8246 | 4.529 | 3.353 |
| 5 | 0.8219 | 4.564 | 3.377 |
| R2 (–) | RMSE (kWh) | MAE (kWh) | |
|---|---|---|---|
| 1 | −0.3242 | 12.445 | 10.578 |
| 3 | 0.5323 | 7.396 | 6.128 |
| 5 | 0.7629 | 5.265 | 4.199 |
| 7 | 0.8281 | 4.484 | 3.413 |
| 9 | 0.8424 | 4.292 | 3.184 |
| 10 | 0.8427 | 4.288 | 3.167 |
| 15 | 0.8353 | 4.389 | 3.227 |
| 20 | 0.8262 | 4.508 | 3.331 |
| Model | Training Dataset | Testing Dataset | ||
|---|---|---|---|---|
| RMSE (kWh) | R2 (–) | RMSE (kWh) | MAE (kWh) | |
| ET | 4.284 | 0.8427 | 4.288 | 3.167 |
| SVR | 4.252 | 0.8453 | 4.253 | 3.090 |
| DHN | 3.087 | 0.8491 | 4.200 | 3.027 |
| Factor/Variable | Actual E.C. Data | DHN | ET | SVR |
|---|---|---|---|---|
| Mean | 37.08 | 37.16 | 37.48 | 37.09 |
| Median | 35.2 | 35.46 | 35.88 | 35.68 |
| Standard Deviation | 10.82 | 9.88 | 9.51 | 9.82 |
| Sample Variance | 116.98 | 97.68 | 90.51 | 96.51 |
| Kurtosis | 1.14 | 0.62 | 1.10 | 0.97 |
| Skewness | 0.96 | 0.82 | 0.93 | 0.88 |
| Range | 69.90 | 64.30 | 58.25 | 63.88 |
| Minimum | 17.2 | 16.84 | 22.87 | 18.31 |
| Maximum | 87.1 | 81.14 | 81.12 | 82.19 |
| Sum | 121,981.7 | 122,245.60 | 123,308.75 | 122,015.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.W.; Mouraud, A.; Rezgui, Y.; Mourshed, M. Deep Highway Networks and Tree-Based Ensemble for Predicting Short-Term Building Energy Consumption. Energies 2018, 11, 3408. https://doi.org/10.3390/en11123408
Ahmad MW, Mouraud A, Rezgui Y, Mourshed M. Deep Highway Networks and Tree-Based Ensemble for Predicting Short-Term Building Energy Consumption. Energies. 2018; 11(12):3408. https://doi.org/10.3390/en11123408
Chicago/Turabian StyleAhmad, Muhammad Waseem, Anthony Mouraud, Yacine Rezgui, and Monjur Mourshed. 2018. "Deep Highway Networks and Tree-Based Ensemble for Predicting Short-Term Building Energy Consumption" Energies 11, no. 12: 3408. https://doi.org/10.3390/en11123408
APA StyleAhmad, M. W., Mouraud, A., Rezgui, Y., & Mourshed, M. (2018). Deep Highway Networks and Tree-Based Ensemble for Predicting Short-Term Building Energy Consumption. Energies, 11(12), 3408. https://doi.org/10.3390/en11123408





