Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation
Abstract
1. Introduction
2. Numerical Method for Vertical Axis Current Turbine under Forced Oscillation
2.1. Turbine Load
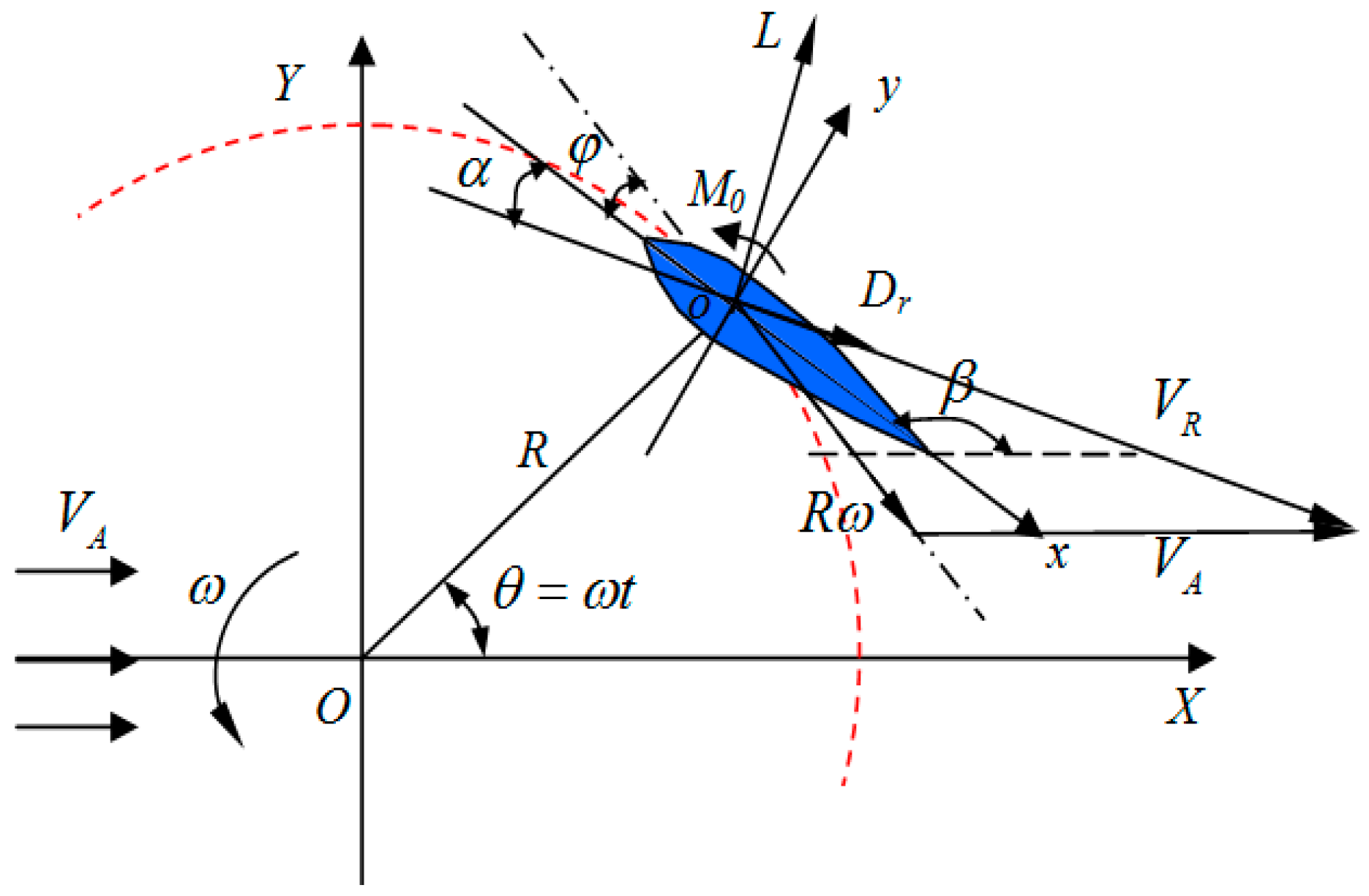
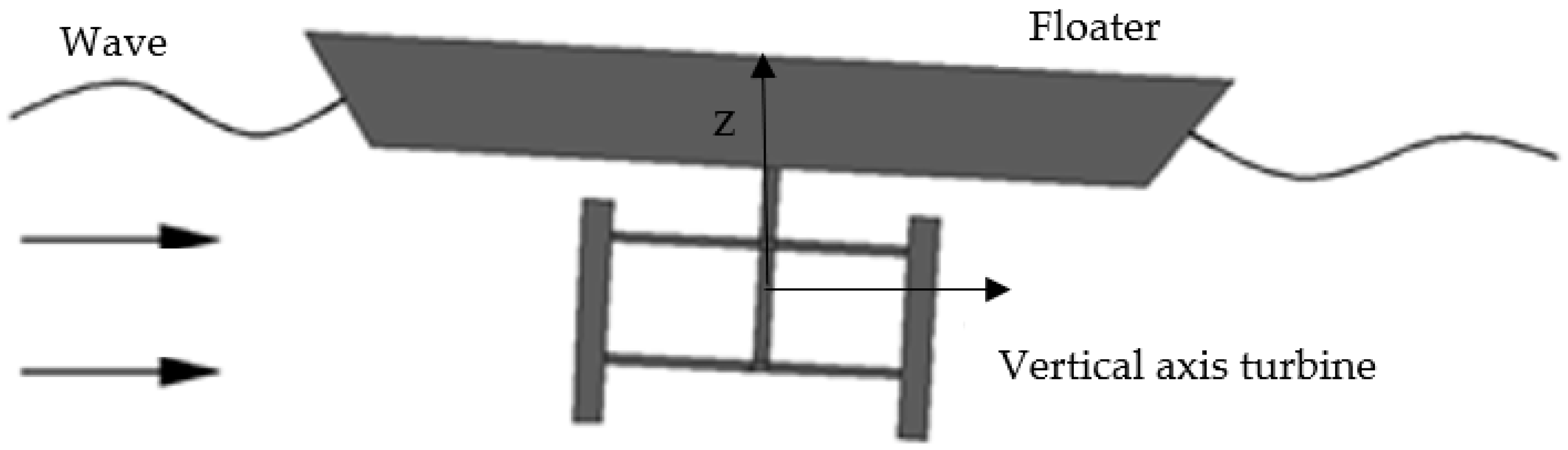
2.2. Hydrodynamic Analysis of the Vertical Axis Current Turbine under Forced Oscillation
- The VACT is connected to the floater through its shaft and the shaft is fixed onto the floater. The motion of the whole system is harmonic with a small oscillation amplitude.
- The spokes and main shaft of the turbine are assumed to have no effects on the turbine’s hydrodynamic characteristics.
- The diameter of the rotor is small compared to the wave length. The velocity of water particles caused by the incident wave is constant at water depth direction.
- VACT can be seen as a slender body and strip theory could be used.
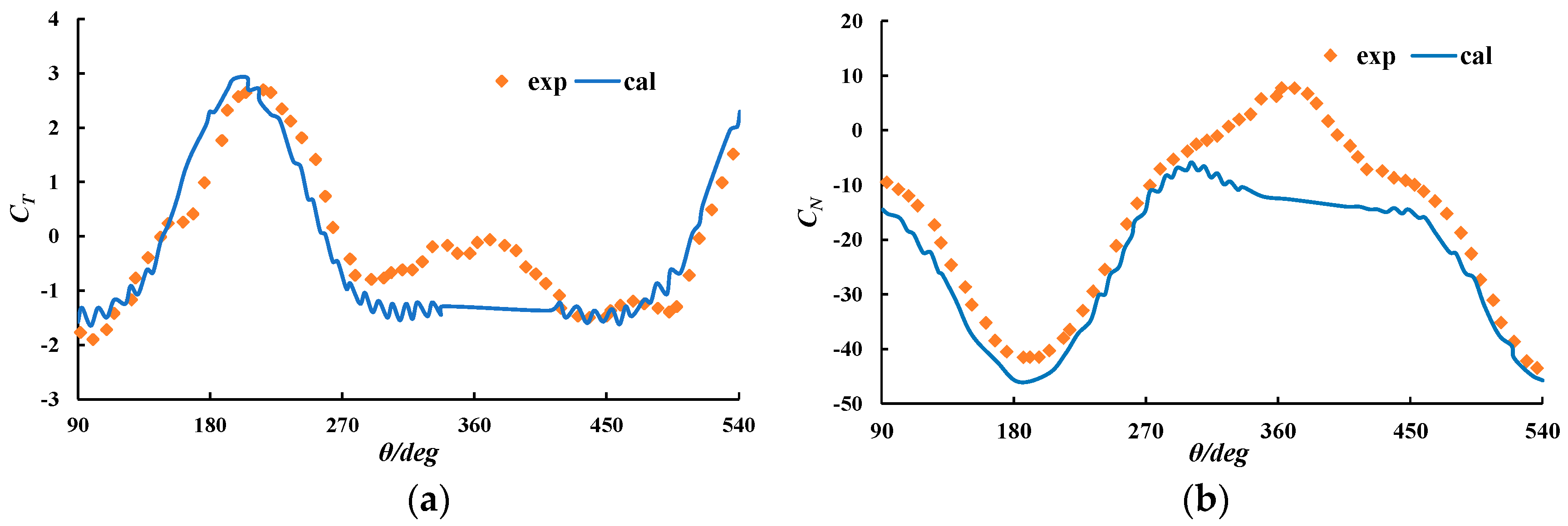
3. Validation of CFX Results
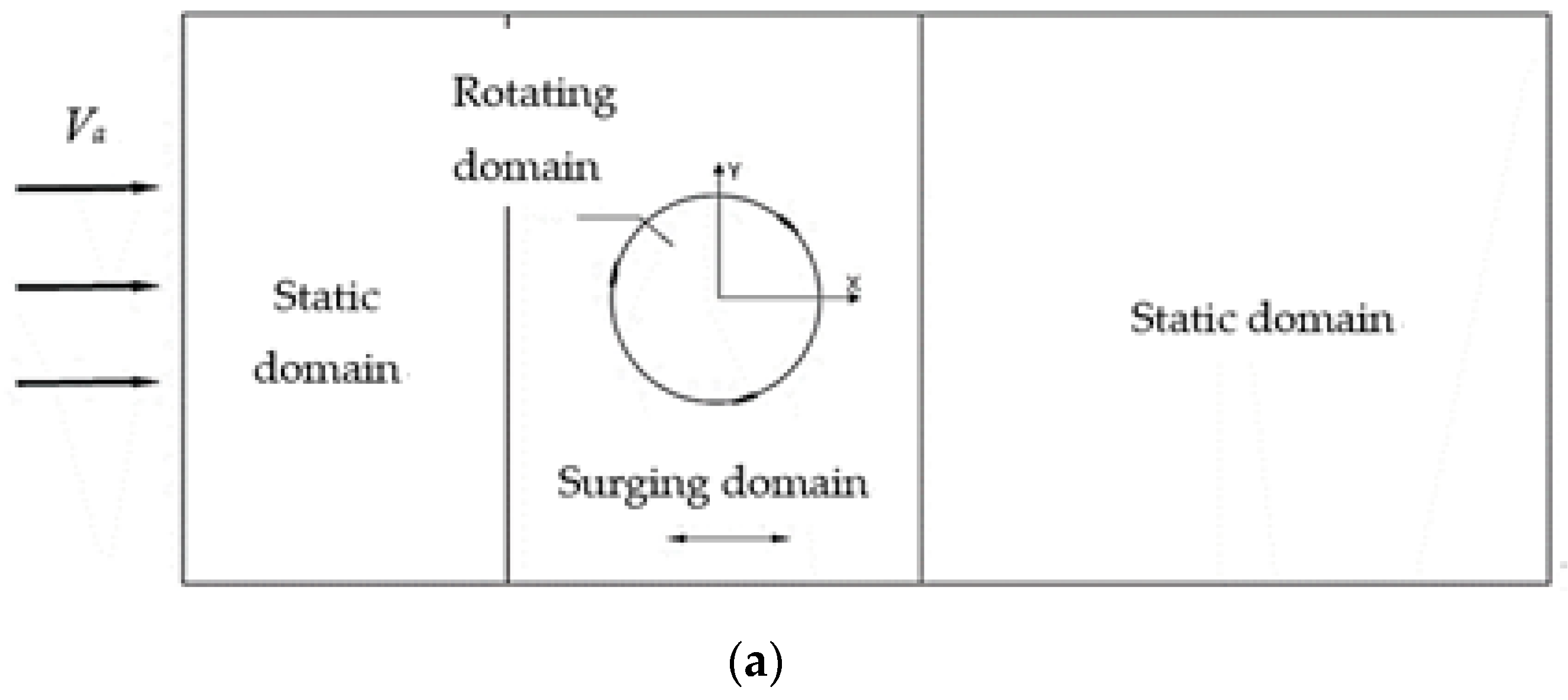
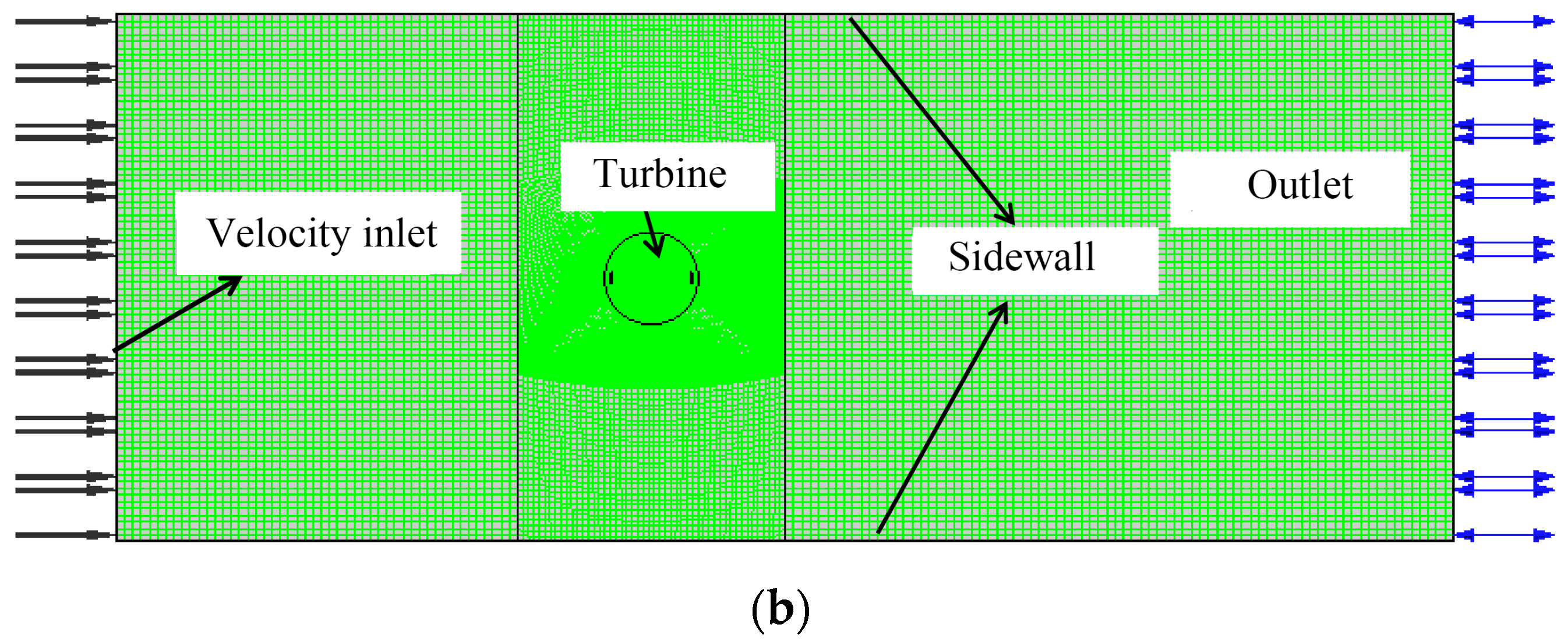
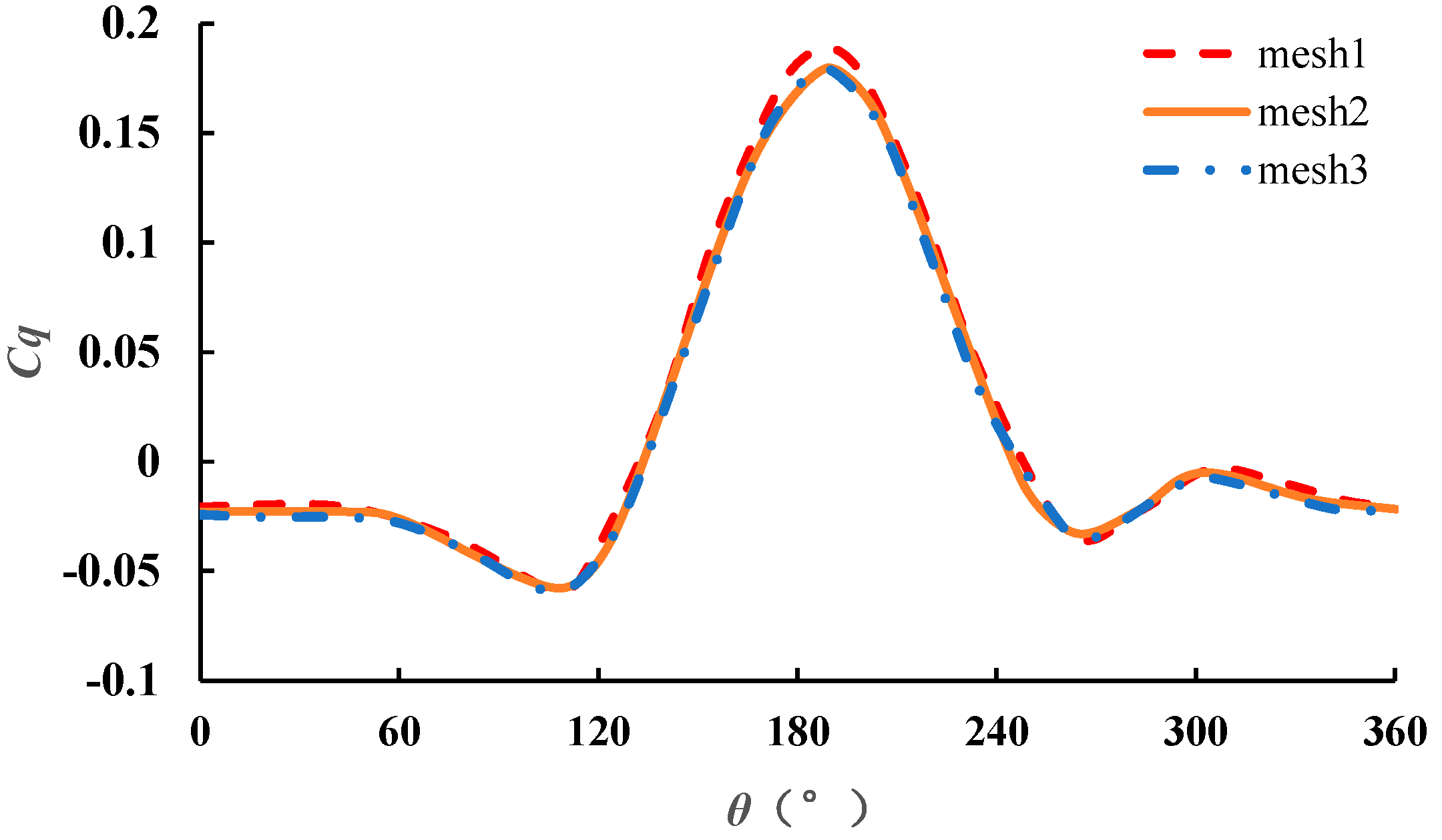
3.1. Validation of Grid Independence
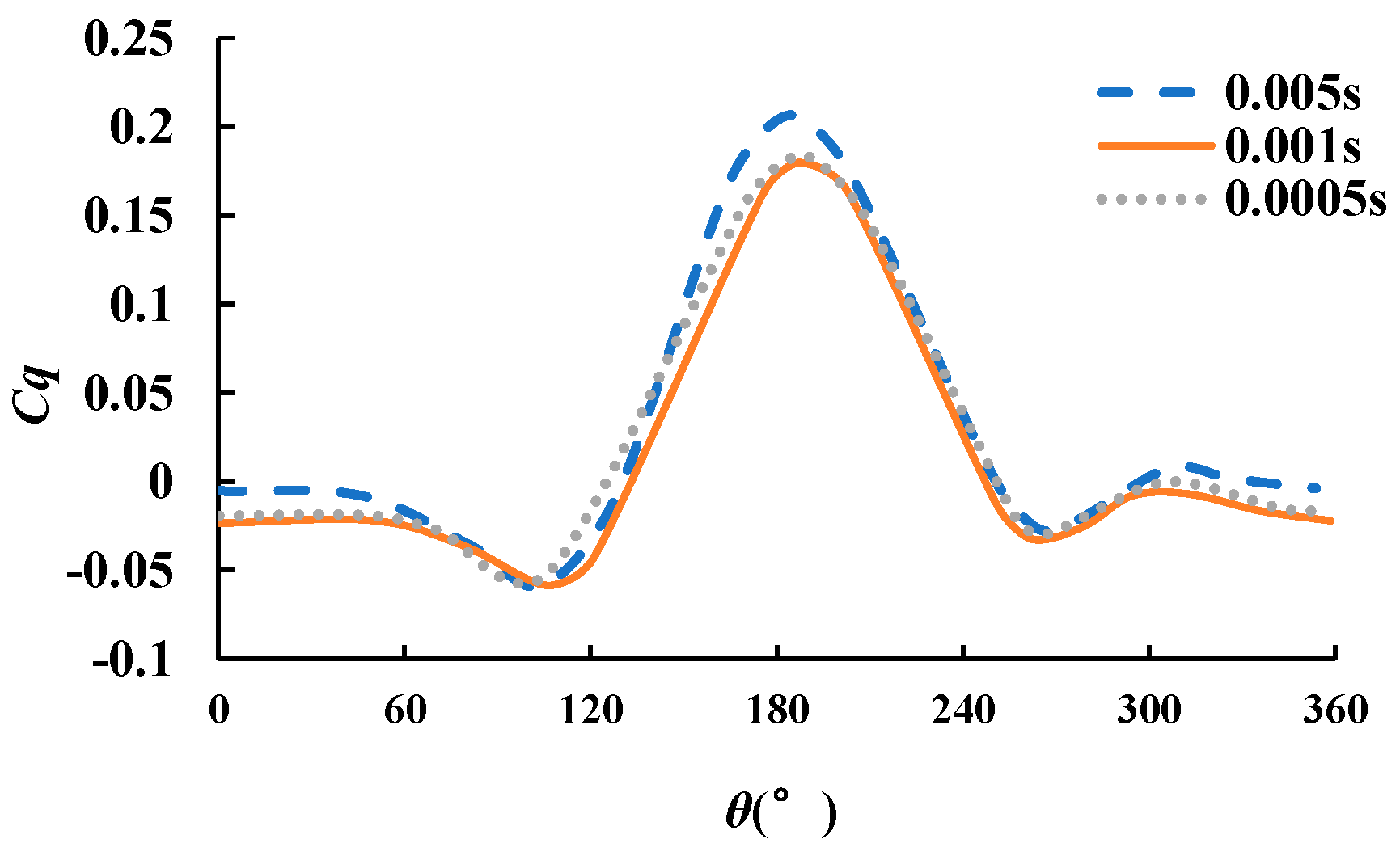
3.2. Validation of Time Step
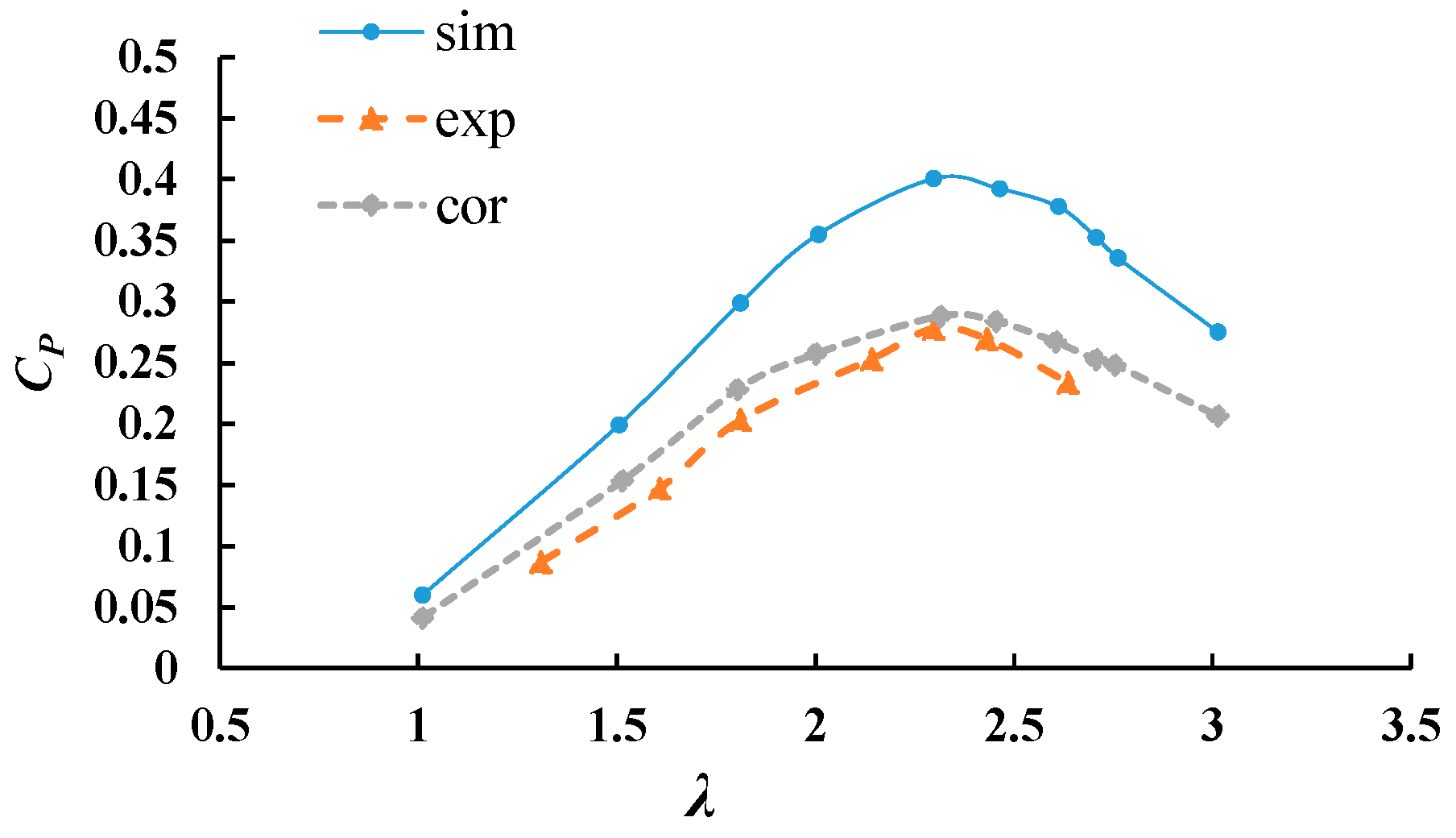
3.3. Comparision between Experiments and Numerical Simulation
4. Results from Hydrodynamic Analysis of the Rotor Under Forced Oscillation
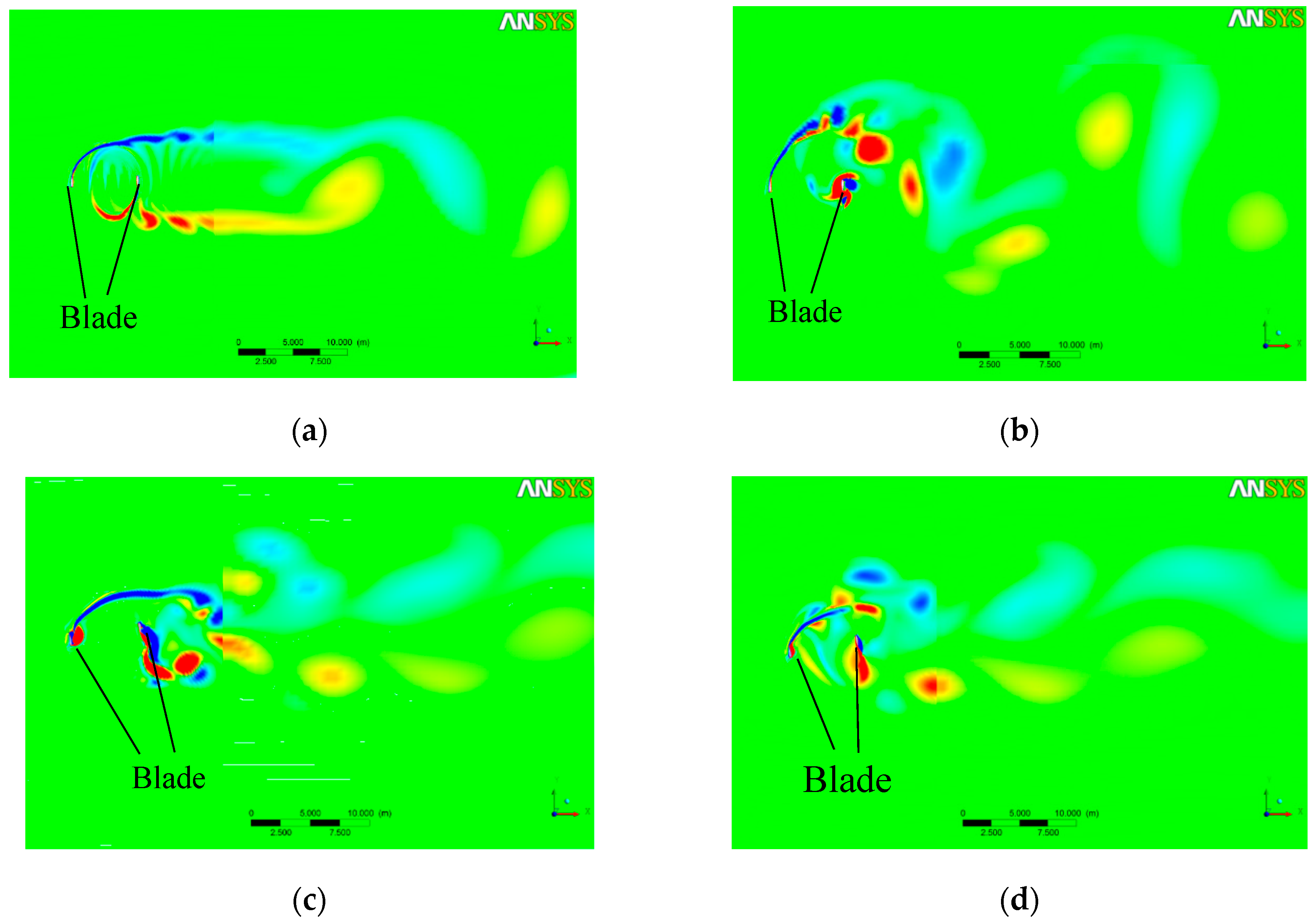
4.1. Flow Field Analysis Under Forced Oscillation
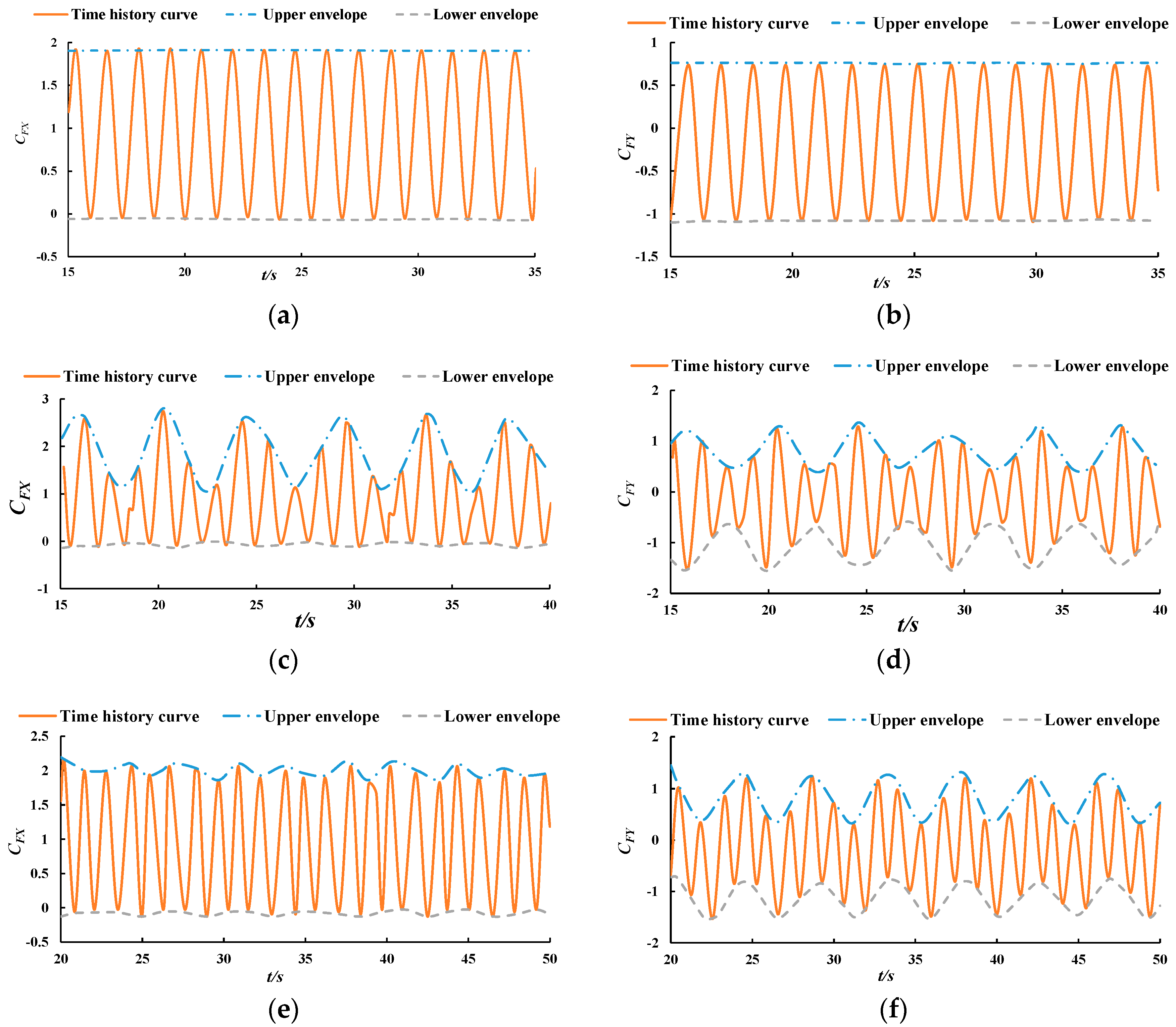
4.2. Analysis of Loads on the Rotor of the Turbine
4.3. Analysis of Loads on the Blade of the Rotor
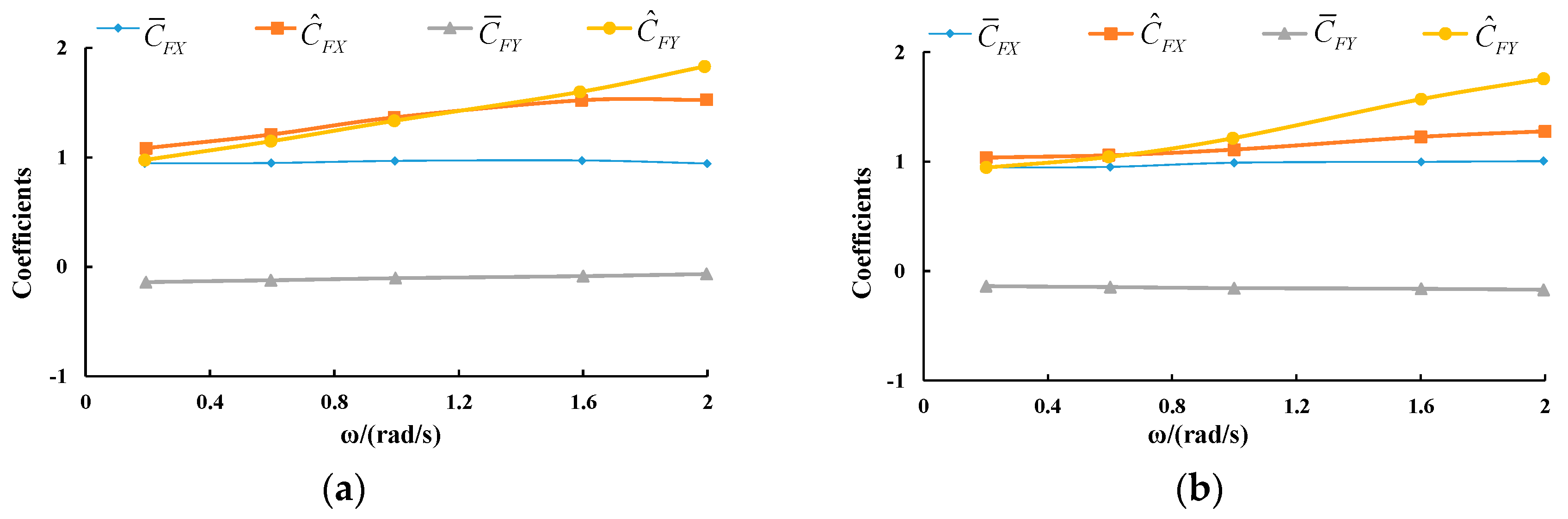
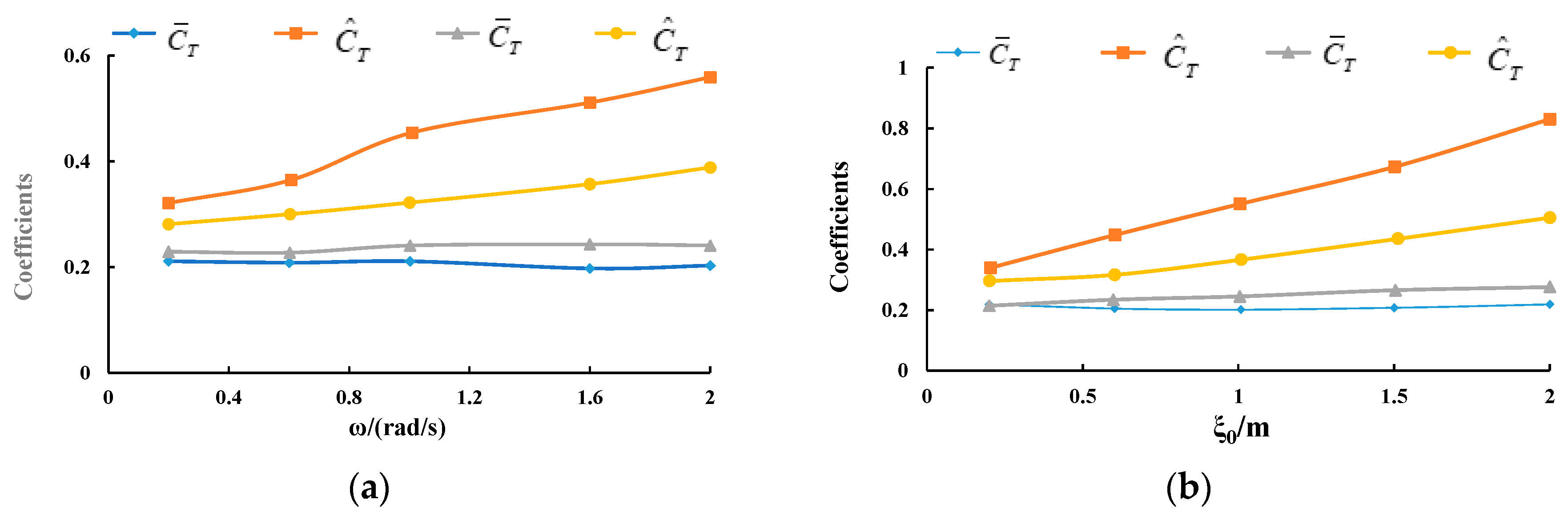
4.4. Effects of Oscillating Frequency
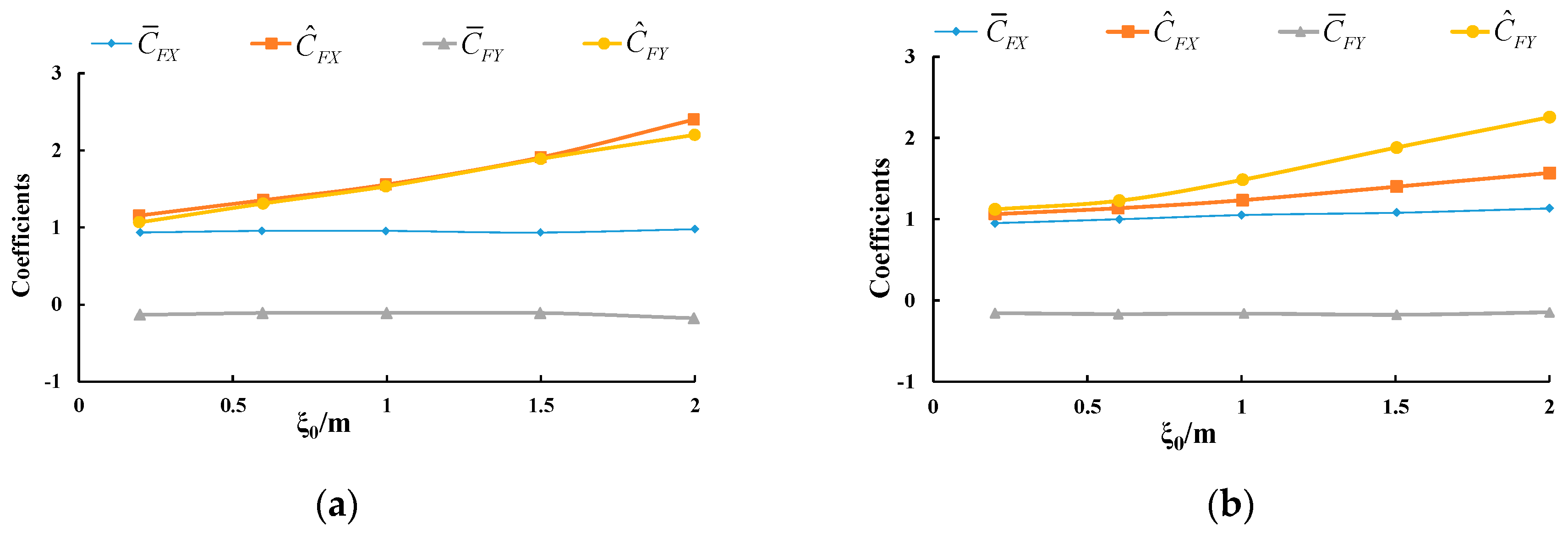
4.5. Effects of Oscillating Amplitude
4.6. Analysis of Torque
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Incoming flow velocity | |
| Lift force of a single blade | |
| Drag force of a single blade | |
| Torque acting on the o axis of the airfoil | |
| Force along the chord line | |
| Force perpendicular to the chord line | |
| Blade tangential force | |
| Radial blade force | |
| Thrust of the rotor | |
| Lateral force of the rotor | |
| Torque of a single blade | |
| SST | Shear Stress Turbulence |
| N-S | Navier-Stokes |
| LES | Large eddy simulation |
| RANS | Reynolds-averaged Navier–Stokes |
| Y plus | Dimensionless wall distance |
| CEL | Computer expression language |
| Cp | Power output efficiency |
| Mean thrust of the rotor | |
| Fluctuation of the amplitude | |
| Solidarity of the turbine | |
| TSR | Tip speed ratio |
| MCT | marine current turbine |
| VAW | Ts vertical axis wind turbines |
References
- Rourke, F.O.; Boyle, F.; Reynolds, A. Tidal energy update 2009. Appl. Energy 2010, 87, 398–409. [Google Scholar] [CrossRef]
- Bahaj, A.B.S. Generating electricity from the oceans. Renew. Sustain. Energy Rev. 2011, 15, 3399–3416. [Google Scholar] [CrossRef]
- Magagna, D.; Margheritini, L.; Alessi, A.; Bannon, E.; Boelman, E.; Bould, D.; Coy, V.; De Marchi, E.; Frigaard, P.; Guedes Soares, C.; et al. Workshop on Identification of Future Emerging Technologies in the Ocean Energy Sector—27th March 2018, Ispra, Italy; EUR29315 EN; European Commission: Luxembourg, 2018; ISBN 978-92-79-92587-0. [Google Scholar]
- Jun, D.; Zhong, S.H.; Xi, W.; Jie, Y. Current research progress of water turbine. Renew. Energy 2010, 28, 130–133. [Google Scholar]
- Denny, E. The economics of tidal energy. Energy Policy 2009, 37, 1914–1924. [Google Scholar] [CrossRef]
- Mehmood, N. Tidal current technologies: Green and renewable. In Proceedings of the 2011 4th IEEE International Conference on Computer Science and Information Technology (ICCSIT2011), Chengdu, China, 10–12 June 2011. [Google Scholar]
- Sheng, Q.-H.; Tang, F.-D.; Wang, H.-F.; Cao, X.-F.; Zhao, W.-M.; Jin, Z.-G.; Han, D.-F.; Zhang, L. The design of 2 × 150 kW floating vertical-axis tidal current independent generating system. In Proceedings of the Symposium of the 16th China Marine (Coastal) Engineering Symposia, Dalian, China, 4–7 August 2013; pp. 758–763. [Google Scholar]
- Zhang, L.; Wang, L.-B.; Li, F.-L. Streamtube models for performance prediction of vertical-axis variable-pitch turbine for tidal current energy conversion. J. Harbin Eng. Univ. 2004, 25, 261–266. [Google Scholar]
- Yang, B.; Shu, X.-W. Hydrofoil optimization and experimental validation in helical vertical axis turbine for power generation from marine current. Ocean Eng. 2012, 42, 35–46. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Batten, W.M.J.; McCann, G. Experimental verifications of numerical predictions for the hydrodynamic performance of a horizontal axis marine current turbines. Renew. Energy 2007, 32, 2479–2490. [Google Scholar] [CrossRef]
- Mccann, G.; Rawlinson, R.; Garrad, H.; Partners Ltd. (Bristol UK). Development of a design tool for current turbines. Smith, 2005. [Google Scholar]
- Batten, W.M.; Bahaj, A.S.; Molland, A.F.; Chaplin, J.R. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Maganga, F.; Germain, G.; King, J.; Pinon, G.; Rivoalen, E. Experimental characterization of flow effects on marine current turbine behavior and on its wake properties. IET Renew. Power Gen. 2010, 4, 498–509. [Google Scholar] [CrossRef]
- Lust, E.E.; Luznik, L.; Flack, K.A.; Walker, J.M.; Van Benthem, M.C. The influence of surface gravity waves on marine current turbine performance. Int. J. Mar. Energy 2013, 3, 27–40. [Google Scholar] [CrossRef]
- Fernandez-Rodriguez, E.; Stallard, T.J.; Stansby, P.K. Experimental study of extreme thrust on a tidal stream rotor due to turbulent flow and with opposing waves. J. Fluids Struct. 2014, 51, 354–361. [Google Scholar] [CrossRef]
- Ai, K.; Avital, E.J.; Korakianitis, T.; Samad, A.; Venkatesan, N. Surface wave effect on marine current turbine, modelling and analysis. In Proceedings of the International Conference on Mechanical and Aerospace Engineering, London, UK, 18–22 July 2016; pp. 180–184. [Google Scholar]
- Guo, X.; Gao, Z.; Yang, J.; Moan, T.; Lu, H.; Li, X.; Lu, W. The Effects of Surface Waves and Submergence on the Performance and Loading of a Tidal Turbine. In Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering (ASME 2017), Trondheim, Norway, 25–30 June 2017; p. V07BT06A055. [Google Scholar]
- Yan, J.; Deng, X.; Korobenko, A.; Bazilevs, Y. Free-surface flow modeling and simulation of horizontal-axis tidal-stream turbines. Comput. Fluids 2017, 158, 157–166. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS CFX; Ansys Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Lanzafame, R.; Mauro, S.; Messina, M. 2D CFD Modeling of H-Darrieus Wind Turbines Using a Transition Turbulence Model. Energy Procedia 2014, 45, 131–140. [Google Scholar] [CrossRef]
- Lam, H.F.; Peng, H.Y. Study of wake characteristics of a vertical axis wind turbine by two- and three-dimensional computational fluid dynamics simulations. Renew. Energy 2016, 90, 386–398. [Google Scholar] [CrossRef]
- Ferreira, C.S.; Bussel, G.V.; Kuik, G.V. 2D CFD Simulation of Dynamic Stall on a Vertical Axis Wind Turbine: Verification and Validation with PIV Measurements. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Danao, L.A.; Howell, R. Effects on the Performance of Vertical Axis Wind Turbines with Unsteady Wind Inflow: A Numerical Study. In Proceedings of the AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Migliore, P.G. Comparison of NACA 6-series and 4-digit airfoils for Darrieus wind turbines. J. Energy 1983, 7, 291–292. [Google Scholar] [CrossRef]
- Yang, B.; Lawn, C. Three-dimensional effects on the performance of a vertical axis tidal turbine. Ocean Eng. 2013, 58, 1–10. [Google Scholar] [CrossRef]
- Alidadi, M.; Calisal, S. A numerical method for calculation of power output from ducted vertical axis hydro-current turbines. Comput. Fluids 2014, 105, 76–81. [Google Scholar] [CrossRef]
- Dai, Y.M.; Gardiner, N.; Lam, W.H. CFD modelling strategy of a straight-bladed vertical axis marine current turbine. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010. [Google Scholar]
- Wang, L.B.; Zhang, L.; Zeng, N.D. A potential flow 2-D vortex panel model: Applications to vertical axis straight blade tidal turbine. Energy Convers. Manag. 2007, 48, 454–461. [Google Scholar] [CrossRef]
- Yang, Z.; Deng, B.Q.; Shen, L. Direct numerical simulation of wind turbulence over breaking waves. J. Fluid Mech. 2018, 850, 120–155. [Google Scholar] [CrossRef]
- Alberello, A.; Pakodzi, C.; Nelli, F.; Bitner-Gregersen, E.M.; Toffoli, A. Three dimensional velocity field underneath a breaking rogue wave. In Proceedings of the OMAE, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.D.; Afgan, I.; Stallard, T.; Stansby, P.K. Fluctuating Loads on a Tidal Turbine Due to Velocity Shear and Turbulence: Comparison of CFD with Field Data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef]
- Mooney, K.G.; Maric, T.; Hopken, J. The OpenFOAM Technology Primer; Source flux: Duisburg, Germany, 2014. [Google Scholar]
- Ma, Y.; Hu, C.; Li, Y.; Li, L.; Deng, R.; Jiang, D. Hydrodynamic Performance Analysis of the Vertical Axis Twin-Rotor Tidal Current Turbine. Water 2018, 10, 1694. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three-dimensional numerical simulations of straight-bladed vertical axis tidal turbines investigating power output, torque ripple and mounting forces. Renew. Energy 2015, 83, 67–77. [Google Scholar] [CrossRef]
- Li, Y.; Calisal, S.M. Three-dimensional effects and arm effects on modeling a vertical axis current turbine. Renew. Energy 2010, 35, 2325–2334. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. The influence of turbulence model and two and three-dimensional domain selection on the simulated performance characteristics of vertical axis tidal turbines. Renew. Energy 2017, 105, 106–116. [Google Scholar] [CrossRef]
- Strickland, J.H.; Webster, B.T.; Nguyen, T. A vortex model of the Darrieus turbine: An analytical and Experimental Study. J. Fluids Eng. 1979, 101, 500–505. [Google Scholar] [CrossRef]


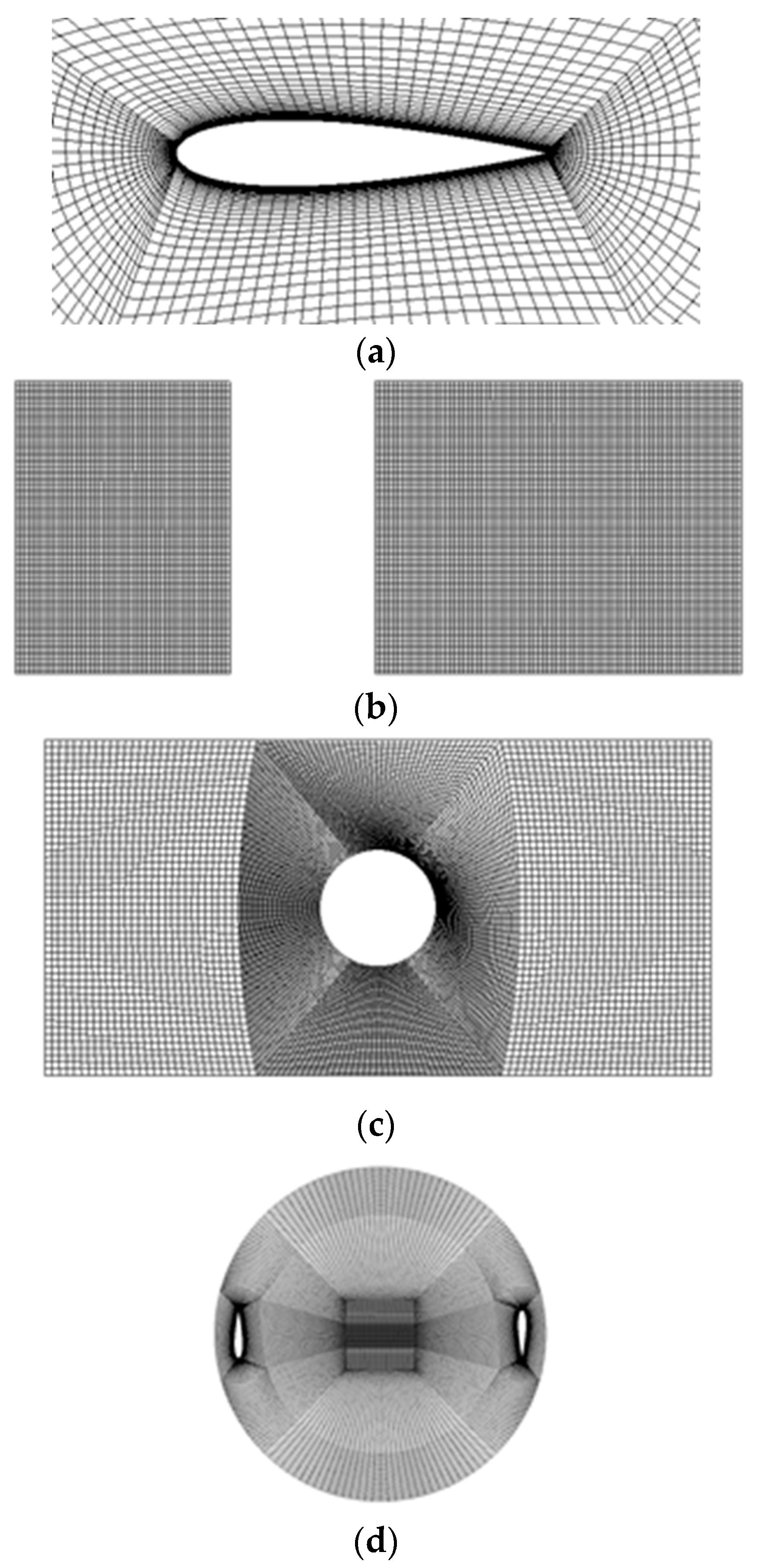


| Number of Blades | Turbine Diameter (m) | Chord Length (m) | Aspect Ratio | Compactness |
|---|---|---|---|---|
| 2 | 6 | 0.9 | 6.5 | 0.0955 |
| Mesh | Total Mesh Quantity (×103) | Y+ | Solution Time | Total Boundary Mesh Layer | Thickness of the First Layer |
|---|---|---|---|---|---|
| 1 | 45 | 21.5–38.2 | 4 h | 30 | 0.0004 m |
| 2 | 119 | 2.65–4.76 | 12 h | 30 | 0.0001 m |
| 3 | 274 | 0.83–1.96 | 26 h | 30 | 0.00005 m |
| Diameter (m) | Numer of Blades | Cord Length (m) | Air Foil | Aspect Ratio |
|---|---|---|---|---|
| 0.8 m | 2 | 0.12 | NACA0018 | 1.5 |
| Diameter D/m | Blades Number Z | Chord Length C/m | Airfoil | Rotation Speed /rad−1 |
|---|---|---|---|---|
| 1.22 | 2 | 0.0914 | NACA0012 | 0.749 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Hu, C.; Li, Y.; Deng, R. Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation. Energies 2018, 11, 3349. https://doi.org/10.3390/en11123349
Ma Y, Hu C, Li Y, Deng R. Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation. Energies. 2018; 11(12):3349. https://doi.org/10.3390/en11123349
Chicago/Turabian StyleMa, Yong, Chao Hu, Yulong Li, and Rui Deng. 2018. "Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation" Energies 11, no. 12: 3349. https://doi.org/10.3390/en11123349
APA StyleMa, Y., Hu, C., Li, Y., & Deng, R. (2018). Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation. Energies, 11(12), 3349. https://doi.org/10.3390/en11123349




