The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations
Abstract
1. Introduction
- Actual energy captured by TECs requiring consideration of device ‘water to wire’ efficiency factor that accounts for hydrodynamic, mechanical and electrical losses.
- Intra-array spacing of devices relative to the plan area of model cells.
- Support structure form drag associated with each TEC.
- Any associated energy losses in downstream wake mixing and free stream velocity interaction between devices.
- To incorporate tidal energy extraction at device scale.
- To test the performance of the modelled hydrodynamics.
- To compare array-averaging with device-scale results.
- To quantify associated uncertainty.
2. Materials and Methods
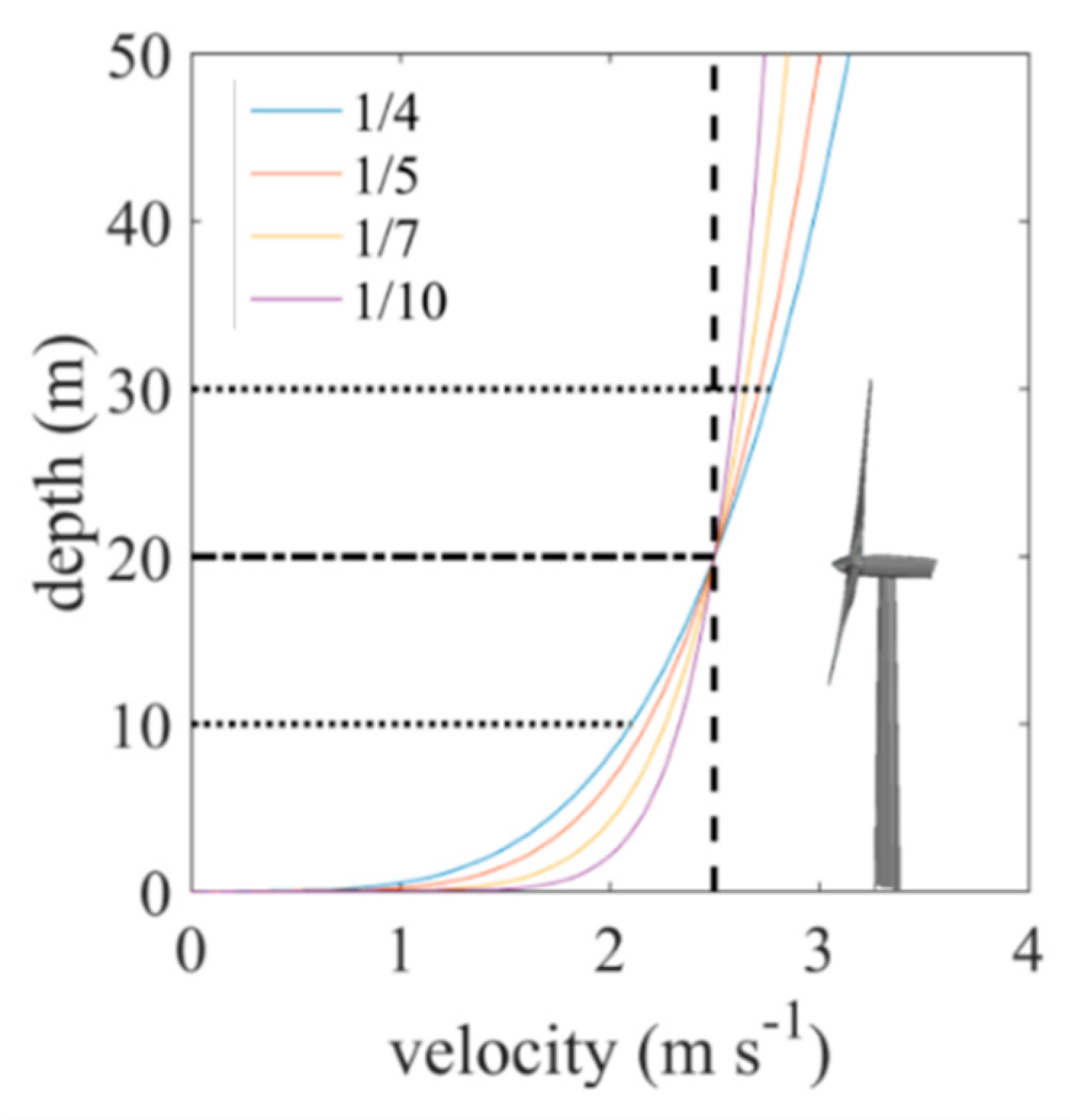
2.1. Seabed Stress Term
2.2. Blockage Ratio
2.3. Mesh Resolution Dependency
2.4. Turbulence Closure Schemes
- Zero equation models (constant viscosity, mixing-length, free-shear layer etc.)
- One equation models (Eddy viscosity concept, Bradshaw et al. etc.)
- Two equation models (k-Ɛ, k-ω, ASM etc.)
- Seven equation model (Reynolds turbulent stress/flux)
- Constant viscosity (CV, the default in Telemac)
- Elder model
- k-epsilon (k-Ɛ) model
- Smagorinski model
2.5. Constant Viscosity Scheme
2.6. Depth-Averaged K-Epsilon Scheme
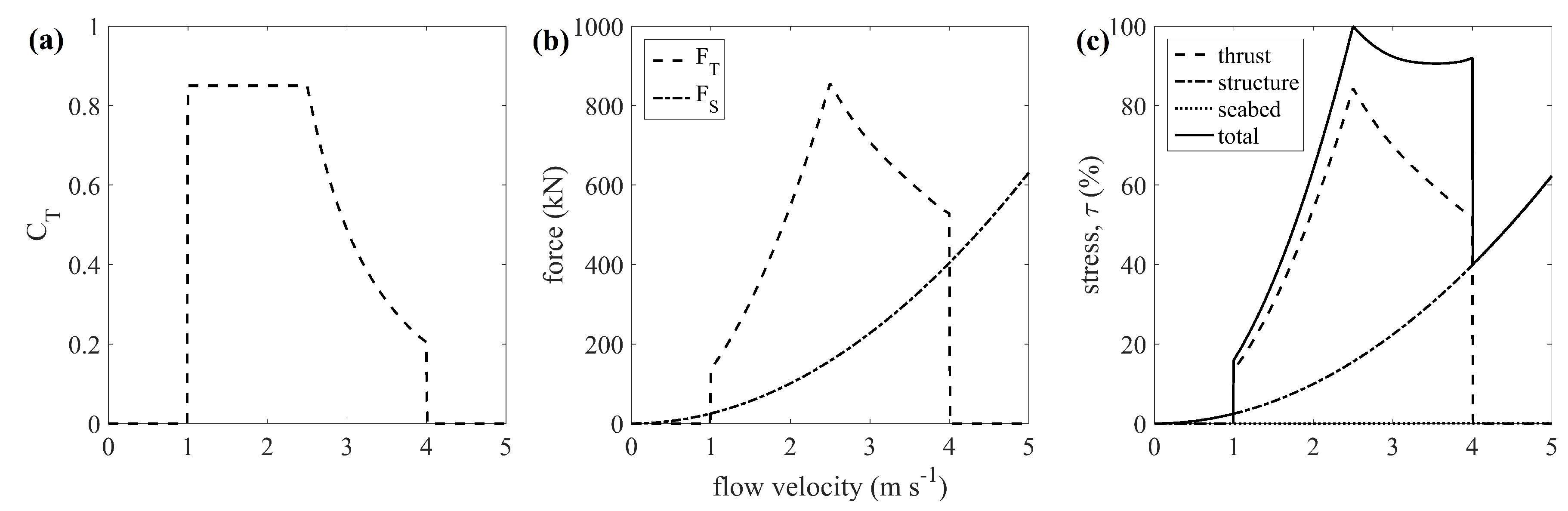
2.7. Energy Extraction Term
- number of TECs
- center position coordinates of each TEC
- the length and width of the grid area occupied by each TEC
- orientation of center axis of TEC to x axis
- TEC rotor radius
- TEC upstream reference velocity distance
- TEC structural drag coefficient
2.8. Method Validation
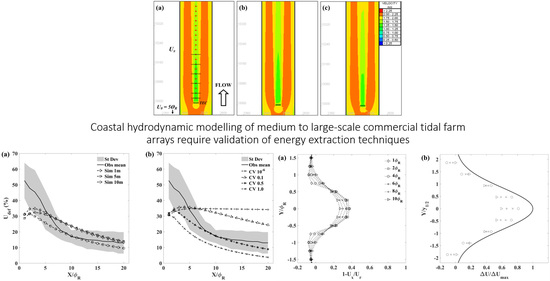
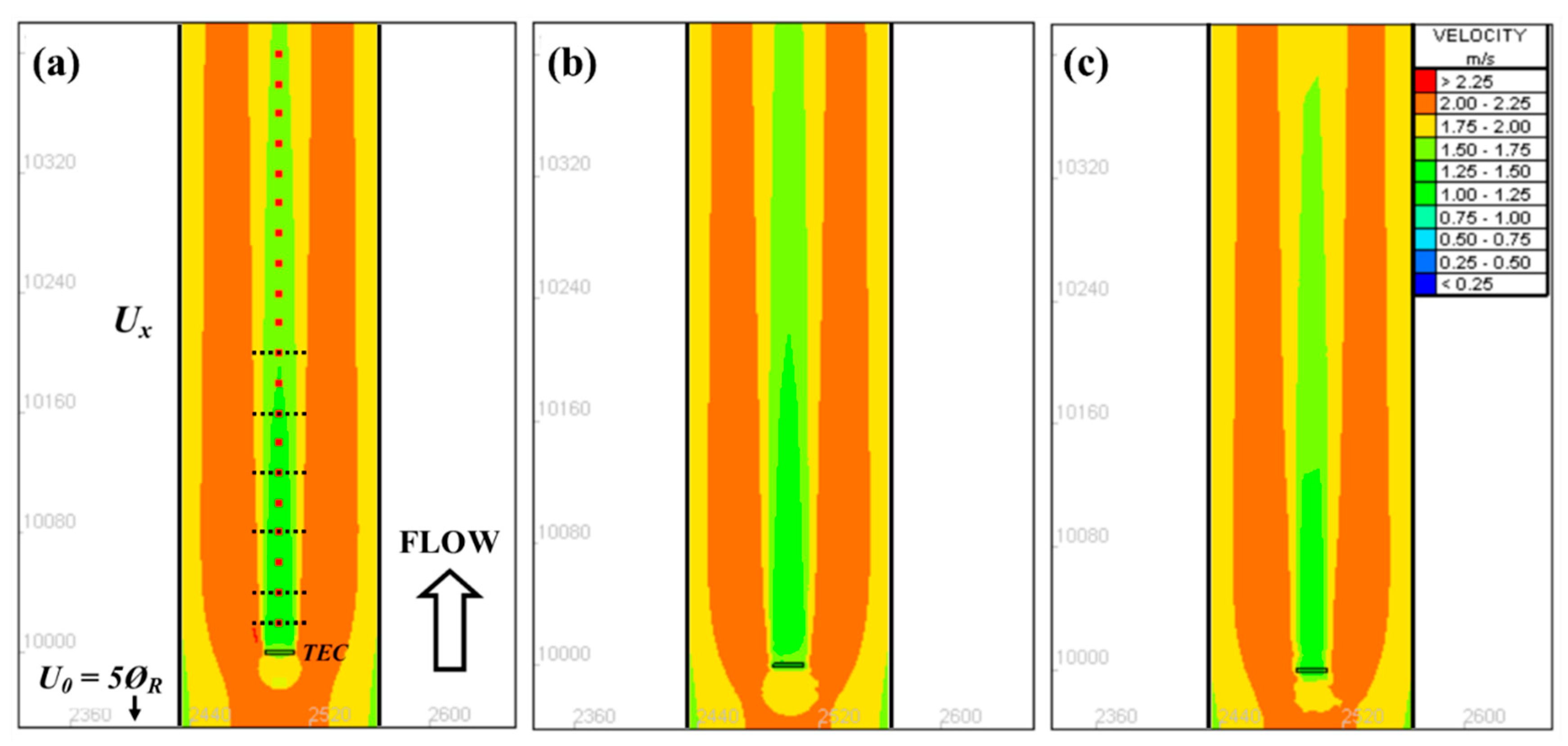
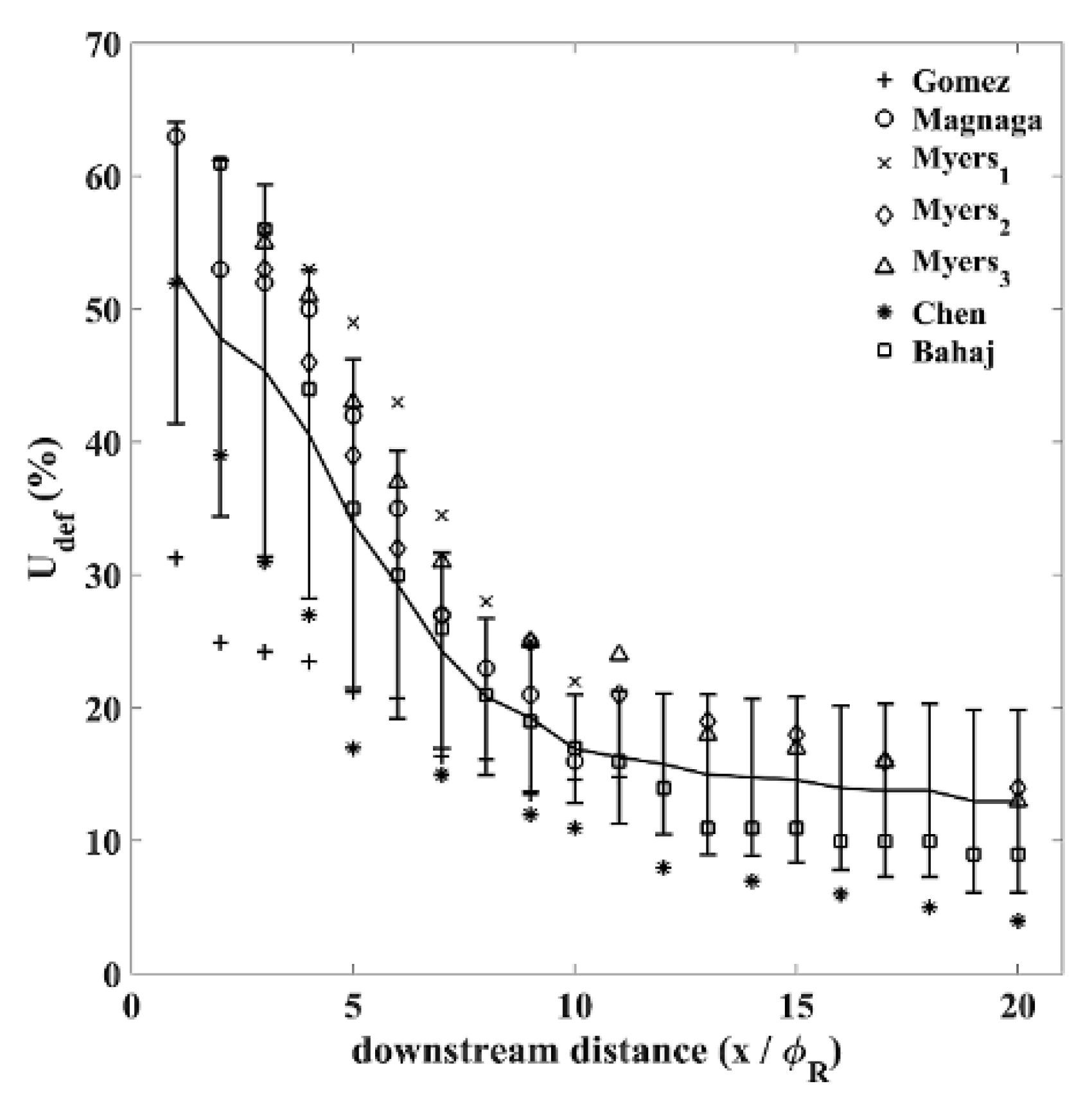
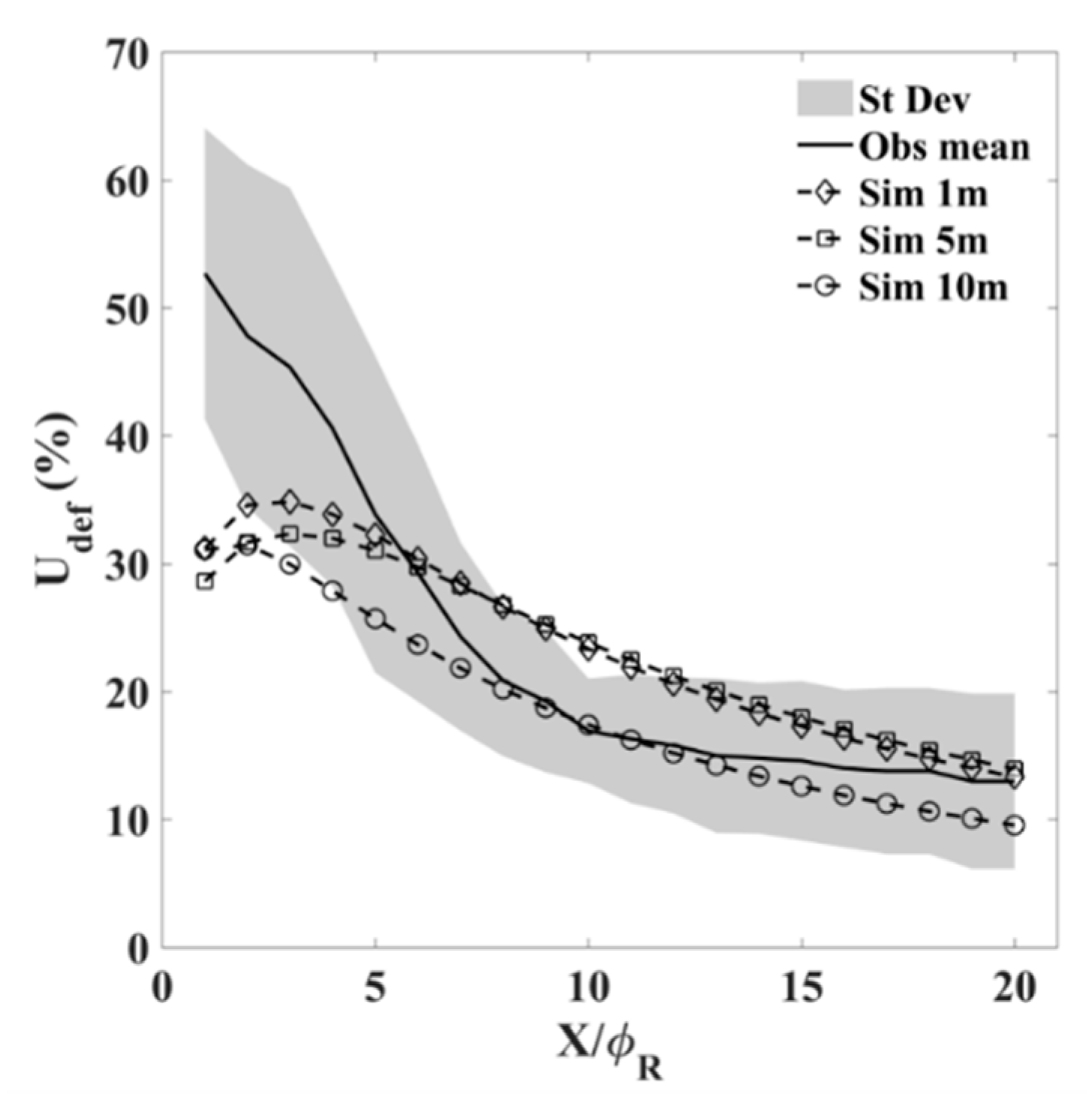
2.9. Axial Wake Centreline Velocity Deficit Profile
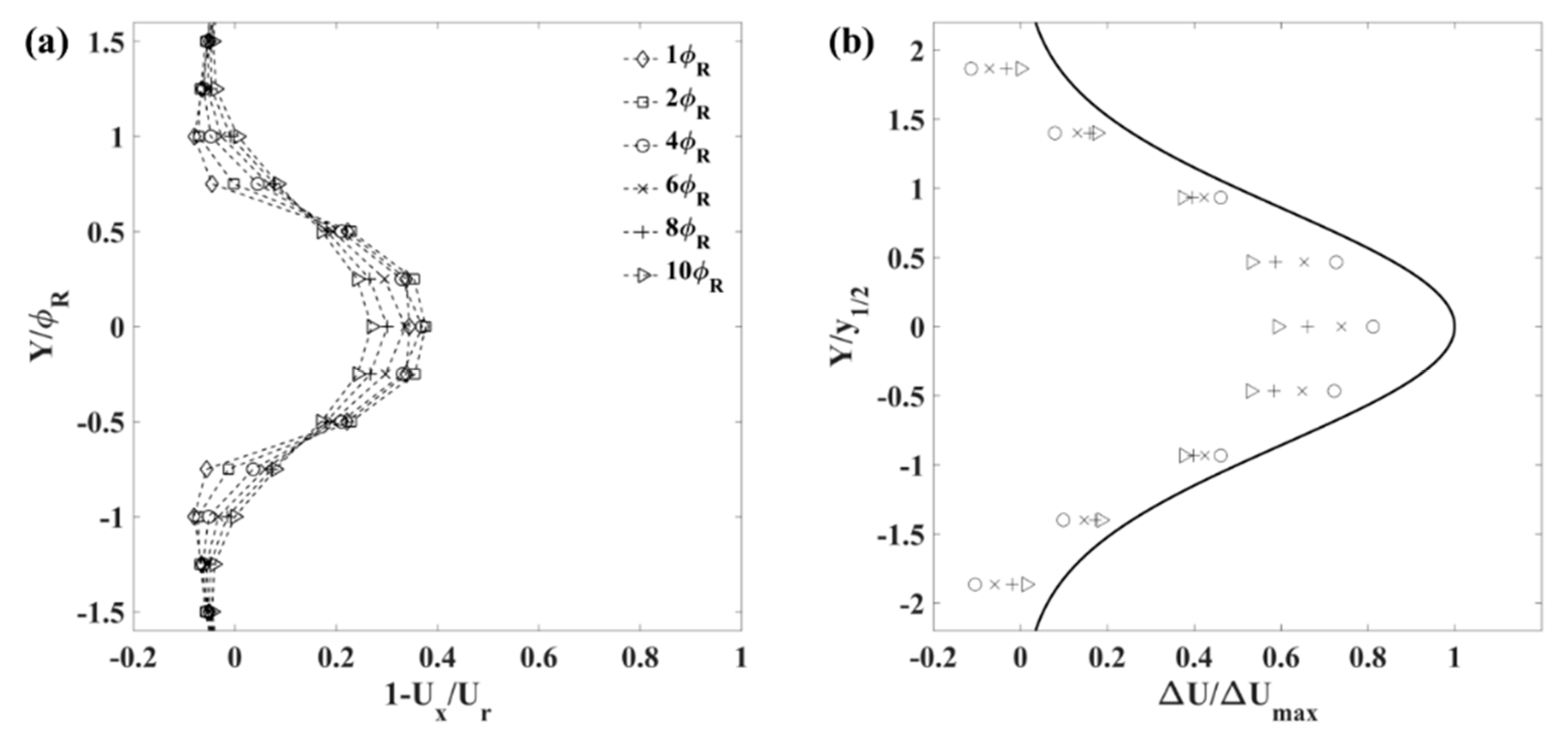
2.10. Transverse Wake Profile
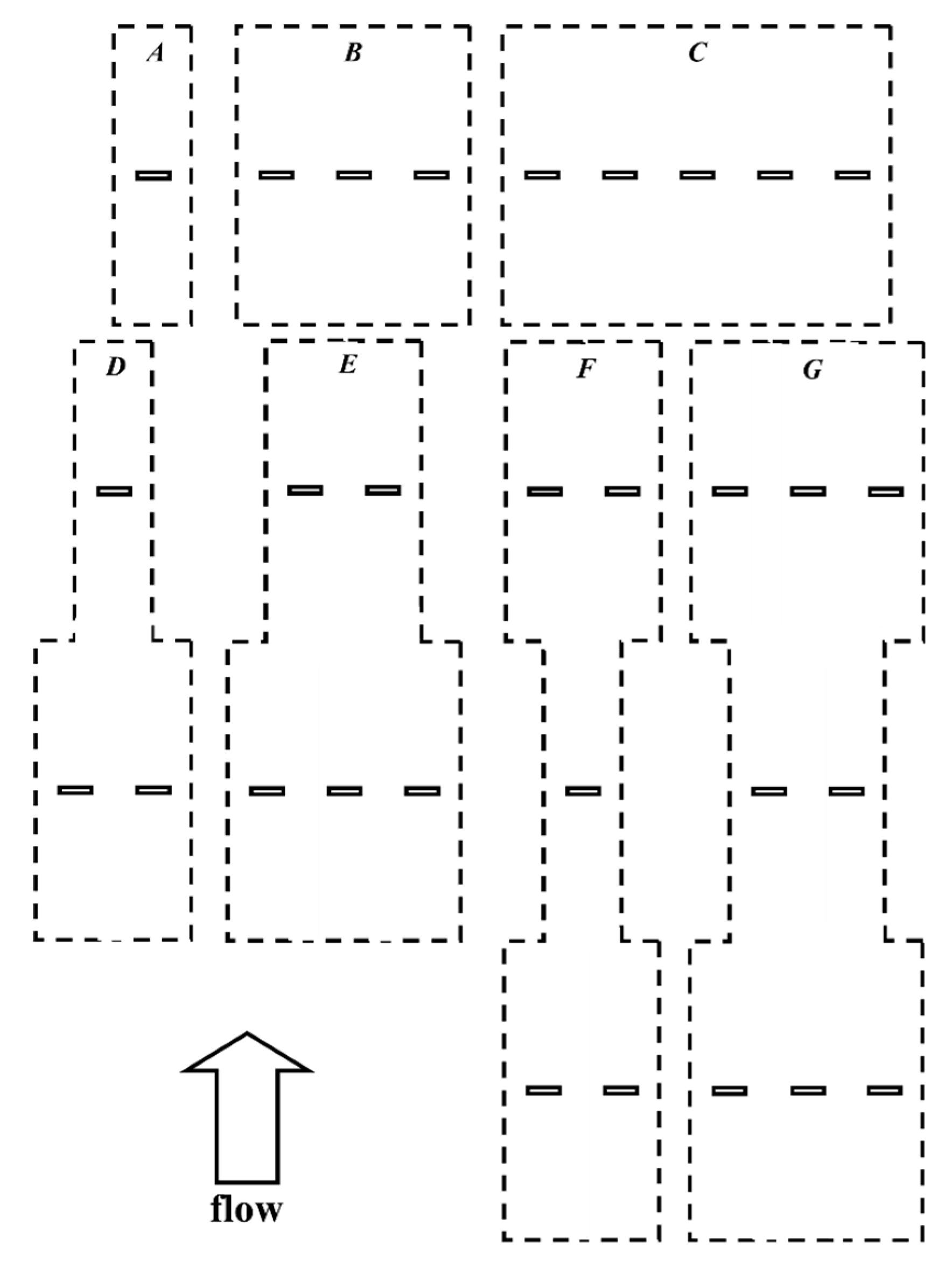
2.11. Array-Scale Evaluation
3. Results
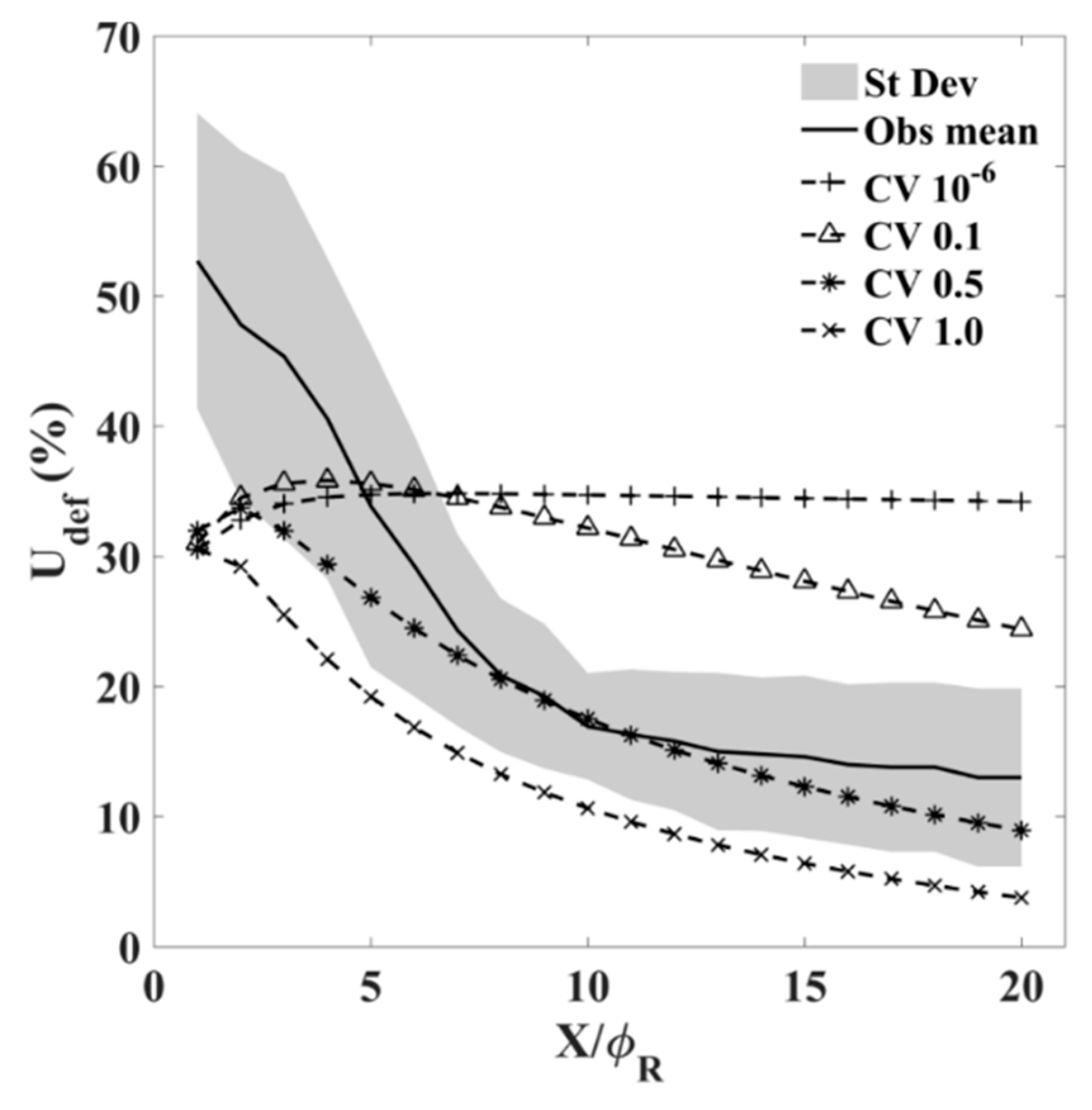
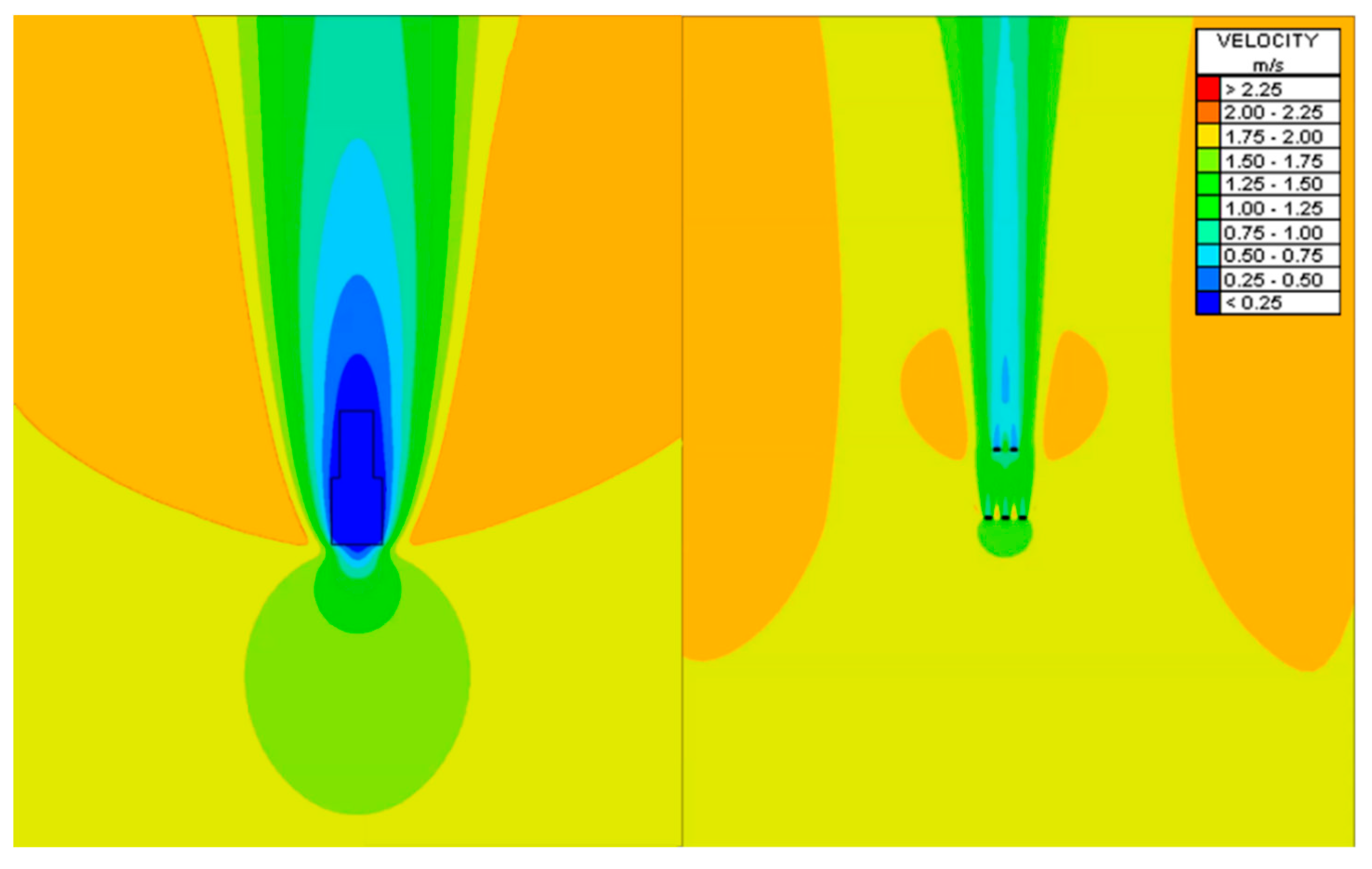
3.1. Single Device Validation
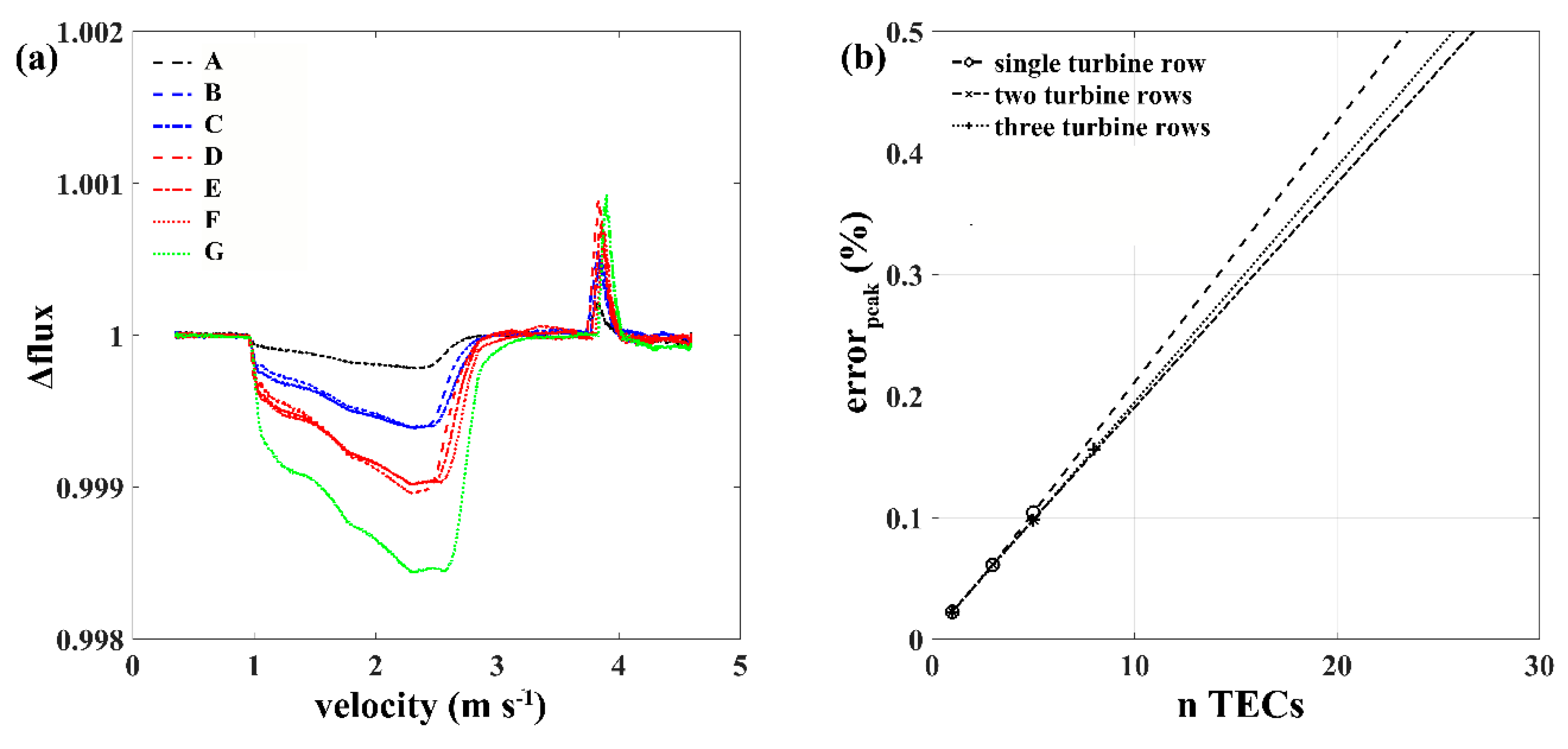
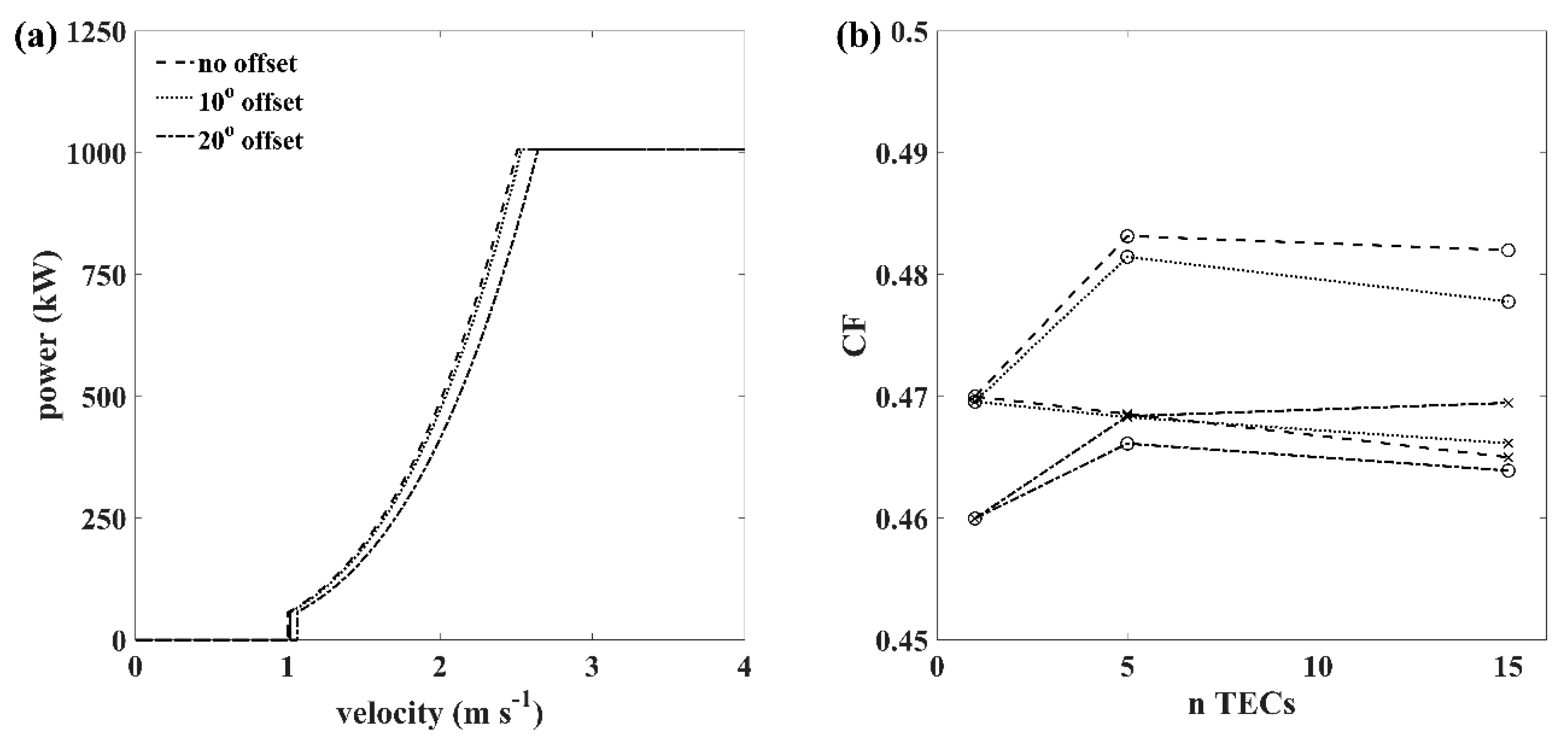
3.2. Array-Scale Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Formatted Data File 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | ||||||||||||||
| X1 | Y1 | L1 | W1 | THETA1 | R1 | DD1 | CD1 | EFFIN1 | EFFRAT1 | VIN1 | VRAT1 | VOUT1 | MH1 | MD1 |
| X2 | Y2 | L2 | W2 | THETA2 | R2 | DD2 | CD2 | EFFIN2 | EFFRAT2 | VIN2 | VRAT2 | VOUT2 | MH2 | MD2 |
| : | : | : | : | : | : | : | : | : | : | : | : | : | : | : |
| XN | YN | LN | WN | THETAN | RN | DDN | CDN | EFFINN | EFFRATN | VINN | VRATN | VOUTN | MHN | MDN |
Appendix B
| Turbulence Scheme | Mesh Resolution (m) | Coefficient | R2 | RMSE (%) |
|---|---|---|---|---|
| Constant Viscosity | 1 | 10−6 | <0.01 | 17.03 |
| 1 | 0.1 | <0.01 | 12.84 | |
| 1 | 0.5 | 0.67 | 7.34 | |
| 1 | 1.0 | 0.13 | 11.92 |
References
- Roche, R.C.; Walker-Springett, K.; Robins, P.E.; Jones, J.; Veneruso, G.; Whitton, T.A.; Piano, M.; Ward, S.L.; Duce, C.E.; Waggitt, J.J.; et al. Research priorities for assessing potential impacts of emerging marine renewable energy technologies: Insights from developments in Wales (UK). Renew. Energy 2016, 99, 1327–1341. [Google Scholar] [CrossRef]
- Magnaga, D.; Uihlein, A. Ocean energy development in Europe: Current status and future perspectives. Int. J. Mar. Energy 2015, 11, 84–104. [Google Scholar] [CrossRef]
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Robins, P.E.; Neill, S.P.; Lewis, M.J. Impacts of tidal-stream arrays in relation to the natural variability of sedimentary processes. Renew. Energy 2014, 72, 311–321. [Google Scholar] [CrossRef]
- The European Marine Energy Centre Ltd. (EMEC). Assessment of Tidal Energy Resource—Marine Renewable Energy Guides; BSI: London, UK, 2009; Available online: http://www.emec.org.uk/assessment-of-tidal-energy-resource/ (accessed on 29 May 2017).
- Frost, C.H.; Evans, P.S.; Harrold, M.J.; Mason-Jones, A.; O’Doherty, T.; O’Doherty, D.M. The impact of axial flow misalignment on a tidal turbine. Renew. Energy 2017, 113, 1333–1344. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, B.; Lin, J.; Wang, S. Experimental study of wake structure behind a horizontal axis tidal stream turbine. Appl. Energy 2017, 196, 82–96. [Google Scholar] [CrossRef]
- Uihlein, A.; Magagna, D. Wave and tidal current energy—A review of the current state of research beyond technology. Renew. Sustain. Energy Rev. 2016, 58, 1070–1081. [Google Scholar] [CrossRef]
- Work, P.A.; Haas, K.A.; Defne, Z.; Gay, T. Tidal sream energy site assessment via three-dimensional model and measurements. Appl. Energy 2013, 102, 510–519. [Google Scholar] [CrossRef]
- Fang, H.; Xianwen, B.; Benxia, L.; Qianqian, L. The assessment of extractable tidal energy and the effect of tidal energy turbine deployment on the hydrodynamics in Zhoushan. Acta Oceanol. Sin. 2015, 34, 86–91. [Google Scholar]
- Yang, Z.; Wang, T.; Copping, A.E. Modeling tidal stream energy extraction and its effects on transport processes in a tidal channel and bay system using a three-dimensional coastal ocean model. Renew. Energy 2013, 50, 605–613. [Google Scholar] [CrossRef]
- Neill, S.P.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
- Plew, D.R.; Stevens, C.L. Numerical modelling of the effect of turbines on currents in a tidal channel—Tory Channel, New Zealand. Renew. Energy 2013, 57, 269–282. [Google Scholar] [CrossRef]
- Lewis, M.; Neill, S.P.; Robins, P.E.; Hashemi, M.R. Resource Assessment for future generations of tidal-sream energy arrays. Energy 2015, 83, 403–415. [Google Scholar] [CrossRef]
- Robins, P.E.; Neill, S.P.; Lewis, M.J.; Ward, S.L. Characterising the spatial and temporal variability of the tidal-stream energy resource over the northwest European shelf seas. Appl. Energy 2015, 147, 510–522. [Google Scholar] [CrossRef]
- Piano, M.; Neill, S.P.; Lewis, M.J.; Robins, P.E.; Hashemi, M.R.; Davies, A.G.; Ward, S.L.; Roberts, M.J. Tidal stream resource assessment uncertainty due to flow asymmetry and turbine yaw misalignment. Renew. Energy 2017, 114, 1363–1375. [Google Scholar] [CrossRef]
- Piano, M.; Ward, S.; Robins, P.; Neill, S.; Lewis, M.; Davies, A.G.; Powell, B.; Wyn-Owen, A.; Hashemi, M.R. Characterizing the tidal energy resource of the West Anglesey Demonstration Zone (UK), using Telemac-2D and field observations. In Proceedings of the Telemac & Mascaret Users Conference, Daresbury, UK, 15–16 October 2015. [Google Scholar]
- Neill, S.P.; Hashemi, M.R. Fundamentals of Ocean Renewable Energy: Generating Electricity from the Sea, 1st ed.; Academic Press: Cambridge, MA, USA, 2018; ISBN 9780128104484. [Google Scholar]
- Martin-Short, R.; Hill, J.; Kramer, S.C.; Avdis, A.; Allison, P.A.; Piggott, M.D. Tidal resource extraction in the Pentland Firth, UK: Potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew. Energy 2015, 76, 596–607. [Google Scholar] [CrossRef]
- Perez-Ortiz, A.; Pescatore, J.; Bryden, I. A systematic approach to undertake tidal energy resource assessment with Telemac-2D. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC), Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- International Electrotechnical Commission. IEC 62600-201 TS: Marine Energy-Wave, Tidal and Other Water Current Converters-Part 201: Tidal Energy Resource Assessment and Characterization; IEC & BSI: Vancouver, BC, Canada, 2014; Available online: https://webstore.iec.ch/publication/22099 (accessed on 3 June 2016).
- Divett, T.; Vennell, R.; Stevens, C. Optimisation of multiple turbine arrays in a channel with tidally reversing flow by numerical modelling with adaptive mesh. Philos. Trans. R. Soc. London, Ser. A: Math. Phys. Eng. Sci. 2013, 371, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Masters, I.; Williams, A.; Croft, T.N.; Togneri, M.; Edmunds, M.; Zangiabadi, E.; Fairley, I.; Karunarathna, H. A Comparison of Numerical Modelling Techniques for Tidal Stream Turbine Analysis. Energies 2015, 8, 7833–7853. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Alvarez, M.; Sanchez, M.; Iglesias, G. Assessment of the impacts of tidal stream energy through high-resolution numerical modelling. Energy 2013, 61, 541–554. [Google Scholar] [CrossRef]
- Shives, M.; Crawford, C.; Hiles, C.; Walters, R. Combining numerical methods for basin and turbine scales for improved modelling of in-situ turbine arrays. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC), Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Shives, M.; Crawford, C.; Grovue, S. A tuned actuator cylinder approach for predicting cross-flow turbine performance with wake interaction and channel blockage effects. Int. J. Mar. Energy 2017, 18, 30–56. [Google Scholar] [CrossRef]
- Ahmed, A.; Afgan, I.; Apsley, D.D.; Stallard, T.; Stansby, P.K. CFD simulations of a full-scale tidal turbine: comparison of LES and RANS with field data. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar]
- Stallard, T.; Collings, R.; Feng, T.; Whelan, J. Interactions between tidal turbine wakes: experimental study of a group of three-bladed rotors. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [PubMed]
- Kramer, S.C.; Piggott, M.D. A correction to the enhanced bottom drag parameterisation of tidal turbines. Renew. Energy 2016, 92, 385–396. [Google Scholar] [CrossRef]
- Villaret, C.; Hervouet, J.-M.; Kopmann, R.; Merkel, U.; Davies, A.G. Morphodynamic modeling using the Telemac finite-element system. Comput. Geosci. 2013, 53, 105–113. [Google Scholar] [CrossRef]
- Supercomputing Wales. Available online: https://www.supercomputing.wales/#hero (accessed on 30 Augest 2018).
- Soulsby, R. Dynamics of Marine Sands, 1st ed.; Thomas Telford Publications: London, UK, 1997; ISBN 072772584X. [Google Scholar]
- Guillou, N.; Thiebot, J. The impact of seabed rock roughness on tidal stream power extraction. Energy 2016, 112, 762–773. [Google Scholar] [CrossRef]
- Gaurier, B.; Germain, G.; Facq, J.V.; Johnstone, C.M.; Grant, A.D.; Day, A.H.; Nixon, E.; de Felice, F.; Constanzo, M. Tidal energy “Round Robin” tests—comparisons between towing tank and circulating tank results. Int. J. Mar. Energy 2015, 12, 87–109. [Google Scholar] [CrossRef]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows, 1st ed.; John Wiley and Sons: New York, NY, USA, 2007; ISBN 9780470035580. [Google Scholar]
- Melvin, J.; Kaufman, R.; Lim, H.; Kaman, T.; Rao, P.; Glimm, J. Macro and micro issues in turbulent mixing. Sci. Ch. Technol. Sci. 2013, 56, 2355–2360. [Google Scholar] [CrossRef]
- Hanjalic, K. Closure Models for Incompressible Turbulent Flows. Delft University of Technology, Delft, 2004. Available online: https://www.researchgate.net/file.PostFileLoader.html?id=53898c5fd039b1bd3a8b45c0&assetKey=AS%3A273543839846420%401442229341759 (accessed on 4 November 2017).
- Rodi, W. Turbulence Models and Their Application in Hydraulics, 3rd ed.; A.A. Balkema: Rotterdam, The Netherland, 2000. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.C.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters, 1st ed.; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Haverson, D.; Bacon, J.; Smith, H. Modelling the far field impacts of a tidal energy development at Ramsey Sound. In Proceedings of the XXI Telemac and Mascaret User Club, Grenoble, France, 15–17 October 2014. [Google Scholar]
- Haverson, D.; Bacon, J.; Smith, H.C.; Venugopal, V.; Xiao, Q. Cumulative Impact Assessment of Tidal Stream Energy Extraction in the Irish Sea. Ocean Eng. 2017, 137, 417–428. [Google Scholar] [CrossRef][Green Version]
- Fallon, D.; Hartnett, M.; Olbert, A.; Nash, S. The effects of array configuration on the hydro-environmental impacts of tidal turbines. Renew. Energy 2014, 64, 10–25. [Google Scholar] [CrossRef]
- Rastogi, A.K.; Rodi, W. Predictions of heat and mass transfer in open channels. J. Hydraul. Div. ASCE 1978, HY3, 397–420. [Google Scholar]
- Shives, M.; Crawford, C. Tuned actuator disk approach for predicting tidal turbine performance with wake interaction. Int. J. Mar. Energy 2017, 17, 1–20. [Google Scholar] [CrossRef]
- Batten, W.M.; Bahaj, A.S.; Molland, A.F.; Chaplin, J.R. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Baston, S.; Waldman, S.; Side, J. Modelling Energy Extraction in Tidal Flows: TerraWatt Position Paper Revision 3.1. TerraWatt Consortium, July 2015. Available online: https://www.researchgate.net/profile/Susana_Baston/publication/283008185_Modelling_energy_extraction_in_tidal_flows_Terawatt_position_paper_revision_31/links/5652efa108aefe619b18e368/Modelling-energy-extraction-in-tidal-flows-Terawatt-position-paper-revision-31.pdf (accessed on 5 January 2016).
- Joly, A.; Pham, C.-T.; Andreewsky, M.; Saviot, S.; Fillot, L. Using the DRAGFO subroutine to model Tidal Energy Converters in Telemac-2D. In Proceedings of the XXII Telemac & Mascaret Users Conference, Daresbury, UK, 15–16 October 2015. [Google Scholar]
- Waldman, S.M.; Genet, G.; Baston, S.; Side, J. Correcting for mesh size dependency in a regional model’s representation of tidal turbines. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar]
- Bahaj, A.S.; Myers, L.E.; Thomson, M.D.; Jorge, N. Characterising the wake of horizontal axis marine current turbines. In Proceedings of the 7th European Wave and Tidal Energy Conference (EWTEC), Porto, Portugal, 11–14 September 2007. [Google Scholar]
- Myers, L.; Bahaj, A.S. Near wake properties of horizontal axis marine current turbines. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Maganga, F.; Pinon, G.; Germain, G.; Rivoalen, E. Wake properties characterisation of marine current turbines. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010. [Google Scholar]
- Gomez, M.G.; Grant, A. Marine Current Turbines: Array Effects. Energy Systems Research Unit. Master’s Thesis, University of Strathclyde, Glasgow, UK, September 2008. [Google Scholar]
- Myers, L.E.; Bahaj, A.S. Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators. Ocean Eng. 2010, 37, 218–227. [Google Scholar] [CrossRef]
- Abolghasemi, M.A.; Piggott, M.D.; Spinneken, J.; Vire, A.; Cotter, C.J.; Crammond, S. Simulating tidal turbines with multi-scale mesh optimisation techniques. J. Fluids Struct. 2016, 66, 69–90. [Google Scholar] [CrossRef]
- Stallard, T.; Feng, T.; Stansby, P.K. Experimental study of the mean wake of a tidal stream rotor in a shallow turbulent flow. J. Fluids Struct. 2015, 54, 235–246. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivolean, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Roc, T.; Greaves, D.; Thyng, K.M.; Conley, D.C. Tidal turbine representation in an ocean circulation model: Towards realistic applications. Ocean Eng. 2014, 78, 95–111. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G.; Neill, S. The influence of waves on the tidal kinetic energy resource at a tidal stream energy site. Appl. Energy 2016, 180, 402–415. [Google Scholar] [CrossRef]
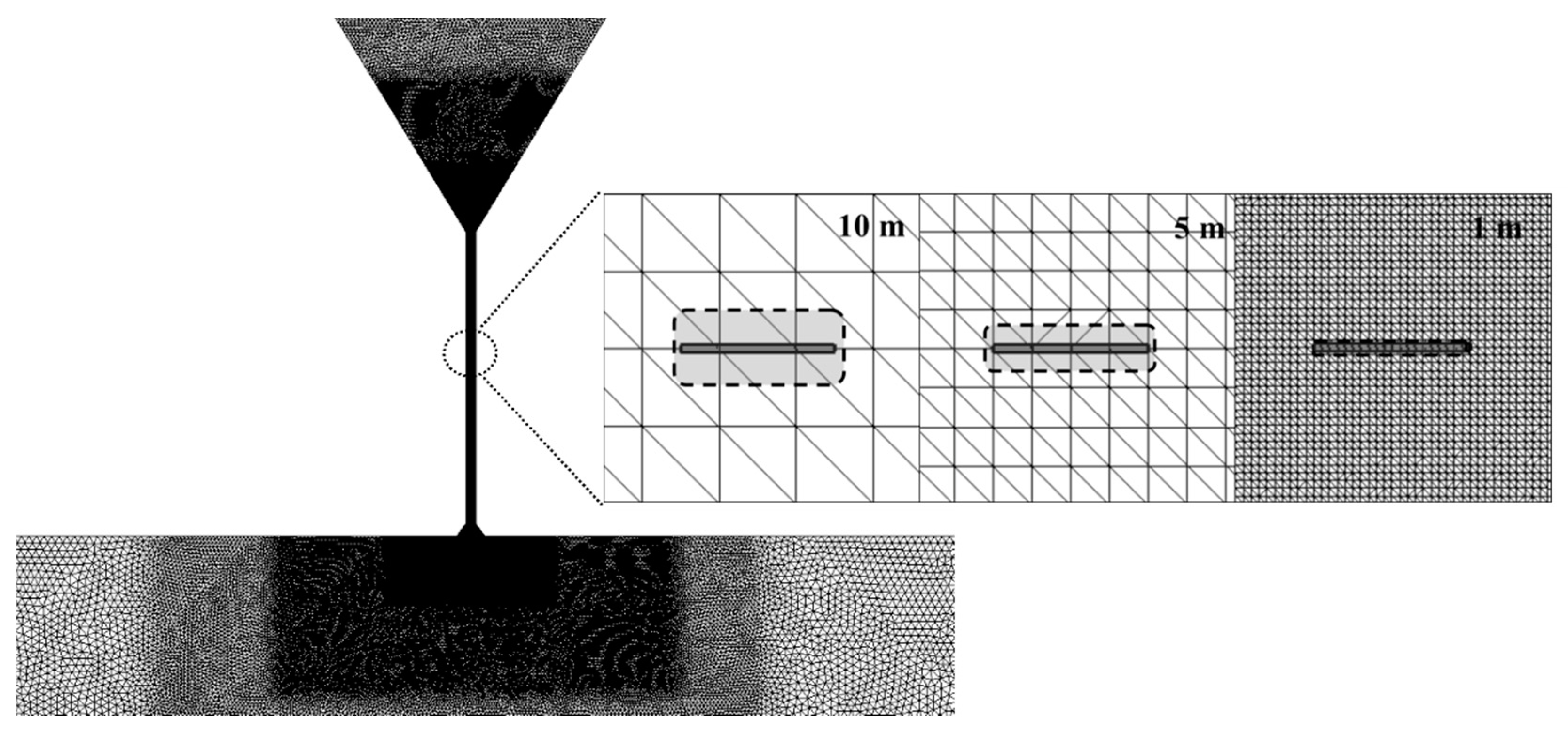
| Grid Resolution (m) | Defined TEC Area (m2) | Model Approximated Area (m2) | Error (%) |
|---|---|---|---|
| 10 | 20 | 133.3 | 566.7 |
| 5 | 20 | 83.3 | 316.7 |
| 1 | 20 | 20.7 | 3.4 |
| Parameter | Value |
|---|---|
| Monopile diameter, (m) | 5.00 |
| Hub height, H (m) | 22.50 |
| Rotor diameter, (m) | 20.00 |
| Cut-in speed, VIN (m s−1) | 1.00 |
| Cut-out speed, VOUT (m s−1) | 4.00 |
| Rated speed, VRAT (m s−1) | 2.50 |
| Cut-in efficiency, EffIN | 0.35 |
| Rated efficiency, EffRAT | 0.40 |
| Structural drag coefficient, CD | 0.60 |
| Upstream reference velocity distance, DD (m) |
| Turbulence Scheme | Mesh Resolution (m) | Coefficient | R2 | RMSE (%) |
|---|---|---|---|---|
| k-epsilon | 1 | 10−6 | 0.69 | 7.16 |
| 5 | 10−6 | 0.58 | 8.28 | |
| 10 | 10−6 | 0.61 | 8.02 |
| Array Layout | CF Change (%) | ||
|---|---|---|---|
| nTECs | Offset 10° | Offset 20° | |
| 1 | +0.04 | +1.00 | |
| Inline–single row | 5 | +0.18 | +1.71 |
| 15 | +0.42 | +1.81 | |
| Staggered–dual row | 5 | +0.02 | +0.01 |
| 15 | −0.11 | −0.45 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piano, M.; Robins, P.E.; Davies, A.G.; Neill, S.P. The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations. Energies 2018, 11, 2852. https://doi.org/10.3390/en11102852
Piano M, Robins PE, Davies AG, Neill SP. The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations. Energies. 2018; 11(10):2852. https://doi.org/10.3390/en11102852
Chicago/Turabian StylePiano, Marco, Peter E. Robins, Alan G. Davies, and Simon P. Neill. 2018. "The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations" Energies 11, no. 10: 2852. https://doi.org/10.3390/en11102852
APA StylePiano, M., Robins, P. E., Davies, A. G., & Neill, S. P. (2018). The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations. Energies, 11(10), 2852. https://doi.org/10.3390/en11102852