Thermal Performance Enhancement of a Cross-Flow-Type Maisotsenko Heat and Mass Exchanger Using Various Nanofluids
Abstract
1. Introduction
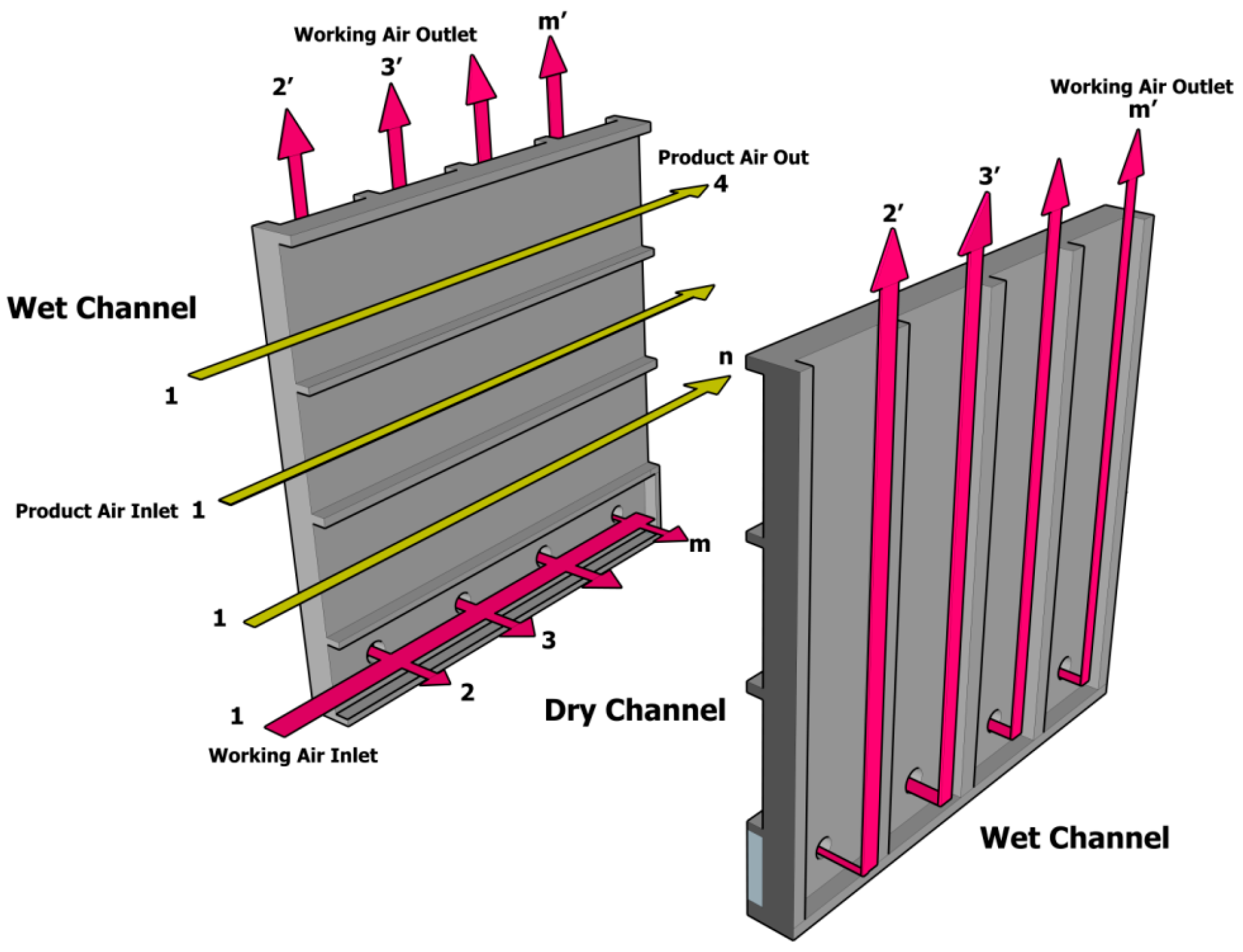
2. Mathematical Description
2.1. Energy and Mass Balance Laws
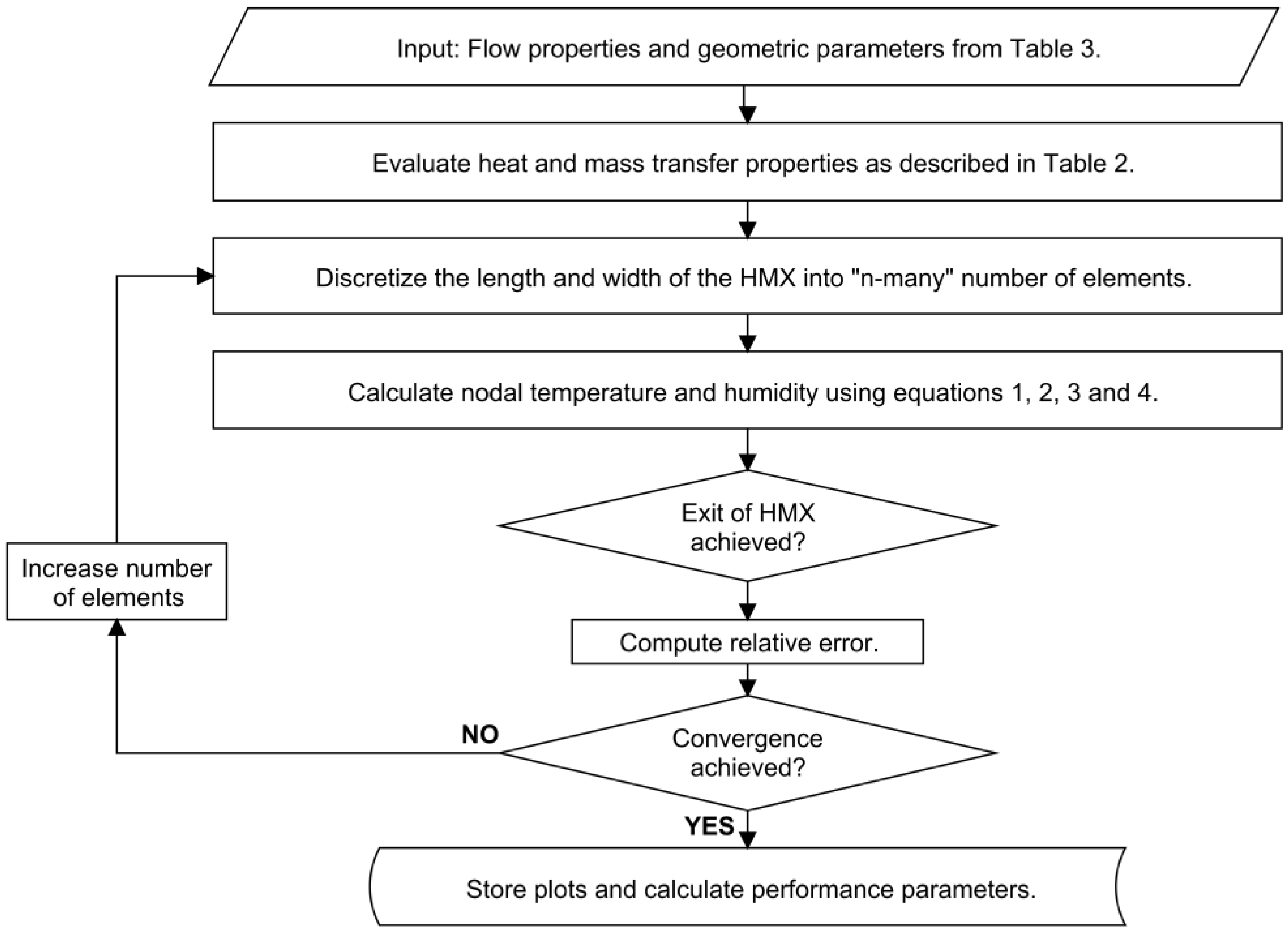
2.2. Calculation of Heat and Mass Transfer Parameters of the HMX
2.3. Performance Parameters
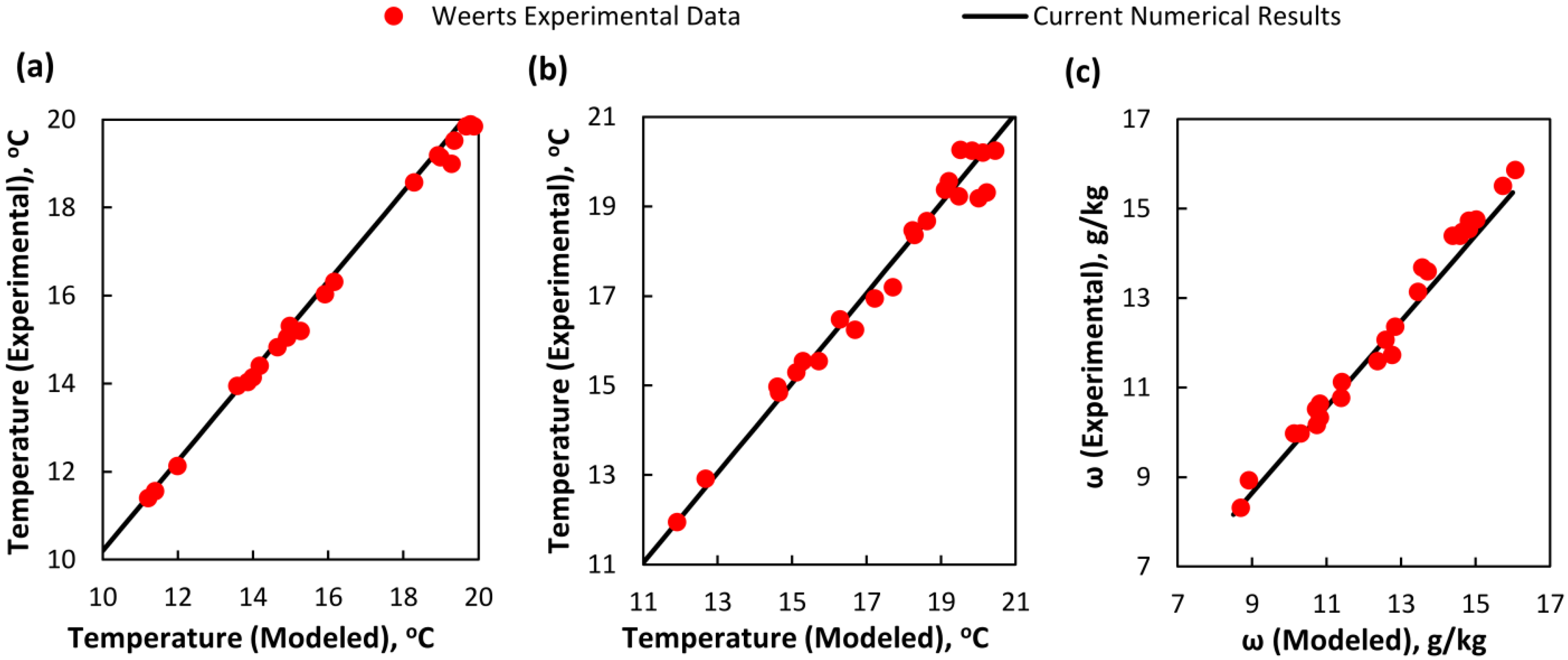
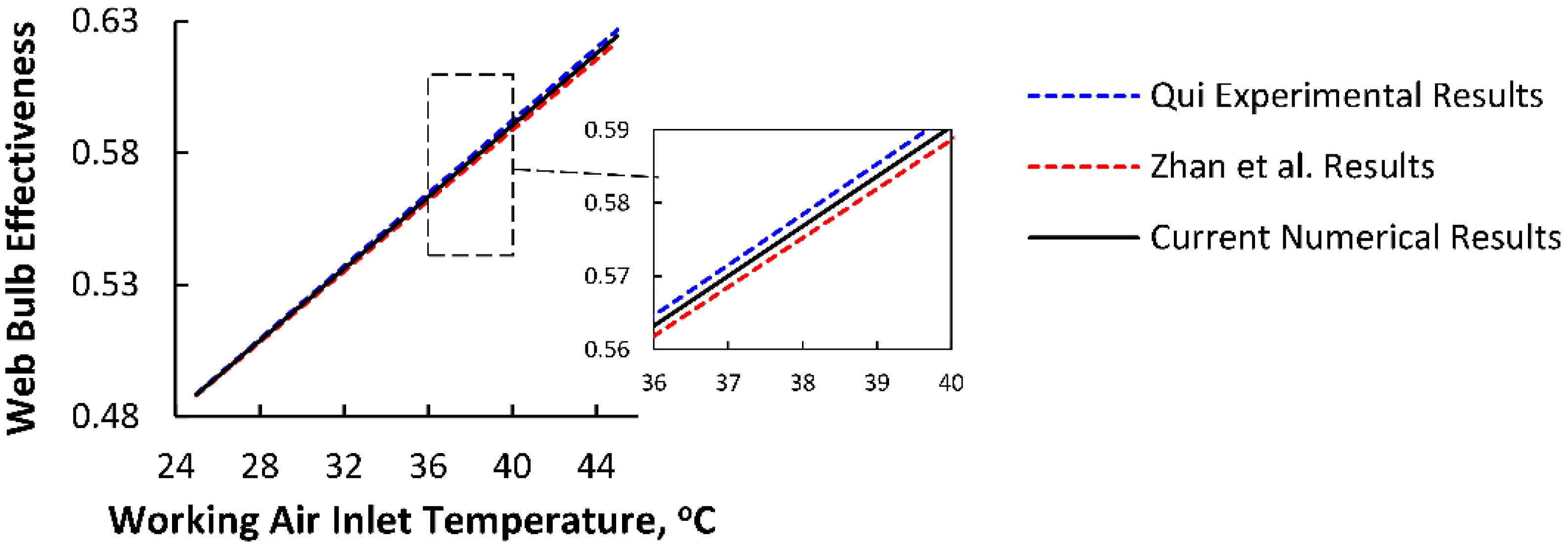
3. Validation of Numerical Approach
3.1. Comparison with an M50 Air Cooler [43] (Part I)
3.2. Comparison with a TAC-150 [44] (Part II)
4. Modelling Setup
5. Results and Discussion
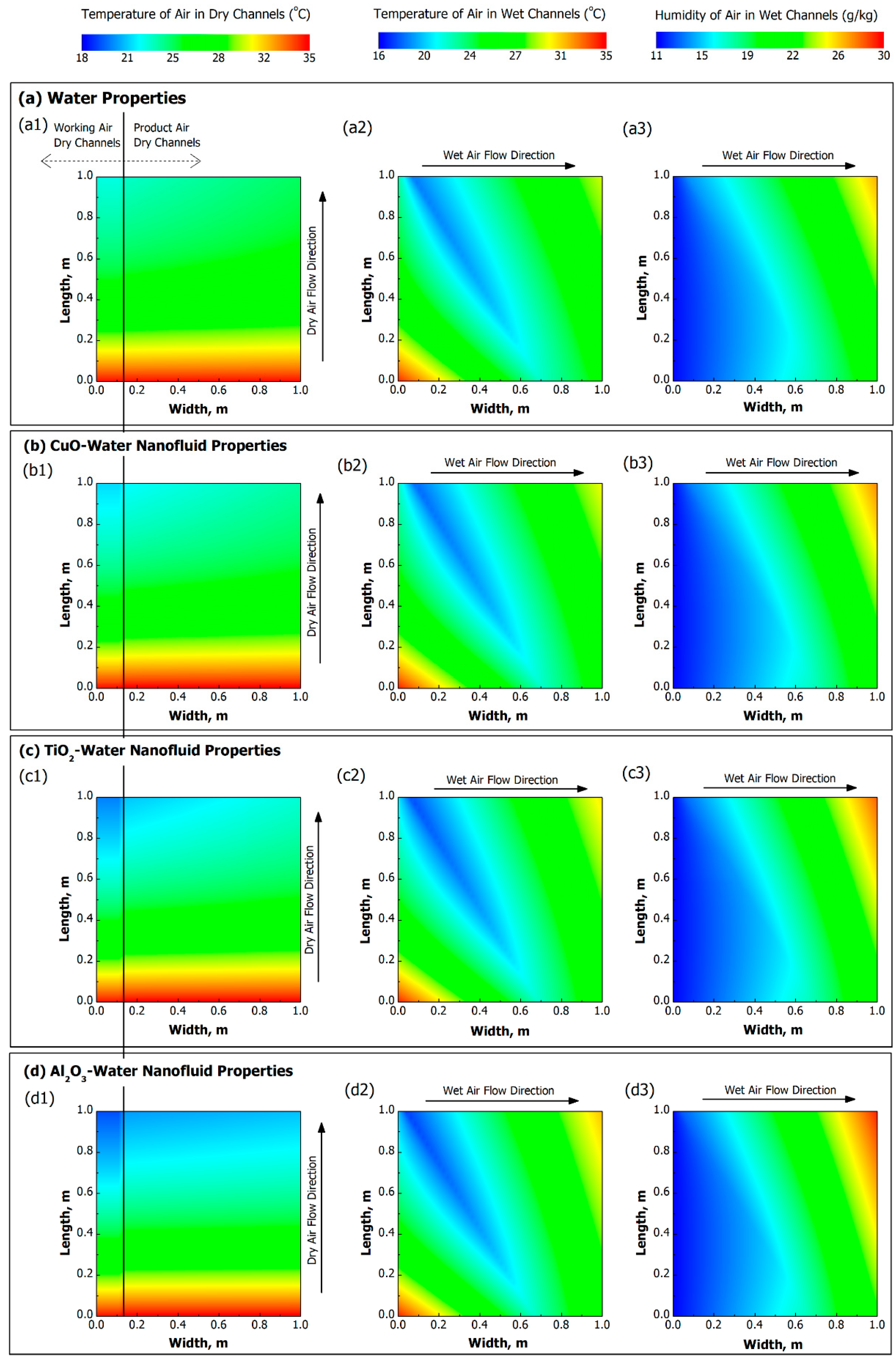
5.1. Heat and Mass Transfer Characteristics of the HMX
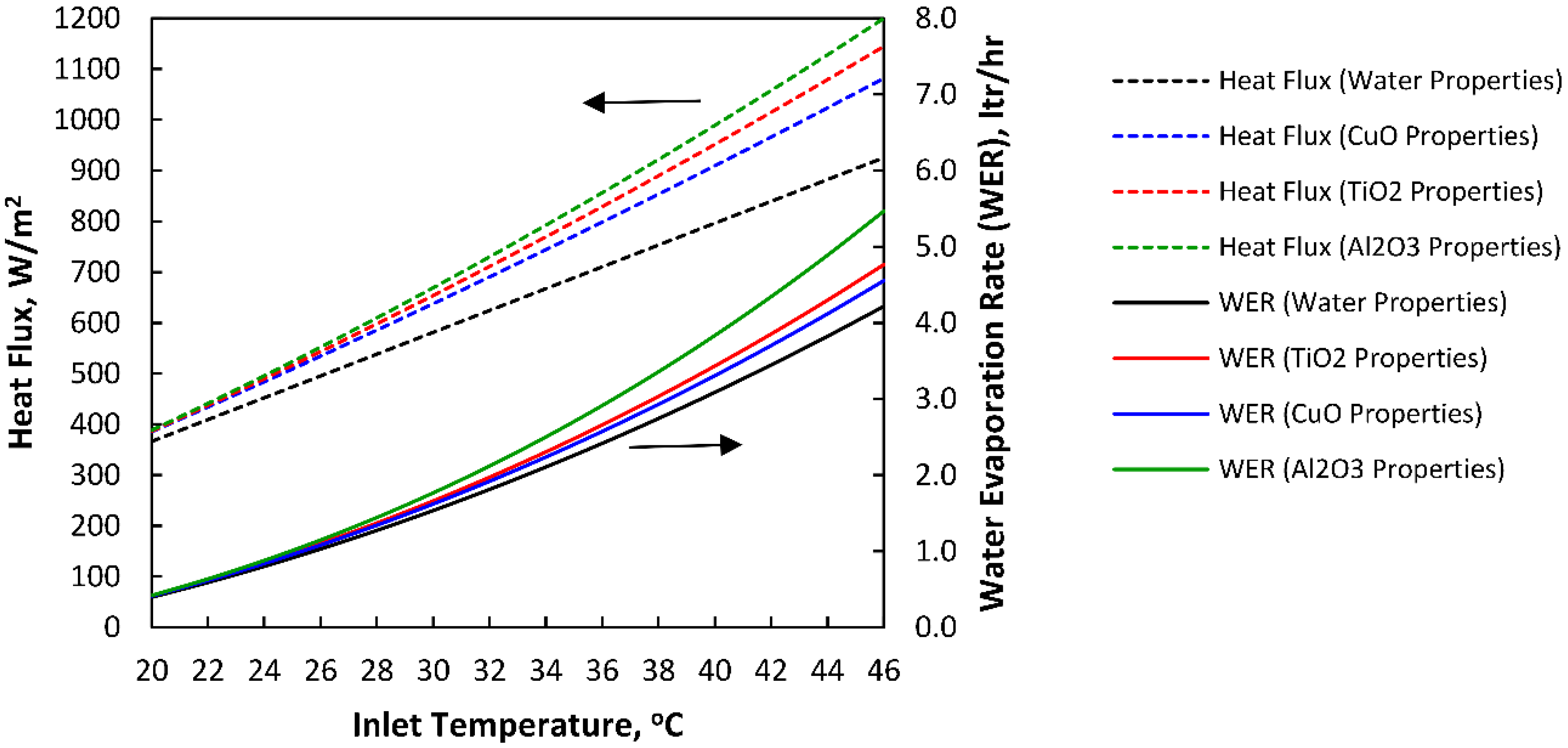
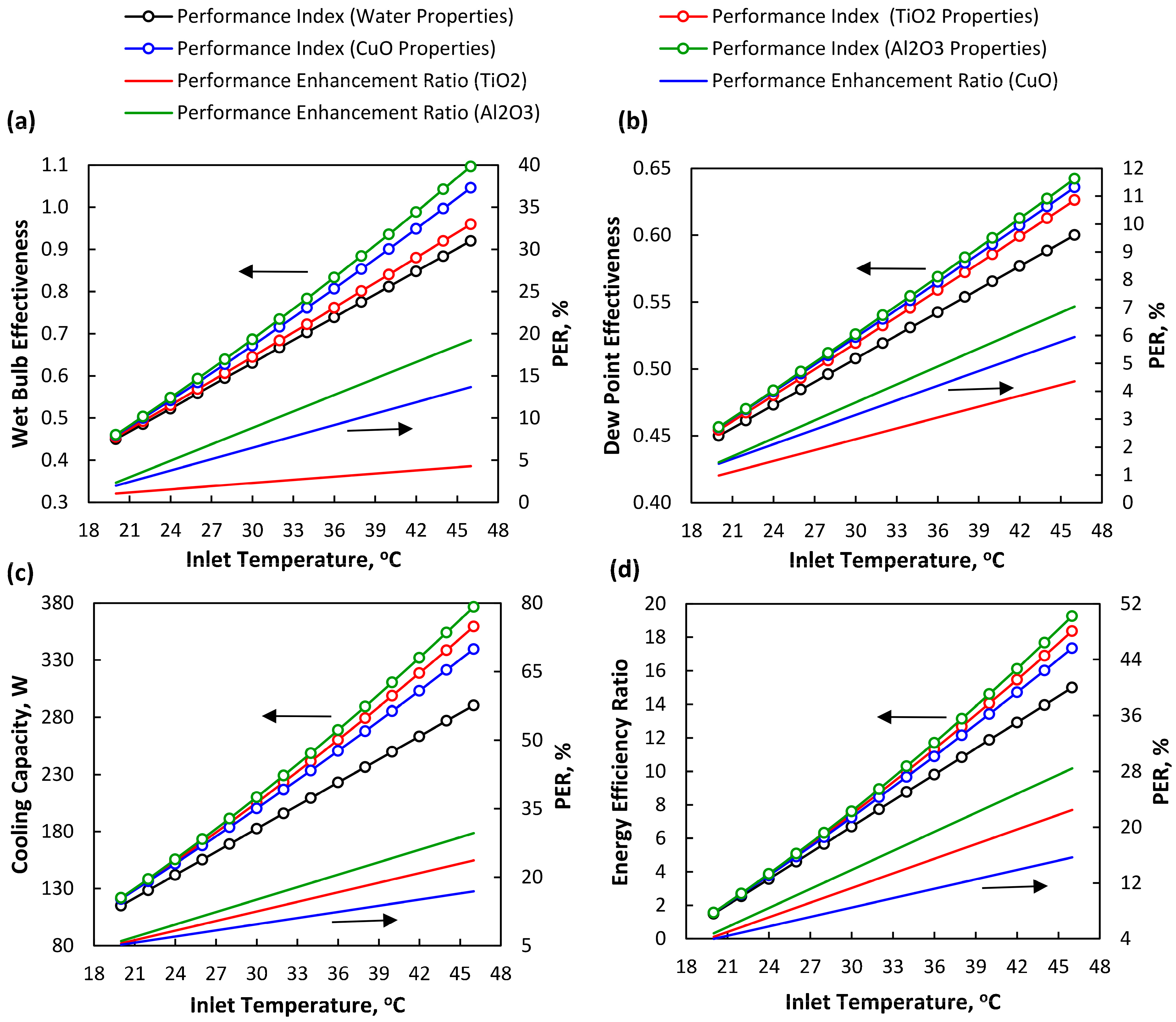
5.2. Performance of HMX Considering Different Types of Nanofluids
5.3. Parametric Study for Alumina Oxide Nanoparticles in the Wet Channel of the HMX
5.3.1. Influence of Particle Volume Fraction on Cooling Performance
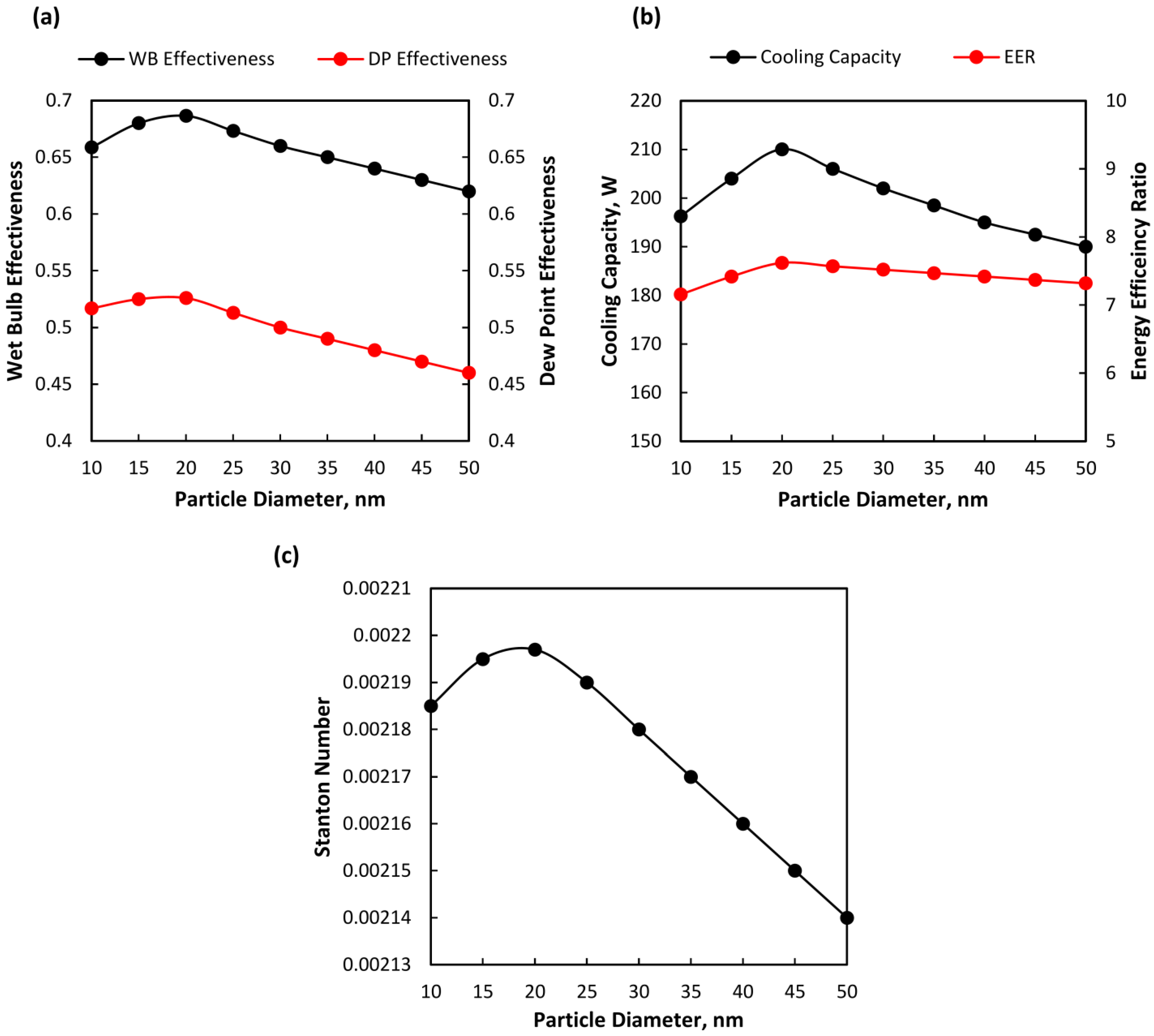
5.3.2. Influence of Particle Diameter on Cooling Performance
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Heat Transfer Surface Area, m2 | |
| Height, m | |
| Width, m | |
| Specific Heat of Fluid, J/(kg·K) | |
| Hydraulic Diameter, m | |
| Molecule Diameter, m | |
| Enthalpy, kJ/kg | |
| Convective Heat Transfer Coefficient, W/(m2·K) | |
| Convective Mass Transfer Coefficient, (kg·m2)/s | |
| Latent Heat of Evaporation, kJ/kg | |
| Thermal Conductivity, W/(m·K) | |
| Length of Channel, m | |
| Mass Flow Rate of Fluid, kg/s | |
| Nusselt Number | |
| Peclet Number | |
| Performance Enhancement Ratio, % | |
| Performance Index | |
| Prandtl Number | |
| Rate of Heat, W | |
| Reynolds Number | |
| Schmidt Number | |
| Sherwood Number | |
| Temperature, °C | |
| Velocity of the Fluid, m/s | |
| Particle Brownian Velocity, m/s | |
| Greek Letters | |
| Thermal Diffusivity, m2/s | |
| Mass Diffusivity, m2/s | |
| Effectiveness | |
| Dynamic Viscosity, (N·s)/m2 | |
| Absolute Humidity, kg/kg | |
| Density, kg/m3 | |
| Cooling Capacity, W | |
| Volume Fraction of Nanofluid | |
| Mean Free Path of Fluid Molecules, nm | |
| Subscripts | |
| Dry Bulb | |
| Dew Point | |
| Dry Channel | |
| Experimental | |
| Inlet | |
| Related to Mass Transfer | |
| Related to Nanofluid | |
| Outlet | |
| Nanoparticle | |
| Product Air | |
| Saturated | |
| Water | |
| Working Air | |
| Wet Bulb | |
| Wet Channel | |
References
- Emdadi, Z.; Asim, N.; Yarmo, M.A.; Shamsudin, R.; Mohammad, M.; Sopian, K. Green material prospects for passive evaporative cooling systems: Geopolymers. Energies 2016, 9. [Google Scholar] [CrossRef]
- Martínez, P.J.; Llorca, C.; Pla, J.A.; Marténez, P. Experimental validation of the simulation model of a DOAS equipped with a desiccant wheel and a vapor compression refrigeration system. Energies 2017, 10, 1330. [Google Scholar] [CrossRef]
- Ma, Y.; Saha, S.C.; Miller, W.; Guan, L. Parametric analysis of design parameter effects on the performance of a solar desiccant evaporative cooling system in brisbane, Australia. Energies 2017, 10, 849. [Google Scholar] [CrossRef]
- Tariq, R.; Sheikh, N.A.; Xamán, J.; Bassam, A. An innovative air saturator for humidification-dehumidification desalination application. Appl. Energy 2018, 228, 789–807. [Google Scholar] [CrossRef]
- Tariq, R.; Sheikh, N.A. Numerical heat transfer analysis of Maisotsenko Humid Air Bottoming Cycle—A study towards the optimization of the air-water mixture at bottoming turbine inlet. Appl. Therm. Eng. 2018, 133, 49–60. [Google Scholar] [CrossRef]
- Noroozi, A.; Veneris, Y.S. Thermal Assessment of a Novel Combine Evaporative Cooling Wind Catcher. Energies 2018, 11, 442. [Google Scholar] [CrossRef]
- Li, S.; Jeong, J.-W. Energy Performance of Liquid Desiccant and Evaporative Cooling-Assisted 100% Outdoor Air Systems under Various Climatic Conditions. Energies 2018, 11, 1377. [Google Scholar] [CrossRef]
- Boukhanouf, R.; Alharbi, A.; Ibrahim, H.G.; Amer, O.; Worall, M. Computer modelling and experimental investigation of building integrated sub-wet bulb temperature evaporative cooling system. Appl. Therm. Eng. 2017, 115, 201–211. [Google Scholar] [CrossRef]
- Lin, J.; Wang, R.Z.; Kumja, M.; Bui, T.D.; Chua, K.J. Modelling and experimental investigation of the cross-flow dew point evaporative cooler with and without dehumidification. Appl. Therm. Eng. 2017, 121, 1–13. [Google Scholar] [CrossRef]
- Fakhrabadi, F.; Kowsary, F. Optimal design of a regenerative heat and mass exchanger for indirect evaporative cooling. Appl. Therm. Eng. 2016, 102, 1384–1394. [Google Scholar] [CrossRef]
- Tariq, R.; Zhan, C.; Zhao, X.; Sheikh, N.A. Numerical study of a regenerative counter flow evaporative cooler using alumina nanoparticles in wet channel. Energy Build. 2018, 169, 430–443. [Google Scholar] [CrossRef]
- Pandelidis, D.; Anisimov, S.; Rajski, K.; Brychcy, E.; Sidorczyk, M. Performance comparison of the advanced indirect evaporative air coolers. Energy 2017, 135, 138–152. [Google Scholar] [CrossRef]
- Khalid, O.; Ali, M.; Sheikh, N.A.; Ali, H.M.; Shehryar, M. Experimental analysis of an improved Maisotsenko cycle design under low velocity conditions. Appl. Therm. Eng. 2016, 95, 288–295. [Google Scholar] [CrossRef]
- Zhan, C.; Zhao, X.; Smith, S.; Riffat, S.B. Numerical study of a M-cycle cross-flow heat exchanger for indirect evaporative cooling. Build. Environ. 2011, 46, 657–668. [Google Scholar] [CrossRef]
- Zhan, C.; Duan, Z.; Zhao, X.; Smith, S.; Jin, H.; Riffat, S. Comparative study of the performance of the M-cycle counter-flow and cross-flow heat exchangers for indirect evaporative cooling - Paving the path toward sustainable cooling of buildings. Energy 2011, 36, 6790–6805. [Google Scholar] [CrossRef]
- Anisimov, S.; Pandelidis, D.; Danielewicz, J. Numerical analysis of selected evaporative exchangers with the Maisotsenko cycle. Energy Convers. Manag. 2014, 88, 426–441. [Google Scholar] [CrossRef]
- Pandelidis, D.; Anisimov, S.; Drag, P. Performance comparison between selected evaporative air coolers. Energies 2017, 10. [Google Scholar] [CrossRef]
- Xu, P.; Ma, X.; Zhao, X.; Fancey, K.S. Experimental investigation on performance of fabrics for indirect evaporative cooling applications. Build. Environ. 2016, 110, 104–114. [Google Scholar] [CrossRef]
- Duan, Z.; Zhao, X.; Li, J. Design, fabrication and performance evaluation of a compact regenerative evaporative cooler: Towards low energy cooling for buildings. Energy 2017, 140, 506–519. [Google Scholar] [CrossRef]
- Xu, P.; Ma, X.; Zhao, X.; Fancey, K. Experimental investigation of a super performance dew point air cooler. Appl. Energy 2017, 203, 761–777. [Google Scholar]
- Lee, J.; Lee, D.Y. Experimental study of a counter flow regenerative evaporative cooler with finned channels. Int. J. Heat Mass Transf. 2013, 65, 173–179. [Google Scholar] [CrossRef]
- Weerts, B.A. NSIDC Green Data Center Project: Coolerado and Modeling an Application of the Maisotsenko Cycle. Master’s Thesis, University of Colorado, Boulder, CO, USA, 2012. [Google Scholar]
- Pinto, R.V.; Fiorelli, F.A.S. Review of the mechanisms responsible for heat transfer enhancement using nanofluids. Appl. Therm. Eng. 2016, 108, 720–739. [Google Scholar] [CrossRef]
- Maheshwary, P.B.; Handa, C.C.; Nemade, K.R. A comprehensive study of effect of concentration, particle size and particle shape on thermal conductivity of titania/water based nanofluid. Appl. Therm. Eng. 2017, 199, 79–88. [Google Scholar] [CrossRef]
- Albadr, J.; Tayal, S.; Alasadi, M. Case Studies in Thermal Engineering Heat transfer through heat exchanger using Al 2 O 3 nanofluid at different concentrations. Case Stud. Therm. Eng. 2013, 1, 38–44. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; de Risi, A.; Laforgia, D. Cooling of electronic devices: Nanofluids contribution. Appl. Therm. Eng. 2017, 127, 421–435. [Google Scholar] [CrossRef]
- Anisimov, S.; Pandelidis, D. Numerical study of the Maisotsenko cycle heat and mass exchanger. Int. J. Heat Mass Transf. 2014, 75, 75–96. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Single-phase and two-phase treatments of convective heat transfer enhancement with nanofluids—A state-of-the-art review. Int. J. Therm. Sci. 2016, 100, 75–97. [Google Scholar] [CrossRef]
- Vanaki, S.M.; Ganesan, P.; Mohammed, H.A. Numerical study of convective heat transfer of nanofluids: A review. Renew. Sustain. Energy Rev. 2016, 54, 1212–1239. [Google Scholar] [CrossRef]
- Beck, M.P.; Yuan, Y.; Warrier, P.; Teja, A.S. The effect of particle size on the thermal conductivity of alumina nanofluids. J. Nanopart. Res. 2009, 11, 1129–1136. [Google Scholar] [CrossRef]
- Chiam, H.W.; Azmi, W.H.; Adam, N.M.; Ari, M.K.A.M. Numerical study of nanofluid heat transfer for different tube geometries—A comprehensive review on performance. Int. Commun. Heat Mass Trans. 2017, 86, 60–70. [Google Scholar] [CrossRef]
- Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—An overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, G.E. Heat Transfer and Pressure Drop of Liquids in Tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, M. Mass transfer in MHD flow of alumina water nanofluid over a flat plate under slip conditions. Alexandria Eng. J. 2015, 54, 383–387. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Welty, J.; Wicks, C.; Wilson, R.; Rorrer, G. Fundamentals of Momentum, heat, and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Yang, L.; Xu, J.; Du, K.; Zhang, X. Recent developments on viscosity and thermal conductivity of nanofluids. Powder Technol. 2017, 317, 348–369. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y. Convective heat transfer and flow characteristics of Cu-water nanofluid. Sci. China Ser. E Technol. Sci. 2002, 45, 408–416. [Google Scholar]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U.S. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Pandelidis, D.; Anisimov, S.; Worek, W.M. Comparison study of the counter-flow regenerative evaporative heat exchangers with numerical methods. Appl. Therm. Eng. 2015, 84, 211–224. [Google Scholar] [CrossRef]
- Maisotsenko, V.E.; Gillan, L.; Heaton, T.L.; Gillan, A.D. Method and Plate Apparatus for Dew Point Evaporative Cooler. U.S. Patent 09,966,928, 27 September 2001. [Google Scholar]
- Catalogue Data of the Fiber Heat and Mass Exchanger (Natural Air Conditioner); ISAW Corporation Limited: Hangzhou, China, 2005.
- Qiu, G. A Novel Evaporative/Desiccant Cooling System. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2007. [Google Scholar]
- EES: Engineering Equation Solver|F-Chart Software: Engineering Software. Available online: http://www.fchart.com/ees/ (accessed on 28 September 2018).
- Bolotin, S.; Vager, B.; Vasilijev, V. Comparative analysis of the cross-flow indirect evaporative air coolers. Int. J. Heat Mass Transf. 2015, 88, 224–235. [Google Scholar] [CrossRef]
- Ashrafmansouri, S.S.; Nasr Esfahany, M. Mass transfer in nanofluids: A review. Int. J. Therm. Sci. 2014, 82, 84–90. [Google Scholar] [CrossRef]
- Jradi, M.; Riffat, S. Experimental and numerical investigation of a dew-point cooling system for thermal comfort in buildings. Appl. Energy 2014, 132, 524–535. [Google Scholar] [CrossRef]
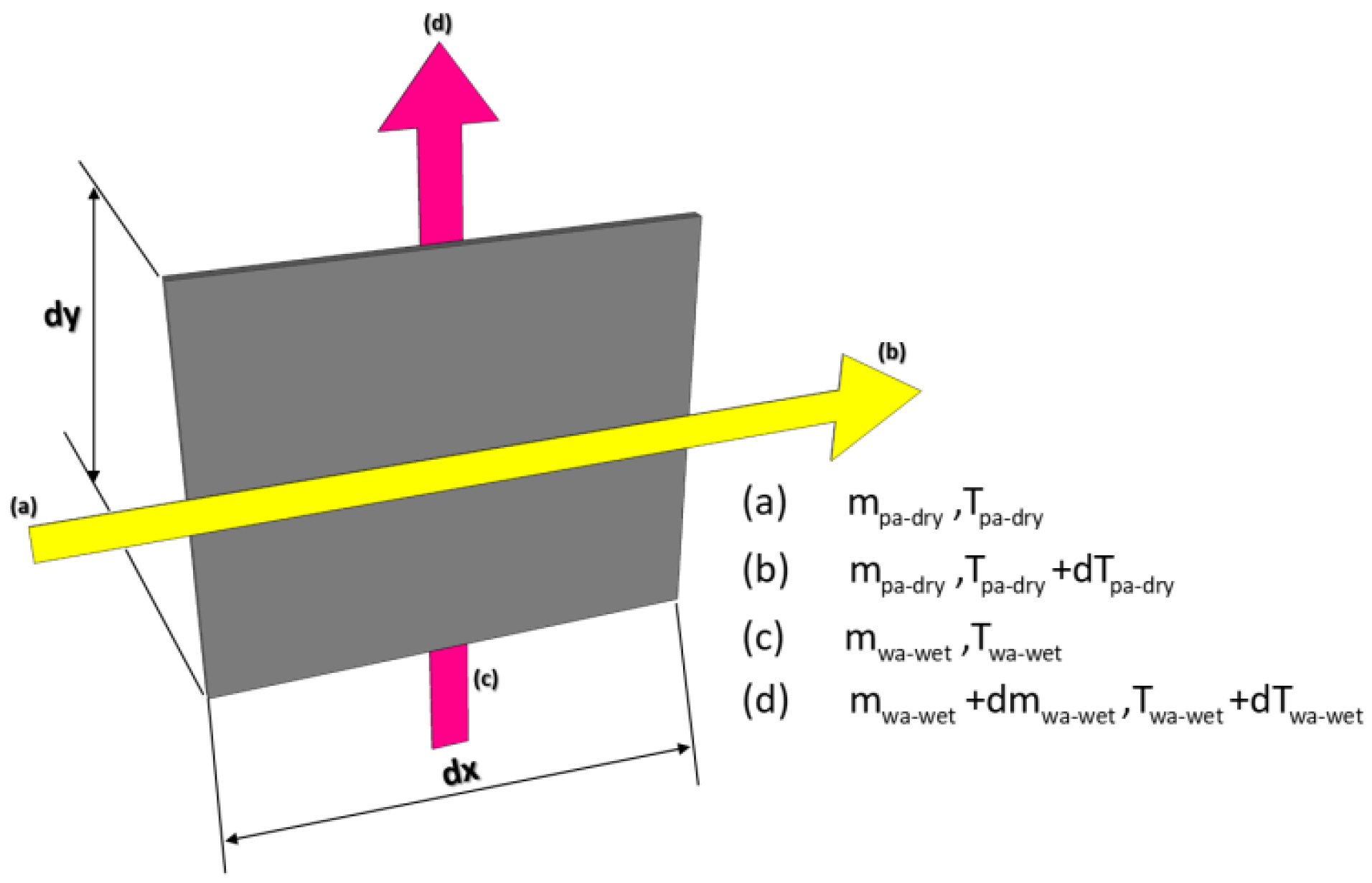

| Parameter | Equation | |
|---|---|---|
| Energy Balance | ||
| Product Air Channel (Temperature Distribution) | (1) | |
| Working Air Dry Channel (Temperature Distribution) | (2) | |
| Working Air Wet Channel (Temperature Distribution) | (3) | |
| Mass Balance Equation: | ||
| Working Air Wet Channel (Humidity Distribution) | (4) | |
| Parameter | Equation | |
|---|---|---|
| Product Air and Working Air Dry Channel | ||
| Hydraulic Diameter | (5) | |
| Reynolds Number | (6) | |
| Nusselt Number [33] | (7) | |
| Convective Heat Transfer Coefficient | (8) | |
| Working Air Wet Channel | ||
| Hydraulic Diameter | (9) | |
| Reynolds Number | (10) | |
| Nusselt Number [33] | (11) | |
| Convective Heat Transfer Coefficient | (12) | |
| Mass Diffusivity of Nanofluid [34] | (13) | |
| Mass Diffusivity of Nanofluid and Air [35] | (14) | |
| Schmidt Number | (15) | |
| Sherwood Number [36] | (16) | |
| Convective Mass Transfer Coefficient | (17) | |
| Nanofluid Properties | ||
| Thermal Conductivity [37] | (18) | |
| Specific Heat [38] | (19) | |
| Density [38] | (20) | |
| Thermal Diffusivity [39] | (21) | |
| Viscosity [31] | (22) | |
| Prandtl Number of Nanofluid | (23) | |
| Brownian Motion [40] | (24) | |
| Reynolds Number | (25) | |
| Peclet Number [41] | (26) | |
| Nusselt Number (Laminar) [32] | (27) | |
| Convective Heat Transfer Coefficient | (28) | |
| No. | Parameters | Quantity | Units |
|---|---|---|---|
| 1 | Intake air flow rate | 1095 to 4050 | m3/h |
| 2 | Supply-to-working air flow rate ratio | 1:1 | - |
| 3 | Inlet air temperature | 17.3 to 32.3 | °C |
| 4 | Inlet relative humidity | 7.4 to 62.9 | % |
| 5 | Number of product air channels | 39 | - |
| 6 | Product air channel height | 3.81 | mm |
| 7 | Working air channel height | 2.54 | mm |
| 8 | Channel width | 23.4 | mm |
| No. | Instrument | Usage | Accuracy | Manufacturer |
|---|---|---|---|---|
| 1 | HMP45C temperature sensor | To measure the temperature of working air and product air. | 0.05 °C | Campbell Scientific |
| 2 | HMP45C humidity sensor | To measure the relative humidity of working air and product air. | 2% | Campbell Scientific |
| 3 | ZW-007 temperature sensor | To measure the inlet air temperature. | 0.21 °C | HOBO |
| 4 | ZW-007 humidity sensor | To measure the inlet air relative humidity. | 2.5% | HOBO |
| 5 | 407123 hot wire anemometers | To measure the velocity profile of the air flow. | 3.0% | Extech Instruments |
| 6 | Fieldpiece HS26 stick meter with thermocouple ATH4 accessory head | To measure the temperature of the HMX filling surface. | 1 °C | Fieldpiece |
| No. | Parameters | Quantity | Units |
|---|---|---|---|
| 1 | Relative humidity of inlet air | 50 | % |
| 2 | Dry bulb temperature of inlet air | 25–45 | °C |
| 3 | Overall dimensions | 270 × 290 × 250 | mm3 |
| 4 | Length of primary air section | 192 | mm |
| 5 | Number of dry channels | 7 | - |
| No. | Instrument | Usage | Accuracy | Manufacturer |
|---|---|---|---|---|
| 1 | HMP45A hygrometer sensor | To measure the temperature of air flow. | Operating range: −40 °C to +50 °C Storage temperature range: −40 °C to +80 °C Settling time: 500 ms | Vaisala |
| 2 | HMP45A hygrometer sensor | To measure the relative humidity of air flow. | Operating range: 0.8% to 100% Accuracy: (1) ±2% RH for 0–90% of range. (2) ±3% RH for 90–100% of range. | Vaisala |
| No. | Parameters | Quantity | Units |
|---|---|---|---|
| 1 | Working Air Inlet DB Temperature | 35 | °C |
| 2 | Working Air Inlet Absolute Humidity | 11.2 | g/kg |
| 3 | Total Flow Rate of Inlet Air | 228 | m3/h |
| 4 | Product Air Flow Rate | 150 | m3/h |
| 5 | Working Air Flow Rate | 78 | m3/h |
| 6 | Particle Volume Fraction | 0.8 | % |
| 7 | Diameter of Nanoparticles | 20 | nm |
| 8 | Length of Dry Channels | 1 | m |
| 9 | Length of Wet Channels | 1 | m |
| 10 | Width of Channels | 314 | mm |
| 11 | Height of Channels | 5 | mm |
| 12 | Working Air Dry Channels | 33 | - |
| 13 | Product Air Dry Channels | 5 | - |
| 14 | Working Air Wet Channels | 32 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tariq, R.; Zhan, C.; Ahmed Sheikh, N.; Zhao, X. Thermal Performance Enhancement of a Cross-Flow-Type Maisotsenko Heat and Mass Exchanger Using Various Nanofluids. Energies 2018, 11, 2656. https://doi.org/10.3390/en11102656
Tariq R, Zhan C, Ahmed Sheikh N, Zhao X. Thermal Performance Enhancement of a Cross-Flow-Type Maisotsenko Heat and Mass Exchanger Using Various Nanofluids. Energies. 2018; 11(10):2656. https://doi.org/10.3390/en11102656
Chicago/Turabian StyleTariq, Rasikh, Changhong Zhan, Nadeem Ahmed Sheikh, and Xudong Zhao. 2018. "Thermal Performance Enhancement of a Cross-Flow-Type Maisotsenko Heat and Mass Exchanger Using Various Nanofluids" Energies 11, no. 10: 2656. https://doi.org/10.3390/en11102656
APA StyleTariq, R., Zhan, C., Ahmed Sheikh, N., & Zhao, X. (2018). Thermal Performance Enhancement of a Cross-Flow-Type Maisotsenko Heat and Mass Exchanger Using Various Nanofluids. Energies, 11(10), 2656. https://doi.org/10.3390/en11102656






