Application of Wind as a Renewable Energy Source for Passive Cooling through Windcatchers Integrated with Wing Walls
Abstract
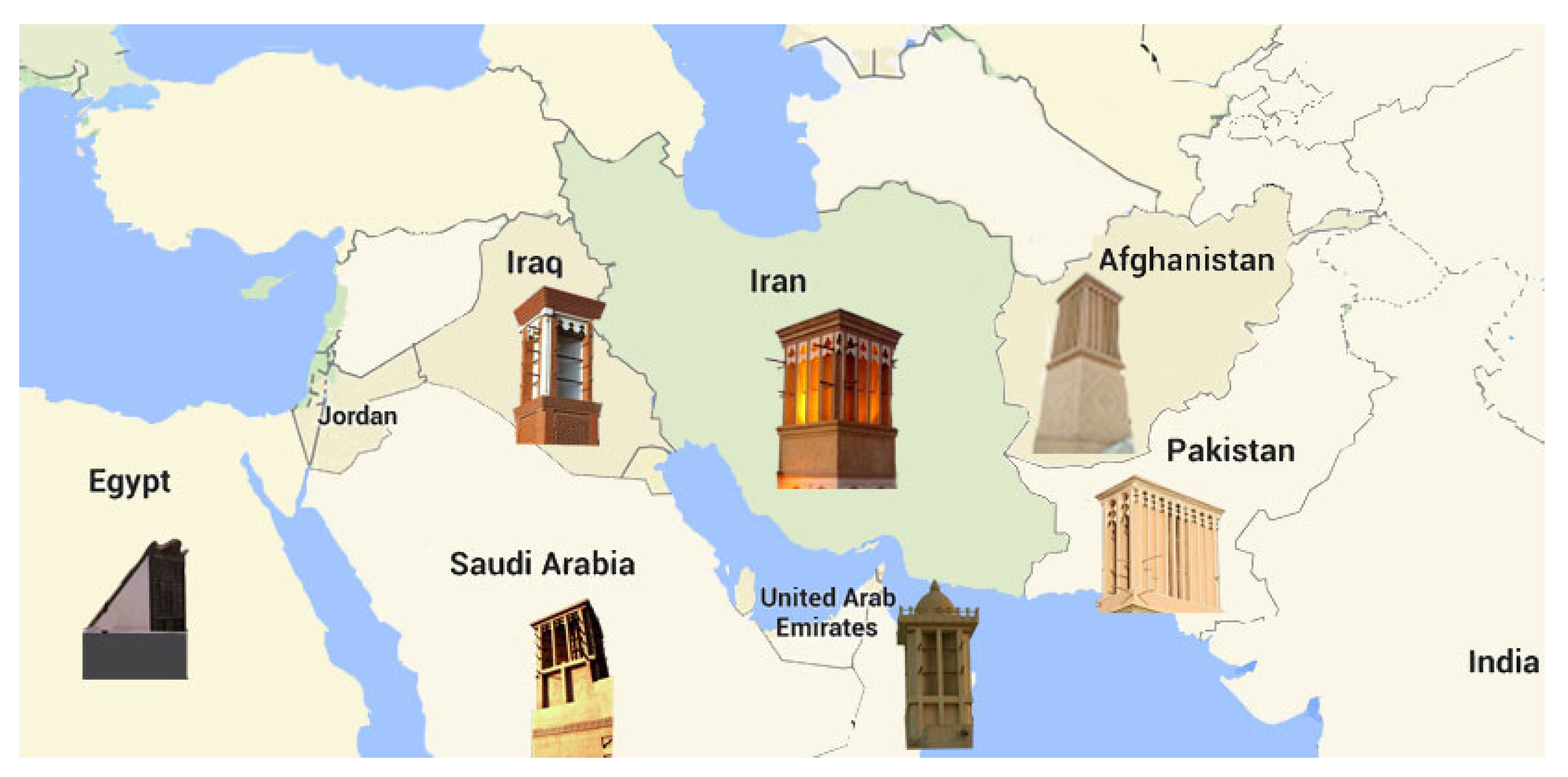
:1. Introduction
2. Literature Review
3. Materials and Methods
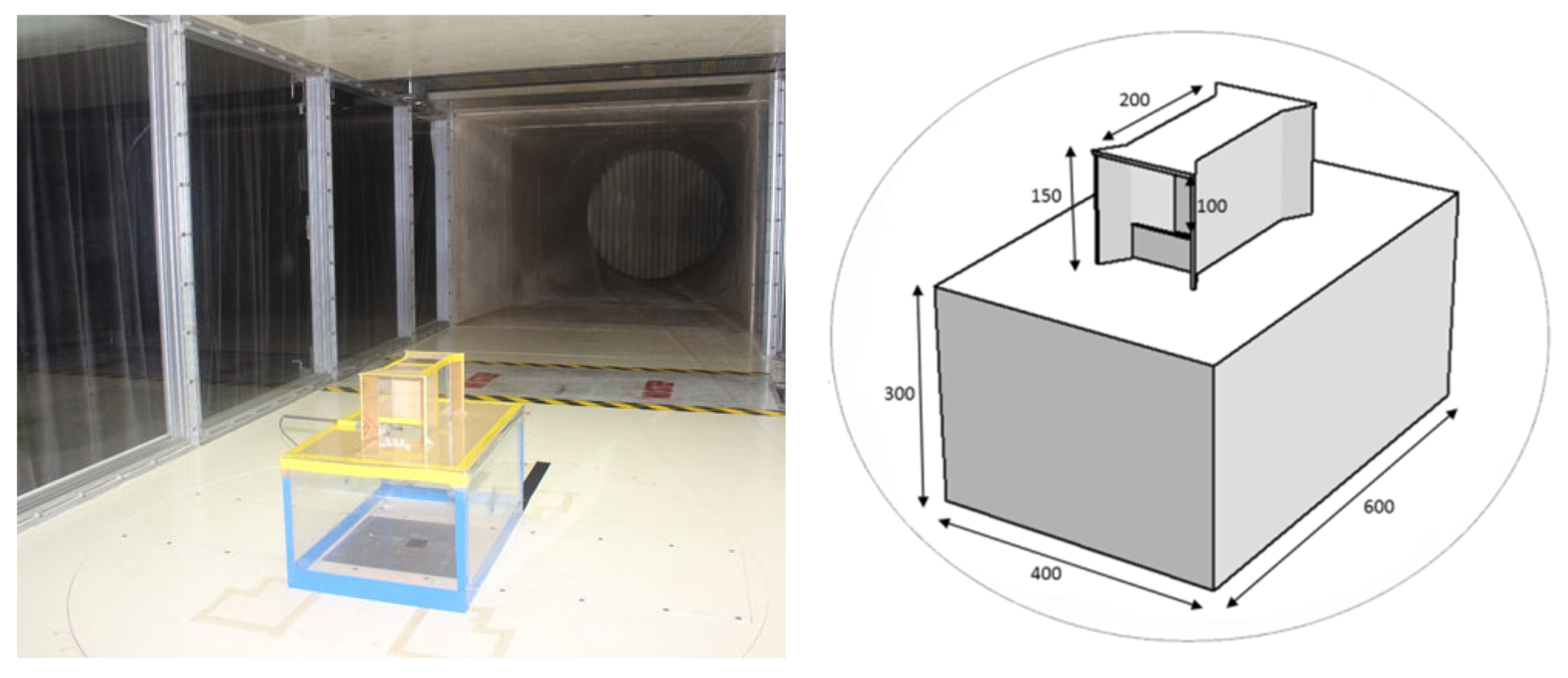
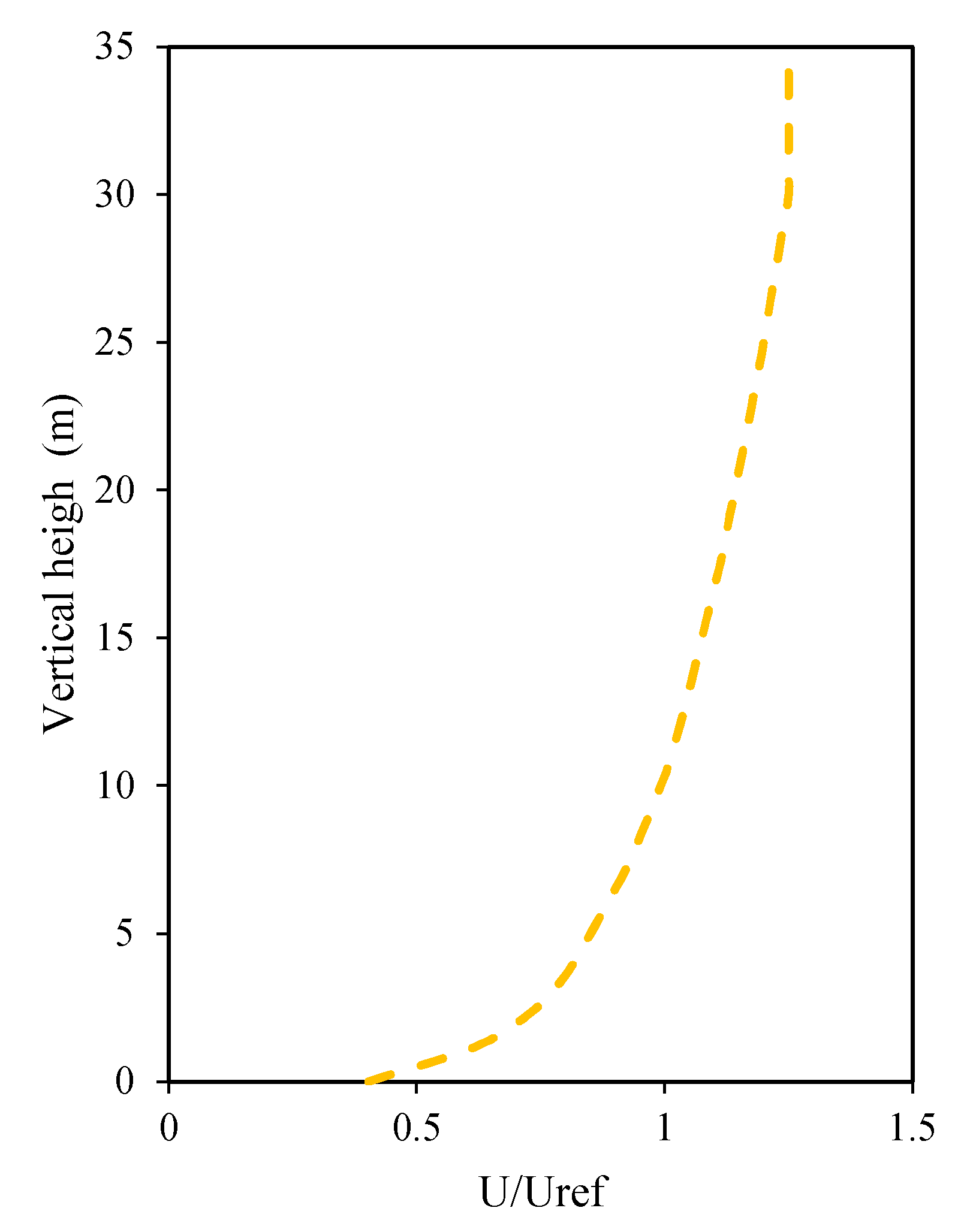
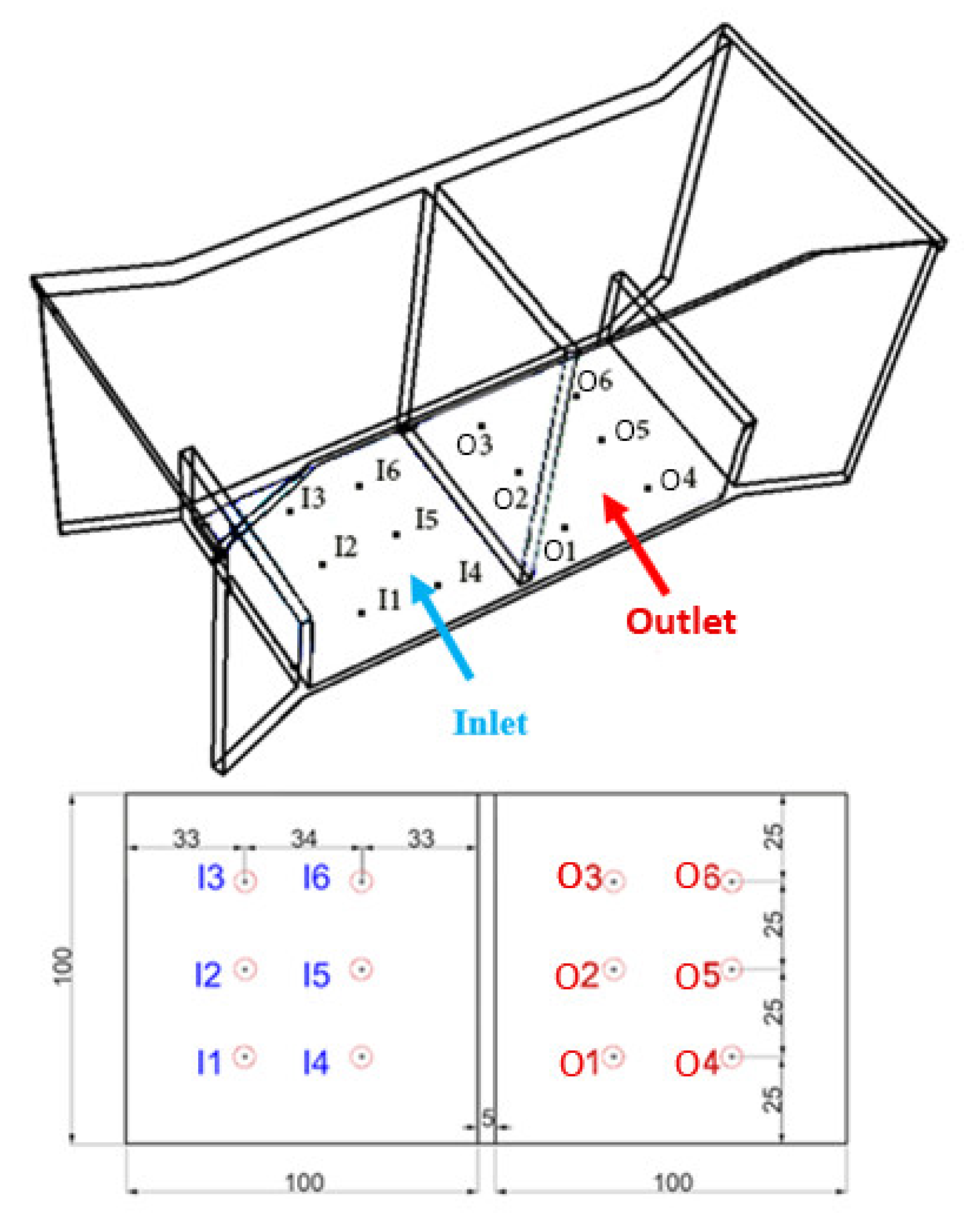
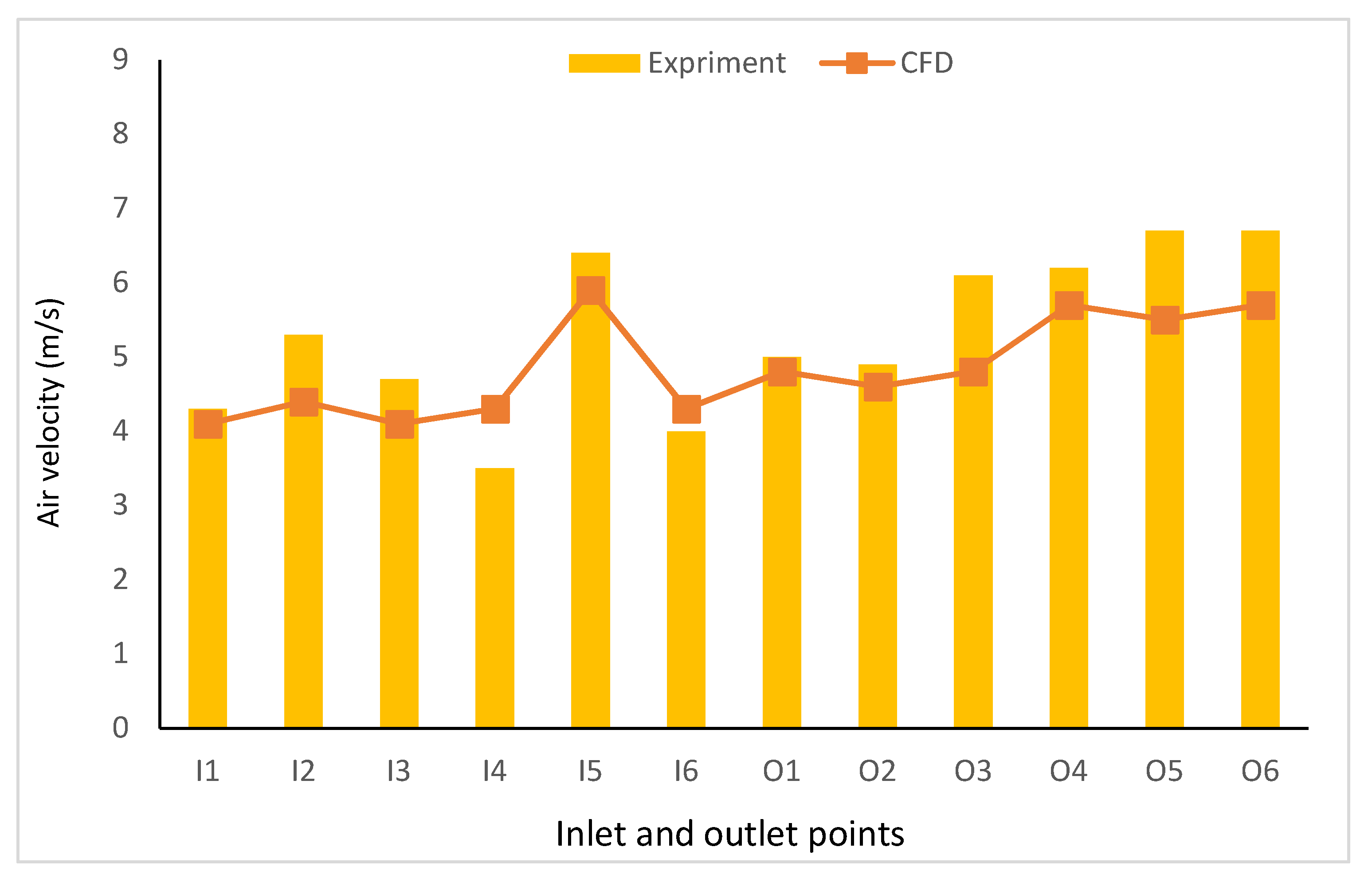
3.1. Validation with Experimental Data
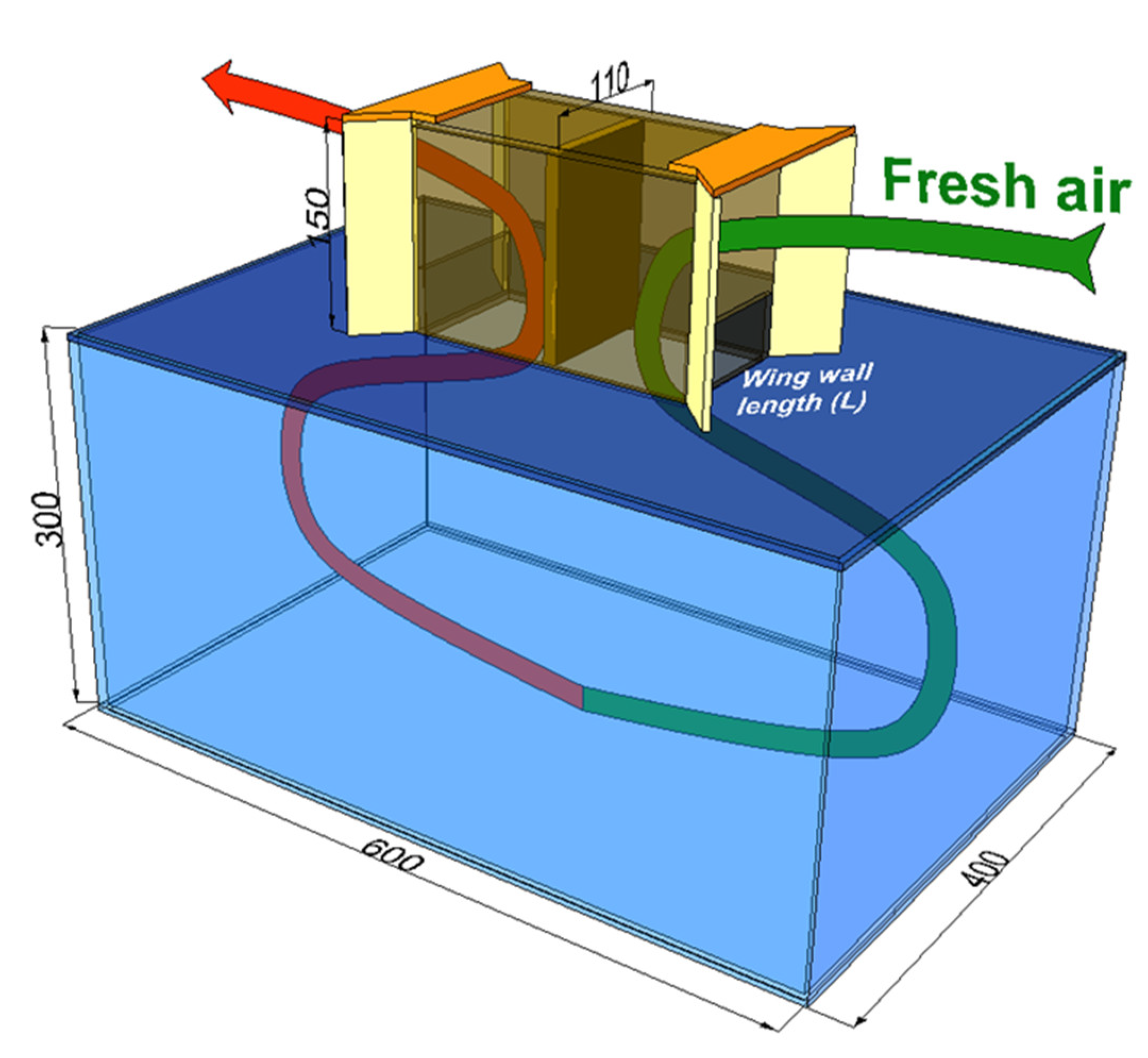
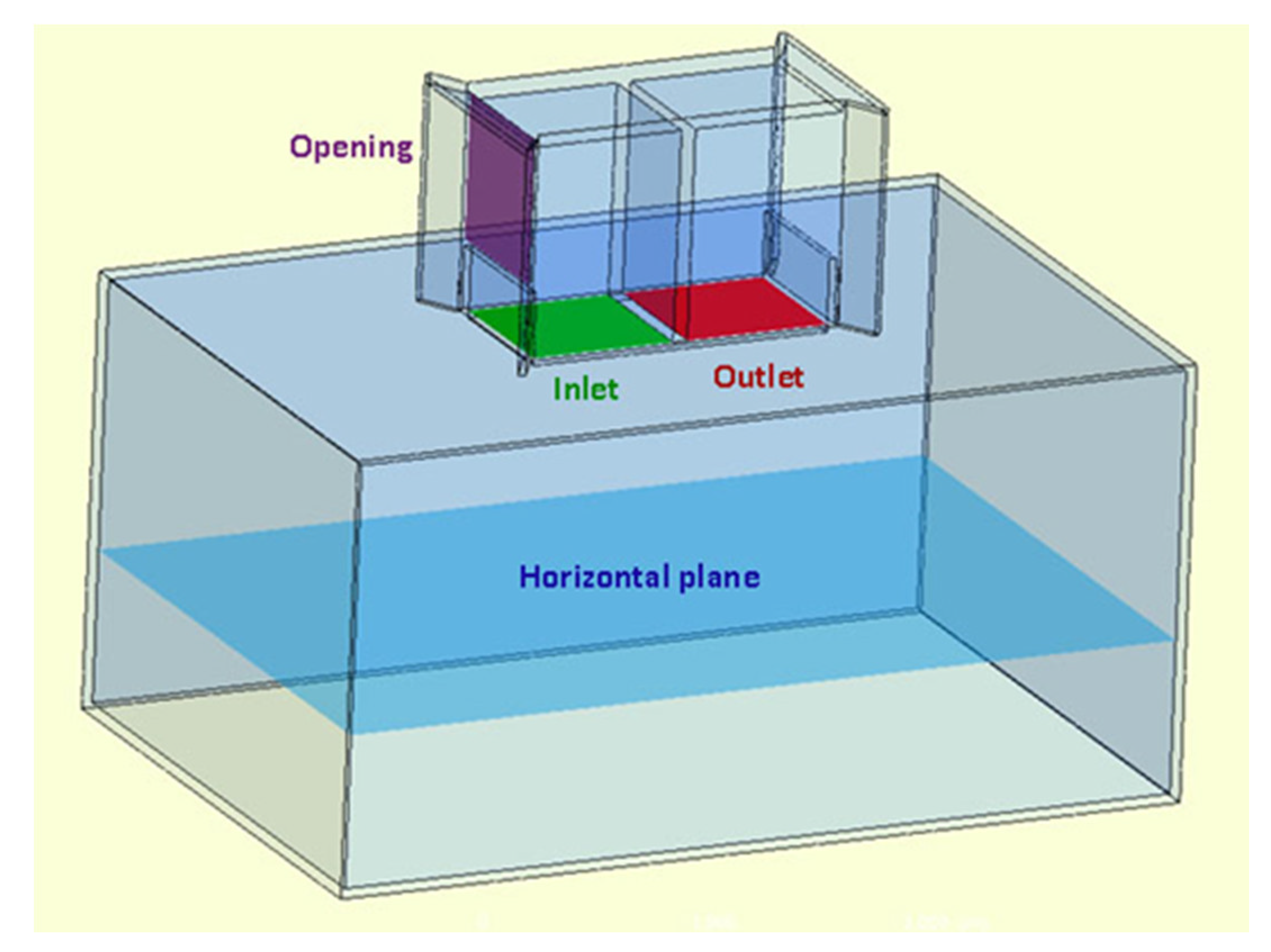
3.2. CFD Study of Windcatcher Performance
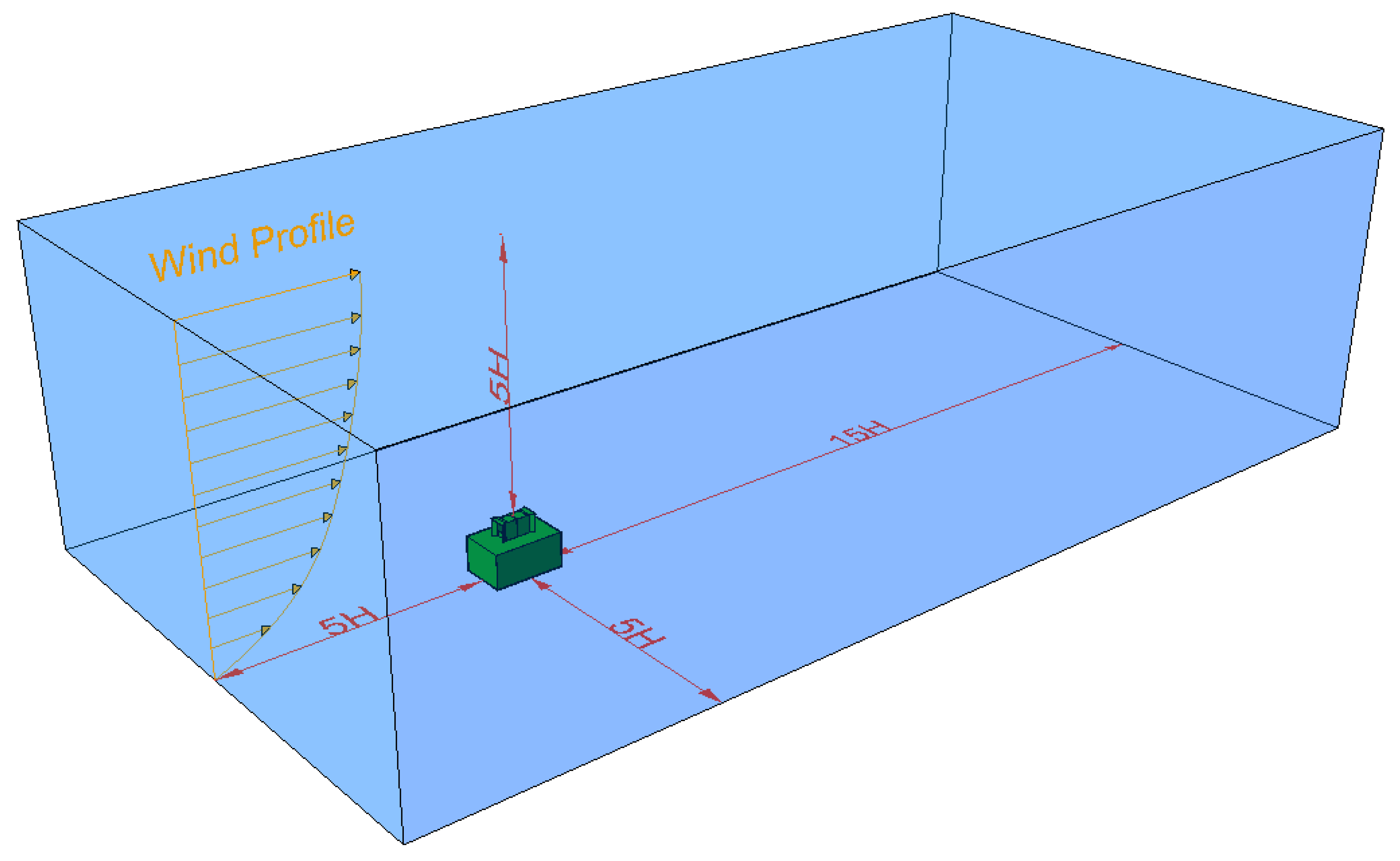
3.2.1. Mesh Generation
3.2.2. Boundary Conditions
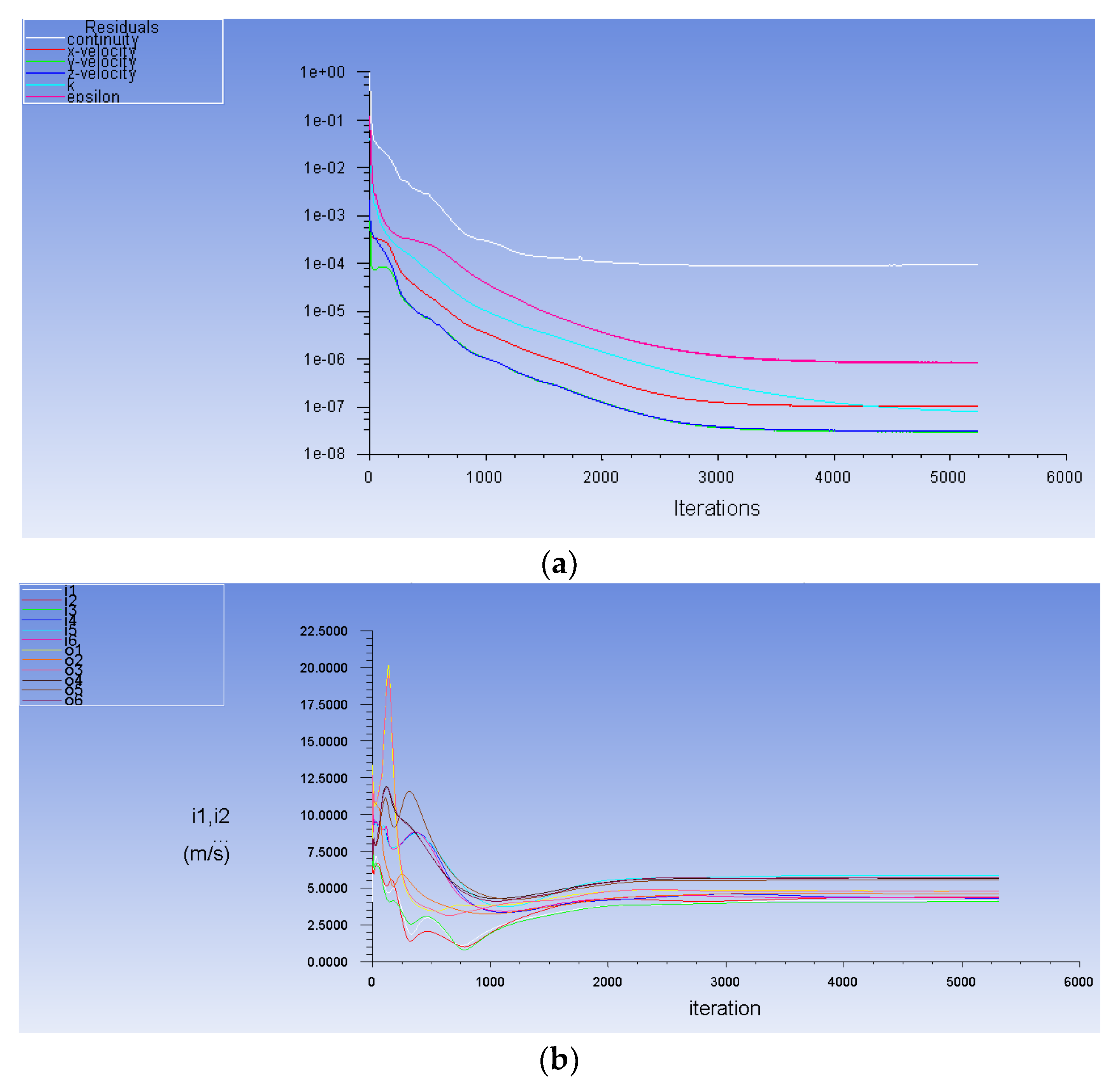
3.2.3. Solution Convergence and Flux Balance
4. Results and Discussion
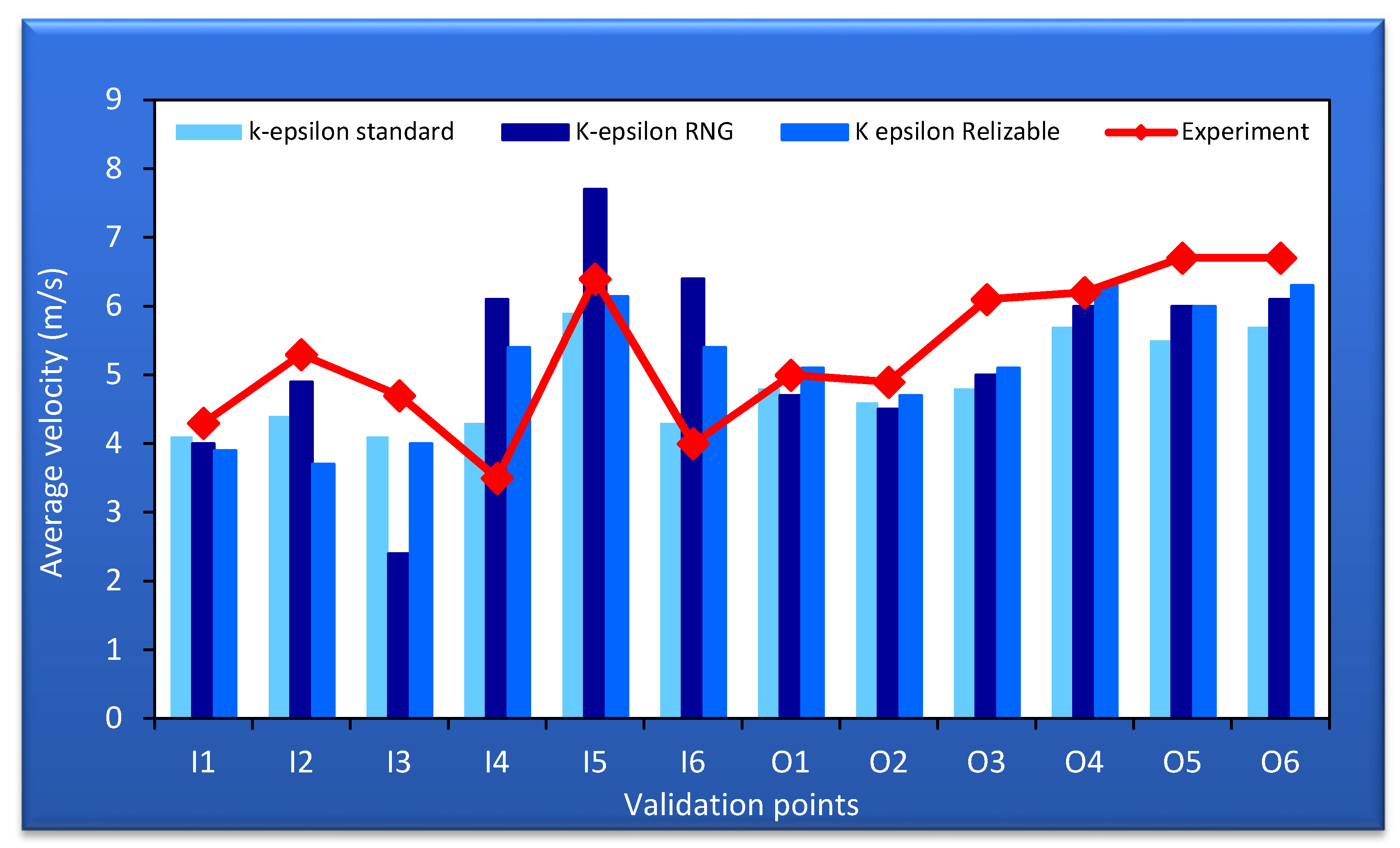
4.1. Validation and Sensitivity Analysis
4.1.1. Sensitivity Analysis
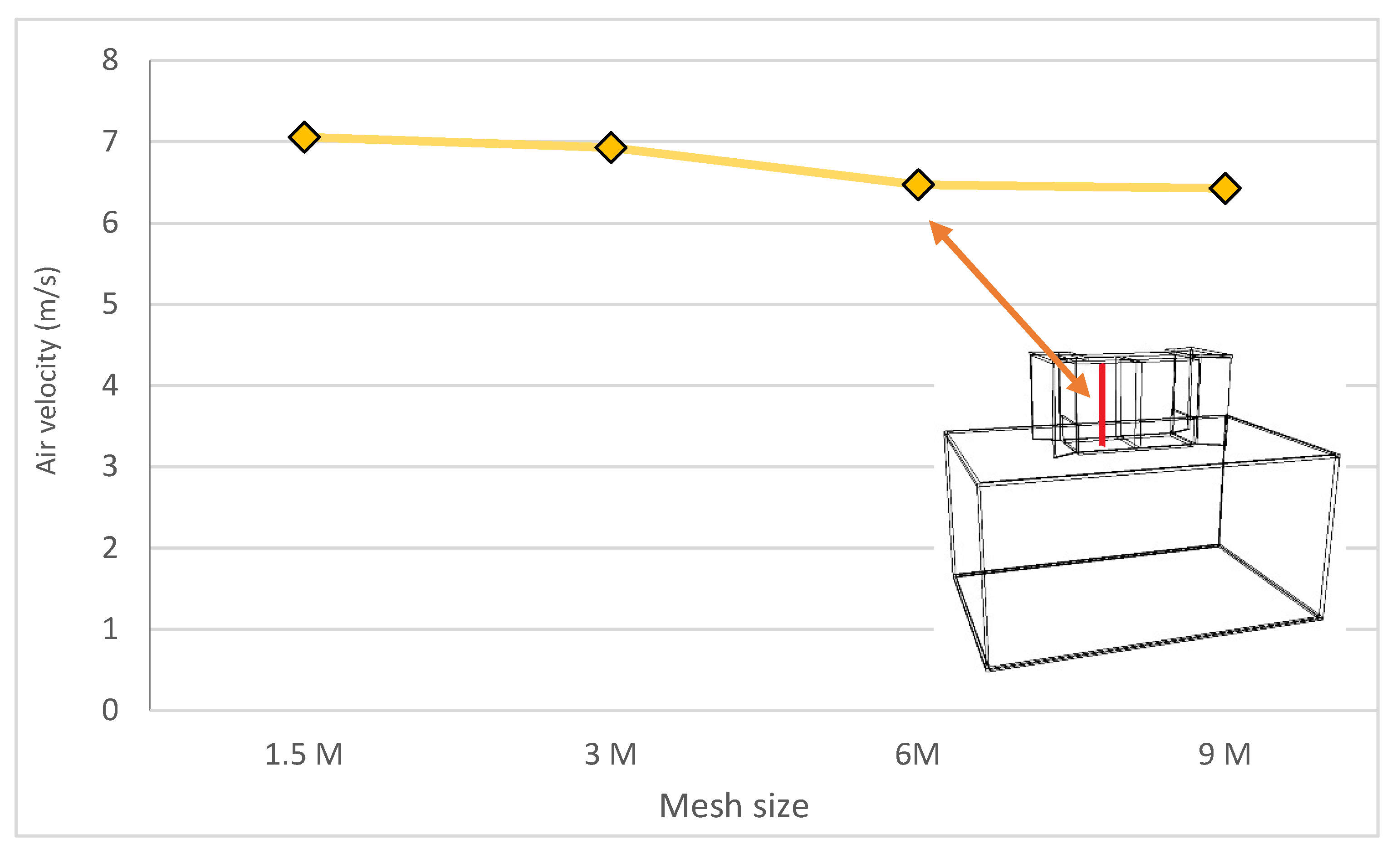
Grid Adaption
Sensitivity Analysis of Turbulence Model
4.2. The Effect of Wing Wall Length on Ventilation Performance.
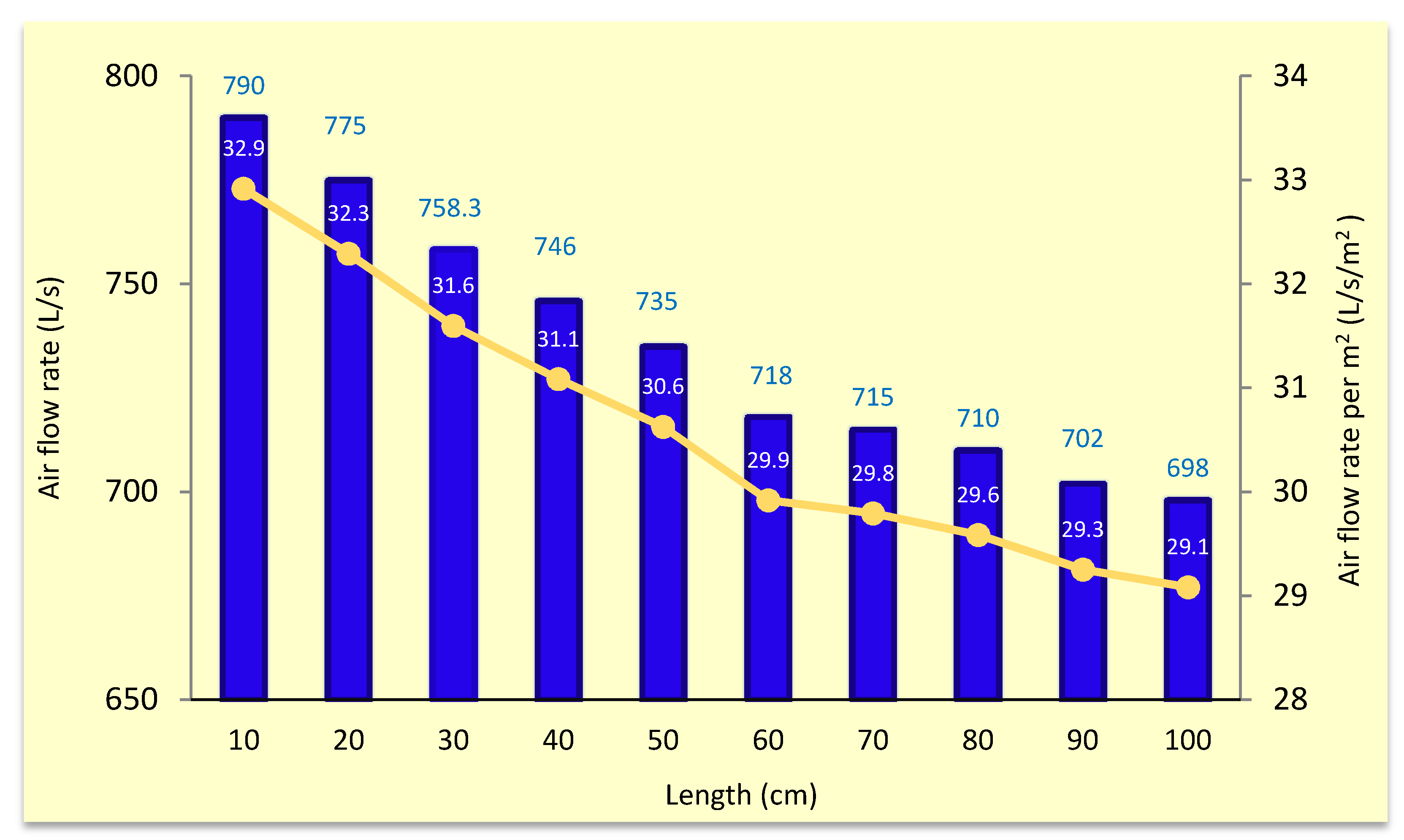
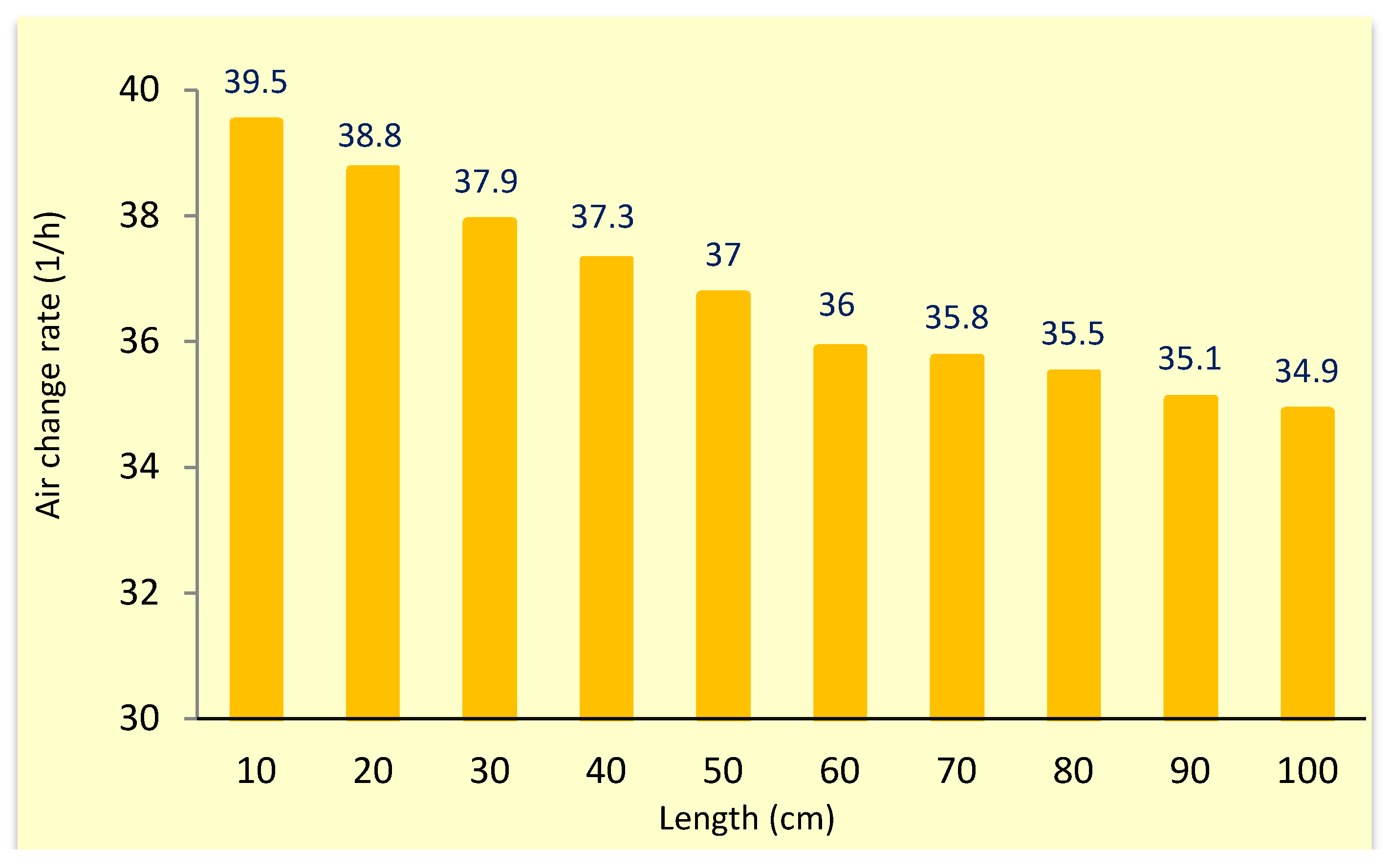
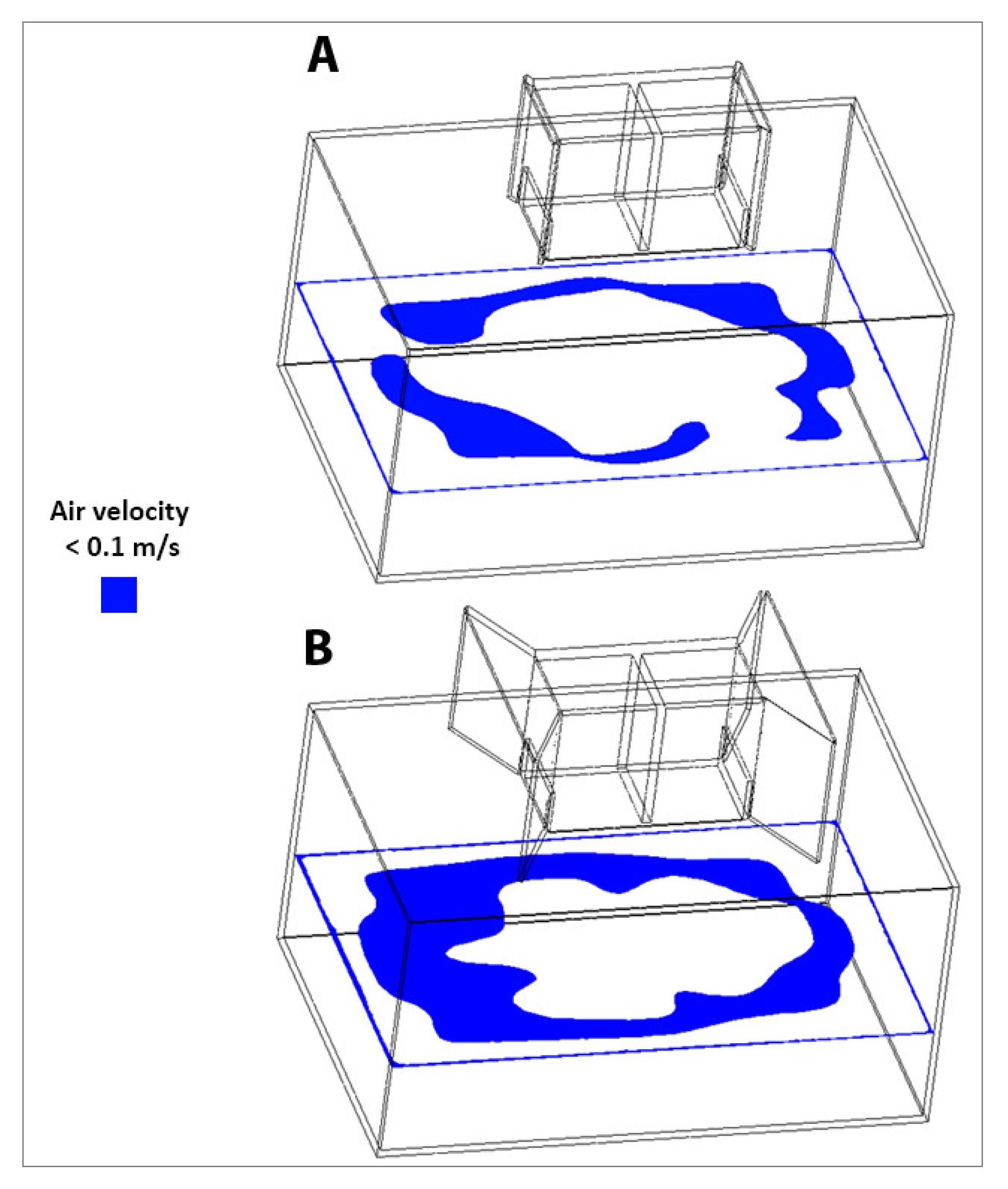
4.2.1. Air Flow in Inlet
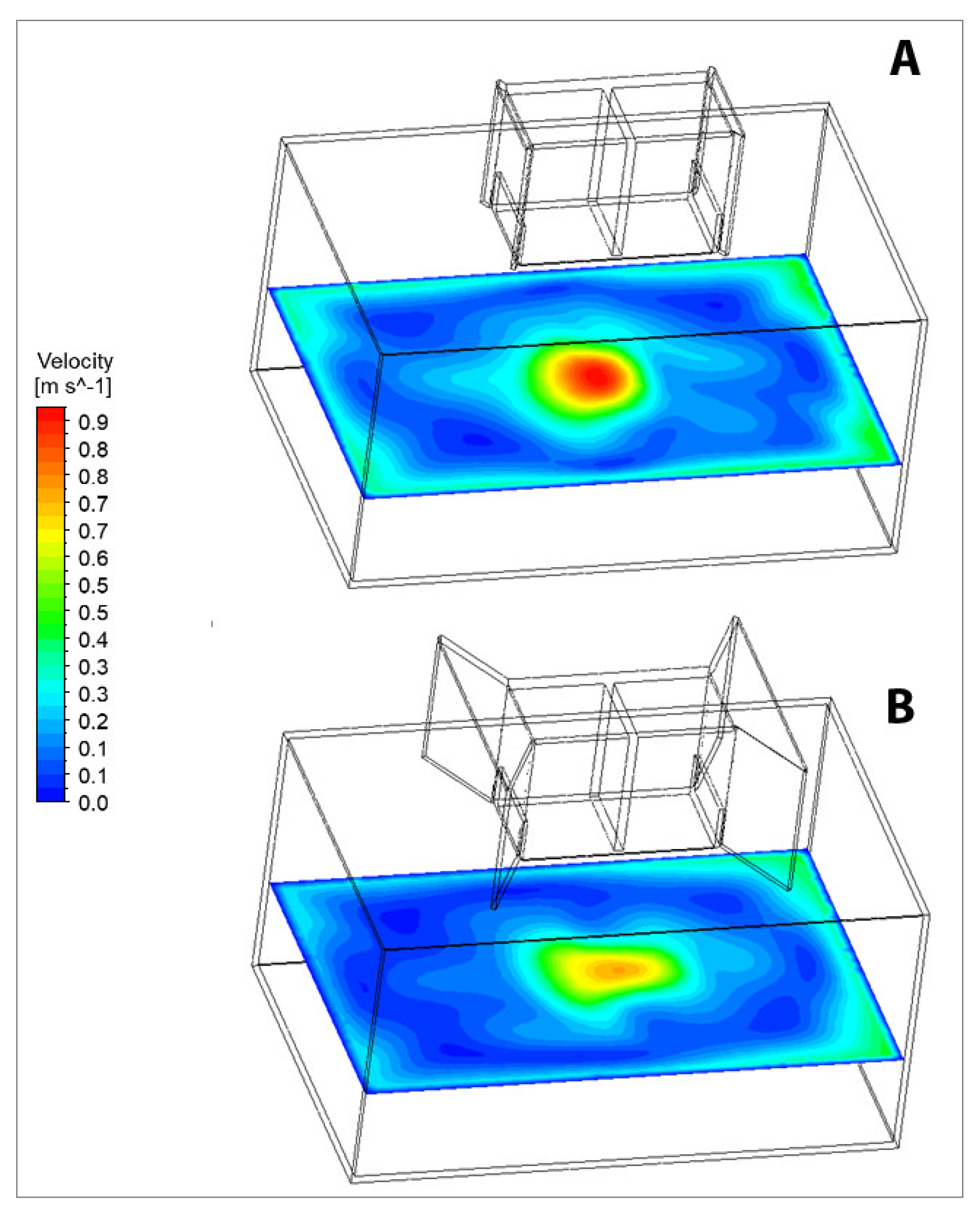
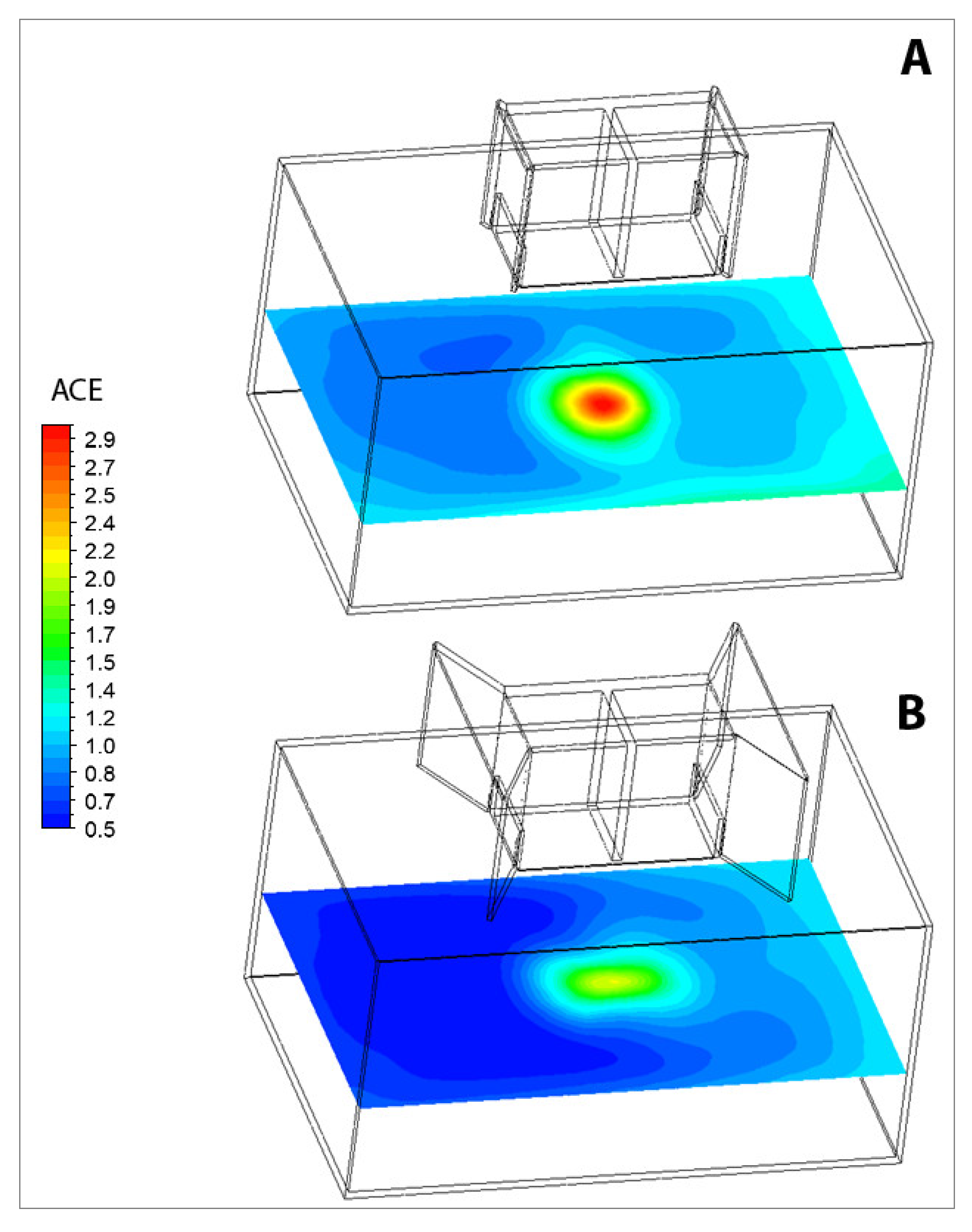
4.2.2. The IAQ Parameters on Horizontal Plane
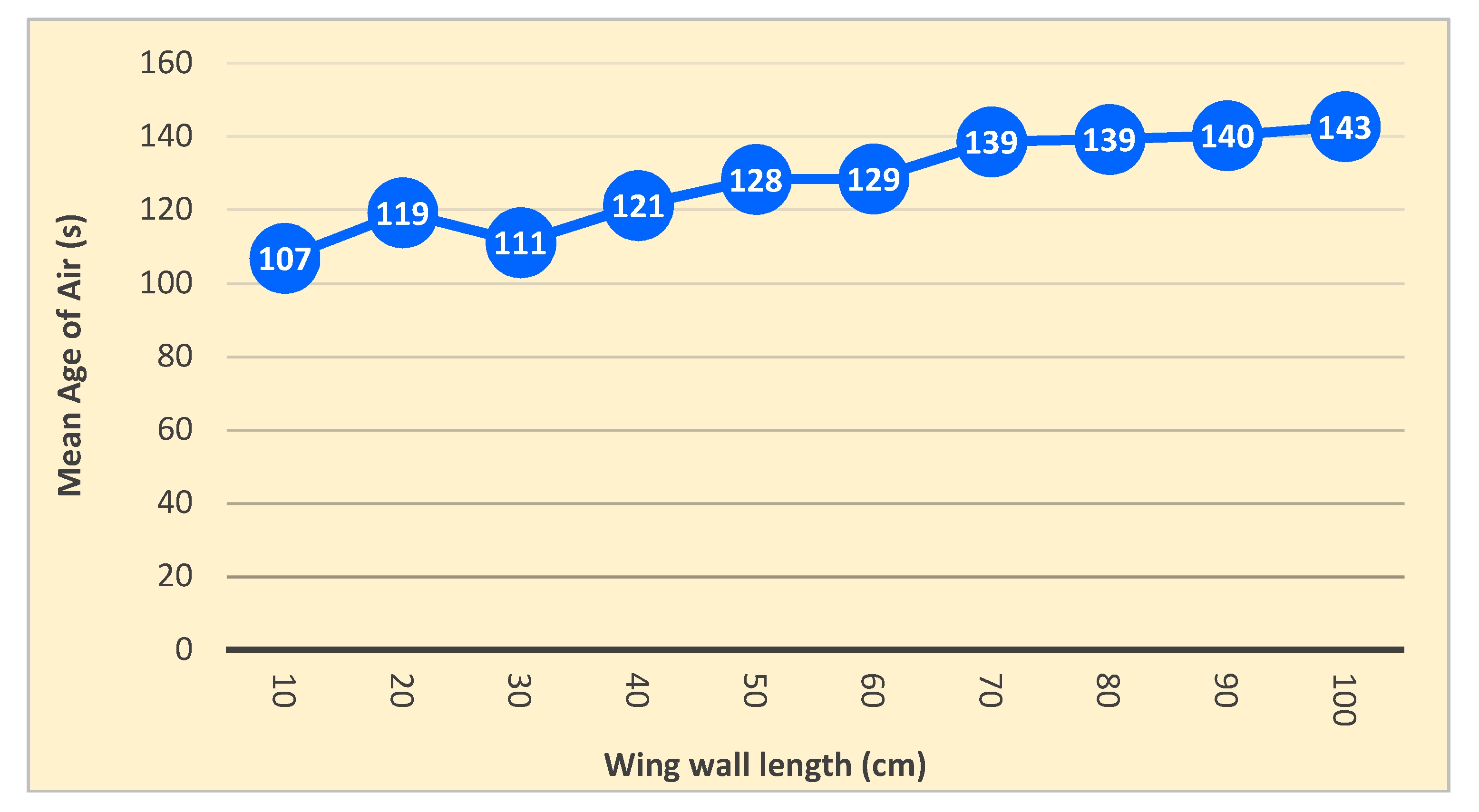
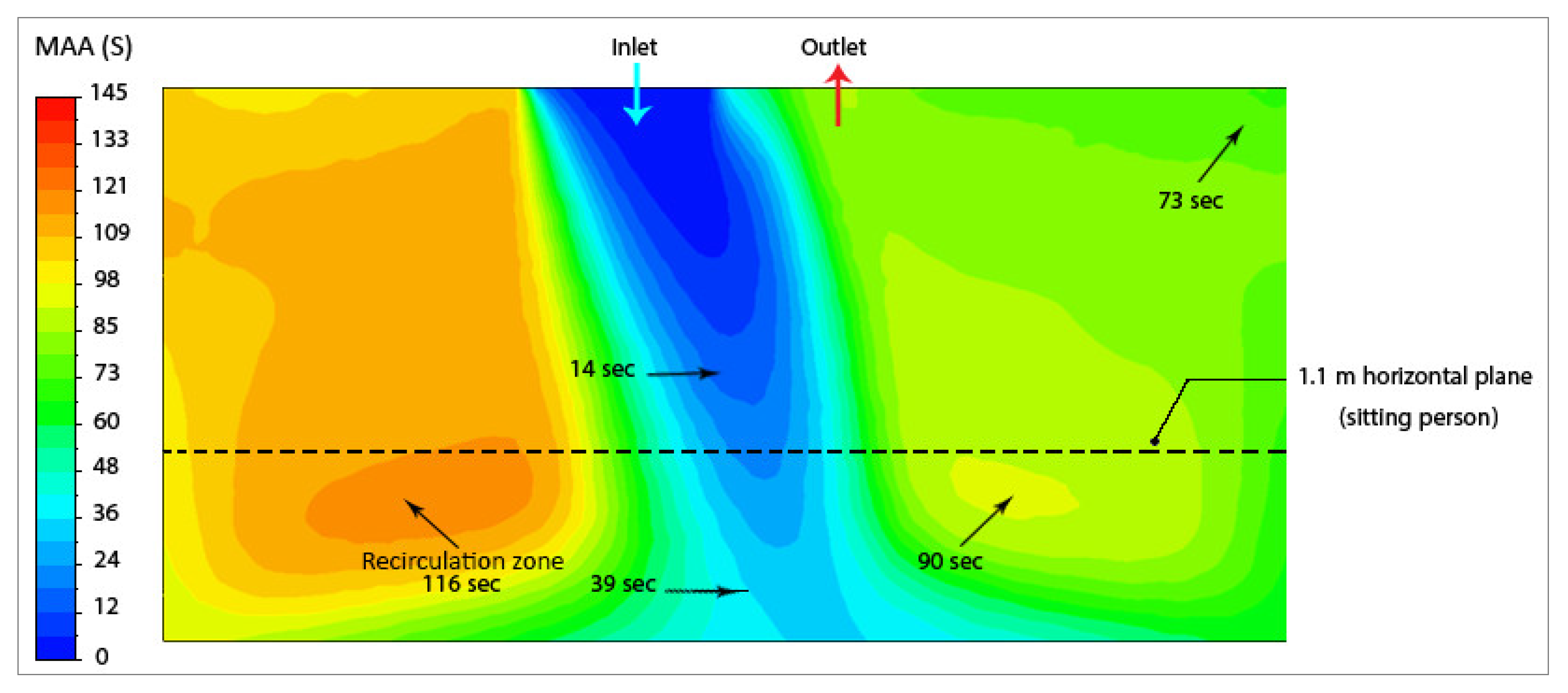
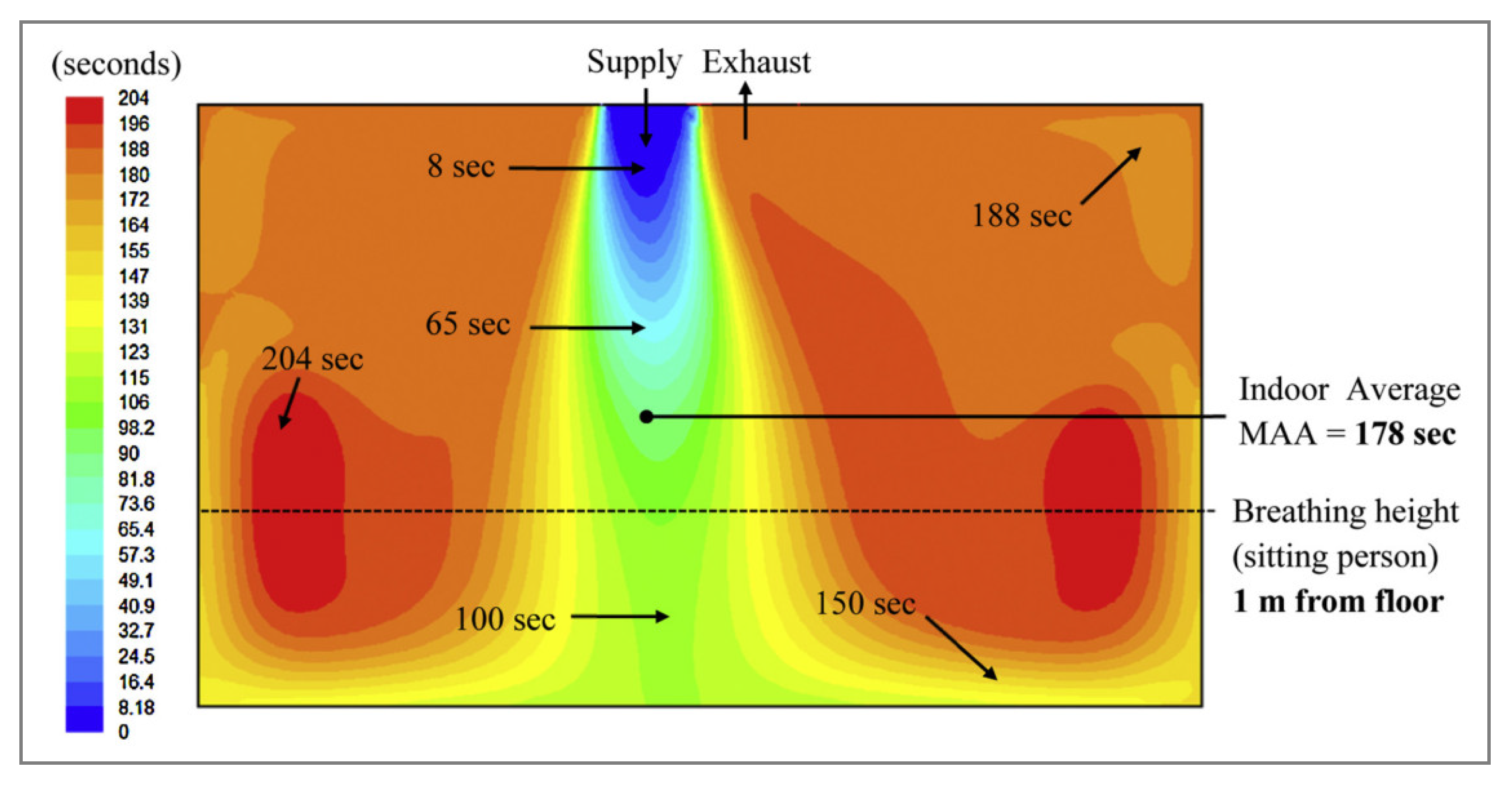
Mean Age of Air
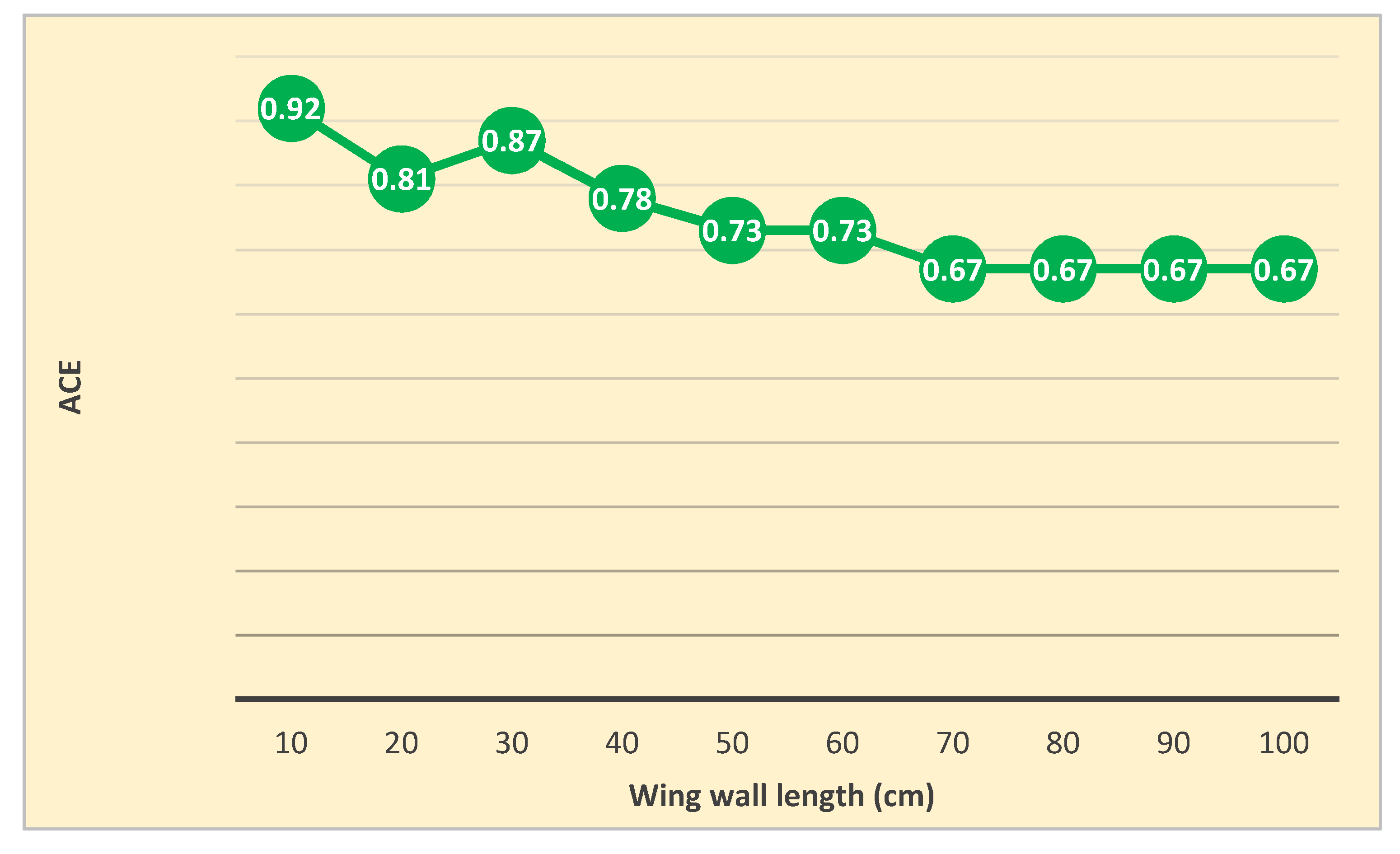
Air Change Effectiveness
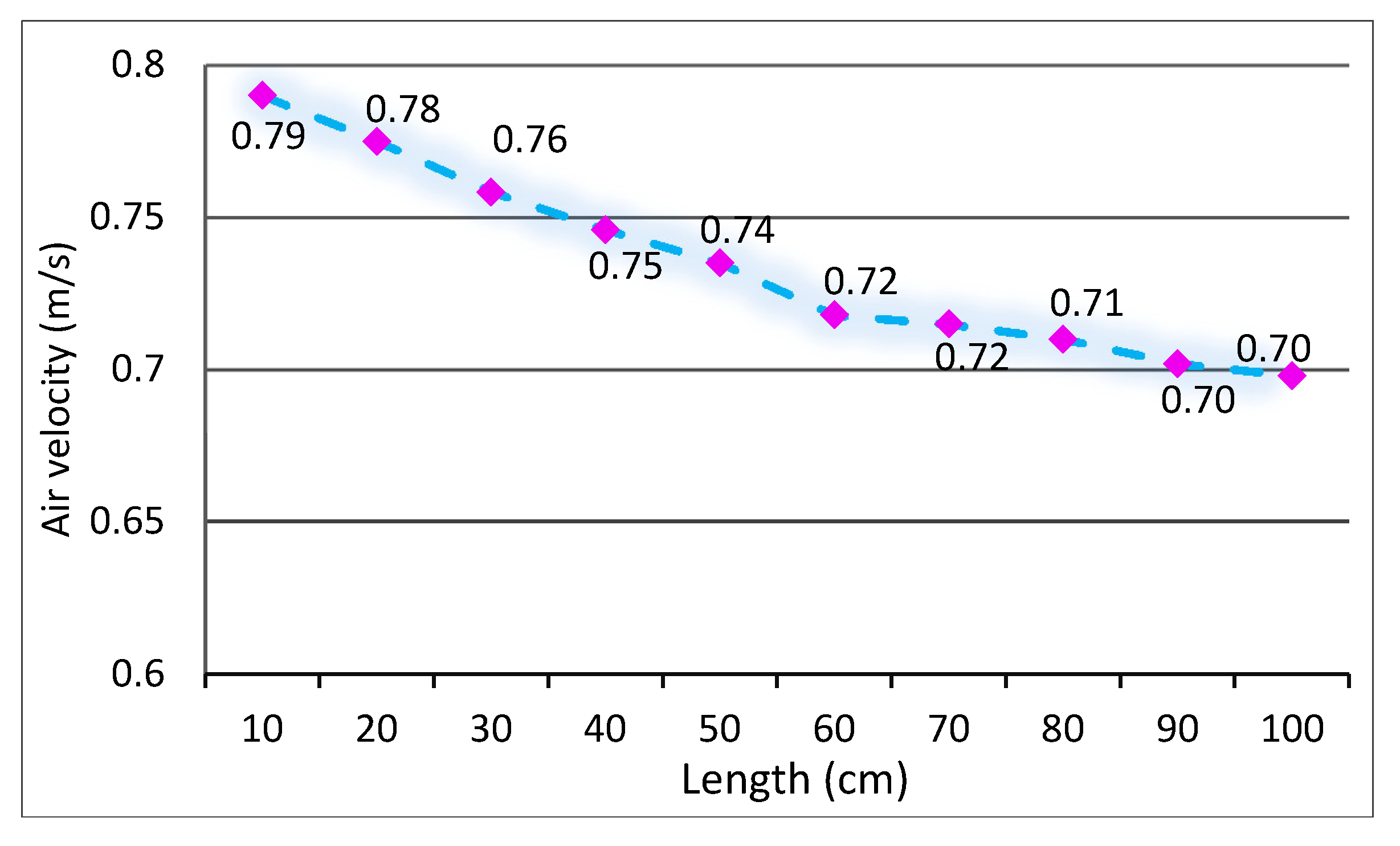
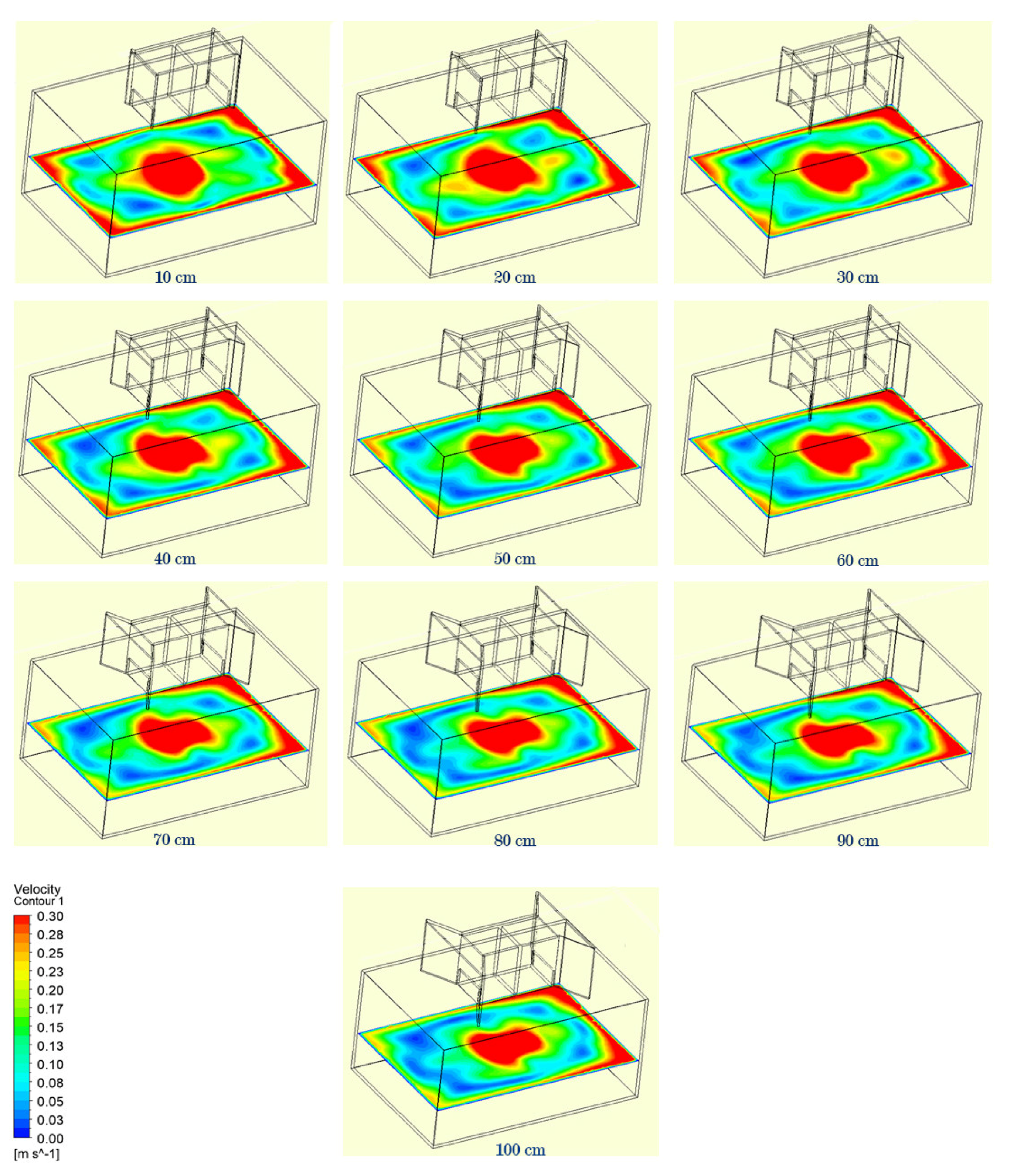
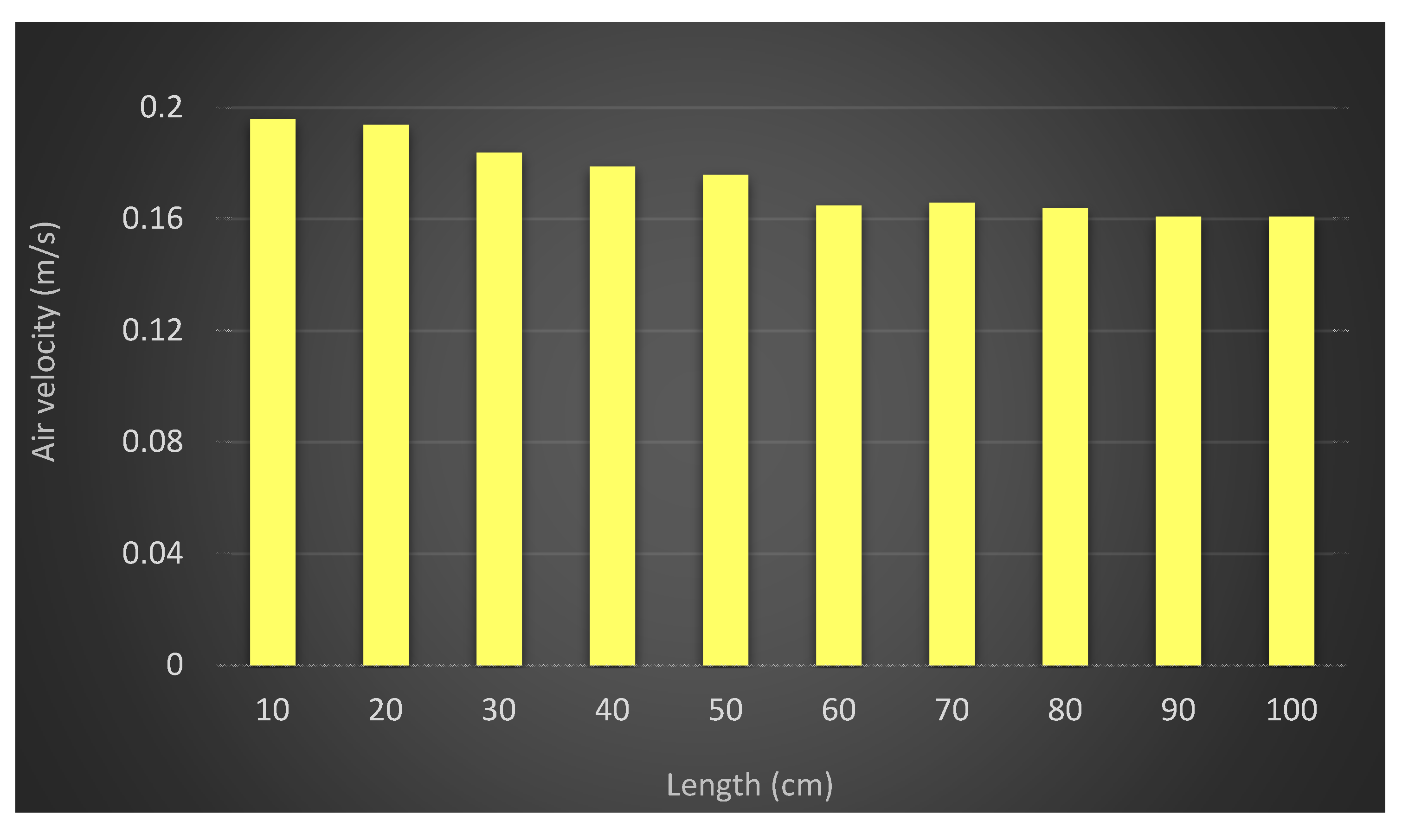
Comparison between 10 cm and 100 cm length
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-sectional area (m2) |
| turbulence dissipation rate | |
| density | |
| molecular dynamic viscosity | |
| g | gravitational acceleration (m/s2) |
| K | turbulence kinetic energy |
| H | height (m) |
| l | kinematic viscosity (m2/s) |
| L | length (m) |
| P | pressure (Pa) |
| Po | total pressure (Pa) |
| Ps | static pressure (Pa) |
| q | air density (kg/m3) |
| Q | volume flow rate (m3/s) |
| Re | Reynolds number |
| t | time (s) |
| TWIW | two-sided windcatcher intertied with wing wall |
| u | x-direction velocity |
| v | y-direction velocity |
| w | z-direction velocity |
| W | width (m) |
| X, Y, Z | Cartesian co-ordinates (m) |
References
- Jazizadeh, F.; Ghahramani, A.; Becerik-Gerber, B.; Kichkaylo, T.; Orosz, M. User-led decentralized thermal comfort driven HVAC operations for improved efficiency in office buildings. Energy Build. 2014, 70, 398–410. [Google Scholar] [CrossRef]
- Yang, L.; Yan, H.; Lam, J.C. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Iannaccone, G.; Imperadori, M.; Masera, G. Smart-ECO Buildings Towards 2020/2030: Innovative Technologies for Resource Efficient Buildings, 1st ed.; Springer: London, UK, 2014; ISBN 3319002694. [Google Scholar]
- Castilla, M.; Álvarez, J.D.; Ortega, M.G.; Arahal, M.R. Neural network and polynomial approximated thermal comfort models for HVAC systems. Build. Environ. 2013, 59, 107–115. [Google Scholar] [CrossRef]
- Chenari, B.; Dias Carrilho, J.; Gameiro da Silva, M. Towards sustainable, energy-efficient and healthy ventilation strategies in buildings: A review. Renew. Sustain. Energy Rev. 2016, 59, 1426–1447. [Google Scholar] [CrossRef]
- Santamouris, M.; Kolokotsa, D. Passive cooling dissipation techniques for buildings and other structures: The state of the art. Energy Build. 2013, 57, 74–94. [Google Scholar] [CrossRef]
- Elmualim, A.A. Evaluating the Performance Of Windcatchers For Natural Ventilation. Ph.D. Thesis, The University of Reading, Reading, UK, 2003. [Google Scholar]
- Hughes, B.R.; Abdul Ghani, S.A. A numerical investigation into the effect of windvent dampers on operating conditions. Build. Environ. 2009, 44, 237–248. [Google Scholar] [CrossRef]
- Environmental Protection Agency. Indoor Air Fact; United States Environmental Protection Agency: Washington, DC, USA, 1991. [Google Scholar]
- Calautit, J.K.; O’Connor, D.; Hughes, B.R. Determining the optimum spacing and arrangement for commercial wind towers for ventilation performance. Build. Environ. 2014, 82, 274–287. [Google Scholar] [CrossRef] [Green Version]
- Calautit, J.K.; Hughes, B.R.; O’Connor, D.; Shahzad, S.S. Numerical and experimental analysis of a multi-directional wind tower integrated with vertically-arranged heat transfer devices (VHTD). Appl. Energy 2017, 185, 1120–1135. [Google Scholar] [CrossRef] [Green Version]
- Zomorodian, Z.S.; Tahsildoost, M.; Hafezi, M. Thermal comfort in educational buildings: A review article. Renew. Sustain. Energy Rev. 2016, 59, 895–906. [Google Scholar] [CrossRef]
- Daghigh, R. Assessing the thermal comfort and ventilation in Malaysia and the surrounding regions. Renew. Sustain. Energy Rev. 2015, 48, 681–691. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, Z.; Malkawi, A. Investigating natural ventilation potentials across the globe: Regional and climatic variations. Build. Environ. 2017, 122, 386–396. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A. Estimating natural ventilation potential for high-rise buildings considering boundary layer meteorology. Appl. Energy 2017, 193, 276–286. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Liu, Z.; Freeman, R.B. Energy saving potential of natural ventilation in China: The impact of ambient air pollution. Appl. Energy 2016, 179, 660–668. [Google Scholar] [CrossRef] [Green Version]
- Elmualim, A.A.; Awbi, H.B. Post occupancy evaluation of a building employing windcatchers for summer ventilation. Facilities 2003, 21, 323–332. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R. Measurement and prediction of the indoor airfolw in a room ventilated with a commercial wind tower. Energy Build. 2014, 84, 367–377. [Google Scholar] [CrossRef]
- Hughes, B.R.; Chaudhry, H.N.; Ghani, S.A. A review of sustainable cooling technologies in buildings. Renew. Sustain. Energy Rev. 2011, 15, 3112–3120. [Google Scholar] [CrossRef]
- Jomehzadeh, F.; Nejat, P.; Calautit, J.K.; Yusof, M.B.M.; Zaki, S.A.; Hughes, B.R.; Yazid, M.N.A.W.M. A review on windcatcher for passive cooling and natural ventilation in buildings, Part 1: Indoor air quality and thermal comfort assessment. Renew. Sustain. Energy Rev. 2017, 70, 736–756. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.; Kirby, R. The Performance of Natural Ventilation Windcatchers in Schools—A Comparison between Prediction and Measurement. Int. J. Vent. 2010, 9, 273–286. [Google Scholar] [CrossRef]
- Monodraught Square Classic Windcatcher. Available online: http://www.ellis.co.nz/media/444887/windcatcher-classic-square-.pdf (accessed on 11 April 2018).
- Siew, C.C.; Che-Ani, A.I.; Tawil, N.M.; Abdullah, N.A.; Mohd-Tahir, M. Classification of natural ventilation strategies in optimizing energy consumption in Malaysian office buildings. Procedia Eng. 2011, 20, 363–371. [Google Scholar] [CrossRef]
- Chungloo, S.; Tienchutima, C. The effect of wing-walls and balcony on wind induced ventilation in high-rise residential units. JARS 2011, 8, 109–120. [Google Scholar]
- Allocca, C.; Chen, Q.; Glicksman, L.R. Design analysis of single-sided natural ventilation. Energy Build. 2003, 35, 785–795. [Google Scholar] [CrossRef]
- Al-Kodmany, K. Eco-Towers: Sustainable Cities in the Sky; WIT Press: Ashurst, UK, 2015; ISBN 1784660175. [Google Scholar]
- Givoni, B. Passive Low Energy Cooling of Buildings; John Wiley & Sons: Hoboken, NJ, USA, 1994; ISBN 0471284734. [Google Scholar]
- Hughes, B.R.; Calautit, J.K.; Ghani, S.A. The development of commercial wind towers for natural ventilation: A review. Appl. Energy 2012, 92, 606–627. [Google Scholar] [CrossRef]
- Mak, C.M.; Niu, J.L.; Lee, C.T.; Chan, K.F. A numerical simulation of wing walls using computational fluid dynamics. Energy Build. 2007, 39, 995–1002. [Google Scholar] [CrossRef]
- Liu, C.-H. Computational fluid dynamic analysis of the function of wing walls for natural ventilation in high-rise buildings. In Proceedings of the Annual Research Conference of the Royal Institution of Chartered Surveyors, London, UK, 7–8 Sepetember 2006. [Google Scholar]
- Nejat, P.; Calautit, J.K.; Majid, M.Z.; Hughes, B.R.; Zeynali, I.; Jomehzadeh, F. Evaluation of a two-sided windcatcher integrated with wing wall (as a new design) and comparison with a conventional windcatcher. Energy Build. 2016, 126, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Afshin, M.; Sohankar, A.; Manshadi, M.D.; Esfeh, M.K. An experimental study on the evaluation of natural ventilation performance of a two-sided wind-catcher for various wind angles. Renew. Energy 2016, 85, 1068–1078. [Google Scholar] [CrossRef]
- Ghadiri, M.H.; Lukman, N.; Ibrahim, N.; Mohamad, M.F. Computational Analysis of Wind-Driven Natural Ventilation in a Two Sided Rectangular Wind Catcher. Int. J. Vent. 2013, 12, 51–61. [Google Scholar] [CrossRef]
- Montazeri, H.; Montazeri, F.; Azizian, R.; Mostafavi, S. Two-sided wind catcher performance evaluation using experimental, numerical and analytical modeling. Renew. Energy 2010, 35, 1424–1435. [Google Scholar] [CrossRef]
- Chandra, S.; Fairey, P.; Houston, M.; Kerestecioglu, A.A. Wing walls to improve natural ventilation. Full-scale results and design strategies. In Proceedings of the 8th National Passive Solar Conference, Sante Fe, NM, USA, 7–9 September 1983; pp. 855–860. [Google Scholar]
- Mak, C.M.; Cheng, C.; Niu, J.L. The Application of computational fluid dynamics to the assessment of green features in buildings: Part 1: Wing walls. Archit. Sci. Rev. 2005, 48, 121–134. [Google Scholar] [CrossRef]
- Mozaffari, F. Indoor Natural Ventilation with Wing Wall in Balcony in Medium-Rise Building in Hot and Humid Climate. Ph.D. Thesis, Universiti Teknologi Malaysia, Johor Bahru, Malaysia, 2015. [Google Scholar]
- Dehghan, A.A.; Esfeh, M.K.; Manshadi, M.D. Natural ventilation characteristics of one-sided wind catchers: Experimental and analytical evaluation. Energy Build. 2013, 61, 366–377. [Google Scholar] [CrossRef]
- Hughes, B.R.; Cheuk-Ming, M. A study of wind and buoyancy driven flows through commercial wind towers. Energy Build. 2011, 43, 1784–1791. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R.; Chaudhry, H.N.; Ghani, S.A. CFD analysis of a heat transfer device integrated wind tower system for hot and dry climate. Appl. Energy 2013, 112, 576–591. [Google Scholar] [CrossRef] [Green Version]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. COST Action 732, Best Practice Guideline for the CFD Simulation of Flows in The Urban Environment; COST: Brussels, Belgium, 2007. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Tominaga, Y.; Akabayashi, S.; Kitahara, T.; Arinami, Y. Air flow around isolated gable-roof buildings with different roof pitches: Wind tunnel experiments and CFD simulations. Build. Environ. 2015, 84, 204–213. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere Publishing Corp: New York, NY, USA, 1977. [Google Scholar]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Montazeri, H.; Montazeri, F. CFD simulation of cross-ventilation in buildings using rooftop wind-catchers: Impact of outlet openings. Renew. Energy 2018, 118, 502–520. [Google Scholar] [CrossRef]
- ANSYS Incorporated ANSYS 14.5 FLUENT Theory Guide. Available online: http://www.ansys.com (accessed on 15 April 2018).
- Liu, P. A Modelling Study of Segmentation of Naturally Ventilated Tall Office Buildings in A Hot and Humid Climate. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2012. [Google Scholar]
- Elmualim, A.A. Dynamic modelling of a wind catcher/tower turret for natural ventilation. Build. Serv. Eng. Res. Technol. 2006, 27, 165–182. [Google Scholar] [CrossRef]
- American Society of Heating Refrigerating and Air-Conditioning Engineers. ASHRAE Standard 62.1: Ventilation for Acceptable Indoor Air Quality; ASHRAE: Atlanta, Georgia, 2007. [Google Scholar]
- Mundt, E.; Mathisen, H. Ventilation Effectiveness; Federation of European Heating, Ventilation and Air Conditioning Associations (REHVA): Stockholm, Sweden, 2004. [Google Scholar]

| Factor | Domain |
|---|---|
| Macro-climate | Fluid zone |
| Micro-Climate | Fluid zone |
| Walls | Top: Symmetry |
| Side: Symmetry | |
| Bottom: Wall | |
| Velocity Inlet | ABL Profile |
| Pressure Outlet | 0 Pa |
| Operating Pressure | Atmospheric |
| Viscous Model | k-ε (standard) |
| Near-Wall Treatment | Standard wall functions |
| Solver Type | Pressure-based |
| Time | Steady |
| Gravity | 9.81 m/s2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nejat, P.; Jomehzadeh, F.; Hussen, H.M.; Calautit, J.K.; Abd Majid, M.Z. Application of Wind as a Renewable Energy Source for Passive Cooling through Windcatchers Integrated with Wing Walls. Energies 2018, 11, 2536. https://doi.org/10.3390/en11102536
Nejat P, Jomehzadeh F, Hussen HM, Calautit JK, Abd Majid MZ. Application of Wind as a Renewable Energy Source for Passive Cooling through Windcatchers Integrated with Wing Walls. Energies. 2018; 11(10):2536. https://doi.org/10.3390/en11102536
Chicago/Turabian StyleNejat, Payam, Fatemeh Jomehzadeh, Hasanen Mohammed Hussen, John Kaiser Calautit, and Muhd Zaimi Abd Majid. 2018. "Application of Wind as a Renewable Energy Source for Passive Cooling through Windcatchers Integrated with Wing Walls" Energies 11, no. 10: 2536. https://doi.org/10.3390/en11102536
APA StyleNejat, P., Jomehzadeh, F., Hussen, H. M., Calautit, J. K., & Abd Majid, M. Z. (2018). Application of Wind as a Renewable Energy Source for Passive Cooling through Windcatchers Integrated with Wing Walls. Energies, 11(10), 2536. https://doi.org/10.3390/en11102536






