High-Precision Speed Control Based on Multiple Phase-Shift Resonant Controllers for Gimbal System in MSCMG
Abstract
:1. Introduction
- (1)
- Torque ripples caused by high-speed rotor dynamic imbalance in a gimbal servo system for MSCMG are first discussed and modeled.
- (2)
- The absolute closed-loop stability and robustness of the overall system is ensured by the proposed MPRC approach and the phase angle is adjusted for wide and multiple resonant frequency-varying conditions.
- (3)
- The design and tuning processes of the MPRC are discussed and simplified. These are important and practical, especially for a gimbal servo system with multiple frequency RCs both in current and speed control loops.
2. Dynamics Modeling and Periodic Disturbance Analysis of Gimbal System
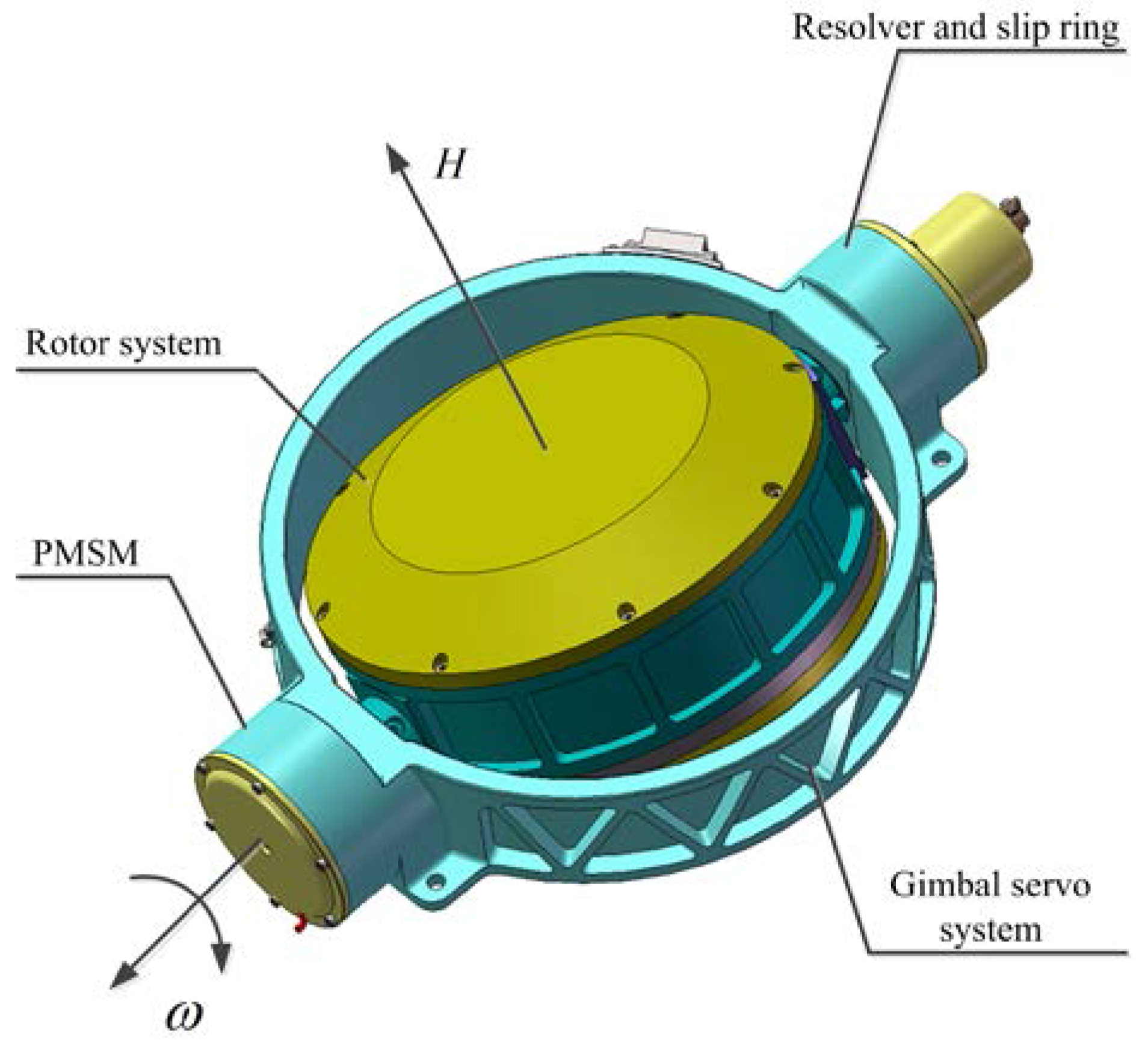
2.1. Model of Gimbal Servo System
2.2. Periodic Disturbance Analysis
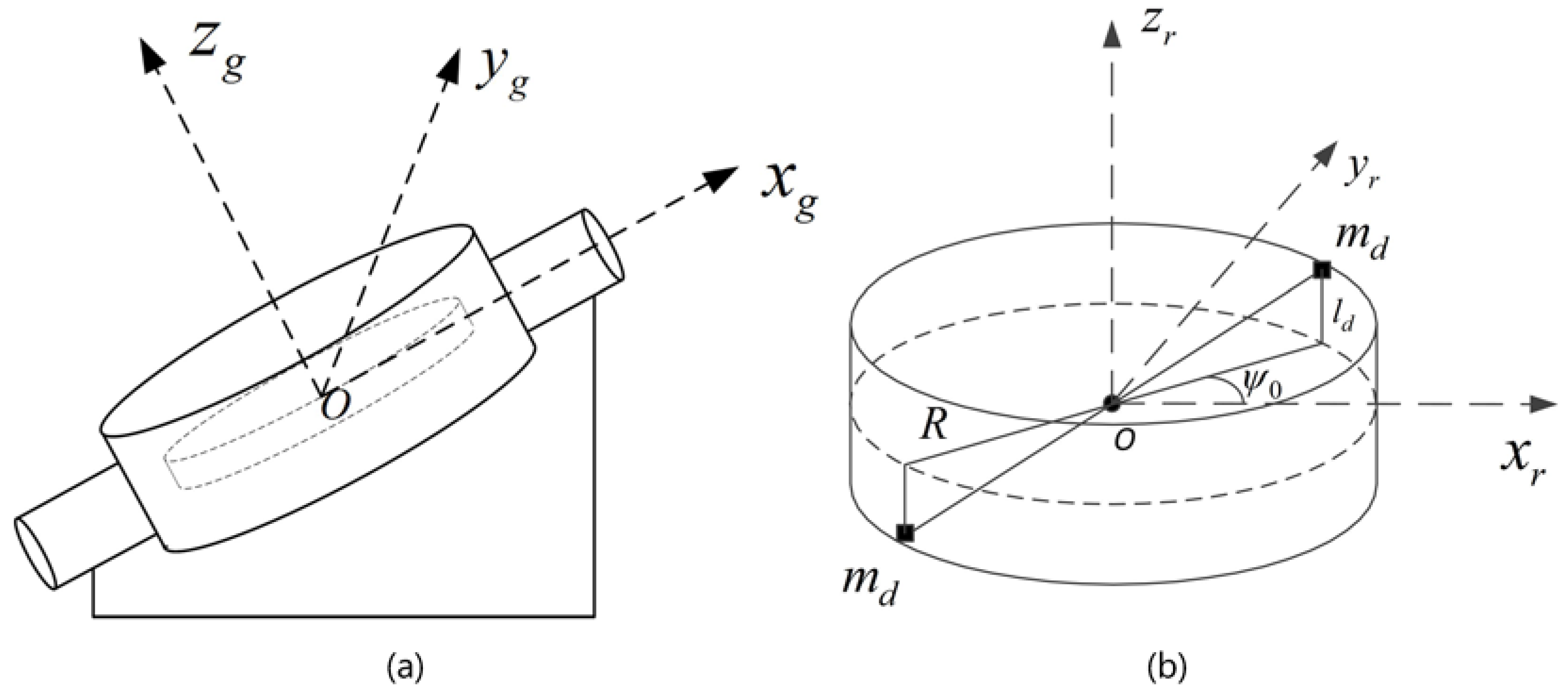
2.2.1. Gyro Torque Caused by Dynamic Unbalance
2.2.2. Cogging Torque
2.2.3. Flux Harmonics
3. MPRC for Periodic Disturbance Suppression
3.1. Multiple Phase-Shift Resonant Controllers
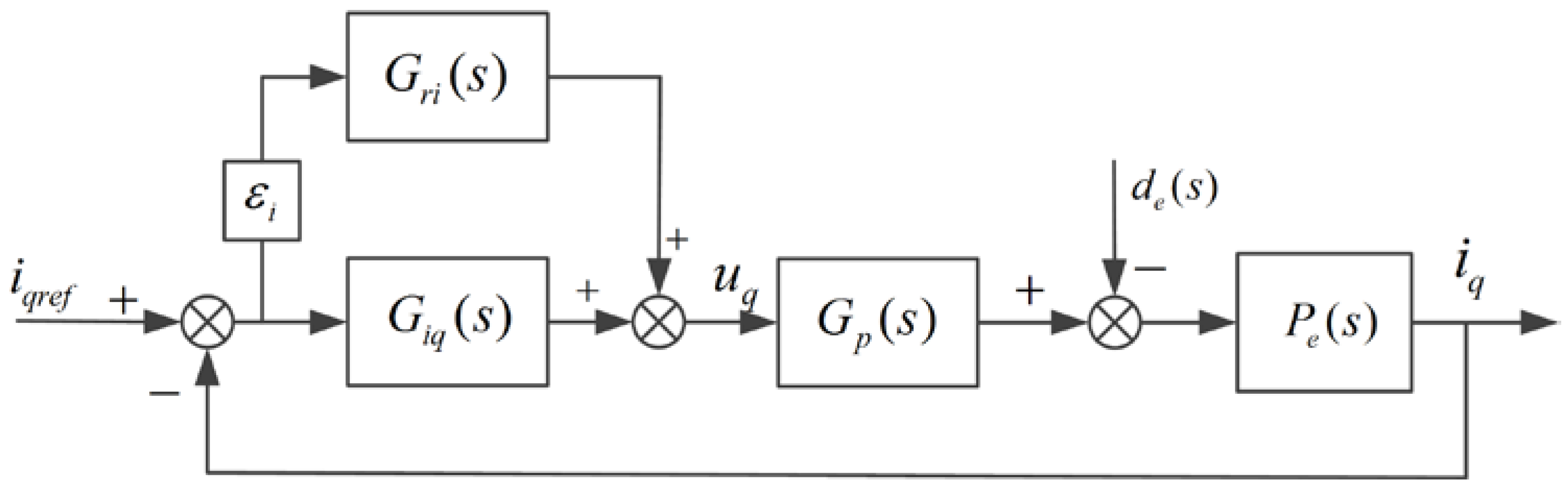
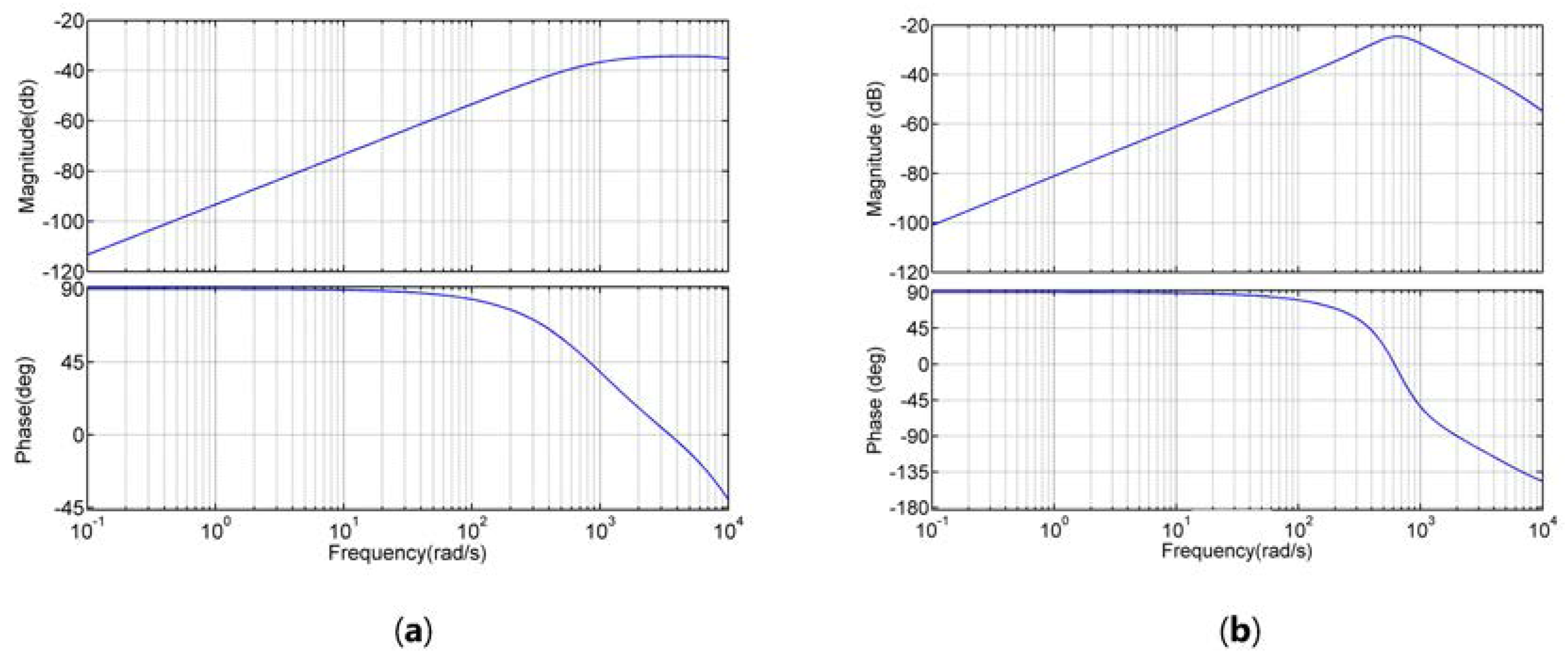
3.2. Design and Analysis of the Current MPRC
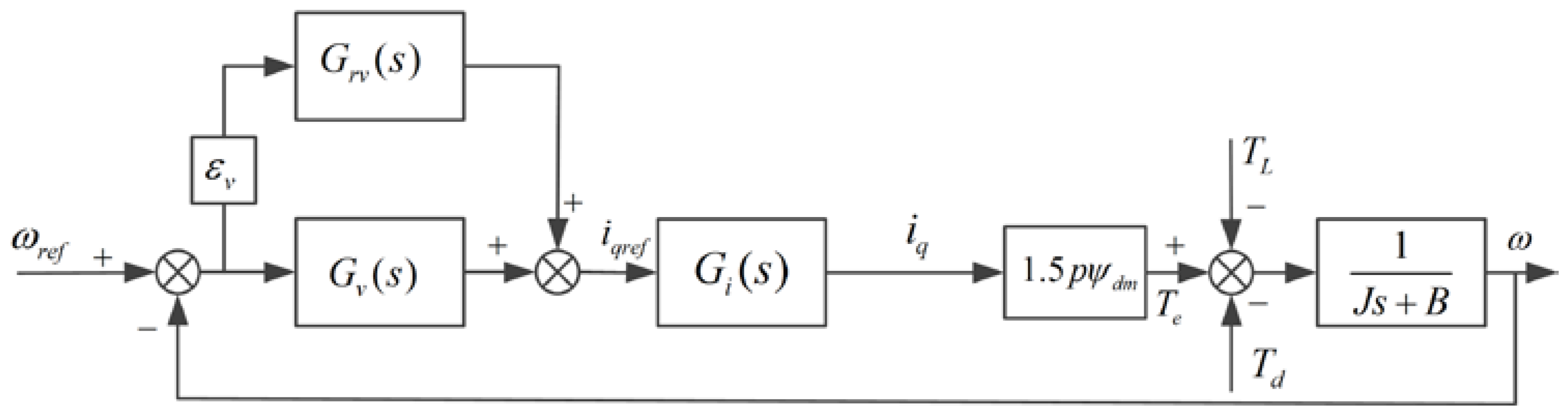
3.3. Design and Analysis of the Speed MPRC
4. Simulation and Experimental Verification
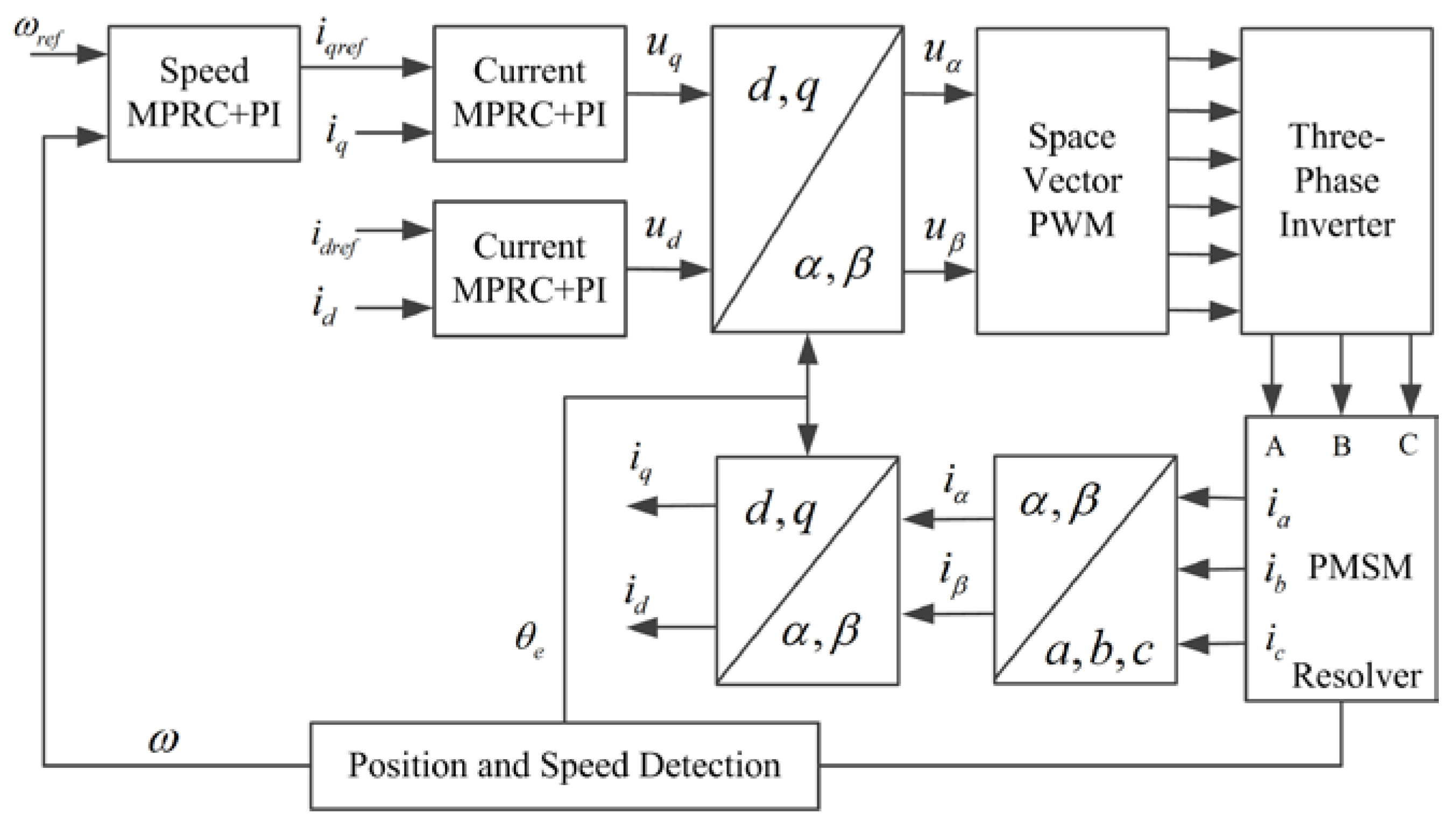
4.1. Simulation and Experimental Setup
4.2. Simulation Results
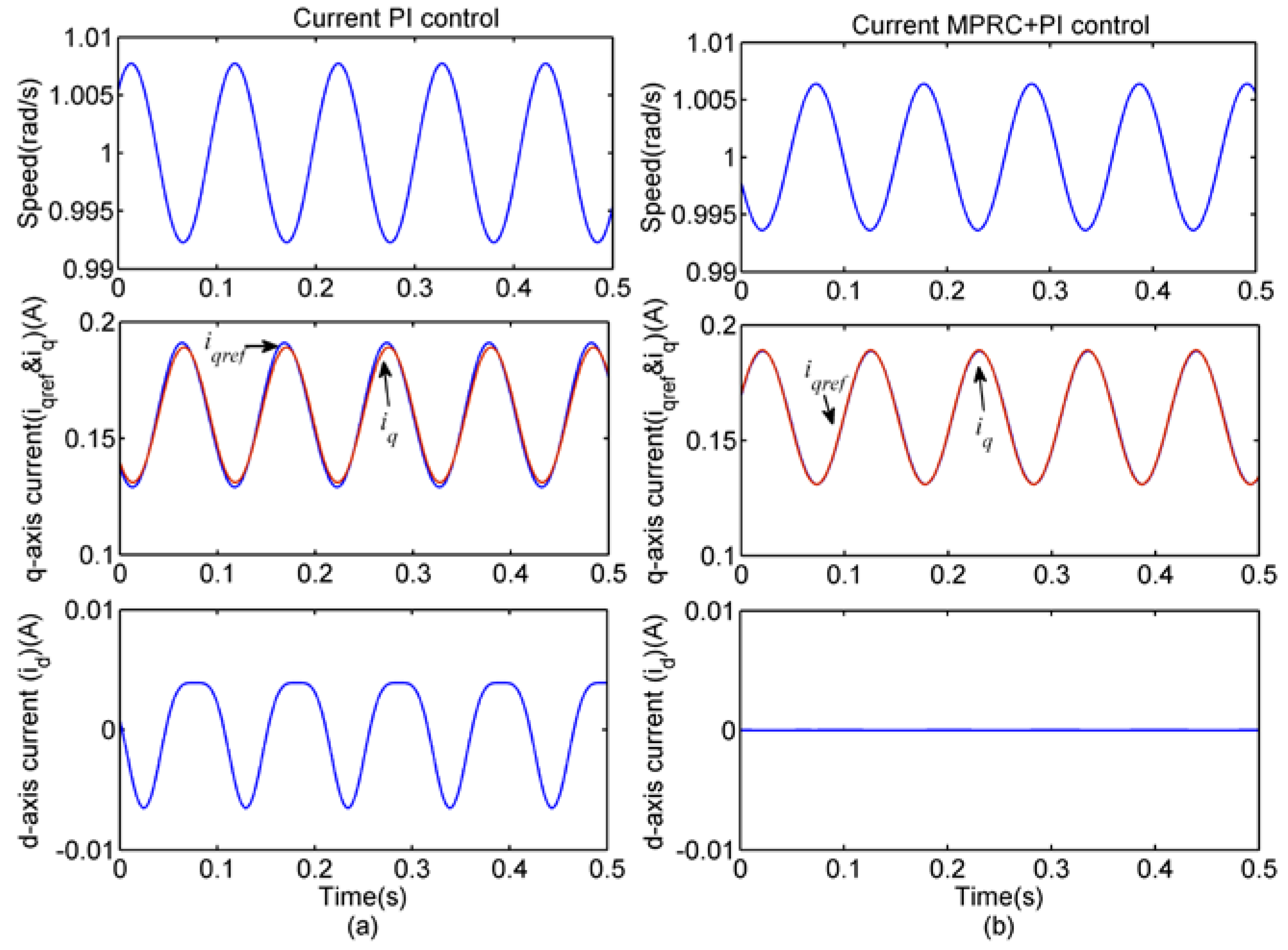
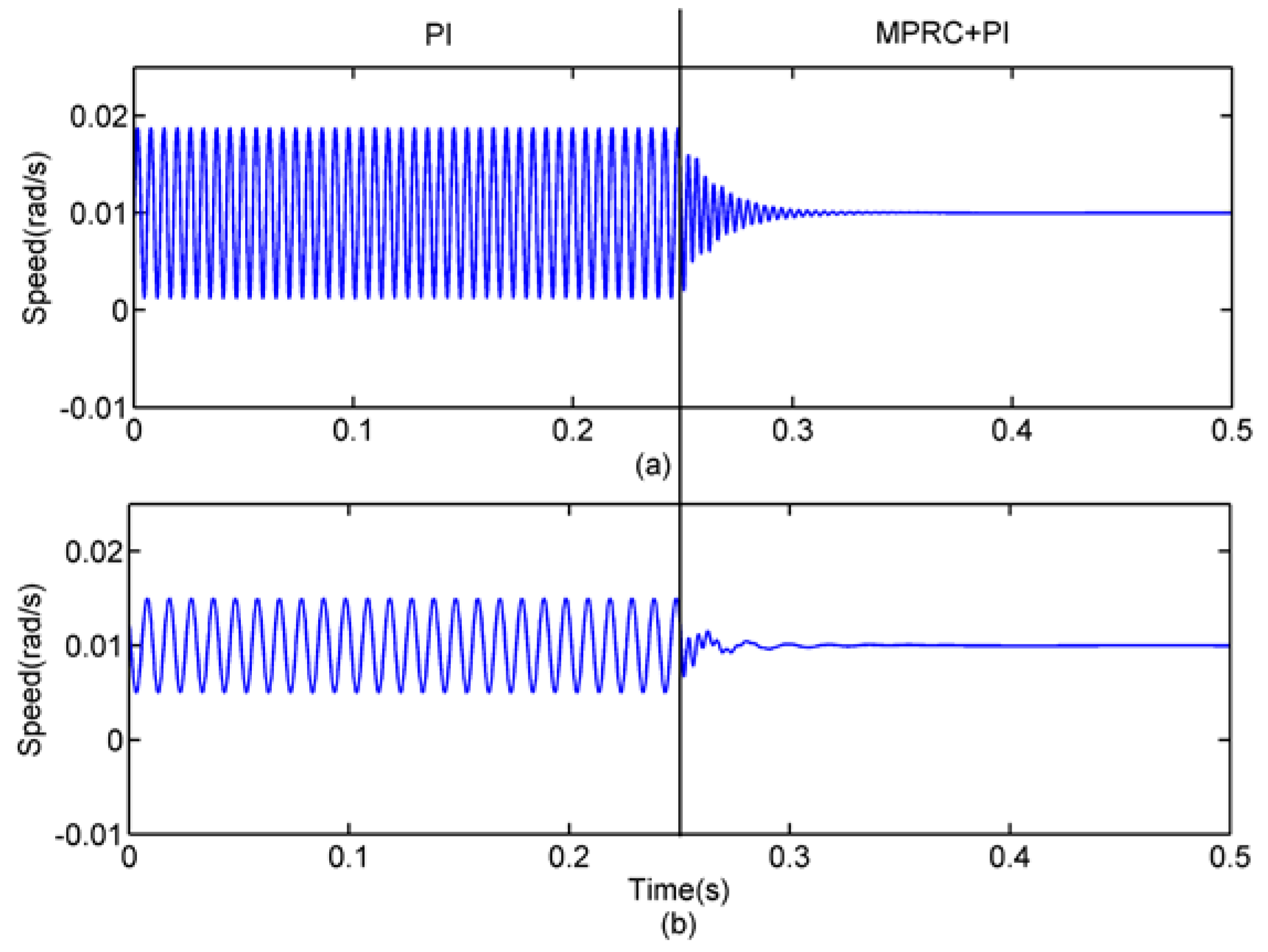
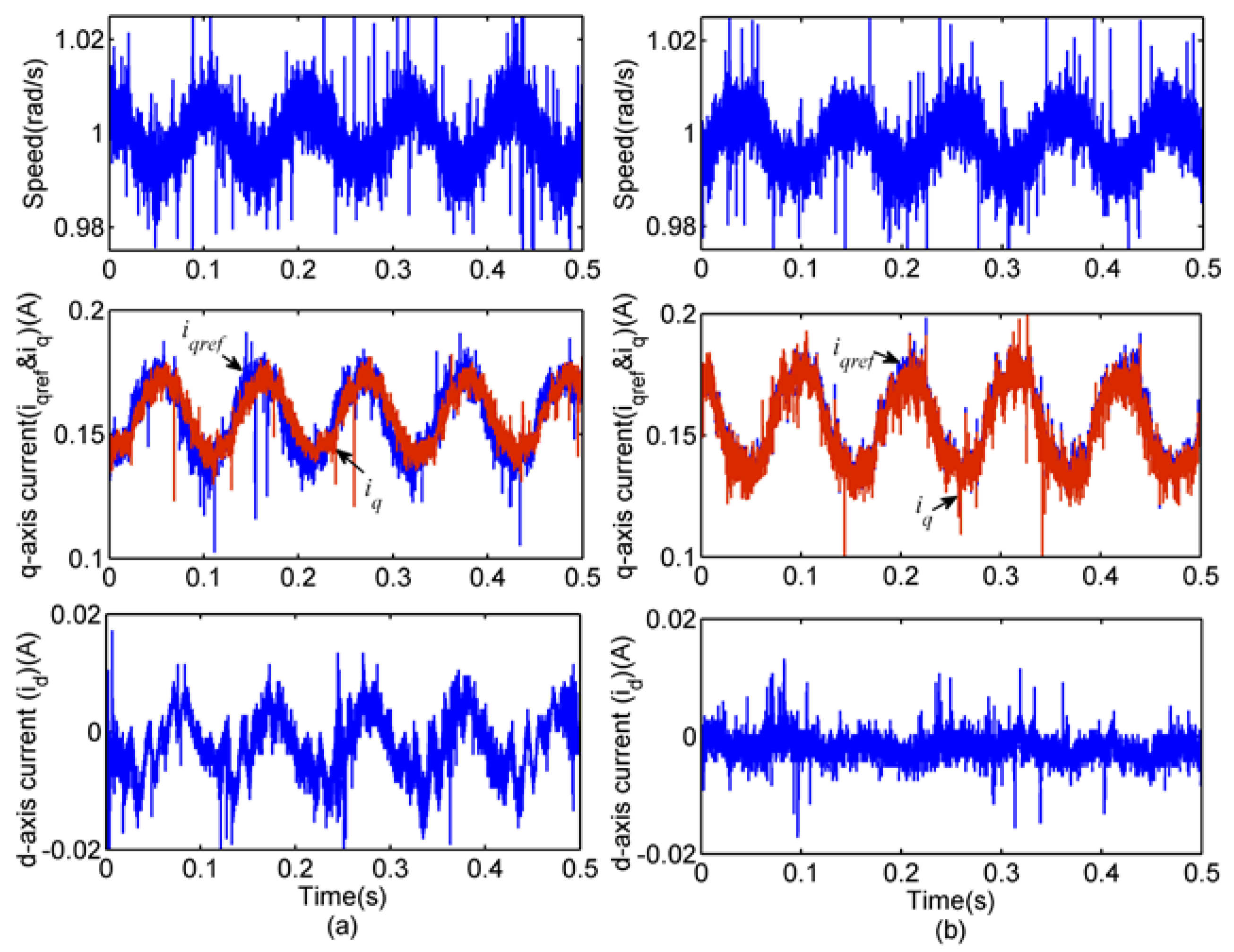
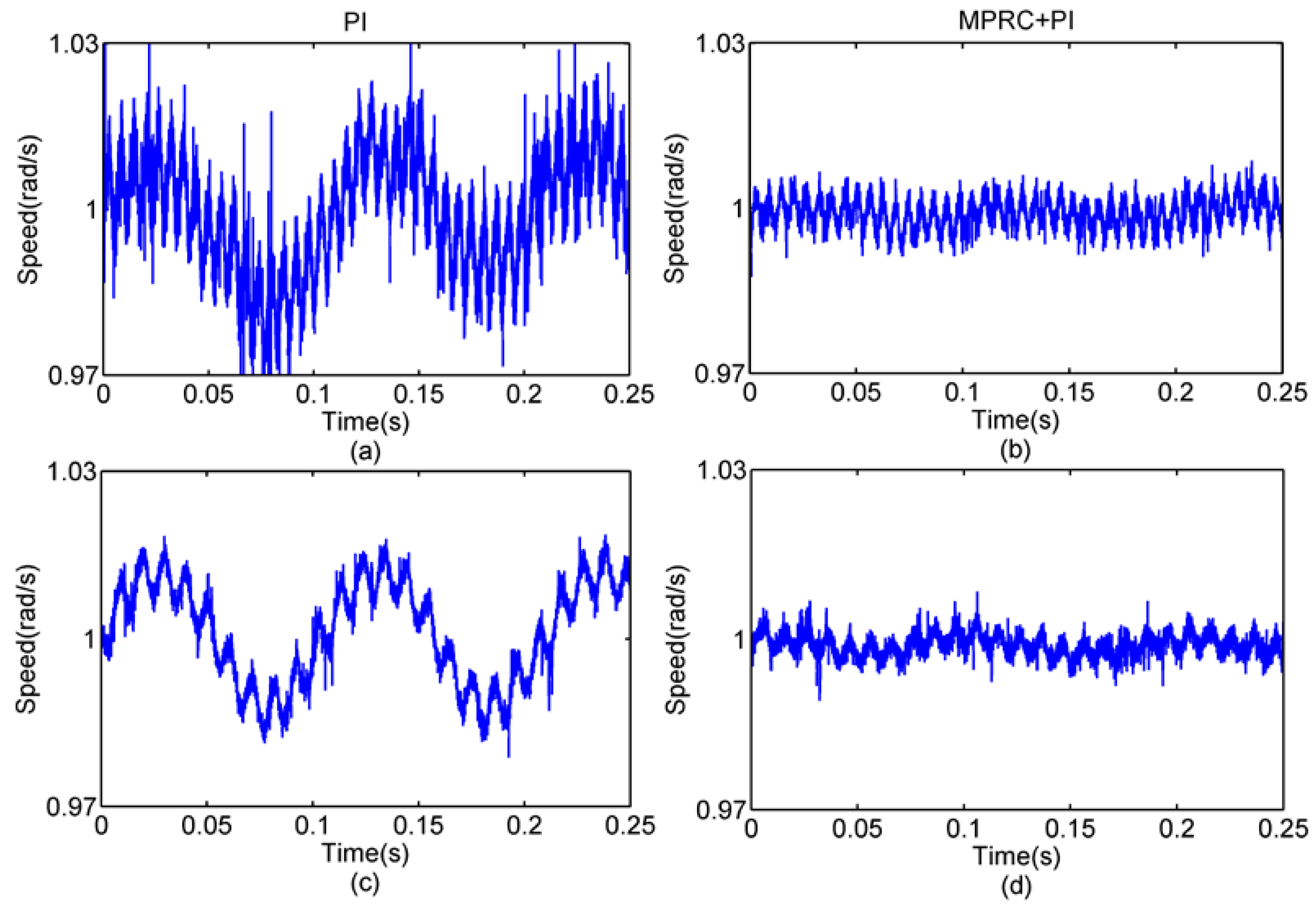
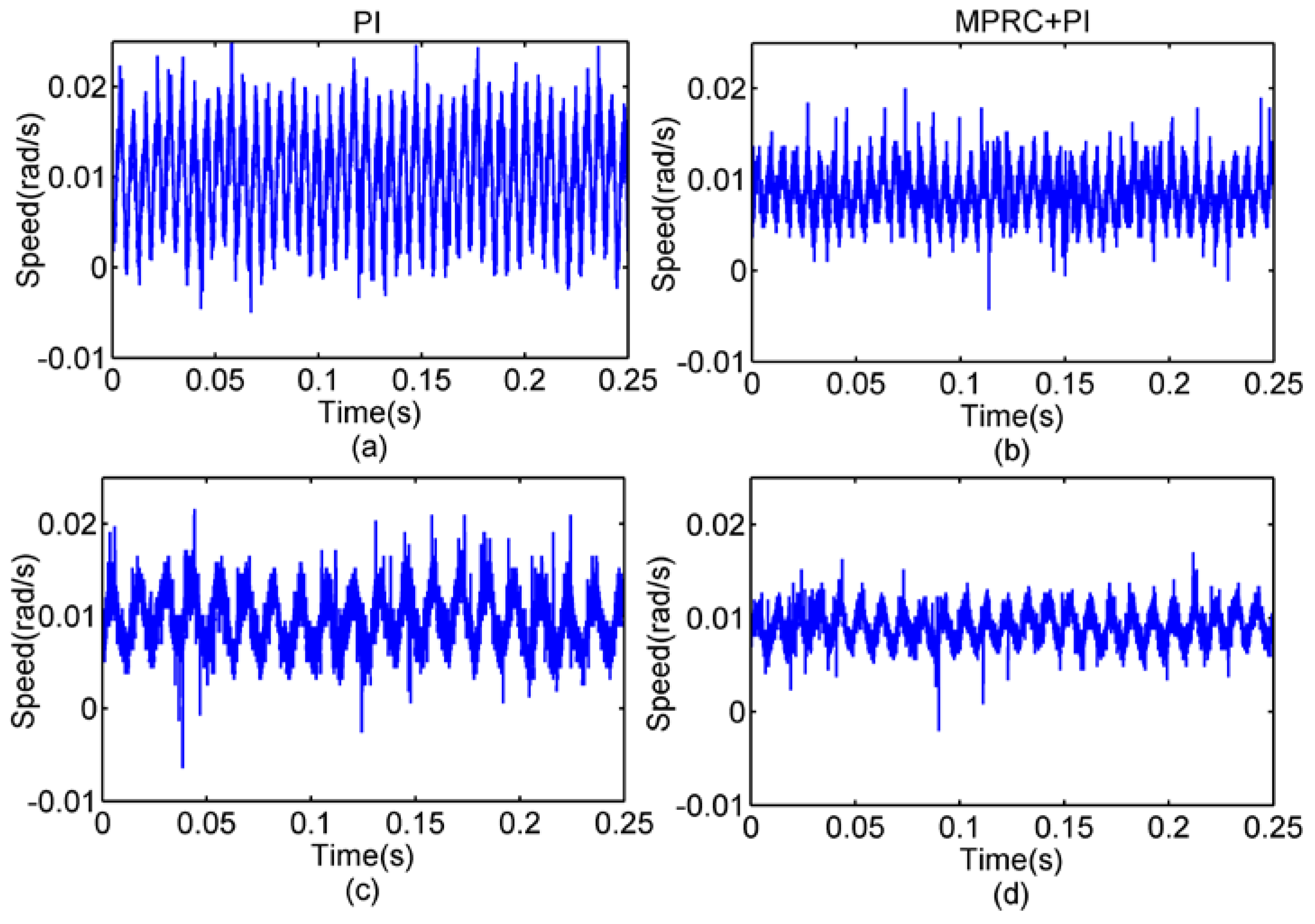
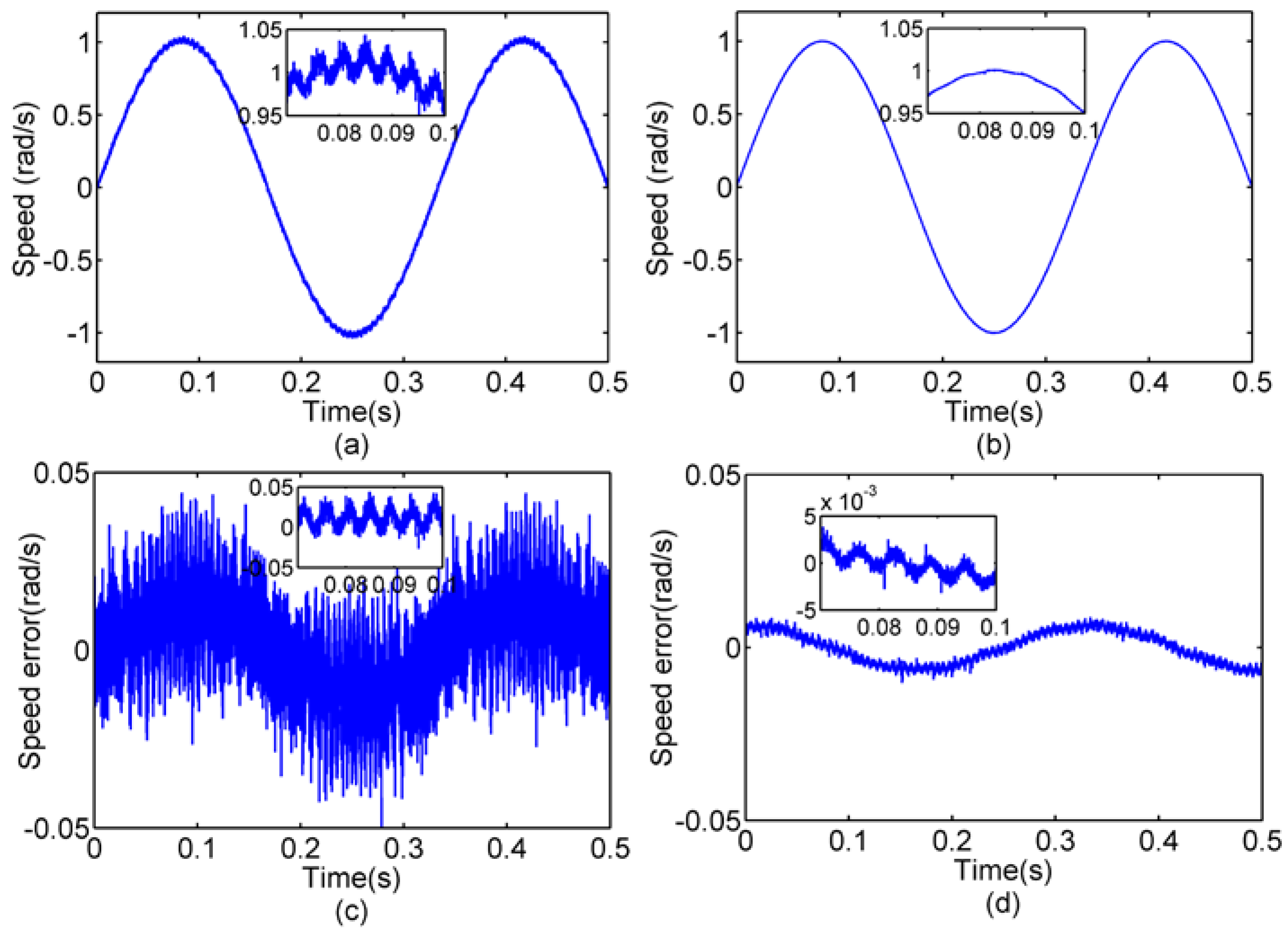
4.2.1. Simulation 1—Harmonic Current Suppression
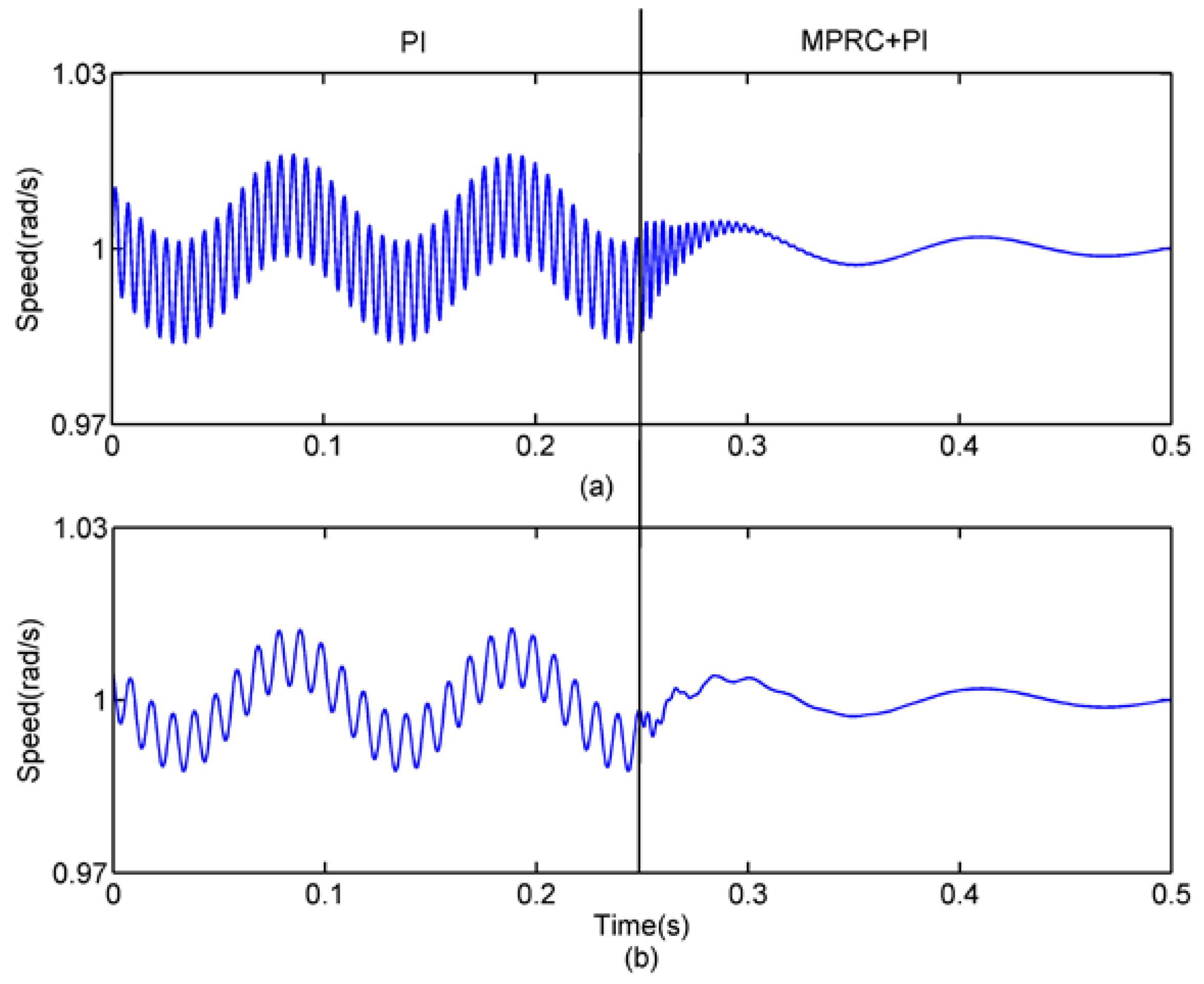
4.2.2. Simulation 2—Speed Ripple Suppression
4.3. Experiment Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bhat, S.; Tiwari, P. Controllability of spacecraft attitude using control moment gyroscopes. IEEE Trans. Autom. Control 2009, 54, 585–590. [Google Scholar] [CrossRef]
- Fang, J.; Ren, R. High-precision control for a single-gimbal magnetically suspended control moment gyro based on inverse system method. IEEE Trans. Ind. Electron. 2011, 58, 4331–4342. [Google Scholar] [CrossRef]
- Cui, P.; Li, S. Suppression of Harmonic current in active-passive magnetically suspended CMG using improved repetitive controller. IEEE/ASME Trans. Mechatron. 2016, 63, 6962–6970. [Google Scholar] [CrossRef]
- Han, B.; Zheng, S. Integral design and analysis of passive magnetic bearing and active radial magnetic bearing for agile satellite application. IEEE Trans. Magn. 2016, 21, 2132–2141. [Google Scholar]
- Dhaouadi, R.; Ghorbel, F. A new dynamic model of hysteresis in harmonic drives. IEEE Trans. Ind. Electron. 2003, 50, 1165–1171. [Google Scholar] [CrossRef]
- Chou, M.; Liaw, C. Dynamic control and diagnostic friction estimation for an SPMSM-driven satellite reaction wheel. IEEE Trans Ind. Electron. 2011, 58, 4693–4707. [Google Scholar] [CrossRef]
- Han, S.; Lee, J. Friction and uncertainty compensation of robot manipulator using optimal recurrent cerebellar model articulation controller and elasto-plastic friction observer. IET Control Theory Appl. 2011, 5, 2120–2141. [Google Scholar] [CrossRef]
- Verbert, K.; Toth, J. Adaptive friction compensation: A globally stable approach. IEEE/ASME Trans. Mechatron. 2016, 21, 351–363. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, D. Friction compensation based on time delay control and internal model control for gimbal system in MSCMG. IEEE Trans Ind. Electron. 2017, 64, 3798–3807. [Google Scholar] [CrossRef]
- Li, H.; Zheng, S. Precise control for gimbal system of double gimbal control moment gyro based on cascade extended state observer. IEEE Trans Ind. Electron. 2017, 64, 4653–4661. [Google Scholar] [CrossRef]
- Liu, T.; Huang, S. Cogging torque reduction by slot-opening shift for permanent magnet machines. IEEE Trans. Magn. 2013, 49, 4028–4031. [Google Scholar] [CrossRef]
- Parsa, L.; Hao, L. Interior permanent magnet motors with reduced torque pulsation. IEEE Trans Ind. Electron. 2008, 55, 602–609. [Google Scholar] [CrossRef]
- Chai, S.; Wang, L. A cascade MPC control structure for a PMSM with speed ripple minimization. IEEE Trans. Ind. Electron. 2013, 60, 2978–2987. [Google Scholar] [CrossRef]
- Hu, X.; Li, H. Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans. Ind. Electron. 2012, 59, 1171–1183. [Google Scholar]
- Flieller, D.; Nguyen, N. A self-learning solution for torque ripple reduction for nonsinusoidal permanent-magnet motor drives based on artificial neural networks. IEEE Trans. Ind. Electron. 2013, 61, 655–666. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S. Torque ripple minimization in PM synchronous motors using iterative learning control. IEEE Trans. Power Electron. 2004, 19, 272–279. [Google Scholar] [CrossRef]
- Mattavelli, P.; Tubiana, L. Torque-ripple reduction in PM synchronous motor drives using repetitive current control. IEEE Trans. Power Electron. 2005, 20, 1423–1431. [Google Scholar] [CrossRef]
- Eren, S.; Pahlevani, M. A digital current control technique for grid-connected AC/DC converters used for energy storage systems. IEEE Trans. Power Electron. 2017, 32, 3970–3988. [Google Scholar] [CrossRef]
- Li, B.; Hang, L. Robust proportional resonant regulator for grid-connected voltage souce inverter (VSI) using direct pole placement design method. IET Power Electron. 2012, 5, 1367–1373. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, M. Proportional-resonant controller and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Iacchetti, M.; Marques, G. Torque ripple reduction in a DFIF-DC system by resonant current controllers. IEEE Trans. Power Electron. 2015, 30, 4244–4254. [Google Scholar] [CrossRef]
- Zeng, J.; Degobert, P. Minimum torque ripple control of permanent magnet synchronous motor in the stationary reference frame. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15–18 May 2005; pp. 667–673. [Google Scholar]
- Yepes, A.; Francisco, F. Fernandez-Comesana, P. Torque ripple minimization in surface-mounted PM drives by means of PI + multi-resonant controller in synchronous reference frame. In Proceedings of the IECON 2010 Conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2010; pp. 1017–1022. [Google Scholar]
- Gao, J.; Wu, X. Torque ripple minimization of permanent magnet synchronous motor using a new proportional resonant controller. IET Power Electron. 2017, 10, 208–214. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional–integral–resonant controller. IEEE Trans Ind. Electron. 2015, 62, 2123–2134. [Google Scholar] [CrossRef]
- Francis, B.; Wonham, W. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]



| Parameters | Values | Unit |
|---|---|---|
| Rated speed | 150 | rpm |
| Pole pairs | 10 | - |
| Slot | 60 | - |
| Torque constant | 1.1 | Nm/A |
| Stator resistance | 7.4 | |
| d axes inductance | 6 | mH |
| q axes inductance | 6 | mH |
| Inertia | 0.024 | kg·m2 |
| Parameters | Values | Unit | Parameters | Values | Unit |
|---|---|---|---|---|---|
| 38 | v/A | 13 | A s/rad | ||
| 42,000 | v/A | 8900 | A s/rad | ||
| 0.00005 | s | 8000 | - | ||
| 10,000 | - | 0.6 | - |
| Control Method | Speed of High-Speed Rotor (rpm) | Amplitude of Hrmonics in Speed | ||
|---|---|---|---|---|
| 60 rad/s | 628 rad/s | 1047 rad/s | ||
| PI | 6000 | 0.013 | 0.005 | - |
| MPRC+PI | 6000 | 0.002 | 0.0012 | - |
| PI | 10,000 | 0.013 | - | 0.0095 |
| MPRC+PI | 10,000 | 0.002 | - | 0.002 |
| Control Method | Speed of High-Speed Rotor (rpm) | Amplitude of Harmonics in Speed | ||
|---|---|---|---|---|
| 0.6 rad/s | 628 rad/s | 1047 rad/s | ||
| PI | 6000 | 0.0001 | 0.005 | - |
| MPRC+PI | 6000 | 0.0001 | 0.0013 | - |
| PI | 10,000 | 0.0001 | - | 0.0095 |
| MPRC+PI | 10,000 | 0.0001 | - | 0.002 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Wang, Q.; Liu, K. High-Precision Speed Control Based on Multiple Phase-Shift Resonant Controllers for Gimbal System in MSCMG. Energies 2018, 11, 32. https://doi.org/10.3390/en11010032
Feng J, Wang Q, Liu K. High-Precision Speed Control Based on Multiple Phase-Shift Resonant Controllers for Gimbal System in MSCMG. Energies. 2018; 11(1):32. https://doi.org/10.3390/en11010032
Chicago/Turabian StyleFeng, Jian, Qing Wang, and Kun Liu. 2018. "High-Precision Speed Control Based on Multiple Phase-Shift Resonant Controllers for Gimbal System in MSCMG" Energies 11, no. 1: 32. https://doi.org/10.3390/en11010032
APA StyleFeng, J., Wang, Q., & Liu, K. (2018). High-Precision Speed Control Based on Multiple Phase-Shift Resonant Controllers for Gimbal System in MSCMG. Energies, 11(1), 32. https://doi.org/10.3390/en11010032





