Esterification Optimization of Crude African Palm Olein Using Response Surface Methodology and Heterogeneous Acid Catalysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterization of MT-KSF Catalyst
2.3. Response Surface Methodology (RSM)
2.4. Experimental Design
3. Results
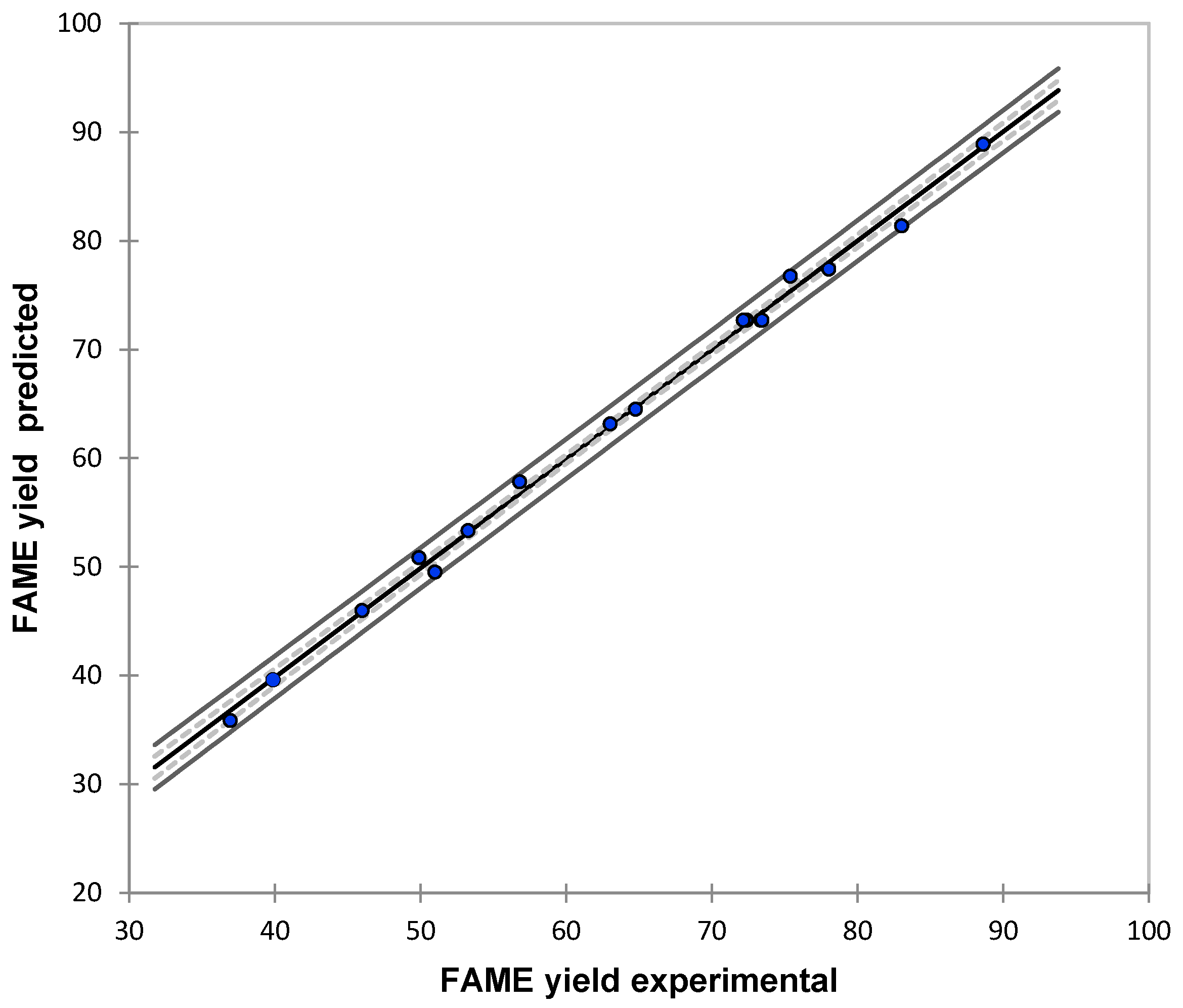
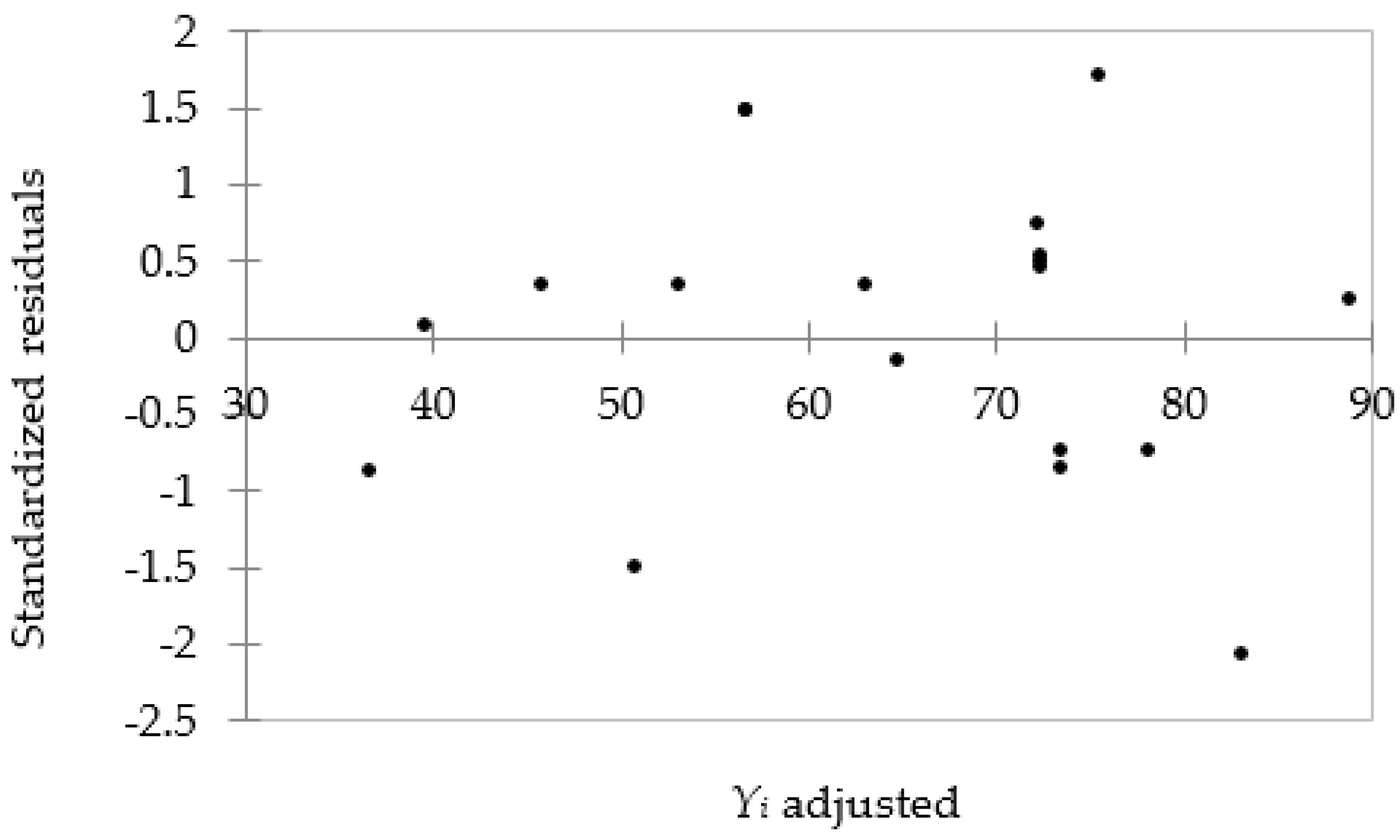
3.1. Modeling Results
3.2. Analysis of Variance (ANOVA)
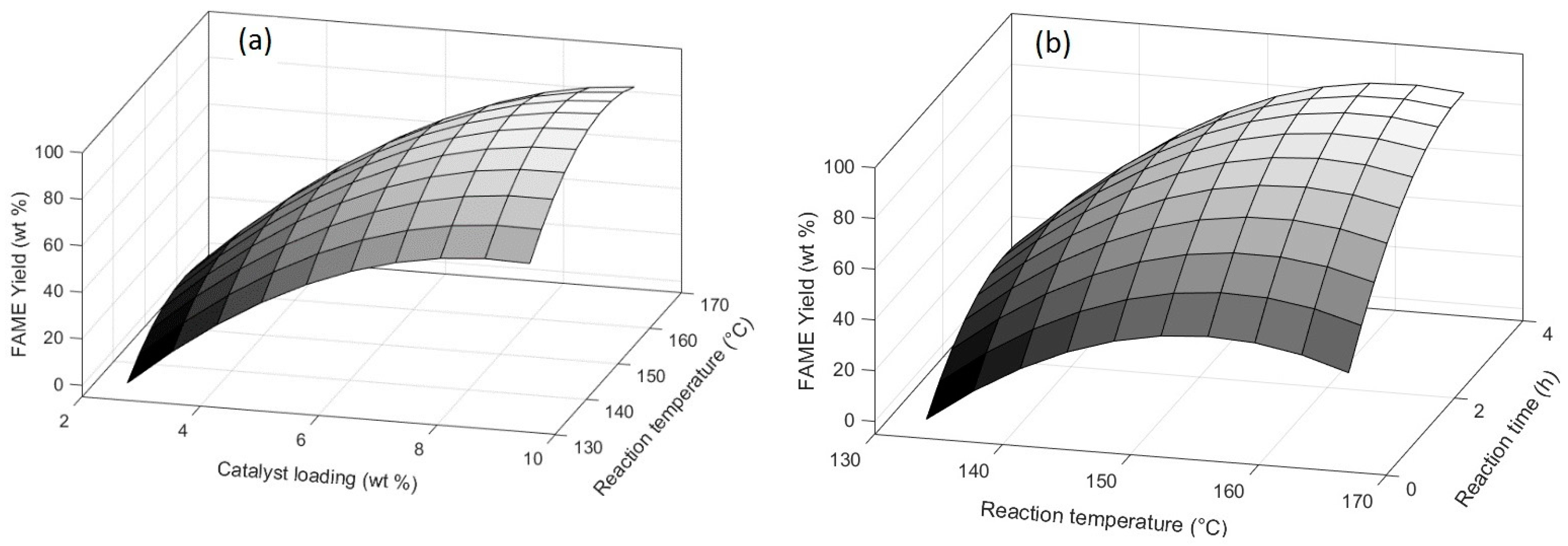
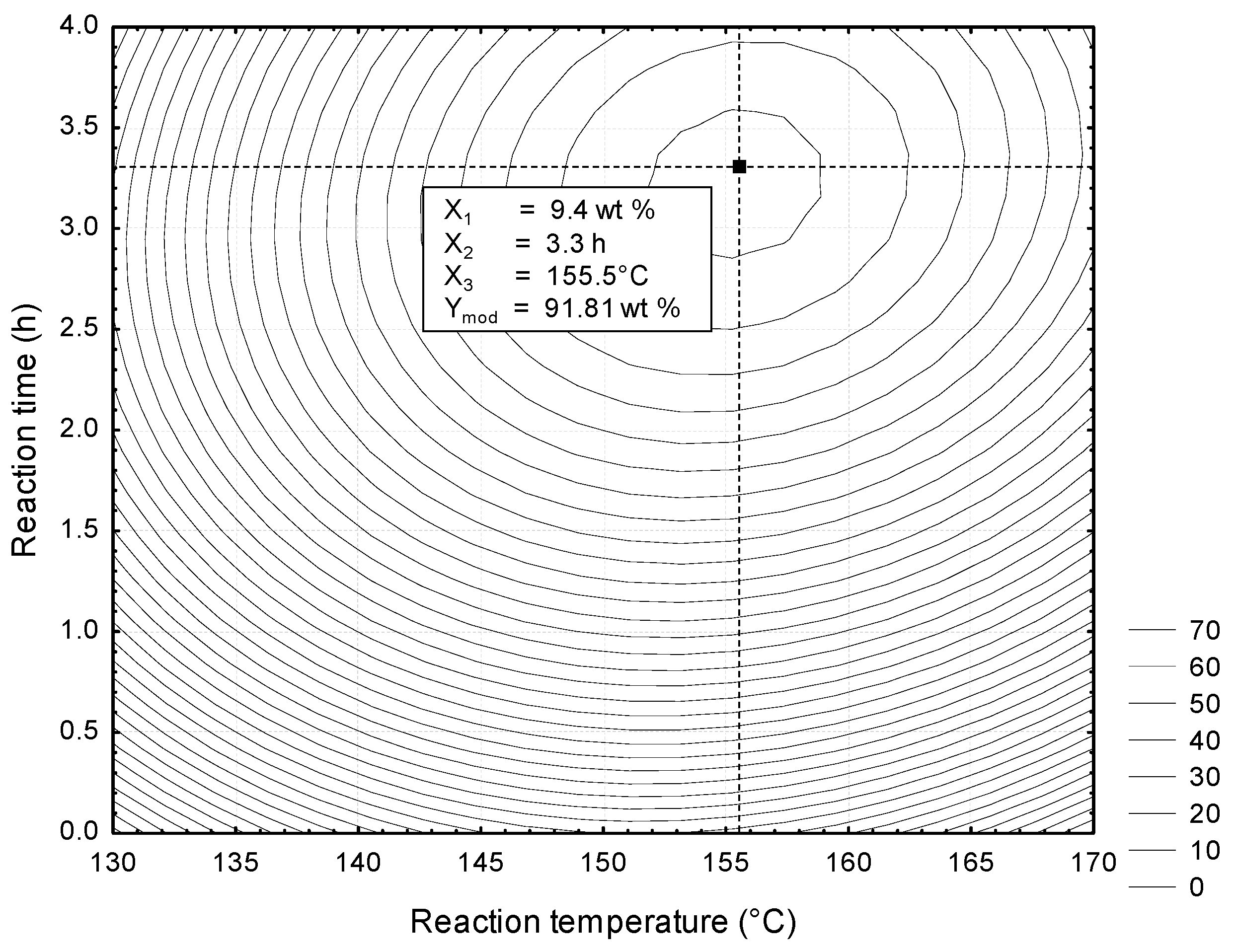
3.3. Optimization
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guerrero, P.A.; Anguebes, F.F.; Castelán, E.M.; Ramos, V.M.; Zarracino, R.G.; Loría, J.C.Z.; Quiroz, A.V.C. Fourier transform infrared-attenuated total reflectance (FTIR-ATR) spectroscopy and chemometric techniques for the determination of adulteration in petrodiesel/biodiesel blends. Química Nova 2014, 37, 392–397. [Google Scholar]
- Seyboth, K.; Sverrisson, F.; Appavou, F.; Brown, A.; Epp, B.; Leidreiter, A.; Lins, C.; Musolino, E.; Murdock, H.E.; Petrichenko, K.; et al. Renewables 2016 Global Status Report; REN21: Paris, France, 2016. [Google Scholar]
- Abdul Kapor, N.Z.; Maniam, G.P.; Rahim, M.H.A.; Yusoff, M.M. Palm fatty acid distillate as a potential source for biodiesel production—A review. J. Clean. Prod. 2017, 143, 1–9. [Google Scholar] [CrossRef]
- Sato, R.T.; Stroppa, P.H.F.; Da Silva, A.D.; De Oliveira, M.A.L. Fast GC-FID method for monitoring acidic and basic catalytic transesterification reactions in vegetable oils to methyl ester biodiesel preparation. Química Nova 2016, 39, 352–355. [Google Scholar] [CrossRef]
- Sebayang, A.H.; Hassan, M.H.; Ong, H.C.; Dharma, S.; Silitonga, A.S.; Kusumo, F.; Mahlia, T.M.I.; Bahar, A.H. Optimization of reducing sugar production from Manihot glaziovii starch using response surface methodology. Energies 2017, 10, 35. [Google Scholar] [CrossRef]
- Santos, F.D.; da Conceição, L.R.V.; Ceron, A.; de Castro, H.F. Chamotte clay as potential low cost adsorbent to be used in the palm kernel biodiesel purification. Appl. Clay Sci. 2017, 149, 41–50. [Google Scholar] [CrossRef]
- Lin, C.Y.; Lin, Y.W. Fuel characteristics of biodiesel produced from a high-acid oil from soybean soapstock by supercritical-methanol transesterification. Energies 2012, 5, 2370–2380. [Google Scholar] [CrossRef]
- Uribarrí, A.; Zabala, A.; Sáchez, J.; Arenas, E.; Chandler, C.; Rincón, M.; González, E.; Aiello Mazzarri, C. Evaluación del potencial de la borra de café como materia prima para la producción de biodiesel. Multiciencias 2014, 14, 129–139. [Google Scholar]
- Lotero, E.; Liu, Y.; Lopez, D.E.; Suwannakarn, K.; Bruce, D.A.; Goodwin, J.G. Synthesis of biodiesel via acid catalysis. Ind. Eng. Chem. Res. 2005, 44, 5353–5363. [Google Scholar] [CrossRef]
- Johnston, M.; Holloway, T. A global comparison of national biodiesel production potentials. Environ. Sci. Technol. 2007, 41, 7967–7973. [Google Scholar] [CrossRef] [PubMed]
- Jahirul, M.I.; Koh, W.; Brown, R.J.; Senadeera, W.; O’Hara, I.; Moghaddam, L. Biodiesel production from non-edible beauty leaf (Calophyllum inophyllum) oil: Process optimization using response surface methodology (RSM). Energies 2014, 7, 5317–5331. [Google Scholar] [CrossRef]
- Farobie, O.; Matsumura, Y. State of the art of biodiesel production under supercritical conditions. Prog. Energy Combust. Sci. 2017, 63, 173–203. [Google Scholar] [CrossRef]
- Özbay, N.; Oktar, N.; Tapan, N.A. Esterification of free fatty acids in waste cooking oils (WCO): Role of ion-exchange resins. Fuel 2008, 87, 1789–1798. [Google Scholar] [CrossRef]
- Silva, C.D.; Oliveira, J.V. Biodiesel production through non-catalytic supercritical transesterification: Current state and perspectives. Braz. J. Chem. Eng. 2014, 31, 271–285. [Google Scholar] [CrossRef]
- Trentin, C.M.; Lima, A.P.; Alkimim, I.P.; Da Silva, C.; De Castilhos, F.; Mazutti, M.A.; Oliveira, J.V. Continuous production of soybean biodiesel with compressed ethanol in a microtube reactor using carbon dioxide as co-solvent. Fuel Process. Technol. 2011, 92, 952–958. [Google Scholar] [CrossRef]
- Reddy, C.R.; Iyengar, P.; Nagendrappa, G.; Prakash, B.S.J. Esterification of dicarboxylic acids to diesters over Mn+-montmorillonite clay catalysts. Catal. Lett. 2005, 101, 87–91. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, C.; Wu, D.; He, S.; Ren, B. A Simple Method of Preparation of High Silica Zeolite y and Its Performance in the Catalytic Cracking of Cumene. J. Nanotechnol. 2016, 2016, 1486107. [Google Scholar] [CrossRef]
- Son, S.M.; Kimura, H.; Kusakabe, K. Esterification of oleic acid in a three-phase, fixed-bed reactor packed with a cation exchange resin catalyst. Bioresour. Technol. 2011, 102, 2130–2132. [Google Scholar] [CrossRef] [PubMed]
- Ferella, F.; Di Celso, G.M.; De Michelis, I.; Stanisci, V.; Vegliò, F. Optimization of the transesterification reaction in biodiesel production. Fuel 2010, 89, 36–42. [Google Scholar] [CrossRef]
- Ali, O.M.; Mamat, R.; Najafi, G.; Yusaf, T.; Ardebili, S.M.S. Optimization of biodiesel-diesel blended fuel properties and engine performance with ether additive using statistical analysis and response surface methods. Energies 2015, 8, 14136–14150. [Google Scholar] [CrossRef]
- Corral Bobadilla, M.; Lostado Lorza, R.; Escribano García, R.; Somovilla Gómez, F.; Vergara González, E. An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions. Energies 2017, 10, 130. [Google Scholar] [CrossRef]
- Wan Omar, W.N.N.; Saidina Amin, N.A. Optimization of heterogeneous biodiesel production from waste cooking palm oil via response surface methodology. Biomass Bioenergy 2011, 35, 1329–1338. [Google Scholar] [CrossRef]
- Ramos, M.J.; Fernández, C.M.; Casas, A.; Rodríguez, L.; Pérez, Á. Influence of fatty acid composition of raw materials on biodiesel properties. Bioresour. Technol. 2009, 100, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Guerrero-Peña, A.; Anguebes-Franseschi, F.; Castelán-Estrada, M.; Morales-Ramos, V.; Córdova-Quiroz, A.V.; Zavala-Loría, J.C.; Bolaños-Reinoso, E. Optimization of the biodiesel synthesis using crude African palm oil (Elaeis guineensis Jacq). Agrociencia 2013, 47, 649–659. [Google Scholar]
- Lozada, I.; Islas, J.; Grande, G. Environmental and economic feasibility of palm oil biodiesel in the Mexican transportation sector. Renew. Sustain. Energy Rev. 2010, 14, 486–492. [Google Scholar] [CrossRef]
- Aricetti, J.A.; Tubino, M. A green and simple visual method for the determination of the acid-number of biodiesel. Fuel 2012, 95, 659–661. [Google Scholar] [CrossRef]
- Knothe, G. Analyzing biodiesel: Standards and other methods. J. Am. Oil Chem. Soc. 2006, 83, 823–833. [Google Scholar] [CrossRef]
- Gao, L.; Teng, G.; Xiao, G.; Wei, R. Biodiesel from palm oil via loading KF/Ca-Al hydrotalcite catalyst. Biomass Bioenergy 2010, 34, 1283–1288. [Google Scholar] [CrossRef]
- Di Serio, M.; Tesser, R.; Pengmei, L.; Santacesaria, E. Heterogeneous Catalysts for Biodiesel Production. Energy Fuels 2008, 22, 207–217. [Google Scholar] [CrossRef]
- Ma, H.; Li, S.; Wang, B.; Wang, R.; Tian, S. Transesterification of Rapeseed Oil for Synthesizing Biodiesel by K/KOH/γ-Al2O3 as Heterogeneous Base Catalyst. J. Am. Oil Chem. Soc. 2008, 85, 263–270. [Google Scholar] [CrossRef]
- Pires, J.; Brasil, B.; Araújo, M.E.M. Reduction of free fatty acids in acidic nonedible oils by modified K10 clay. J. Am. Oil Chem. Soc. 2013, 90, 555–561. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 2. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. 1951, 13, 1–45. [Google Scholar]
- Le Van, S.; Chon, B.H. Chemical flooding in heavy-oil reservoirs: From technical investigation to optimization using response surface methodology. Energies 2016, 9, 711. [Google Scholar] [CrossRef]
- Brassard, P.; Godbout, S.; Raghavan, V.; Palacios, J.H.; Grenier, M.; Zegan, D. The production of engineered biochars in a vertical auger pyrolysis reactor for carbon sequestration. Energies 2017, 10, 388. [Google Scholar] [CrossRef]
- Su, C.-H. Kinetic study of free fatty acid esterification reaction catalyzed by recoverable and reusable hydrochloric acid. Bioresour. Technol. 2013, 130, 522–528. [Google Scholar] [CrossRef] [PubMed]
- Tesser, R.; Di Serio, M.; Guida, M.; Nastasi, M.; Santacesaria, E. Kinetics of oleic acid esterification with methanol in the presence of triglycerides. Ind. Eng. Chem. Res. 2005, 44, 7978–7982. [Google Scholar] [CrossRef]
- Espinosa Guzmán, A.; May Tzuc, O.; Balam Pantí, I.; Reyes Trujeque, J.; Pérez Quintana, I.; Bassam, A. Modelado de partículas PM10 y PM2.5 Mediante Redes Neuronales Artificiales sobre clima tropical de San Francisco de Campeche, México. Química Nova 2017, 40, 1025–1034. [Google Scholar]
- Melero, J.A.; Bautista, L.F.; Morales, G.; Iglesias, J.; Briones, D. Biodiesel production with heterogeneous sulfonic acid-functionalized mesostructured catalysts. Energy Fuels 2009, 23, 539–547. [Google Scholar] [CrossRef]
- Boey, P.L.; Ganesan, S.; Maniam, G.P.; Khairuddean, M.; Efendi, J. A new heterogeneous acid catalyst for esterification: Optimization using response surface methodology. Energy Convers. Manag. 2013, 65, 392–396. [Google Scholar] [CrossRef]
- Charoenchaitrakool, M.; Thienmethangkoon, J. Statistical optimization for biodiesel production from waste frying oil through two-step catalyzed process. Fuel Process. Technol. 2011, 92, 112–118. [Google Scholar] [CrossRef]
- Wiley, J.; Hepburn, K.; Levenspiel, O. Chemical Reaction Engineering. In Proceedings of the 3rd European Symposium on Chemical Reaction Engineering, Amsterdam, The Netherlands, 15–17 September 1964; Volume 19. [Google Scholar]
- Boffito, D.C.; Pirola, C.; Galli, F.; Di Michele, A.; Bianchi, C.L. Free fatty acids esterification of waste cooking oil and its mixtures with rapeseed oil and diesel. Fuel 2013, 108, 612–619. [Google Scholar] [CrossRef]
- Nandiwale, K.Y.; Niphadkar, P.S.; Deshpande, S.S.; Bokade, V.V. Esterification of renewable levulinic acid to ethyl levulinate biodiesel catalyzed by highly active and reusable desilicated H-ZSM-5. J. Chem. Technol. Biotechnol. 2014, 89, 1507–1515. [Google Scholar] [CrossRef]
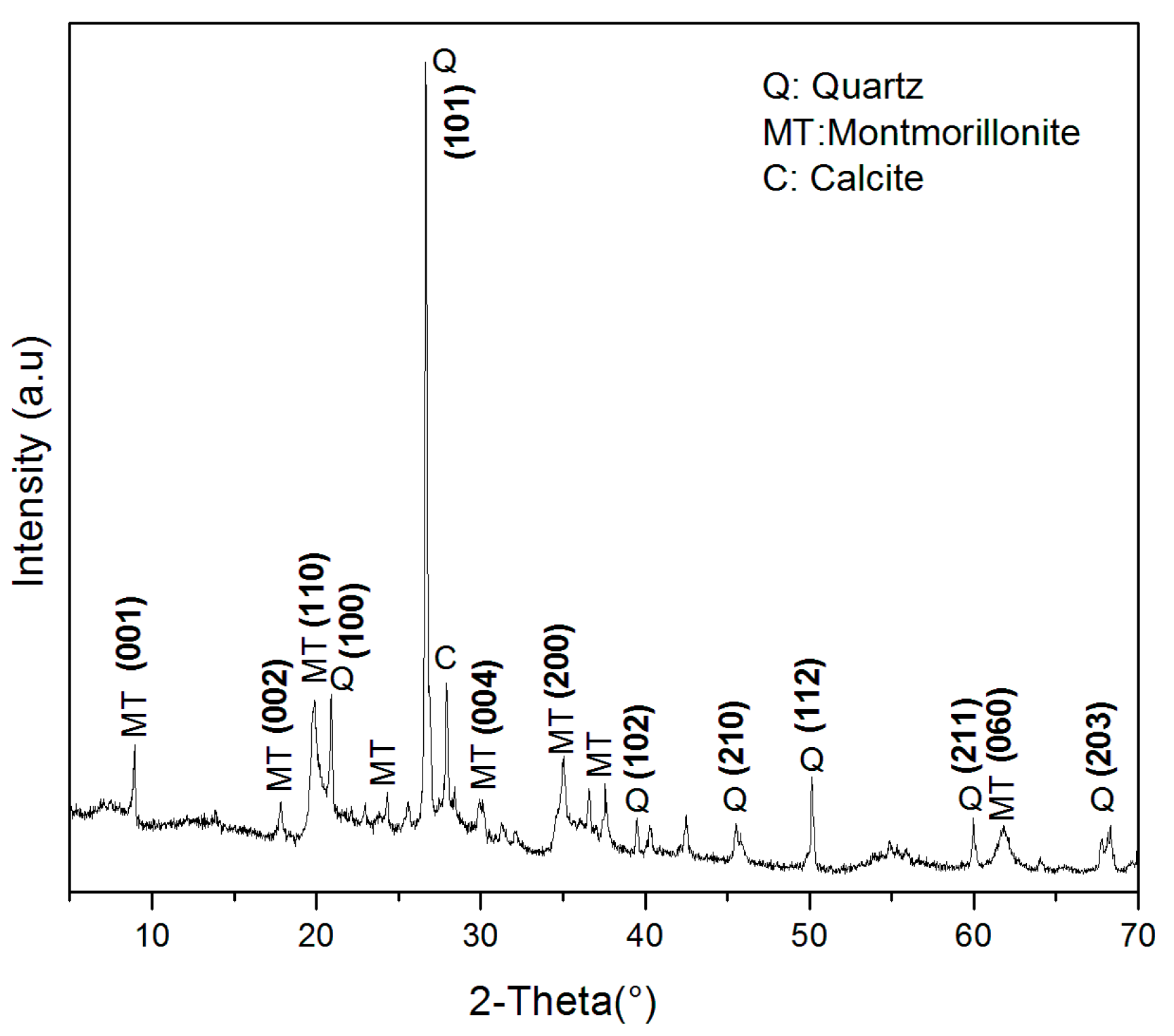

| Punctual Analysis | O | Mg | Al | Si | S | K | Ca | Fe | Total (%) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Zone 1 (Figure 2a) | A | 67.57 | 1.76 | 7.37 | 17.32 | 2.53 | 0.66 | 0.52 | 2.26 | 100 |
| B | 77.53 | 1.81 | 6.02 | 5.87 | 7.49 | 0.44 | 0 | 0.84 | 100 | |
| Zone 2 (Figure 2b) | C | 70.46 | 1.24 | 5.54 | 9.89 | 6.61 | 1.35 | 0.28 | 4.63 | 100 |
| D | 69.15 | 1.55 | 7.56 | 17.28 | 2.1 | 0.23 | 0.38 | 1.73 | 100 | |
| E | 77.95 | 1.97 | 6.05 | 4.52 | 8.6 | 0 | 0 | 0.91 | 100 | |
| F | 78.01 | 1.96 | 5.79 | 5.34 | 7.62 | 0.23 | 0.17 | 0.87 | 100 | |
| G | 69.84 | 0.53 | 3.05 | 15.89 | 5.08 | 1.02 | 0.81 | 3.78 | 100 | |
| H | 69.42 | 0.82 | 4.81 | 20.83 | 2.5 | 0.26 | 0.38 | 0.98 | 100 | |
| Statistics | O | Mg | Al | Si | S | K | Ca | Fe | Si/Al | Ca/Al | Mg/Al | Ca/Mg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max. | 78.01 | 1.97 | 7.56 | 20.83 | 8.6 | 1.35 | 0.81 | 4.63 | 2.75 | 0.107 | 0.261 | 0.411 |
| Min. | 67.57 | 0.53 | 3.05 | 4.52 | 2.1 | 0.23 | 0.17 | 0.84 | 1.48 | 0.056 | 0.105 | 0.321 |
| Average | 72.49 | 1.46 | 5.77 | 12.12 | 5.32 | 0.79 | 0.49 | 2 | 2.1 | 0.085 | 0.253 | 0.336 |
| SD * | 1.8 | 0.2 | 0.6 | 8.4 | 1.09 | 0.18 | 0.3 | 0.63 | 0.21 | 0.009 | 0.03 | 0.014 |
| Run | X1 | X2 | X3 | Yexp |
|---|---|---|---|---|
| (wt %) | (°C) | (h) | (wt %) | |
| 1 | 4(−1) | 140(−1) | 1(−1) | 34.13 |
| 2 | 8(+1) | 140(−1) | 1(−1) | 49.89 |
| 3 | 4(−1) | 160(+1) | 1(−1) | 39.87 |
| 4 | 8(+1) | 160(+1) | 1(−1) | 56.79 |
| 5 | 4(−1) | 140(−1) | 3(+1) | 53.26 |
| 6 | 8(+1) | 140(−1) | 3(+1) | 75.38 |
| 7 | 4(−1) | 160(+1) | 3(+1) | 63.02 |
| 8 | 8(+1) | 160(+1) | 3(+1) | 88.61 |
| 9 | 2.6(−2) | 150(0) | 2(0) | 45.98 |
| 10 | 9.4(+2) | 150(0) | 2(0) | 83.02 |
| 11 | 6(0) | 133.2(−2) | 2(0) | 50.98 |
| 12 | 6(0) | 166.2(+2) | 2(0) | 64.75 |
| 13 | 6(0) | 150(0) | 0.32(−2) | 36.92 |
| 14 | 6(0) | 150(0) | 3.68(+2) | 78.01 |
| 15 | 6(0) | 150(0) | 2(0) | 72.31 |
| 16 | 6(0) | 150(0) | 2(0) | 72.37 |
| 17 | 6(0) | 150(0) | 2(0) | 73.35 |
| 18 | 6(0) | 150(0) | 2(0) | 72.34 |
| 19 | 6(0) | 150(0) | 2(0) | 73.44 |
| 20 | 6(0) | 150(0) | 2(0) | 72.15 |
| Variable | Range and Levels | |||||
|---|---|---|---|---|---|---|
| Code | −1.68 (−α) | −1 | 0 | 1 | +1.68 (+α) | |
| Concentration of catalyst (wt %) | X1 | 2.6 | 4 | 6 | 8 | 9.4 |
| Reaction temperature (°C) | X2 | 133.2 | 140 | 150 | 160 | 166.2 |
| Reaction time (h) | X3 | 0.32 | 1 | 2 | 3 | 3.68 |
| Yexp | Ymod | |Error| |
|---|---|---|
| (wt %) | (wt %) | (%) |
| 34.13 | 34.98 | 2.5 |
| 49.89 | 50.87 | 2.0 |
| 39.87 | 39.63 | 0.6 |
| 56.79 | 57.84 | 1.8 |
| 53.26 | 53.35 | 0.2 |
| 75.38 | 76.76 | 1.8 |
| 63.02 | 63.18 | 0.3 |
| 88.61 | 88.91 | 0.3 |
| 45.98 | 46.01 | 0.1 |
| 83.02 | 81.38 | 2.0 |
| 50.98 | 49.54 | 2.8 |
| 64.75 | 64.53 | 0.3 |
| 36.92 | 35.88 | 2.8 |
| 78.01 | 77.41 | 0.8 |
| 72.31 | 72.71 | 0.6 |
| 72.37 | 72.71 | 0.5 |
| 73.35 | 72.71 | 0.9 |
| 72.34 | 72.71 | 0.5 |
| 73.44 | 72.71 | 1.0 |
| 72.15 | 72.71 | 0.8 |
| Effect | Degrees of Freedom | RMSE | F-Value | p-Value |
|---|---|---|---|---|
| Model | 18 | 4764.34 | 6717.71 | 0 |
| Intercept | 1 | 413.25 | 323.48 | 0 |
| X1 | 1 | 8.92 | 6.98 | 0.02465 |
| 1 | 144.93 | 113.46 | 0.00014 | |
| X2 | 1 | 431.23 | 337.56 | 0.00001 |
| 1 | 441.99 | 345.98 | 0.00001 | |
| X3 | 1 | 3.33 | 2.61 | 0.13736 |
| 1 | 465.14 | 364.11 | 0.00001 | |
| X2 | 1 | 2.68 | 2.09 | 0.17815 |
| X3 | 1 | 28.24 | 22.10 | 0.00084 |
| X3 | 1 | 13.39 | 10.48 | 0.00891 |
| Error | 10 | 1.28 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anguebes-Franseschi, F.; Abatal, M.; Bassam, A.; Escalante Soberanis, M.A.; May Tzuc, O.; Bucio-Galindo, L.; Cordova Quiroz, A.V.; Aguilar Ucan, C.A.; Ramirez-Elias, M.A. Esterification Optimization of Crude African Palm Olein Using Response Surface Methodology and Heterogeneous Acid Catalysis. Energies 2018, 11, 157. https://doi.org/10.3390/en11010157
Anguebes-Franseschi F, Abatal M, Bassam A, Escalante Soberanis MA, May Tzuc O, Bucio-Galindo L, Cordova Quiroz AV, Aguilar Ucan CA, Ramirez-Elias MA. Esterification Optimization of Crude African Palm Olein Using Response Surface Methodology and Heterogeneous Acid Catalysis. Energies. 2018; 11(1):157. https://doi.org/10.3390/en11010157
Chicago/Turabian StyleAnguebes-Franseschi, Francisco, Mohamed Abatal, Ali Bassam, Mauricio A. Escalante Soberanis, Oscar May Tzuc, Lauro Bucio-Galindo, Atl Victor Cordova Quiroz, Claudia Alejandra Aguilar Ucan, and Miguel Angel Ramirez-Elias. 2018. "Esterification Optimization of Crude African Palm Olein Using Response Surface Methodology and Heterogeneous Acid Catalysis" Energies 11, no. 1: 157. https://doi.org/10.3390/en11010157
APA StyleAnguebes-Franseschi, F., Abatal, M., Bassam, A., Escalante Soberanis, M. A., May Tzuc, O., Bucio-Galindo, L., Cordova Quiroz, A. V., Aguilar Ucan, C. A., & Ramirez-Elias, M. A. (2018). Esterification Optimization of Crude African Palm Olein Using Response Surface Methodology and Heterogeneous Acid Catalysis. Energies, 11(1), 157. https://doi.org/10.3390/en11010157








