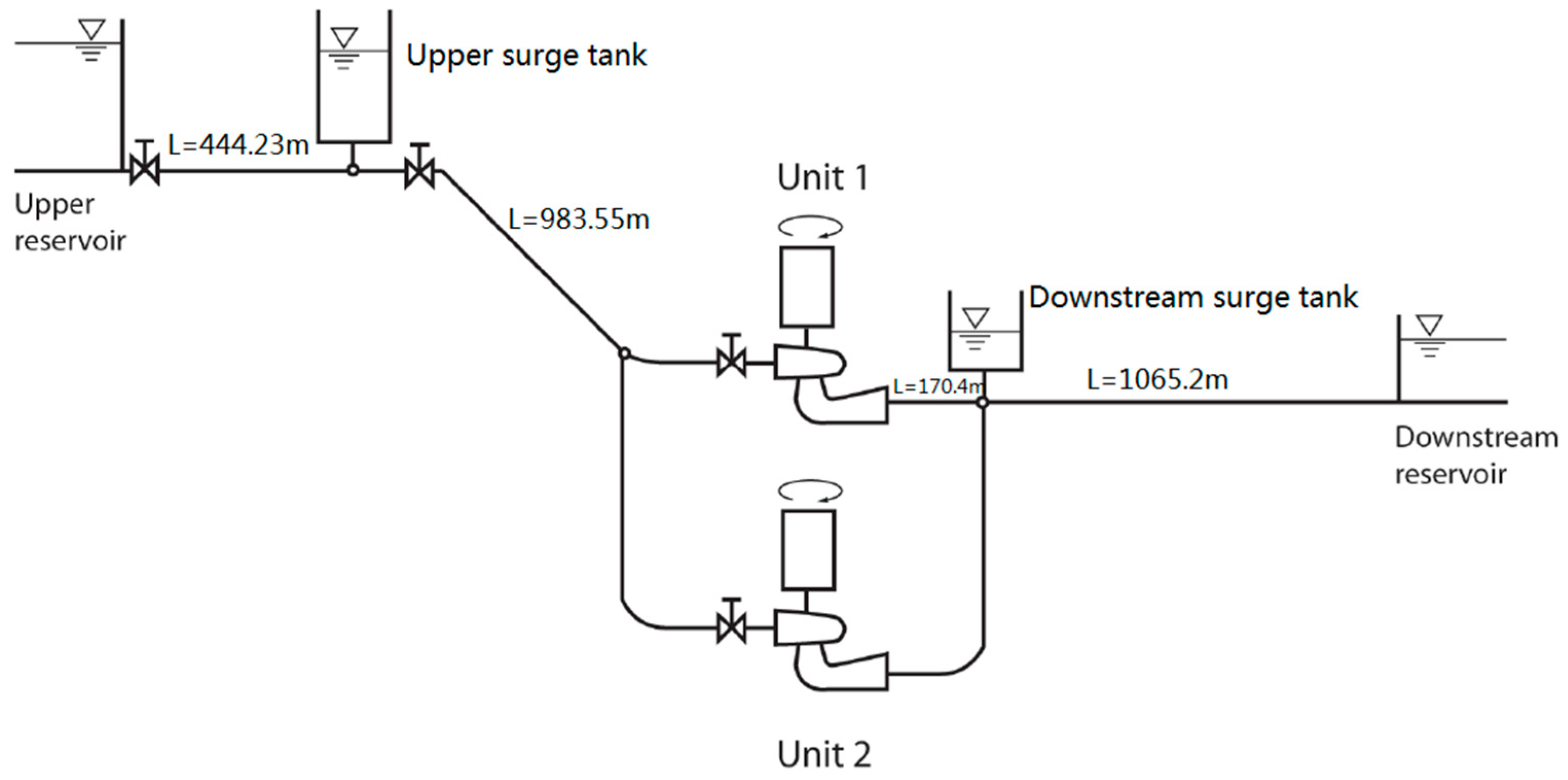
1. Introduction
Nowadays, the increase of energy demand and the depletion of fossil fuel have necessitated the large-scale utilization of renewable energy (RE). More and more REs, like wind and solar power have access to power grid [
1]. Due to the intermittent of the wind and solar power, the stability of the power grid that contains large capacity of RE has become a severe problem. Energy storage devices like batteries [
2,
3], flywheels [
4] and pumped storage units (PSUs) [
5] are indispensable in RE- connected power systems to mitigate this problem. Among these, PSUs might be the most economical and mature tool for power storage [
6]. In addition, PSUs have good performance in peak load shaving, frequency regulation and emergency response in power systems [
7]. In recent years, with the increasing scale of RE-integrated power systems, a considerable amount of work [
8,
9,
10,
11] has been carried out to study large-scale pumped storage facilities integrated with the grid-connected wind or solar power systems. In [
8], joint operation of REs and energy storage devices like PSUs is studied in the energy and ancillary service market. In [
9], the scheduling problem of a hybrid energy system containing intermittent solar power and pumped hydro storage (PHES) system has been investigated. In [
10], a flexibility-based reserve scheduling method for energy storage system with PSUs has been developed to improve the flexibility of the power system. In [
11], a model for transient stability analysis of a combined wind-pumped storage generation system is studied. Furthermore, this new generation model will be installed in El Hierro Island, in Spain. In those system or facilities where PSUs have been extensively adopted, the control quality of PSUs could not be neglected.
As a kind of hydropower generating unit, one of the merits of PSUs is their quick start-up, while a PSU could start and transfer to no-load condition from static status within 100 s and increase the power output to rated value within several minutes. This merit makes it able to quickly respond to RE power intermitting and load fluctuation, and keep the stability of the power system containing large-scale RE. The unit start-up related problems have attracted great interest of researchers. In [
12], Saboya et al. proposes a start-up decision method by using machine learning-based system for providing secondary frequency control for a power grid. In [
13], experimental investigations of transient pressure variations in a high head Francis turbine during start-up. A control system model of a hydropower unit was built and the start-up process was simulated in [
14].
PSU start-up usually refers to the process of unit starting in turbine mode. This process begins at the time the guide vane is beginning to move and ends at the time the unit connects to the grid. PSU start-up is a complex control problem. Multiple control models exist in start-up processes. The traditional and actually applied start-up strategy of PSUs mainly contains two phases [
15], namely the open-loop type and the close-loop type [
16]. In the first phase, a direct guide vane control (DGVC) is adopted, which is usually open-loop, while the governor drives the guide vane (GV) as a given law. In the second phase, a closed-loop PID control is applied to track the rated rational speed and maintain the stability. The open-loop DGVC law provides the trajectory of guide vane opening (GVO), which could be a one-stage polyline or two-stage polyline. Take the two-stage DGVC as an example, in a two-stage strategy, the guide vane will firstly open to start opening, which is about twice as much as the no-load opening, and then keep the opening for a while; until the rotational speed rises to a threshold, guide vane opening is adjusted to the no-load opening. In the second phase, a closed-loop PID control is switched in to stabilize the rotational speed as soon as it reaches a threshold value.
Although the traditional strategies are applicable, there are two main drawbacks, which are: (1) parameters of GVO trajectory in the open-loop DGVC are difficult to set, which are always selected by experience; (2) study on optimization of start-up strategy is not sufficient. In order to handle these problems, researches have tried efforts. Bao et al. designed an “open-closed loop” GVO trajectory and the results indicated that a fast and smooth start-up process could been achieved [
17]. Zhang et al. proposed a new DGVC strategy, which integrates the open-loop and close-loop trajectories in DGVC, aiming at balancing the start-up time and control quality [
18]. In [
7], Yang and Yang tried to modify the conventional open-loop DGVC law and the improved strategy has proved to be effective in promoting start-up performance. Besides, more efforts have been made in optimization of start-up strategies. Zhou et al. [
19] selected a constant rational speed growth rate as the objective, so it’s easier to control the frequency change in the whole start-up process. The results also indicate that indices of rotation torque, axial thrust fluctuation as well as the pressure fluctuating of penstock could be improved except for the quick-start index. Dynamic control indices have been chosen as optimization objectives in designing an adaptively fast fuzzy fractional order PID controller in the second phase of start-up process and the simulation results demonstrates that the new controller could enhance the dynamic performance and stability of the pumped storage unit governing systems in the start-up process [
20]. Although control quality indices are often considered in start-up strategy optimization, the start-up time is always neglected. An excellent start-up strategy should be built on indices concerning both quickness and control quality. Pannatier et al. presented the start-up and synchronization procedures of large variable-speed pump-turbine units in pumping mode. By the optimization of the start-up time, it leads to a significant decrease of the start-up time [
21].
As for parameter tuning for control system of hydropower generating units, meta-heuristic algorithms have been successfully applied [
22,
23]. Moreover, some popular meta-heuristic algorithms, such as Genetic Algorithm (GA) [
24], particle swarm optimization (PSO) [
25], Ant Colony Optimization (ACO) algorithm [
26], and Gravitational Search Algorithm (GSA) [
27,
28,
29] have been adopted to solve optimization problems. Although numerous meta-heuristic algorithms have been proposed and applied to solve different optimization problems, there is no specific algorithm which can solve all optimization problems. For optimization of start-up strategy, a powerful algorithm is essential to achieve the desired goal.
Flocks of sheep, which is a common swarm in nature, also show intelligence in social activities. In foraging ground, the strolling of sheep implies individual exploration, and the bellwether is the leading elite that affects the swarm movement. Many swarm intelligence (SI) techniques are inspired by foraging and search behaviors. However, there is no SI technique in the literature mimicking the Herding Effect, which is a well-known phenomenon in the sheep flock. Motivated by this interesting behavior, a new meta-heuristic optimization algorithm is proposed in this paper. The mathematical model of the social behavior of a sheep flock, as well as investigation of its abilities in solving benchmark problems, will be fully discussed before applying it in start-up strategy optimization of PSU.
Motivated by the above discussion, a new integrated start-up method for PSU is proposed in this paper, while a two phase’s closed-loop startup strategy is designed, and optimization scheme is built for parameter optimization of the strategy. Moreover, in order to promote the optimization performance, new meta-heuristic algorithm is studied. This paper presents a novel meta-heuristic called Artificial Sheep Algorithm (ASA) based on social behaviors of sheep flock. The mathematically model of the social behavior of sheep flock, as well as investigation of its abilities in solving complicated problems, will be fully discussed.
The remaining part of this paper is organized as follows:
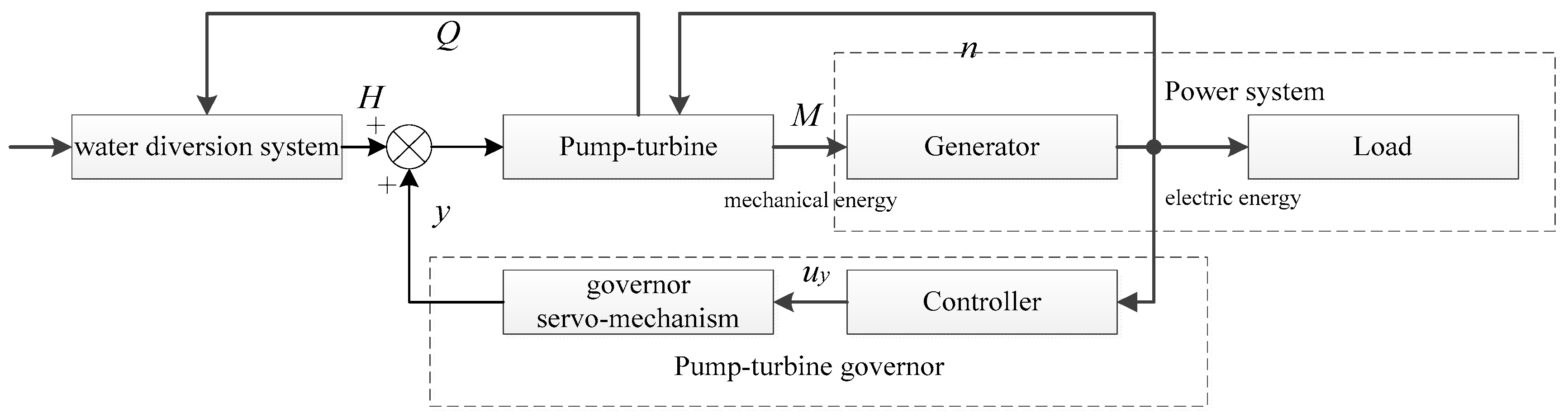
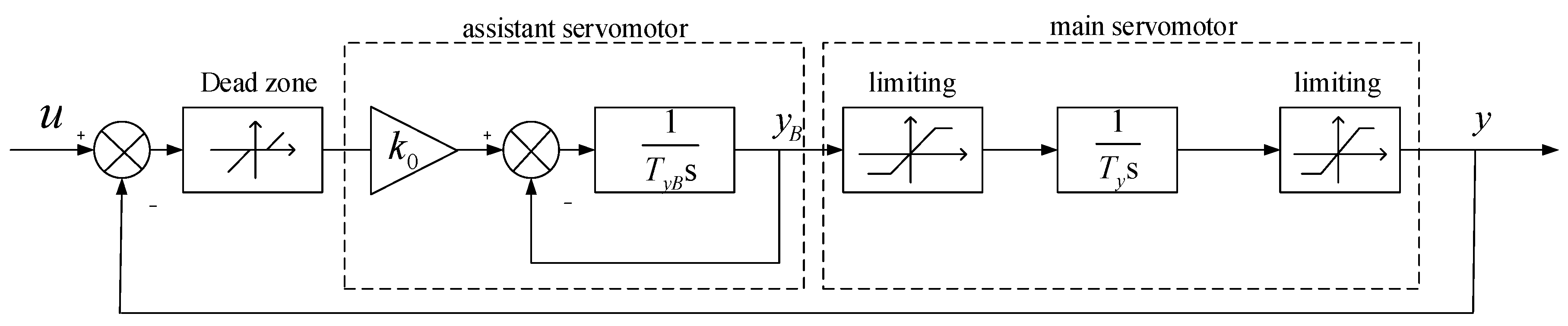
Section 2 establishes a mathematical of Pump-Turbine Governing System which composed of PID controller, governor servo-mechanism, water diversion system, pump-turbine and generator.
Section 3 introduces the theoretical knowledge of ASA.
Section 4 delineates specific operations of traditional start-up and the proposed integrated start-up strategy. In
Section 5, the performances of optimization schemes and integrated start-up strategy are analyzed by comparison experiment. The conclusions are summarized in the
Section 6.
3. Artificial Sheep Algorithm
Optimization of parameters in the start-up strategy is an important task in this paper. A novel meta-heuristic called Artificial Sheep Algorithm (ASA) based on the social behaviors of sheep flocks is proposed and used to optimize the parameters. A series of test experiments are conducted to evaluate the performance of the proposed ASA.
Sheep flocks are always regarded as a scattered organization. Although they are loose, and can collide with each other in group activities, they have the habitual nature of following and moving towards the bellwether who is the strongest in the group. As sheep appear to blindly follow, people always associate them with conformity. Actually, the behavior of this social group has undergone ten million years of natural testing. From the perspective of SI, the loose individuals indicate random diversity, the blind herd behavior indicates high-efficiency positive feedback, and the bellwether leading implements the sharing of information in the whole group. This paper is inspired by the herd behavior of sheep flock and tries to simulate a novel meta-heuristic optimization algorithm with some artificial measures.
The social behaviors of sheep flock are attractive, and two main behaviors, namely the free strolling of individuals and strong leading of bellwether. In a sheep flock, the strongest sheep is called the bellwether, acting as the leader of the swarm. When fleeing from a predator or foraging, the individual will follow the bellwether by moving as close as possible. When strolling or playing, individuals are loose and always move randomly in their own local region.
3.1. Theoretical Knowledge of Algorithm
Consider a sheep flock with
N sheep, the position of the
ith sheep at specific time “
t” is defined as:
where
represents the position of
ith sheep in the
dth dimension,
D is the dimension of the position.
For solving a minimization problem:
where
is the lower boundary of the searing space, and
is the upper boundary of the searing space. The objective function value of the
ith agent at time “
t” is expressed as
.
Leading of bellwether
The influence of the bellwether is decisive. When the bellwether moves with a big stride, individuals will adjust their motion trajectory to follow the bellwether closely. The position of the bellwether should be recorded and inherited, and this position is denoted as . The influence of the bellwether acting on the ith sheep is expressed as bellwether vector, denoted by .
The bellwether vector that affects the movement of the
ith agent,
i = 1, …,
N, is defined as:
where
is the influence scope of the bellwether playing on the
ith sheep on the
dth dimension,
,
,
is the coefficient of leading scope,
rand1 is a random number generated in [−1, 1],
w is a dynamic weight that linearly decreased from 1 to 0 over the course of iterations.
The coefficient c1 is a random value whose center is 1, and its radius is determined by the parameter , which is selected from [0, 1]. The is a control parameter, which influences the consensus effect of the bellwether in defining the distance vector. When tends to 1, it emphasizes the consensus influence of the bellwether; when tends to 0, it enhances the stochastic components. The coefficient c2 is a random dynamic number that is automatically generated, and its random range is linearly decreased over the course of iterations.
Individual strolling
Every individual of flock forages autonomously in a local area, and this behavior is called “self-awareness”. The mathematical model of “individual strolling” to represent shelf-awareness of sheep individual in the process of foraging is proposed as follow. We define a location vector to denote self-awareness in foraging.
The shelf-awareness vector that affects the movement of the
ith agent,
i = 1, …,
N, is defined as:
where
is a random number generated from [0, 1], the term
is used to generate periodic random.
The vector represents the self-driven behavior and local random search of a sheep, which consists of a series of nonlinear operations. The parameter is a positive number that modulates the amplitude of the strolling step. As increases, the sheep’s jump steps increase exponentially and vice versa. As a result, this parameter controls the resolution of individual exploration. The value of should be chosen according to the search scope of the optimization problem.
In a sheep flock, the direction of the sheep flock is determined by the lead of the bellwether and the autonomous foraging. Based on the discussion above, the movement of a sheep is affected by its self-awareness and the summoning of the bellwether. The individuals in artificial sheep flock will automatically update their positions as follows:
where
is linearly decreased from 1 to 0 over the course of iterations and
r3 is random number generated in [0, 1].
Competition strategy
In ASA, competition mechanism is designed to keep the diversity of the flock. For a minimum problem, at a specific time “t”, calculate the average value of N objective function values of the flock , and the minimal objective function value .
For the
ith sheep, if the elimination criteria as following is satisfied:
Then, the ith sheep is eliminated and reinitialized between .
3.2. The Optimized Procedures of Algorithm
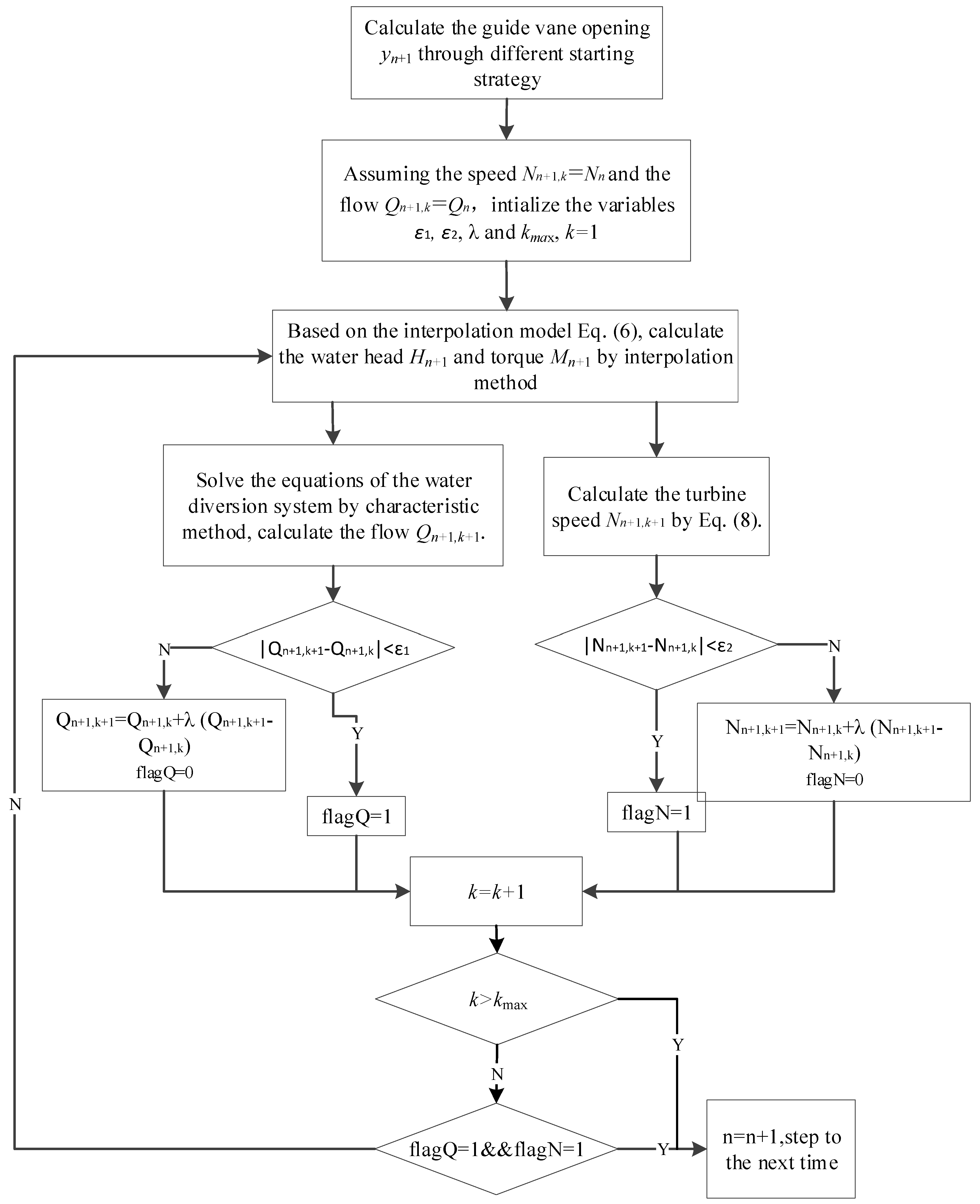
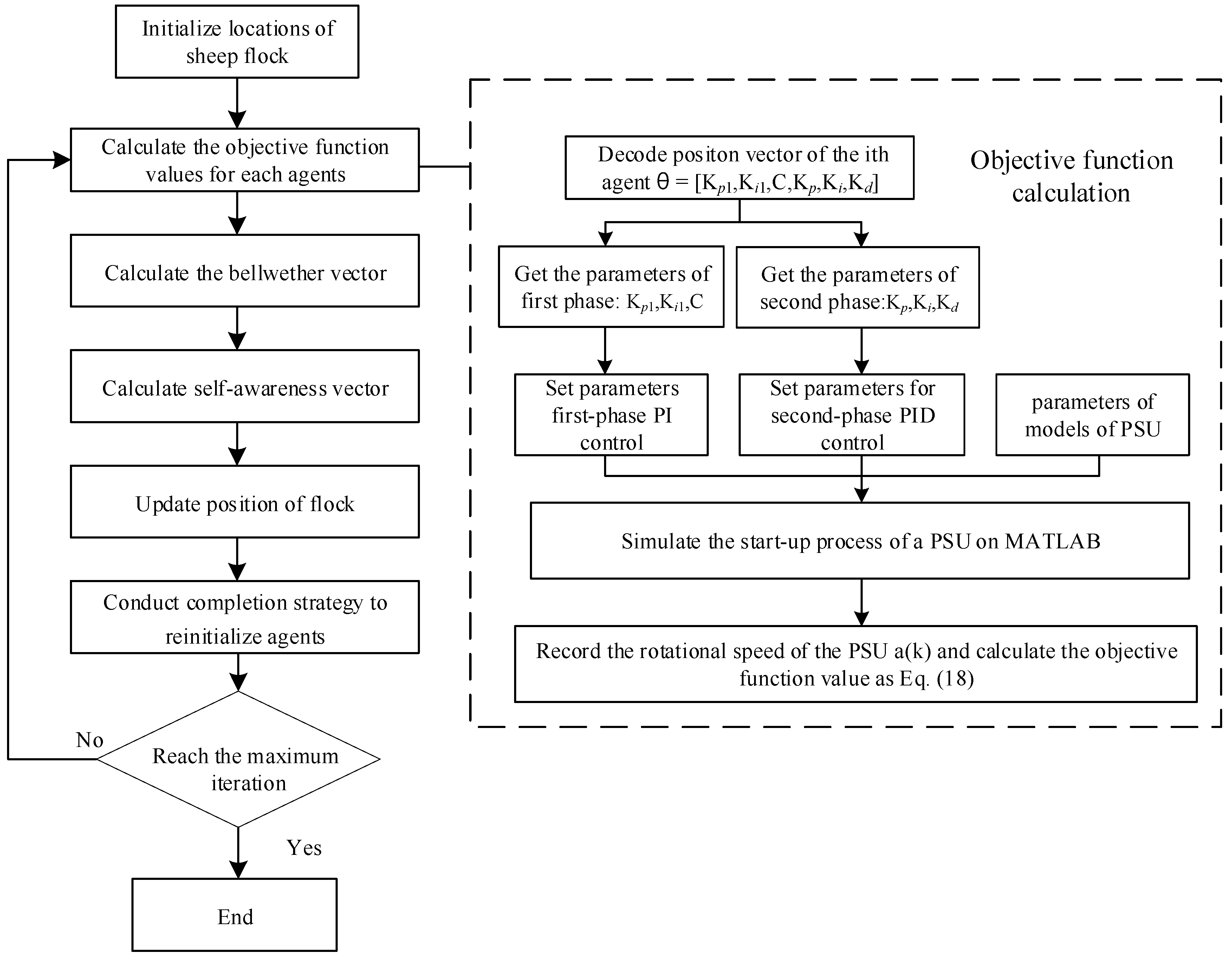
The whole idea and the specific architecture of ASA have been clearly presented in above paragraphs. The flow chart of ASA optimization is illustrated in
Figure 7. Accordingly, the main steps of the ASA is summarized as follows.
Step 1: Initialization. Initialize locations of sheep flock with N sheep in the solution space with boundaries , and calculate the objective function value , i = 1,…,N; set the first sheep as the bellwether ; set other control parameters: the initial scope coefficient of leading and the modulation coefficient of strolling ; set the total number of iteration T, and the current number of iteration t = 0.
Step 2: Calculate the objective function values of agents , i = 1,…,N, and update the bellwether by conducting: if then , .
Step 3: Calculate the bellwether vector , i = 1,…,N, according to the Equation (13).
Step 4: Calculate self-awareness vector , i = 1,…,N, according to the Equation (14).
Step 5: Updating position of flock according to the Equation (15).
Step 6: Judge whether sheep need to be eliminated according to the Equation (16) and reinitialize the same number of new sheep between .
Step 7: t = t + 1; if t > Tmax, end and output bellwether’s position as the final solution; else, go to Step 2.
The ASA is inspired by the behavior of the sheep flock and the complete optimization mechanism of ASA algorithm has been established now.
3.3. Experimental Study and Comparison Results on Benchmark Functions
To evaluate the performance of the proposed ASA, as well as other seven meta-heuristic optimization algorithms, i.e., Particle Swarm Optimization (PSO) [
25], Differential Evolution (DE) [
39], Ant Colony Optimization for continuous domain (ACO
R) [
40], Artificial Bee Colony (ABC) [
41], Cuckoo Search (CS) [
42], Gravitational Search Algorithm (GSA) [
27], and Grey Wolf Optimizer (GWO) [
43], were applied to solve 13 standard benchmark functions. The selected algorithms are representatives of evolutionary, physics-based and SI based meta-heuristics. In these algorithms, the newly developed meta-heuristics are included. The following experiments are conducted on MATLAB (R2016a, MathWorks, Natick, MA, USA).
3.3.1. Benchmark Functions
Table 1 and
Table 2 present the benchmark functions used in our experimental study. The employed benchmark functions can be divided into two groups: unimodal, multimodal test functions with high dimension. The unimodal test functions have only one global optimal value, so they are often used to test the ability of exploitation of algorithms, as shown in
Table 1. The multimodal test functions with high dimension have many local optimal values expect for the global optimum, so they are most difficult to optimize, as shown in
Table 2.
In these tables,
D is the dimension of function,
fopt is the minimum value of the function, and searching space is a subset of
. The minimum value (
fopt) of the functions of
Table 1 and
Table 2 are zero, except for F
8 which has a minimum value of −418.9829 ×
D. The optimum location (
Xopt) for functions of
Table 1 and
Table 2, are in [0]
D, except for F
5, F
12 and F
13 with
Xopt in [1]
D and F
8 in [420.96]
D.
3.3.2. Parameters of Algorithms
A set of fair parameters obtained by a simple trail-and-error procedure was adopted for ASA. For a fair comparison, the recommended parameters of PSO, DE, ACOR, ABC, CS, GSA and GWO were used to tackle these problems. In order to conduct a fair comparison, the maximum number of iteration was chosen to 1000 and the population size of all algorithms was set to 30 (i.e., N = 30) in all experiences in this section. Other parameters of the comparative algorithms were set as follows:
3.3.3. Comparison Results on Benchmark Functions
All experiences were repeated 30 times independently. The mean value, the best value, as well as the standard deviation, of the optimal objective function values of 30 runs, were reported for unimodal functions in
Table 3 and for multimodal test functions with high dimension in
Table 4.
The unimodal test functions are relatively simple to optimize because they only have one global optimal value. From
Table 3, it is clear that the ASA has a very good performance for the unimodal test functions. The ASA algorithm shows obvious advantage over the competitors in the remainder of high dimension unimodal functions, except for F
4 and F
6. The multimodal test functions with high dimension are relatively difficult to optimize because they have many local optimal values and one optimal global value. The ASA also has significant performance, as shown in
Table 4. Generally, the ASA algorithm has shown an obvious advantage over the competitors on high dimensional benchmark functions F
1–F
13. Furthermore, optimization processes of the comparative algorithms were given in
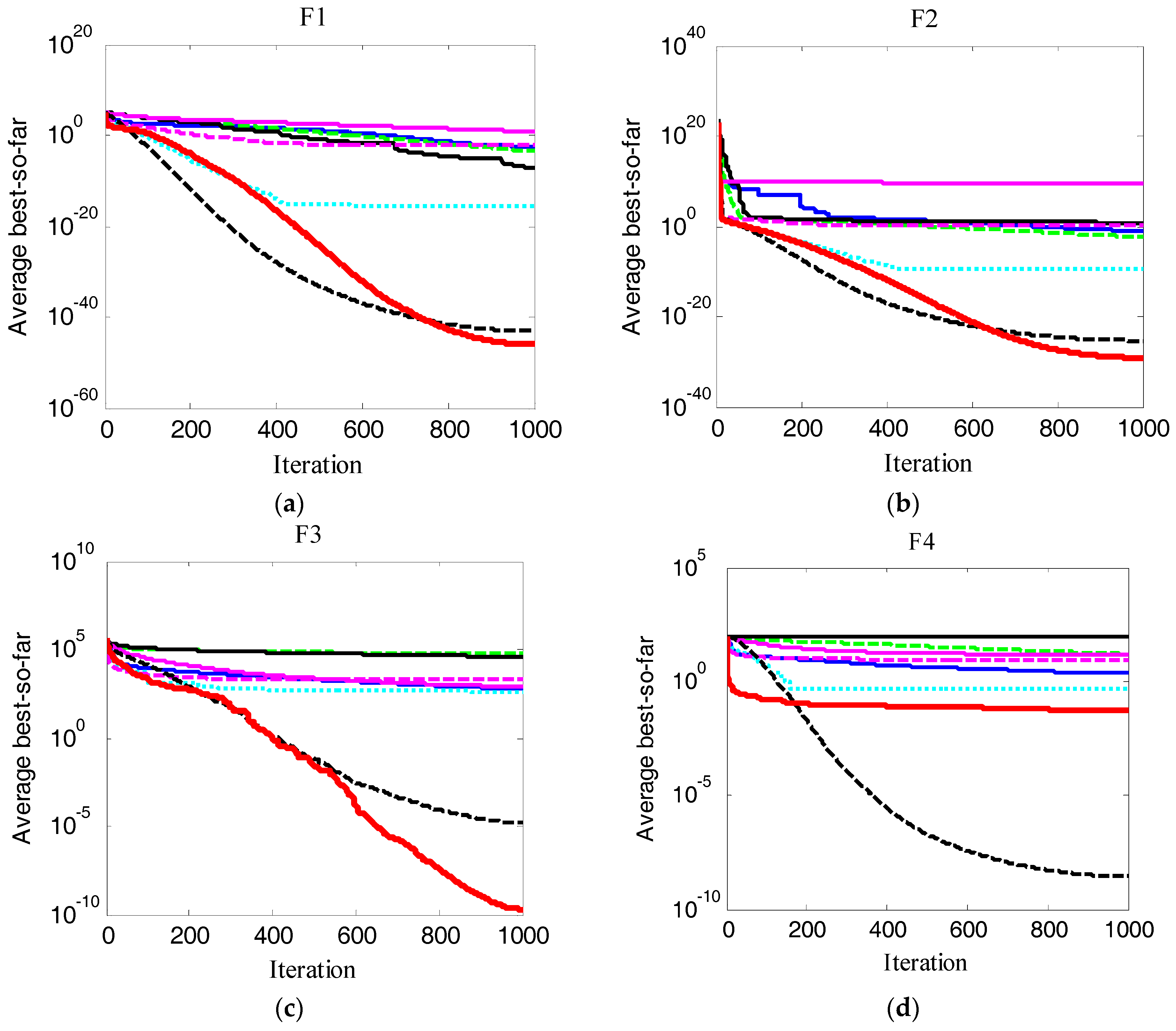
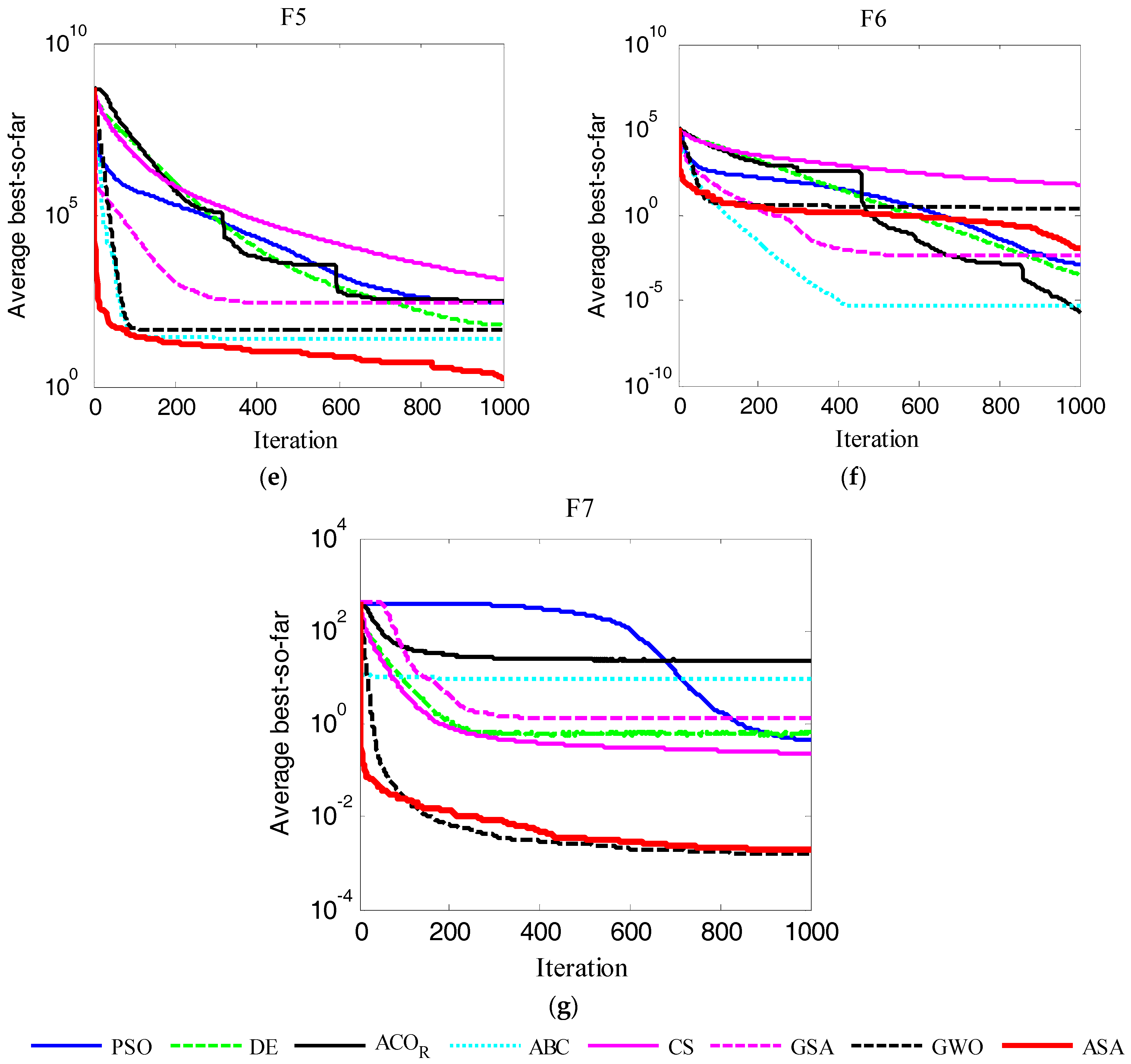
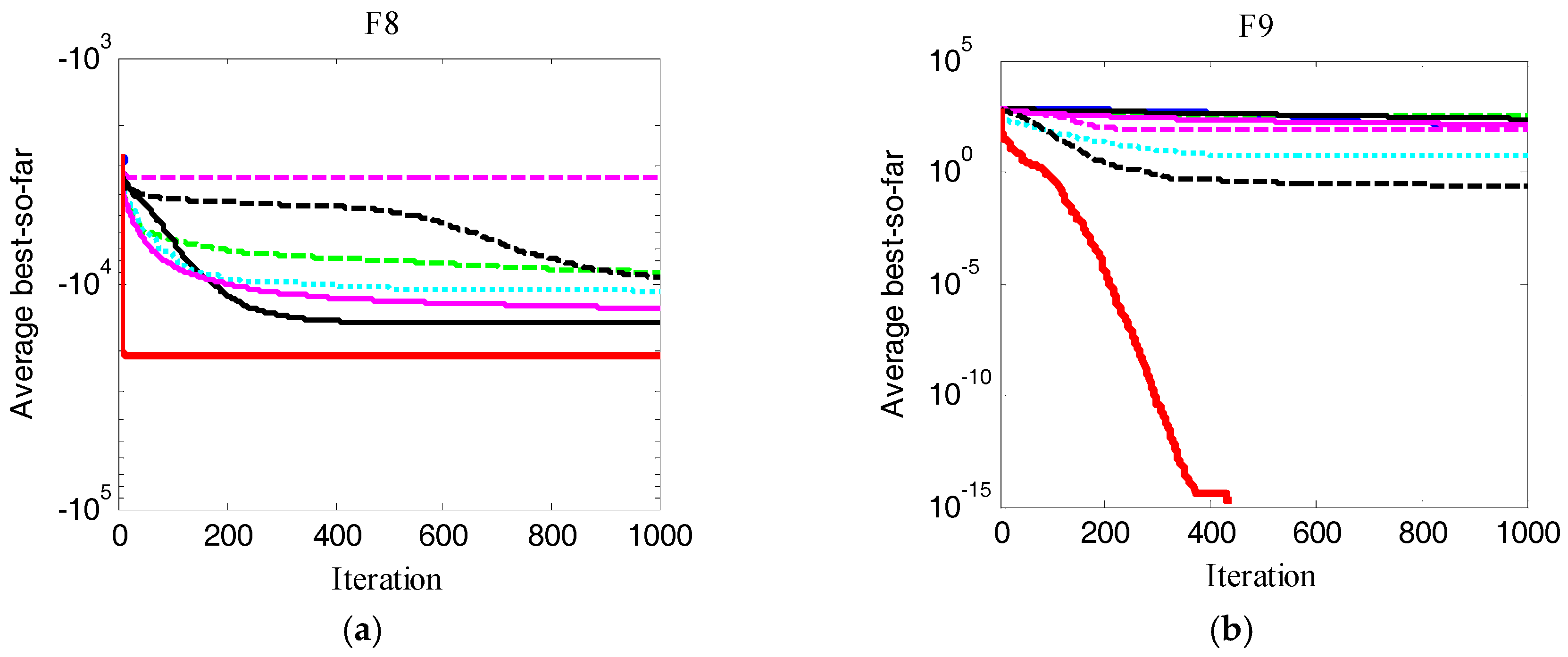
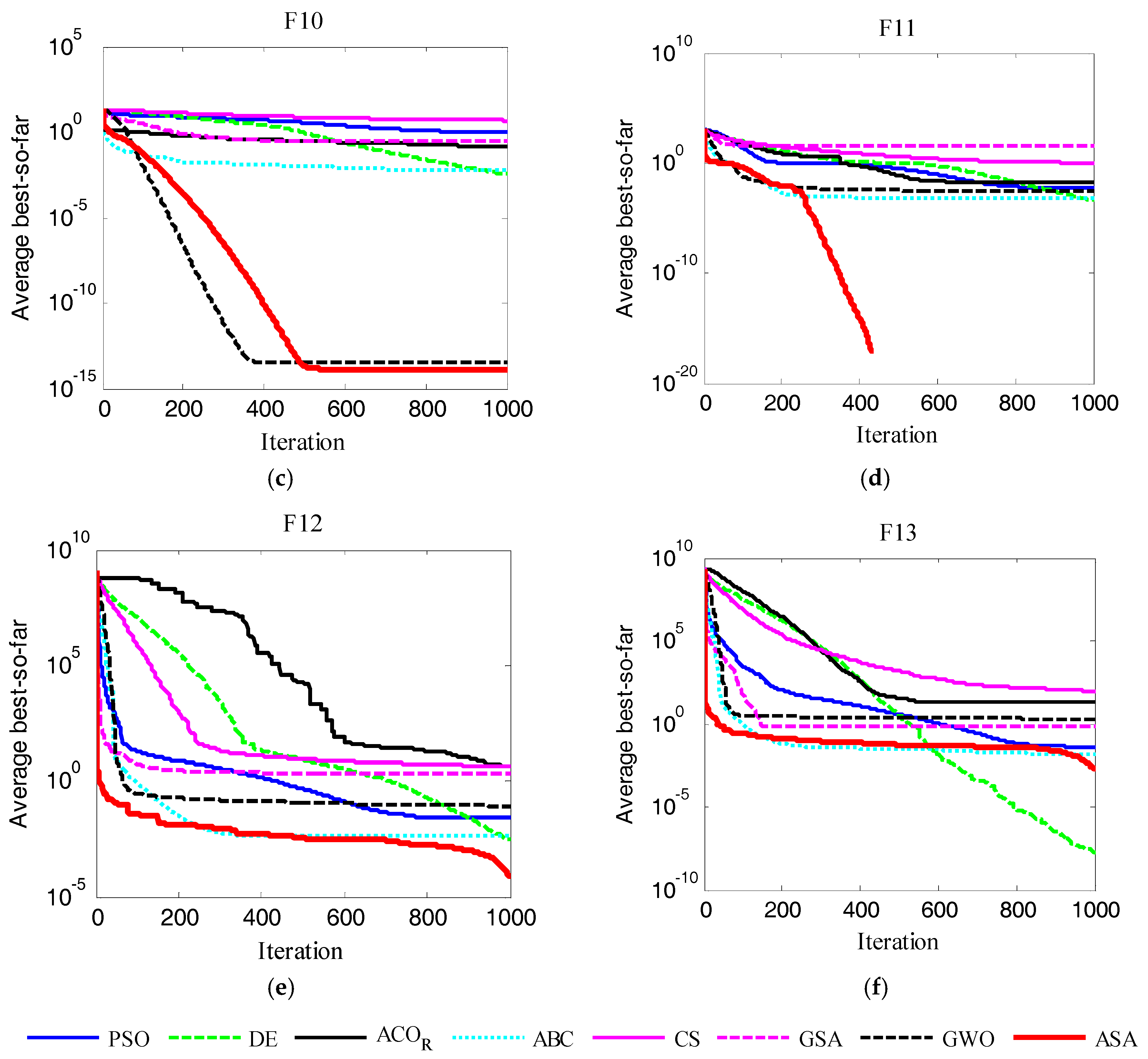
Figure 8 and
Figure 9. The values shown in these figures were the average of “best so far” in iterations achieved from 30 runs. The “best so far” is the best objective function value searched by the artificial sheep flock at certain iteration.
Figure 8 shows the average “best so far” in iterations obtained by the eight methods on the unimodal functions F
1–F
7. From
Figure 8 ASA performance is superior to the seven methods in the optimization process on all high dimensional unimodal functions except for F
4 and F
6.
Figure 9 shows the average iteration processes obtained by the eight methods on the multimodal functions F
8–F
13. From
Figure 9, it is demonstrated that ASA performs the best compared with another seven methods on F
8–F
12. ASA has advantages over other algorithms, except for DE, in the optimization process of F
13. From these figures, it was seen that the ASA had a faster converge speed compared with other approaches. In particular, ASA had a very good performance on high dimensional test functions.
4. An Integrated Start-Up Method for Pumped Storage Units
4.1. Traditional Start-Up Strategies of a PSU
The traditional start-up method of a PSU contains two phases. In the first phase, the control system of the PSU is open-loop, in which the feedback signal of rotational speed of pump-turbine is not adopted and used for control. In this phase, the control system undertakes a kind of direct guide vane control (DGVC). After receiving the start-up command, governor will control the guide vane to tract a DGVC trajectory. As the rational speed of pump-turbine increase to a threshold value, the second phase starts. At that moment, the control system is closed-loop, while the feedback signal of pump-turbine speed is used for control. The system is then under a speed control mode. In the second phase, PID control is adopted for the purpose of adjusting and maintaining the stability of pump-turbine speed referring to the rated speed.
4.1.1. The First Phase: Direct Guide Vane Control
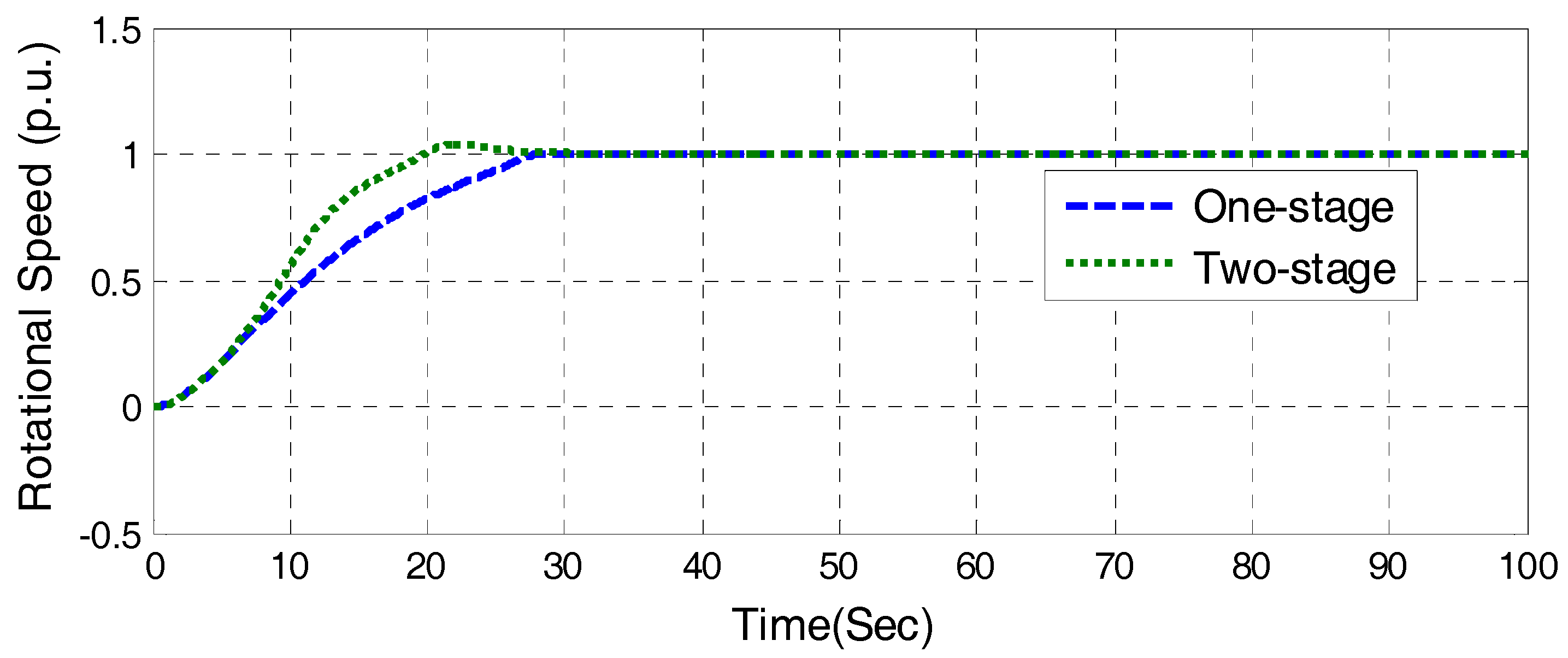
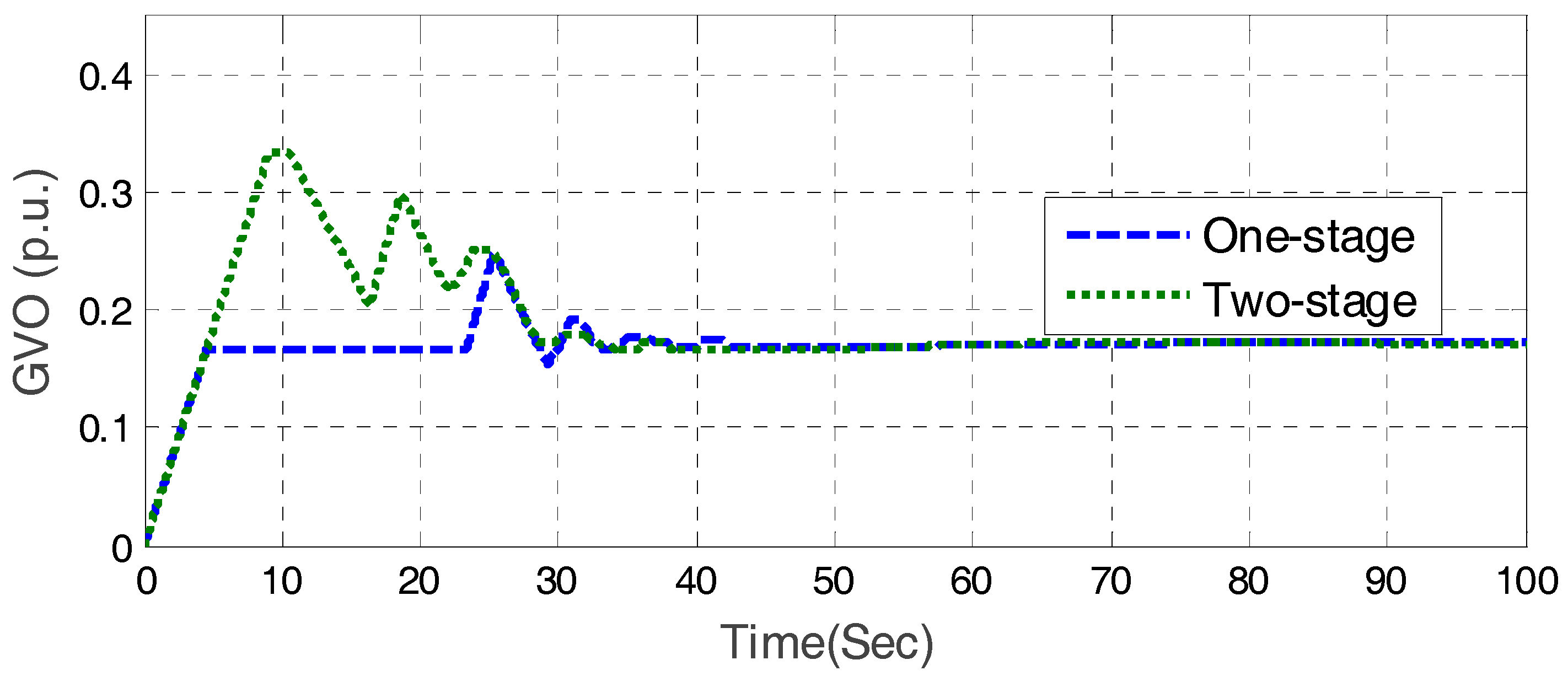
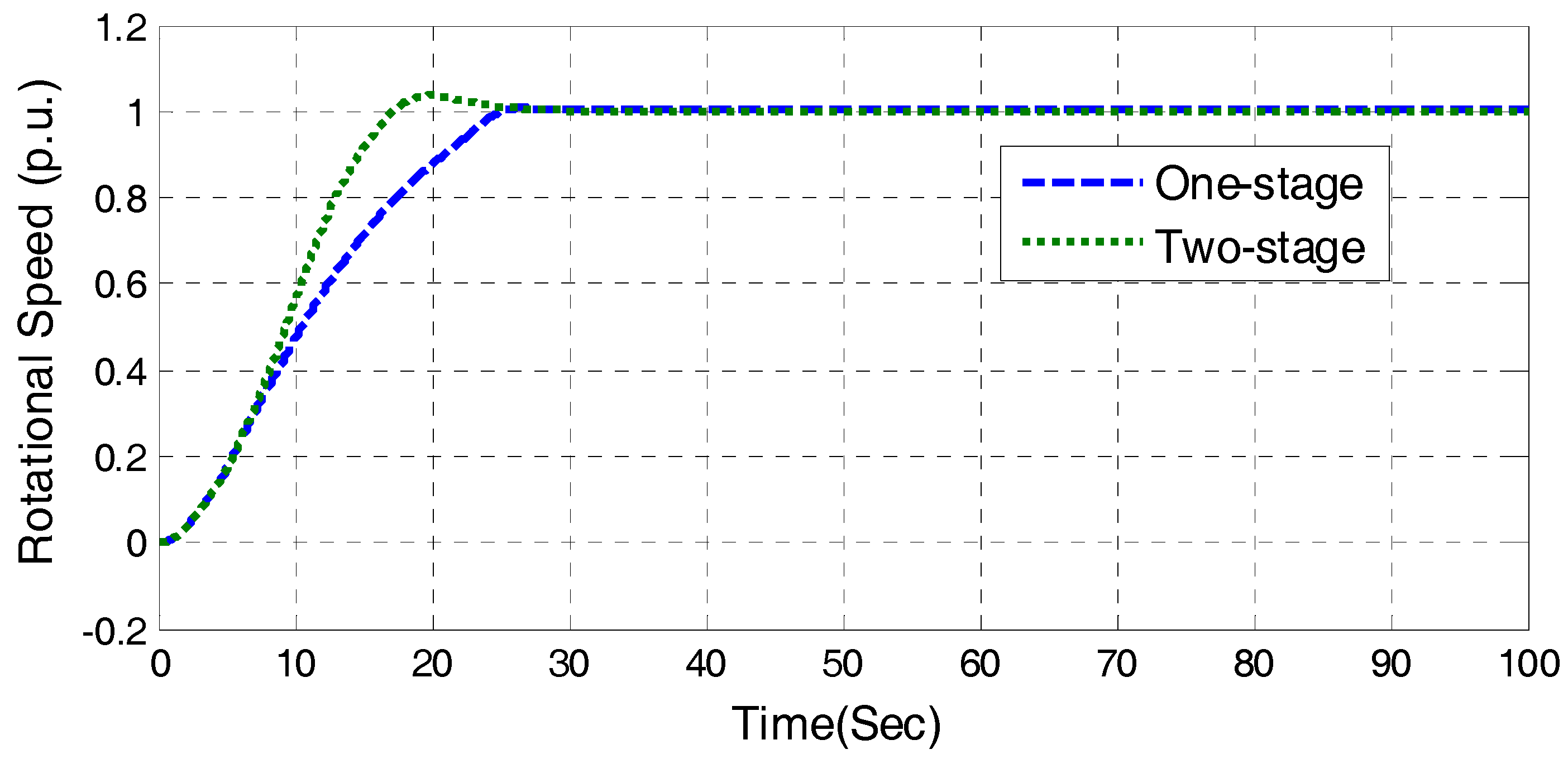
One-stage DGVC
The guide value opens as the highest speed to no-load opening, while the rotational speed of unit will increase. As the speed reaches 90% of the rated value, a closed-loop PID control will be switched on to adjust and maintain the stability of speed for grid connection. The one-stage DGVC is illustrated in
Figure 10.
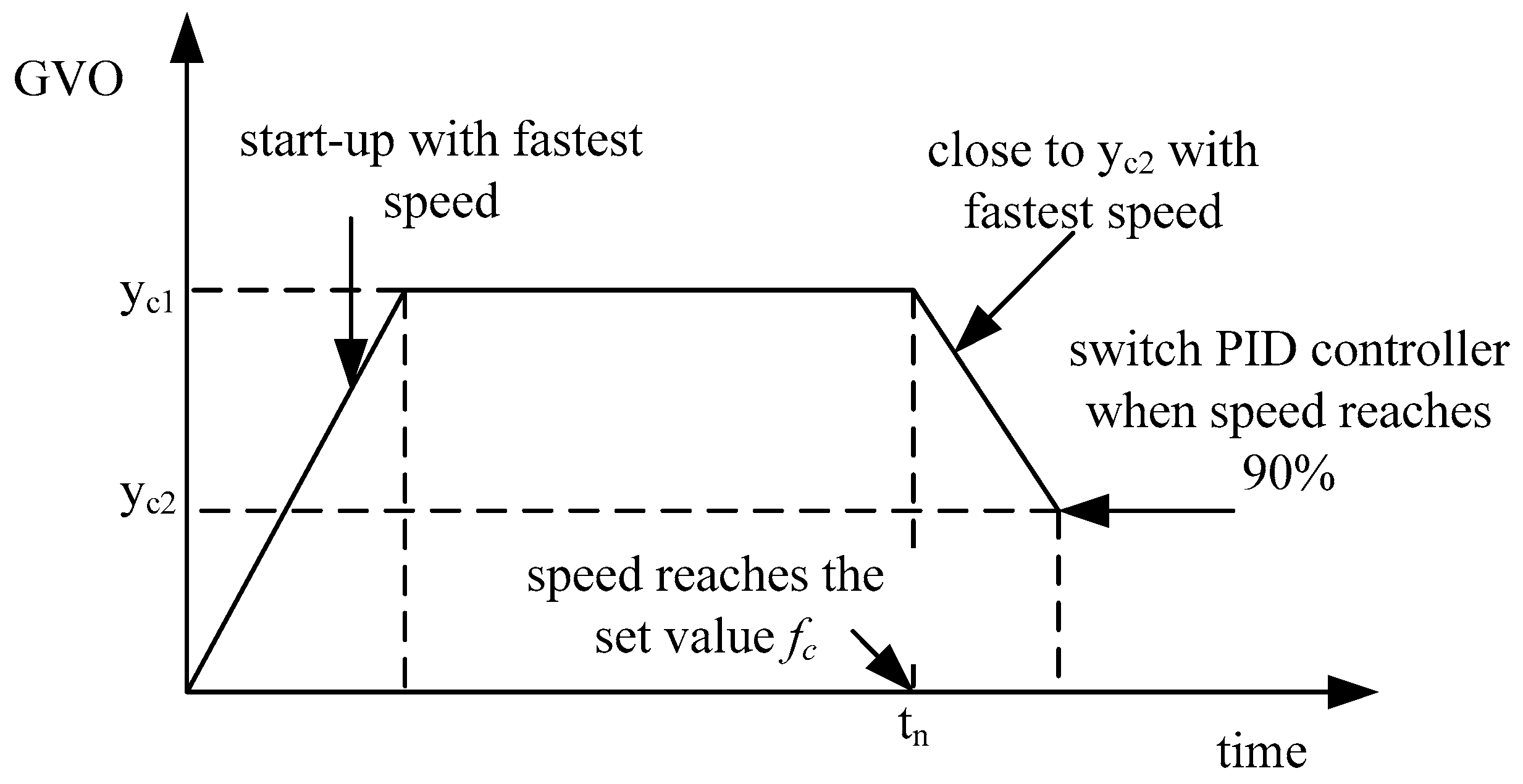
Two-stage DGVC
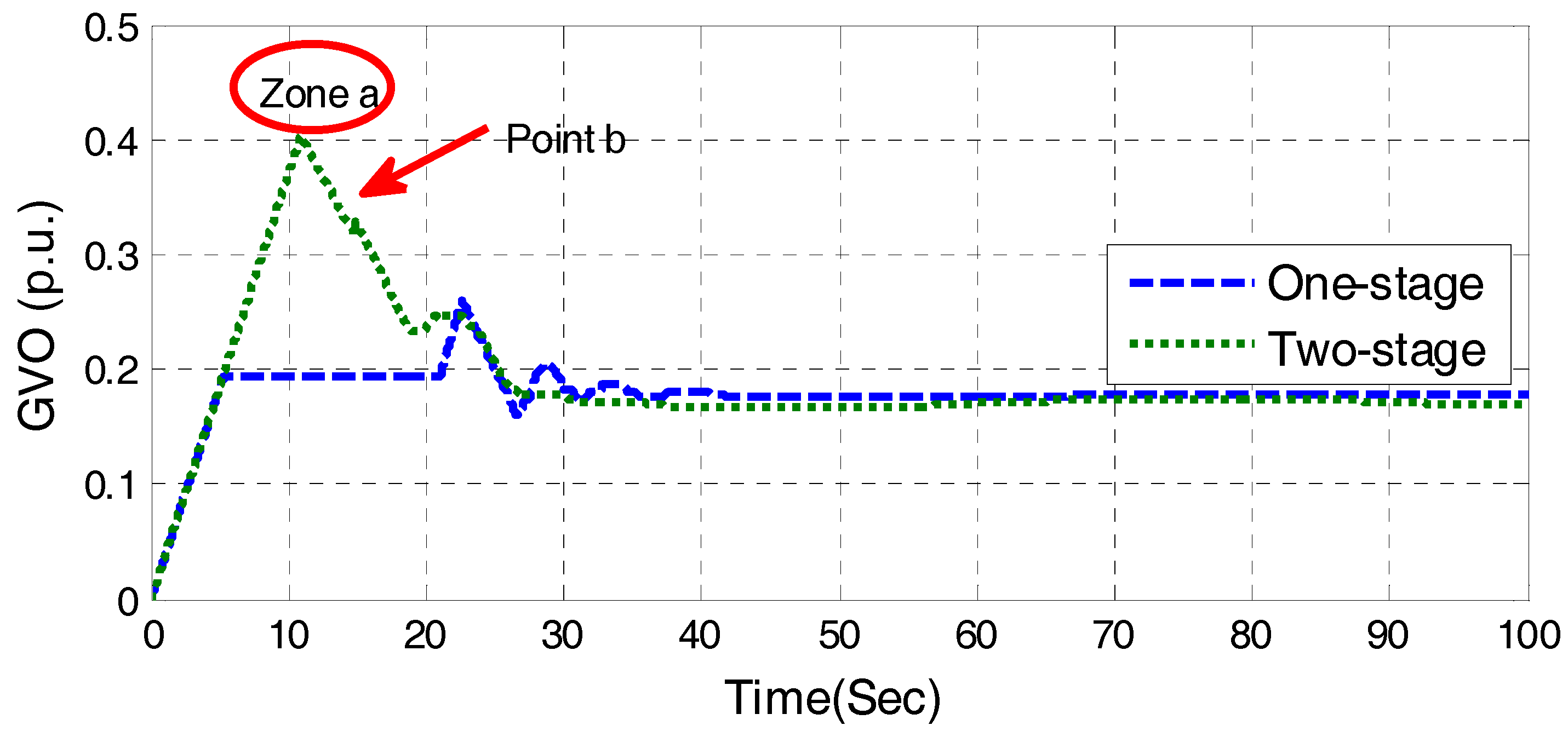
The guide vane opens rapidly to start opening (opening is about twice as much as the no-load opening) with the fastest speed, and keep the opening for a period, until the speed rises to a set value
nc (
nc is usually 60% of the rated speed). The guide vane opening is then adjusted to the no-load opening immediately. After the speed reaches 90% of the rated value, the PID control is switched on. The illustration of the two-stage DGVC is shown in
Figure 11.
4.1.2. The Second Phase: PID Control
As mentioned above, following the open-loop direct guide vane control, the closed-loop PID control will be switched on when the pump-turbine speed reaches a threshold value, which is usually set as 90% of the rated speed. Though the PID controller is a very traditional design, it is still one of the favorite and most widely used controllers for many industrial process control applications. This is due to its simple structure, satisfactory control effect and acceptable robustness [
45,
46]. The PID controller is easier to understand due to intuitive simplicity of the algorithm and simple meaning of its tuning parameters proportional (
Kp), integral (
Ki) and derivative (
Kd).
In the following, the start-up strategy composed of open-loop one-stage DGVC and closed-loop PID control is named the one-stage start-up strategy. The start-up strategy composed of open-loop two-stage DGVC and closed-loop PID control is named the two-stage start-up strategy.
4.2. Optimization Variables for Start-Up Strategies
In order to improve the start-up performance, the parameters in the start-up strategies could be optimized. Traditionally, PID control parameters are often optimized to enhance the control performance for a quick and smooth PSU start-up. The tuning parameter vector for a PID controller is .
The parameters of the DGVC could also be optimized, though this has seldom been researched. For a one-stage DGVC, the maximum value yc and the rising slope of guide vane kc can be used as parameters to be optimized, as . The parameters to be optimized of a two-stage DGVC are the maximum value of the guide vane opening yc1, the minimum value after guide vane closure yc2 and the set frequency fc when the guide vane began to decrease, as .
In this paper, optimization experiments of the traditional two-phase start-up strategies are grouped into two categories:
Scheme A: optimization of PID controller. In practice, parameters of the DGVC are set as a rule of thumb. The PID parameter vector is optimized. In these categories, one-stage DGVC and two-stage DGVC can be selected corresponding.
Scheme B: optimization of DGVC. DGVC parameters are optimized, the parameters of PID controller are kept the same as the optimized parameters of Scheme A.
4.3. An Integrated Start-Up Method
In order to improve the performance of the start-up process of PSUs, a new integrated start-up strategy and the relevant optimization method are proposed. This strategy is composed of two phases, in which a closed-loop PI control, instead of the open-loop GVO control, is applied in the first phase to open GVO, and a closed-loop PID control is switched on once the speed reaches the threshold. In the first phase, a closed-loop PI control is conducted to open the GVO to accelerate the rotational speed, while the control target is to keep the ratio of differential speed and speed deviation to be a constant:
where
dΔ
a/
dt is the speed differential speed; Δ
a is deviation of speed. When the speed is close to the rated speed (about 98% of the rated speed), the governor will switch to the PID controller to track the rated speed.
Parameters of the integrated start-up strategy can be optimized synchronously. Parameters of the first phase include parameters Kp1, Ki1, of PI controller, and the constant C in Equation (17). Parameters of the second phase are that of PID controller, Kp, Ki, and Kd. Therefore, the optimization vector is .
4.3.1. Objective Function
The objective function for start-up strategy optimization is an integral performance index to evaluate the control performances, including overshoot and start-up time. The Integral Time Absolute Error (ITAE) [
47] index is used as the objective function as defined by:
where
is parameter vector to be optimized,
k is the sample number,
Ns is the number of samples,
T(
k) is the sample time,
a(
k) is the relative value of unit speed.
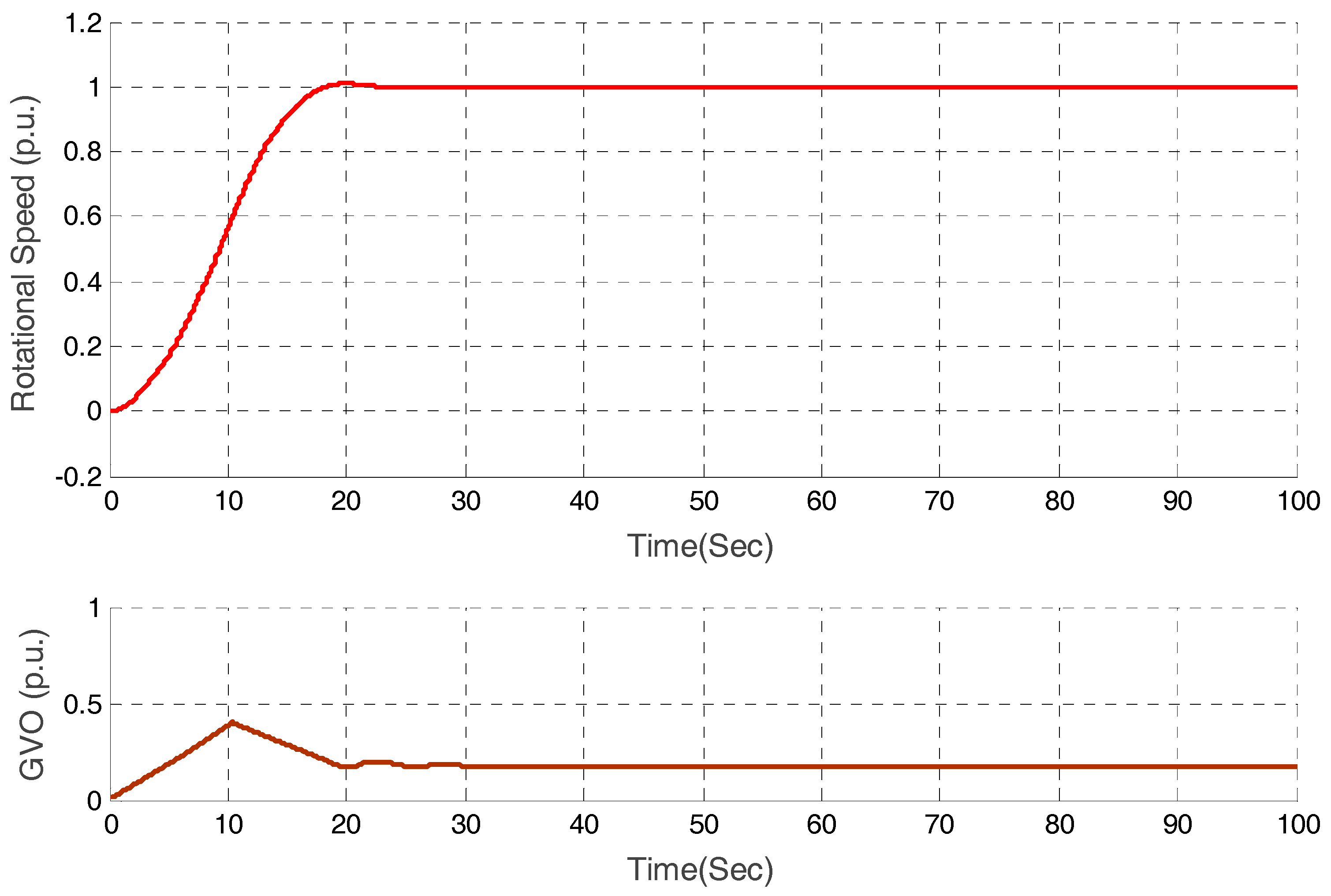
In order to assess the performance of the proposed integrated start-up methods quantitatively, three indices about overshoot, start-up time and steady-state error are presented:
amax is the relative value of the peak speed,
ts called the start-up time is the corresponding time when the relative value of the speed reaches rated relative speed 1 and the steady-state error means the deviation of the actual rotational unit speed and rated relative speed 1 that can’t be eliminate. Here, considering the constraints of the experiment, we choose the steady-state error at 100 s. The specific description is shown in
Figure 12.
4.3.2. Procedures
In the proposed method, the ASA is used to optimize the objective function, while optimization parameters are elements in
. As for optimization of traditional start-up strategies, i.e., Scheme A and Scheme B, the objective function is also selected as the ITAE function, while the optimization vectors are
,
, respectively. Take optimization of the integrated start-up strategy as an example, the detail flow chart of start-up strategy optimization based on the ASA is shown in
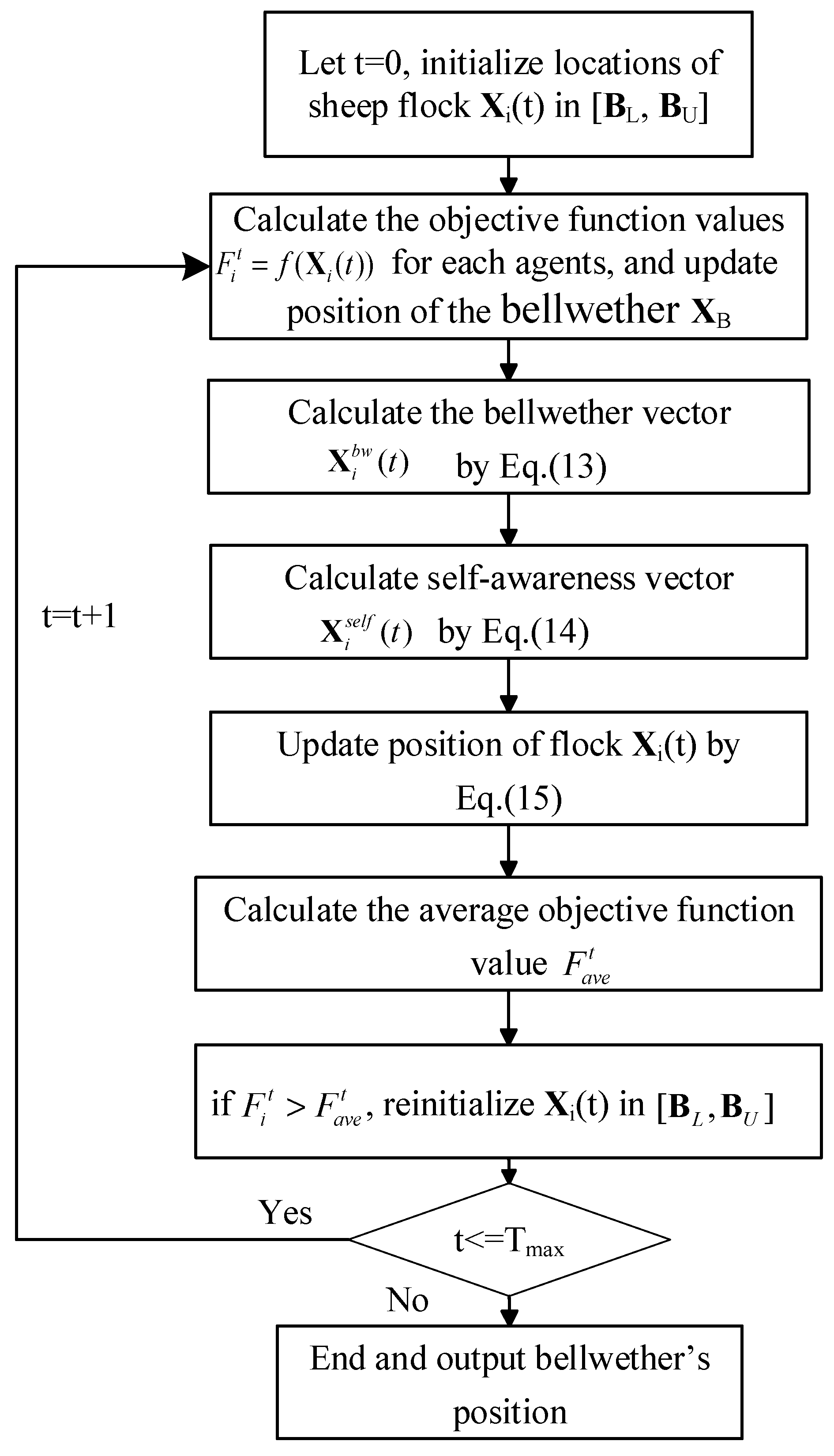
Figure 13. To illuminate the procedures briefly, the main steps are summarized as follows.
Step 1: Initialization. Initialize locations of a sheep flock with N sheep in the solution space with boundaries , set the first sheep as the bellwether , ; set other control parameters: the initial scope coefficient of leading and the modulation coefficient of strolling ; set the total number of iteration Tmax, and the current number of iteration t = 0.
Step 2: Objective function calculation. For the ith (i = 1, .., N) agent, the objective function value is calculated as three steps:
Step 2.1: Decode Xi, and get the control parameters of the first phase Kp1, Ki1, and C, and parameters of second phase Kp, Ki, Kd.
Step 2.2: Set these parameters for controllers and start the established PTGS simulation plant to simulate the start-up process of PSU; sample and record system outputs including the unit speed a(k), opening of guide vanes y(k).
Step 2.3: Calculate the objective function value by Equation (18), and let .
Step 3: Implement other iterative procedures of ASA as described in Section 3.2;
Step 4: Set, t = t + 1; if t > Tmax, stop simulation and output bellwether’s position as the final solution; or else, go to Step 2.
6. Conclusions
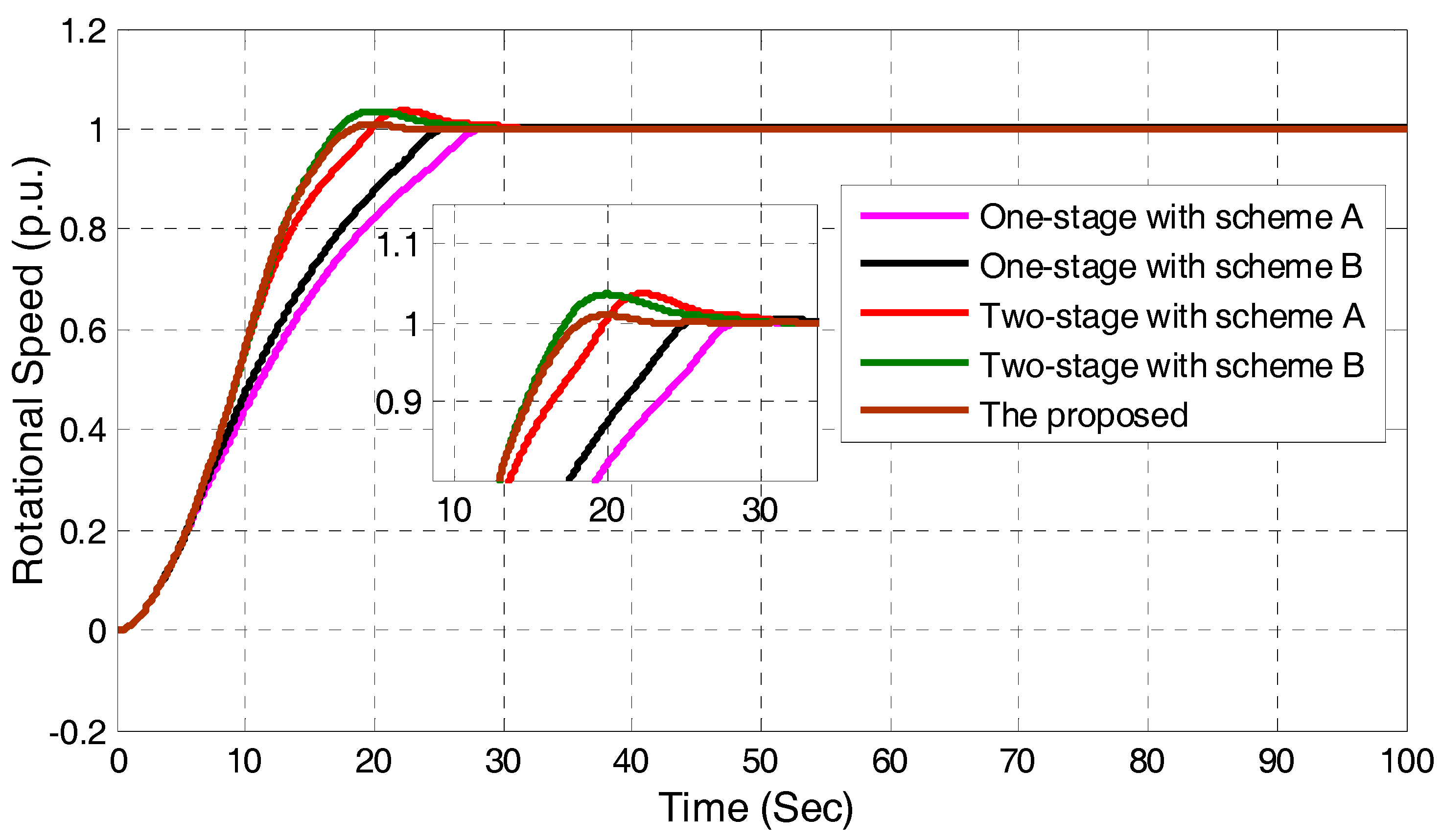
In order to improve the start-up process indices, a new integrated start-up method is proposed. In this method, a two-phase closed-loop start-up strategy is designed, while PI control is applied to quickly open the guide vane with a specially designed control target in the first phase, and PID control is adopted to adjust the rotational speed of a PSU to track the rated value in the second phase. What’s more, an integrated optimization method is used to synchronously tune the parameters of the PI and PID controllers.
To solve this complicated optimization problem, the ASA, a novel meta-heuristic that mimics the social behaviors of sheep, has been proposed and fully verified by comparing it with seven popular meta-heuristics on 13 typical benchmark functions. The results show that the ASA significantly outperforms all competitors for high dimension numerical functions.
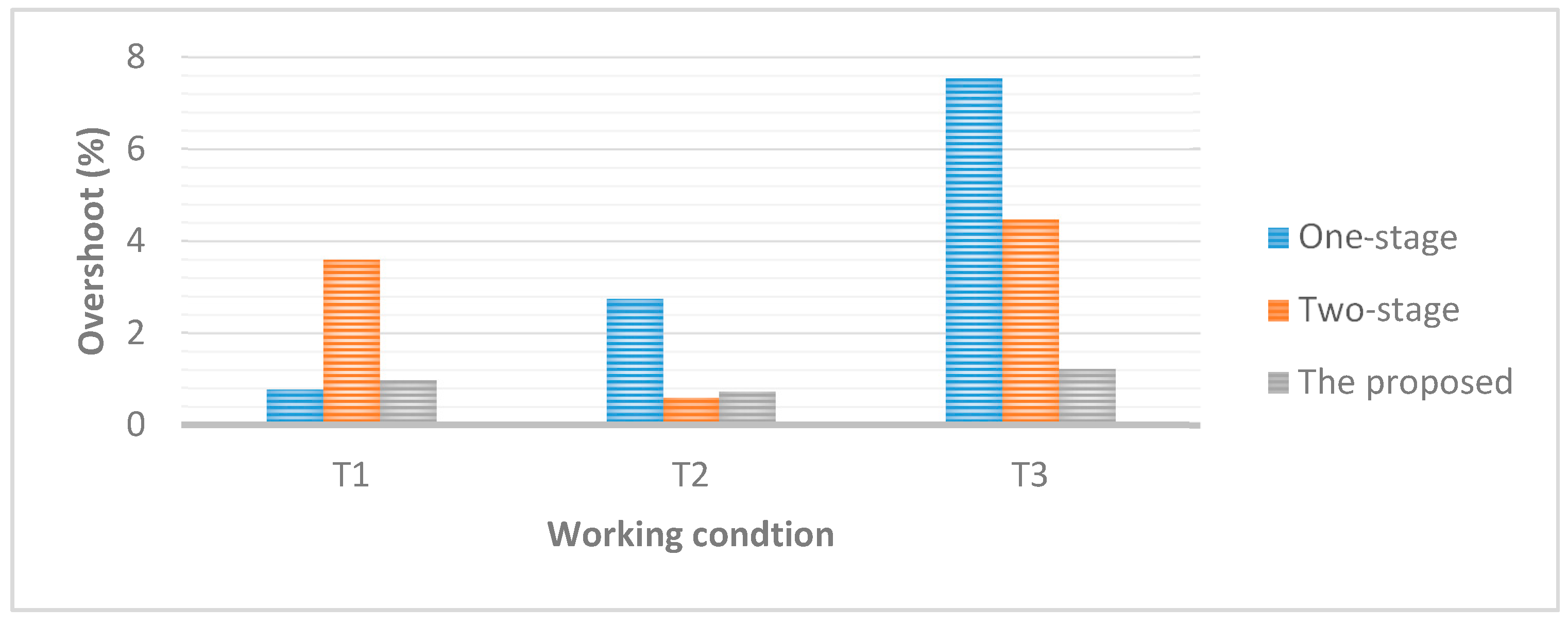
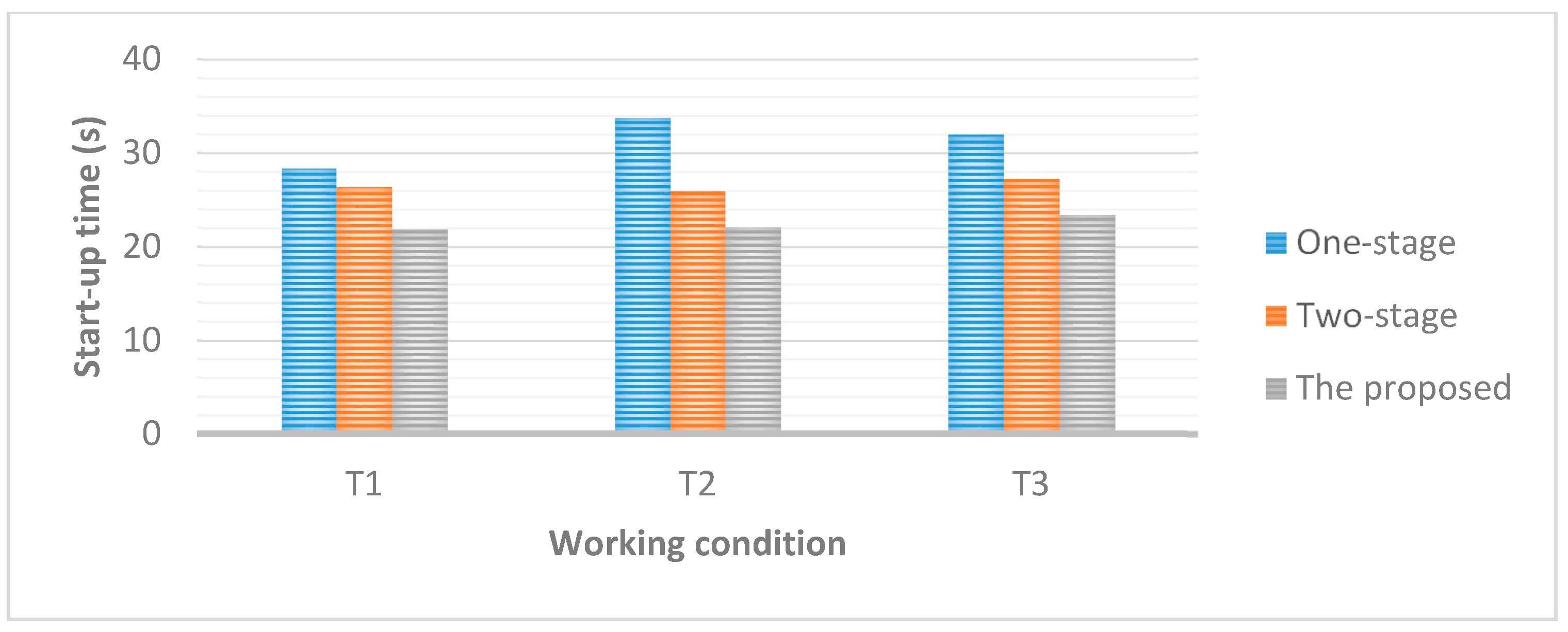
Based on the mathematical model of PSUs, the control system, PTGS, has been modeled and simulated in MATLAB, and simulation experiments on different start-up strategies have been conducted. The proposed method has been compared with the traditional one-stage DGVC, and two-stage DGVC strategies with different optimization schemes. The experimental results have revealed that the proposed integrated start-up method shows great advantages in terms of performance indices, i.e., overshoot, start-up time, compared with the traditional start-up strategies. The start-up time could be improved by as much as 34%, while maintaining the overshoot under a low level. The significant improvements on these key indices is interesting and merit further application in real PSUs.