Using a Multiobjective Approach to Compare Multiple Design Alternatives—An Application to Battery Dynamic Model Tuning
Abstract
:1. Introduction
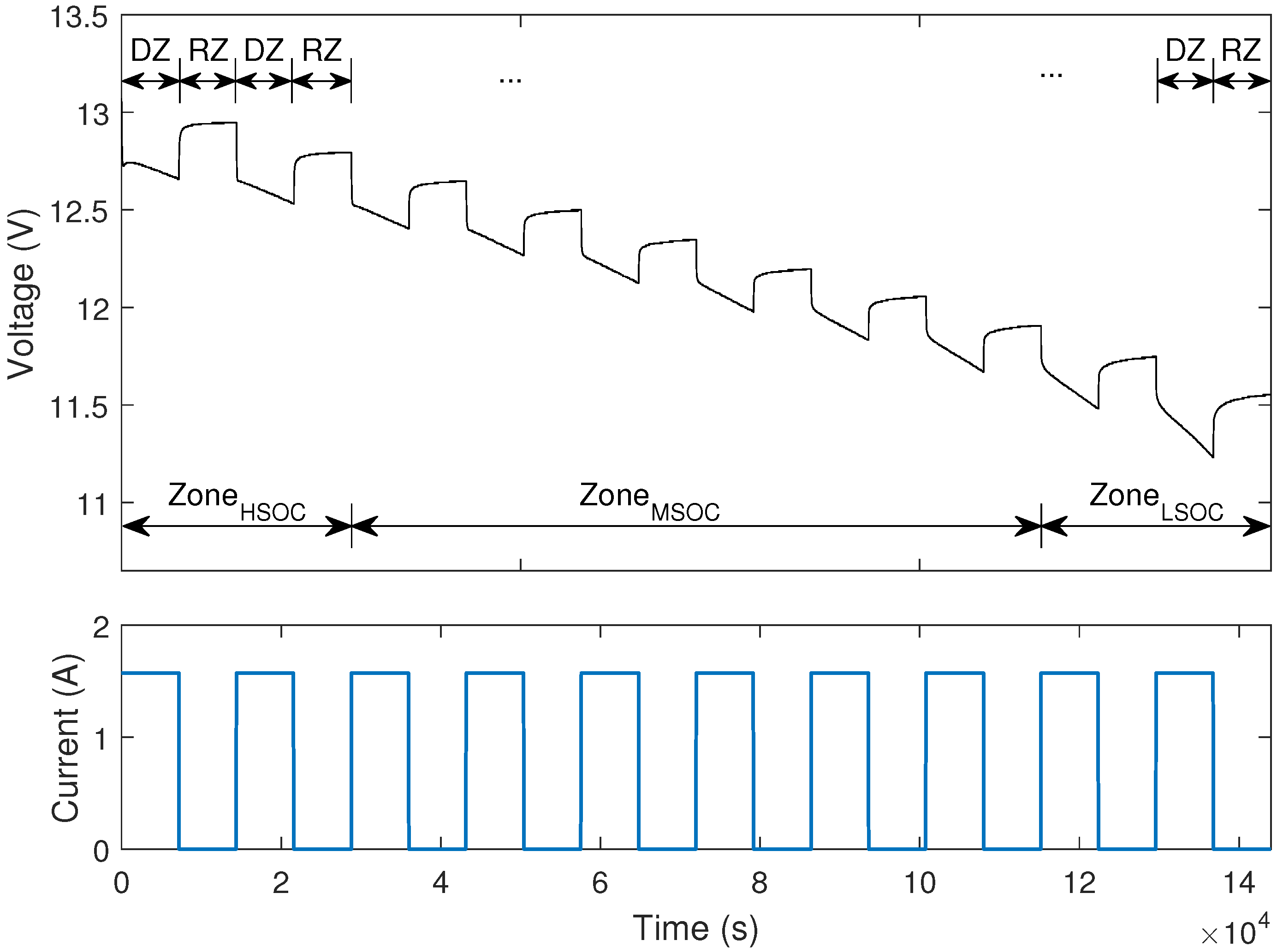
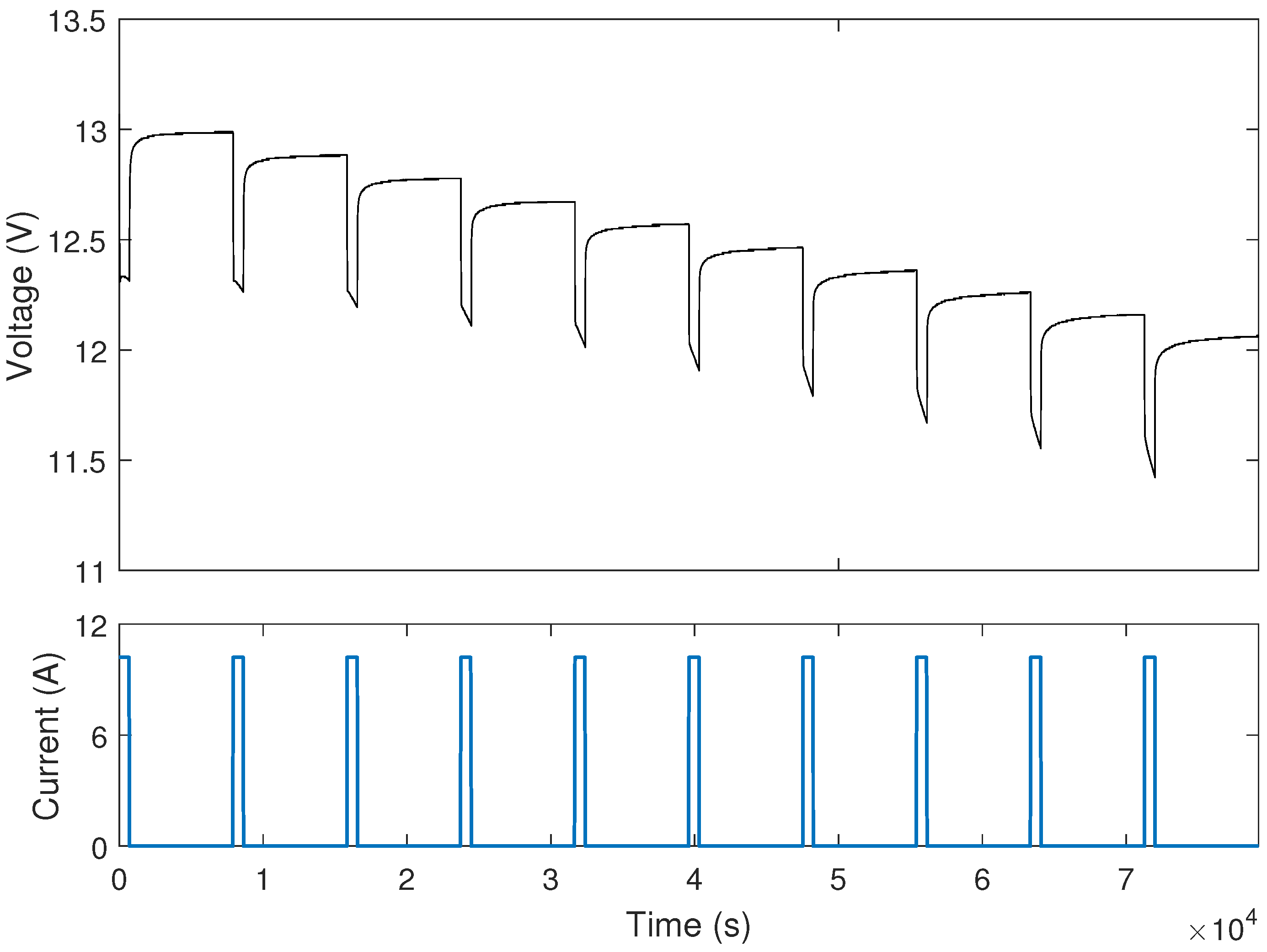
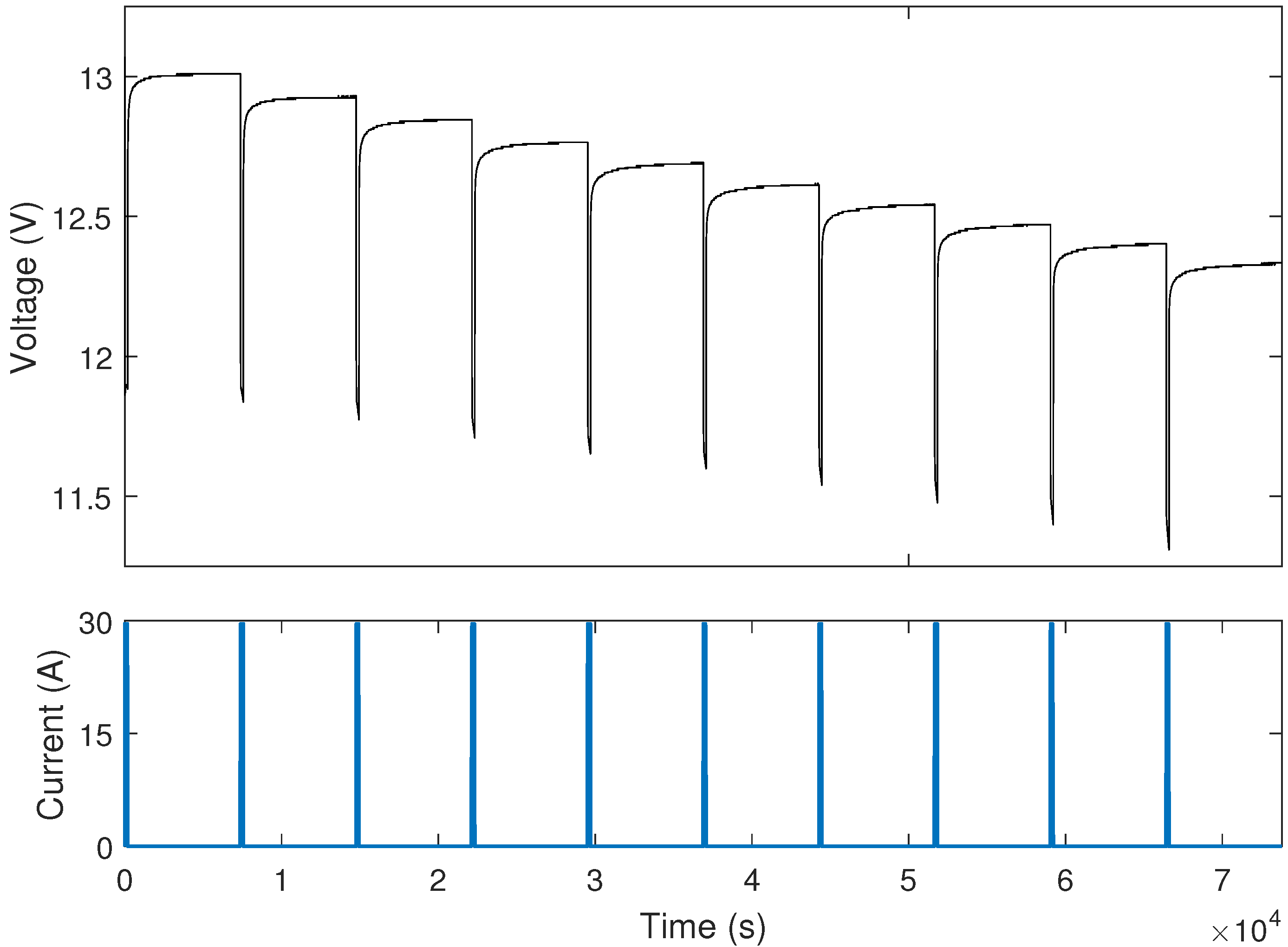
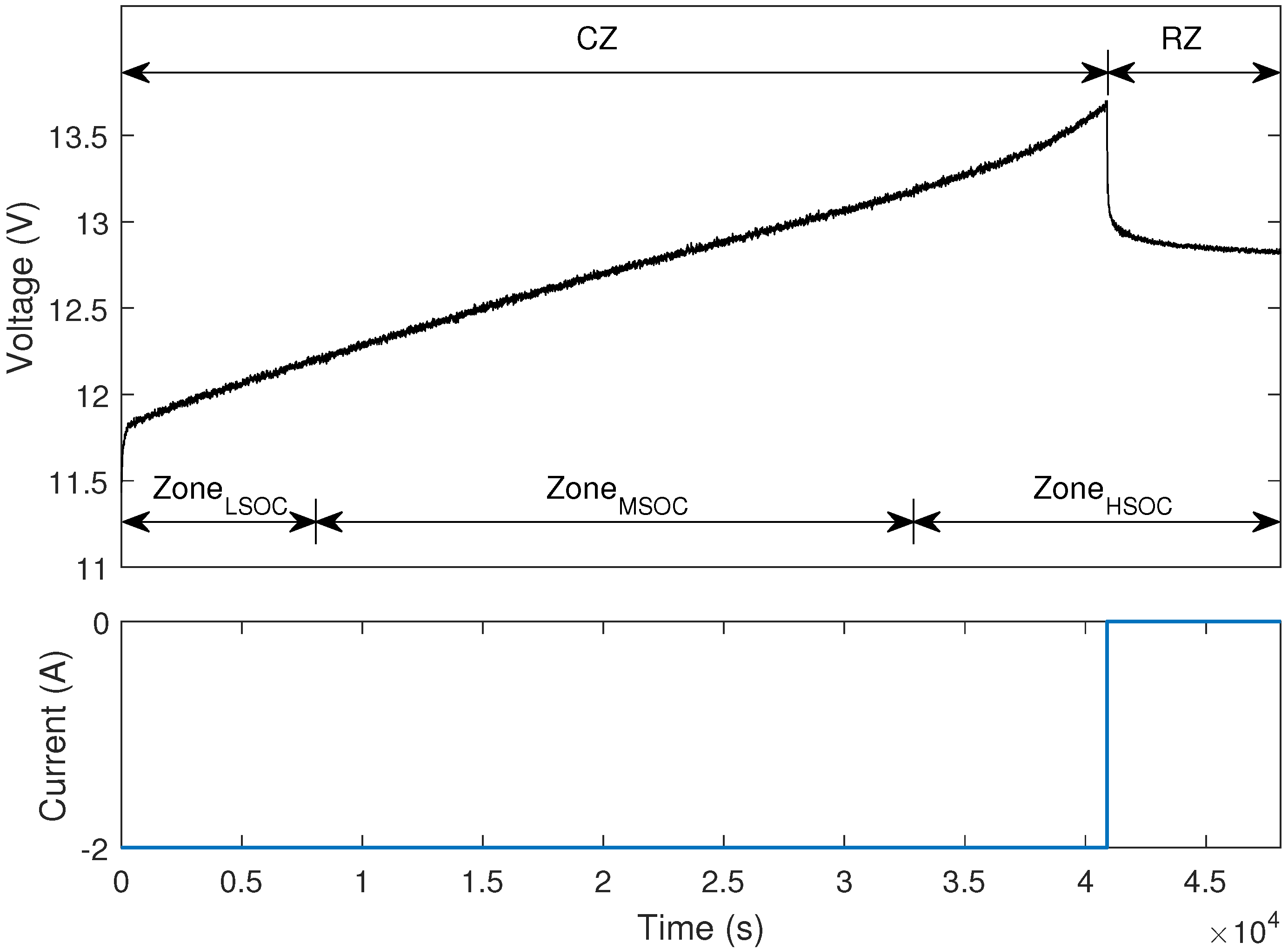
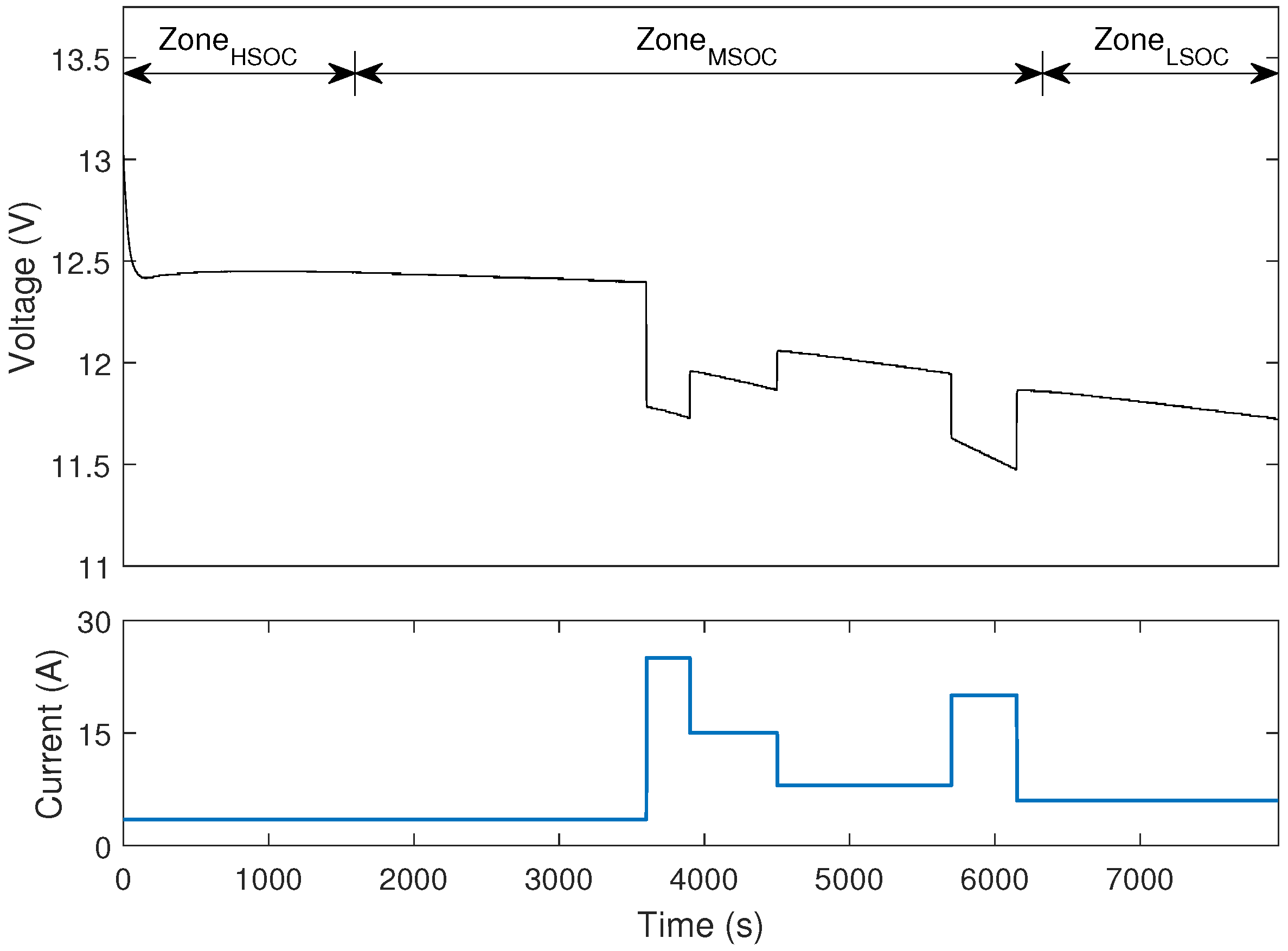
2. Experimental Tests
3. Dynamic Models of the Battery
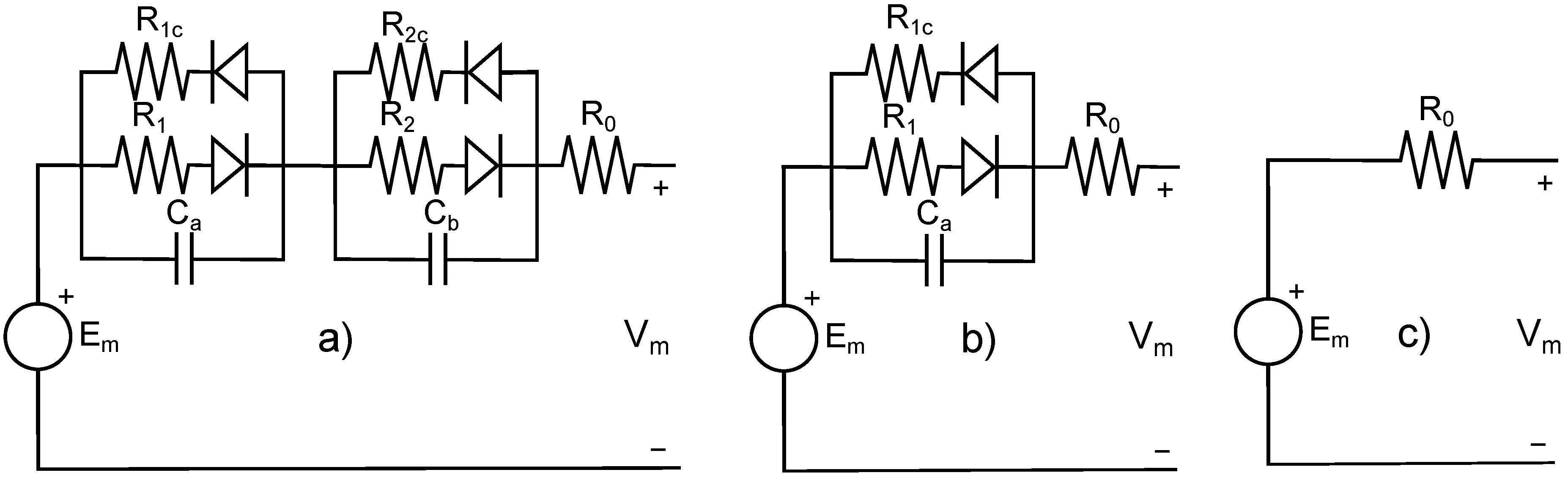
3.1. Complete Model
3.1.1. Open Circuit Voltage
3.1.2. State of Charge
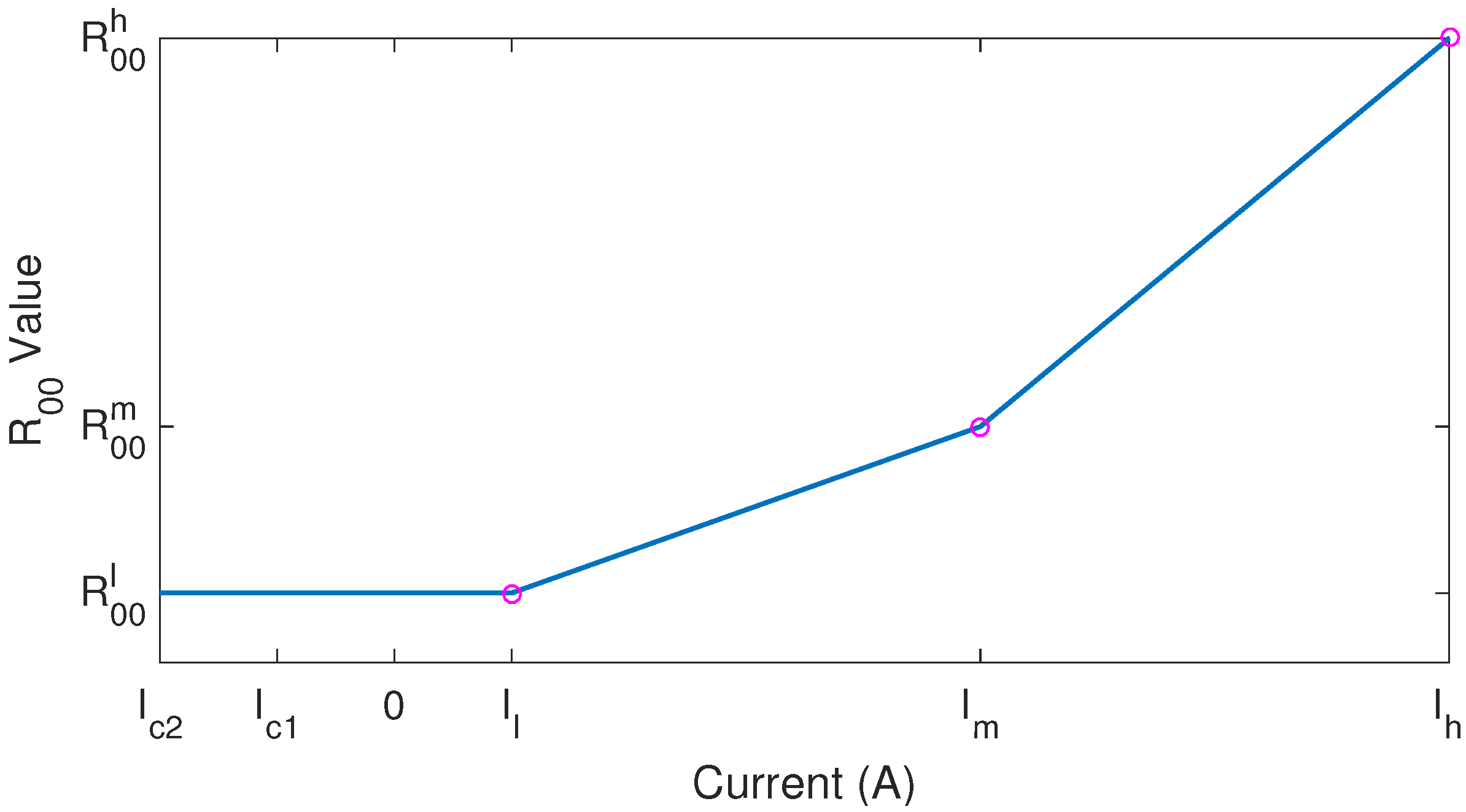
3.1.3. Resistance
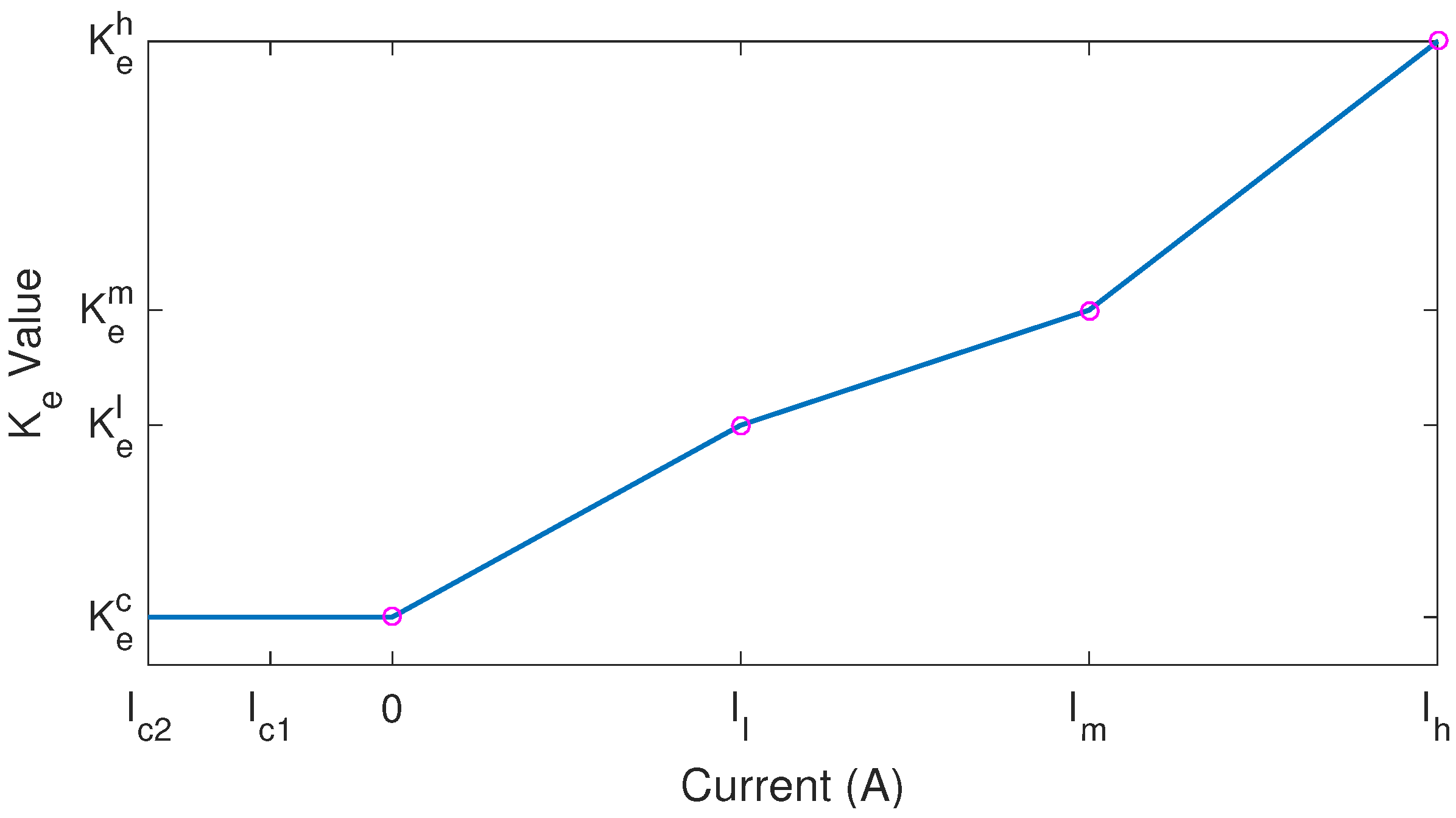
3.1.4. First RC Circuit (, and )
3.1.5. Second RC Circuit (, and )
3.2. Intermediate Model
3.3. Simple Model
4. Multiobjective Optimization Problem For Electrical Model Identification
4.1. Decision Space
4.2. Objectives
4.3. The Multiobjective Optimization Problem
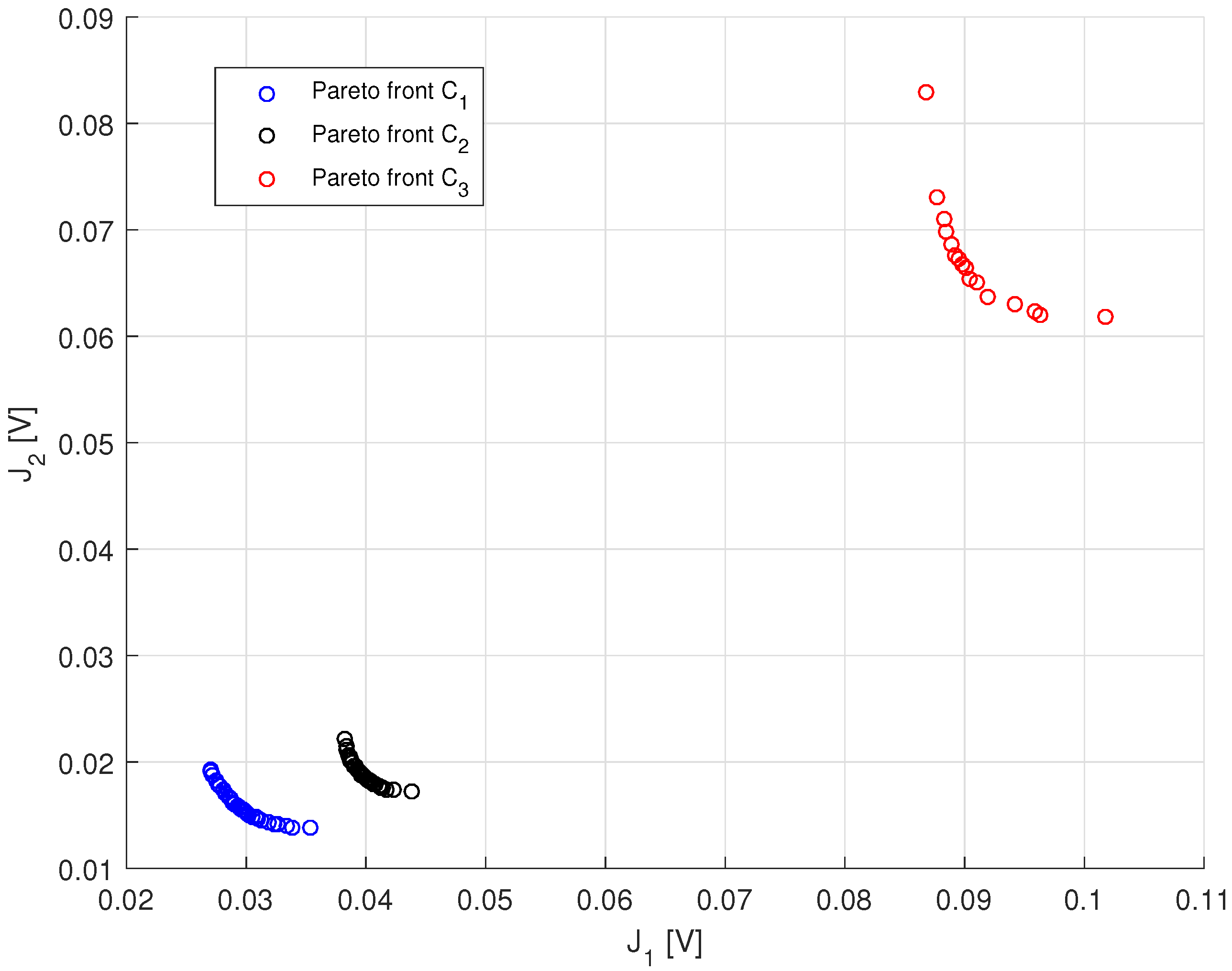
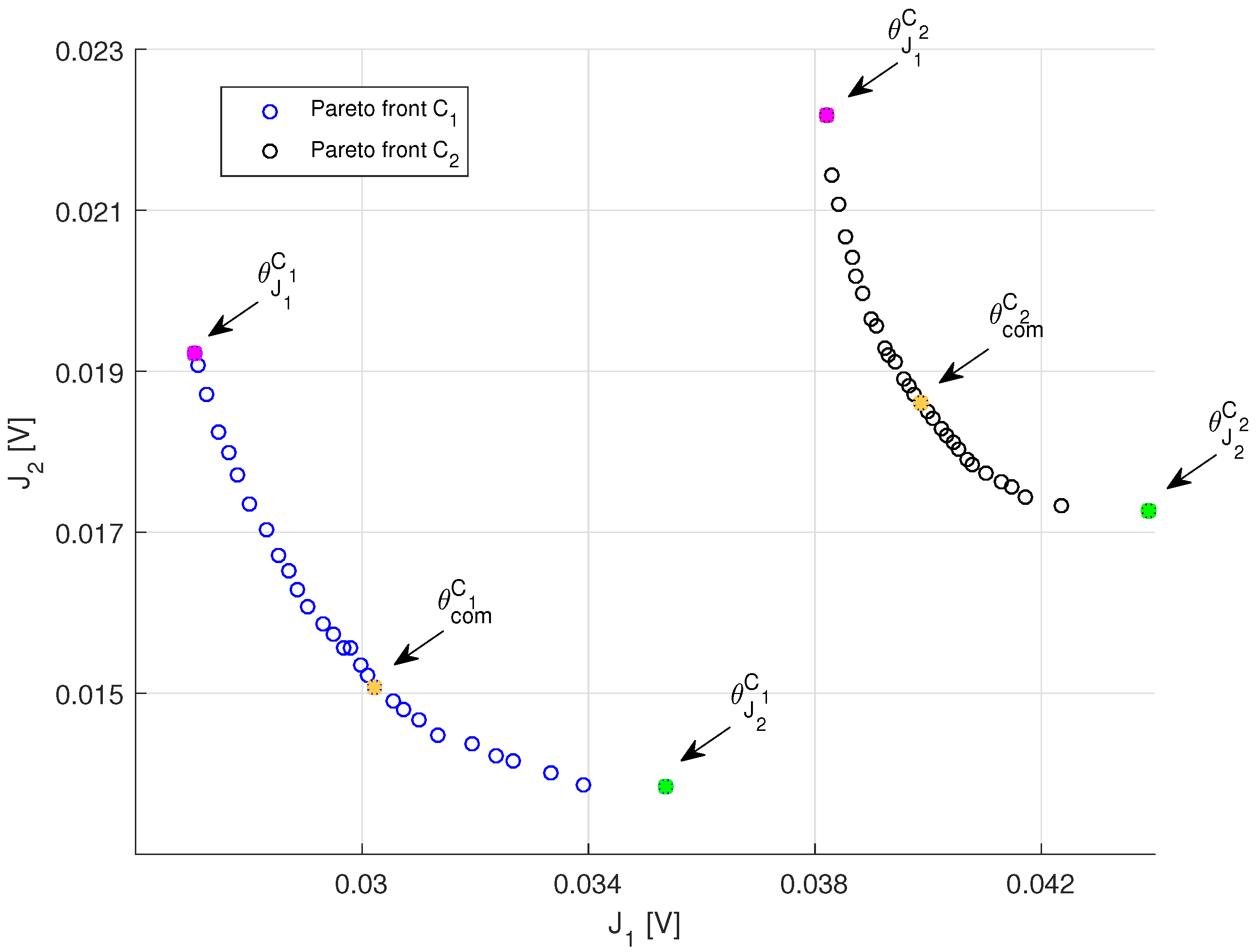
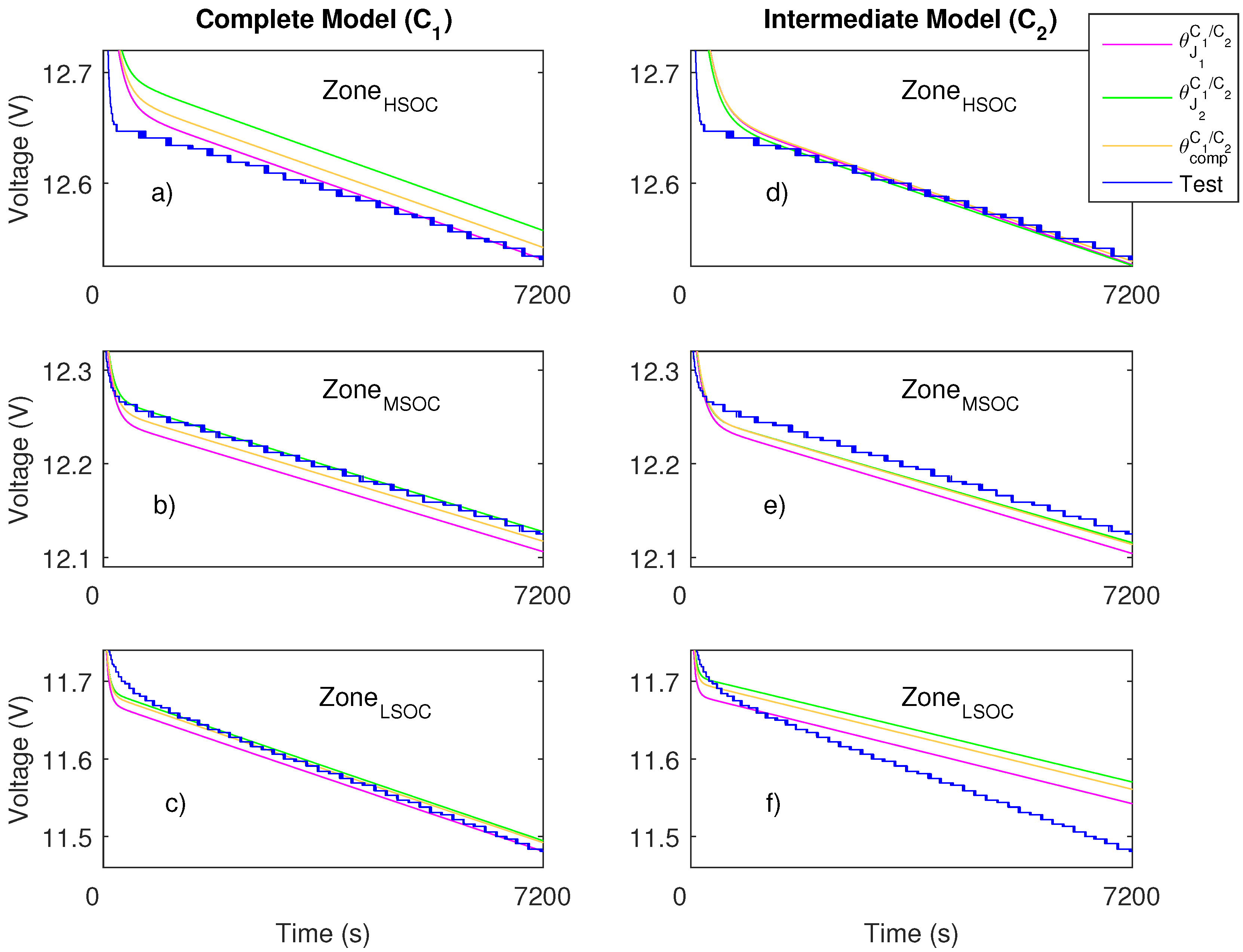
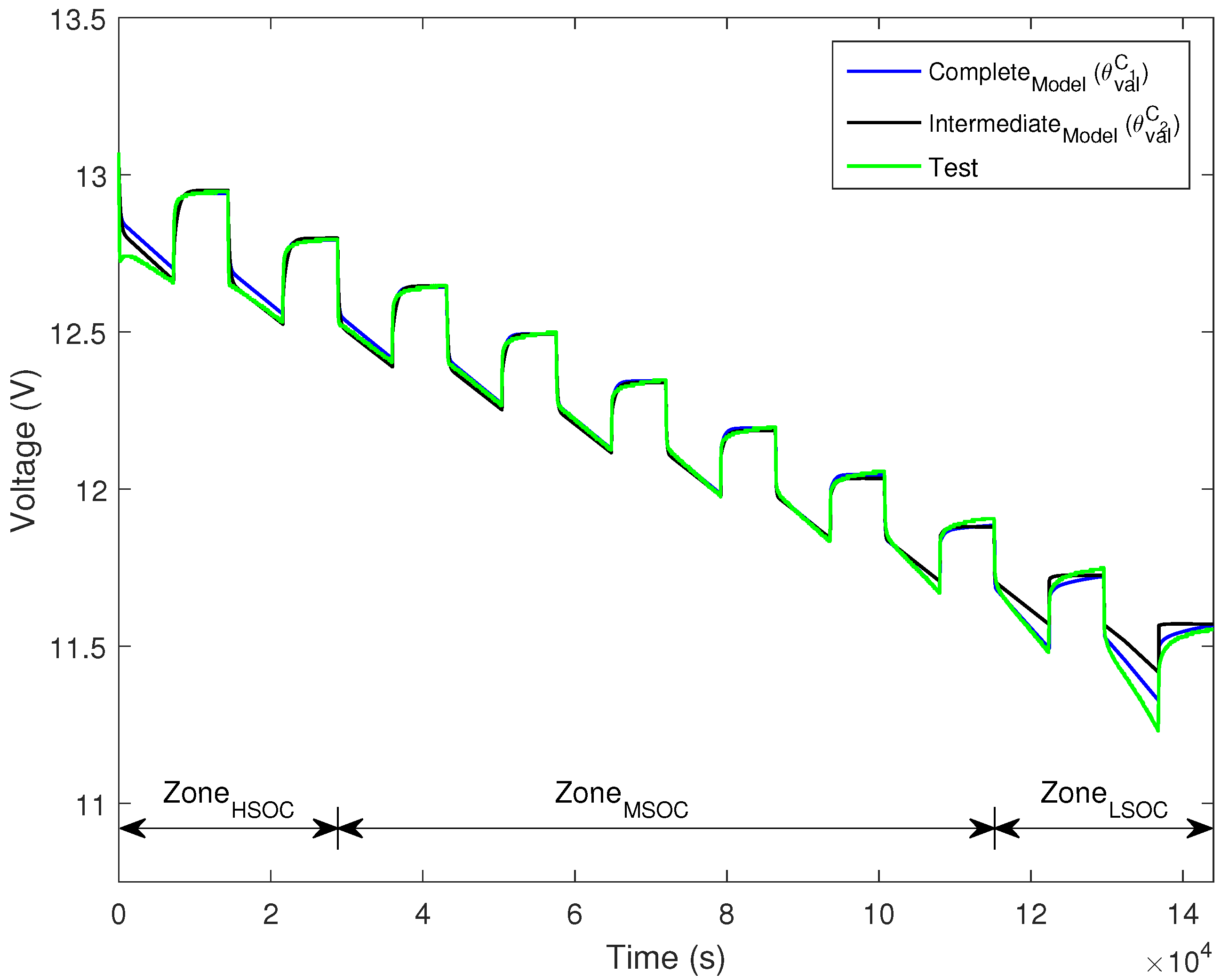
5. Results and Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mattson, C.A.; Messac, A. Concept selection using s-Pareto frontiers. AIAA J. 2003, 41, 1190–1198. [Google Scholar] [CrossRef]
- Mattson, C.A.; Messac, A. Pareto frontier based concept selection under uncertainty, with visualization. Optim. Eng. 2005, 6, 85–115. [Google Scholar] [CrossRef]
- Chang, W.Y. The state of charge estimating methods for battery: A review. ISRN Appl. Math. 2013, 2013. [Google Scholar] [CrossRef]
- Lee, D.T.; Shiah, S.J.; Lee, C.M.; Wang, Y.C. State-of-charge estimation for electric scooters by using learning mechanisms. IEEE Trans. Veh. Technol. 2007, 56, 544–556. [Google Scholar] [CrossRef]
- Hua, C.C.; Tasi, T.Y.; Chuang, C.W.; Shr, W.B. Design and implementation of a residual capacity estimator for lead-acid batteries. In Proceedings of the 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 2018–2023. [Google Scholar]
- Ramadass, P.; Haran, B.; Gomadam, P.M.; White, R.; Popov, B.N. Development of first principles capacity fade model for Li-ion cells. J. Electrochem. Soc. 2004, 151, A196–A203. [Google Scholar] [CrossRef]
- Sanchis, J.; Martínez, M.A.; Blasco, X. Integrated multiobjective optimization and a priori preferences using genetic algorithms. Inf. Sci. 2008, 178, 931–951. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Sanchis, J.; Blasco, X.; Freire, R.Z. Evolutionary multi-objective optimisation with preferences for multivariable PI controller tuning. Expert Syst. Appl. 2016, 51, 120–133. [Google Scholar] [CrossRef]
- Herrero, J.; Blasco, X.; Martínez, M.; Ramos, C.; Sanchis, J. Non-linear robust identification of a greenhouse model using multi-objective evolutionary algorithms. Biosyst. Eng. 2007, 98, 335–346. [Google Scholar] [CrossRef]
- Deb, K.; Sindhya, K.; Hakanen, J. Multi-objective optimization. In Decision Sciences: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; pp. 145–184. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization. In International Series in Operations Research and Management Science, 12nd ed.; Spring: Berlin, Germany, 1999. [Google Scholar]
- Bonissone, P.P.; Subbu, R.; Lizzi, J. Multicriteria decision making (MCDM): A framework for research and applications. IEEE Comput. Intell. Mag. 2009, 4, 48–61. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Blasco, X.; Sanchis, J.; Herrero, J.M. Comparison of design concepts in multi-criteria decision-making using level diagrams. Inf. Sci. 2013, 221, 124–141. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B. Applications of Multi-Objective Evolutionary Algorithms, 1st ed.; World Scientific: Singapore, 2004. [Google Scholar]
- You, D.; Zhang, H.; Chen, J. A simple model for the vanadium redox battery. Electrochimica Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Malik, A.; Zhang, Z.; Agarwal, R.K. Extraction of battery parameters using a multi-objective genetic algorithm with a non-linear circuit model. J. Power Sources 2014, 259, 76–86. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Xu, L.; Wang, J.; Chen, Q. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Convers. Manag. 2012, 53, 33–39. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A.; Dekkiche, A.I. A generic battery model for the dynamic simulation of hybrid electric vehicles. In Proceedings of the Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar]
- Einhorn, M.; Conte, F.V.; Kral, C.; Fleig, J. Comparison, selection, and parameterization of electrical battery models for automotive applications. IEEE Trans. Power Electron. 2013, 28, 1429–1437. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 1–10. [Google Scholar]
- Wang, J.; Cao, B.; Chen, Q.; Wang, F. Combined state of charge estimator for electric vehicle battery pack. Control Eng. Pract. 2007, 15, 1569–1576. [Google Scholar] [CrossRef]
- Moubayed, N.; Kouta, J.; El-Ali, A.; Dernayka, H.; Outbib, R. Parameter identification of the lead-acid battery model. In Proceedings of the 33rd IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–6. [Google Scholar]
- Ceraolo, M. New dynamical models of lead-acid batteries. IEEE Trans. Power Syst. 2000, 15, 1184–1190. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Garcia-Nieto, S.; Sanchis, J.; Blasco, F.X. Controller tuning by means of multi-objective optimization algorithms: A global tuning framework. IEEE Trans. Control Syst. Technol. 2013, 21, 445–458. [Google Scholar] [CrossRef]
- Herrero, J.; Reynoso-Meza, G.; Martínez, M.; Blasco, X.; Sanchis, J. A smart-distributed Pareto front using the ev-MOGA evolutionary algorithm. Int. J. Artif. Intell. Tools 2014, 23, 1450002. [Google Scholar] [CrossRef]
- Herrero, J.M.; García-Nieto, S.; Blasco, X.; Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L. Optimization of sonic crystal attenuation properties by ev-MOGA multiobjective evolutionary algorithm. Struct. Multidiscip. Optim. 2009, 39, 203. [Google Scholar] [CrossRef]
- Herrero, J.; Blasco, X.; Sánchez-Pérez, J.; Redondo, J. Design of sound phase diffusers by means of multiobjective optimization approach using ev-MOGA evolutionary algorithm. Struct. Multidiscip. Optim. 2016, 53, 861–879. [Google Scholar] [CrossRef]



| Parameter | Description | Value | Unit |
|---|---|---|---|
| I | Battery current (input) | - | A |
| Battery temperature (input) | - | C | |
| Open-circuit voltage at full charge | 13.1 | V | |
| Constant, which depends on , , and | - | V/C | |
| Constant | 1.24 | - | |
| No-load capacity at 0 C | 25.62 | Ah | |
| Constant | 0.64 | - | |
| Constant | 0.34 | - | |
| Nominal battery current | 1.57 | A | |
| Electrolyte freezing temperature | −40 | C | |
| Resistor, whose value depends on , , , , and | - | ||
| First RC resistor, whose value depends on , , , , and | - | ||
| First RC resistor, whose value depends on and | - | ||
| Second RC resistor, whose value depends on , and | - | ||
| Resistor of the second RC circuit | - | ||
| First RC capacitor | - | F | |
| Second RC capacitor | - | F | |
| When , this is considered a low current | 1.57 | A | |
| When , this is considered a medium current | 10.2 | A | |
| When , this is considered a high current | 29.6 | A | |
| First charge current | −2 | A | |
| Second charge current | −4 | A | |
| When , this is considered a very low SOC | 20 | % | |
| When : low SOC | 37.5 | % | |
| When : medium SOC | 55 | % | |
| When : high SOC | 90 | % |
| SOC | ||
|---|---|---|
| High | Very Low | |
| High Current, | ||
| Medium Current, | ||
| Low Current, | ||
| SOC | ||||
|---|---|---|---|---|
| High | Medium | Low | Very Low | |
| High Current | 0 | - | - | |
| Medium Current | 0 | 0 | - | |
| Low Current | 0 | 0 | 0 | |
| 0.004 | 0.0075 | ||||
| 0.0052 | 0.008 | ||||
| 0.0045 | 0.0075 | ||||
| 0.0075 | 0.015 | ||||
| 0.008 | 0.23 | ||||
| 0.019 | 0.07 | ||||
| 0.035 | 0.25 | ||||
| 0.05 | 0.7 | ||||
| 0.1 | 1.65 | ||||
| 0.35 | 1.9 | ||||
| 0.0065 | 0.0225 | ||||
| 1e-5 | 1e-3 | ||||
| 0.01 | 0.04 | ||||
| 1e-4 | 0.0035 | ||||
| 0.08 | 0.2 | ||||
| 0.008 | 0.04 | ||||
| −0.0065 | −0.045 | ||||
| 0.31 | 0.45 | ||||
| 750 | 2000 | ||||
| 1.15 | 1.75 | ||||
| 0.022 | 0.05 | ||||
| 0.075 | 0.55 | ||||
| 0.025 | 0.045 | ||||
| 1.5e5 | 2.5e5 |
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| 0.0251 | 0.0323 | 0.0385 | 0.12 | ||||
| 0.703 | 1.36 | 0.0119 | |||||
| 0.0253 | 0.139 | 0.0129 | |||||
| −0.0581 | 0.399 | – | – |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pajares, A.; Blasco, X.; Herrero, J.M.; Simarro, R. Using a Multiobjective Approach to Compare Multiple Design Alternatives—An Application to Battery Dynamic Model Tuning. Energies 2017, 10, 999. https://doi.org/10.3390/en10070999
Pajares A, Blasco X, Herrero JM, Simarro R. Using a Multiobjective Approach to Compare Multiple Design Alternatives—An Application to Battery Dynamic Model Tuning. Energies. 2017; 10(7):999. https://doi.org/10.3390/en10070999
Chicago/Turabian StylePajares, Alberto, Xavier Blasco, Juan Manuel Herrero, and Raúl Simarro. 2017. "Using a Multiobjective Approach to Compare Multiple Design Alternatives—An Application to Battery Dynamic Model Tuning" Energies 10, no. 7: 999. https://doi.org/10.3390/en10070999
APA StylePajares, A., Blasco, X., Herrero, J. M., & Simarro, R. (2017). Using a Multiobjective Approach to Compare Multiple Design Alternatives—An Application to Battery Dynamic Model Tuning. Energies, 10(7), 999. https://doi.org/10.3390/en10070999







