Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting
Abstract
:1. Introduction
2. Methodology of SVRCQBA Model
2.1. Support Vector Regression (SVR) Model
2.2. Chaotic Quantum Bat Algorithm (CQBA)
2.2.1. Bat Algorithm (BA)
2.2.2. Quantum Computing for BA
2.2.3. Chaotic Quantum Global Perturbation
- (1)
- Generate chaotic disturbance bats. For each (i = 1, 2, …, N), apply Equation (26) to generate d random numbers, (j = 1, 2, …, d). Then, the Equations (27) and (28) are used to map these numbers, , into (with valued from −1 to 1). Set as the qubit (with quantum state, ) amplitude, , of .
- (2)
- Determine the bats with better fitness. Calculate fitness value of each bat from current QBA, and arrange these bats to be a sequence in the order of fitness values. Then, select the bats with the th ranking ahead in the fitness values.
- (3)
- Form the new CQBA population. Mix the chaotic perturbation bats with the bats which are with better fitness selected from current QBA, and form a new population that contains new N bats, and named it as CQBA population.
- (4)
- Complete global chaotic perturbation. After obtaining the new CQBA population, take the new CQBA population as the new population of QBA, and continue to execute the QBA process.
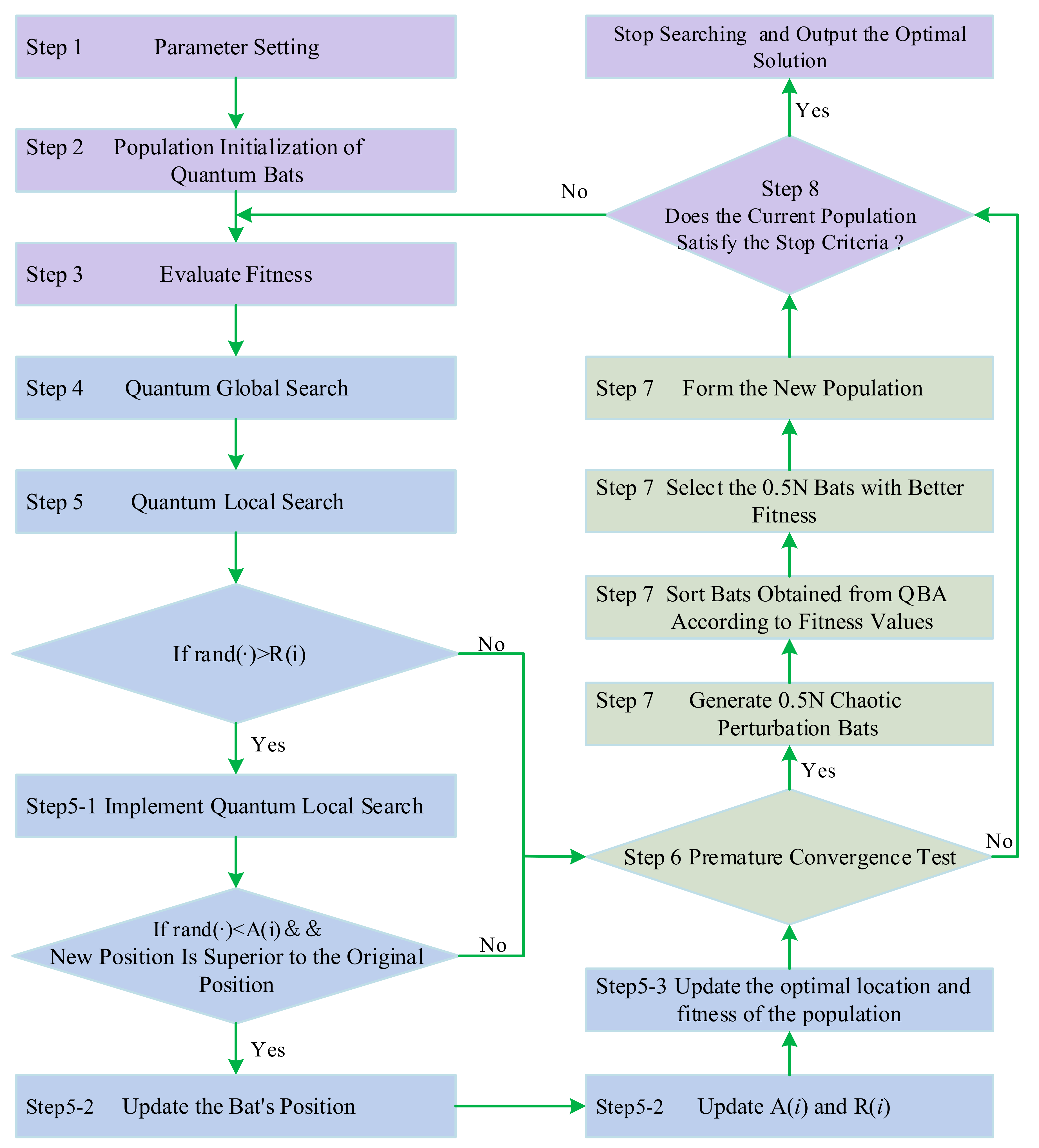
2.2.4. Implementation Steps of CQBA
- Step 1
- Parameter Setting. Initialize the population size, N; maximal iteration, gen_max; expected criteria, ; pulse emission rate, R(i); maximum and minimum of emission frequencies, and , respectively.
- Step 2
- Population Initialization of Quantum Bats. According to quantum bat population initialization strategy, initialize quantum bat population randomly.
- Step 3
- Evaluate Fitness. Evaluate the objective fitness by employing the coding information of quantum bats. Each probability amplitude of qubit is corresponding to an optimization variable in solution space. Assumed that the jth qubit of the bat is , the element’s value of the qubit is between the interval, [−1, 1]; the solution space variable corresponding to that is , set the element’s value be between the interval, [aj, bj]. Then, the solution could be calculated by the equal proportion relationship (i.e., Equations (29) and (30)),
- Step 4
- Quantum Global Search. According to quantum bat global search strategy, employ Equations (20) and (23) to implement the global search process of quantum bats, update the optimal location and fitness of the population.
- Step 5
- Quantum Local Search. This step considers two situations to implement quantum local search.
- Step 5.1
- If , use Equations (22) and (23), around the optimal bat of the current population, to implement quantum local search, and obtain the new position; else, go to Step 6.
- Step 5.2
- If and the new position is superior to the original position, then, update the bat’s position, and employ Equations (13) and (14) to update A(i) and R(i), respectively, go to Step 5.3; else, go to Step 6.
- Step 5.3
- Update the optimal location and fitness of the population. Go to Step 6.
- Step 6
- Premature Convergence Test. To improve the global disturbance efficiency, set the expected criteria , when the population aggregation degree is higher, the global chaotic disturbance for population should be executed once. The mean square error (MSE), as shown in Equation (34), is used to evaluate the premature convergence status,where, N is the number of forecasting samples, is the actual value of the ith period; is average objective value of the current status; can be obtained by Equation (35),
- Step 7
- Chaotic Global Perturbation. Based on cat mapping, i.e., the GCPS as illustrated Section 2.2.1, generate chaotic perturbation bats, sort bats obtained from QBA according to fitness values, and select the th bats with better fitness. Then, form the new population which includes the chaotic perturbation bats and the bats with better fitness selected from current QBA. After forming the new population, the QBA is implemented continually.
- Step 8
- Stop Criteria. If the number of search steps is greater than a given maximum search step, gen_max, then, the coded information of the best bat among the current population is determined as parameters (, C, ) of an SVR model; otherwise, go back to Step 4 and continue searching the next generation.
3. Experimental Examples
3.1. Data Set of Numerical Examples
3.2. The SVRCQBA Load Forecasting Model
3.2.1. Parameters Setting in CQBA Algorithm
3.2.2. Forecasting Accuracy Evaluation Index
3.2.3. Forecasting Performance Improvement Tests
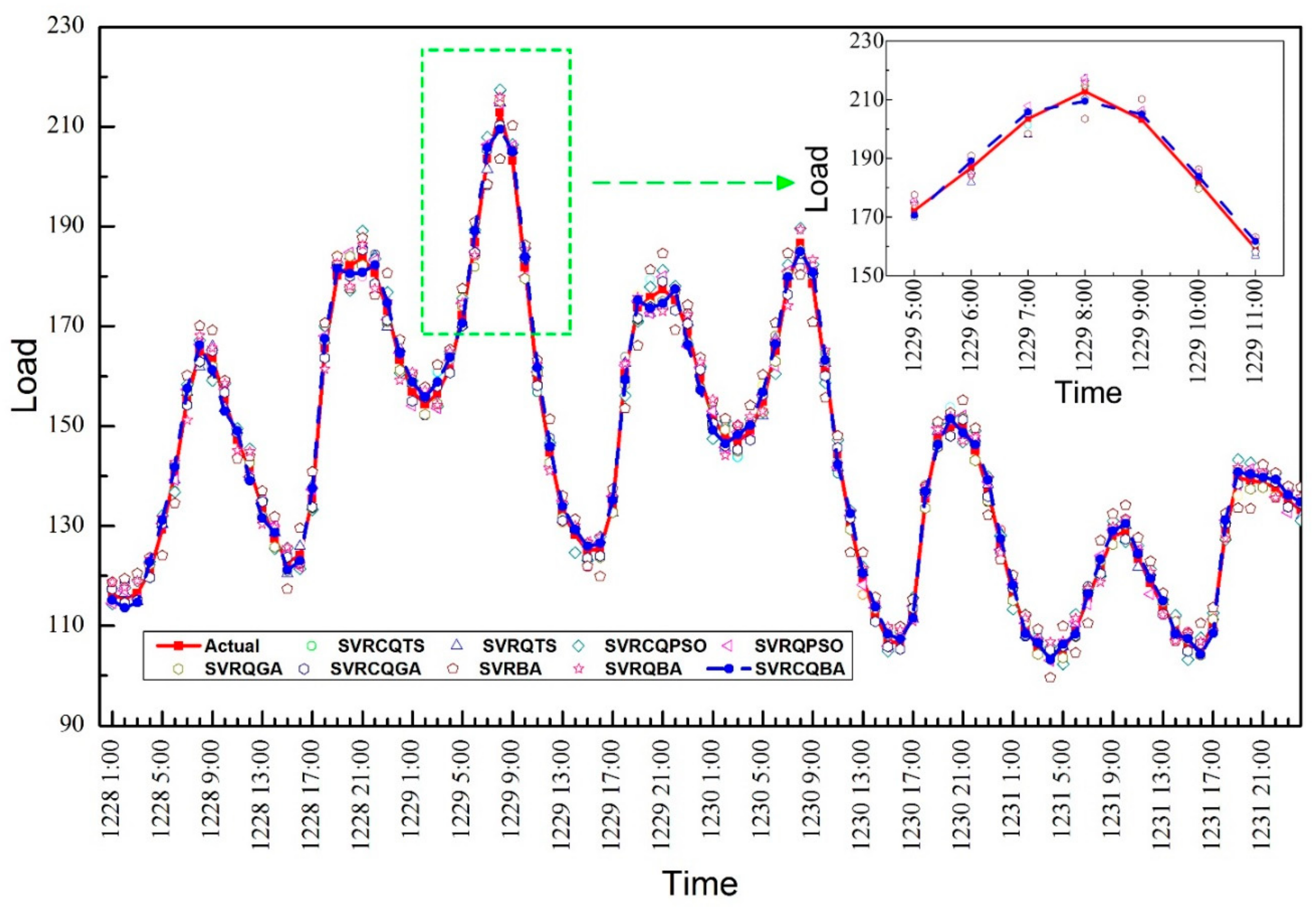
3.2.4. Forecasting Results and Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiao, L.; Wang, J.; Hou, R.; Wu, J. A combined model based on data pre-analysis and weight coefficients optimization for electrical load forecasting. Energy 2015, 82, 524–549. [Google Scholar] [CrossRef]
- Bunn, D.W.; Farmer, E.D. Comparative models for electrical load forecasting. Int. J. Forecast. 1986, 2, 241–242. [Google Scholar]
- Fan, G.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Li, Y.; Zhu, S.; Zhao, J. Techniques of applying wavelet de-noising into a combined model for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2014, 62, 816–824. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karampelas, P.; Karamousantas, D.C.; Katsikas, S.K.; Chatzarakis, G.E.; Skafidas, P.D. Electricity demand load forecasting of the Hellenic power system using an ARMA model. Electr. Power Syst. Res. 2010, 80, 256–264. [Google Scholar] [CrossRef]
- Zhang, M.; Bao, H.; Yan, L.; Cao, J.; Du, J. Research on processing of short-term historical data of daily load based on Kalman filter. Power Syst. Technol. 2003, 9, 39–42. [Google Scholar]
- Maçaira, P.M.; Souza, R.C.; Oliveira, F.L.C. Modelling and forecasting the residential electricity consumption in Brazil with pegels exponential smoothing techniques. Procedia Comput. Sci. 2015, 55, 328–335. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J. Forecasting natural gas consumption in China by Bayesian model averaging. Energy Rep. 2015, 1, 216–220. [Google Scholar] [CrossRef]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Ertugrul, Ö.F. Forecasting electricity load by a novel recurrent extreme learning machines approach. Int. J. Electr. Power Energy Syst. 2016, 78, 429–435. [Google Scholar] [CrossRef]
- Bennett, C.J.; Stewart, R.A.; Lu, J.W. Forecasting low voltage distribution network demand profiles using a pattern recognition based expert system. Energy 2014, 67, 200–212. [Google Scholar] [CrossRef]
- Akdemir, B.; Çetinkaya, N. Long-term load forecasting based on adaptive neural fuzzy inference system using real energy data. Energy Procedia 2012, 14, 794–799. [Google Scholar] [CrossRef]
- Hooshmand, R.-A.; Amooshahi, H.; Parastegari, M. A hybrid intelligent algorithm based short-term load forecasting approach. Int. J. Electr. Power Energy Syst. 2013, 45, 313–324. [Google Scholar] [CrossRef]
- Mahmoud, T.S.; Habibi, D.; Hassan, M.Y.; Bass, O. Modelling self-optimised short term load forecasting for medium voltage loads using tunning fuzzy systems and artificial neural networks. Energy Convers. Manag. 2015, 106, 1396–1408. [Google Scholar] [CrossRef]
- Niu, D.X.; Shi, H.; Wu, D.D. Short-term load forecasting using Bayesian neural networks learned by hybrid Monte Carlo algorithm. Appl. Soft Comput. 2012, 12, 1822–1827. [Google Scholar] [CrossRef]
- Hanmandlu, M.; Chauhan, B.K. Load forecasting using hybrid models. IEEE Trans. Power Syst. 2011, 26, 20–29. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Lou, C.W.; Dong, M.C. A novel random fuzzy neural networks for tackling uncertainties of electric load forecasting. Int. J. Electr. Power Energy Syst. 2015, 73, 34–44. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J.; De Moor, B. Optimal control by least squares support vector machines. Neural Netw. 2001, 14, 23–35. [Google Scholar] [CrossRef]
- Sankar, R.; Sapankevych, N.I. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000; ISBN 978-0-387-98780-4. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; ISBN 978-0-471-03003-4. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; The MIT Press: Cambridge, MA, USA, 2002; ISBN 978-0-262-19475-4. [Google Scholar]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector machine for function approximation, regression estimation, and signal processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- Antonanzas, J.; Urraca, R.; Martinez-De-Pison, F.J.; Antonanzas-Torres, F. Solar irradiation mapping with exogenous data from support vector regression machines estimations. Energy Convers. Manag. 2015, 100, 380–390. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. A recurrent support vector regression model in rainfall forecasting. Hydrol. Process. 2007, 21, 819–827. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; de Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; de Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Modeling and prediction of Turkey’s electricity consumption using Support Vector Regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Hong, W.-C.; Dong, Y.; Zhang, W.; Chen, L.-Y.; Panigrahi, B.K. Cyclic electric load forecasting by seasonal SVR with chaotic genetic algorithm. Int. J. Electr. Power Energy Syst. 2013, 44, 604–614. [Google Scholar] [CrossRef]
- Ju, F.-Y.; Hong, W.-C. Application of seasonal SVR with chaotic gravitational search algorithm in electricity forecasting. Appl. Math. Model. 2013, 37, 9643–9651. [Google Scholar] [CrossRef]
- Geng, J.; Huang, M.-L.; Li, M.-W.; Hong, W.-C. Hybridization of seasonal chaotic cloud simulated annealing algorithm in a SVR-based load forecasting model. Neurocomputing 2015, 151, 1362–1373. [Google Scholar] [CrossRef]
- Peng, L.-L.; Fan, G.-F.; Huang, M.-L.; Hong, W.-C. Hybridizing DEMD and quantum PSO with SVR in electric load forecasting. Energies 2016, 9, 221. [Google Scholar] [CrossRef]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. ISBN 978-3-642-12537-9. [Google Scholar]
- Yang, X.-S. Nature Inspired Meta-heuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010; pp. 97–104. ISBN 978-1-905986-28-6. [Google Scholar]
- Sheng, X.-H.; Ye, C.-M. Application of bat algorithm to permutation flow-shop scheduling problem. Ind. Eng. J. 2013, 16, 119–124. [Google Scholar]
- Komarasamy, G.; Wahi, A. An optimized k-means clustering technique using bat algorithm. Eur. J. Sci. Res. 2012, 84, 263–273. [Google Scholar]
- Yang, X.-S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Yang, X.-S. Bat algorithm for multi-objective optimization. Int. J. Bio-Inspired Comput. 2011, 3, 267–274. [Google Scholar] [CrossRef]
- Huang, M.-L. Hybridization of chaotic quantum particle swarm optimization with SVR in electric demand forecasting. Energies 2016, 9, 426. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lin, B.-Y. Application of hybrid quantum tabu search with support vector regression (SVR) for load forecasting. Energies 2016, 9, 873. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lin, B.-Y. Applications of the chaotic quantum genetic algorithm with support vector regression in load forecasting. Energies 2017, 10, 1832. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Ma, L.; Zhang, H.-Z. Quantum bat algorithm for function optimization. J. Syst. Manag. 2014, 23, 717–722. [Google Scholar]
- Moss, C.F.; Sinha, S.R. Neurobiology of echolocation in bats. Curr. Opin. Neurobiol. 2003, 13, 751–758. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Wang, P.; Yuan, Y.; Huang, Y.; Zhang, X. A new quantum inspired chaotic artificial bee colony algorithm for optimal power flow problem. Energy Convers. Manag. 2015, 100, 1–9. [Google Scholar] [CrossRef]
- Peng, A.N. Particle swarm optimization algorithm based on chaotic theory and adaptive inertia weight. J. Nanoelectron. Optoelectron. 2017, 12, 404–408. [Google Scholar] [CrossRef]
- Li, M.-W.; Geng, J.; Hong, W.-C.; Chen, Z.-Y. A novel approach based on the Gauss-vSVR with a new hybrid evolutionary algorithm and input vector decision method for port throughput forecasting. Neural Comput. Appl. 2017, 28, S621–S640. [Google Scholar] [CrossRef]
- Li, M.-W.; Hong, W.-C.; Geng, J.; Wang, J. Berth and quay crane coordinated scheduling using chaos cloud particle swarm optimization algorithm. Neural Comput. Appl. 2017, 28, 3163–3182. [Google Scholar] [CrossRef]
- Global Energy Forecasting Competition. 2014. Available online: http://www.drhongtao.com/gefcom/ (accessed on 28 November 2017).
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 134–144. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
| Optimization Algorithms | Parameters | MAPE of Testing (%) | Computation Time (Seconds) | ||
|---|---|---|---|---|---|
| C | |||||
| SVRQPSO [43] | 9.000 | 42.000 | 0.180 | 1.960 | 635.73 |
| SVRCQPSO [43] | 19.000 | 35.000 | 0.820 | 1.290 | 986.46 |
| SVRQTS [44] | 25.000 | 67.000 | 0.090 | 1.890 | 489.67 |
| SVRCQTS [44] | 12.000 | 26.000 | 0.320 | 1.320 | 858.34 |
| SVRQGA [45] | 5.000 | 79.000 | 0.380 | 1.750 | 942.82 |
| SVRCQGA [45] | 6.000 | 54.000 | 0.620 | 1.170 | 1327.24 |
| SVRBA | 8.000 | 37.000 | 0.750 | 3.160 | 326.87 |
| SVRQBA | 13.000 | 61.000 | 0.560 | 1.744 | 549.68 |
| SVRCQBA, | 11.000 | 76.000 | 0.670 | 1.098 | 889.36 |
| Indexes | SVRQPSO [43] | SVRCQPSO [43] | SVRQTS [44] | SVRCQTS [44] | SVRQGA [45] | SVRCQGA [45] |
|---|---|---|---|---|---|---|
| MAPE (%) | 1.9600 | 1.3200 | 1.8900 | 1.2900 | 1.7500 | 1.1700 |
| RMSE | 2.9358 | 1.9909 | 2.8507 | 1.9257 | 1.6584 | 1.4927 |
| MAE | 2.8090 | 1.8993 | 2.7181 | 1.8474 | 1.6174 | 1.4522 |
| Indexes | SVRBA | SVRQBA | SVRCQBA | |||
| MAPE (%) | 3.1600 | 1.7442 | 1.0982 | |||
| RMSE | 4.7312 | 2.5992 | 1.4835 | |||
| MAE | 4.5234 | 2.4968 | 1.4372 | |||
| Compared Models | Wilcoxon Signed-Rank Test | ||
|---|---|---|---|
| α = 0.025; W = 2328 | α = 0.005; W = 2328 | p-Value | |
| SVRCQBA vs. SVRQPSO | 1087 T | 1087 T | 0.00220 ** |
| SVRCQBA vs. SVRCQPSO | 1184 T | 1184 T | 0.00156 ** |
| SVRCQBA vs. SVRQTS | 1123 T | 1123 T | 0.00143 ** |
| SVRCQBA vs. SVRCQTS | 1246 T | 1246 T | 0.00234 ** |
| SVRCQBA vs. SVRQGA | 1207 T | 1207 T | 0.00183 ** |
| SVRCQBA vs. SVRCQGA | 1358 T | 1358 T | 0.00578 * |
| SVRCQBA vs. SVRBA | 874 T | 874 T | 0.00278 ** |
| SVRCQBA vs. SVRQBA | 1796 T | 1796 T | 0.00614 * |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.-W.; Geng, J.; Wang, S.; Hong, W.-C. Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting. Energies 2017, 10, 2180. https://doi.org/10.3390/en10122180
Li M-W, Geng J, Wang S, Hong W-C. Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting. Energies. 2017; 10(12):2180. https://doi.org/10.3390/en10122180
Chicago/Turabian StyleLi, Ming-Wei, Jing Geng, Shumei Wang, and Wei-Chiang Hong. 2017. "Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting" Energies 10, no. 12: 2180. https://doi.org/10.3390/en10122180
APA StyleLi, M.-W., Geng, J., Wang, S., & Hong, W.-C. (2017). Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting. Energies, 10(12), 2180. https://doi.org/10.3390/en10122180






