Performance Recovery of Natural Draft Dry Cooling Systems by Combined Air Leading Strategies
Abstract
:1. Introduction
2. Modeling and Approaches
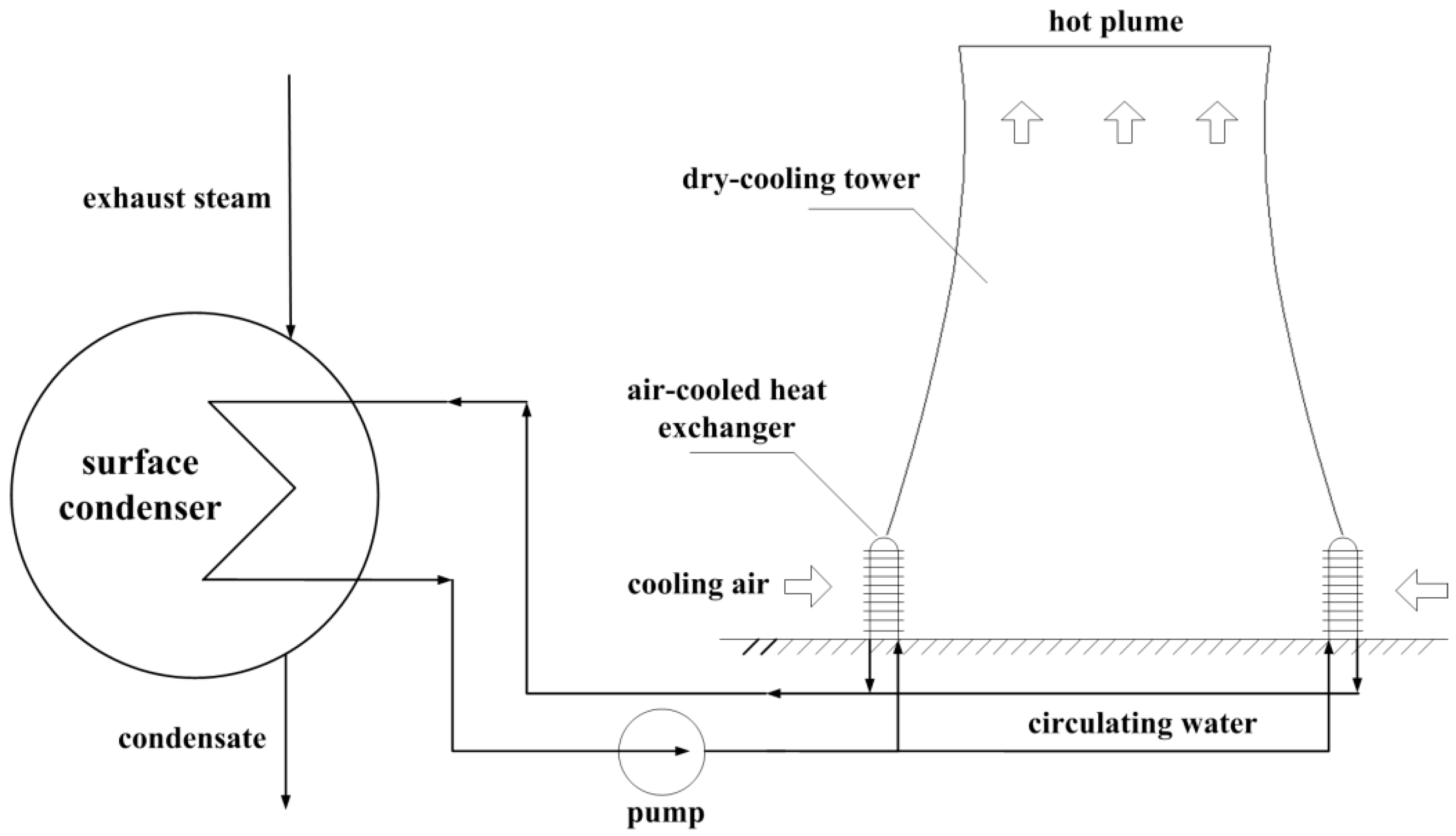
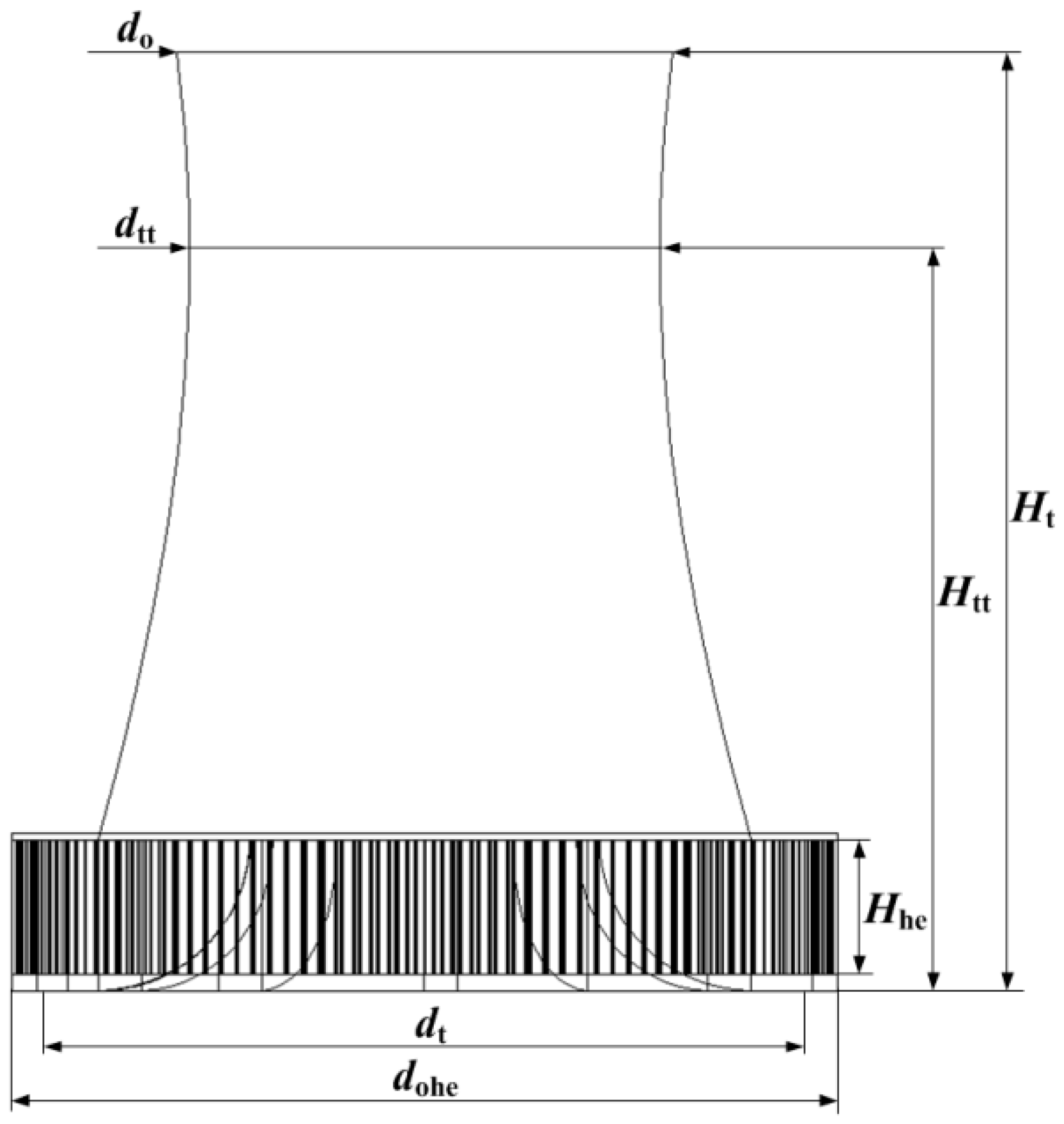
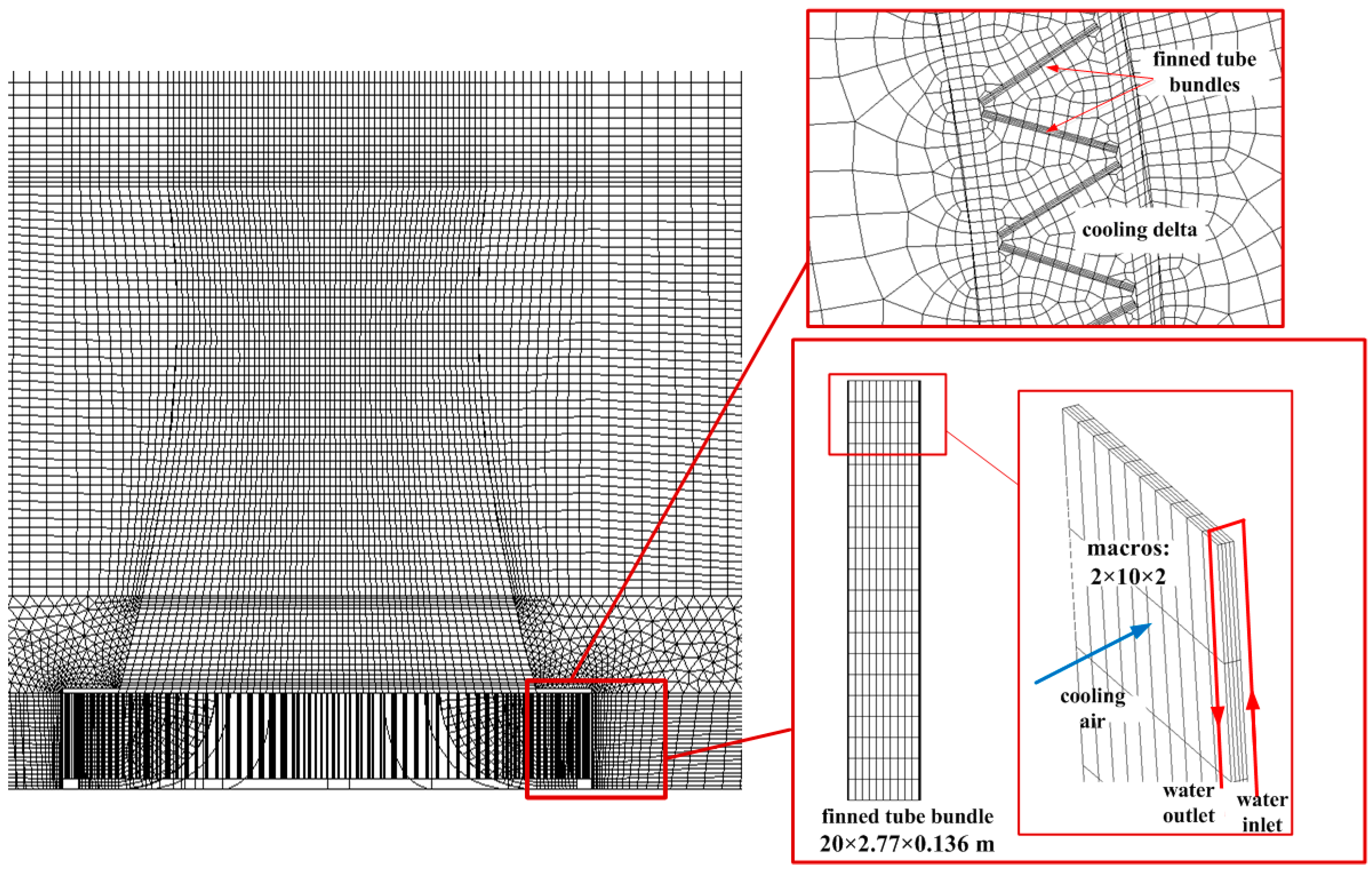
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Macro Heat Exchanger Model
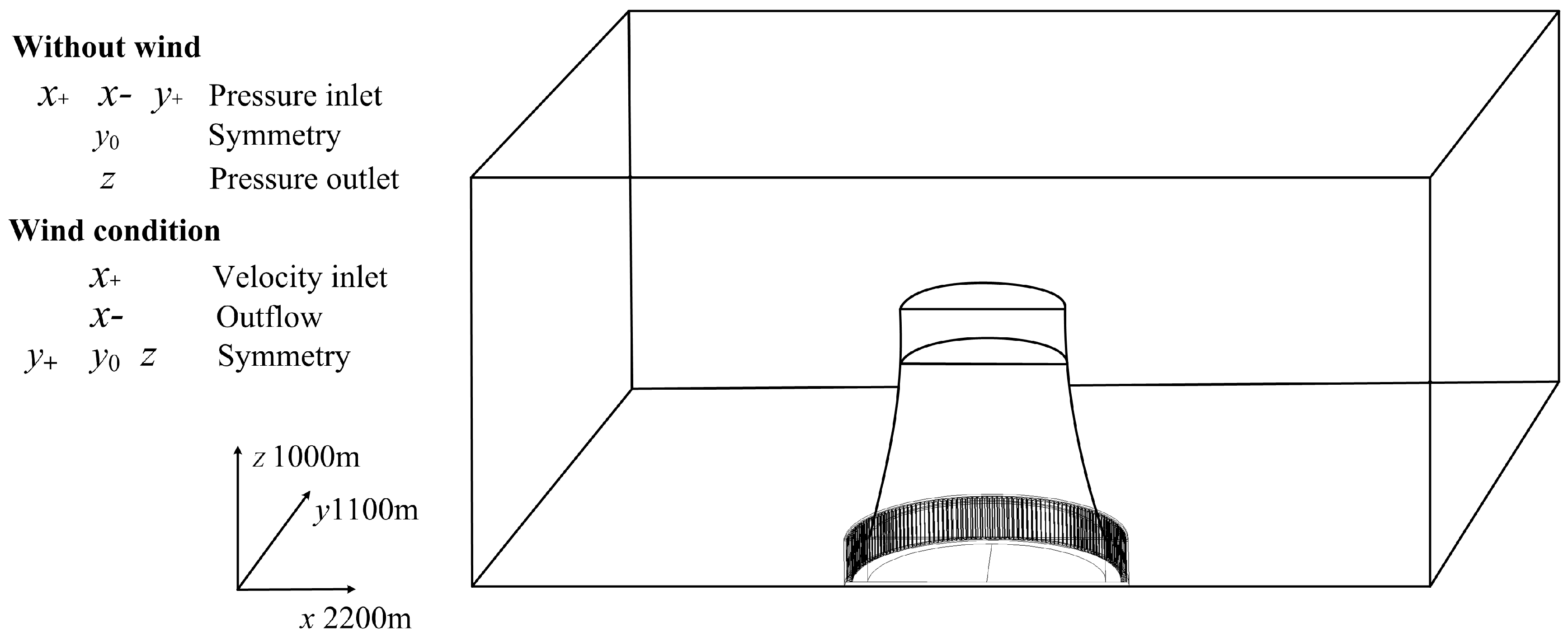
2.2.2. Conservation Equations and Numerical Approach
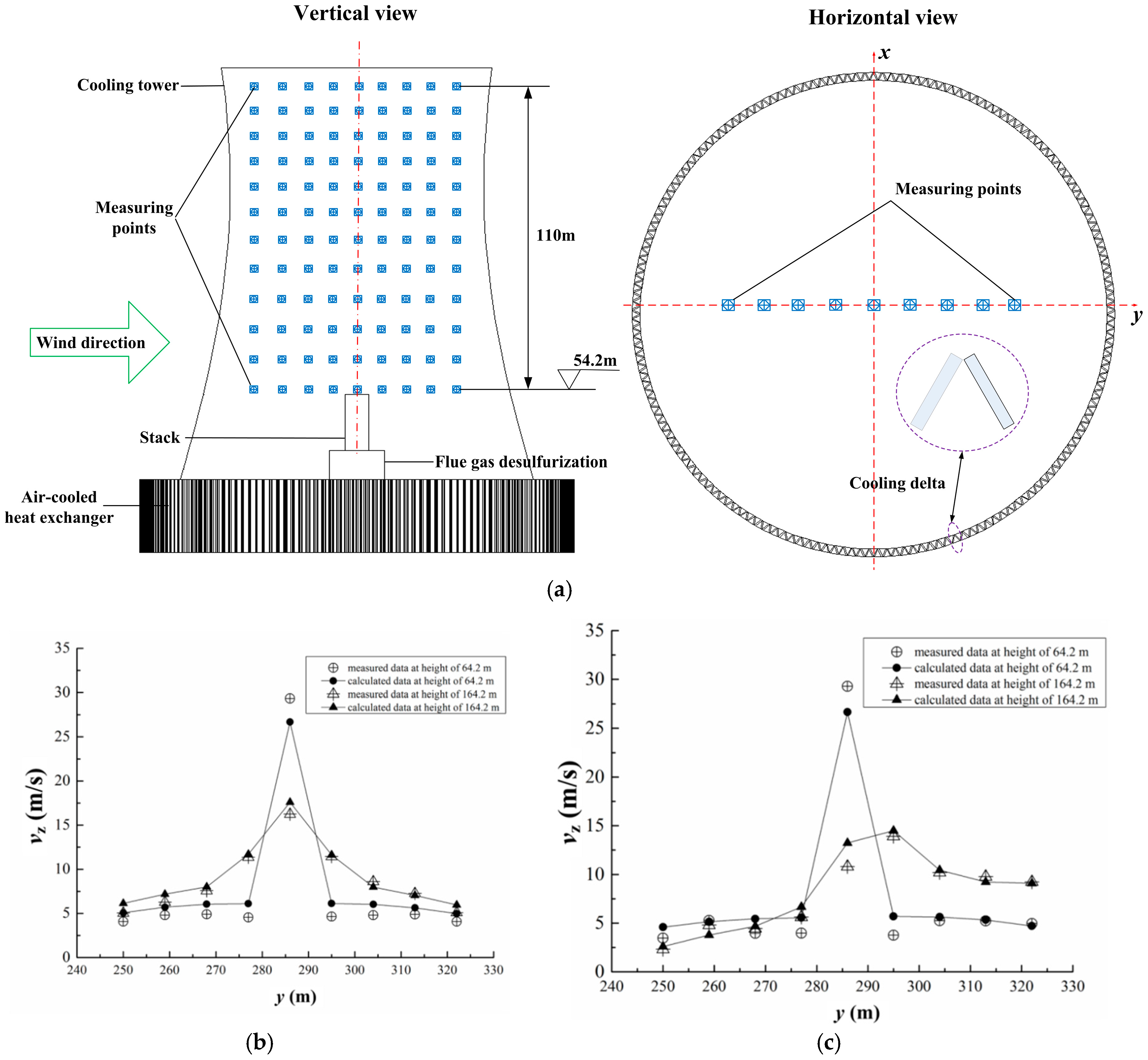
2.3. Experimental Validation
3. Results and Discussion
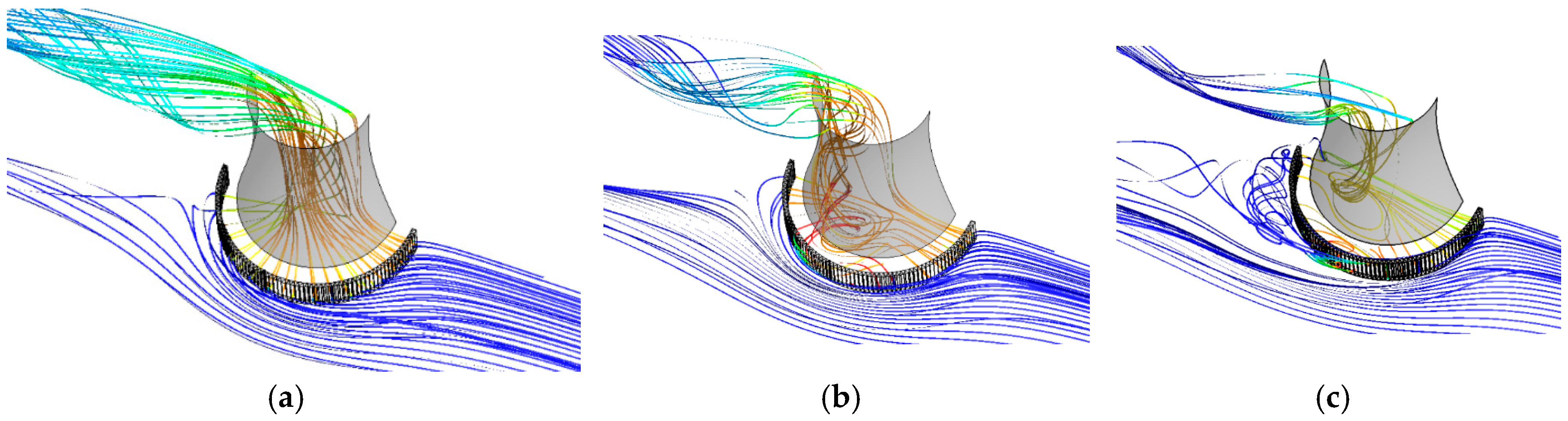
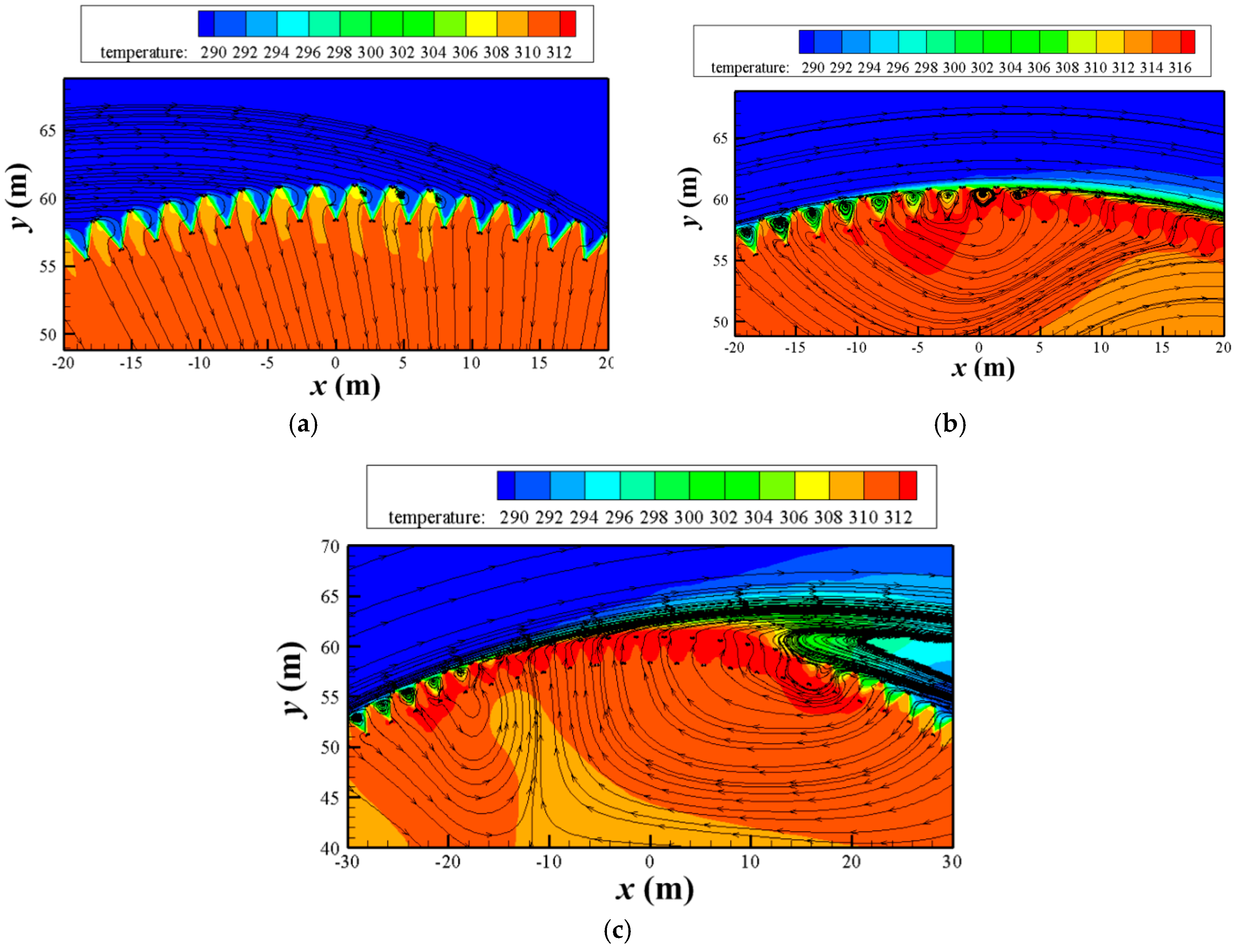
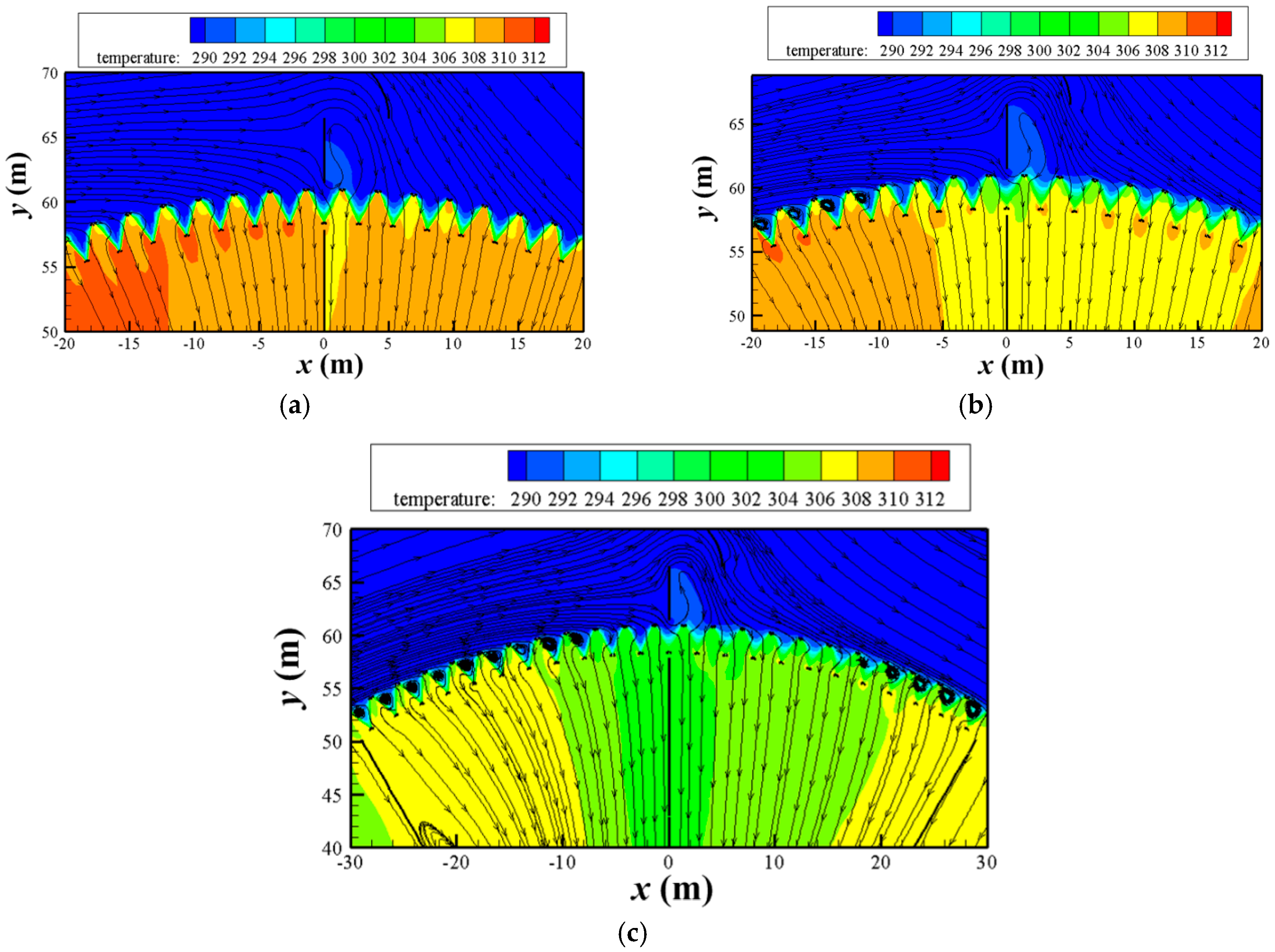
3.1. With No Air Leading
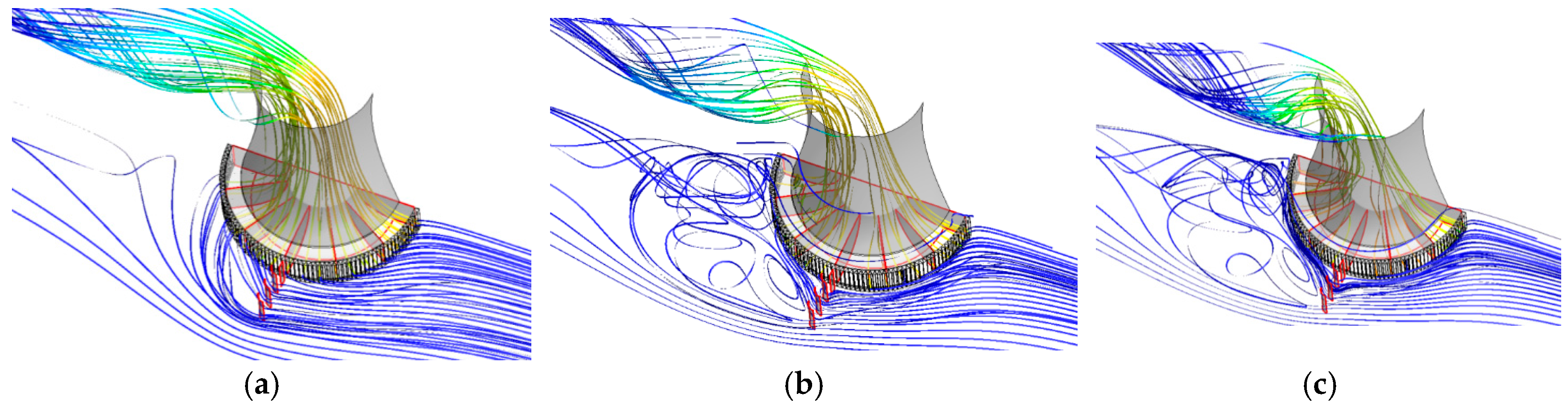
3.1.1. Streamlines
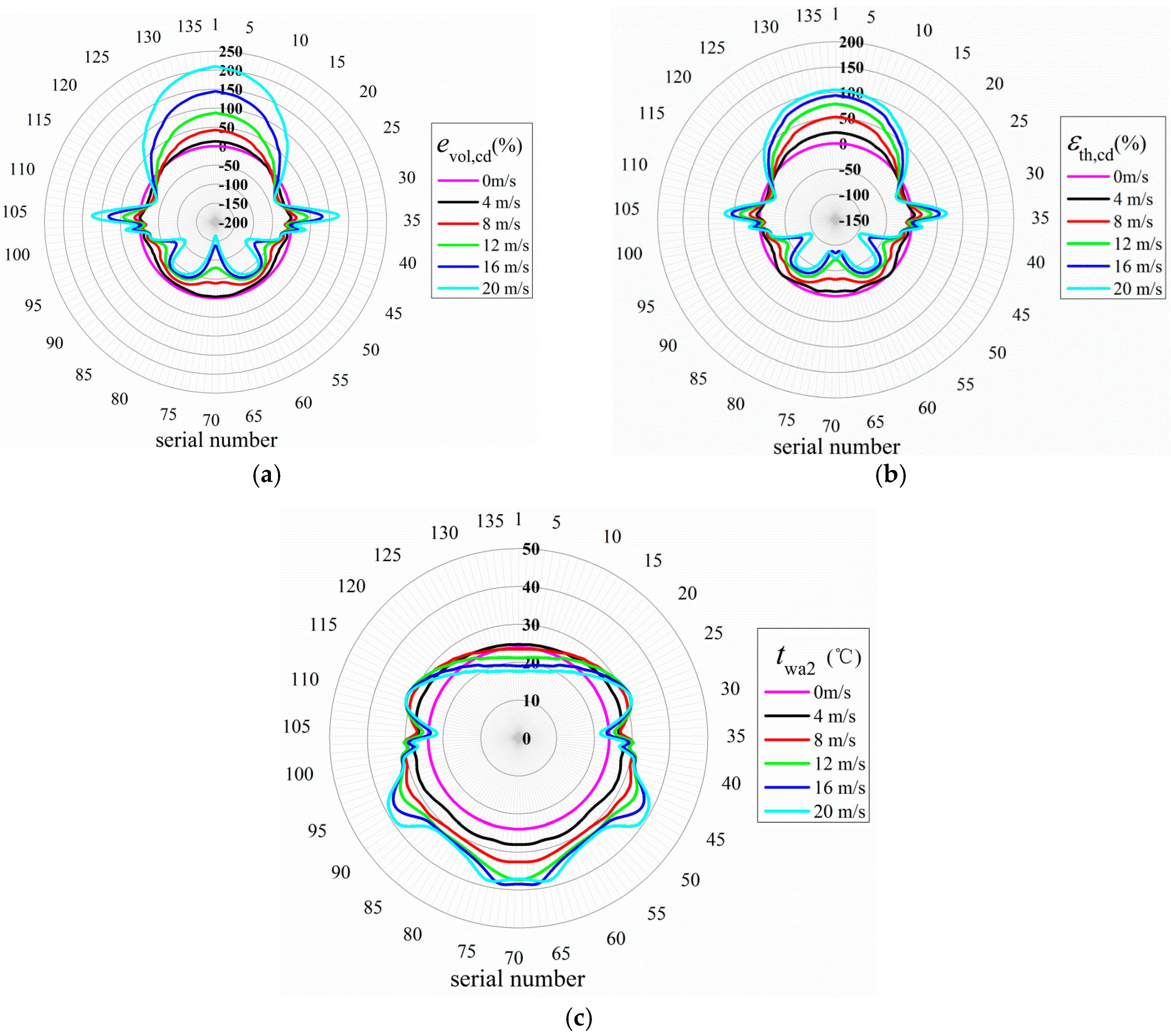
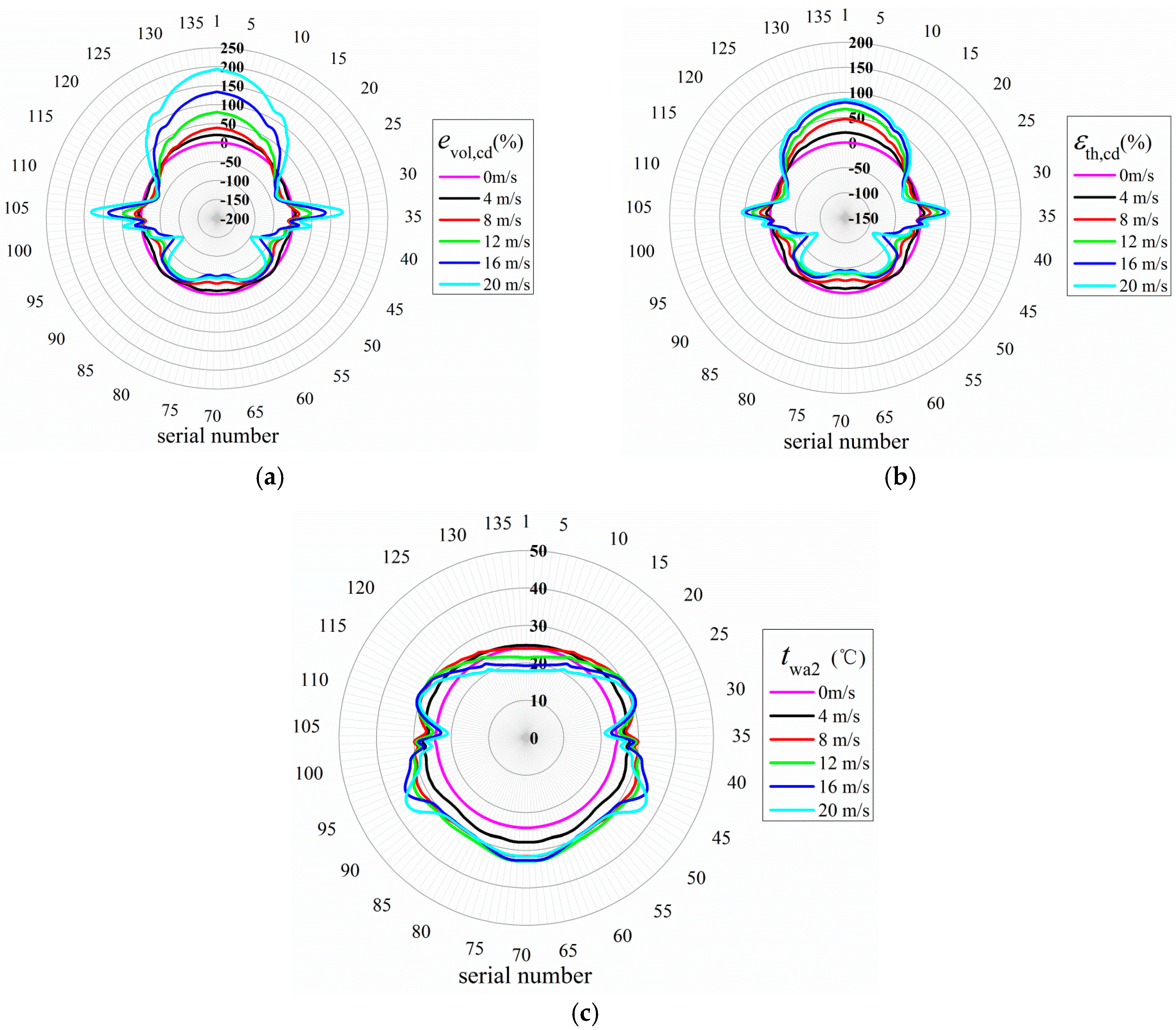
3.1.2. Performances of Cooling Deltas
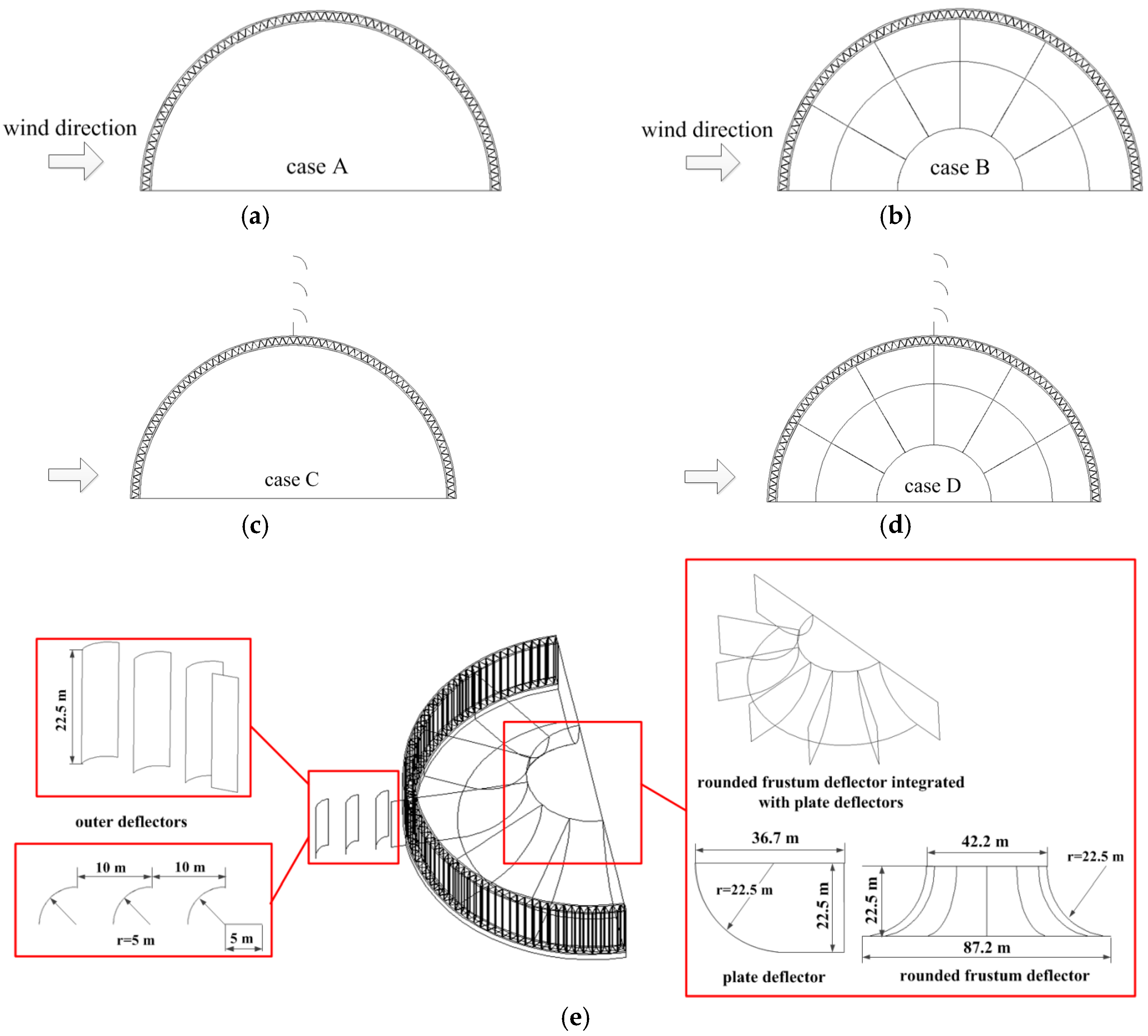
3.2. With Air Leading Strategies
3.2.1. Streamlines
3.2.2. Performances of Cooling Deltas
3.3. Overall Performance
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kroger, D. Air-Cooled Heat Exchangers and Cooling Towers: Thermal-Flow Performance Evaluation and Design; PennWell Corporation: Tulsa, OK, USA, 2004. [Google Scholar]
- Wei, Q.; Zhang, B.; Liu, K.; Du, X.; Meng, X. A study of the unfavorable effects of wind on the cooling efficiency of dry cooling towers. J. Wind Eng. Ind. Aerodyn. 1995, 54–55, 633–643. [Google Scholar] [CrossRef]
- Yang, L.; Wu, X.; Du, X.; Yang, Y. Dimensional characteristics of wind effects on the performance of indirect dry cooling system with vertically arranged heat exchanger bundles. Int. J. Heat Mass Transf. 2013, 67, 853–866. [Google Scholar] [CrossRef]
- Ma, H.; Si, F.; Li, L.; Yan, W.; Zhu, K. Effects of ambient temperature and crosswind on thermo-flow performance of the tower under energy balance of the indirect dry cooling system. Appl. Therm. Eng. 2015, 78, 90–100. [Google Scholar] [CrossRef]
- Lu, Y.; Guan, Z.; Gurgenci, H.; Hooman, K.; He, S.; Bharathan, D. Experimental study of crosswind effects on the performance of small cylindrical natural draft dry cooling towers. Energy Convers. Manag. 2015, 91, 238–248. [Google Scholar] [CrossRef]
- Zhao, Y.; Long, G.; Sun, F.; Li, Y.; Zhang, C. Numerical study on the cooling performance of dry cooling tower with vertical two-pass column radiators under crosswind. Appl. Therm. Eng. 2015, 75, 1106–1117. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, F.; Li, Y.; Long, G.; Yang, Z. Numerical study on the cooling performance of natural draft dry cooling tower with vertical delta radiators under constant heat load. Appl. Energy 2015, 149, 225–237. [Google Scholar] [CrossRef]
- Yang, L.; Chen, L.; Du, X.; Yang, Y. Effects of ambient winds on the thermo-flow performances of indirect dry cooling system in a power plant. Int. J. Therm. Sci. 2013, 64, 178–187. [Google Scholar] [CrossRef]
- Goodarzi, M. A proposed stack configuration for dry cooling tower to improve cooling efficiency under crosswind. J. Wind Eng. Ind. Aerodyn. 2010, 98, 858–863. [Google Scholar] [CrossRef]
- Goodarzi, M. Proposing a new technique to enhance thermal performance and reduce structural design wind loads for natural drought cooling towers. Energy 2013, 62, 164–172. [Google Scholar] [CrossRef]
- Goodarzi, M.; Ramezanpour, R. Alternative geometry for cylindrical natural draft cooling tower with higher cooling efficiency under crosswind condition. Energy Convers. Manag. 2014, 77, 243–249. [Google Scholar] [CrossRef]
- Liao, H.; Yang, L.; Du, X.; Yang, Y. Influences of height to diameter ratios of dry-cooling tower upon thermo-flow characteristics of indirect dry cooling system. Int. J. Therm. Sci. 2015, 94, 178–192. [Google Scholar] [CrossRef]
- Liao, H.; Yang, L.; Du, X.; Yang, Y. Triangularly arranged heat exchanger bundles to restrain wind effects on natural draft dry cooling system. Appl. Therm. Eng. 2016, 99, 313–324. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, W.; Yang, L.; Du, X.; Yang, Y. A novel natural draft dry cooling system with bilaterally arranged air-cooled heat exchanger. Int. J. Therm. Sci. 2017, 112, 318–334. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. The performance of natural draft dry cooling towers under crosswind: CFD study. Int. J. Energy Res. 2004, 28, 147–161. [Google Scholar] [CrossRef]
- Goodarzi, M.; Keimanesh, R. Heat rejection enhancement in natural draft cooling tower using radiator-type windbreakers. Energy Convers. Manag. 2013, 71, 120–125. [Google Scholar] [CrossRef]
- Goodarzi, M.; Keimanesh, R. Numerical analysis on overall performance of Savonius turbines adjacent to a natural draft cooling tower. Energy Convers. Manag. 2015, 99, 41–49. [Google Scholar] [CrossRef]
- Lu, Y.; Guan, Z.; Gurgenci, H.; Zou, Z. Windbreak walls reverse the negative effect of crosswind in short natural draft dry cooling towers into a performance enhancement. Int. J. Heat Mass Transf. 2013, 63, 162–170. [Google Scholar] [CrossRef]
- Lu, Y.; Gurgenci, H.; Guan, Z.; He, S. The influence of windbreak wall orientation on the cooling performance of small natural draft dry cooling towers. Int. J. Heat Mass Transf. 2014, 79, 1059–1069. [Google Scholar] [CrossRef]
- Lu, Y.; Guan, Z.; Gurgenci, H.; Alkhedhair, A.; He, S. Experimental investigation into the positive effects of a tri-blade-like windbreak wall on small size natural draft dry cooling towers. Appl. Therm. Eng. 2016, 105, 1000–1012. [Google Scholar] [CrossRef]
- Zhao, Y.; Long, G.; Sun, F.; Li, Y.; Zhang, C.; Liu, J. Effect mechanism of air deflectors on the cooling performance of dry cooling tower with vertical delta radiators under crosswind. Energy Convers. Manag. 2015, 93, 321–331. [Google Scholar] [CrossRef]
- Gu, H.; Wang, H.; Gu, Y.; Yao, J. A numerical study on the mechanism and optimization of wind-break structures for indirect air-cooling towers. Energy Convers. Manag. 2016, 108, 43–49. [Google Scholar] [CrossRef]
- Ma, H.; Si, F.; Kong, Y.; Zhu, K.; Yan, W. Wind-break walls with optimized setting angles for natural draft dry cooling tower with vertical radiators. Appl. Therm. Eng. 2017, 112, 326–339. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Liu, P.; Li, Z.; Lv, J.; Ni, W. The cooling performance of a natural draft dry cooling tower under crosswind and an enclosure approach to cooling efficiency enhancement. Appl. Energy 2017, 186, 336–346. [Google Scholar] [CrossRef]
- Zavaragh, H.; Ceviz, M.; Tabar, M. Analysis of windbreaker combinations on steam power plant natural draft dry cooling towers. Appl. Therm. Eng. 2016, 99, 550–559. [Google Scholar] [CrossRef]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. Performance improvement of natural draft dry cooling system by interior and exterior windbreaker configurations. Int. J. Heat Mass Transf. 2016, 96, 42–63. [Google Scholar] [CrossRef]
- Wang, W.; Yang, L.; Du, X.; Yang, Y. Anti-freezing water flow rates of various sectors for natural draft dry cooling system under wind conditions. Int. J. Heat Mass Transf. 2016, 102, 186–200. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.; Du, X.; Yang, Y. Performance improvement of natural draft dry cooling system by water flow distribution under crosswinds. Int. J. Heat Mass Transf. 2017, 108, 1924–1940. [Google Scholar] [CrossRef]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. A novel layout of air-cooled condensers to improve thermo-flow performances. Appl. Energy 2016, 165, 244–259. [Google Scholar] [CrossRef]


| Parameters | Symbol | Value |
|---|---|---|
| Height of tower | Ht | 140 m |
| Base diameter of tower | db | 114 m |
| Outlet diameter of tower | do | 78 m |
| Throat height of tower | Htt | 110 m |
| Throat diameter of tower | dtt | 74 m |
| Height of air-cooled heat exchanger | Hhe | 20 m |
| Outlet diameter of heat exchanger | dohe | 122 m |
| Number of cooling deltas | ncd | 136 |
| Pressure Loss Coefficients | |||||||||
| σ | Ki | Ke | a | b | |||||
| 0.492 | 0 | 0 | 0.9255 | −0.34123 | |||||
| Effectiveness Versus Velocity | |||||||||
| va (m/s) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
| εhe | 0.75584 | 0.63524 | 0.55515 | 0.49612 | 0.4501 | 0.41289 | 0.38201 | 0.35588 | 0.33342 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Chen, L.; Huang, X.; Yang, L.; Du, X. Performance Recovery of Natural Draft Dry Cooling Systems by Combined Air Leading Strategies. Energies 2017, 10, 2166. https://doi.org/10.3390/en10122166
Wang W, Chen L, Huang X, Yang L, Du X. Performance Recovery of Natural Draft Dry Cooling Systems by Combined Air Leading Strategies. Energies. 2017; 10(12):2166. https://doi.org/10.3390/en10122166
Chicago/Turabian StyleWang, Weijia, Lei Chen, Xianwei Huang, Lijun Yang, and Xiaoze Du. 2017. "Performance Recovery of Natural Draft Dry Cooling Systems by Combined Air Leading Strategies" Energies 10, no. 12: 2166. https://doi.org/10.3390/en10122166
APA StyleWang, W., Chen, L., Huang, X., Yang, L., & Du, X. (2017). Performance Recovery of Natural Draft Dry Cooling Systems by Combined Air Leading Strategies. Energies, 10(12), 2166. https://doi.org/10.3390/en10122166






