Directionality Effects of Aligned Wind and Wave Loads on a Y-Shape Semi-Submersible Floating Wind Turbine under Rated Operational Conditions
Abstract
:1. Introduction
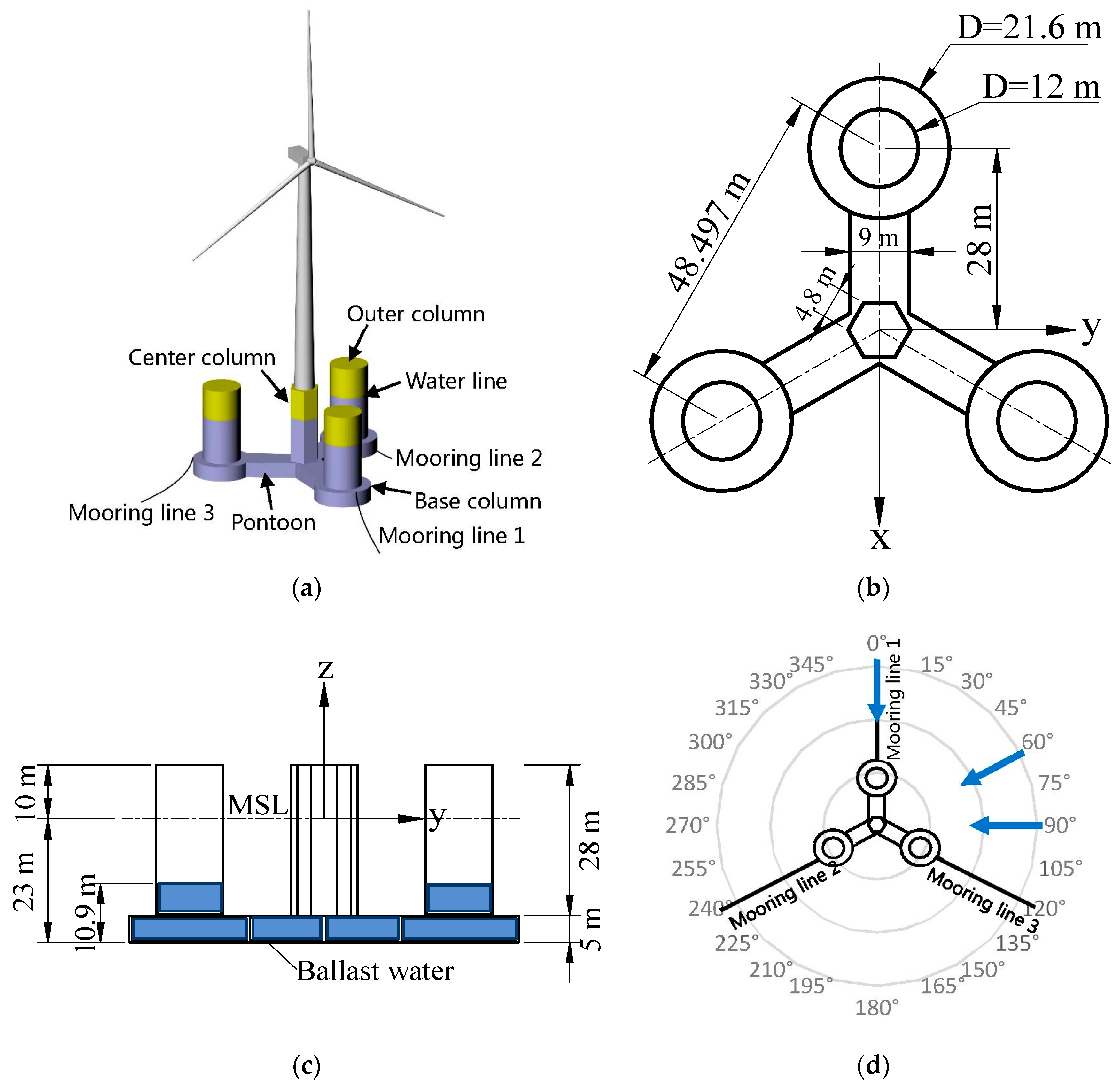
2. The Specification of the Semi-Submersible Floating Wind Turbine
- (1)
- Prestressed concrete is used to construct the major structure, which is expected to reduce manufacturing cost and a better resistance against corrosion and fatigue compared with steel;
- (2)
- Three rectangle section pontoons are arranged between the outer columns and the center column for connection, providing sufficient strength and stiffness for the platform. No brace arm is designed so as to reduce fatigue occurred at the joints [8];
- (3)
- The base columns and large-section pontoons are helpful to provide space for ballast, lower the center of gravity and alleviate the motion response, especially the heave motion.
3. Setup of the Model Tests
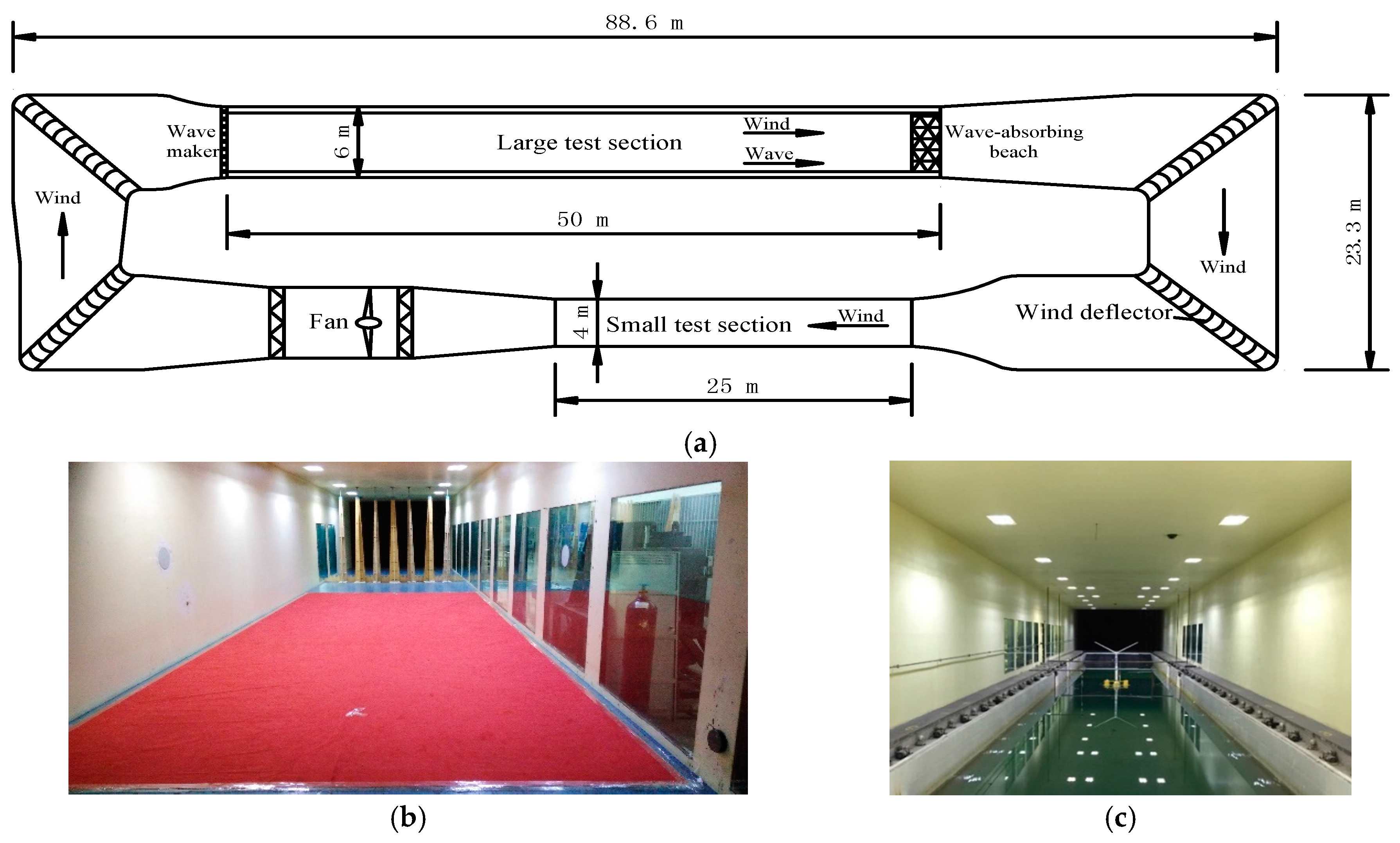
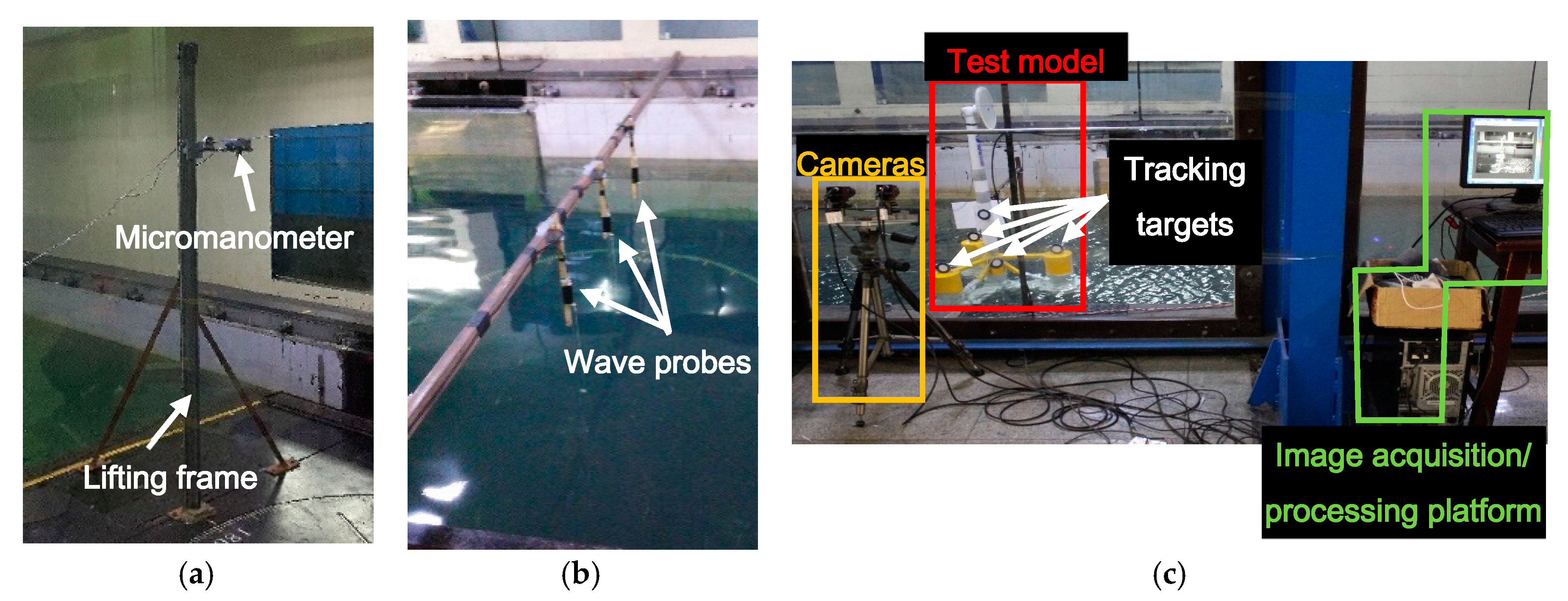
3.1. Test Facility
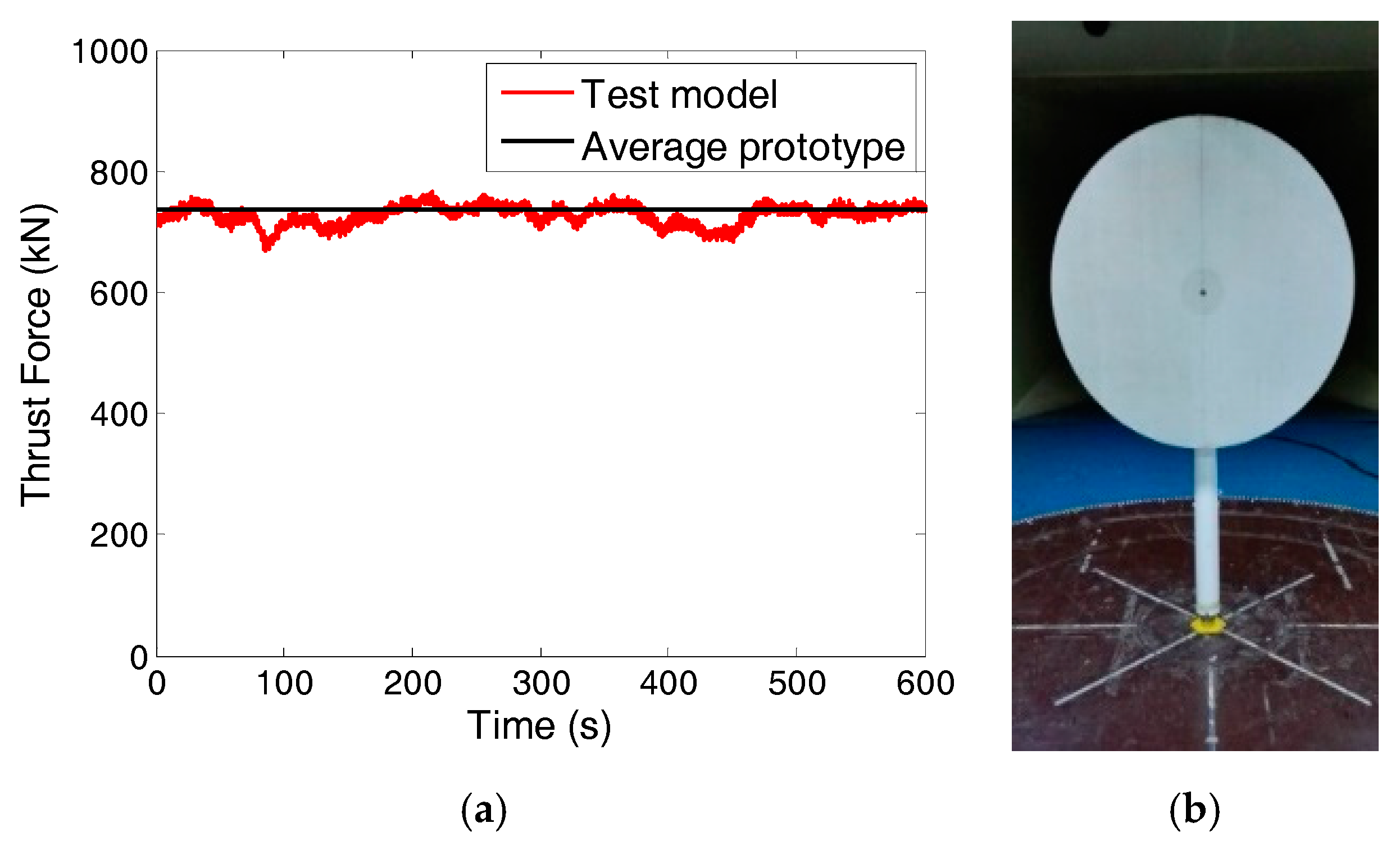
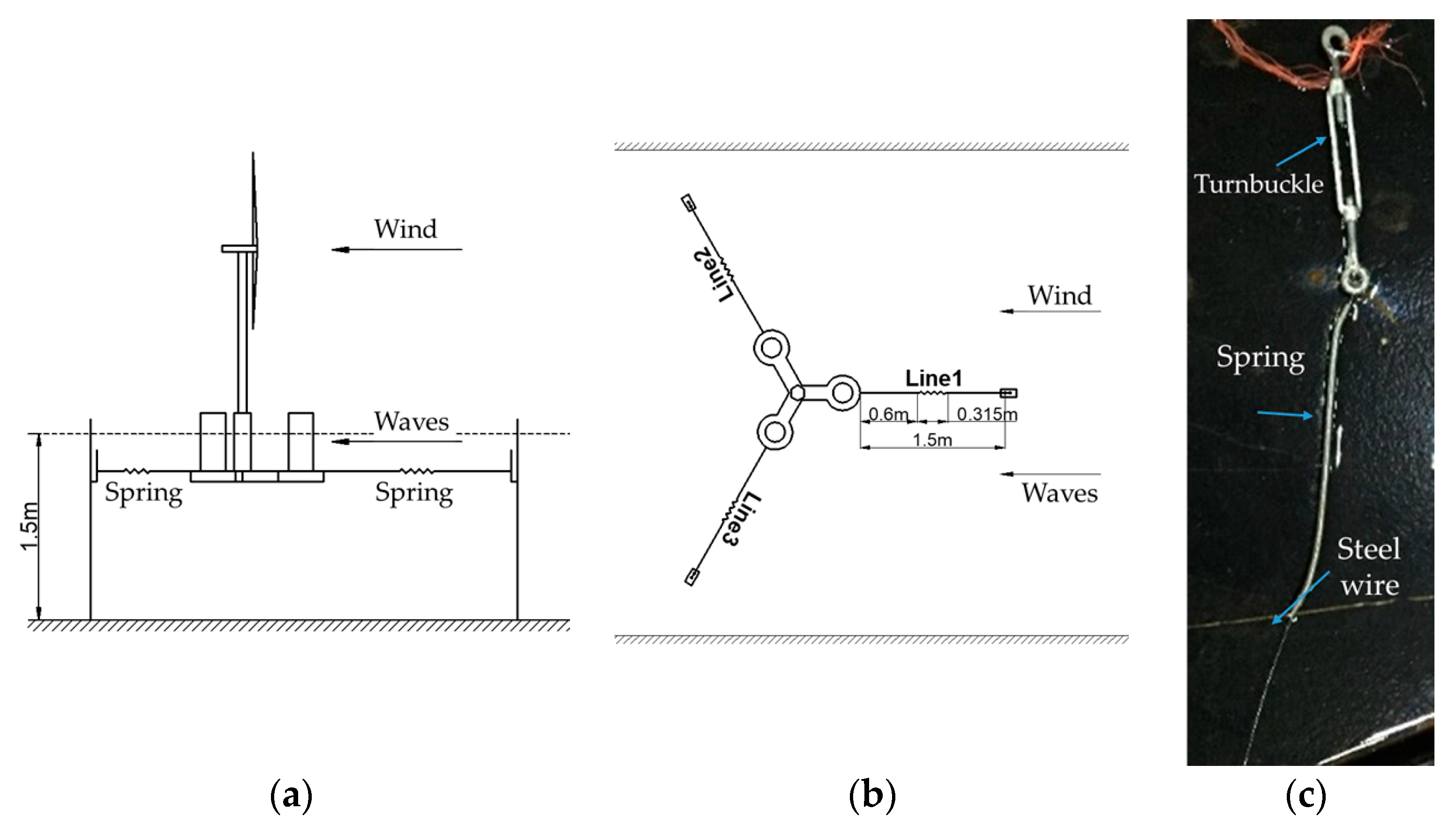
3.2. Experimental Models
3.3. Measuring Instruments
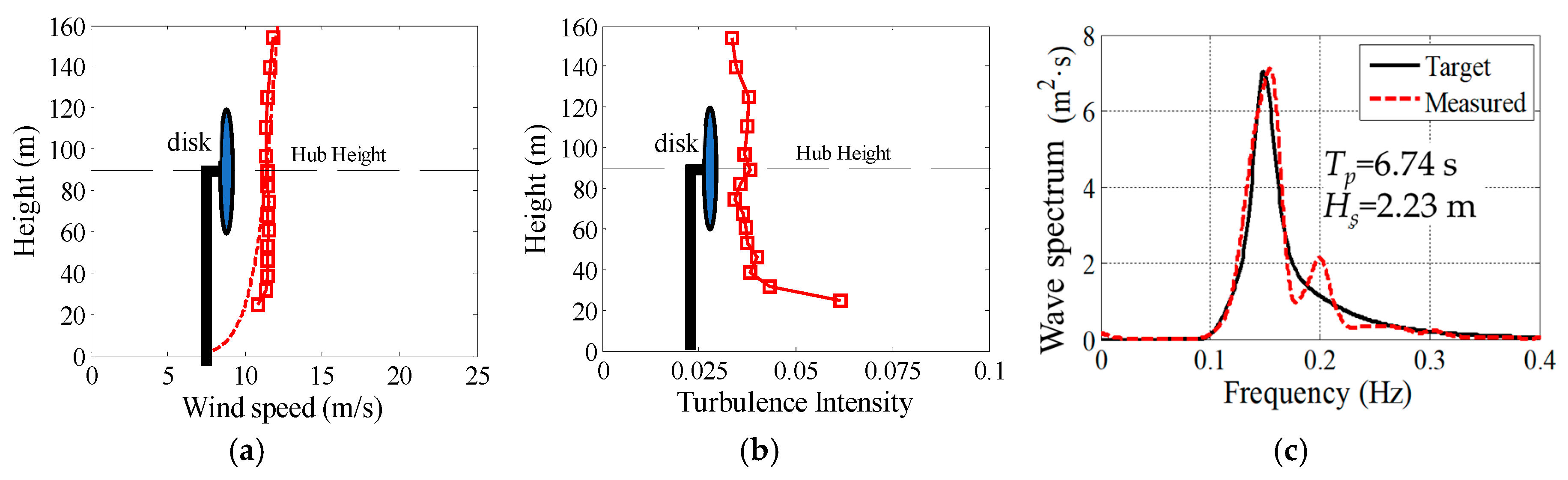
3.4. Wind and Wave Environment Calibration Tests
3.5. Test Matrix
4. Numerical Simulations
4.1. Hydrodynamics Modeling
4.2. Aerodynamics Modeling
4.3. Mooring Line Modeling
4.4. Structural Modeling of the Tower
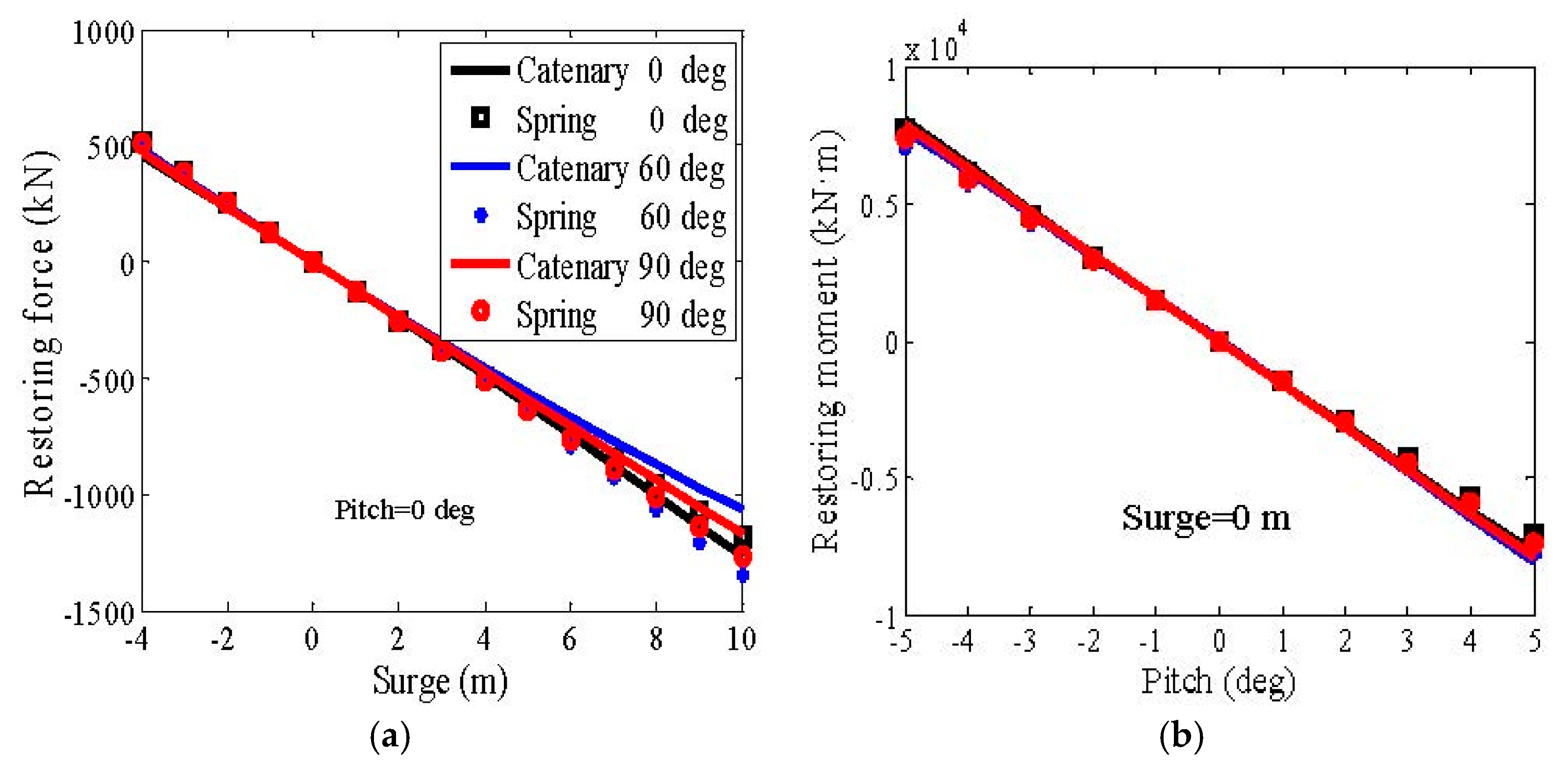
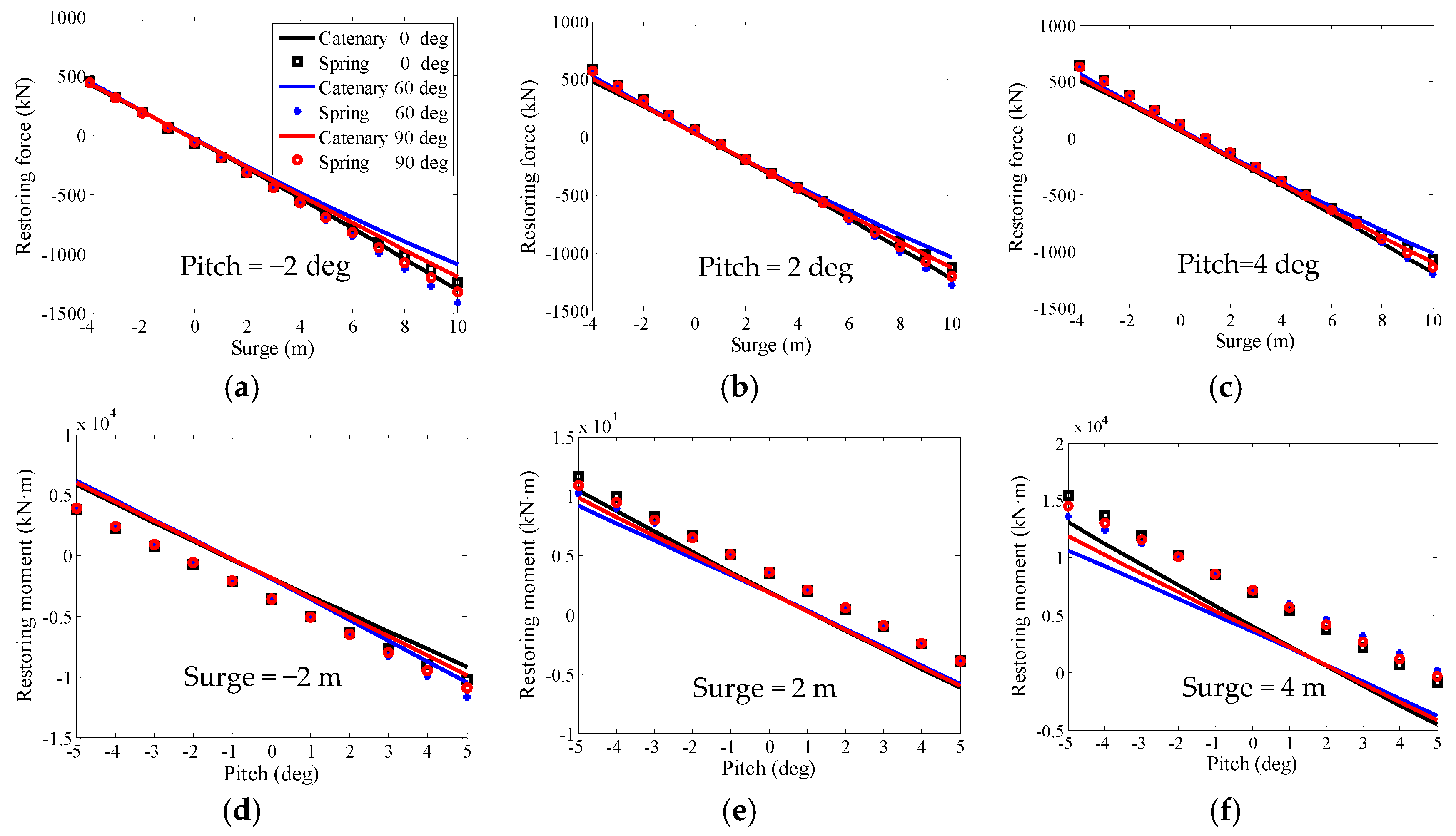
5. Results and Discussion
5.1. Free Decay Tests
5.2. Regular Wave Tests
5.3. Steady Wind Tests
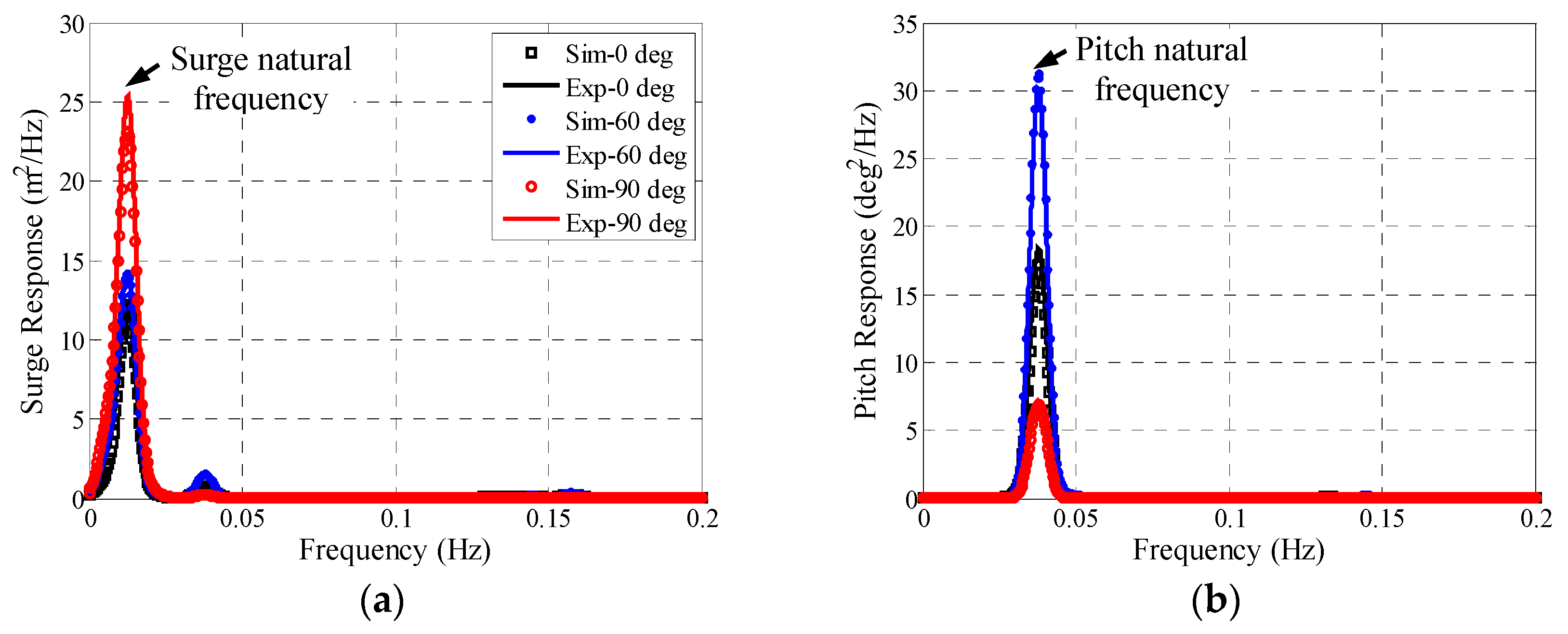
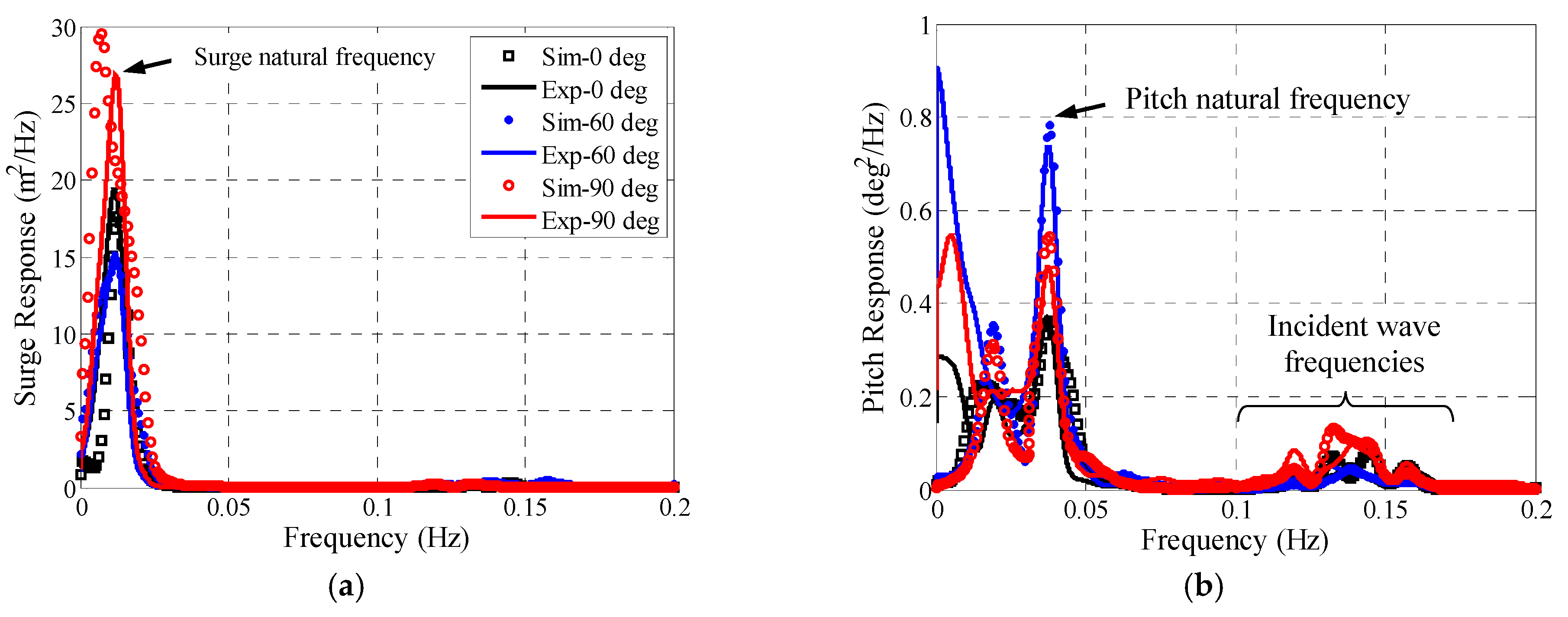
5.4. Irregular Wave Tests
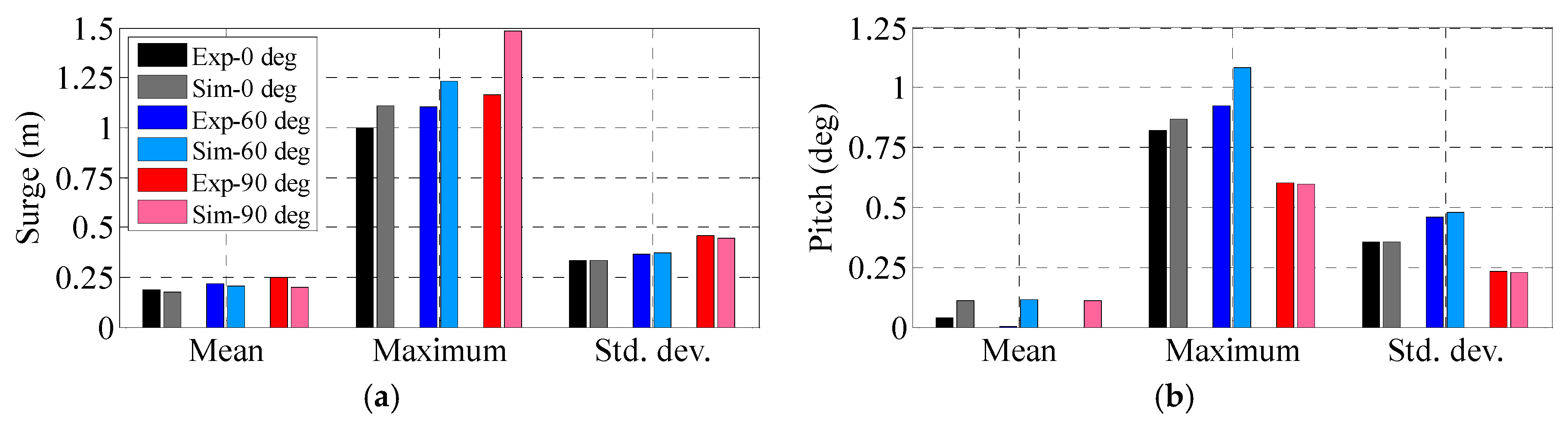
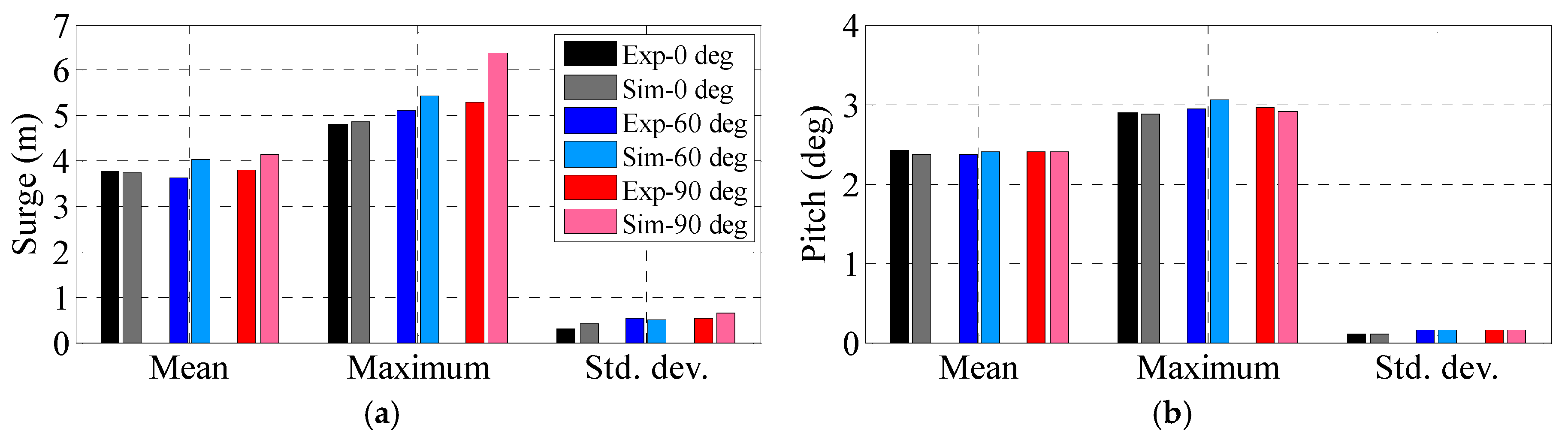
5.5. Combined Wind and Waves Tests
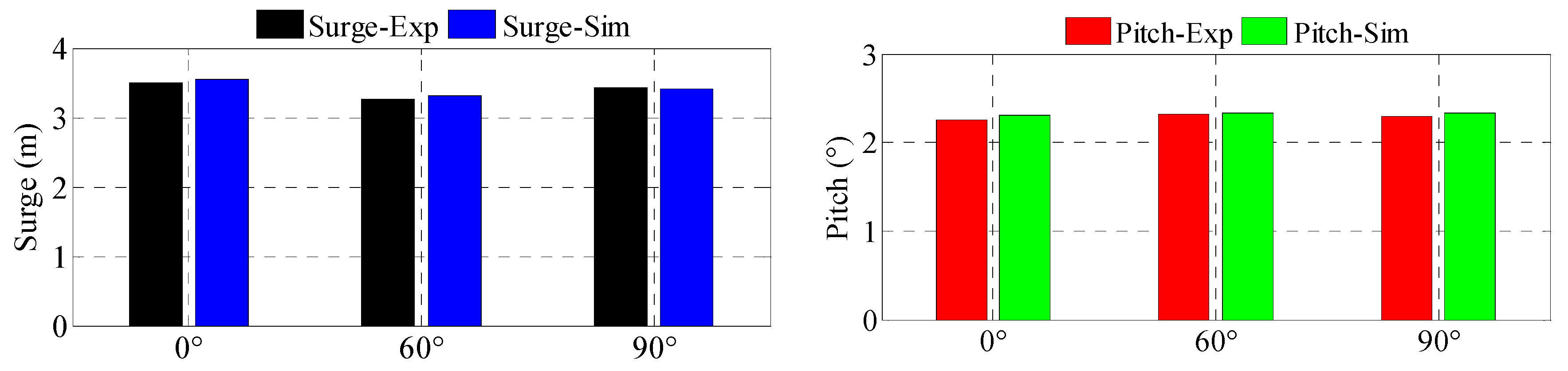
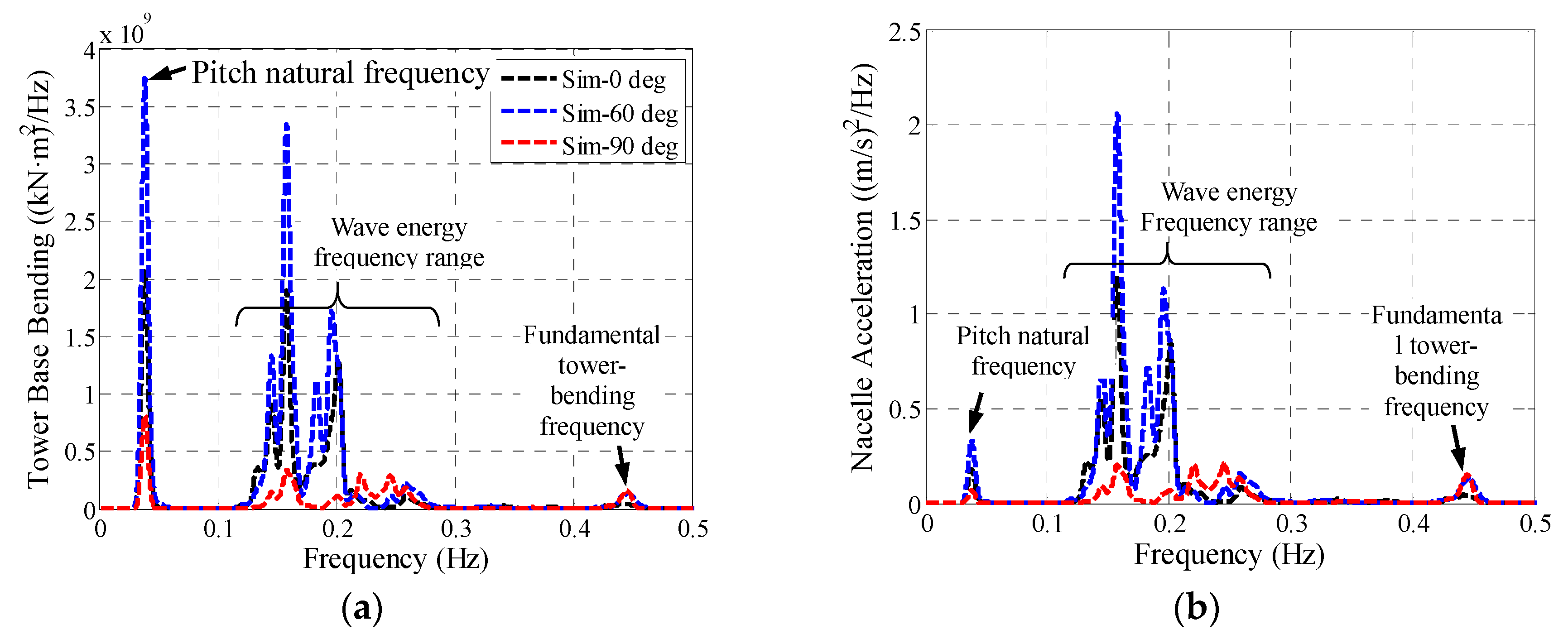
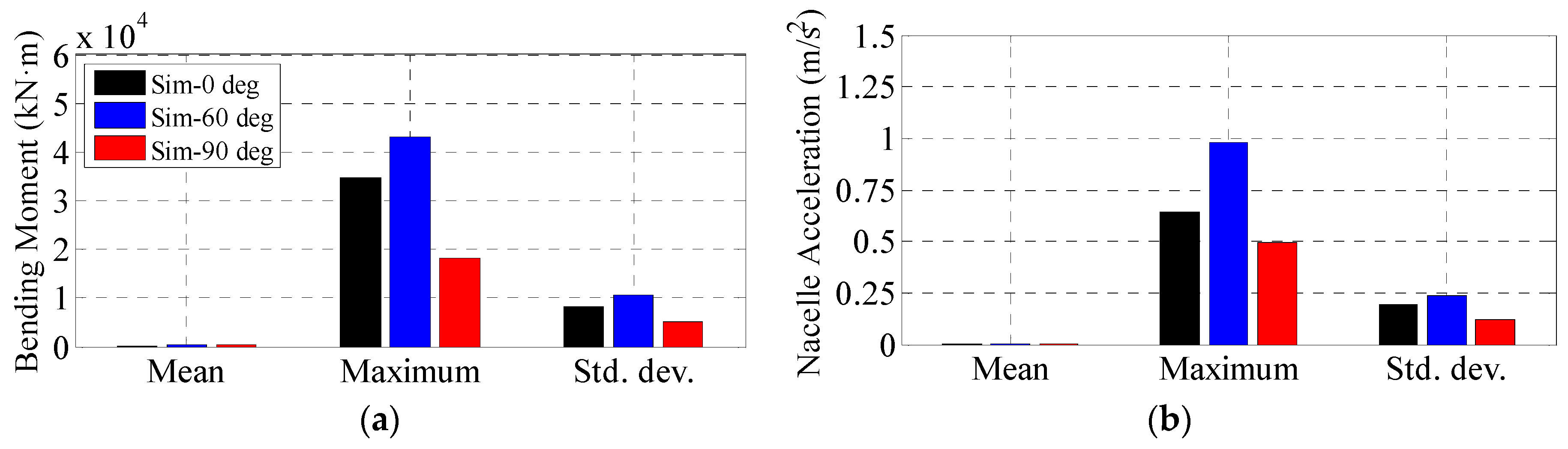
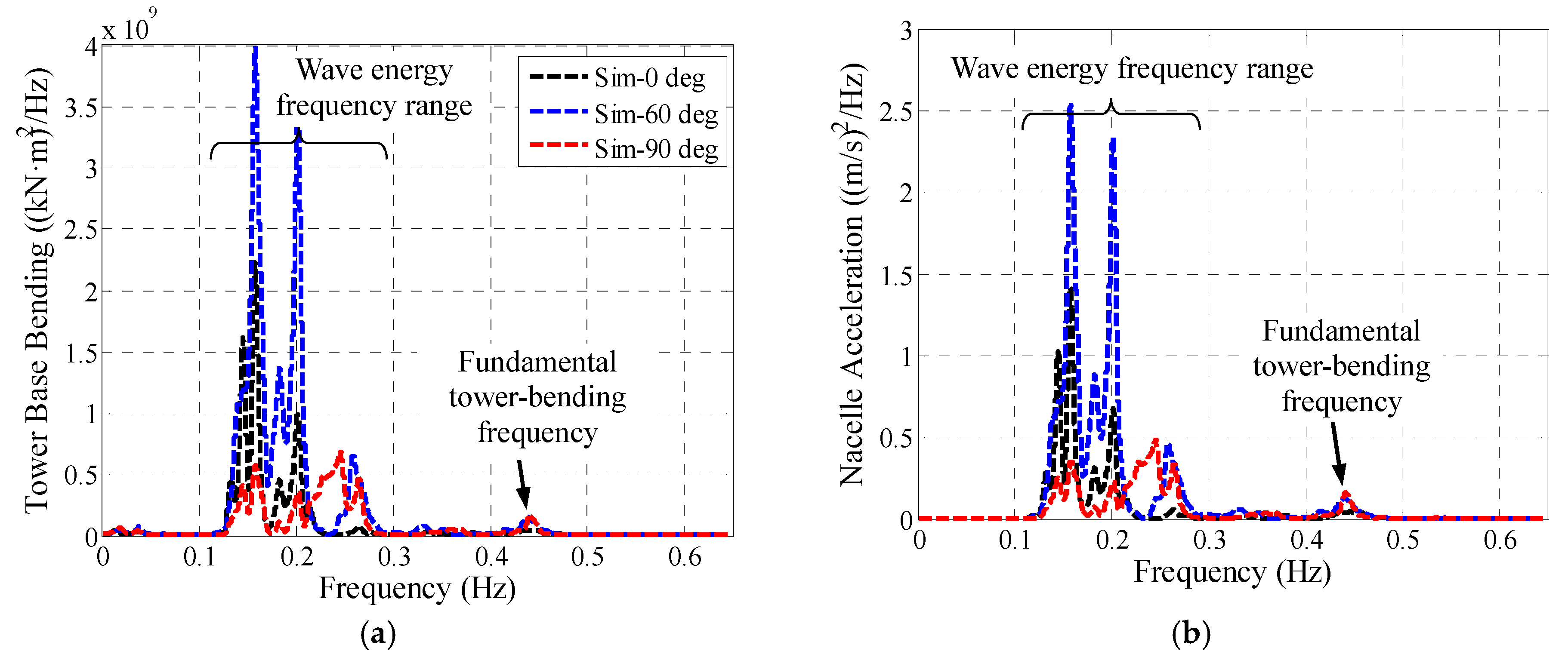
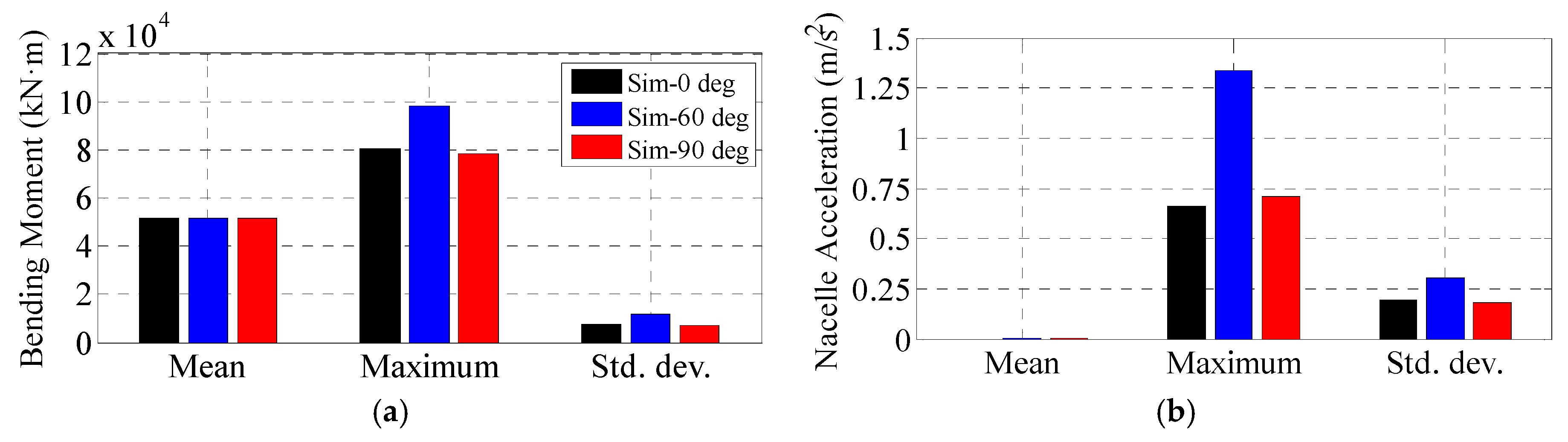
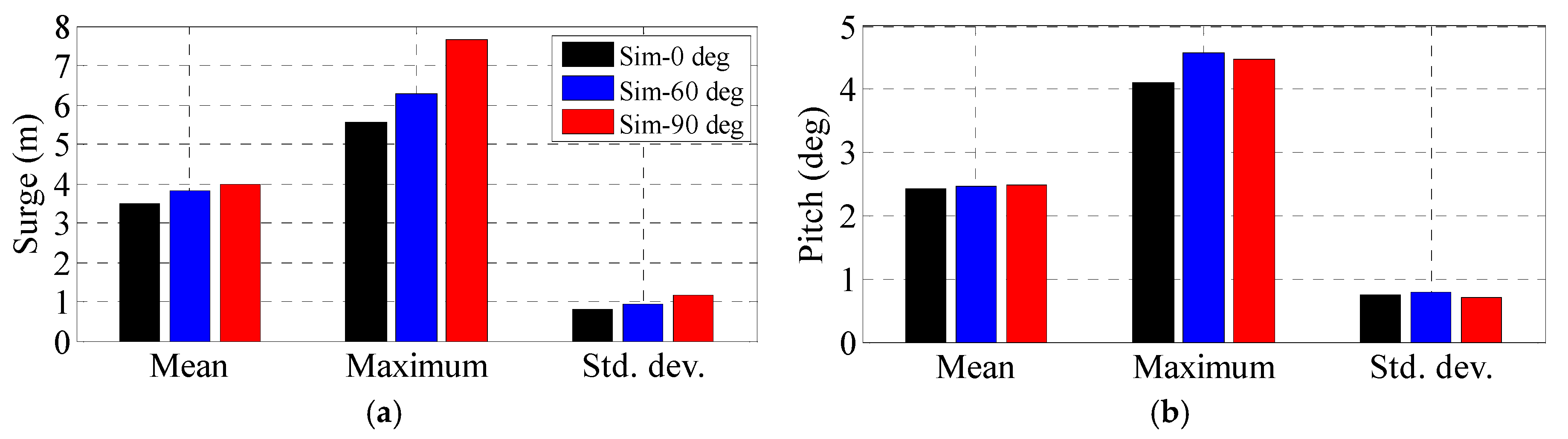
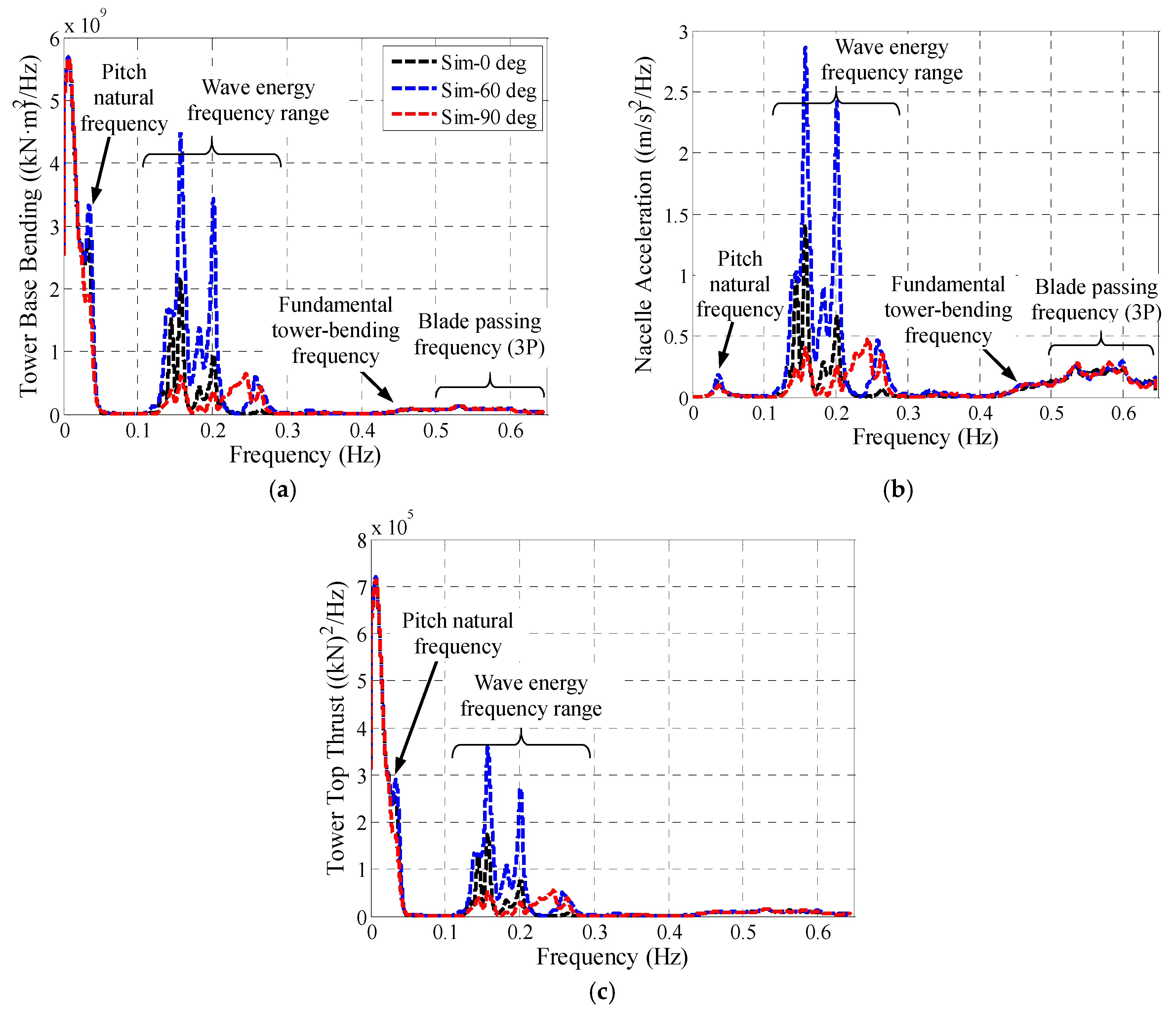
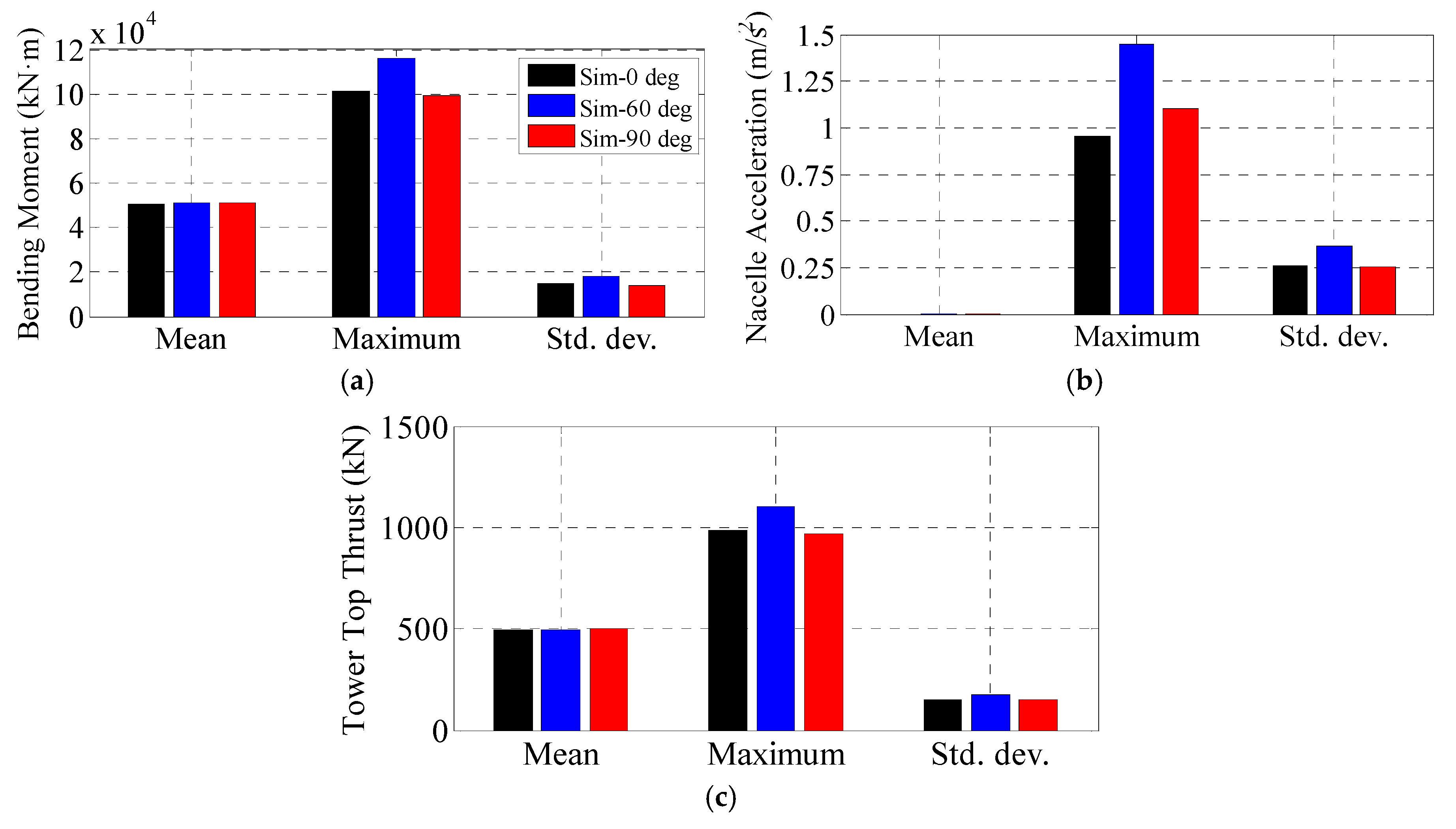
5.6. Simulations with a Fully Operational Wind Turbine and Realistic Wind and Waves
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Breton, S.; Moe, G. Status, plans and technologies for offshore wind turbines in Europe and North America. Renew. Energy 2009, 34, 646–654. [Google Scholar] [CrossRef]
- Ederer, N. The market value and impact of offshore wind on the electricity spot market: Evidence from Germany. Appl. Energy 2015, 154, 805–814. [Google Scholar] [CrossRef]
- Esteban, M.; Leary, D. Current developments and future prospects of offshore wind and ocean energy. Appl. Energy 2012, 90, 128–136. [Google Scholar] [CrossRef]
- Musial, W.; Butterfield, S.; Boone, A. Feasibility of floating platform systems for wind turbines. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Stiesdal, H. Hywind: The world’s first floating MW-scale wind turbine. Wind Dir. 2009, 52, 1–9. [Google Scholar]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 33104. [Google Scholar] [CrossRef]
- Fukushima Offshore Wind Consortium. Fukushima Floating Offshore Wind Farm Demonstration Project (Fukushima FORWARD). Available online: http://www.fukushima-forward.jp/pdf/pamphlet3.pdf (accessed on 8 December 2017).
- Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine: An alternative concept for offshore wind technology. Renew. Energy 2015, 83, 126–143. [Google Scholar] [CrossRef]
- Bruinsma, N. Validation and Application of a Fully Nonlinear Numerical Wave Tank. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 83, 433–449. [Google Scholar] [CrossRef]
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. J. Renew. Sustain. Energy 2013, 5, 023116. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.M.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Report No. NREL/TP-5000-60601; Contract No. DE-AC36-08-GO28308; National Renewable Energy Laboratory: Golden, CO, USA, 2014.
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; Report No. NREL/EL-500-38230; Contract No. DE-AC36-99-GO10337; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Michailides, C.; Gao, Z.; Moan, T. Experimental study of the functionality of a semisubmersible wind turbine combined with flap-type Wave Energy Converters. Renew. Energy 2016, 93, 675–690. [Google Scholar] [CrossRef]
- Gao, Z.; Moan, T.; Wan, L.; Michailides, C. Comparative numerical and experimental study of two combined wind and wave energy concepts. J. Ocean Eng. Sci. 2016, 1, 36–51. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z. Experimental investigation of aerodynamic effect–induced dynamic characteristics of an OC4 semi-submersible floating wind turbine. Proc. Inst. Mech. Eng. Part M 2017. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Thys, M.; Sauder, T.; Chabaud, V.; Sæther, L.O. Real-Time Hybrid Model Testing of a Braceless Semi-Submersible Wind Turbine: Part II—Experimental Results. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar]
- Naess, A.; Moan, T. Stochastic Dynamics of Marine Structures; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wan, L.; Greco, M.; Lugni, C.; Gao, Z.; Moan, T. A combined wind and wave energy-converter concept in survival mode: Numerical and experimental study in regular waves with a focus on water entry and exit. Appl. Ocean Res. 2017, 63, 200–216. [Google Scholar] [CrossRef]
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, University of Colorado, Golden, CO, USA, 2007. [Google Scholar]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef]
- Wang, L.; Sweetman, B. Multibody dynamics of floating wind turbines with large-amplitude motion. Appl. Ocean Res. 2013, 43, 1–10. [Google Scholar] [CrossRef]
- Ormberg, H.; Bachynski, E.E. Global analysis of floating wind turbines: Code development, model sensitivity and benchmark study. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2012. [Google Scholar]
- Philippe, M.; Babarit, A.; Ferrand, P. Effect of wave direction relative to wind on the motions of offshore floating wind turbine systems. In Proceedings of the 3rd International Conference and Exhibition on Ocean Energy, Bilbao, Spain, 6–8 October 2010; Ocean Energy Systems: Lisbon, Spain, 2010. [Google Scholar]
- Philippe, M.; Babarit, A.; Ferrant, P. Modes of response of an offshore wind turbine with directional wind and waves. Renew. Energy 2013, 49, 151–155. [Google Scholar] [CrossRef]
- Wayman, E.N. Coupled Dynamics and Economic Analysis of Floating Wind Turbine Systems. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Ramachandran, G.K.V.; Bredmose, H.; Sorensen, J.N.; Jensen, J.J. Fully Coupled Three-Dimensional Dynamic Response of a Tension-Leg Platform Floating Wind Turbine in Waves and Wind. J. Offshore Mech. Arct. Eng. 2014, 136, 020901. [Google Scholar] [CrossRef]
- Barj, L. Influence of Met-Ocean Conditions on the Loads Analysis of a Floating Wind Turbine. Master’s Thesis, The Pennsylvania State University, State College, PA, USA, 2013. [Google Scholar]
- Barj, L.; Stewart, S.; Stewart, G.; Lackner, M.; Jonkman, J.; Robertson, A.; Matha, D. Wind/wave misalignment in the loads analysis of a floating offshore wind turbine. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2014. [Google Scholar]
- Bachynski, E.E.; Kvittem, M.I.; Luan, C.; Moan, T. Wind-wave misalignment effects on floating wind turbines: Motions and tower load effects. J. Offshore Mech. Arct. Eng. 2014, 136, 0419024. [Google Scholar] [CrossRef]
- Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine subjected to misaligned wave and wind. J. Renew. Sustain. Energy 2016, 83, 126–143. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Report No. NREL/TP-500-38060; Contract No. DE-AC36-08-GO28308; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Martin, H.R. Development of a Scale Model Wind Turbine for Testing of Offshore Floating Wind Turbine Systems. Master’s Thesis, University of Maine, Orono, ME, USA, 2011. [Google Scholar]
- Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for wind/wave basin testing of floating offshore wind turbines. J. Offshore Mech. Arct. Eng. 2012, 136, 020905. [Google Scholar]
- Fowler, M.J.; Kimball, R.W.; Thomas, I.D.A.; Goupee, A.J. Design and testing of scale model wind turbines for use in wind/wave basin model tests of floating offshore wind turbines. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Wan, L.; Gao, Z.; Moan, T. Experimental and numerical study of hydrodynamic responses of a combined wind and wave energy converter concept in survival modes. Coast. Eng. 2015, 104, 151–169. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Experimental and numerical comparisons of hydrodynamic responses for a combined wind and wave energy converter concept under operational conditions. Renew. Energy 2016, 93, 87–100. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Comparative experimental study of the survivability of a combined wind and wave energy converter in two testing facilities. Ocean Eng. 2016, 111, 82–94. [Google Scholar] [CrossRef]
- Det Norske Veritas. Recommended practice dnv-rp-c205. In Environmental Conditions and Environmental Loads; Det Norske Veritas: Oslo, Norway, 2010. [Google Scholar]
- Ishihara, T.; Phuc, P.V.; Sukegawa, H.; Shimada, K.; Ohyama, T. A study on the dynamic response of a semi-submersible floating offshore wind turbine system Part 1: A water tank test. In Proceedings of the 12th International Conference on Wind Engineering, Gairns, Australia, 1–6 July 2007; Australasian Wind Engineering Society: Gairns, Australia, 2007. [Google Scholar]
- Shan, B.; Zheng, S.; Ou, J. Free vibration monitoring experiment of a stayed-cable model based on stereovision. Measurement 2015, 76, 228–239. [Google Scholar] [CrossRef]
- Shan, B.; Zheng, S.; Ou, J. A stereovision-based crack width detection approach for concrete surface assessment. KSCE J. Civ. Eng. 2016, 20, 803–812. [Google Scholar] [CrossRef]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Lee, C. WAMIT Theory Manual; Massachusetts Institute of Technology: Cambridge, MA, USA, 1995. [Google Scholar]
- Duarte, T.; Sarmento, A.; Jonkman, J. Effects of second-order hydrodynamic forces on floating offshore wind turbines. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2014. [Google Scholar]
- Bayati, I.; Jonkman, J.; Robertson, A.; Platt, A. The Effects of Second-Order Hydrodynamics on a Semisubmersible Floating Offshore Wind Turbine; Report No. NREL/CP-5000-61752; Contract No. DE-AC36-08-GO28308; National Renewable Energy Laboratory: Golden, CO, USA, 2014.
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M. Importance of second-order difference-frequency wave-diffraction forces in the validation of a fast semi-submersible floating wind turbine model. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Roald, L.; Jonkman, J.; Robertson, A.; Chokani, N. The effect of second-order hydrodynamics on floating offshore wind turbines. Energy Procedia 2013, 35, 253–264. [Google Scholar] [CrossRef]
- Bir, G. User’s Guide to BModes (Software for Computing Rotating Beam-Coupled Modes); Report No. NREL/TP-500-39133; Contract No. DE-AC36-99-GO10337; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J. Overview of the TurbSim Stochastic Inflow Turbulence Simulator; Report No. NREL/TP-500-41137; Contract No. DE-AC36-99-GO10337; National Renewable Energy Laboratory: Golden, CO, USA, 2007.
- International Electrotechnical Commission. Wind Turbines—Part 1: Design Requirements; IEC61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]

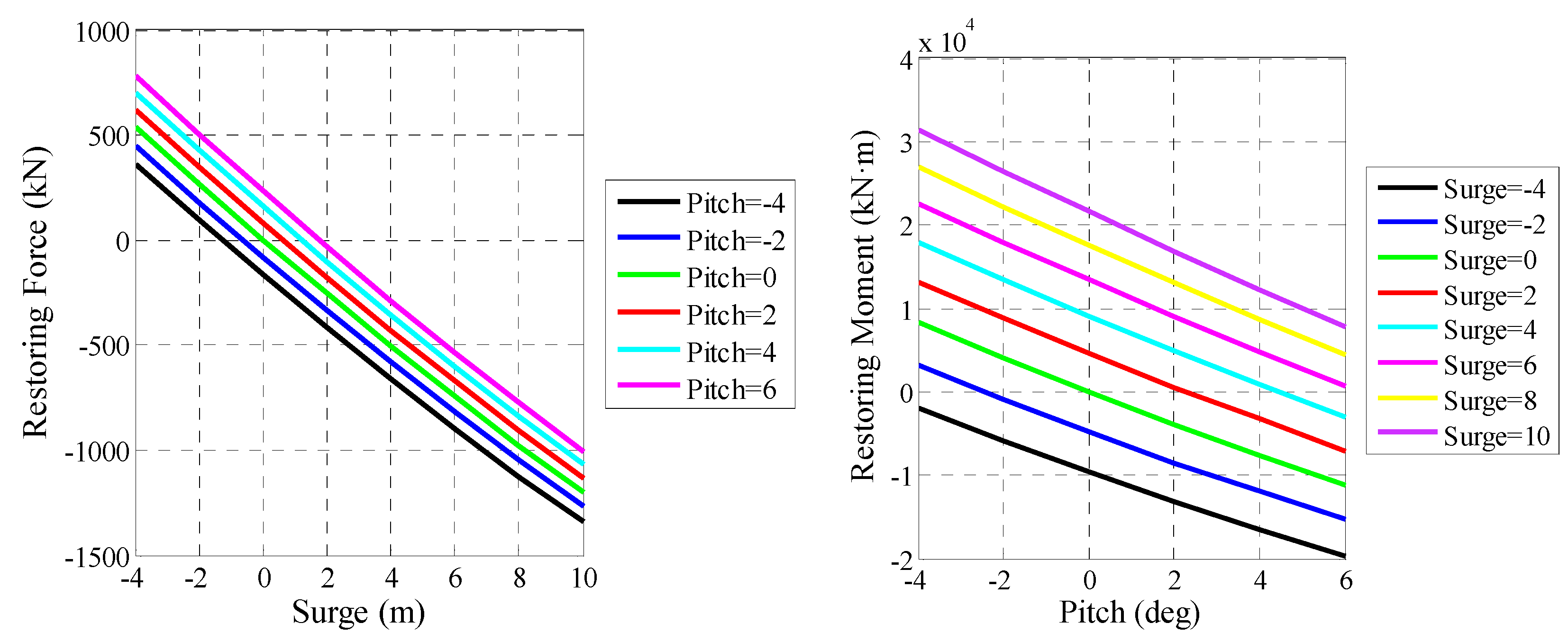

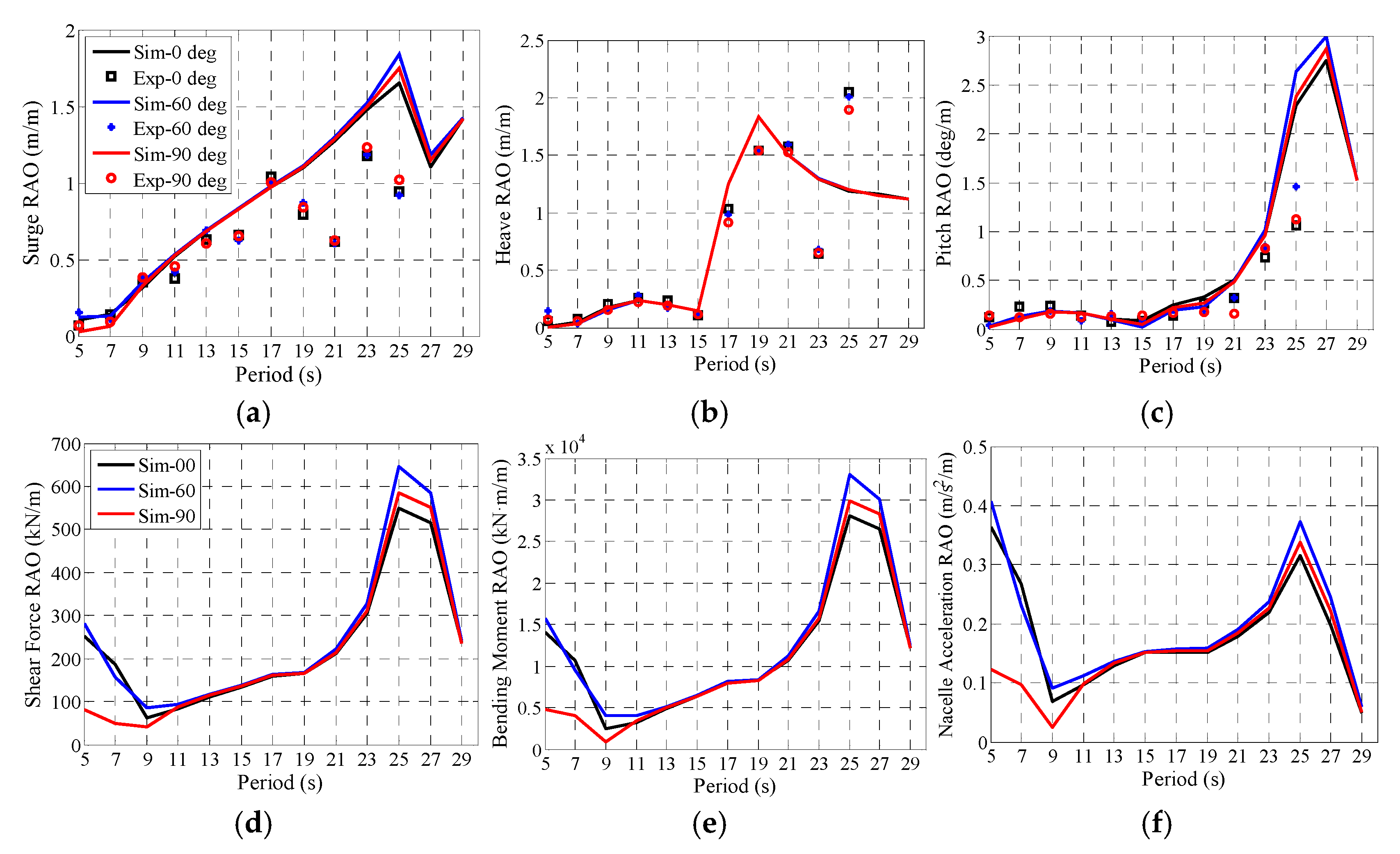
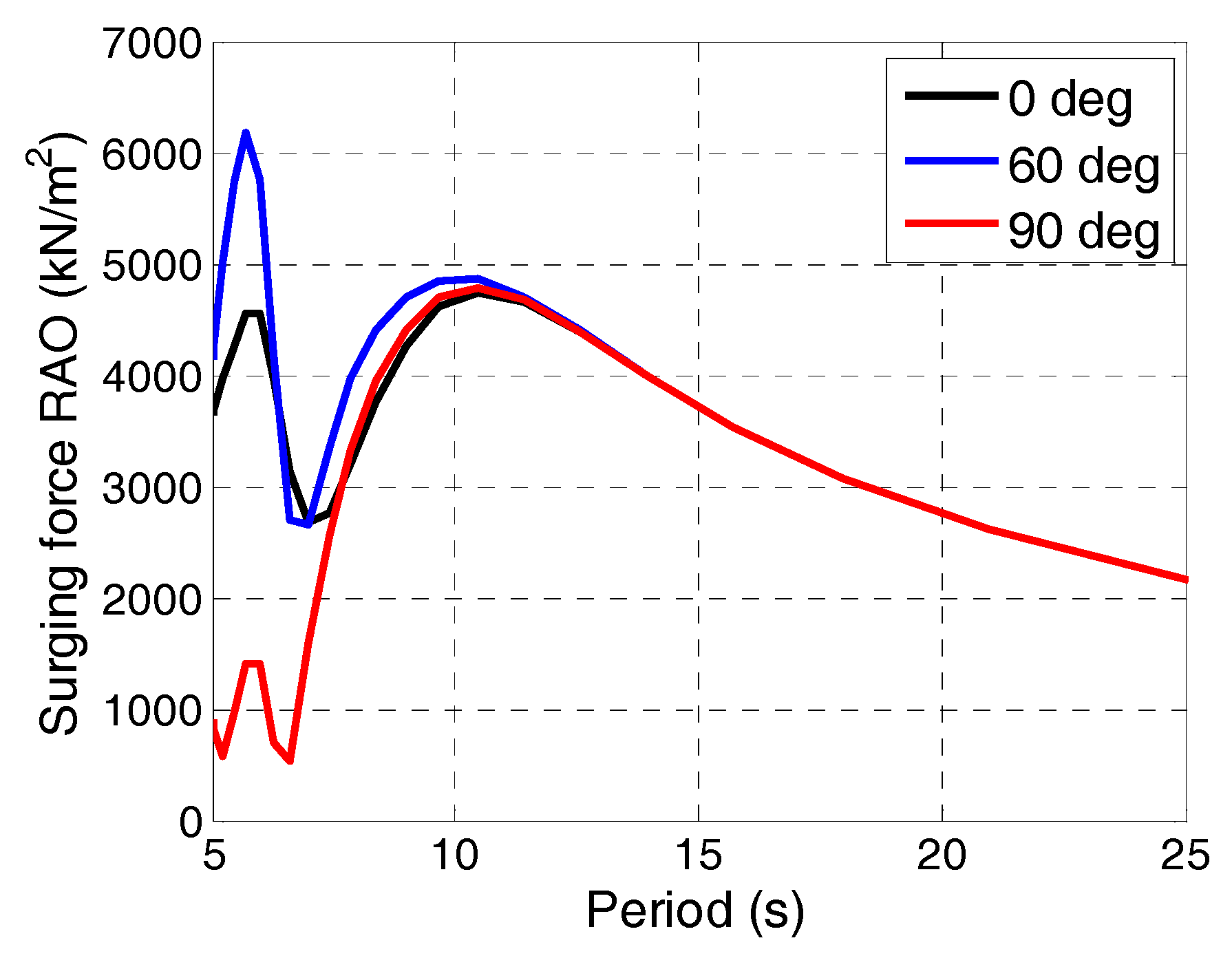
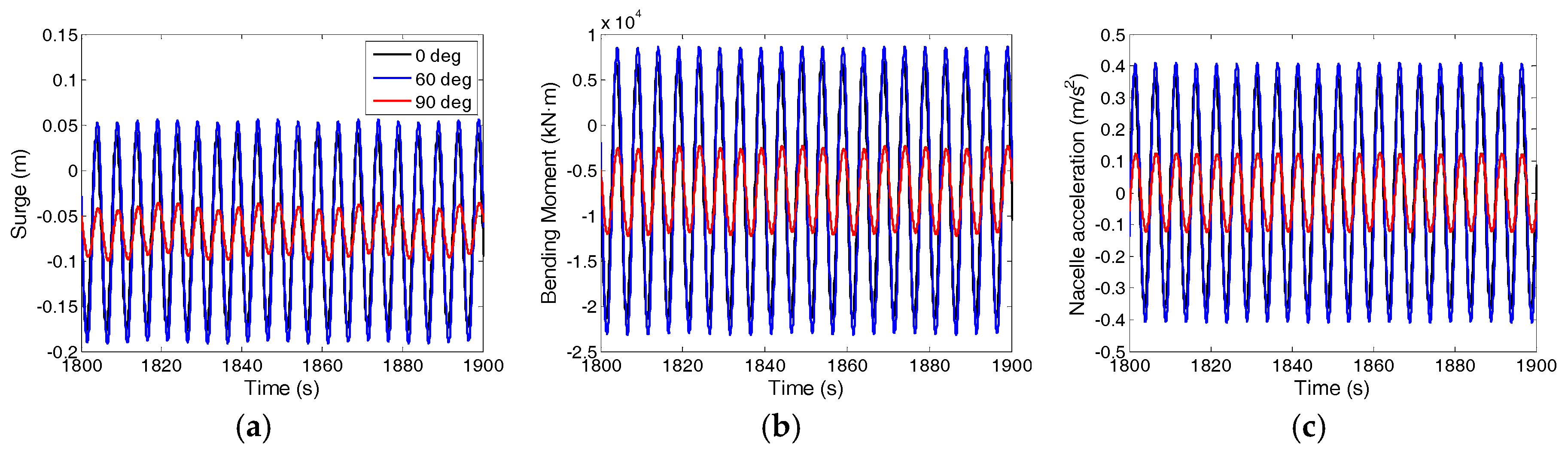



| Structural Properties | Value without Wind Turbine | Value with Wind Turbine |
|---|---|---|
| Mass, including ballast (kg) | 1.4560 × 107 | 1.5237 × 107 |
| Center of mass (CM) location below MSL (m) | 16.063 | 11.797 |
| Roll inertia around CM (kg·m2) | 5.780 × 109 | 1.109 × 1010 |
| Pitch inertia around CM (kg·m2) | 5.780 × 109 | 1.109 × 1010 |
| Yaw inertia around CM (kg·m2) | 9.630 × 109 | 9.970 × 109 |
| Properties | Value |
|---|---|
| Number of mooring lines | 3 |
| Depth of fairleads below MSL (m) | 18 |
| Depth of anchors below MSL (m) | 90 |
| Horizontal distance between anchors and the z-axis (m) | 424.8 |
| Unstretched length of mooring line (m) | 392 |
| Diameter of mooring line (m) | 0.08 |
| Equivalent apparent mass in fluid per unit length (kg/m) | 136.248 |
| Equivalent extensional stiffness (MN) | 50 |
| Category | Closed Return Wind Tunnel with Two Test Sections |
|---|---|
| Sizes of the small test section | 4.0 m (W) × 3.0 m (H) × 25 m (L) |
| Sizes of the large test section | 6.0 m (W) × 3.6 m (H) × 50 m (L) |
| Sizes of the wave flume | 5.0 m (W) × 4.5 m (H) × 50 m (L) |
| Maximum wind speed | 50 m/s for the small test section |
| 30 m/s for the large test section | |
| Maximum wave height | 0.4 m |
| Range of wave periods | 0.5 s to 5 s |
| Tests | Wind Speed at Hub Height (m/s) | Wave Period (s) | Wave Height (m) | Wind/Wave Headings |
|---|---|---|---|---|
| Free decay tests | - | - | - | - |
| Regular wave tests | - | 5:2:15 | 1.8 | 0°/60°/90° |
| - | 17:2:25 | 2 | ||
| Wind-only tests | 11.5 | - | - | 0°/60°/90° |
| Irregular wave tests | - | 6.74 | 2.23 | 0°/60°/90° |
| Combined wind and wave tests | 11.5 | 6.74 | 2.23 | 0°/60°/90° |
| DOF | Tests | Simulations | Relative Errors |
|---|---|---|---|
| Surge | 80.5 s | 79.9 s | −0.7% |
| Sway | 79.7 s | 78.6 s | −1.4% |
| Heave | 17.7 s | 17.6 s | −0.6% |
| Roll | 25.8 s | 26.0 s | 0.8% |
| Pitch | 26.0 s | 26.0 s | 0% |
| Yaw | 79.0 s | 79.7 s | 0.9% |
| DOF | Global Quadratic Coefficient |
|---|---|
| Surge | 4.0 × 106 N·s2/m2 |
| Sway | 4.0 × 106 N·s2/m2 |
| Heave | 1.0 × 106 N·s2/m2 |
| Roll | 2.0 × 109 N·m·s2/rad2 |
| Pitch | 2.0 × 109 N·m·s2/rad2 |
| Yaw | 4.0 × 109 N·m·s2/rad2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Shan, B.; Xiao, Y.; Li, C.; Hu, G.; Song, X.; Liu, Y.; Hu, Y. Directionality Effects of Aligned Wind and Wave Loads on a Y-Shape Semi-Submersible Floating Wind Turbine under Rated Operational Conditions. Energies 2017, 10, 2097. https://doi.org/10.3390/en10122097
Zhou S, Shan B, Xiao Y, Li C, Hu G, Song X, Liu Y, Hu Y. Directionality Effects of Aligned Wind and Wave Loads on a Y-Shape Semi-Submersible Floating Wind Turbine under Rated Operational Conditions. Energies. 2017; 10(12):2097. https://doi.org/10.3390/en10122097
Chicago/Turabian StyleZhou, Shengtao, Baohua Shan, Yiqing Xiao, Chao Li, Gang Hu, Xiaoping Song, Yongqing Liu, and Yimin Hu. 2017. "Directionality Effects of Aligned Wind and Wave Loads on a Y-Shape Semi-Submersible Floating Wind Turbine under Rated Operational Conditions" Energies 10, no. 12: 2097. https://doi.org/10.3390/en10122097
APA StyleZhou, S., Shan, B., Xiao, Y., Li, C., Hu, G., Song, X., Liu, Y., & Hu, Y. (2017). Directionality Effects of Aligned Wind and Wave Loads on a Y-Shape Semi-Submersible Floating Wind Turbine under Rated Operational Conditions. Energies, 10(12), 2097. https://doi.org/10.3390/en10122097






