Abstract
Several control schemes specifically designed to operate inverter-based industrial microgrids during voltage sags have been recently proposed. This paper first classifies these control schemes in three categories and then performs a comparative analysis of them. Representative control schemes of each category are selected, described and used to identify the main features and performance of the considered category. The comparison is based on the evaluation of several indexes, which measure the power quality of the installation and utility grid during voltage sags, including voltage regulation, reactive current injection and transient response. The paper includes selected simulation results from a 500 kVA industrial microgrid to validate the expected features of the considered control schemes. Finally, in view of the obtained results, the paper proposes an alternative solution to cope with voltage sags, which includes the use of a static compensator in parallel with the microgrid. The novelty of this proposal is the suitable selection of the control schemes for both the microgrid and the static compensator. The superior performance of the proposal is confirmed by the analysis of the quality indexes. Its practical limitations are also revealed, showing that the topic studied in this paper is still open for further research.
1. Introduction
An inverter-based microgrid is a combination of power generation units, energy storage systems and loads in a single, controllable power system [1,2,3]. The presence of power inverters as interfaces for the generation and storage components offers flexible operation, high power quality and reliable power delivery [4,5]. Two modes of operation in both the microgrid and the power inverters make these well-known characteristics possible. On the one hand, the microgrid operates normally in grid-connected mode, interconnected to the utility grid. In some circumstances, it can intentionally separate from the grid and operate autonomously as an independent island, which is known as islanded mode [6,7,8]. On the other hand, the power inverters can be programmed to equivalently operate as power-controlled current or voltage sources, depending on the needs of the microgrid [8]. As current sources, the inverters are responsible for injecting the amount of active and reactive power set by the power references. As voltage sources, the inverters contribute to support the microgrid voltage, including amplitude and frequency regulation [9].
An industrial microgrid is a practical application of the concepts of inverter-based microgrids to the power supply of industrial processes [10]. In this context, the principal requirement is the power supply of the priority loads uninterruptedly [11,12]. Typically, the loads are electrical machines in charge of a continuous process in a production line. The manufacturing of paper or plastic film are two examples of a production line requiring reliable power delivery to avoid damaging materials during the production process. The possibility to operate the industrial microgrid in islanded mode is essential in this application to guarantee the continuous operation during power events and grid faults [13,14]. Other types of microgrids have been studied in the literature including residential, commercial, institutional, military and remote microgrids [15,16,17]. They have specific requirements such as variable profile high-power loads, physical and cyber security and forced islanded operation, to name just a few. However, this work focuses on the study of industrial microgrids.
The large-scale integration of renewable energy sources in transmission and distribution networks has led network operators to define low voltage ride through requirements, in order to avoid the sudden disconnection of significant amounts of power in case of severe voltage sags while providing, at the same time, local voltage support through the injection of reactive current [18,19]. Therefore, the power inverters of these energy sources must respond to grid code requirements demanding for reactive current injection. Such requirements were designed for predominantly inductive grids and thus they are not the most appropriated ones regarding industrial microgrid environments where the predominance of inductive coupling is in cause [19].
The control system is a key element in the operation and performance of microgrids [20]. In this application, the control system is typically organized in a central controller responsible to perform the energy management of the microgrid and in local controllers in charge of the power processing of the inverters. Particularly, during grid voltage sags, the local controllers are fundamental to avoid sudden tripping of the inverters, which could lead to a utility grid blackout if the mitigation actions are not properly implemented. Several control schemes specifically designed to operate microgrids during voltage sags have been recently presented. This paper first analyzes the recent literature and then classifies these control schemes in three categories, according to the operation modes of both the microgrid and the inverters: grid-connected current-source (GCCS) schemes [21,22,23,24,25], islanded voltage-source (IVS) schemes [26,27] and grid-connected voltage-source (GCVS) schemes [28,29,30]. On the one hand, GCCS schemes usually consider a fixed current-injection angle of 90 degrees (i.e., a predominant inductive coupling, as mentioned above) [21,22,23,24], thus providing a non-optimal voltage support during the voltage sag. The three control schemes presented in [25] solve this problem by using a current-injection angle defined by the angle of the impedance seen from the generator output. The three alternatives inject active and reactive current via (1) positive sequence only; (2) negative sequence only; and (3) both positive and negative sequences. These representative control schemes are selected in this study to identify the main features and performances of the GCCS schemes. On the other hand, both IVS and GCVS schemes are based on the droop control method, which has been extensively studied in the literature. The differences between the operation and performance of these schemes during voltage sags in an industrial microgrid are evaluated in this study by selecting the control configuration presented in [27,30].
This paper introduces an analytical tool to compare the performance of the considered control schemes. The comparative analysis is based on the evaluation of several indexes, which measure the power quality of the installation and utility grid during voltage sags, including voltage regulation, reactive current injection and transient response. Three voltage sags with different amplitudes of the positive and negative sequence components are considered in the evaluation test to examine the control operation for different faulty scenarios. This performance comparison constitutes the first contribution of this study. In view of the results of the analysis, this paper proposes an alternative solution to cope with voltage sags, which includes the use of a static compensator (STATCOM) in parallel with the microgrid [31]. Two proposals are introduced in this study according to the operation of the microgrid in grid-connected or in islanded mode, while the STATCOM remains continuously connected to the utility grid during the voltage sag. The novelty and second contribution of these two proposals are the suitable selection of the control schemes for both the microgrid and the STATCOM. The superior performance of the proposals is confirmed by the analysis of the quality indexes for the three faulty scenarios. Their practical limitations are also detailed, showing that the topic studied in this paper is still open for further research.
This paper is organized as follows. Section 2 formulates the problem to be solved in an industrial microgrid. Section 3 presents the grid-faulty control schemes considered in this study. Section 4 performs the comparative analysis of these control schemes. This section includes selected simulation results to validate the results of the analysis. Section 5 introduces the original control solution and discusses its advantages and limitations. Section 6 is the conclusion.
2. Problem Statement
This section presents the problem statement, including the description of the 500 kVA industrial microgrid, the definition of the power quality indexes and the problem formulation.
2.1. Industrial Microgrid
Figure 1 shows the diagram of the 500 kVA industrial installation considered in this study. It has two buildings, a factory with a nominal power of 320 kW and a second building with offices with 80 kW of nominal power. In the factory, the production process requires 250 kW at full load, which is the priority load of the microgrid. The installation has two generators, G1 (46 kVA) and G2 (230 kVA), placed on the roof of the buildings. They use photovoltaic (PV) technology and batteries to smooth the generation capacity and to have an energy reserve. The sizing of the generators was carried out taking into account the priority load with a certain margin for the compensation of power losses. The microgrid is connected to the utility grid at the point of common coupling (PCC) through the switch S, which is closed in grid-connected mode and open in islanded mode. The diagram shows the equivalent impedances of the microgrid, which account for the impedances of cables, lines and transformers. Although the transformers are not explicitly shown, the diagram indicates the voltage levels in several locations of the microgrid. The voltage and current of the generators are also marked in the diagram.
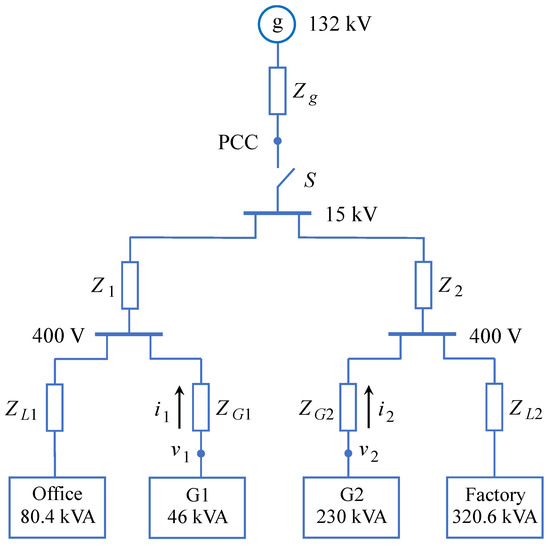
Figure 1.
Diagram of the 500 kVA microgrid considered in this study.
The nominal values of the microgrid components are listed in Table 1. The impedances included in the table account for the impedances of cables, lines and transformers. In the particular case of transformers, the impedances are referred to their low-voltage sides. During islanded mode, only the supply of priority loads is guaranteed in the microgrid. Note that local generators have enough capacity to supply these loads with enough room for the compensation of power losses.

Table 1.
Nominal values of the microgrid components.
Figure 2 shows a diagram with the main components of each generator. The PV source and the batteries regulate the voltage of the DC bus. They include a DC/DC boost converter and a battery charger to correctly perform the tracking of the maximum power point of the PV panels and to charge/discharge the batteries, respectively. The inverter delivers active and reactive power to the microgrid commanded by the local control scheme. The inputs of the controller are the measured voltage and current of the inverter while the outputs are the gate signals for the power switches .
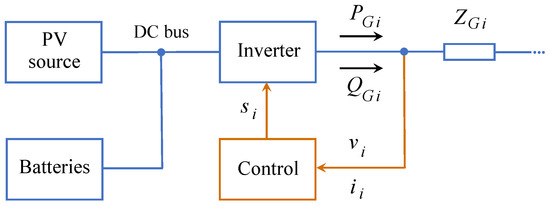
Figure 2.
Diagram of the components of the generators.
2.2. Power Quality Indexes
Below is a definition of the indexes used in this study to evaluate the power quality of the microgrid during a voltage sag. The ideal value of these indexes is also indicated. Other disturbances also affect the power quality of microgrids, including harmonics, flickers and DC current injection [32,33,34]. They are not taken into account in this study, which focusses only on the disturbances caused by voltage sags.
The voltage regulation is characterized by two factors, which measure the per unit (p.u.) amplitude of the positive and negative sequence voltages
where and are the amplitudes of the sequence voltages expressed in volts and is the base voltage in volts. In an ideal balanced system, these factors take the values = 1 and = 0.
Reactive current injection is a typical requirement that is intended to provide local voltage support during voltage sag occurrence, and therefore increase grid resiliency by reducing the risk of under-voltage generation tripping. Reactive current can be injected through positive and negative sequences. The amplitude of these sequences are written in p.u. as
where and are the amplitudes of the sequence currents expressed in amps and is the base current in amps. The ideal value of both and is 1. However, this ideal value cannot be simultaneously supplied by both sequence currents without surpassing the maximum current of the generator. Therefore, in practice, a good result is reached when and take values as high as possible while respecting the limitation imposed by the maximum current. Particular attention should be given to weak networks with low short-circuit currents in which the injection of maximum current increases the risk of over-voltage generation tripping [19,20]. In these scenarios, appropriate control actions must be implemented to address this problem including active power curtailment, reactive current regulation, and so on [35,36].
The transient response of the microgrid during voltage sags is characterized by the settling time of the generators. Two quality indexes are considered for each generator, according to the transition from normal to faulty conditions and from faulty to normal conditions . In general, these indexes are defined as
where is the initial time of the transition in seconds and is the final time when the measured signal reaches the 98% of its steady-state value in seconds. Ideally, = 0. In a real system, this value is not possible and a as small as possible is desired.
2.3. Problem Formulation
The first objective of this study is to compare the performance of the selected control schemes. The superior scheme is the one with the better quality factors defined in the previous section (i.e., the scheme with quality factors as near as possible to the ideal values). The second objective is to propose novel control schemes that improve the state-of-the-art control solutions.
Once the problems addressed in this study are formulated (and solved in following sections), the contributions of the paper can be identified as follows: (1) the performance comparison between the considered control schemes that leads to the identification of the most appropriate one to operate industrial microgrids during voltage sags, and (2) the two novel control schemes and policies designed to operate an industrial microgrid with a STATCOM connected in the PCC of the installation, which provides superior performance in terms of static and dynamic characteristics compared to control solutions known so far.
3. Control Schemes
This section briefly describes the control schemes designed to operate industrial microgrids during voltage sags. All these schemes are formulated in αβ domain. Note that the transformation from abc to αβ frame is intentionally omitted in the diagrams shown in next figures.
3.1. GCCS Control Schemes
In this case, the microgrid operates in grid-connected mode during the voltage sag. Figure 3a shows a simplified diagram of the microgrid in this operation mode with the switch S closed.
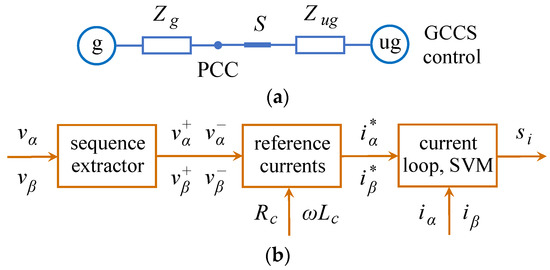
Figure 3.
GCCS control schemes: (a) diagram of the power system; (b) diagram of the control scheme.
Figure 3b shows a general block diagram of all the GCCS control schemes. The input signals to this diagram are the αβ domain voltages and while the outputs are the gate signals for the power switches (see Figure 2). The GCCS control schemes have in common a voltage sequence extractor [37], a current control loop [38] and a space vector modulator (SVM). The main difference between them relies in the way the reference currents are generated. Usually, the reference currents are designed by considering a current injection angle of 90 degrees (i.e., by assuming that the impedance is dominantly inductive). In this study, the injection angle is calculated for each injection point using the impedance seen from the output side of the generators [25]. The control parameters for this impedance are and for its real and imaginary parts, as shown in Figure 3b. The use of a particular impedance for each generator is a shared property of the three different ways to implement the reference currents presented below.
3.1.1. Control Scheme for Injecting Maximum Current via Positive Sequence Only
The objective of the first control scheme (GCCS1) is to increase the positive sequence voltage as much as possible. To this end, the scheme is based on injecting the maximum current during the voltage sag via positive sequence only. In this case, the optimal injection angle is defined in [25] as
Therefore, the reference currents can be written as [25]
where and are the positive sequence voltages, is the amplitude of these voltages, is the maximum amplitude of the generator current and
3.1.2. Control Scheme for Injecting Maximum Current via Negative Sequence Only
The objective of the second control scheme (GCCS2) is to decrease the negative sequence voltage as much as possible. To this end, the scheme is based on injecting the maximum current during the voltage sag via negative sequence only. The optimal injection angle and the reference currents are defined in [25] as
where and are the negative sequence voltages and is the amplitude of these voltages.
3.1.3. Control Scheme for Injecting Maximum Current via Positive and Negative Sequences
The objective of the third control scheme (GCCS3) is to increase the difference between the amplitudes of the positive and negative sequence voltages as much as possible. In fact, this is an intermediate solution between the previous control schemes since it simultaneously increases the positive sequence voltage and decreases the negative sequence voltage to accomplish the control objective. To this end, the scheme injects the maximum current during the voltage sag via positive and negative sequences. In addition, this scheme has an optimal injection angle for each sequence, which are defined as [25]
where is the angle between the positive and negative sequence voltages. Note that in this third control scheme the injection angles rely on both the impedance seen from the output side of the generator and the voltage sag characteristics through the angle . During the voltage sag, this angle must be measured in real time as
In fact, if the angle between the sequence voltages is out of the range , Equations (14) and (15) produce correct results only if the following correction is applied [25]
For angles inside the range , the value obtained from Equation (18) must be directly used in Equations (14) and (15).
In GCCS3 control scheme, the reference currents for injecting maximum current via positive and negative sequences can be written as [25]
where
3.2. IVS Control Scheme
In this control strategy, the microgrid operates in islanded mode during the voltage sag; see Figure 4a. Therefore, the inverters are responsible to regulate the microgrid voltage. To this end, a voltage loop is essential in this control scheme to force the inverters to behave as voltage sources. Figure 4b shows the diagram of the IVS control scheme. The voltage loop regulates the voltage by forcing and to follow the references and accurately [9]. The outputs of the voltage loop are the reference currents and , which are given to the current loop and the SVM.
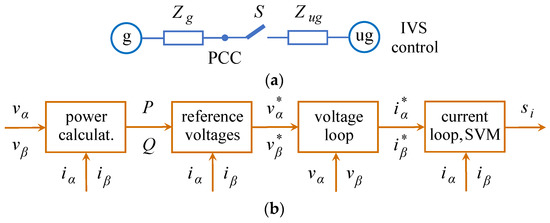
Figure 4.
IVS control scheme: (a) diagram of the power system; (b) diagram of the control scheme.
The droop control method makes possible to operate several inverters simultaneously as voltage sources [5,8]. It is based on reducing the amplitude and frequency of the reference voltages according to the reactive Q and active P powers delivered by the inverter [17,26,27]
In Equations (26) and (27), and are the references for voltage amplitude and frequency, n and m are the gains of the droop equations, and and are the references for active and reactive power. Typically, P and Q are obtained by filtering the instantaneous active and reactive powers, expressed in Equations (28) and (29), with a first-order low-pass filter which cutoff frequency is
The principle of operation of the droop method can be appreciated with the help of Equations (26) and (27). On the one hand, the frequency is a global variable in a power system and in steady-state all the elements in this system operate at the same frequency. Thus, from Equation (27), the following relation can be written for the inverters i and j [39]
revealing the capacity of active power sharing of the inverters. In other words, the active power delivered by each inverter is proportional to the active power of the other inverters. In the particular case that the control parameters are designed as and , then all the inverters supply the same power in steady-state. It is worth mentioning that the capacity of active power sharing is reached without using the communication service of the microgrid, i.e., with only local measures in the inverter (voltage and current to be more precise, as seen in Figure 4b). On the other hand, the voltage is a local variable and different voltages are observed in steady-state in different points of the power system, for . In this case, from Equation (26), it is possible to write
Therefore, the voltage error induces a deviation in the reactive power sharing that depends on the gains and .
In droop-controlled inverters, a virtual impedance is usually programmed in local controllers to improve stability, controllability and transient response without losing power efficiency (due to its virtual, non-physical nature) [4,26]. Considering this impedance, the reference voltages can be written as [27]
where and are the resistance and inductance of the virtual impedance.
As Figure 3a depicts, with GCCS control schemes, the microgrid operates connected to the utility grid during the voltage sags. For this reason, the voltage at the output side of the inverters usually contains positive and negative sequences and the GCCS scheme processes these sequences separately, as seen for example in Equations (20) and (21). However, in IVS control schemes, the microgrid is disconnected from the utility grid during the voltage sag, as Figure 4a shows, and thus there is no negative sequence voltage at the output side of the inverters induced by the unbalanced voltage sag. As a consequence, the IVS scheme processes directly the voltage measured at the output side of the inverters without extracting its positive and negative components, as shown in Figure 4b.
3.3. GCVS Control Scheme
The objective of the GCVS scheme is to eliminate the negative sequence voltage in the PCC while contributing to the support of the positive sequence voltage [28]. As a difference to GCCS3 control scheme, the inverters are programmed in this case to operate as grid-connected voltage sources. To this end, the droop method is used again, but now with a different configuration compared to the IVS approach due to: (1) the microgrid operates in grid-connected mode, see Figure 5a; and (2) positive and negative sequences are processed separately [29,30]. The diagram of the GCVS scheme is depicted in Figure 5b–d, and it is described below.
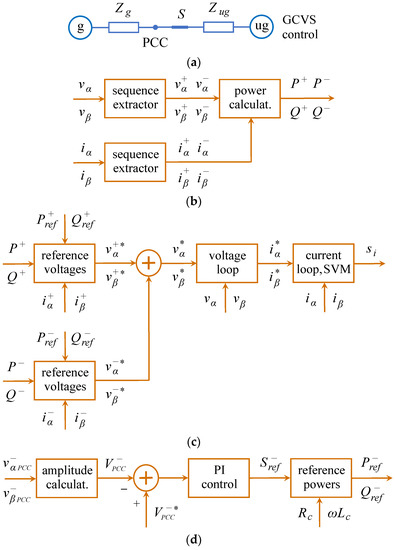
Figure 5.
GCVS control scheme: (a) diagram of the power system; (b) calculation of positive and negative sequence active and reactive powers; (c) generation of reference voltages, voltage and current control loops and SVM; (d) generation of negative sequence active and reactive powers.
Figure 5b shows a diagram for calculating the positive and negative sequence active and reactive powers. It uses two sequence extractors to estimate the positive and negative sequence voltage and current, and a block that calculates the instantaneous power as
As usual, , , and are obtained by filtering the instantaneous powers with a first-order low-pass filter with cutoff frequency
Figure 5c shows some blocks shared with the IVS control scheme, such as the voltage and current loops and the SVM modulator. In addition, it shows two blocks for generating the reference voltages via positive and negative sequences. These blocks are based on a specific re-formulation of the droop method valid for grid-connected conditions. The main differences with the implementation shown in Equations (26) and (27) for islanded mode are: (1) PI controllers instead of only P controllers are used to ensure that active and reactive powers follow their references accurately; and (2) phase angles instead of angular frequencies are used due to the microgrid frequency is fixed by the utility grid frequency . From [30], the voltage amplitude and phase angle of the positive and negative sequence voltages are written as
where , , and are the nominal values of the voltage amplitudes and phase angles and , , , , , , and are the proportional and integral gains of the PI controllers. Then, the positive and negative sequence reference voltages are expressed as
where , and , denote resistance and inductance of the positive and negative sequence virtual impedances, respectively.
Figure 5d shows a diagram for generating the negative sequence active and reactive reference powers. It is based on a PI controller which regulates the amplitude of the negative sequence voltage in the PCC according to the reference voltage . The output of the PI controller is the negative sequence component of the reference apparent power [30]
where and are the gains of the PI controller. The negative sequence reference powers are determined using the angle of the impedance seen from the output side of the generators
As mentioned above, the objective of the GCVS control scheme is to eliminate the amplitude of the negative sequence voltage in the PCC. Theoretically, this objective is accomplished by choosing the reference voltage in the control diagram shown in Figure 5d. However, due to practical limitations, in some cases the negative sequence voltage cannot be completely eliminated due to the insufficient available negative sequence active and reactive powers. In these circumstances, a value for greater than 0 must be set to not saturate the PI controller in Figure 5d.
4. Comparative Analysis of Grid-Faulty Control Schemes
This section presents a comparative analysis of the grid-faulty control schemes considered in this study. Advantages and disadvantages of the control schemes are revealed and the scheme with the best performance during voltage sags is identified. The analysis is validated with MATLAB© (2014a, MathWorks, Natick, MA, USA) simulation results.
4.1. Simulation Setup
The microgrid shown in Figure 1 was programmed in MATLAB© using the SimPowerSystems© toolbox. The control schemes presented in Figure 3, Figure 4 and Figure 5 were modelled in embeddable C code with MATLAB© S-functions blocks. The sampling frequency of these controllers was 10 kHz.
Table 2 lists the parameters of the control schemes. Top, medium and bottom sections report the parameters of GCCS, IVS and GCVS schemes, respectively. It is worth mentioning the large number of control parameters of the GCVS scheme compared to the GCCS scheme. This fact reveals the different complexity of the considered control schemes.

Table 2.
Parameters of the control schemes.
The design of the control parameters has a significant effect on the operation of the microgrid. The design guidelines provided in [17,25,30] are used to properly tune the parameters of GCCS, IVS and GCVS control schemes, respectively. In particular, the gains of the PI controllers only impact on the dynamic characteristics of the microgrid, providing a fast transient response with small overshoot when the design guidelines are observed. The rest of the indices (apart from ) are measured in steady state and do not depend on the gains of the PI controllers.
Three voltage sags are considered below to evaluate the performance of the control schemes. The characteristics of these voltage sags are listed in Table 3. The first voltage sag belongs to the type I category in which the voltage drop in one phase is greater than in the others. The second is a type II voltage sag with two phases with lower voltages than in the last phase. The third is a type III voltage sag with no negative sequence voltage and, thus, with the same amplitude reduction in all the phase voltages. Further details on the classification of the voltage sags as type I, II and III are found in [40]. Using the classification in [32], the three voltage sags are denoted as types C, D and A, respectively.

Table 3.
Characteristics of the voltage sags used in the tests.
4.2. Measured Quality Indexes and Discussion of the Results
Table 4 shows the quality indexes measured for the control schemes considering the type I voltage sag. The column Ideal lists the ideal values of the quality indexes and is included here as a base result for comparison. Green shading is used in this column to highlight the ideal results. The column No inject gives the measured quality indexes when the generators are inactive and allows to observe the characteristics of the voltage sag in different locations of the microgrid. These poor results are emphasized with red shading. For instance, in the PCC, the amplitude of the positive sequence voltage reduces from 1 p.u. to 0. 78 p.u. while the amplitude of the negative sequence voltage increases from 0 p.u. to 0.19 p.u. Another shading is used in the table to denote values close to the ideal (light green).

Table 4.
Quality indexes measured for type I voltage sag.
The column GCCS1 reports the results obtained when using the GCCS1 control scheme. As mentioned above, this scheme injects the maximum current via positive sequence only and, therefore, . The quality index is slightly lower than 1 (ideal value) due to some amount of active current is also injected via positive sequence according to the angle of the impedance seen from the output side of the generators. In any case, this control scheme produces a clear increase in the amplitude of the positive sequence voltage while the amplitude of the negative sequence voltage remains unchanged. As opposed to this, the GCCS2 control scheme injects the maximum current via negative sequence only, thus reducing the amplitude of the negative sequence voltage. The associated results to this scheme are listed in the column GCCS2. Note that, in this case, and then the amplitude of the positive sequence voltage remains unaltered. The results of the last grid-connected current source control scheme are reported in the column GCCS3. In this case, the maximum current is injected via positive and negative sequences, thus both increasing the amplitude of the positive sequence voltage and decreasing the amplitude of the negative sequence voltage. However, the total amount of power is divided between the two sequences and, thus, the results for positive sequence voltage are slightly lower than those for the GCCS1 scheme while for the negative sequence voltage they are slightly higher than those for the GCCS2 scheme. It is worth mentioning that the transient response of the three control schemes is fairly good for both normal-to-faulty and faulty-to-normal transitions.
The column IVS lists the results of the IVS control scheme. In this case, the microgrid is intentionally separated from the utility grid during the voltage sag and, therefore, the regulation of its internal voltage is nearly perfect. The amplitude of the positive sequence voltage is close to 1 while the amplitude of the negative sequence voltage is 0. These excellent results are obtained in different locations of the microgrid. However, the IVS scheme has serious drawbacks. First, the voltage at the PCC is not supported by the islanded microgrid because the switch S is open in this case; see Figure 1. Thus, the voltage measures associated to this point coincide with the non-injection case. Second, the transient response is slow, especially during the faulty-to-normal transition.
The results of the GCVS control scheme are reported in the column GCVS. The measures are quite similar to those obtained for GCCS3 scheme due to, in both cases, reactive current being injected via positive and negative sequences. In order to avoid the saturation of the PI controller shown in Figure 5d, the reference voltage in the GCVS scheme was set to 0.15 p.u; see Table 2. With this value, most of the reactive current is injected via negative sequence, thus slightly improving the regulation of the negative sequence voltage compared to the GCCS3 case. The opposite is observed in Table 4 for the positive sequence voltage, although the improvement with the GCCS3 scheme is small. As a final remark, the transient response of the GCVS scheme is slower than that of the GCCS3 scheme.
Table 5 shows the quality indexes measured for the control schemes considering the type II voltage sag. Compared to type I, this voltage sag is caused by a more severe fault resulting in a lower (higher) amplitude in the positive (negative) sequence component. Anyway, the control schemes operate correctly during the voltage sag providing the expected features. Note that the GCCS3 scheme has superior performance in relation to the other grid-connected control schemes, since it supports both sequences simultaneously. The IVS scheme has excellent results for the nodes within the microgrid, which is even more evident with the type II voltage sag due to the lower residual voltages. For instance, the amplitude of the positive sequence voltage increases from 0.39 p.u. to 0.96 p.u. in several locations of the microgrid. The performance of the GCVS scheme is similar to the GCCS3 performance. To achieve these results, the reference amplitude of the negative sequence voltage in the PCC has been changed from 0.15 p.u. (see Table 2) to 0.25 p.u. due to the higher imbalance measured in type II voltage sag. This is a key parameter for this control scheme that impacts notably in the system performance. It must be generated in real time to adapt correctly to the changing conditions in microgrids. As a negative point, the transient response of the GCVS scheme is slow compared to the GCCS3 dynamics, as reported in Table 5.

Table 5.
Quality indexes measured for type II voltage sag.
Table 6 shows the quality indexes measured for the type III voltage sag. As shown in Table 3, this is a balanced sag without negative sequence voltage. Therefore, the control schemes that process negative sequence voltage are not considered in this test. Note that the GCCS1 control scheme improves the voltage amplitude by almost 0.05 p.u. in the PCC and in 0.1 p.u. in other locations within the microgrid. As expected, the IVS scheme has excellent voltage regulation in the internal nodes of the microgrid while, at the PCC, the voltage remains at the value of no injection (the switch S is open in this case and the microgrid does not contribute to regulate the voltage at the PCC). As in the case of previous sags, the transient response of GCCS1 scheme is superior to those obtained with the IVS scheme.

Table 6.
Quality indexes measured for type III voltage sag.
It is clear that, taking into account the previous analysis, there is no control scheme with all its quality indexes above the indexes of the other schemes. However, for unbalanced sags (type I and type II) it is possible to note that the GCCS3 scheme provides the best support to the PCC voltage for both positive and negative sequences and, therefore, it is probably the best scheme from the point of view of the utility grid. For balanced sags (type III), the best scheme from the perspective of the utility grid is the GCCS1 scheme since the highest voltage amplitude in the PCC is obtained using this control. In addition, the IVS scheme provides an excellent voltage regulation in different locations within the microgrid, being the best choice from the point of view of the microgrid. Section 5 will propose an alternative solution to cope with balanced and unbalanced voltage sags, which includes the use of a STATCOM in parallel with the microgrid. The solution will improve the performance of the control schemes highlighted in this discussion (the GCCS1, GCCS3 and IVS schemes).
4.3. Validation of the Analysis with Transient Simulation Results
This sub-section validates the previous analysis by transient simulation results. A test with the same sequence of events is used for all the control schemes. The test starts with the utility grid in normal condition at t = 0 s. The voltage sag appears at t = 0.1 s and is cleared at t = 0.3 s. The utility grid is in normal condition again in the last interval, from t = 0.3 s to 0.4 s. The control schemes are intentionally inactive during the interval t = 0.1–0.2 s. This period of inactivity is not necessary for the correct operation of the control schemes, but is included here to show the characteristics of the voltage sag when the generators are not injecting power to the utility grid. Therefore, the different characteristics of type I, II and III voltage sags are clearly observed in this inactive interval. For those control schemes operating in islanded mode during the interval t = 0.1–0.3 s, the non-priority loads of the micro-grid are disconnected during the voltage sag. Due to the design of the system, the capacity of the installation only guarantees the supply of the priority loads in islanded mode.
Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show the main waveforms of both generators for type I voltage sag. In particular, Figure 6 shows the results obtained using the GCCS1 control scheme. As expected, this scheme increases the amplitude of the positive sequence voltage in the current injection interval, from t = 0.2 s to 0.3 s, while keeping constant the amplitude of the negative sequence voltage. Therefore, the amplitude of all the phase voltages increase in this interval. In addition, generator 1 injects active and reactive power with a relation of 1 to 2.85 while generator 2 with relation 1 to 3.5, according to the impedance seen from the output side of each generator (see Table 2). Note that this injection is carried out limiting the current to its maximum value.
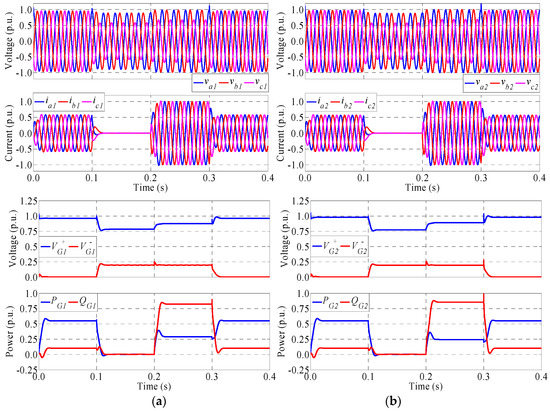
Figure 6.
Main waveforms of (a) generator 1 and (b) generator 2 using the GCCS1 control scheme for type I voltage sag.
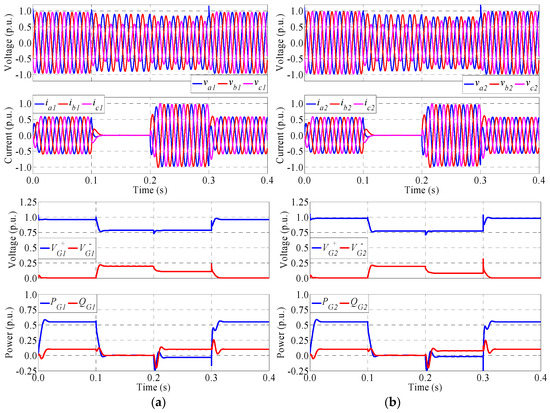
Figure 7.
Main waveforms of (a) generator 1 and (b) generator 2 using the GCCS2 control scheme for type I voltage sag.
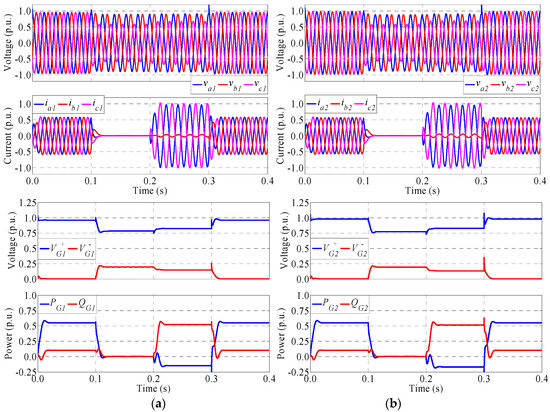
Figure 8.
Main waveforms of (a) generator 1 and (b) generator 2 using the GCCS3 control scheme for type I voltage sag.
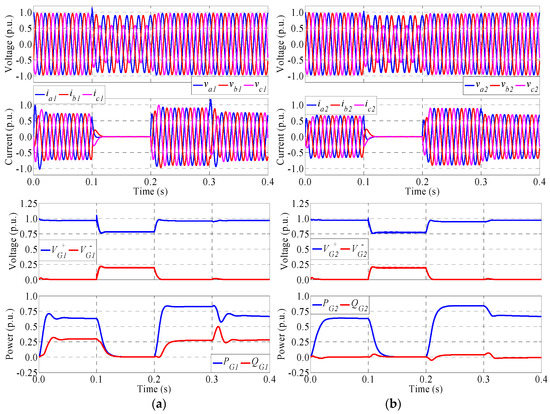
Figure 9.
Main waveforms of (a) generator 1 and (b) generator 2 using the IVS control scheme for type I voltage sag.
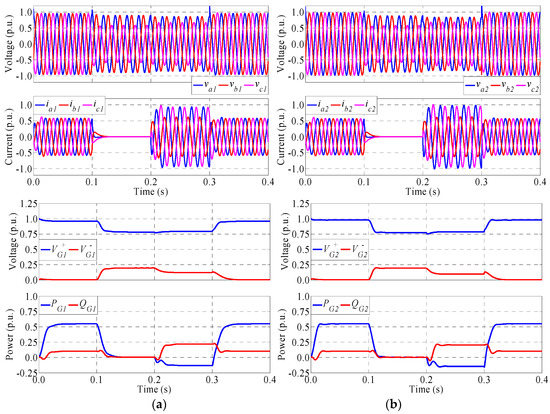
Figure 10.
Main waveforms of (a) generator 1 and (b) generator 2 using the GCVS control scheme for type I voltage sag.
Figure 7 shows the waveforms of the generators using the GCCS2 control scheme. This control reduces the amplitude of the negative sequence voltage while maintaining the amplitude of the positive sequence voltage during the injection interval. The consequence is a reduction in the differences between the amplitudes of all the phase voltages. In other words, the amplitudes of the phase voltages tend to go together as much as possible. To this end, the higher voltage reduces its amplitude and the lower voltage increases it, as shown in the figure. In this case, the active and negative powers are lower compared to the values in the previous scheme, but again, the current is limited to its maximum value. It is worth mentioning that the active power is negative, meaning that this power is absorbed from the utility grid and delivered to the DC bus shown in Figure 2.
Figure 8 shows the main waveforms of the generators using the GCCS3 control scheme. As expected, this scheme simultaneously increases the amplitude of the positive sequence voltage and decreases the amplitude of the negative sequence voltage. The amplitude of the phase voltages both increase and tend to be together at the same time, thus improving the voltage support compared with previous control solutions. The active power is again negative and, hence, delivered to the DC bus of each generator. The injected current is limited to the maximum value, but in this case it is unbalanced. Note that the current injected by phase b in both generators is very small. A common feature of the GCCS control schemes is a good transient response with fast recovery and small (or negligible) overshoots in voltage, current and power.
Figure 9 shows the waveforms of the generators using the IVS control scheme. During the injection interval (from t = 0.2 s to 0.3 s), the voltage regulation in both generators is very good. The positive sequence is nearly recovered to the pre-sag value and the negative sequence is completely removed. This is possible because the microgrid operates in islanded mode in this interval and the generators have enough energy to both regulate the internal voltages and supply the loads (due to the microgrid does not inject power to the utility grid). As negative points, the generators poorly share the reactive power, the transient response is slow and currents and powers have overshoots during transitions, especially in generator 1.
Finally, Figure 10 shows the waveforms of the generators using the GCVS control scheme. In this case, the waveforms are quite similar to those obtained with the GCCS3 scheme; see Figure 8. Both schemes support the voltage by simultaneously increasing the positive sequence and decreasing the negative sequence. The generators in both schemes absorb active power and inject reactive power with slightly different values. The main differences observed in Figure 8 and Figure 10 are: (1) the amplitude of the phase voltages are slightly higher in the GCCS3 scheme; (2) the current unbalance is lower in the GCVS scheme; and (3) the transient response is faster in GCCS3 scheme.
Tests similar to those reported in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 were carried out for type II and III voltage sags. A selection of the results is shown in Figure 11, which compares the waveforms obtained in generator 1 using the GCCS1 and IVS control schemes for type II voltage sag. In addition, Figure 12 shows the same waveforms using the selected control schemes for type III voltage sag. Note that the GCCS1 scheme is preferred in this comparison instead of the GCCS3 scheme (which provides even higher performance for type II voltage sags) since this last scheme cannot be used for type III voltage sag.

Figure 11.
Main waveforms of generator 1 using the (a) GCCS1 and (b) IVS control schemes for type II voltage sag.
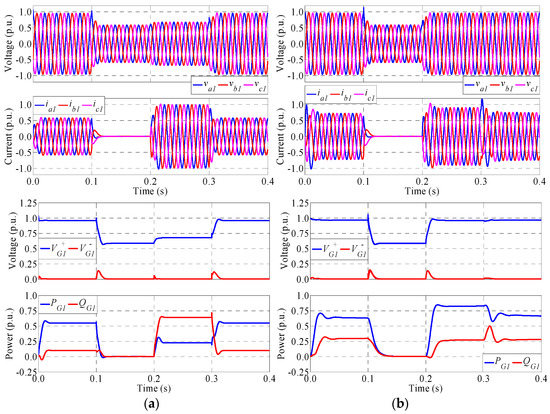
Figure 12.
Main waveforms of generator 1 using the (a) GCCS1 and (b) IVS control schemes for type III voltage sag.
Focusing on the injection interval (from t = 0.2 s to 0.3 s), it is clear from Figure 11 that the IVS control scheme provides better voltage regulation on the output side of generator 1 compared to the GCCS1 scheme. The improvement in voltage regulation is remarkable since the amplitude of negative sequence voltage is high in the type II voltage sag. Although this property is maintained for the type III voltage sag (see Figure 12), the improvement is not as pronounced due to the absence of negative sequence and the higher values of the residual phase voltages. Another point to take into account is that the microgrid is intentionally separated from the utility grid when using the IVS control scheme, which makes the voltage regulation in the PCC better using the GCCS1 scheme; see the previous results of Table 4, Table 5 and Table 6. Finally, it should be noted that the impact of the characteristics of the voltage sags on the transient response of the system is small, as shown in Table 4, Table 5 and Table 6 and in the results of Figure 11 and Figure 12. It is clear in these figures that the GCCS1 control scheme presents a much higher performance in terms of transient response compared to the IVS control. In particular, the transient response is faster and exhibits lower overshoots in voltage, current and power.
5. Control Schemes for the Microgrid with STATCOM
This section presents the operation of the microgrid with STATCOM. Two different control policies are analyzed and the improvement in the quality indexes are discussed in detail. In addition, the practical limitations of this proposal are also highlighted.
A STATCOM is a voltage-regulating device used basically for the injection of reactive current to the utility grid. If connected to a source of power or to an energy storage system, it can also be used to inject active power [41]. This capability is useful for power losses compensation and to grid support in imbalance conditions [42,43].
Figure 13 shows the diagram of the power system with STATCOM indicating the two different operating modes of the microgrid in islanded and grid-connected modes. The STATCOM is included in this solution to improve the power quality of the internal and external points of the microgrid. It is assumed that it is connected at its input side to an energy storage system to be able to inject active power when necessary. In normal conditions, the STATCOM can be used to provide ancillary services to the system (reactive current injection, voltage and current harmonics rejection, among others). During voltage sags, its operation is described below.
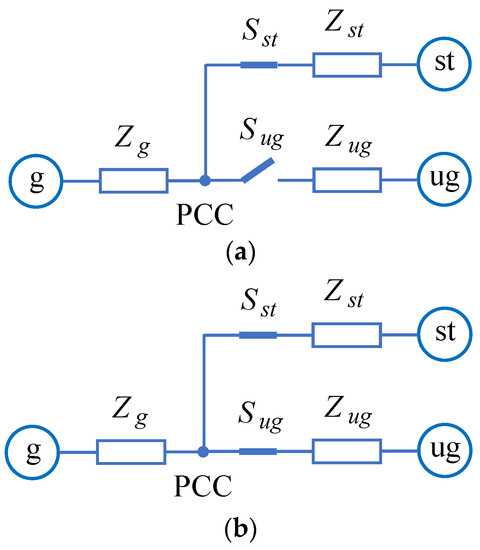
Figure 13.
Diagram of the power system with STATCOM during voltage sags for (a) islanded and (b) grid-connected microgrid.
In the first operating mode, it is assumed that the industrial microgrid, acting as a cell of the utility grid, is required to provide premium power to its priority loads and, at the same time, should also support the upstream distribution grid voltage. Such a demanding set of requirements can be achieved by means of: (1) islanding operation of the industrial microgrid following the voltage sag, which assures premium power to its priority loads; and (2) controlled injection of reactive current by the STATCOM connected to the PCC in order to support the external grid voltage. Therefore, the improvement of the power quality in the utility grid is exclusively performed by the STATCOM. Focusing on the control system, the IVS control scheme is selected in this scenario for the islanded microgrid because of its excellent voltage regulation in different internal points of the microgrid. In addition, for type I and II voltage sags, the GCCS3 control scheme is chosen for the STATCOM as it provides the best support to the PCC voltage for positive and negative sequences, thus improving the power quality of the external grid. Note that this control scheme causes the absorption of some amount of active power from the utility grid, as shown in Figure 8. Therefore, the STATCOM must have the ability to absorb active power, which can be used for charging the installed energy storage system [41,42,43].
In the second operating mode, the microgrid remains connected to the utility grid during voltage sags. In this case, both priority and non-priority loads of the microgrid are uninterruptedly supplied. The STATCOM complements the injection of reactive current provided by the grid-connected microgrid, thus improving the power quality indexes of the installation. For type I and II voltage sags, GCCS3 control scheme is selected for both the microgrid and STATCOM in this grid-connected scenario.
As discussed in the previous section, the presence of negative sequence components in type III voltage sags is residual. Therefore, the GCCS1 control scheme is selected for this type of sags instead of the GCCS3 scheme (which simultaneously processes positive and negative sequence voltages). Table 7 summarizes the control schemes suitable for the microgrid and STATCOM according to the type of voltage sag.

Table 7.
Selected control policies for the microgrid with STATCOM under different voltage sags.
The sizing of the STATCOM has a design trade-off between desired performance in the PCC and cost. Obviously, the characteristics of the PCC voltage during the voltage sag will improve as the nominal power of the STATCOM increases, at the expense of also increasing the cost of the installation. This is in fact the main limitation of this solution.
In this study, the nominal power of the STATCOM is chosen to match the total power of the microgrid generators (i.e., 276 kVA). In addition, the line impedance of the STATCOM is 10.2 mΩ and 33 mΩ. Under these conditions, Table 4 shows the quality indexes of the microgrid with STATCOM in the two considered operating modes measured during the type I voltage sag. The column nIVS lists the measures for the first mode, when the microgrid is islanded during the voltage sag, while the column nGCCS3 shows the measures when the microgrid remains connected to the utility grid. On the one hand, using the new nIVS control, the quality of the voltage in different points of the microgrid is excellent due to the IVS control scheme. In addition, the voltage in the PCC improves in both sequences compared to the previous control schemes thanks to the specific support of the STATCOM. Note also that the transient response of the microgrid is slow as in the IVS control scheme. On the other hand, the transient response of the new nGCCS3 control is faster, a feature shared by the GCCS schemes. In addition, by comparing the results with the basic GCCS3 scheme, it is evident that with the new control policy the voltage support noticeably improves in all the points of the power system, as shown in Table 4.
The results of the new control policies are listed in Table 5 (see columns nIVS and nGCCS3) and Table 6 (see columns nIVS and nGCCS1) for type II and III voltage sags, respectively. Despite of the fact that these sags exhibit different positive and negative sequence amplitudes and angles, the previous remarks are valid also for the new control schemes. The new IVS control provides better support at the internal points of the microgrid, but non-priority loads are not fed during voltage sags. The new GCCS control schemes (GCCS3 scheme for type II voltage sags and GCCS1 scheme for type III voltage sags) improve the transient response and supply all loads, but at the expense of a slightly poor voltage regulation in the internal points of the microgrid.
6. Conclusions
Several control schemes designed to operate industrial microgrids during voltage sags have been compared in this study. The comparison was based on the evaluation of several indexes, which measure the power quality of the installation and utility grid during voltage sags, including voltage regulation, reactive current injection and transient response. Balanced and unbalanced voltage sags are considered to test the performance of the microgrid in different scenarios and to evaluate the impact of these sags on the operation of the studied control schemes. From the study, it is clear that there is no control scheme with all its quality indexes above the indexes of the other schemes. In view of these results, two alternative solutions to cope with voltage sags have been proposed, both including the use of a STATCOM in parallel with the microgrid and considering the microgrid in islanded mode or in grid-connected mode. The shared features of these proposals are: (1) excellent voltage regulation in several points of the microgrid including the PCC; (2) injection of reactive current to the utility grid simultaneously by both positive and negative sequences for type I and II voltage sags; and (3) injection of reactive current via only positive sequence for type III voltage sags. Therefore, the most suitable control scheme for industrial microgrids for any type of voltage sag is identified in this study, which may be considered a significant advance in knowledge for academia and industry communities.
However, the cost of the microgrid deployment with the proposed solution is high due to the inclusion of a STATCOM with high rated power. An open topic for future research is the search for alternative solutions with similar technical features but with lower cost. In addition, the application of the analytical tool for comparing control schemes presented in this paper can be extended to other types of microgrids, including residential, commercial, institutional, military and remote microgrids. Since those microgrids have different requirements, the final results of this future investigation can lead to some different conclusions compared to those obtained in this study.
Acknowledgments
This work has been supported by the European Union Project ELAC2014/ESE0034 and its linked National Projects PCIN-2015-001 (MINECO, Spain), 082-2015 (CONCYTEC, Peru), ERANETLAC/0005/2014 (FCT, Portugal), ERANETLAC/0006/2014 (FCT, Portugal) and 018/16 (MINCYT, Argentina).
Author Contributions
This paper was a collaborative effort between all the authors. All of them contributed to the comparative analysis. In particular, A.C. and M.C. conceived and designed the microgrid installation. F.C., P.C. and M.G. studied the control schemes for the grid-connected operation while C.M. and P.E.M. studied the control schemes for the islanding operation. The inclusion of a STATCOM was proposed by M.C. and analyzed by A.C. All the authors participated in the discussion of the results. A.C. wrote the paper and the rest of the authors reviewed it.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Strbac, G.; Hatziargyriou, N.; Peças Lopes, J.; Moreira, C.; Dimeas, A.; Papadaskalopoulos, D. Microgrids: Enhancing the resilience of the European megagrid. IEEE Power Energy Mag. 2015, 13, 35–43. [Google Scholar] [CrossRef]
- Strasser, T.; Andrén, F.; Kathan, J.; Cecati, C.; Buccella, C.; Siano, P.; Leitão, P.; Zhabelova, G.; Vyatkin, V.; Vrba, P.; et al. A review of architectures and concepts for intelligence in future electric energy systems. IEEE Trans. Ind. Electron. 2015, 62, 2424–2438. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Tale, H.A. Three-phase AC/DC power-flow for balanced/unbalanced microgrids including wind/solar, droop-controlled and electronically-coupled distributed energy resources using radial basis function neural networks. IET Power Electron. 2017, 10, 313–328. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, H.; Cai, H.; Shi, J.; He, X. Power decoupling strategy based on ‘virtual negative resistor’ for inverters in low-voltage microgrids. IET Power Electron. 2016, 9, 1037–1044. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Suvire, G.O.; Molina, M.G.; Mercado, P.E. Improving the integration of wind power generation into AC microgrids using flywheel energy storage. IEEE Trans. Smart Grid 2012, 3, 1945–1954. [Google Scholar] [CrossRef]
- Sun, X.; Liu, B.; Cai, Y.; Zhang, H.; Zhu, Y.; Wang, B. Frequency-based power management for photovoltaic/battery/fuel cell-electrolyser stand-alone microgrid. IET Power Electron. 2016, 9, 2602–2610. [Google Scholar] [CrossRef]
- Peças Lopes, J.A.; Moreira, C.; Madureira, A.G. Defining control strategies for microgrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Derakhshandeh, S.Y.; Masoum, A.S.; Deilami, S.; Masoum, M.A.; Hamedani Golshan, M.E. Coordination of generation scheduling with PEVs charging in industrial microgrids. IEEE Trans. Power Syst. 2013, 28, 3451–3461. [Google Scholar] [CrossRef]
- Haj-ahmed, M.A.; Illindala, M.S. Investigation of protection schemes for flexible distribution of energy and storage resources in an industrial microgrid. IEEE Trans. Ind. Appl. 2015, 51, 2071–2080. [Google Scholar] [CrossRef]
- Tian, J.; Liu, Z.; Shu, J.; Liu, J.; Tang, J. Base on the ultra-short term power prediction and feed-forward control of energy management for microgrid system applied in industrial park. IET Gener. Transm. Distrib. 2016, 10, 2259–2266. [Google Scholar] [CrossRef]
- Vogt, T.; Keuck, L.; Fröhlecke, N.; Böcker, J.; Kempen, S. Analysis of industrial microgrid power curves based on the theory of stochastic variables for control system development and component sizing. In Proceedings of the International Conference on Advances in Green Energy, Thiruvananthapuram, India, 17–18 December 2014. [Google Scholar]
- Eseye, A.T.; Zheng, D.; Zhang, J.; Wei, D. Optimal energy management strategy for an isolated industrial microgrid using a modified particle swarm optimization. In Proceedings of the IEEE International Conference on Power and Renewable Energy, Shanghai, China, 21–23 October 2016. [Google Scholar]
- Bonfiglio, A.; Delfino, F.; Pampararo, F.; Procopio, R.; Rossi, M.; Barillari, L. The smart polygeneration microgrid test-bed facility of Genoa University. In Proceedings of the 47th International Universities Power Engineering Conference, London, UK, 4–7 September 2012. [Google Scholar]
- Bonfiglio, A.; Barillari, L.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R.; Rossi, M.; Bracco, S.; Robba, M. An optimization algorithm for the operation planning of the University of Genoa smart polygeneration microgrid. In Proceedings of the IREP Symposium Bulk Power System Dynamics and Control—IX Optimization, Security and Control of the Emerging Power Grid, Rethymno, Greece, 25–30 August 2013. [Google Scholar]
- Miret, J.; García de Vicuña, L.; Guzman, R.; Camacho, A.; Ghahderijani, M.M. A flexible experimental laboratory for distributed generation networks based on power inverters. Energies 2017, 10, 1589. [Google Scholar] [CrossRef]
- Göksu, Ö.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjær, P.C. Instability of wind turbine converters during current injection to low voltage grid faults and PLL frequency based stability solution. IEEE Trans. Power Syst. 2014, 29, 1683–1691. [Google Scholar] [CrossRef]
- Yang, Y.; Enjeti, P.; Blaabjerg, F.; Wang, H. Wide-scale adoption of photovoltaic energy: Grid code modifications are explored in the distribution grid. IEEE Ind. Appl. Mag. 2015, 21, 21–31. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Moradi Ghahderijani, M.; Castilla, M.; García de Vicuña, L.; Camacho, A.; Torres Martínez, J. Voltage sag mitigation in a PV-based industrial microgrid during grid faults. In Proceedings of the IEEE 26th International Symposium on Industrial Electronics, Edinburgh, UK, 19–21 June 2017. [Google Scholar]
- Lei, Z.; Ai, X.; Cui, M. Coordinated control strategy based on network parameters for voltage sags compensating in microgrid. In Proceedings of the 5th International Conference on Critical Infrastructure, Beijing, China, 20–22 September 2010. [Google Scholar]
- Gkavanoudis, S.I.; Oureilidis, K.O.; Demoulias, C.S. Fault ride-through capability of a microgrid with WTGS and supercapacitor storage during balanced and unbalanced utility voltage sags. In Proceedings of the International Conference on Renewable Energy Research and Applications, Madrid, Spain, 20–23 October 2013. [Google Scholar]
- Hamzeh, M.; Karimi, H.; Mokhtari, H. Harmonic and negative-sequence current control in an islanded multi-bus MV microgrid. IEEE Trans. Smart Grid 2014, 5, 167–176. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; García de Vicuña, L.; Guzman, R. Positive and negative sequence control strategies to maximize the voltage support in resistive-inductive grids during grid faults. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Moradi Ghahderijani, M.; Castilla, M.; Momeneh, A.; Guzmán, R.; García de Vicuña, L. Transient analysis of PV-based industrial microgrids between grid-connected and islanded modes. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Momeneh, A.; Castilla, M.; Moradi Ghahderijani, M.; Camacho, A.; García de Vicuña, L. Design and control of a small-scale industrial microgrid in islanding mode. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Zhao, X.; Savaghebi, M.; Guerrero, J.M.; Vasquez, J.C.; Sun, K.; Wu, X.; Chen, G.; Sun, L. Negative sequence droop method based hierarchical control for low voltage ride-through in grid-interactive microgrids. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Zhao, X.; Meng, L.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M.; Wu, X. A dynamic consensus algorithm based low-voltage ride-through operation of power converters in grid-interactive microgrids. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Zhao, X.; Guerrero, J.M.; Savaghebi, M.; Vasquez, J.C.; Wu, X.; Sun, X. Low-voltage ride-through operation of power converters in grid-interactive microgrids by using negative-sequence droop control. IEEE Trans. Power Electron. 2017, 32, 3128–3142. [Google Scholar] [CrossRef]
- Suvire, G.O.; Mercado, P.E. Combined control of a distribution static synchronous compensator/flywheel energy storage system for wind energy applications. IET Gener. Transm. Distrib. 2012, 6, 483–492. [Google Scholar] [CrossRef]
- Bollen, M.H.J. Understanding Power Quality Problems: Voltage Sags and Interruptions, 1st ed.; Willey-IEEE Press: New York, NY, USA, 2000; pp. 139–252. ISBN 978-0-78-034713-7. [Google Scholar]
- Delfino, B.; Fornari, F.; Procopio, R. An effective SSC control scheme for voltage sag compensation. IEEE Trans. Power Deliv. 2005, 20, 2100–2107. [Google Scholar] [CrossRef]
- Fornari, F.; Procopio, R.; Bollen, M.H.J. SSC compensation capability of unbalanced voltage sags. IEEE Trans. Power Deliv. 2005, 20, 2030–2037. [Google Scholar] [CrossRef]
- Tonkoski, R.; Lopes, L.A.C.; El-Fouly, T.H.M. Coordinated active power curtailment of grid connected PV inverters for overvoltage prevention. IEEE Trans. Sustain. Energy 2011, 2, 139–147. [Google Scholar] [CrossRef]
- Sosa, J.L.; Castilla, M.; Miret, J.; Matas, J.; Al-Turki, Y.A. Control strategy to maximize the power capability of PV three-phase inverters during voltage sags. IEEE Trans. Power Electron. 2016, 31, 3314–3323. [Google Scholar] [CrossRef]
- Matas, J.; Castilla, M.; Miret, J.; García de Vicuña, L.; Guzman, R. An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions. IEEE Trans. Ind. Electron. 2014, 61, 2139–2151. [Google Scholar] [CrossRef]
- Castilla, M.; Miret, J.; Camacho, A.; Matas, J.; García de Vicuña, L. Reduction of current harmonic distortion in three-phase grid-connected photovoltaic inverters via resonant current control. IEEE Trans. Ind. Electron. 2013, 60, 1464–1472. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Guzmán, R.; Borrell, A. Reactive power control for distributed generation power plants to comply with voltage limits during grid faults. IEEE Trans. Power Electron. 2014, 29, 6224–6234. [Google Scholar] [CrossRef]
- Obando-Montaño, A.F.; Carrillo, C.; Cidrás, J.; Díaz-Dorado, E. A STATCOM with supercapacitors for low-voltage ride-through in fixed-speed wind turbines. Energies 2014, 7, 5922–5952. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M. Comparison of two control approaches for stability enhancement using STATCOM with active power injection capability. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Shabestary, M.M.; Mohamed, Y.A.R.I. Advanced voltage support and active power flow control in grid-connected converters under unbalanced conditions. IEEE Trans. Power Electron. 2018, 33, 1855–1864. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).