1. Introduction
Nowadays the domestic hot water and the domestic spacing heating count towards approximately 20% of the total energy consumption in the European Union [
1,
2]. This part is extended to 31% if the ones of industrial and tertiary buildings are considered [
3]. This thermal energy (more than 300 Mtoe) mainly comes from fossil fuels, 66 %, and only 13% from renewable ones. On another hand, about 1% of the total energy consumption is dedicated to the cooling of buildings (all fields).
From an environmental point of view, this energy consumption produces wide CO
and pollutant emissions. These emissions are harmful for the environment (e.g., increase of the world temperature, eutrophication of grounds, etc.) and for humanity. Indeed, the World Health Organization estimates that 5% of the world population die each year due to outside air pollution, mainly due to energy use (e.g., particles, NO
emissions, etc.) [
4].
Therefore, energy systems with high energy efficiency and low pollutant emissions have to be developed and widely used to avoid these issues. The European Union has proposed several energy directives, supported by academia [
5], to encourage the use of a district heating network (DHN) [
6] and their related limitations [
7], renewable sources and combined heat and power plant; in particular, the EU estimates that 50% of its heating and cooling demand should be fed by DHN in 2050 [
8]. Fourth generation district heating networks, widely described in [
9], are one of the future energetic transition solutions as they combine low energy building, high conversion energy systems and smart energy generation. However, the European building stock is quite old—about 40% of the buildings stock was built before 1960 and 45% was built between 1961–1990 [
10]. On the other hand, the new building construction rate is quite limited (about 0.5% in Belgium for example [
11] and less than 0.7% for EU28 [
12]). This leads to a reduced penetration of new low energy buildings and the related fourth generation of the district heating network. Moreover, the energetic performance of the current buildings stock is quite limited [
12]. Thenceforth, other major topics of the energetic transition are to improve the building envelope of current buildings to reduce the heat demand [
13] and to improve the heating systems to supply them [
14]. This contribution tends to propose a methodology compatible with all generations of DHN to perform integration and retrofit studies to improve the current building stock heating.
The focus of this study is performed on DHN given they are an efficient way to supply heat to buildings [
15,
16], especially if they are fed by renewable energy systems capable of reducing CO
emissions [
17]. Therefore, retrofit studies of current neighborhoods or towns should be a part of the energetic transition as well as a retrofit of existing DHN. Indeed, a lot of existing DHN are high temperature DHN (For example, more than 40% of the DHN-delivered heat is from high temperature DHN (>120 °C) in France [
18]) leading to high heat losses.
To perform these studies, simulations and planning tools are required to consider the integration of renewable energy systems and assess their efficiency and influence into the environment while ensuring comfort into buildings. Indeed the heat transport can reach some hours in large DHN due to the reduced speed of the fluid carrier, typically one or two meters per second to limit the electric pump consumption [
19,
20,
21,
22]. Therefore, dynamic simulation tools are also required, while optimizing the operation of existing DHN through dedicated optimized control strategies [
23,
24,
25], which is considered as a future challenge to improve DHN [
9].
Previous works intended to assess the energy, economic and environmental performances of a DHN fed by a biomass CHP plant [
26] and to study with some scenario improvements [
27]. However these works were based on existing heat demand curves to assess global system performance, i.e., only the heating plant was really studied. In this contribution, an extension of these works is proposed to consider the dynamic behavior of DHN and assess the heat demand of consumers while ensuring their comfort. The developed tools are also able to study complex control strategies and renewable sources integration as wind turbines or solar energy systems whose generated heat and power fluctuate more by nature. In this contribution, the control strategy of heat generation is the only solution which is considered.
On the other hand, some professional software is available on the market as Bentley [
28], Modelon [
29] or Schneider Electric [
30] software. However they are dedicated to the optimization of the DHN itself (temperature and electric pump consumption) without considering the part load performance of heating systems such as the CHP plant, the plant subsidies, the comfort inside the buildings or the CO
and pollutant emissions.
The current contribution is intended to present the methodology used to assess the dynamic global system performance. An open-source programming platform is selected and used, namely Modelica [
31], to propose a validated tool for plant owners or for communities considering a DHN as a heating system. Moreover, several existing open-source libraries are available to simulate a lot of DHN and building configurations to make the developed tool as generic as possible. Finally, the developed tool can be used as a decision tool for design or retrofit of such installations as it takes into consideration energy, environmental and cost approaches.
The considered tool is applied to an existing DHN fed by natural gas boilers and biomass CHP plant of the University of Liège. The study of a control strategy is performed to optimize the electric pump consumption while keeping the DHN heat losses at a reasonable level and ensuring the comfort of DHN users.
2. Problem Statement
A district heating network can be seen as the combination of three main components. Basically, it is composed of heat sources, renewable or not, where energy is produced or recovered from processes; sinks, namely buildings; and a network piping that transports energy from one to the other. To size or retrofit a district heating network, several characteristics of each component are required to assess the DHN performances correctly. For example, heat losses due to a determined DHN insulation involve a related overall heat demand; the heat demand profile of the buildings connected to a DHN involves a minimal thermal power of heating installation systems (and so investment costs). Despite some of these characteristics being found in the literature, in this contribution, they are assessed by several models described later to capture a more precise performance of the system and its dynamic behavior to ensure the users’ comfort.
The present research focuses on the dynamic modeling of heat sources and related piping systems. The heat demands of consumers are assessed by internal simulations performed. In order to assess the technical solutions investigated, it is proposed to define several indicators. For this purpose, the economic, energy, environmental and exergy approaches are considered.
The energy approach consists of an assessment of the energy conversion efficiency of an energy system. It is used to quantify the primary energy requirements of a process and the related costs. The environmental one is dedicated to assessing the influence of the process use on the environment. Despite the fact that a lot of environmental criteria are available in Life Cycle Analyses, such as the use and the eutrophication of land and ozone layer depletion, only the CO
and the restricted pollutant emissions will be considered in this contribution. The economic approach is generally the main criterion for the choice of a technical solution. Therefore, several costs have to be considered. Investments, maintenance and operation costs are used to assess the total energy produced cost of a system. Reliable information about generic costs of domestic and industrial energy systems are respectively available in [
32,
33], while energy costs are available in [
34]. However, the proposed tool in this contribution is able to assess precisely the energy costs of a defined scenario case in order to improve them by studying some other, alternative scenarios.
On the other hand, the energetic approach, based on the first law of the thermodynamics, is often misleading in ranking energy systems as it
does not always provide an indicator how the process is near the optimality [
35]. For example, a heat generation system uses, generally, high-grade energy i.e., electricity or fuel in a combustion process which reaches 1500 °C [
36] to produce low-grade energy such as hot water at 55 °C [
37]. In this case, the energy conversion of this combustion process is currently close to one but the quality of the energy is widely degraded. The exergy analysis, which is detailed in the following section, is able to rank energy systems because it is based on the first and the second laws of thermodynamics and states that despite the energy cannot be created or destroyed, its quality can be degraded up to an equilibrium state with the surroundings. Moreover, this analysis is able to point out the parts of the energy process which degrade the available exergy in order to improve them too. Therefore, in a sustainable global energy use, the exergy approach completes the energy approach.
Previously, some works [
26,
27,
36,
38] were performed to assess the performance of district heating systems based on all these approaches. However, they are based on the pseudo-dynamic behavior of the DHN. This involves some limitations while the heat transport delay inside the DHN was not considered, and so the related comfort could not be ensured, especially when the production systems can vary widely as it is the case with the use of renewable energy systems such as thermal solar systems. On the other hand, control strategies, such as heat demand peaks optimization [
25], require dynamic modeling to ensure comfort inside the buildings. So, the current work is a dynamic extension of these previous works, able to consider all these features.
In this contribution, a retrofit of an existing system is studied dynamically. Previously, experimental data measured on the considered DHN show that the difference temperature between the supply and the return line is quite reduced. This behavior leads to a high pumping work and related electric consumption. So, it is proposed to consider a control strategy to minimize the electric pump consumption while ensuring the user’s comfort inside the buildings fed by the DHN which is not currently ensured.
3. Modeling Methods
As discussed previously, three main parts compose a DHN, namely, the production plant, the pipes and the consumers. This section is dedicated to the presentation of the different modeling methods used to assess the performance of these parts based on the indicators required to rank these energy systems.
3.1. Energy Approach
To assess the production system’s energetic performance, unidimensional thermodynamic models were previously implemented and validated on an application test case [
26]. In this model, each subsystem of the energy system is modeled by zero-dimensional components where the relation between the input and output satisfies energy, mass and momentum balances. This modeling method is generic while geometric or specific characteristics can be used as input of the model: heat exchangers geometry; steam turbine, fan or pump characteristics, etc. Thus, energy conversion efficiency can be assessed during the whole year, considering off-design ambient conditions and part load operation of the plant. The heat systems off-design behavior is important to assess the annual mean system efficiency and to provide reliable estimates for energy and cost predictions.
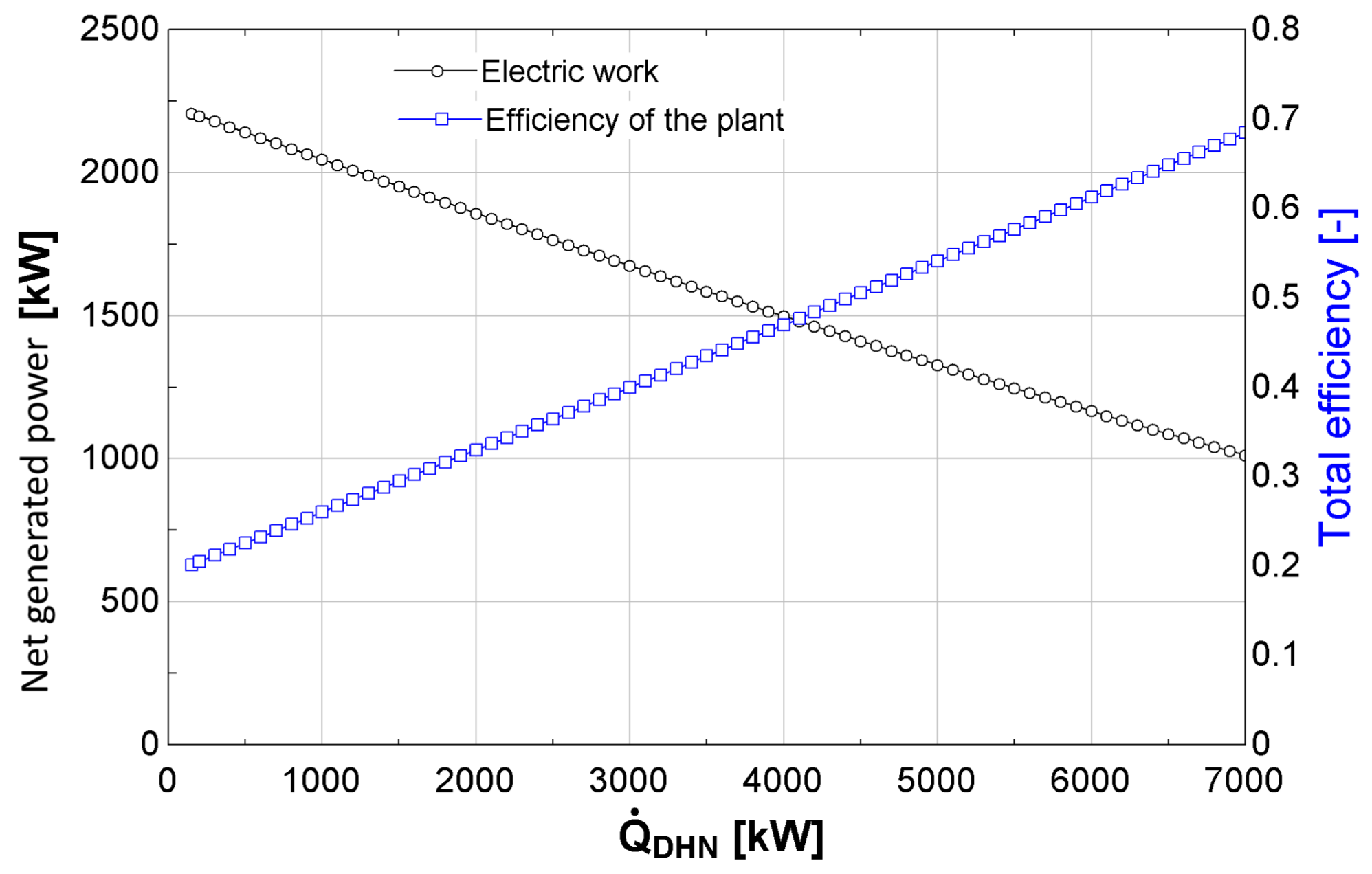
For example, the studied CHP plant, detailed in the application test case section, is composed of steam turbines, heat exchangers and a boiler and is dedicated to produce heat and power.
and
represent respectively the net electrical power and heat generated by the CHP plant.
denotes the primary energy used to generate
and
. The electrical and thermal efficiency are defined respectively as:
The total CHP efficiency is defined as
. The assessed performance of this plant is available in
Figure 1.
This methodology could be extended to each kind of thermodynamic system, renewable or not, to integrate them into the developed tool as it has already been performed for a heat pump in [
27] or through a new dynamic simulation of boilers from [
39]. In this case, the pseudo-dynamic approach is considered, i.e., the assessment for each time step of the performance of the system based on steady state performances (
Figure 1 shows the studied CHP plant steady-state performances in function of the thermal load supplied to the DHN).
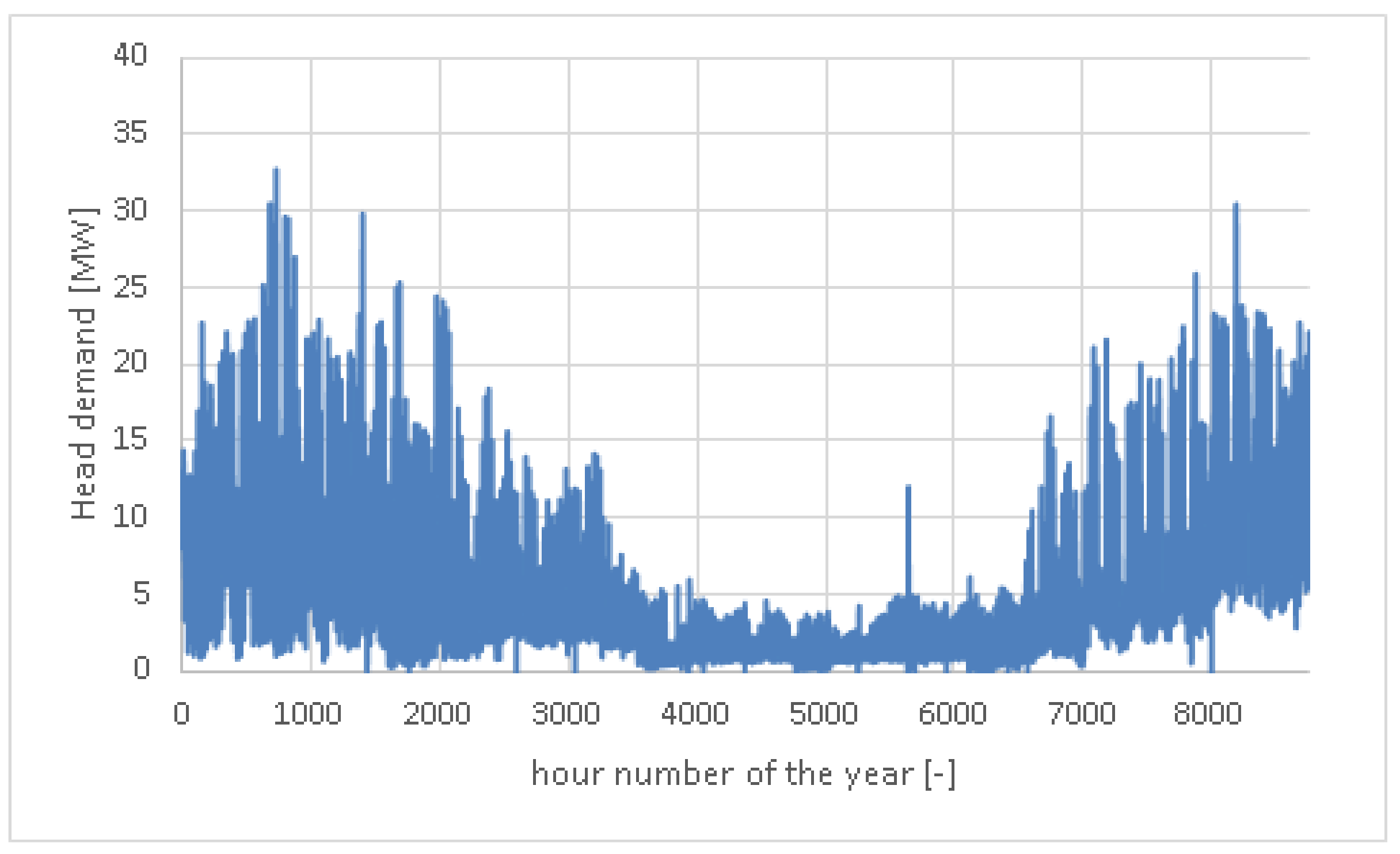
Indeed, the heat demand for a DHN can vary widely during the year (as depicted in
Figure 2) as a function of the users’ habit or climatic conditions. However, these changes generally occur slowly and the corresponding supply heat is limited due to technical constraints. For example, the control valves have mechanical inertia or the control system limits the temperature variation of the DHN to avoid too large an expansion of the material constituting the pipes. Therefore, this pseudo-dynamic modeling can be suitable for the developed tool.
As previously discussed, the heat transport modeling is required to assess the behavior of the heat transport inside a DHN. Indeed the temperature level reached a building has to be beyond a threshold to ensure the comfort inside the building connected to the DHN. Due to the heat transport delay induced by the large distance of piping network and reduced fluid velocity, the dynamic behavior has to be correctly assessed.
The heat transport modeling is based on a plug flow model to assess its dynamic behavior [
40,
41]. It is derived from the Lagrangian approach [
42], i.e., the properties of each fluid particle are considered along their direction as a function of time, considering the energy balance in each cell with its environment [
42]. It is assumed that the fluid carrier is incompressible, which is valid if water is considered and for low pressure variations [
43]. This method was previously analyzed, developed [
44] and validated under Matlab for different operating conditions and pipe layouts [
45], but it has now been successfully ported to Modelica [
46] and the related open-source Modelica library is available in [
47].
To assess the delay time between the entry and the exit of a fluid parcel inside the pipe, the following equation is solved:
where
is the transported quantity,
y is the normalized spatial coordinate,
t is the time, and
the normalized velocity. An approximation of the one-way wave equation was successfully introduced with the
spatialDistribution() operator defined in the Modelica Language Specification [
48].
This model considers the heat transport, thermal inertia of the pipes and the related heat losses.
Heat losses are assessed through a global heat transfer coefficient. The assessment of this coefficient is based on a bi-dimensional steady state heat transfer model, which considers the insulation, geometry and buried layout of the pipes [
26].
A thermal capacity is added to the core pipe model at the outlet of the pipe to account for the thermal inertia of the pipe constituting material as [
49].
The hydraulic behavior is assessed by a previously developed model denoted
HydraulicDiameter of the Annex 60 Library [
50]. In this case, the pressure drop is coupled to the mass flow rate using a quadratic relation.
An interested reader could refer to [
46] for further details.
3.2. Environmental Approach
To complete the analysis from an environmental point of view, a detailed combustion model was previously performed [
36] and validated on several fuels and boiler sizes to assess the CO
and regulated pollutant emissions of biomass combustion such as NO
and SO
. The developed model considers chemical reaction kinetics coupled to a zero-dimensional, steady-state thermodynamic model. The fuel as biomass could be specified as a general model C
H
O
N
S
, where the subscripts are the ratio between the wet basis mass fraction of each component and its molar mass. The model is also able to consider natural gas as fuel under the form C
H
O
N
He
.
The assessed combustion products produced in the exhaust gas are 15 chemical species (H
, O
, H
O, CO, CO
, OH, H, O, N
, N, NO, NO
, CH
, SO
, SO
). While the NO
emissions at the equilibrium were overestimated [
51], a complementary chemical analysis is performed to lead to a corrected thermal NO
formation calculation with the assessment of the fraction of the fuel nitrogen, which is converted into NO
[
52].
The emphasis of the model on the NO emissions is performed to assess if the operator plant requires the use of a de NO fuel system leading to extra investments and operational costs, which are required for the economic indicator.
If other energy sources (electricity or heavy fuel) are used or if the energy conversion process is currently not known, CO
emissions factor can also be retrieved from literature (see
Table 1 for the combustion process reference CO
emissions in Belgium and for electricity consumption).
3.3. Economic Indicator
One of the most critical and decisive criteria for the development of energy systems (DHN or CHP plant for example) is the cost of the energy.
The cost model per unit of thermal energy used herein is derived similarly to the one defined for electricity in [
56]. According to this model, the cost of heat is expressed as:
where
C is the total investment cost and
is the annuity factor, which takes into account for the present value of money and represents the annual repayment for the initial investment expressed in year
. The annuity factor is defined as:
where
d is the discounting rate per year and
N the number of years for which the installation is used (e.g., the life time of the plant).
is the installed thermal power of the CHP plant in MW and
is the equivalent utilization time at rated power output.
embeds the availability factor of the plant (around 92% for a biomass CHP plant [
56]).
is the cost of fuel in €/MWh,
is the fixed cost of operation, maintenance and administration in €/year and
is the variable cost of operation, maintenance and repair in €/MWh.
is the average annual thermal efficiency defined similarly to
yet taking into account the start/stop procedures (if any) and the part load efficiency. These efficiencies are assessed by the thermodynamic modeling described previously.
is the price of electricity in €/MWh while
and
are, respectively, the number of green certificates per MWh of electricity produced (For the Walloon region of Belgium one green certificate is granted for every 456 kg of CO
saving. A maximum of two green certificates are allowed per MWh of electricity produced.) and the unit price of green certificate. The term
is replaced by the premium on the electricity selling when feed-in tariffs are used instead.
is defined as the ratio of the heat delivered to the consumers to the heat produced by the plant depending on the temperature level, the insulation of the network and the ambient conditions.
A reliable estimate of
C,
,
,
d and
N can be found, for example, in [
32,
33,
56]. Neither the influence of fuel cost
nor the one of the supporting policies
will be long discussed herein and representative value of the market in Belgium will be used, as it is relatively straightforward for the reader to include his proper data into the above model.
3.4. Exergy Analysis
The use of energy refers generally to the first law of thermodynamics which states that energy is stored in every device and process and can neither be consumed nor destroyed; it can only be transformed [
57]. As it was discussed previously, this concept is
“inadequate for depicting some important aspects of energy resource utilization” [
57] as energy system performance. The exergy indicates the maximum work potential of a system under determined conditions. There are no conventions widely accepted to define the exergy concept but in the present study, the exergy analysis proposed by [
58] is used. Exergy (Ex) expressed in J/kg is defined as:
where
H stands for the enthalpy [J/kg], S for the entropy [J/kg/K],
T for the temperature [°C] and the subscript
the reference or ’dead’ state. In this study, this reference state is defined as the daily temperature of a location with a pressure of 1 atmosphere. For the fuel exergy calculations, the air studied has a relative humidity of 70% [
59] and a composition defined according to [
60].
This complementary analysis can be useful to point out the design problem of current energy systems or the parts of these systems where the exergy is destroyed to optimize the available exergy [
61]. An example of this analysis is performed in [
62] to study a CHP plant. In this case, the pressure level of an extraction turbine was identified as too high, leading to exergy degradation and related energy efficiency drop.
3.5. Heat Demand Profile
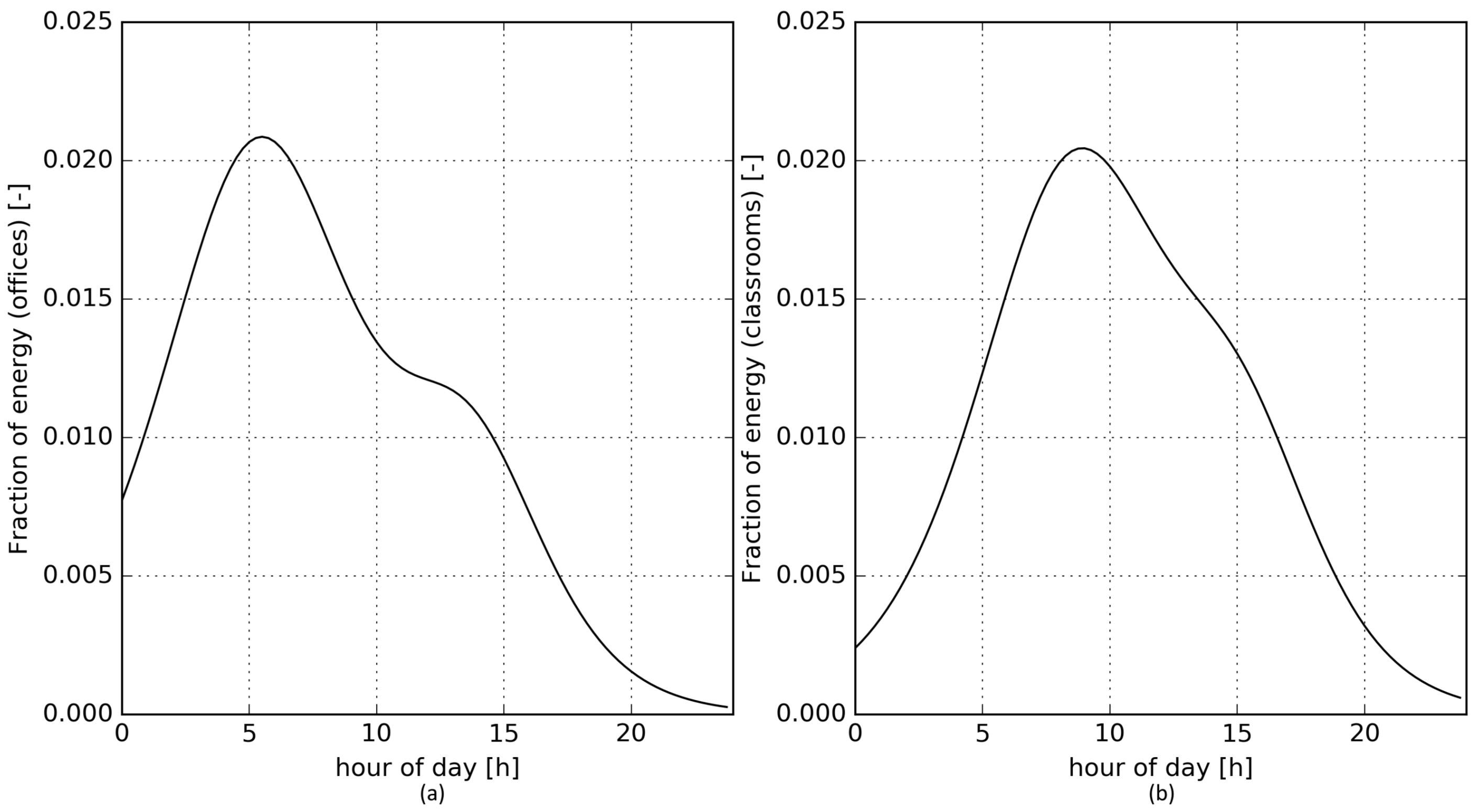
The head demand of consumers can be assessed by experimental data, building performance energy reports or dedicated modeling libraries. In this contribution, internal reports performed to assess the building performance are used. These heat demand profiles are derived as a function of occupancy profile depending on each building to assess the dynamic consumption of each building. A typical heat consumption profile for two studied buildings is available in
Figure 3.
For other building topologies, the internal Modelica library can be used [
63] (It should be available into the Thermocycle Library [
64] soon.) or a more generic library as [
65]. To go one step further, these libraries can be modified to take into account specific dynamic behavior as those appearing in a condensing boiler [
66] as a function of the control strategy.
4. Application Test Case
The application test case studied is the DHN of the University of Liège (The interested reader can refer to [
26] for the detailed configuration of the DHN and the heating plant). It is fed by a biomass CHP plant of a nominal thermal power of 7 MW dedicated to the base heat demand and natural gas back-up boilers (50 MW) to complete it. The nominal power generation of this CHP plant is 2.4 MW. The total length of the DHN is 10 km and the fluid carrier is pressurized (12 bar) hot water at a mean temperature of 120 °C. About 70 buildings (classroom, office rooms, administrative office, a sport center and a hospital) are connected to the DHN for a normalized annual heat demand of 61 GWh and represents a heated area of 470,000 m
whose a quarter is dedicated to the hospital. A typical heat demand curve is available in
Figure 2. During the summer time (between May and October), only the hospital and the sport center (swimming pool) are fed by the DHN. The relative high temperature of the fluid carrier is due to the use of steam by the hospital for his kitchen and its humidification system.
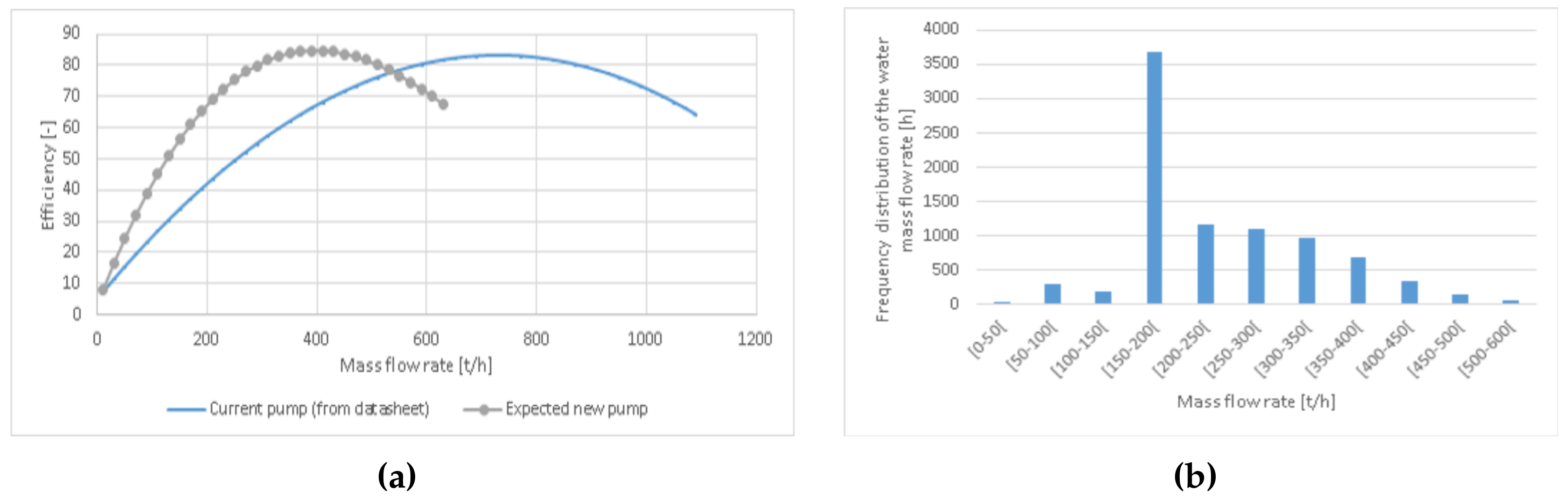
The DHN is assumed to be composed of 23 sections. They are insulated with mineral wool with an identified thermal conductivity of 0.047 W/m/K. The corresponding heat transfer global coefficient is assessed to 0.9 W/K per meter of duct containing the pipes of the DHN. The DHN has operated since the sixties and it is divided into three main pipe networks whose one ensures the hospital back-up and is usually not used. Each main pipe network is fed by pumps whose efficiency in function of the mass flow rate is available in
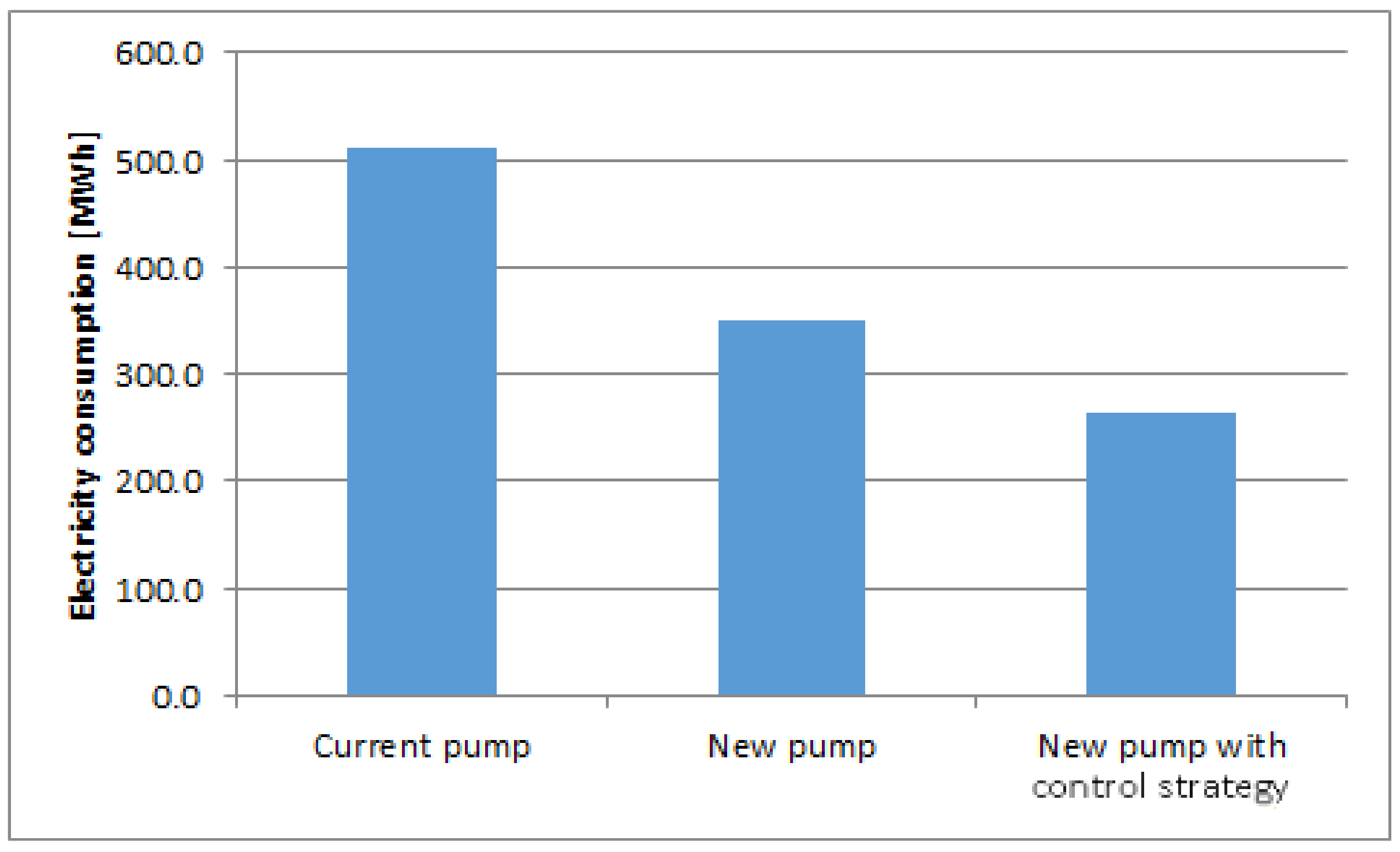
Figure 4a, blue line. Due to specificities of the DHN which are not within the scope of the present contribution, only one main pipe network optimization will be considered in this study. This pipe network works continuously throughout the year while it feeds the hospital and the sport center.
However, the pumps were over sized. Indeed, the mass flow rate of the pipe network is frequently under 200 t/h (over half a year,
Figure 4b) while the nominal mass flow rate reaches about 1000 t/h. The corresponding mass involves that the pump works at an efficiency lower than 45%. On the other hand, the temperature difference between the supply and the return pipe is quite reduced (about 13 °C) while a common temperature difference tends to 30 °C to minimize electric pump work and the DHN heat losses as advised by [
19,
20,
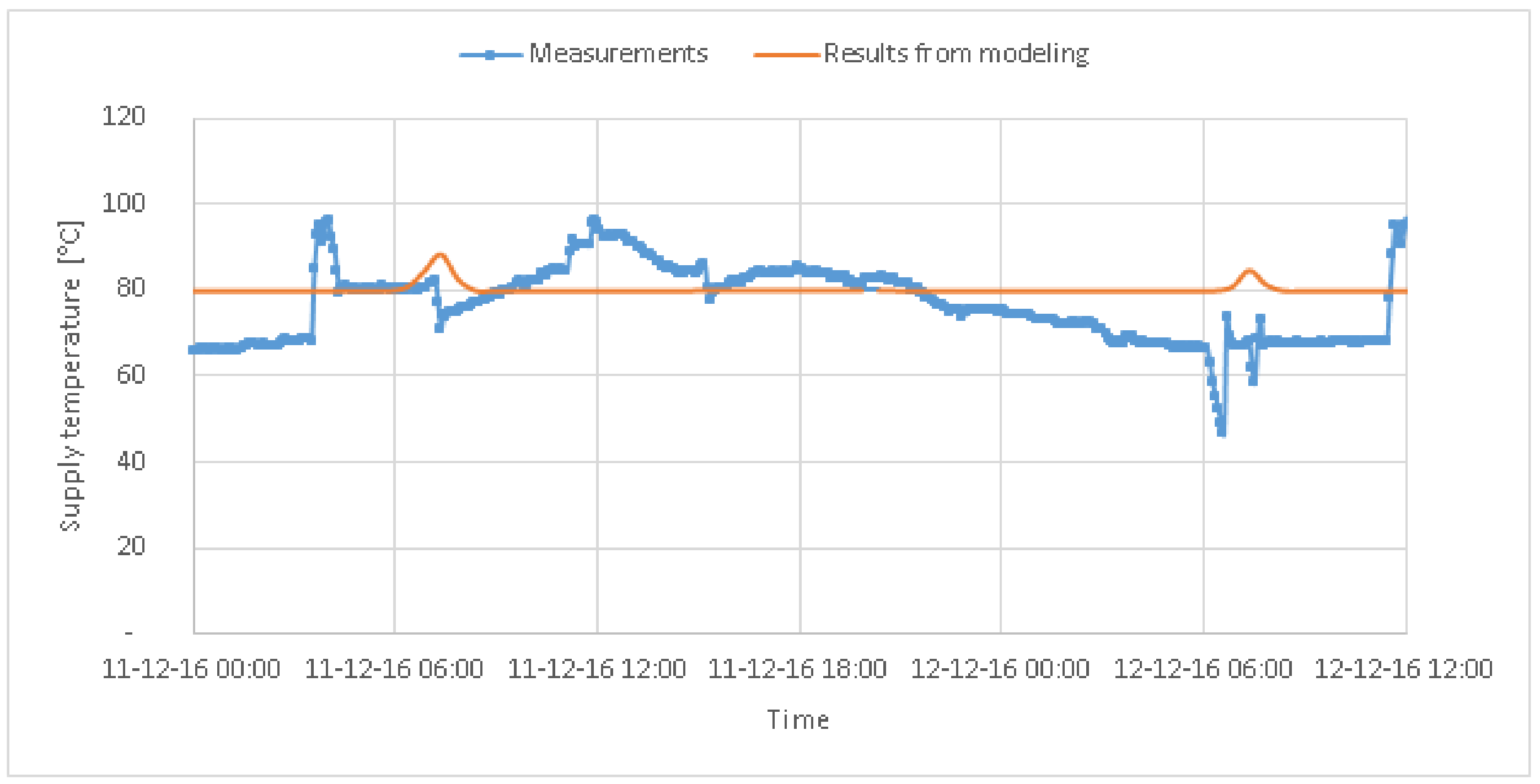
67]. This reduced temperature difference is due to inadequate control strategies of the power injected into the DHN, leading to too high a mass flow rate. On the other hand, some discomfort currently occur in buildings due to too low a supply temperature reaching the furthest buildings from the heating plant. That is why it is proposed to investigate an optimal control strategy to increase the temperature difference while minimizing the mass flow rate, the related pump work and ensuring the building comfort.
To perform economic calculations, the cost of electricity is considered at 112 € per MWh [
34], while the cost of heat identified by the energy and cost modeling for the considered system is about 65 € per MWh [
26].
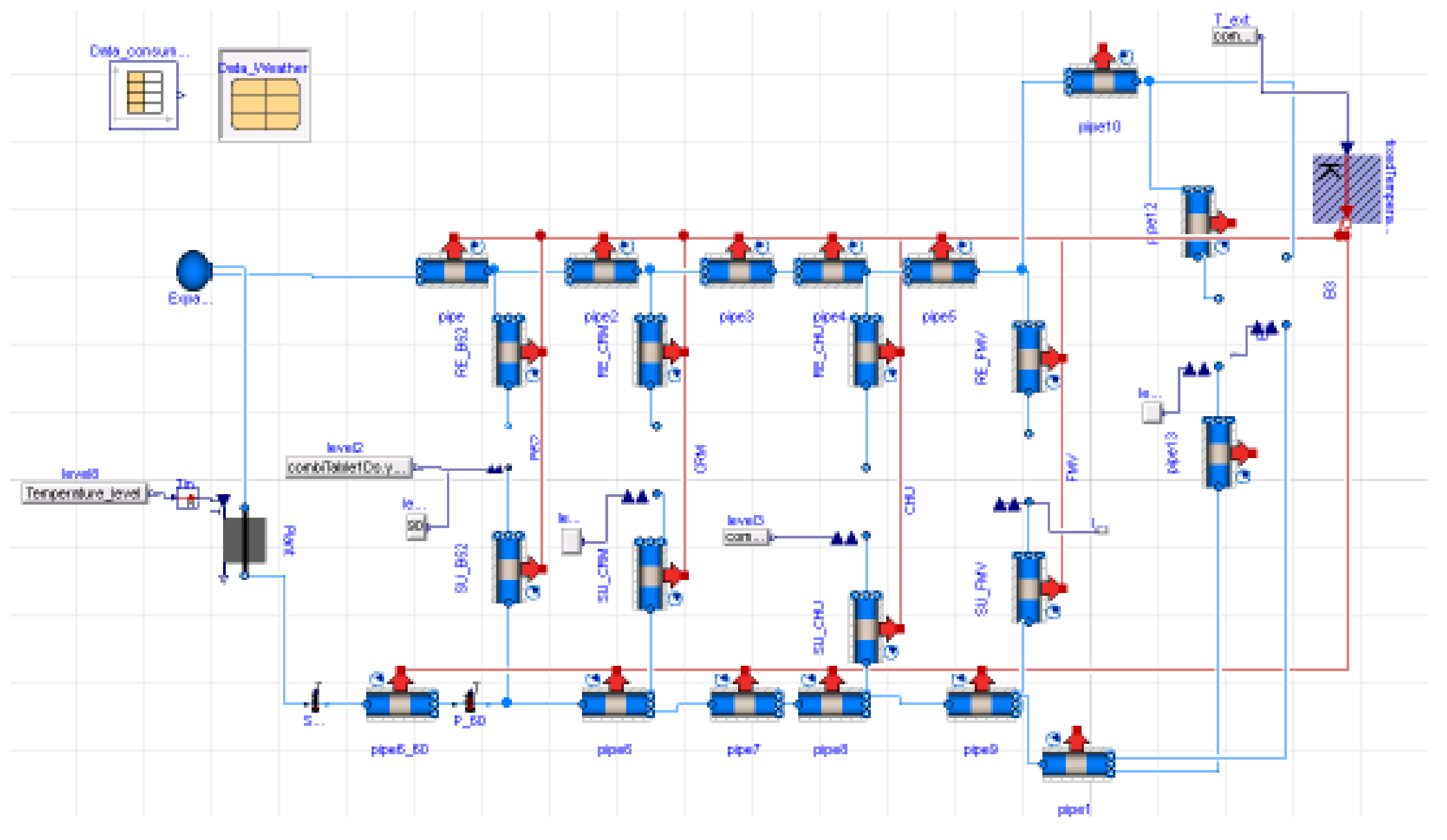
A schematic diagram of the application test case performed under Modelica is available in
Figure 5.
6. Conclusions and Perspectives
District heating networks are considered as a convenient way to supply buildings while reducing CO emissions and introducing renewable energies into the current energy production mix. However, to optimize the profitability of new DHN or perform a retrofit of current DHN installations, some modeling tools are required to investigate several scenario and assess what is the best option. To achieve this, models were developed to assess the behavior and the energetic, economic and environmental performances of the production plant, the pipes of the DHN and the consumers.
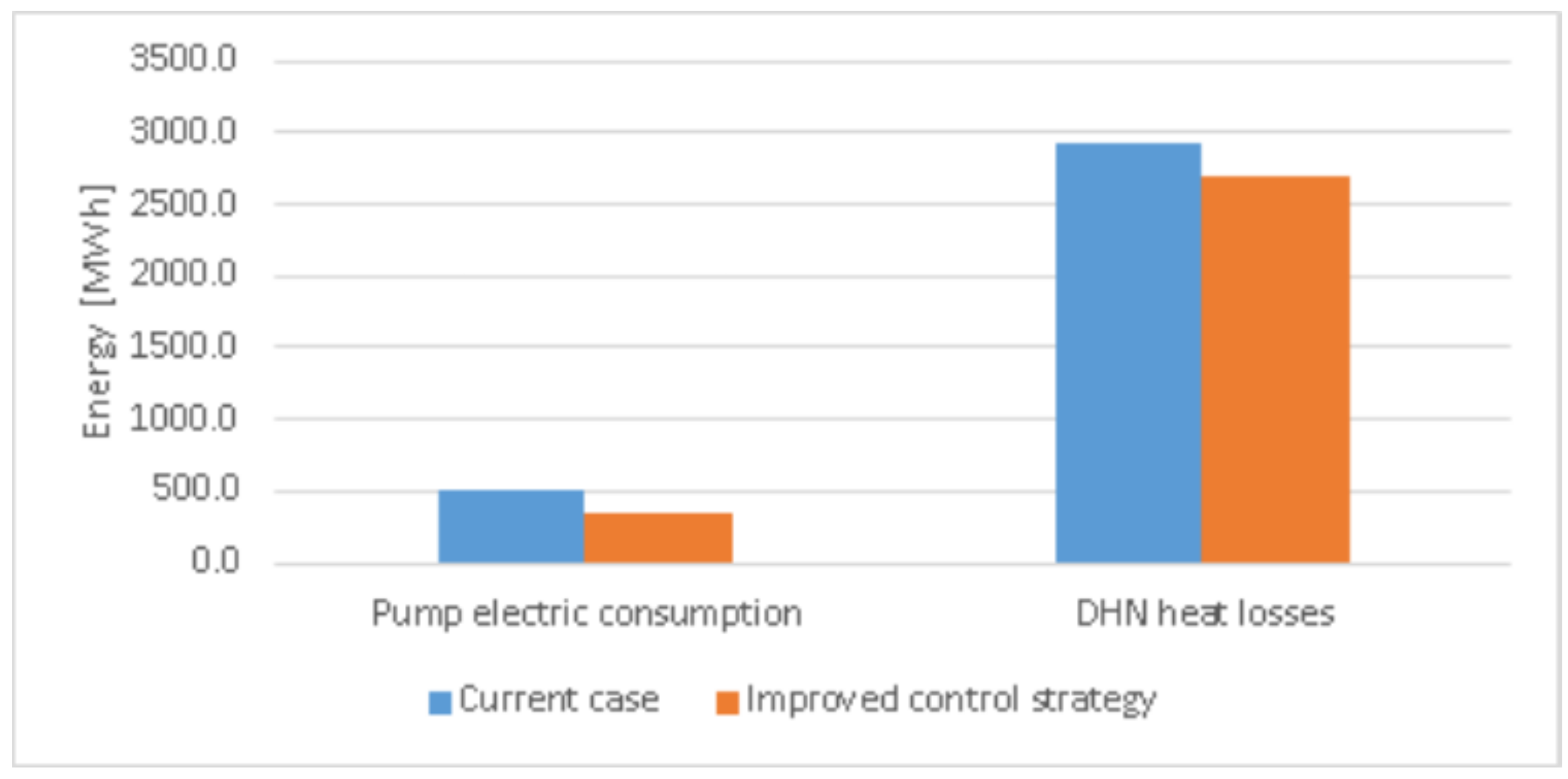
In this contribution, all the models previously developed and validated are implemented into one open-source language, Modelica, to assess the dynamic behavior of such a system. To illustrate the usefulness of the method, an application test case is selected to study an improved control strategy dedicated to reducing the electric pump work while minimizing the DHN heat losses and ensuring the users’ comfort inside the building.
The use of an improved control strategy leads to a significant reduction of the electric consumption of the pump by about 30%. As expected, the heat losses are reduced (%) while the average annual temperature of the DHN is lower due to the higher temperature difference. Another solution to reduce the electric pump consumption is to replace the current over sized pump with a new one. All these results involve CO emissions savings (from 70 to 111 tons per year). Moreover the users’ comfort, which was not previously satisfied, is ensured by this control strategy.
Therefore this contribution has shown that the developed open tool is able to perform a simple or more complex retrofit of DHN installations while ensuring the comfort inside connected buildings and assessing useful indicators to rank the considered scenario.
For perspective, other complex control strategies could be investigated, especially the heat storage inside the network itself, to reduce the peak heat demand due to the night setback for example [
23]. On the other hand, the integration of solar thermal systems will be considered to study the use of the network as a heat storage facility during the summer time, while reducing the CHP plant use and its related emissions.