A New Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Based on Fuzzy Information Granulation and an Optimized Wavelet Neural Network
Abstract
:1. Introduction
2. Fuzzy Information Granulation
- (1)
- Determine the mean value R. R = median(T) where T is the time series put in ascending order.
- (2)
- Determine the lower bound LOW.
- (3)
- Determine the upper bound UP.
- (4)
- Determine the fuzzy particle P.
3. Chaotic Particle Swarm Optimized Wavelet Neural Network
- (1)
- The randomness of the initialization process may result in inferior solutions, affecting the convergence of the evolutionary process.
- (2)
- The solution obtained by this algorithm may be a local optimal solution rather than a global optimal solution.
- (1)
- Initialize the parameters to generate a random D-dimensional vector (z1 = (z11, z12, …, z1D)) with the value of each component being between 0 and 1. Get N vectors z1, z2, …, zn by iteration according to Equation (9). Additionally, transform the components of each vector into the corresponding value range.
- (2)
- Call the WNN to obtain the fitness value of the particles. Select M particles from the N populations to form the initial population. Additionally, generate the initial velocity of the M particles by chaotic series.
- (3)
- Update the individual extremum pBest if the particle fitness value is superior to pBest. Additionally, update the global extremum gBest if the particle fitness value is superior to gBest. Then update the particle’s position and velocity.
- (4)
- Perform chaotic optimization to the current optimal position PgBest = (pg1, pg2, …, pgD). Additionally, map PgBest to 0–1 according to:Let Y = [y1, y2, …, yD]. The chaotic series Y1, Y2, …, Ym is generated after m times iterations by Logistic equation. The chaotic series is then mapped back to the original solution space according to:So the new solution series is Pg1*, Pg2*, …, Pgm*.
- (5)
- Calculate the fitness value of the new solution and replace the position of any particle in the current population with the best solution P*.
- (6)
- Determine whether the termination condition is reached. If not, return to step (3) to continue iteration. Otherwise, the flow terminates and the selected parameters are obtained.
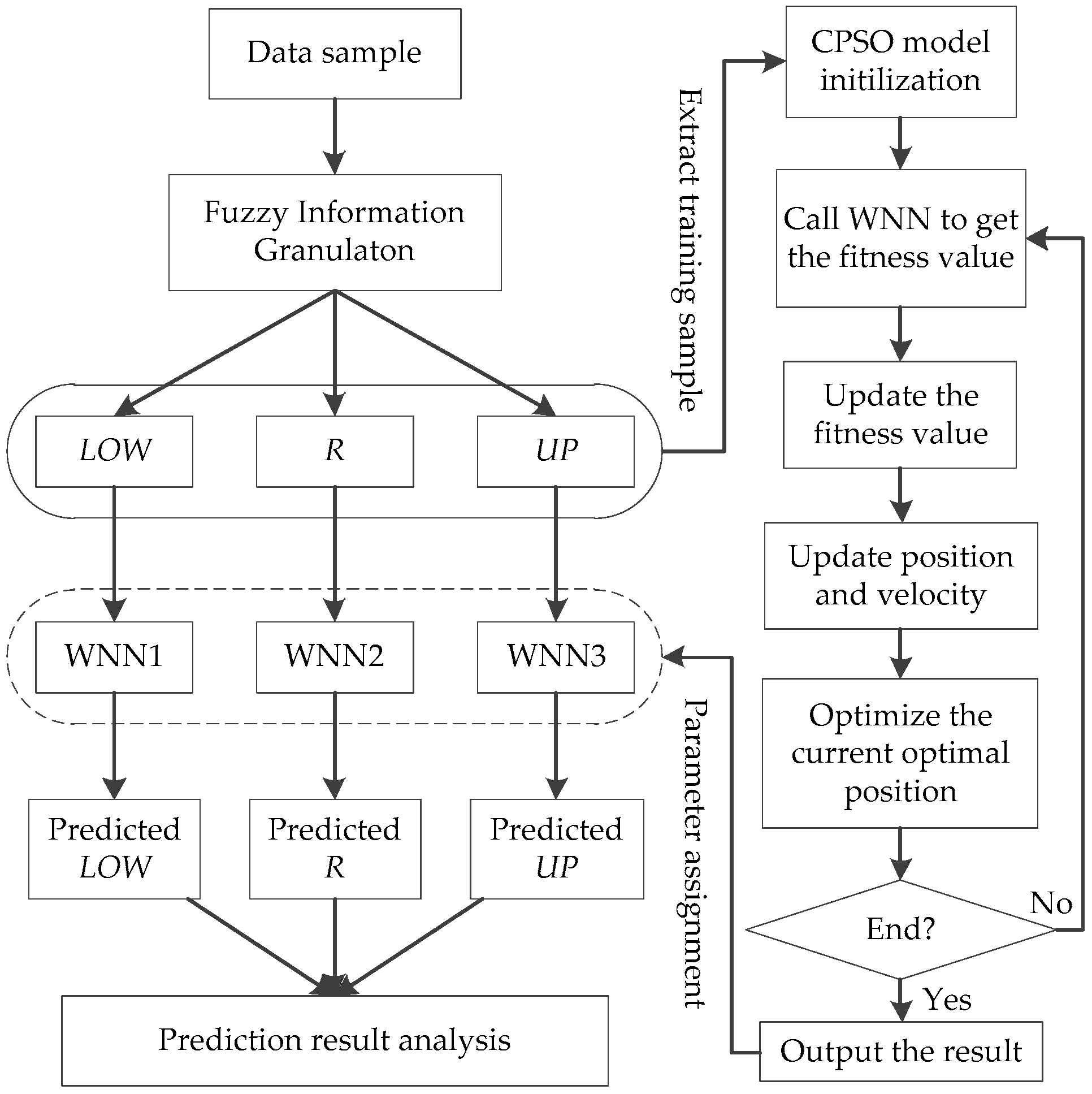
4. Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Range
- (1)
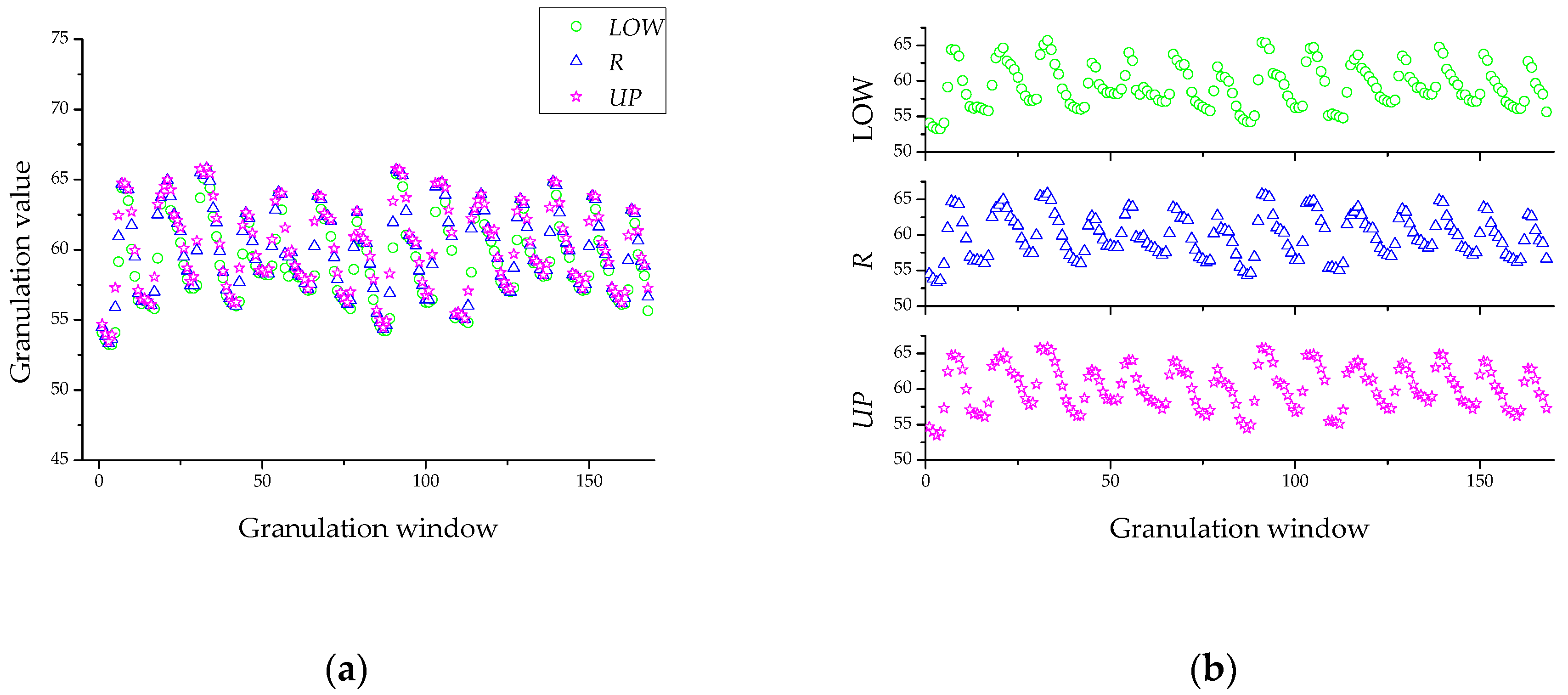
- Extract the sample data. Determine the size of granulation time window according to the sample data. The granulation data should be able to describe the trend of the original sample data. Perform FIG to sample data to obtain LOW, R, and UP.
- (2)
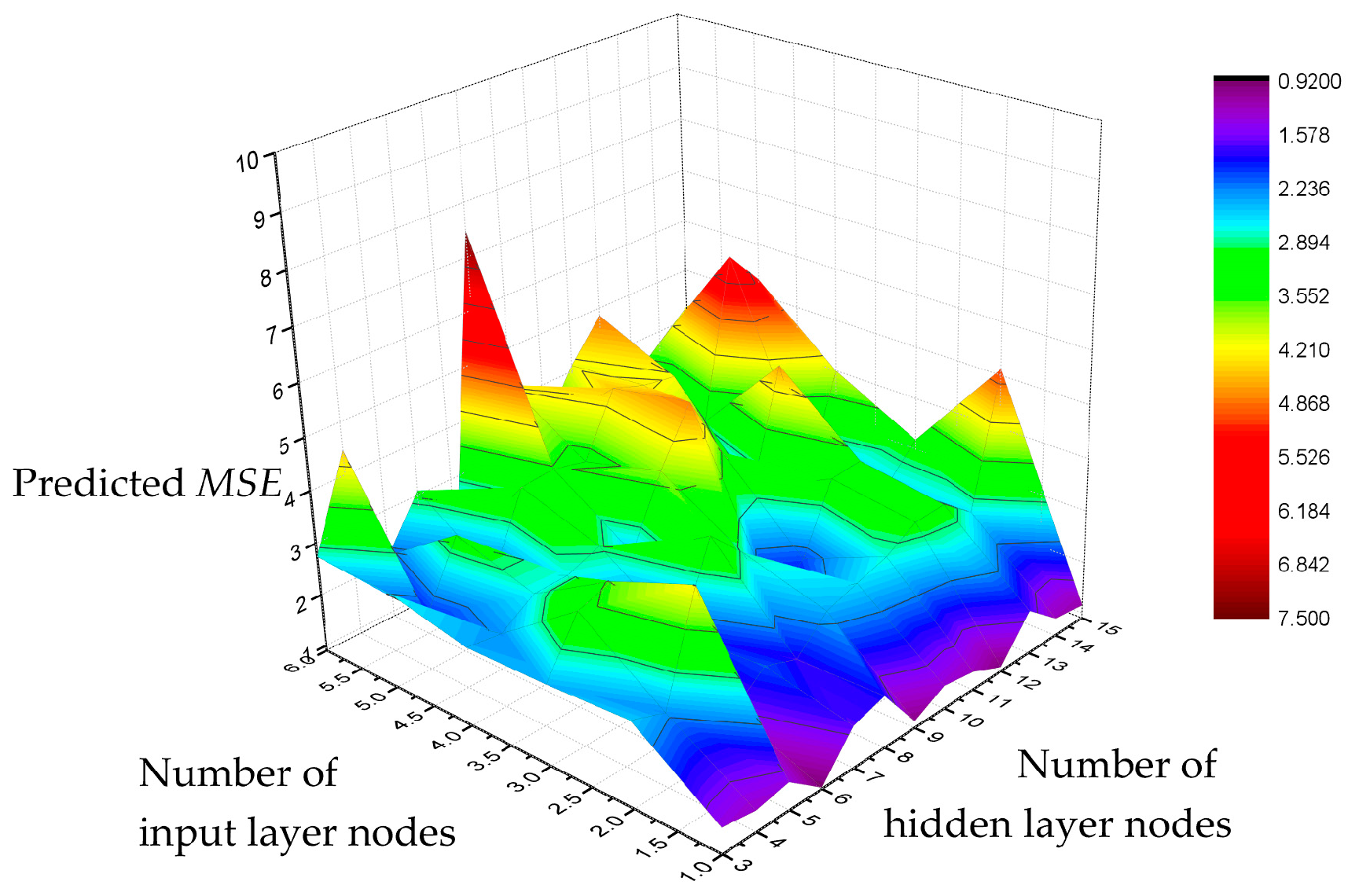
- If the amount of data is huge, the output layer node shall be determined according to forecast demand. The input layer node n shall be determined according to the intrinsic regularity of the historical data. Additionally, the number of hidden layer node shall be m = 2n + 1.If the amount of data to be processed is limited, the output layer node shall be determined according to forecast demand, while the input layer node and the hidden layer node shall be determined by traversing method.
- (3)
- The structural parameters that need to be optimized are determined when the input layer, the hidden layer, and the output layer are determined. Encode the optimization object according to Equation (13), and take Equation (11) to be the fitness value function. Screen the structural parameters of the WNN by CPSO.
- (4)
- Use the designed WNN to predict LOW, R, and UP to obtain the fluctuation range of the TWHT.
- (5)
- Evaluate the performance of the model by the mean square error (MSE), the mean absolute error (MAE), and the correlation coefficient (r), calculated as:
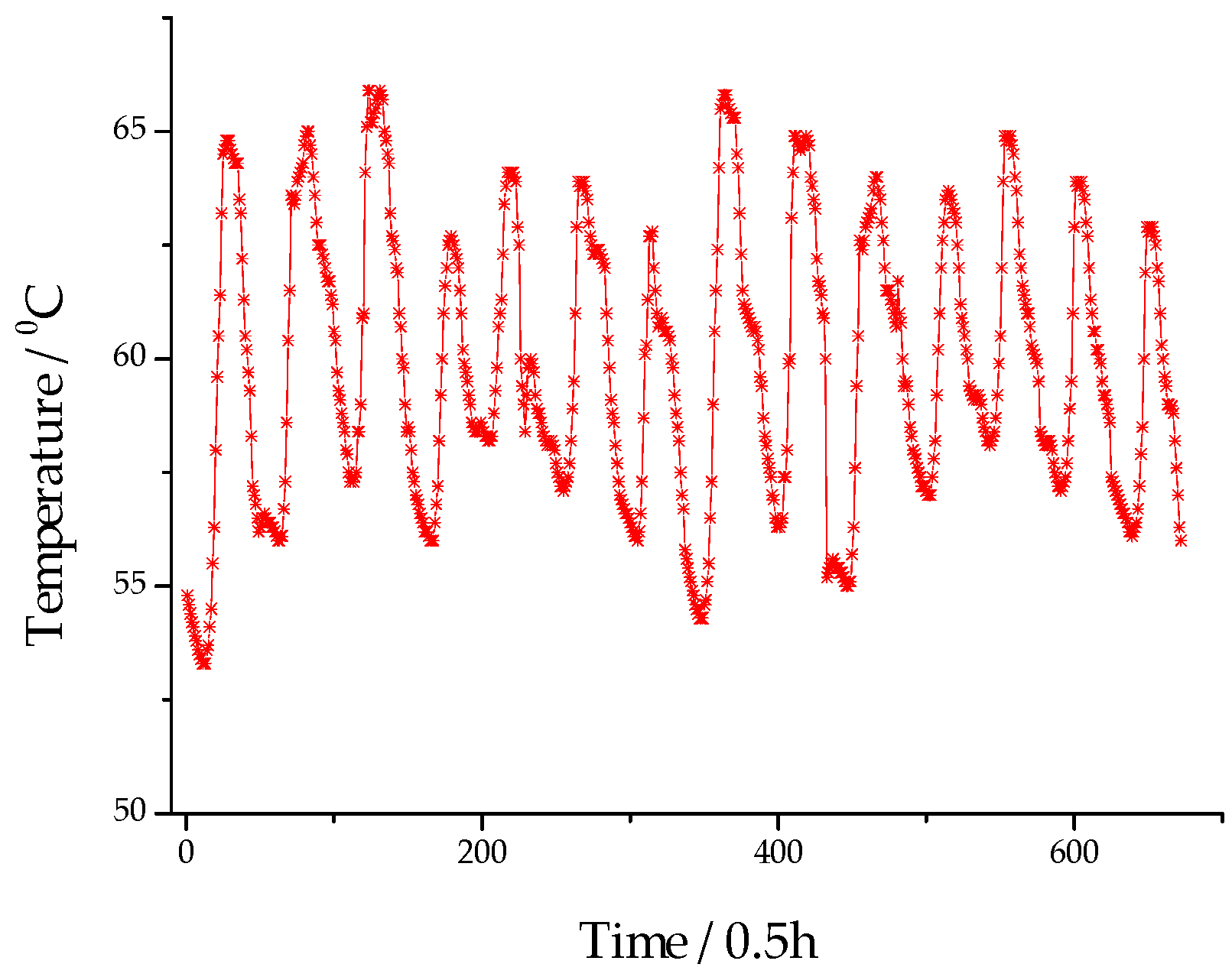
5. Case Study
5.1. Fuzzy Information Granulation
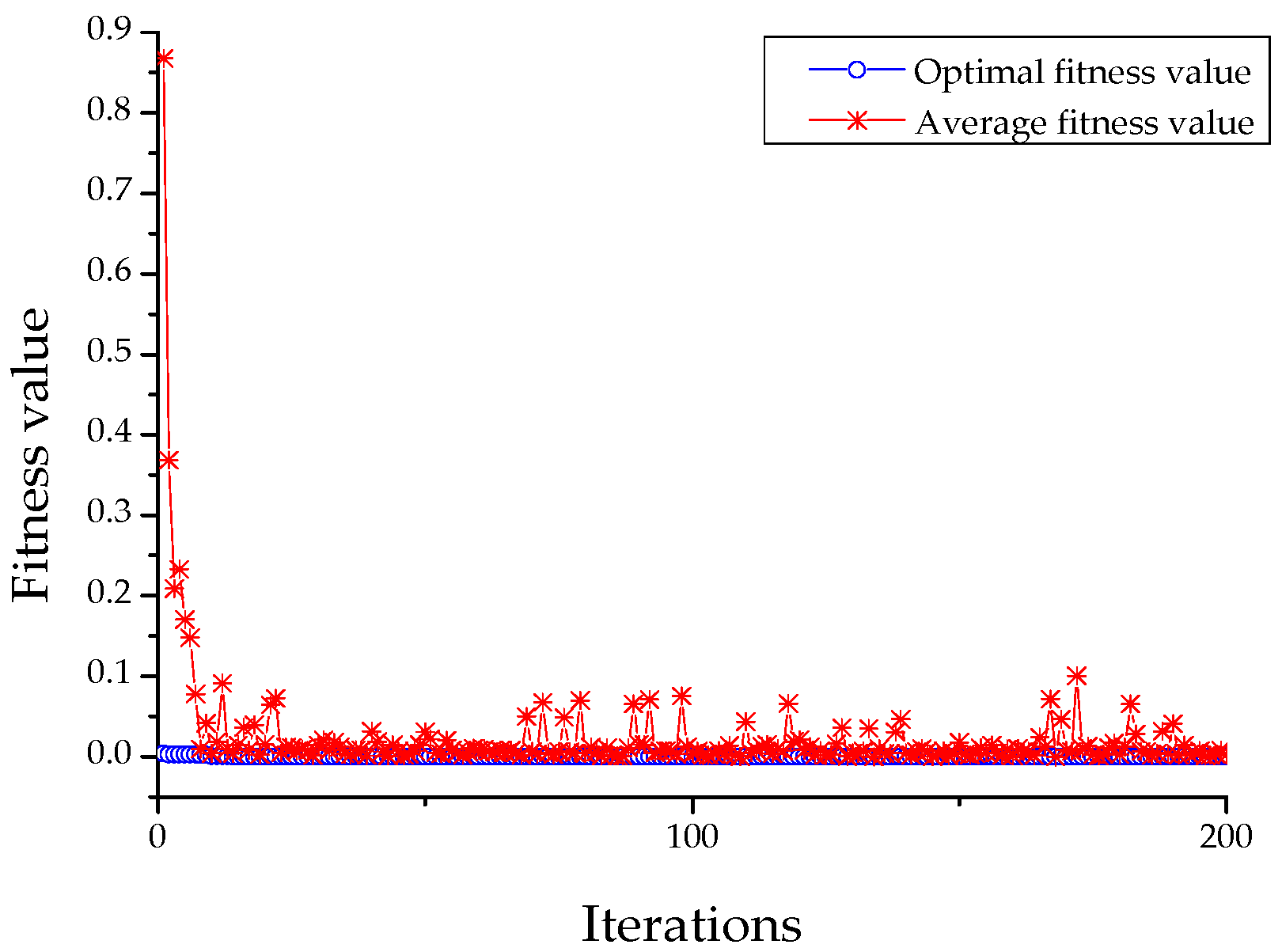
5.2. Establishment of Optimized WNN Prediction Model
- (1)
- The selection of wavelet function.
- (2)
- The number of nodes for the input layer and the hidden layer.
- (3)
- The selection of the input weight wij, the output weight wj, the translation factor bj, and the stretching factor aj.
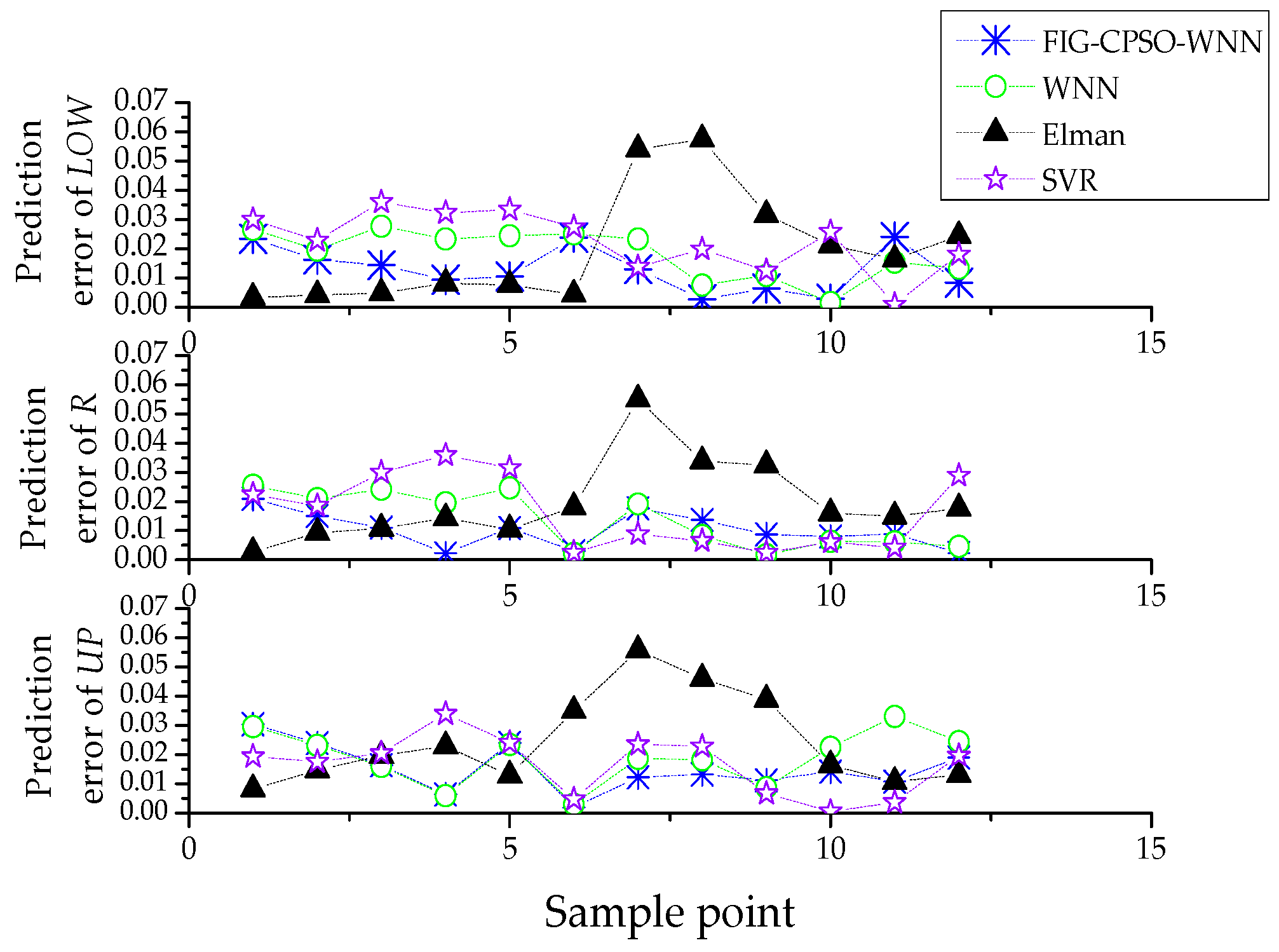
5.3. Comparison of Four Prediction Models
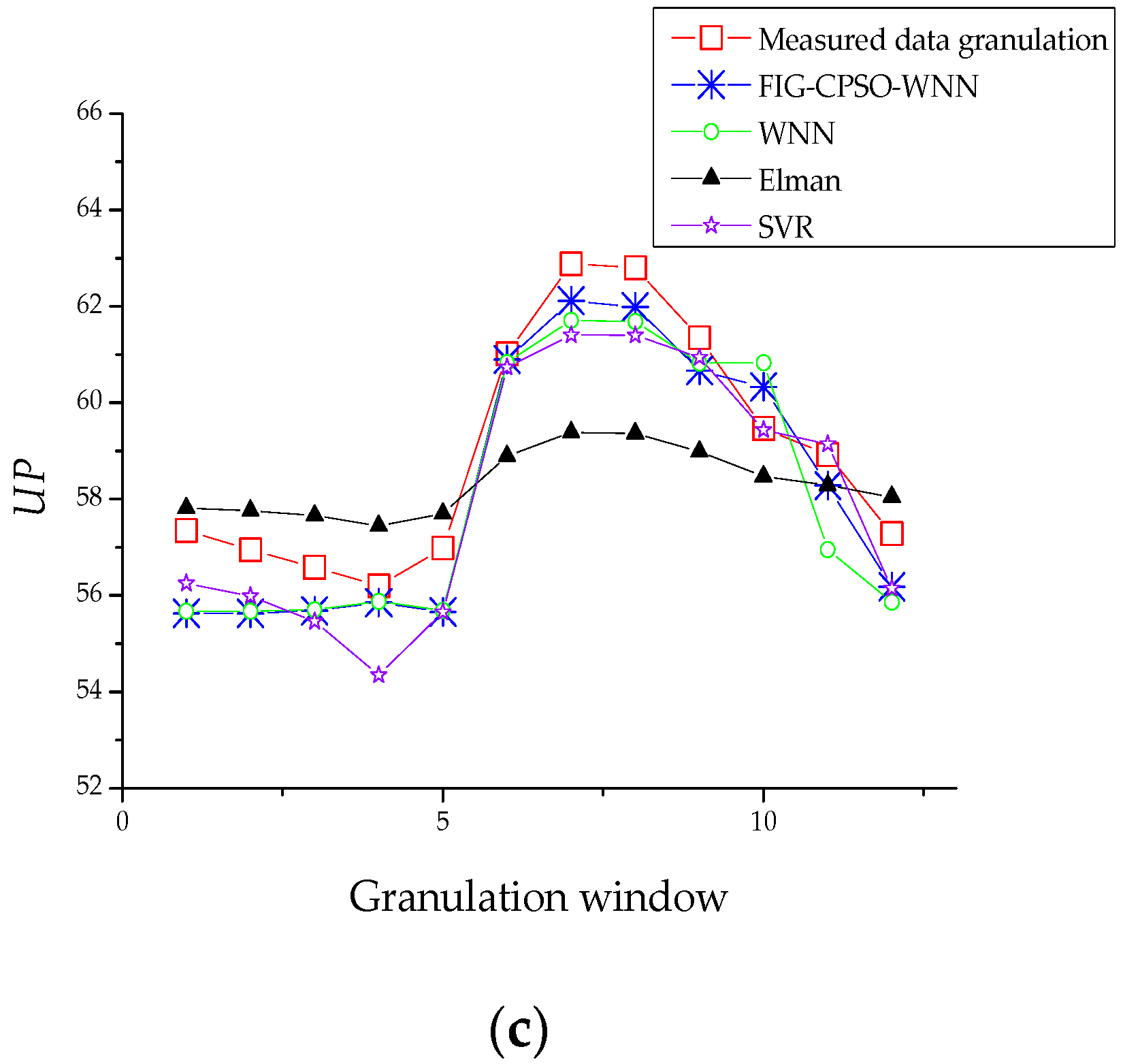
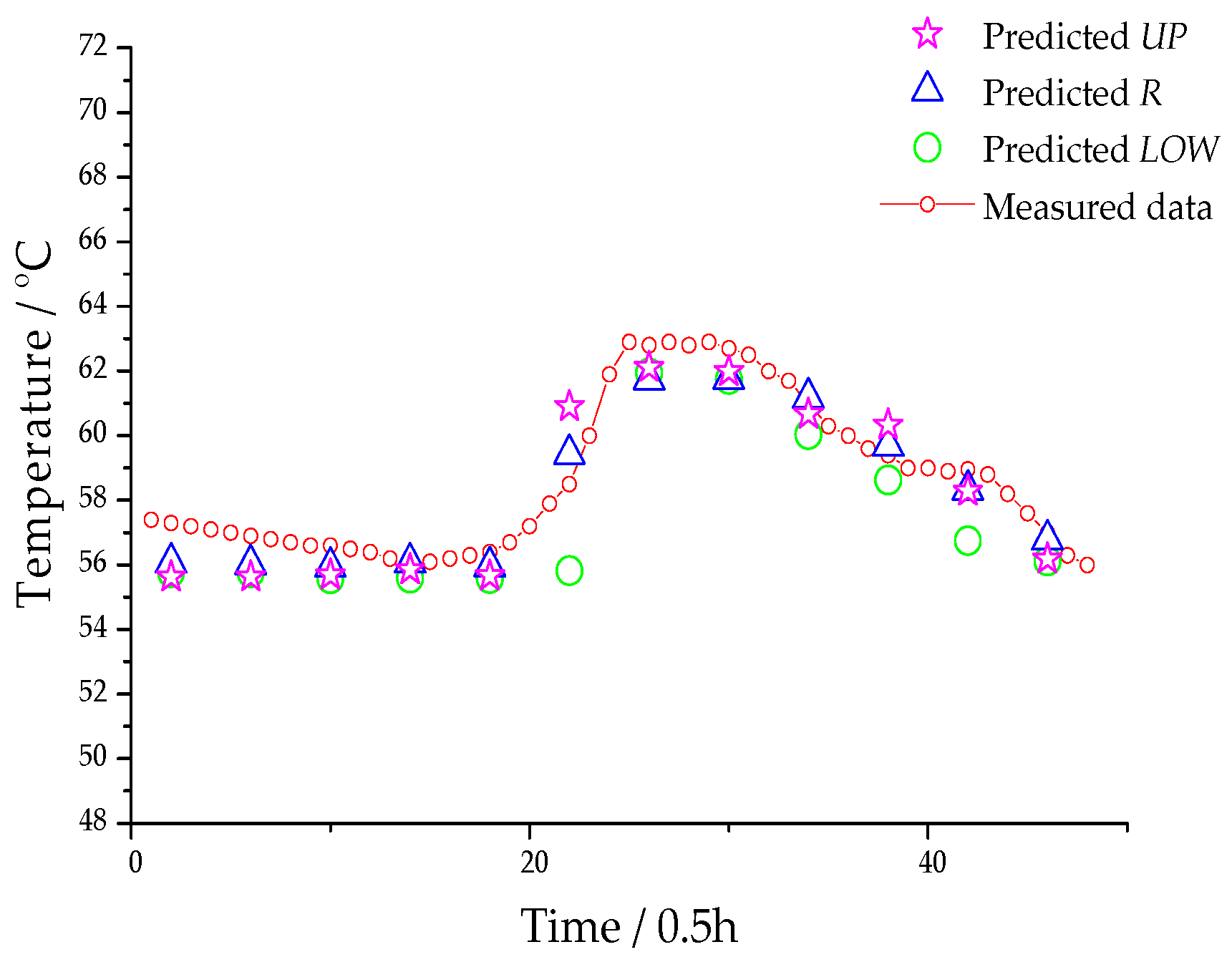
5.4. Comparison of the Predicted Fluctuation Range with the Measured Data
6. Conclusions
- (1)
- Information granulation can extract useful information from the raw data, which reduces the complexity of target data. Additionally, the wavelet neural network (WNN) has a strong nonlinear mapping capability. In this paper, the two methods are combined to make effective predictions of the transformer winding hotspot temperature fluctuation range.
- (2)
- By designing the WNN according to the field data, we obtain a superior prediction performance compared with various prediction models. The feasibility of the FIG-CPSO-WNN model for predicting the transformer winding hotspot temperature fluctuation range is thereby demonstrated.
- (3)
- The proposed model has a high prediction accuracy and guiding significance to the operation and maintenance of transformers. The new model can not only be used in the prediction of transformer winding hotspot temperature fluctuation range, but also provides ideas for prediction modeling in other areas.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pradhan, M.K.; Ramu, T.S. Prediction of hottest spot temperature (HST) in power and station transformers. IEEE Trans. Power Deliv. 2004, 18, 1275–1283. [Google Scholar] [CrossRef]
- Mcnutt, W.J.; Mciver, J.C.; Leibinger, G.E. Direct measurement of transformer winding hotspot temperature. IEEE Trans. Power Appar. Syst. 1984, 103, 1155–1162. [Google Scholar] [CrossRef]
- Assuncao, T.; Silvino, J.L.; Resende, P. Transformer top-oil temperature modeling and simulation. Trans. Eng. Comput. Technol. 2006, 15, 240–245. [Google Scholar]
- Taghikhani, M.A.; Gholami, A. Prediction of hottest spot temperature in power transformer windings with non-directed and directed oil-forced cooling. Electr. Power Energy Syst. 2009, 31, 356–364. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Power Transformers—Part 7: Loading Guide for Oil-Immersed Power Transformers; IEC 60076-7; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- Chen, W.G.; Pan, C.; Yun, Y.X. Power transformer top-oil temperature model based on thermal-electric analogy theory. Eur. Trans. Electr. Power 2009, 19, 341–354. [Google Scholar]
- Chen, W.G.; Xi, H.J.; Su, X.P.; Liu, W. Application of generalized regression neural network to transformer winding hot spot temperature forecasting. High Volt. Eng. 2012, 38, 16–21. [Google Scholar]
- Su, X.P.; Chen, W.G.; Xi, H.J. Winding hotspot temperature prediction for oil-immersed power transformer based on Kalman filter algorithm. High Volt. Eng. 2012, 38, 1909–1916. [Google Scholar]
- Keerthi, S.S.; Lin, C.J. Asymptotic behaviors of support vector machines with Gaussian kernel. Neural Comput. 2003, 15, 1667–1689. [Google Scholar] [CrossRef] [PubMed]
- Van Gestel, T.; Suykens, J.A.K.; Baestaens, D.E.; Lambrechts, A.; Lanckriet, G.; Vandaele, B.; De Moor, B.; Vandewalle, J. Financial time series prediction using least squares support vector machines within the evidence framework. IEEE Trans. Neural Netw. 2001, 12, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Lee, Y.; Yoon, B. Dynamic near-term traffic flow prediction: System-oriented approach based on past experiences. IET Intell. Transp. Syst. 2012, 6, 292–305. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Z.J.; Zhang, M.L. A combined forecasting model for range of wind power fluctuation based on fuzzy information granulation and least squares support. Trans. China Electrotechnol. Soc. 2014, 29, 218–224. [Google Scholar]
- Cui, Y.; Ma, H.; Tapan, S. Transformer hot spot temperature prediction using a hybrid algorithm of support vector regression and information granulation. In Proceedings of the Power and Energy Engineering Conference (APPEEC), Beijing, China, 12–14 April 2015. [Google Scholar]
- Zadeh, L.A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Pawlak, Z. Granularity of knowledge, indiscernibility and rough sets. In Proceedings of the IEEE World Congress on Computational Intelligence, Piscataway, NJ, USA, 4–9 May 1998. [Google Scholar]
- Zhang, Q.; Benveniste, A. Wavelet networks. IEEE Trans. Neural Netw. 1992, 3, 889–898. [Google Scholar] [CrossRef] [PubMed]
- Amjady, N.; Keynia, F. A new neural network approach to short term load forecasting of electrical power systems. Energies 2011, 4, 488–503. [Google Scholar] [CrossRef]
- Maniezzo, V. Genetic evolution of the topology and weight distribution of neural networks. IEEE Trans Neural Netw. 1994, 5, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Bargiela, A.; Pedrycz, W. Granular Computing: An Introduction; Kluwer Academic Publishers: Dodrecht, The Netherlands, 2003. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Chen, Z.; Xiong, R.; Wang, K.; Jiao, B. Optimal energy management strategy of a plug-in hybrid electric vehicle based on a particle swarm optimization algorithm. Energies 2015, 8, 3661–3678. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Teshnehlab, M.; Shoorehdeli, M.A. A novel binary particle swarm optimization. In Proceedings of the IEEE Conference on Control & Automation, Mediterranean, Athens, Greece, 27–29 June 2007. [Google Scholar]
- Swift, G.; Molinski, T.S.; Lehn, W. A fundamental approach to transformer thermal modeling—Part I: Theory and equivalent circuit. IEEE Trans. Power Deliv. 2001, 16, 171–175. [Google Scholar] [CrossRef]
- Lesieutre, B.C.; Hagman, W.H.; Kirtley, J.L. An improved transformer top oil temperature model for use in an on-line monitoring and diagnostic system. IEEE Trans. Power Deliv. 1997, 12, 249–256. [Google Scholar] [CrossRef]

| Rated Parameters | Basic Structural Parameters | ||
|---|---|---|---|
| rated capacity | 24/24/16 MVA | oil weight | 62,000 kg |
| rated voltage | 220/115/37 kV | winding weight | 39,482 kg |
| rated current | 630/1205/2497 A | core weight | 99,658 kg |
| rated frequency | 50 Hz | tank length | 10 m |
| connection type | YNyn0d11 | tank width | 2.5 m |
| cooling method | ONAN | tank height | 4 m |
| Serial Number | wij | aj | bj | wj |
|---|---|---|---|---|
| 1 | 0.8199 | 0.3208 | 0.1225 | 0.3837 |
| 2 | 0.2874 | 0.4802 | 0.6329 | 0.6052 |
| 3 | 0.8830 | 0.2729 | 0.9809 | 0.5076 |
| 4 | 0.5415 | 0.5215 | 0.0292 | 0.3290 |
| 5 | 0.5623 | 0.2805 | 0.4745 | 0.6701 |
| 6 | 0.9254 | 0.2475 | 0.7413 | 0.4753 |
| Prediction Model | SVR | Elman | WNN | FIG-CPSO-WNN | |
|---|---|---|---|---|---|
| MSE | 1.3812 | 1.7679 | 1.1170 | 0.8385 | |
| LOW | MAE | 1.2786 | 1.2362 | 1.0265 | 0.7290 |
| r | 0.9379 | 0.9708 | 0.9457 | 0.9681 | |
| MSE | 1.1378 | 1.6338 | 0.9209 | 0.6830 | |
| R | MAE | 0.9269 | 1.2716 | 0.7743 | 0.5954 |
| r | 0.9785 | 0.9863 | 0.9665 | 0.9689 | |
| MSE | 1.092 | 1.8314 | 1.2137 | 0.9779 | |
| UP | MAE | 0.9432 | 1.5108 | 1.1000 | 0.8828 |
| r | 0.9725 | 0.9946 | 0.9483 | 0.9729 | |
| Time Window | Measured Data | Predicted Data | ||||
|---|---|---|---|---|---|---|
| MIN | MEAN | MAX | LOW | R | UP | |
| 1 | 57.1 | 57.2 | 57.4 | 55.8 | 56.1 | 55.6 |
| 2 | 56.7 | 56.8 | 57 | 55.8 | 56 | 55.6 |
| 3 | 56.4 | 56.5 | 56.6 | 55.6 | 55.9 | 55.7 |
| 4 | 56.1 | 56.2 | 56.2 | 55.6 | 56.1 | 55.9 |
| 5 | 56.3 | 56.3 | 57.2 | 55.6 | 56 | 55.7 |
| 6 | 57.9 | 60 | 61.9 | 55.8 | 59.4 | 60.9 |
| 7 | 62.8 | 62.8 | 62.9 | 61.9 | 61.7 | 62.1 |
| 8 | 62 | 62.5 | 62.9 | 61.7 | 61.8 | 62 |
| 9 | 60 | 61 | 61.7 | 60 | 61.2 | 60.7 |
| 10 | 59 | 59.4 | 59.6 | 58.6 | 59.7 | 60.3 |
| 11 | 58.2 | 58.8 | 60 | 56.7 | 58.3 | 58.3 |
| 12 | 56 | 57 | 57.6 | 56.1 | 56.8 | 56.2 |
| Evaluation Index | LOW | R | UP |
|---|---|---|---|
| MSE | 0.9836 | 0.6318 | 1.1951 |
| MAE | 0.7917 | 0.5417 | 1.1167 |
| r | 0.9666 | 0.9823 | 0.9692 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, W.; Liu, J.; Zhao, T.; Zou, L.; Wang, X. A New Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Based on Fuzzy Information Granulation and an Optimized Wavelet Neural Network. Energies 2017, 10, 1998. https://doi.org/10.3390/en10121998
Zhang L, Zhang W, Liu J, Zhao T, Zou L, Wang X. A New Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Based on Fuzzy Information Granulation and an Optimized Wavelet Neural Network. Energies. 2017; 10(12):1998. https://doi.org/10.3390/en10121998
Chicago/Turabian StyleZhang, Li, Wenfang Zhang, Jinxin Liu, Tong Zhao, Liang Zou, and Xinghua Wang. 2017. "A New Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Based on Fuzzy Information Granulation and an Optimized Wavelet Neural Network" Energies 10, no. 12: 1998. https://doi.org/10.3390/en10121998
APA StyleZhang, L., Zhang, W., Liu, J., Zhao, T., Zou, L., & Wang, X. (2017). A New Prediction Model for Transformer Winding Hotspot Temperature Fluctuation Based on Fuzzy Information Granulation and an Optimized Wavelet Neural Network. Energies, 10(12), 1998. https://doi.org/10.3390/en10121998







