Transactive-Market-Based Operation of Distributed Electrical Energy Storage with Grid Constraints
Abstract
1. Introduction
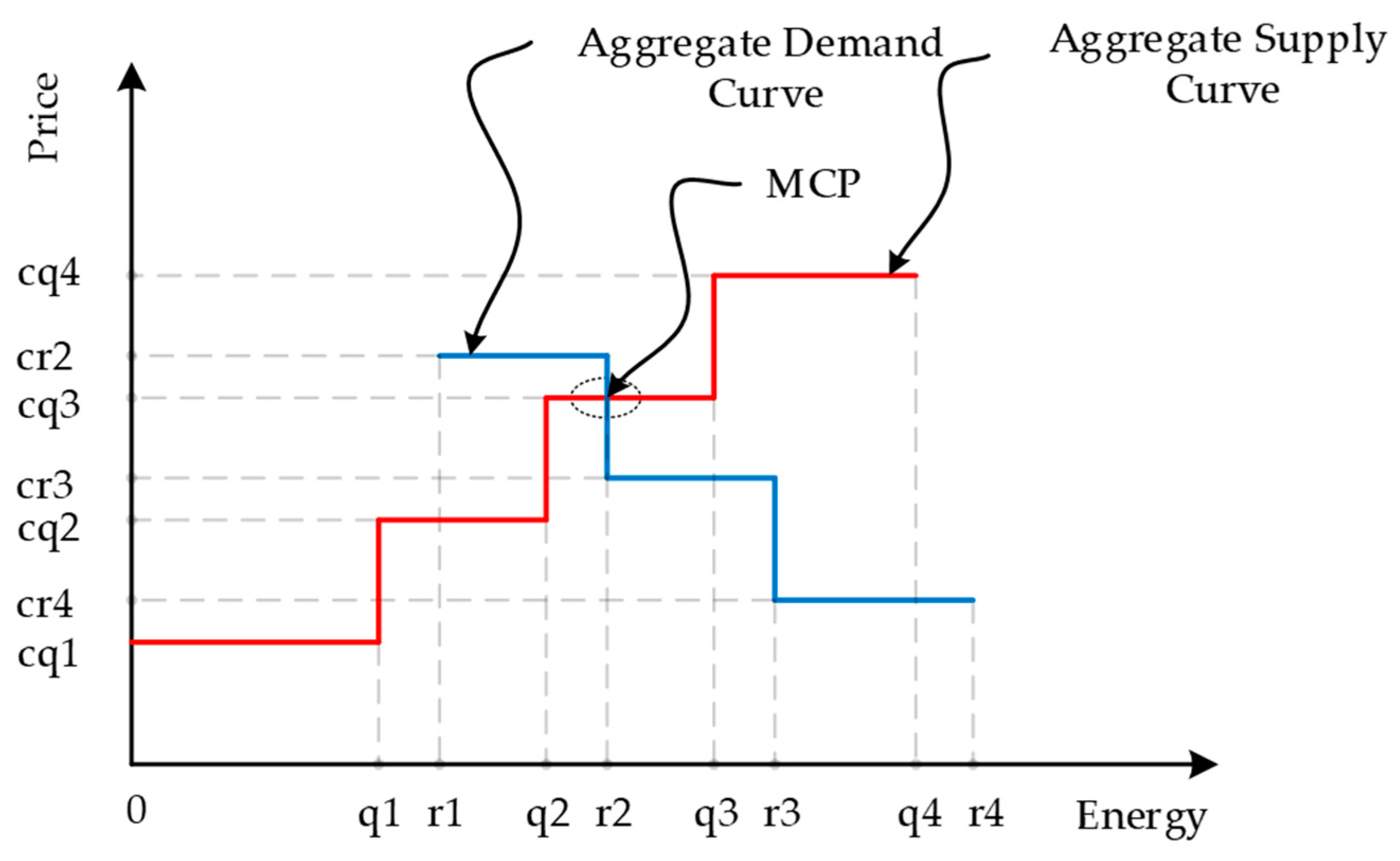
2. Mathematical Formulation
Subject to power flow, load and DG units, line flow, and EES unit constraints
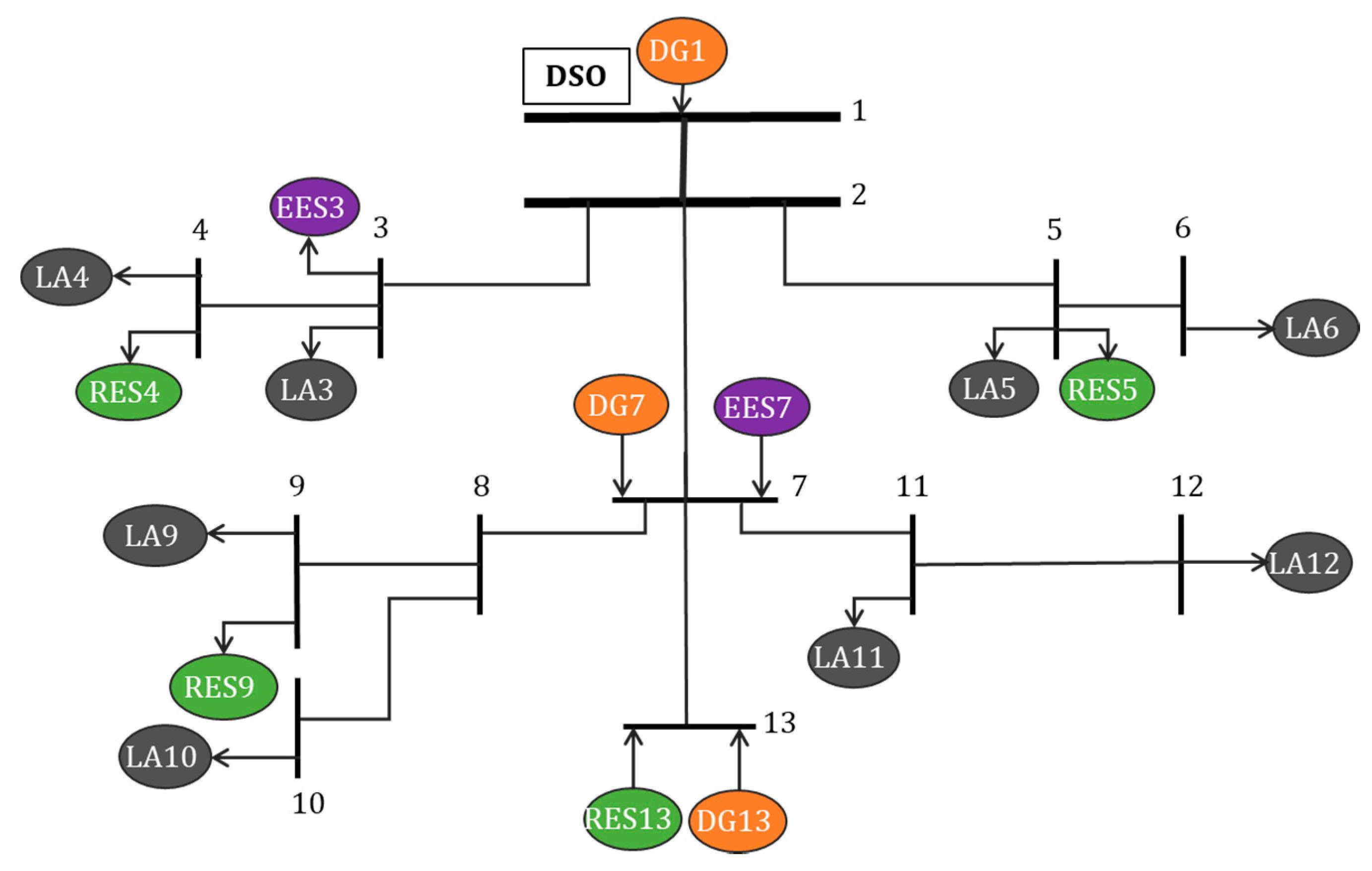
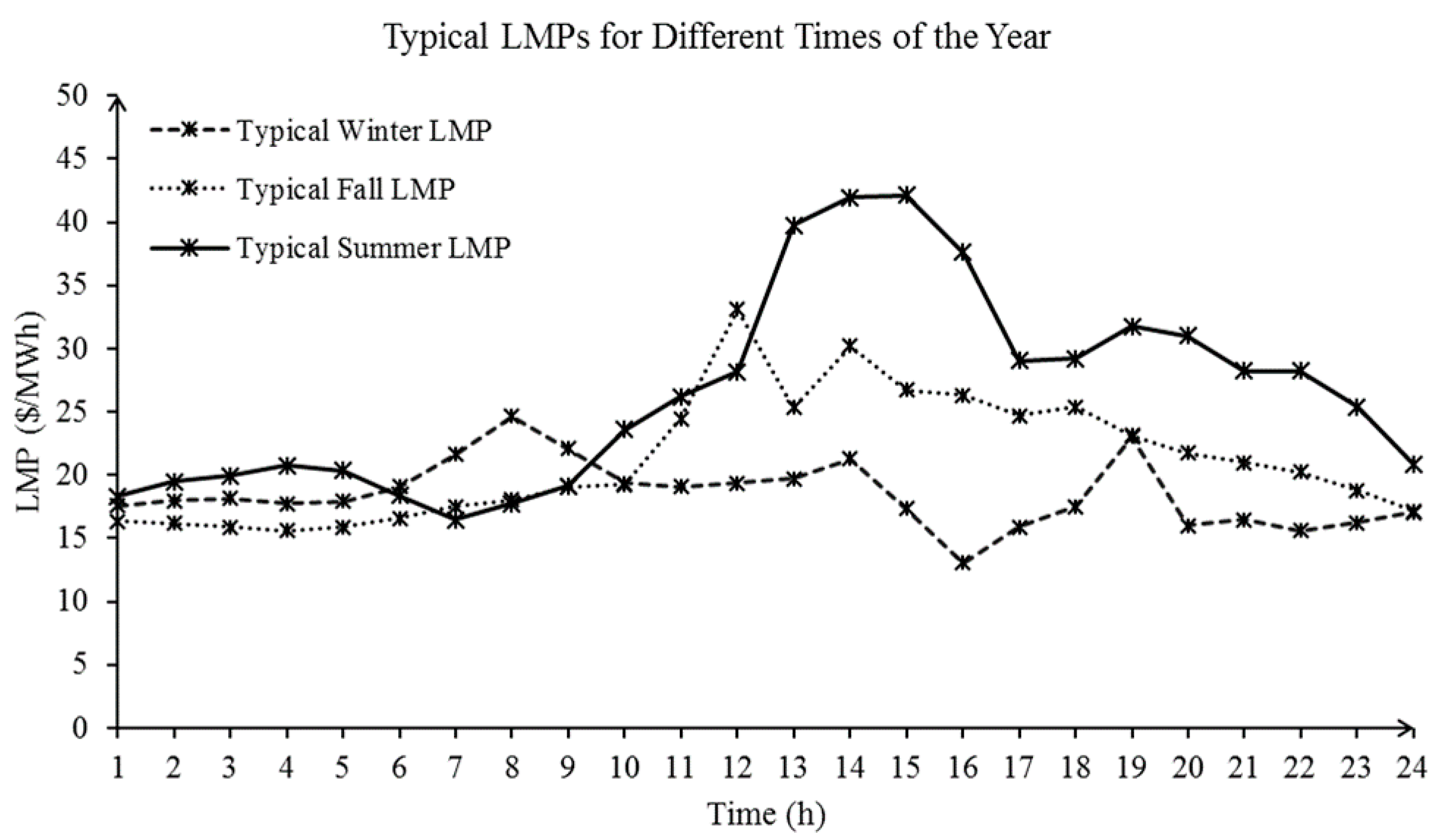
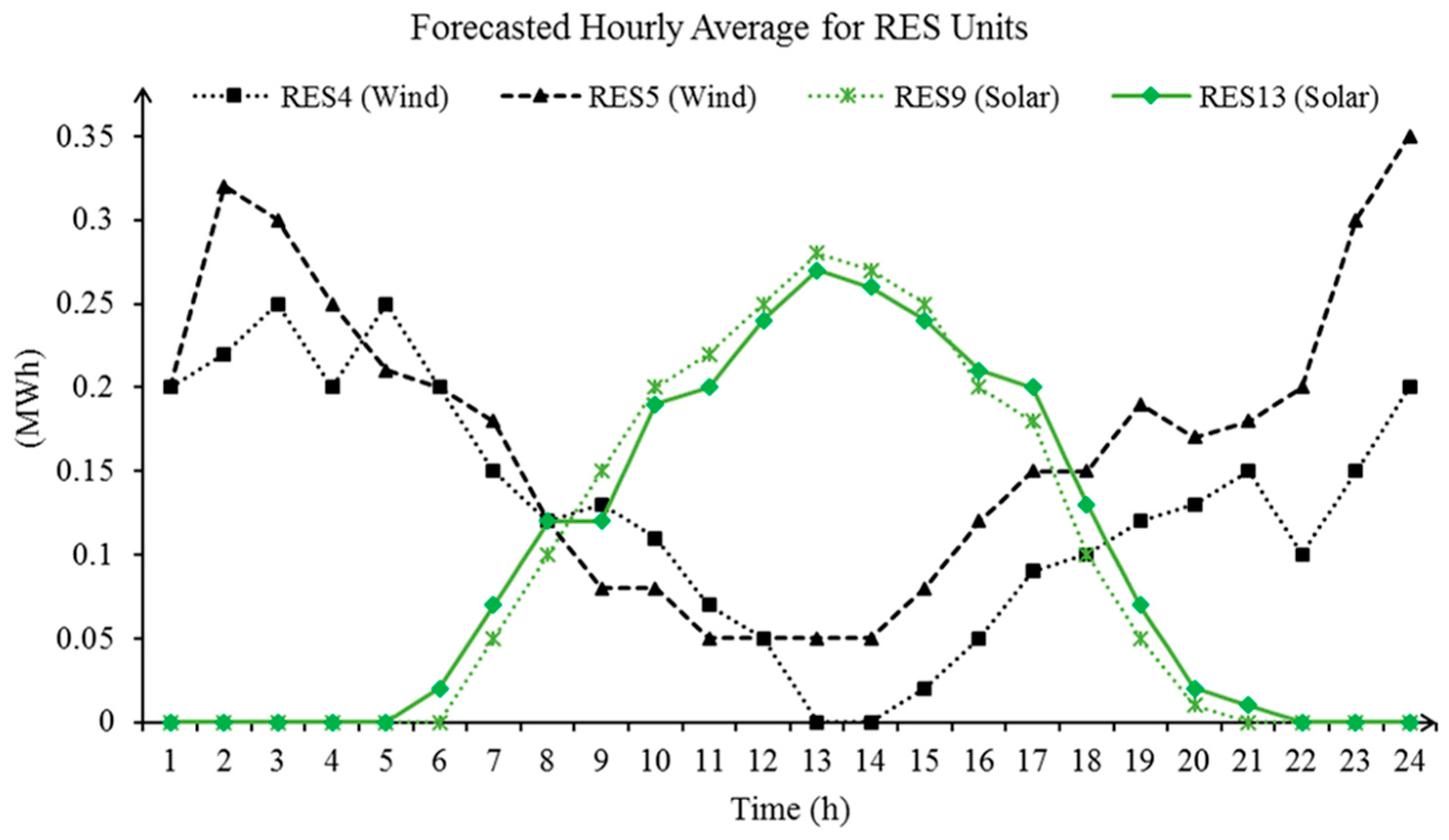
3. Simulation Results
4. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations: | |
| EES | Electrical Energy Storage |
| DG | Distributed Generation |
| LMP | Locational Marginal Price |
| DLMP | Distribution LMP |
| MCP | Market Clearing Price |
| DER | Distributed Energy Resource |
| RES | Renewable Energy Resource |
| LA | Load Aggregator |
| Functions: | |
| Operation cost function | |
| Sets: | |
| Set of timeslots | |
| Set of buses | |
| Set of line segments | |
| Set of load blocks | |
| Set of generation blocks | |
| Set of buses with DG units | |
| Set of buses with EES units | |
| Set of buses with LA units | |
| Indices: | |
| i | Index of distribution bus |
| ij | Distribution line index connecting i to j |
| q | Generation block index |
| r | Load block index |
| Variables: | |
| Real power output at block q of dispatchable unit at bus i at time t | |
| Real power demand at block r of load at bus i at time t | |
| Net real/reactive output of dispatchable generator unit at bus i at time t | |
| Real/reactive power demand of load at bus i at time t | |
| Net real/reactive power output of EES unit at bus i at time t | |
| Extraction (∧)/Injection (∨) of EES unit at bus i at time t | |
| Forecasted real/reactive generation of renewable unit at bus i at time t | |
| Net real/reactive power injection at bus i at t | |
| Real/reactive power flow in line ij at time t | |
| Per unit voltage of bus i at time t | |
| State of charge of EES at bus i at time t | |
| Binary and Integer Variables: | |
| EES unit charging state (1 for charging, 0 for not charging) at time t | |
| EES unit discharging state (1 for discharging, 0 for not discharging) at time t | |
| EES unit charging indicator (Unity ‘1’ only where it starts charging) at time t | |
| EES unit not charging indicator (Unity ‘1’ only where it stops charging) at time t | |
| EES unit discharging indicator (Unity ‘1’ only where it starts discharging) at time t | |
| EES unit not discharging indicator (Unity ‘1’ only where it stops discharging) at time t | |
| EES unit charging counter (counts the number of times is ON) at time t | |
| EES unit discharging counter (counts the number of times is ON) at time t | |
| Parameters: | |
| Substation voltage at time t | |
| Scheduling horizon | |
| MVA limit of line ij | |
| Resistance of line ij | |
| Reactance of line ij | |
| Minimum energy withdraw rate of EES unit | |
| Maximum energy withdraw rate of EES unit | |
| Minimum state of charge of EES unit | |
| Maximum state of charge of EES unit | |
| Self-discharge coefficient of EES unit | |
| Discharge efficiency coefficient of EES unit | |
| Charge efficiency coefficient of EES unit | |
| Minimum number of consecutive discharging hours of EES unit at bus i | |
| Minimum number of consecutive charging hours of EES unit at bus i | |
| Maximum generation in each block q of DG unit i | |
| Maximum real power output of a DG unit at bus i | |
| Minimum real power output of a DG unit at bus i | |
| Maximum load in each block r of load at bus i | |
| Maximum demand of load at bus i | |
| Minimum demand of load at bus i | |
| Fraction of real power of load as reactive power | |
| Fraction of real power of DG as reactive power | |
| Bidding price for charging of EES unit at bus i at time t | |
| Bidding price for discharging of EES unit at bus i at time t | |
| Selling bid at block q of DG unit at bus i at time t | |
| Buying bid in block r of load at bus i at time t | |
References
- Kristov, L.; De Martini, P.; Taft, J.D. A Tale of Two Visions: Designing a Decentralized Transactive Electric System. IEEE Power Energy Mag. 2016, 14, 63–69. [Google Scholar] [CrossRef]
- Barrager, S.M.; Cazalet, E. A Roadmap toward a Sustainable Business and Regulatory Model: Transactive Energy; 51st State; Baker Street Publishing: San Francisco, CA, USA, 2016; pp. 1–29. [Google Scholar]
- Martini, P.; De Kristov, L. Distribution Systems in a High Distributed Resoures Future: Planning, Market Design, Operation and Oversight; Future Electric Utility Regulation Report No. 2: Berkeley, CA, USA, 2015. [Google Scholar]
- Caramani, M.; Ntakou, E.; Hogan, W.W.; Chakrabortty, A.; Schoene, J. Co-Optimization of Power and Reserves in Dynamic T & D Power Markets With Nondispatchable Renewable Generation and Distributed Energy Resources. Proc. IEEE 2016, 104, 807–836. [Google Scholar]
- Parvania, M.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Optimal demand response aggregation in wholesale electricity markets. IEEE Trans. Smart Grid 2013, 4, 1957–1965. [Google Scholar] [CrossRef]
- Herranz, R.; Muñoz San Roque, A.; Villar, J.; Campos, F.A. Optimal demand-side bidding strategies in electricity spot markets. IEEE Trans. Power Syst. 2012, 27, 1204–1213. [Google Scholar] [CrossRef]
- Wu, D.; Aliprantis, D.C.; Ying, L. Load scheduling and dispatch for aggregators of plug-in electric vehicles. IEEE Trans. Smart Grid 2012, 3, 368–376. [Google Scholar] [CrossRef]
- Sardou, I.G.; Khodayar, M.E.; Khaledian, K.; Soleimani-Damaneh, M.; Ameli, M.T. Energy and reserve market clearing with microgrid aggregators. IEEE Trans. Smart Grid 2015, PP, 1–10. [Google Scholar] [CrossRef]
- Gkatzikis, L.; Koutsopoulos, I.; Salonidis, T. The role of aggregators in smart grid demand response markets. IEEE J. Sel. Areas Commun. 2013, 31, 1247–1257. [Google Scholar] [CrossRef]
- Carlini, E.M.; Sbordone, D.A.; Di Pietra, B.; Devetsikiotis, M. The future interaction between virtual aggregator-TSO-DSO to increase DG penetration. In Proceedings of the International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015; pp. 201–205. [Google Scholar]
- Faqiry, M.N.; Das, S. Double-Sided Energy Auction in Microgrid: Equilibrium under Price Anticipation. IEEE Access 2016, 4, 3794–3805. [Google Scholar] [CrossRef]
- Zhang, Y.; Gevorgian, V.; Wang, C.; Lei, X.; Chou, E.; Yang, R.; Li, Q.; Jiang, L. Grid-level application of electrical energy storage. IEEE Power Energy Mag. 2017, 15, 51–58. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Mandel, J.; Morris, J.; Touati, H. The Economics of Battery Storage; Rocky Mountain Institute (RMI): Boulder, CO, USA, 2015. [Google Scholar]
- Telaretti, E.; Ippolito, M.; Dusonchet, L. A simple operating strategy of small-scale battery energy storages for energy arbitrage under dynamic pricing tariffs. Energies 2016, 9, 12. [Google Scholar] [CrossRef]
- Rahimi, F.; Mokhtari, S. From ISO to DSO: Imagining new construct--an independent system operator for the distribution network. Public Util. Fortn 2014, 152, 42–50. [Google Scholar]
- Parhizi, S.; Khodaei, A.; Shahidehpour, M. Market-based vs. Price-based Microgrid Optimal Scheduling. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 Novermber 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Khodayar, M.E. Hourly demand response in day-ahead scheduling considering generating unit ramping cost. IEEE Trans. Power Syst. 2013, 28, 2446–2454. [Google Scholar] [CrossRef]
- Faqiry, M.N.; Zarabie, A.K.; Nassery, F.; Wu, H.; Das, S. A Day Ahead Market Energy Auction for Distribution System Operation. In Proceedings of the IEEE Conference on Electro-Information Technology, Lincoln, NE, USA, 14–17 May 2017; pp. 1–6. [Google Scholar]
- Baringo, L.; Conejo, A.J. Offering Strategy of Wind-Power Producer: A Multi-Stage Risk-Constrained Approach. IEEE Trans. Power Syst. 2016, 31, 1420–1429. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Strategic offering for a wind power producer. IEEE Trans. Power Syst. 2013, 28, 4645–4654. [Google Scholar] [CrossRef]
- Baillo, A.; Cerisola, S.; Fernandez-Lopez, J.M.; Bellido, R. Strategic bidding in electricity spot markets under uncertainty: A roadmap. In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar] [CrossRef]
- Sotkiewicz, P.M.; Vignolo, J.M. Nodal pricing for distribution networks: Efficient pricing for efficiency enhancing DG. IEEE Trans. Power Syst. 2006, 21, 1013–1014. [Google Scholar] [CrossRef]
- Verzijlbergh, R.A.; De Vries, L.J.; Lukszo, Z. Renewable Energy Sources and Responsive Demand. Do We Need Congestion Management in the Distribution Grid? Power Syst. IEEE Trans. 2014, 29, 2119–2128. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Q.; Oren, S.; Huang, S.; Li, R.; Cheng, L. Distribution Locational Marginal Pricing for Optimal Electric Vehicle Charging through Chance Constrained Mixed-Integer Programming. IEEE Trans. Smart Grid 2016, PP, 1. [Google Scholar] [CrossRef]
- O’Connell, N.; Wu, Q.; Østergaard, J.; Nielsen, A.H.; Cha, S.T.; Ding, Y. Day-ahead tariffs for the alleviation of distribution grid congestion from electric vehicles. Electr. Power Syst. Res. 2012, 92, 106–114. [Google Scholar] [CrossRef]
- Kristoffersen, T.K.; Capion, K.; Meibom, P. Optimal charging of electric drive vehicles in a market environment. Appl. Energy 2011, 88, 1940–1948. [Google Scholar] [CrossRef]
- Faqiry, M.N.; Sanjoy, D. Distributed Bi-level Energy Allocation Mechanism with Grid Constraints and Hidden User Information. arXiv, 2017; arXiv:1707.05429. [Google Scholar]
- Wu, H.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. A Game Theoretic Approach to Risk-Based Optimal Bidding Strategies for Electric Vehicle Aggregators in Electricity Markets With. IEEE Trans. Sustain. Energy 2016, 7, 374–385. [Google Scholar] [CrossRef]
- Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar]
- Baran, M.E.; Wu, F.F. Optimal sizing of capacitors placed on a radial distribution system. IEEE Trans. Power Deliv. 1989, 4, 735–743. [Google Scholar] [CrossRef]
- Yeh, H.; Member, S.; Gayme, D.F.; Low, S.H. Adaptive VAR Control for Distribution Circuits With Photovoltaic Generators. IEEE Trans. Power Syst. 2012, 27, 1656–1663. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Kim, J. Decentralized Energy Management System for Networked Microgrids in Grid-Connected and Islanded Modes. IEEE Trans. Smart Grid 2016, 7, 1097–1105. [Google Scholar] [CrossRef]
- Turitsyn, K.; Šulc, P.; Backhaus, S.; Chertkov, M. Distributed control of reactive power flow in a radial distribution circuit with high photovoltaic penetration. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Lamont, J.W.; Fu, J. Cost analysis of reactive power support. IEEE Trans. Power Syst. 1999, 14, 890–898. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Zhong, J. Reactive power as an ancillary service. IEEE Trans. Power Syst. 2001, 16, 294–300. [Google Scholar] [CrossRef]
- Kahn, E.; Baldick, R. Reactive Power is a Cheap Constraint. Int. Assoc. Energy Econ. 2017, 15, 191–201. [Google Scholar]
- Taylor, J.A. Convex Optimization of Power Systems; Cambridge University Press: Cambridge, UK, 2015; ISBN 978110707687. [Google Scholar]
- Divya, K.C.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Mandel, J.; Morris, J.; Touati, H. The Economics of Battery Energy Storage: How Multi-Use, Customer-Sted Batteries Deliver the Most Services and Value to Customers and the Grid; Rocky Mountain Institute: Boulder, CO, USA, 2015; p. 41. [Google Scholar]
- He, G.; Chen, Q.; Kang, C.; Pinson, P.; Xia, Q. Optimal Bidding Strategy of Battery Storage in Power Markets Considering Performance-Based Regulation and Battery Cycle Life. IEEE Trans. Smart Grid 2016, 7, 2359–2367. [Google Scholar] [CrossRef]
- GAMS Development Corporation. General Algebraic Modeling System (GAMS) Release 24.7.4.; GAMS Development Corporation: Washington, DC, USA, 2016. [Google Scholar]
- SPP Locational Marginal Price. Available online: https://marketplace.spp.org/pages/rtbm-lmp-by-location (accessed on 8 October 2017).
- DiOrio, N.; Dobos, A.; Janzou, S. Economic Analysis Case Studies of Battery Energy Storage with SAM; National Renewable Energy Laboratory: Denver, CO, USA, 2015.

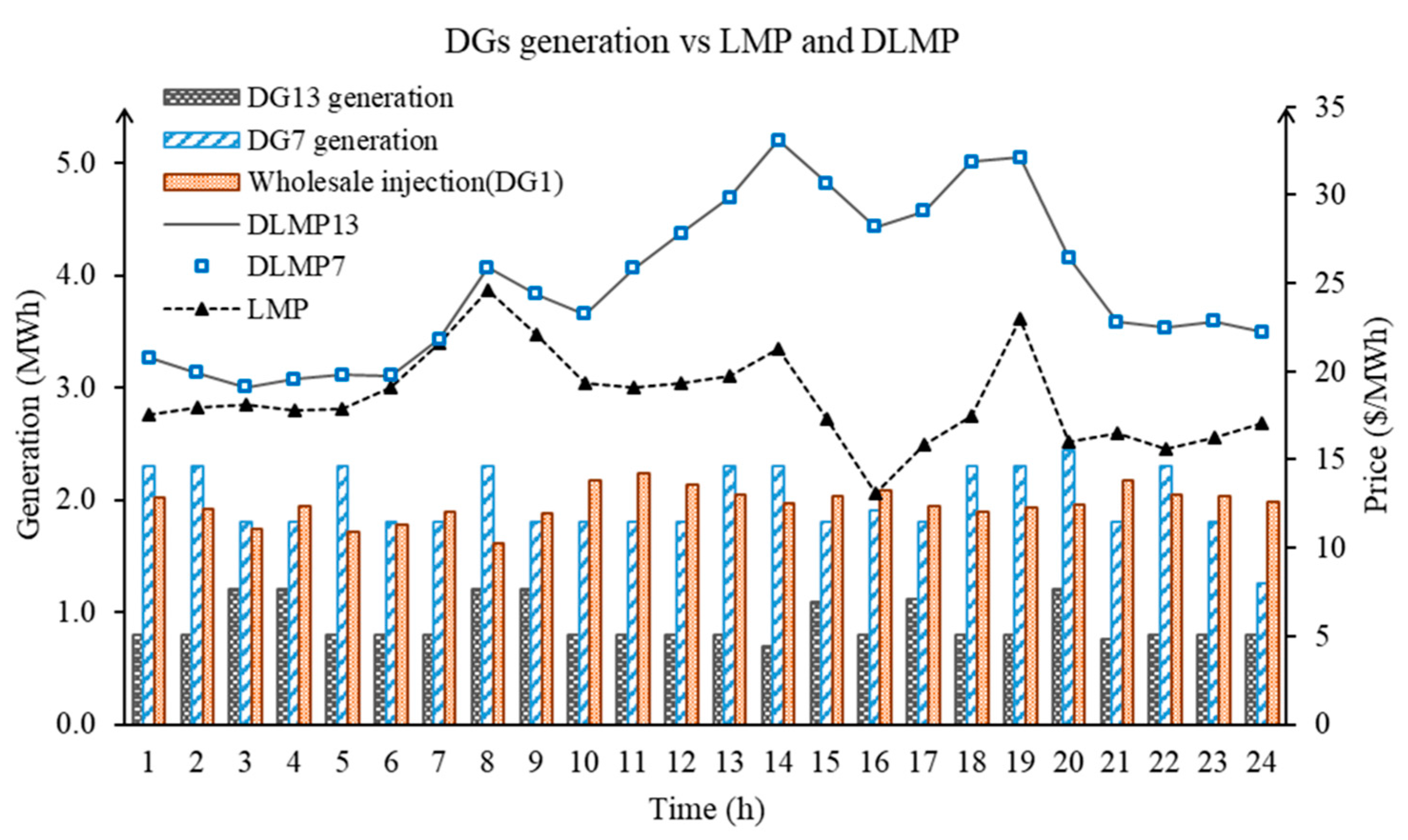
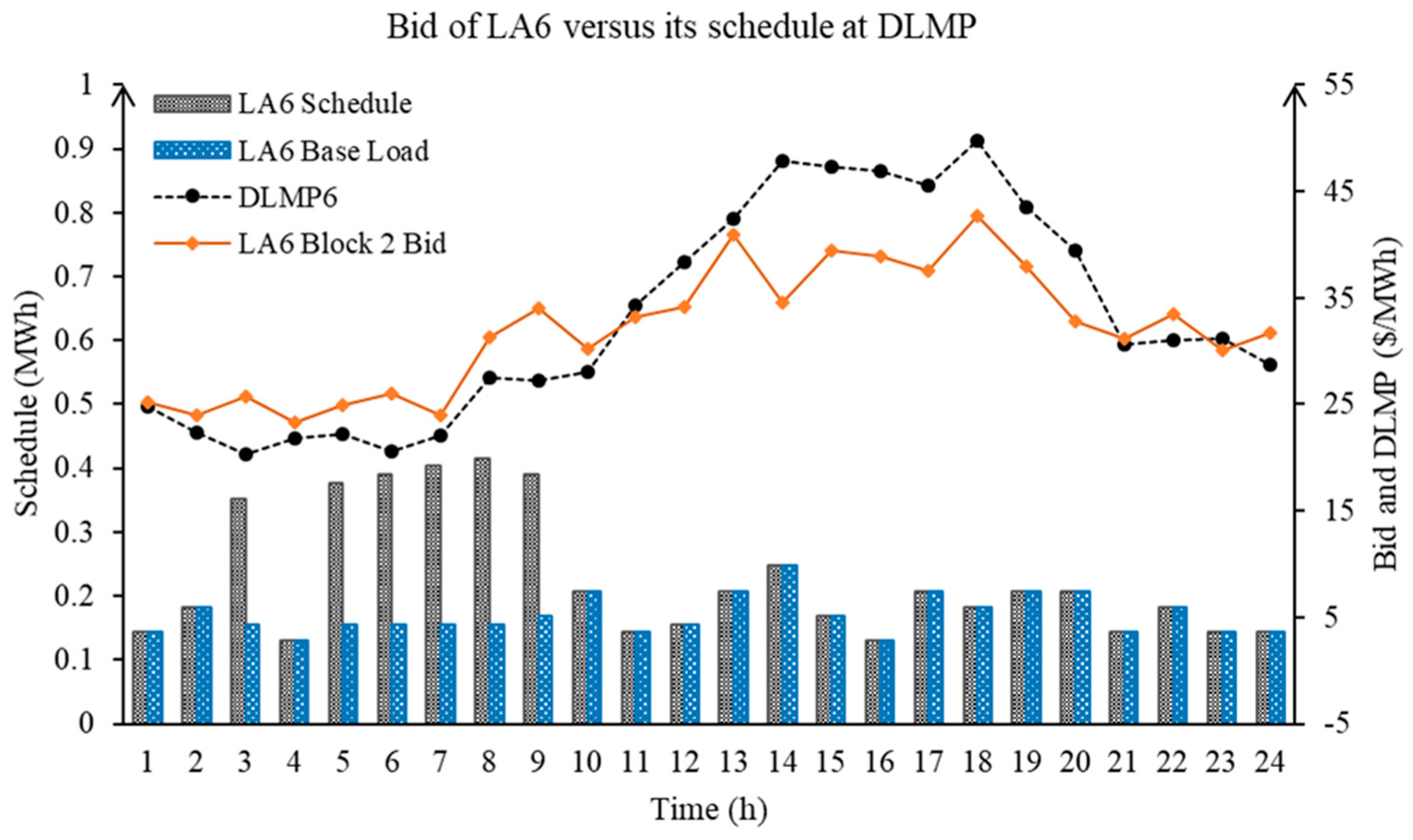
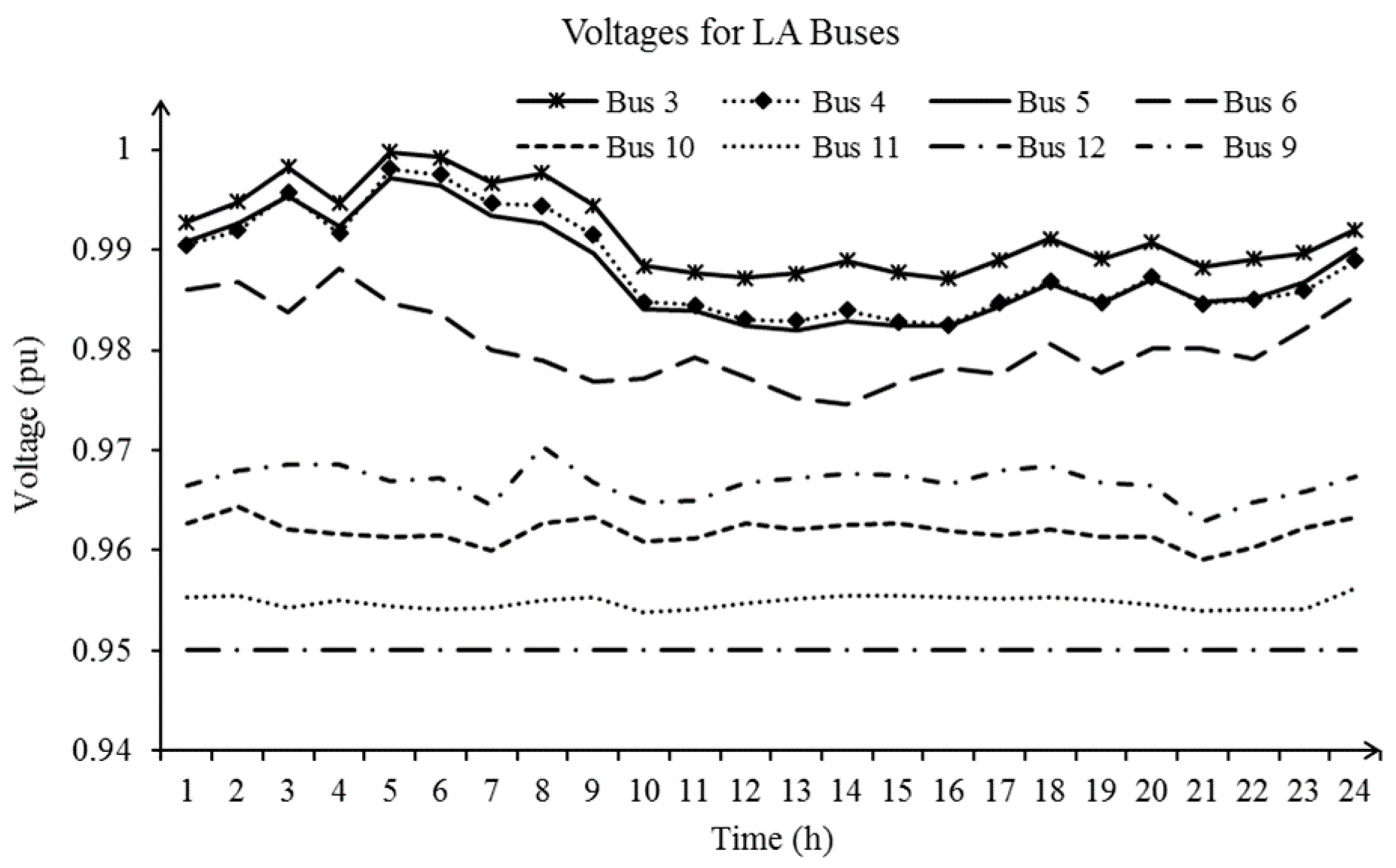
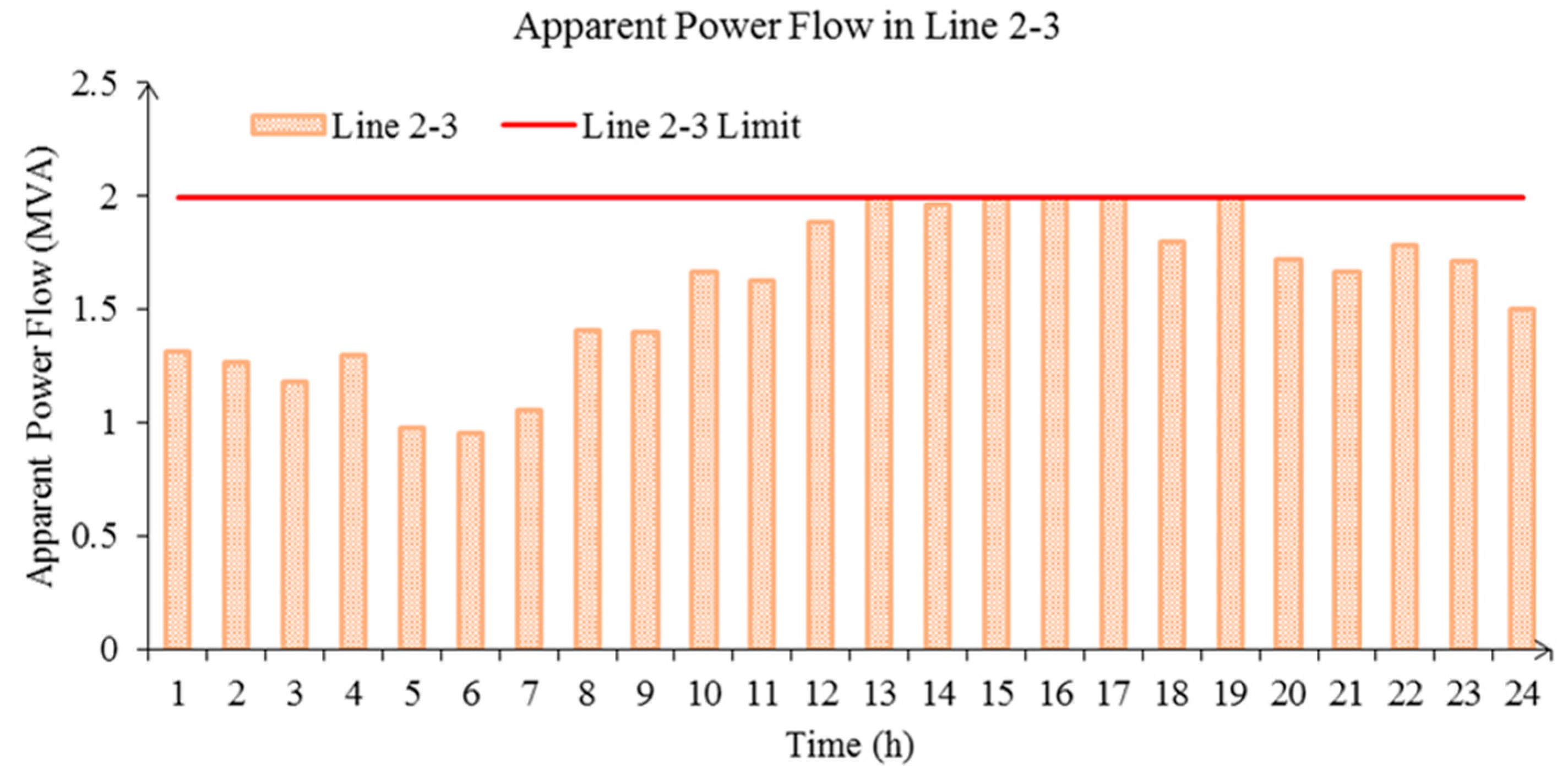
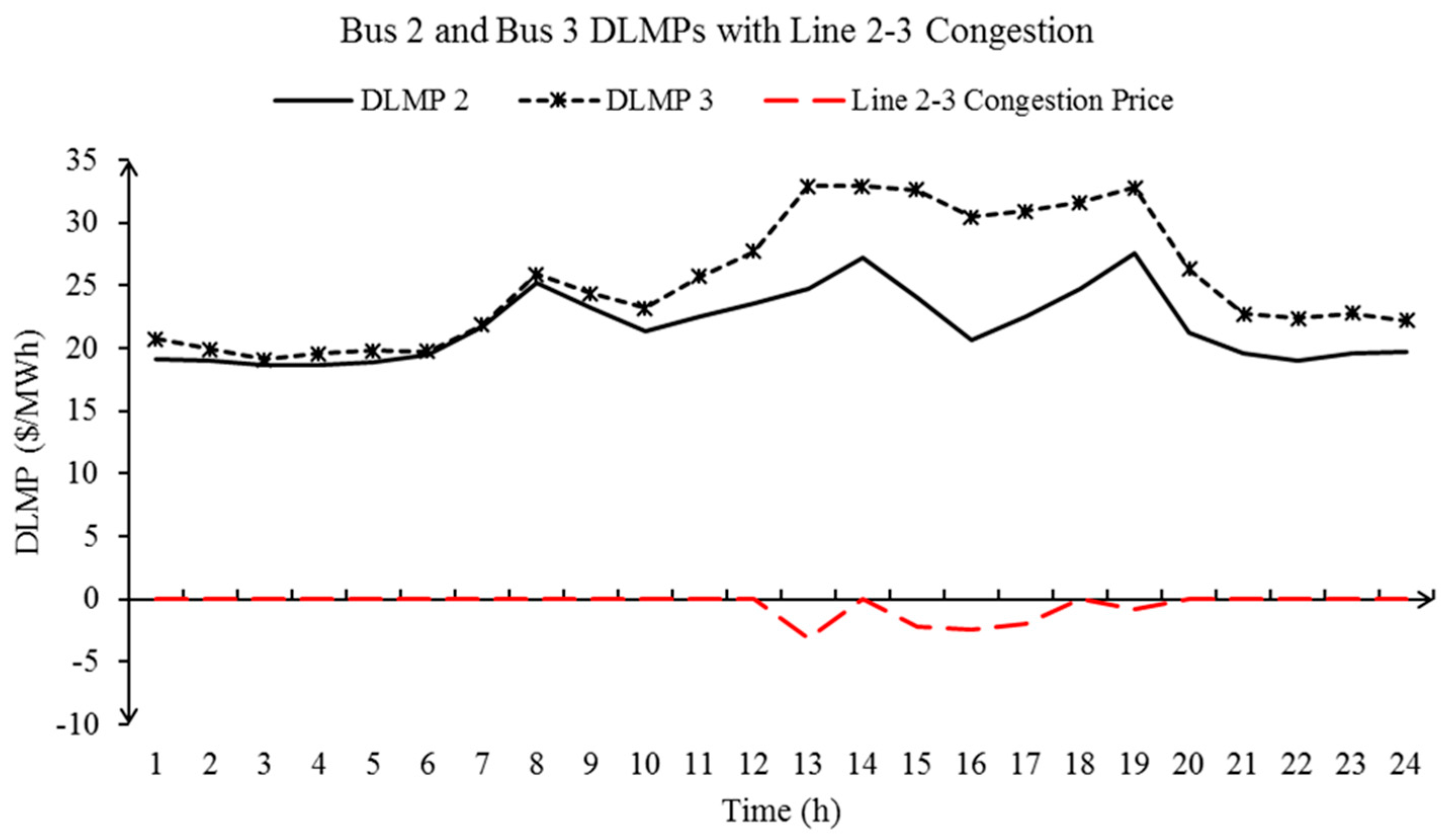
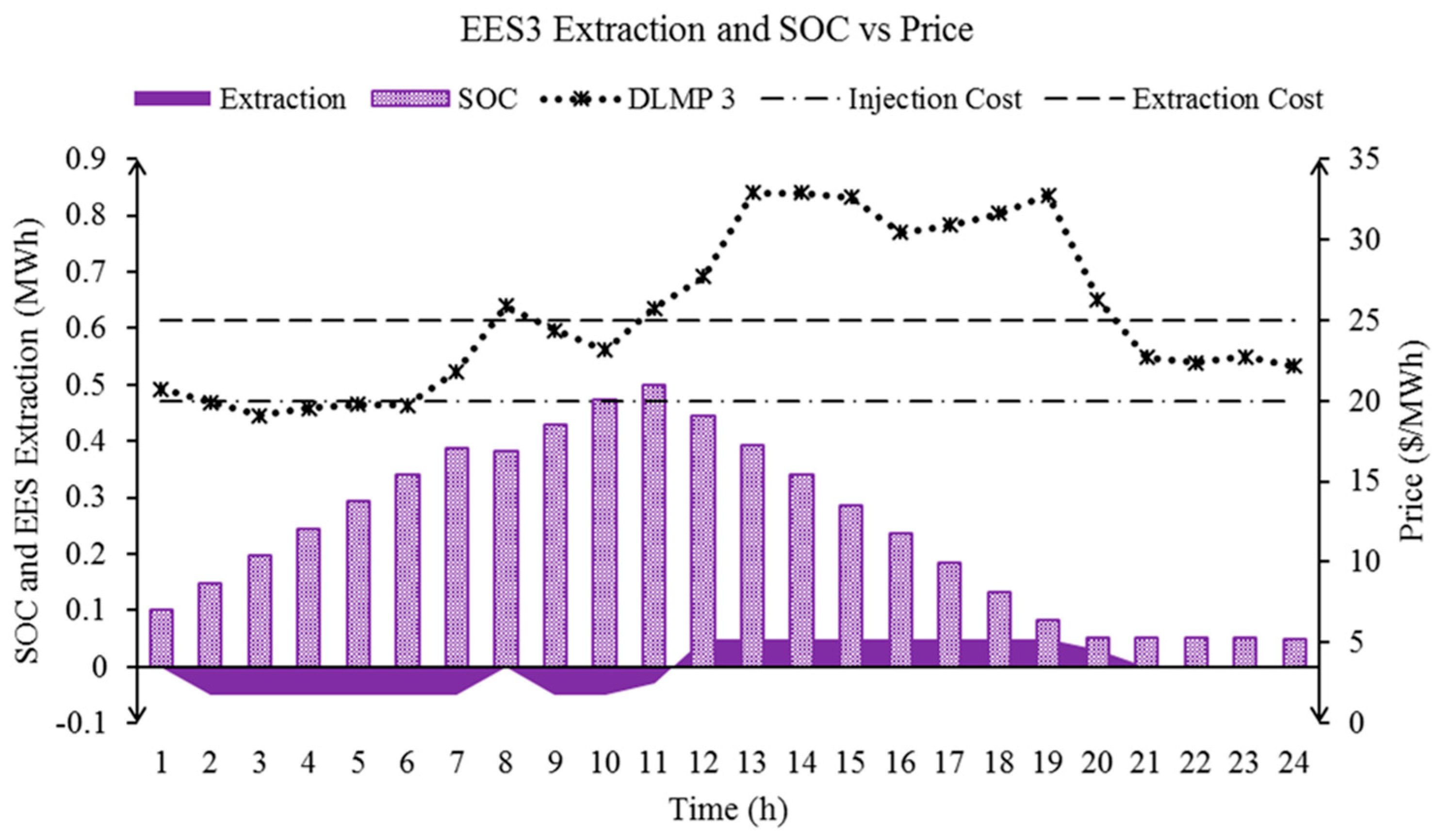
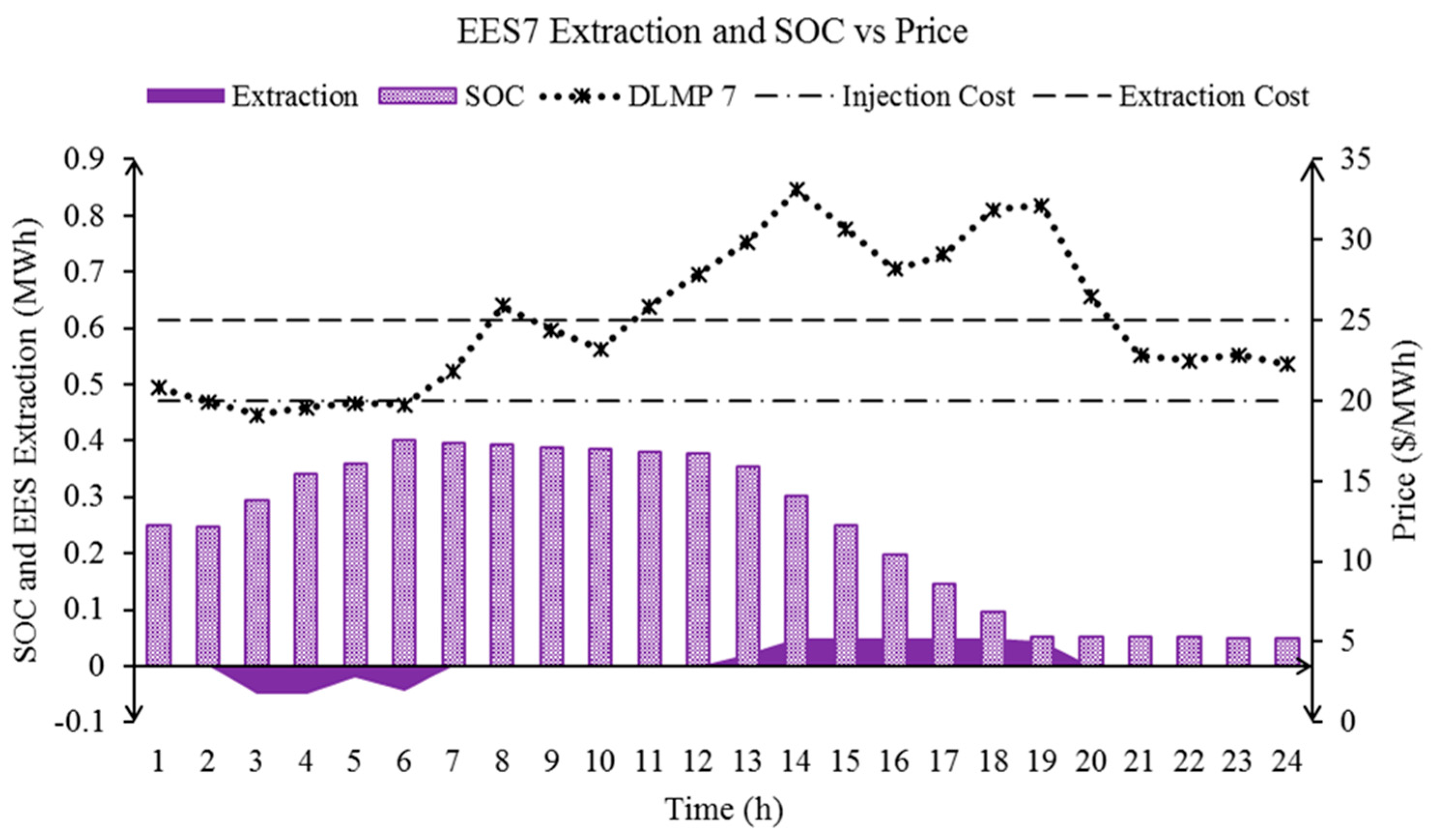
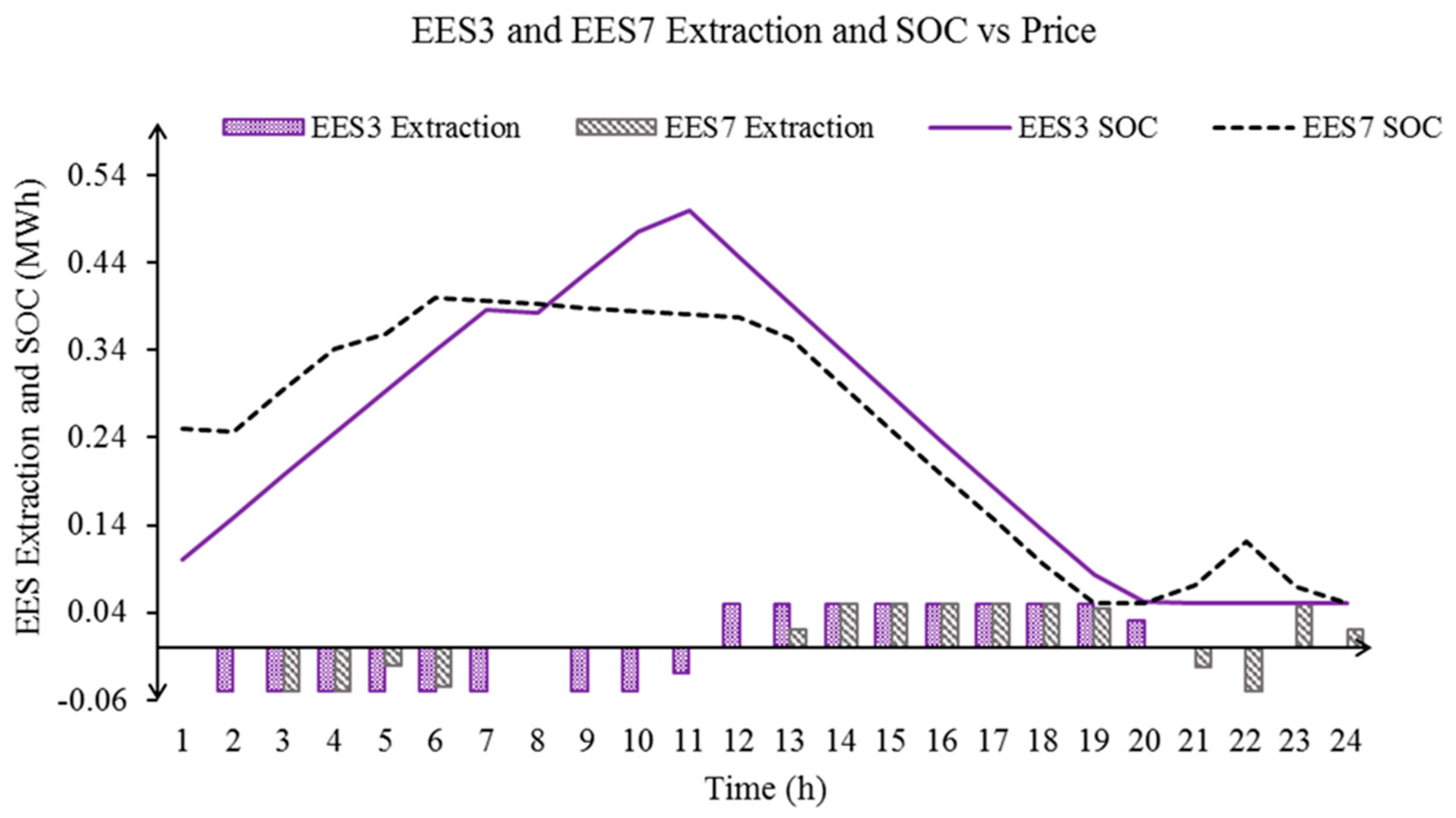
| Bus | Unit | (Min, Max SOC) (MWh) | (Min, Max Power Rate) (MW) | (Min Charge, Discharge Time) (h) | (Injection, ExRaction Cost ($/MWh) | Initial SOC (MWh) |
|---|---|---|---|---|---|---|
| 3 | EES3 | (0.05,0.5) | (0.02,0.05) | (3,3) | (20,25) | 0.1 |
| 7 | EES7 | (0.05,0.4) | (0.02,0.05) | (3,3) | (20,25) | 0.25 |
| Bus No, Unit | DG Bids | |||||
|---|---|---|---|---|---|---|
| Block 1 | Block 2 | Block 3 | ||||
| Bid ($/MWh) | Max Supply (MW) | Bid ($/MWh) | Max Supply (MW)) | Bid ($/MWh) | Max Supply (MW) | |
| 1, DG1 | 39.80 | 10 | N/A | N/A | N/A | N/A |
| 7, DG7 | 30.60 | 1.8 | 32.40 | 0.5 | 35.82 | 0.5 |
| 13, DG13 | 33.75 | 0.8 | 36.72 | 0.4 | 39.15 | 0.3 |
| Bus No, Unit | LA Bid | |||||
|---|---|---|---|---|---|---|
| Block 1 | Block 2 | Block 3 | ||||
| Bid ($/MWh) | Demand (MW) | Bid ($/MWh) | Demand (MW) | Bid ($/MWh) | Demand (MW) | |
| 3, LA3 | N/A | 0.28 | 28.05 | 0.08 | 23.68 | 0.10 |
| 4, LA4 | N/A | 0.38 | 29.29 | 0.09 | 23.75 | 0.17 |
| 6, LA6 | N/A | 0.11 | 25.25 | 0.22 | 20.87 | 0.16 |
| 7, LA7 | N/A | 0.64 | 30.38 | 0.41 | 25.79 | 0.48 |
| 9, LA9 | N/A | 0.28 | 27.91 | 0.14 | 21.05 | 0.17 |
| 10, LA10 | N/A | 0.11 | 27.66 | 0.21 | 22.40 | 0.18 |
| 11, LA11 | N/A | 0.11 | 28.79 | 0.22 | 23.77 | 0.28 |
| 12, LA12 | N/A | 0.46 | 30.73 | 0.30 | 25.93 | 0.19 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faqiry, M.N.; Edmonds, L.; Zhang, H.; Khodaei, A.; Wu, H. Transactive-Market-Based Operation of Distributed Electrical Energy Storage with Grid Constraints. Energies 2017, 10, 1891. https://doi.org/10.3390/en10111891
Faqiry MN, Edmonds L, Zhang H, Khodaei A, Wu H. Transactive-Market-Based Operation of Distributed Electrical Energy Storage with Grid Constraints. Energies. 2017; 10(11):1891. https://doi.org/10.3390/en10111891
Chicago/Turabian StyleFaqiry, M. Nazif, Lawryn Edmonds, Haifeng Zhang, Amin Khodaei, and Hongyu Wu. 2017. "Transactive-Market-Based Operation of Distributed Electrical Energy Storage with Grid Constraints" Energies 10, no. 11: 1891. https://doi.org/10.3390/en10111891
APA StyleFaqiry, M. N., Edmonds, L., Zhang, H., Khodaei, A., & Wu, H. (2017). Transactive-Market-Based Operation of Distributed Electrical Energy Storage with Grid Constraints. Energies, 10(11), 1891. https://doi.org/10.3390/en10111891






