Harmonic Adaptability Remote Testing Method for Offshore Wind Turbines
Abstract
:1. Introduction
2. Testing System Configuration, Requirement and Procedure
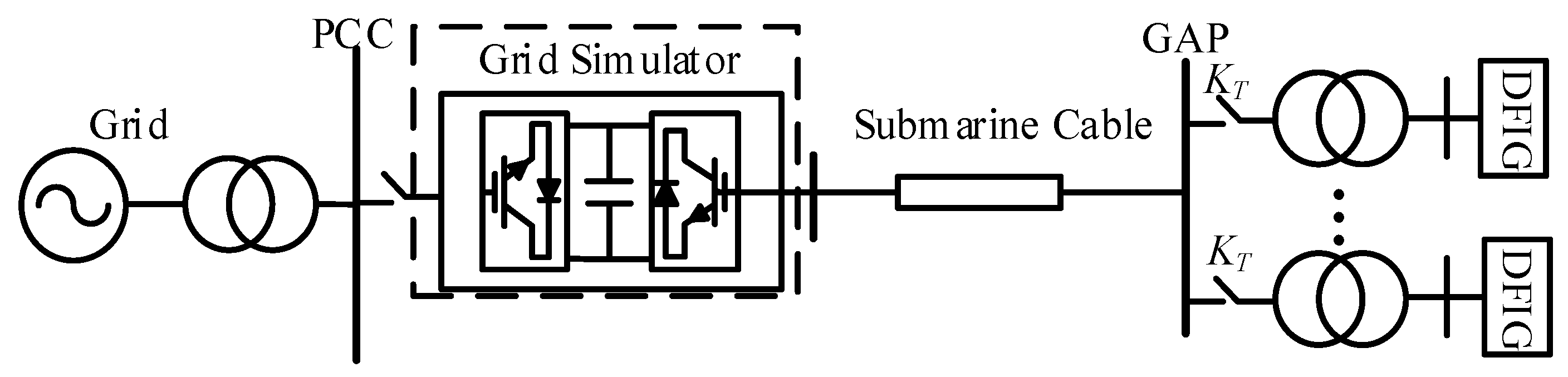
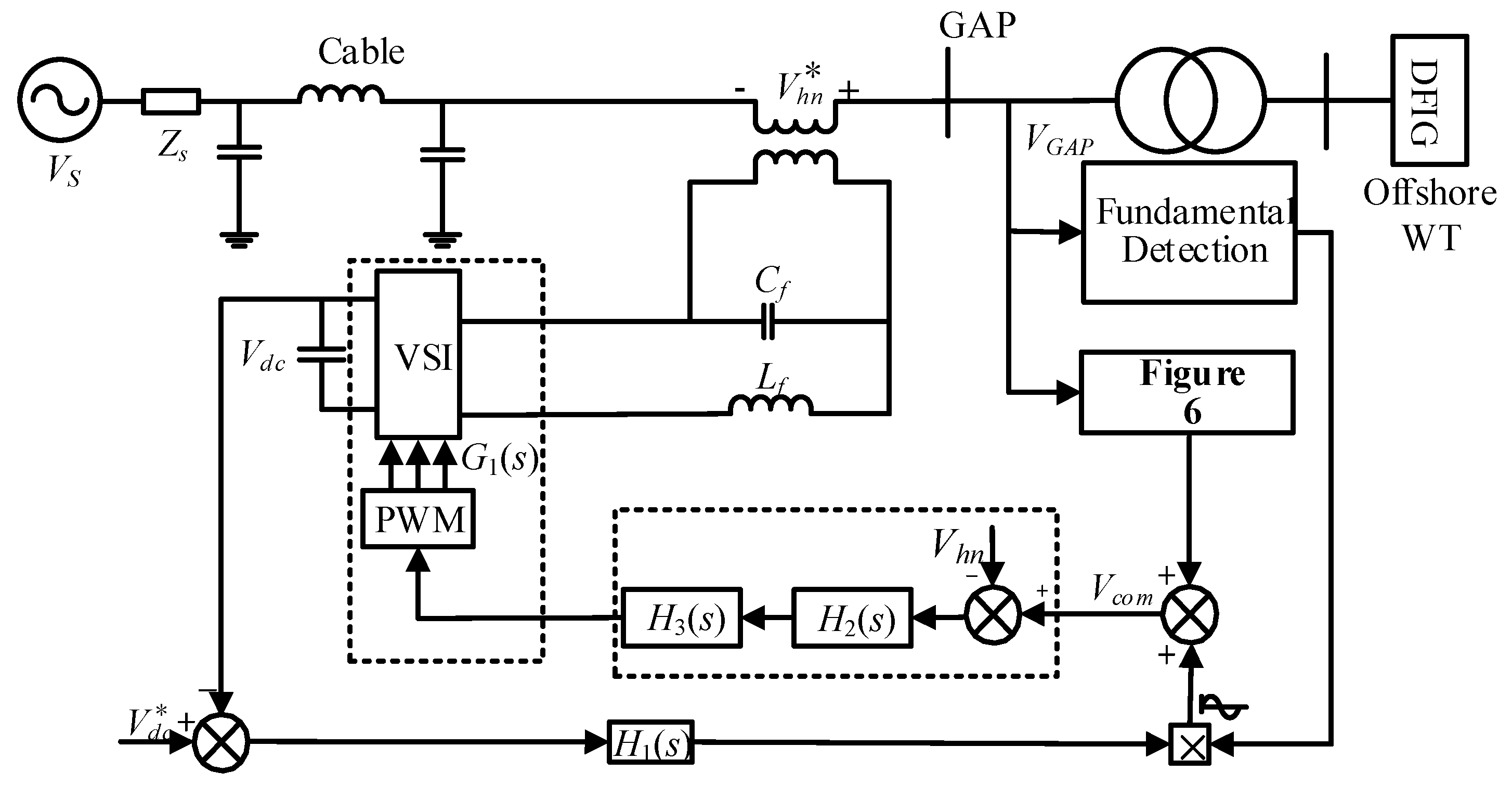
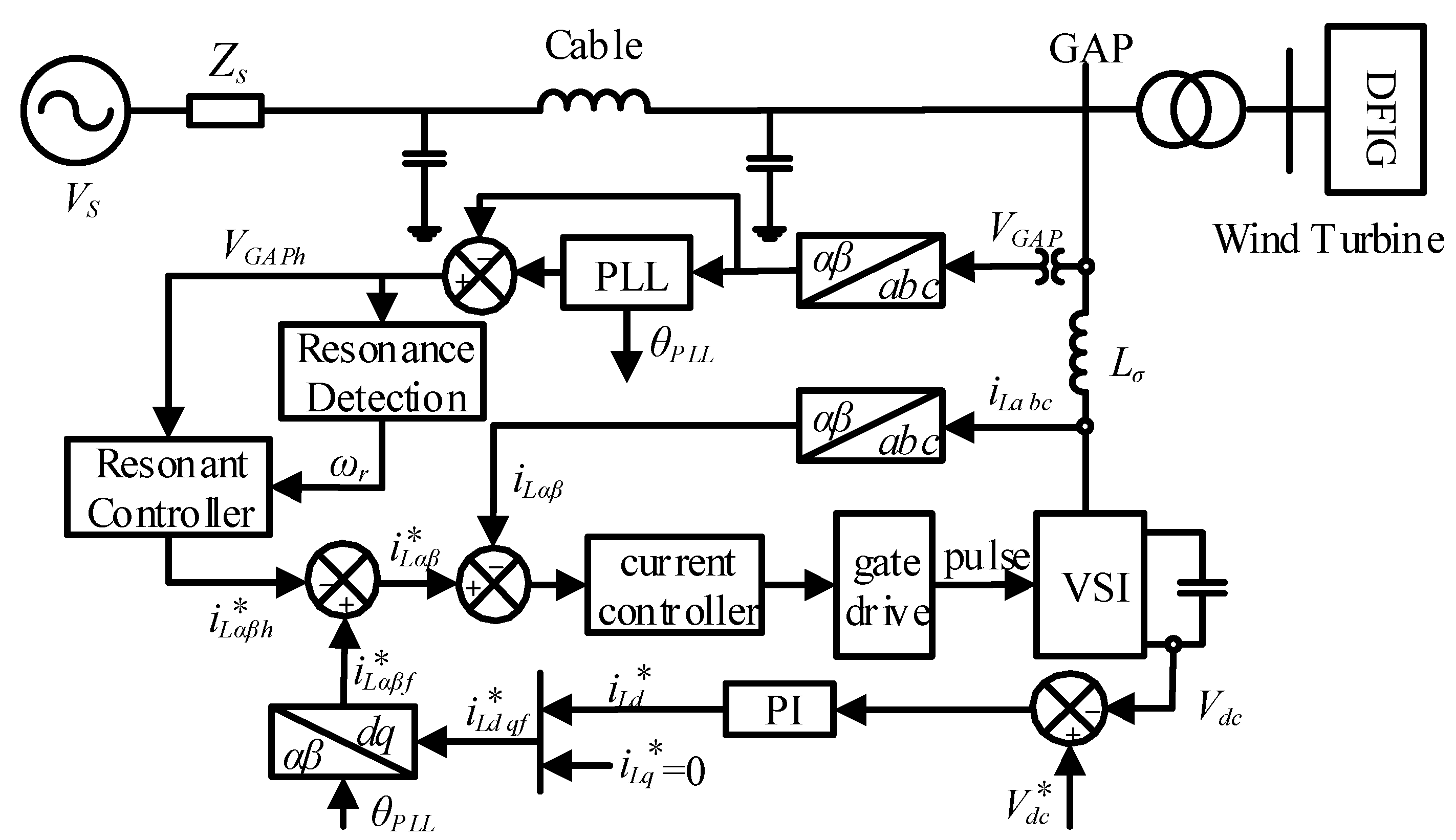
2.1. Testing System Configuration
2.2. Harmonic Adaptability Testing Requirement
2.3. Harmonic Adaptability Testing Procedure
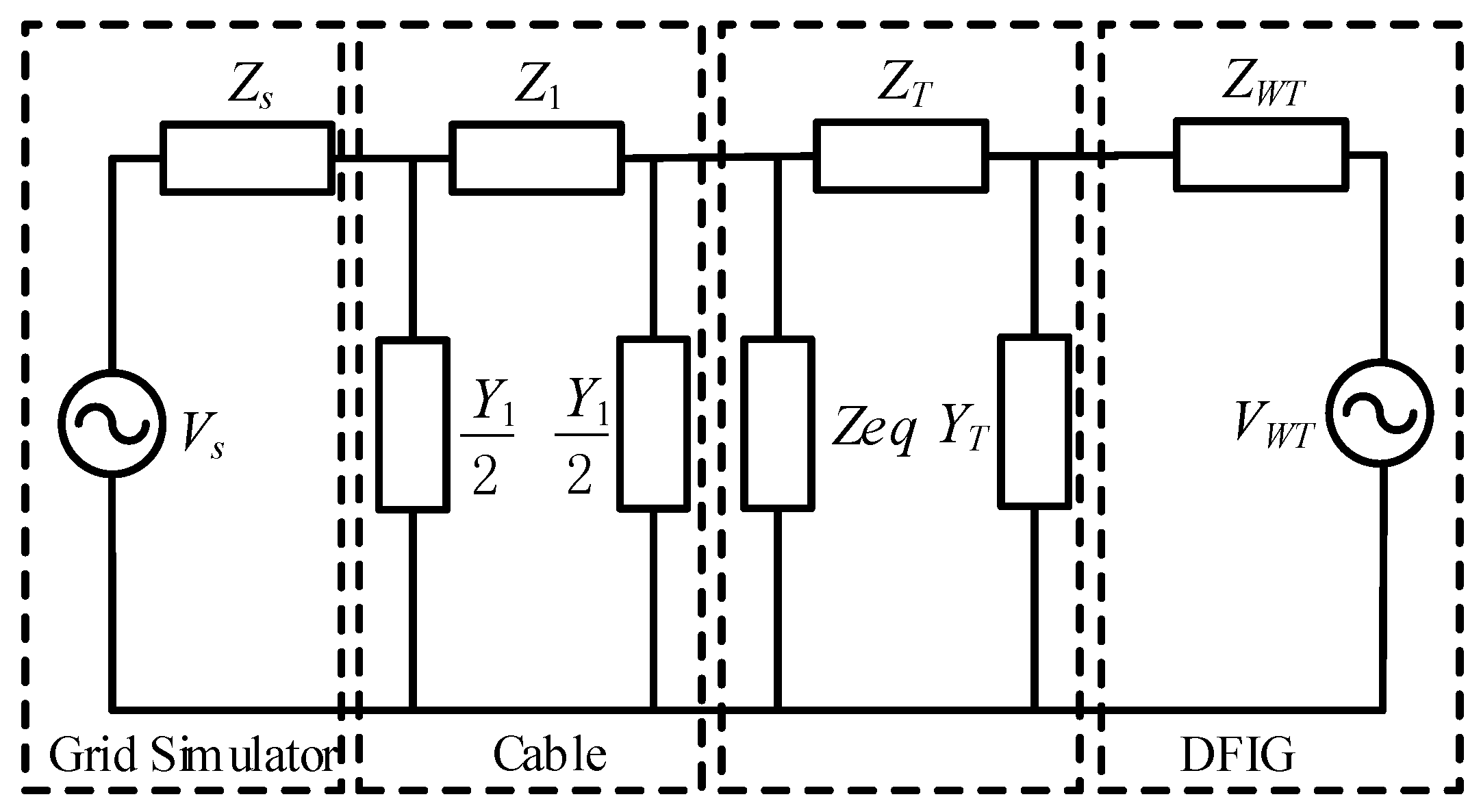
3. Effects of Submarine Cables on Harmonic Adaptability Testing
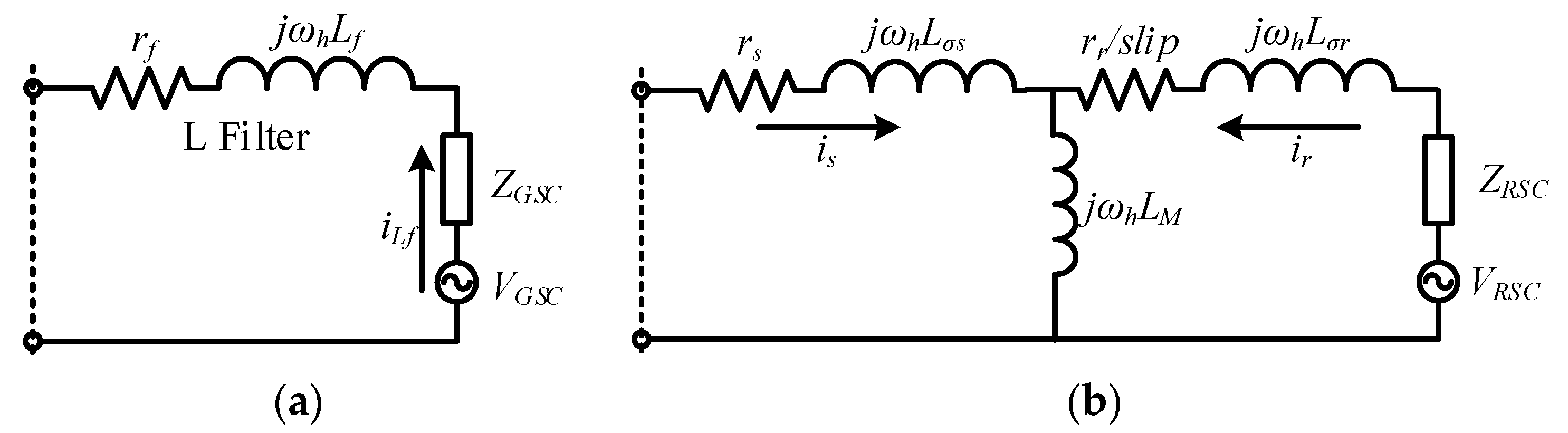
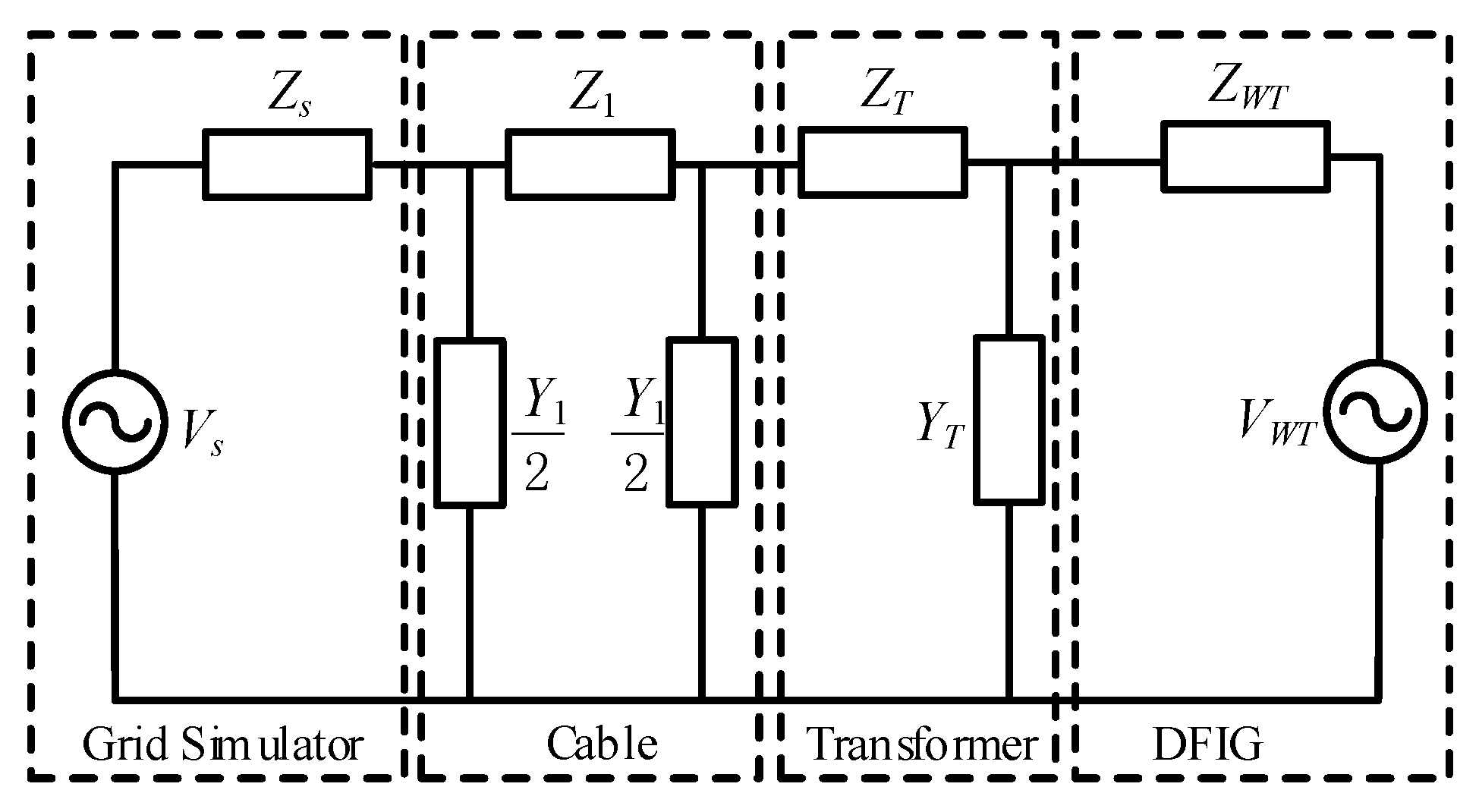
3.1. Equivalent Circuit of the System
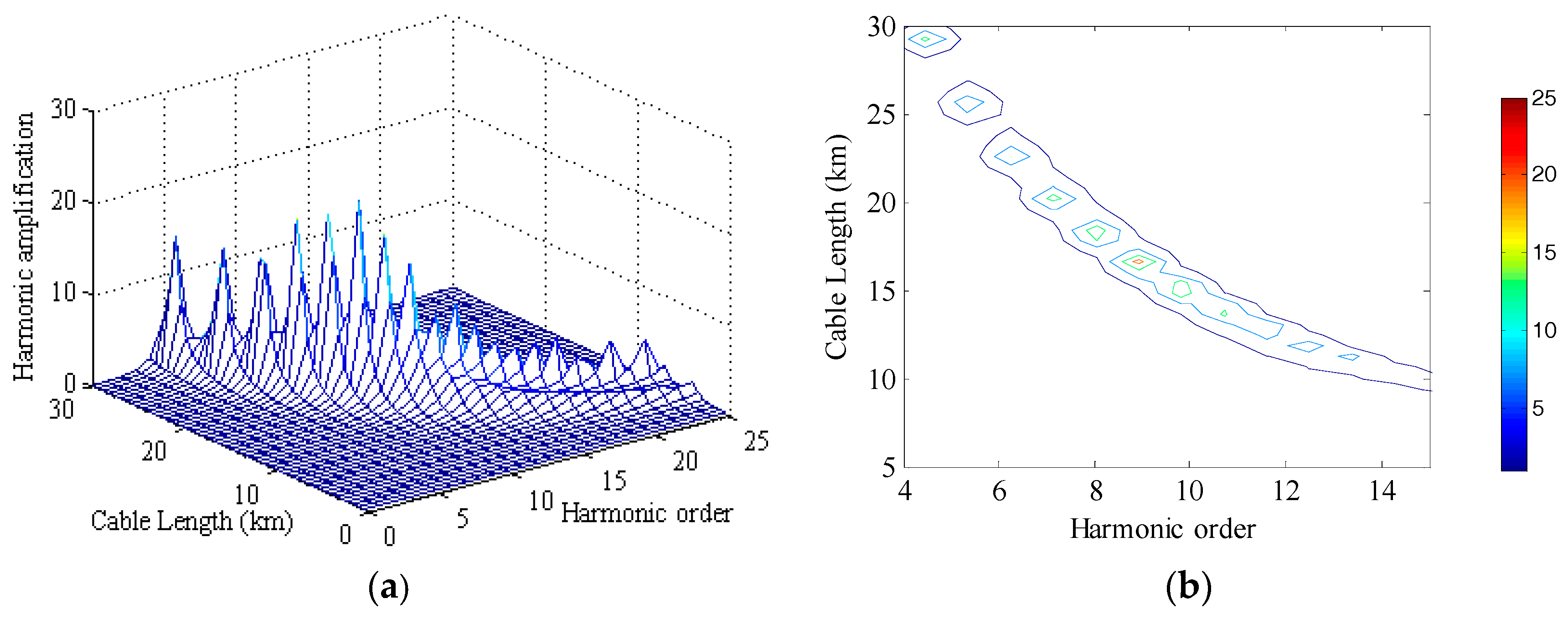
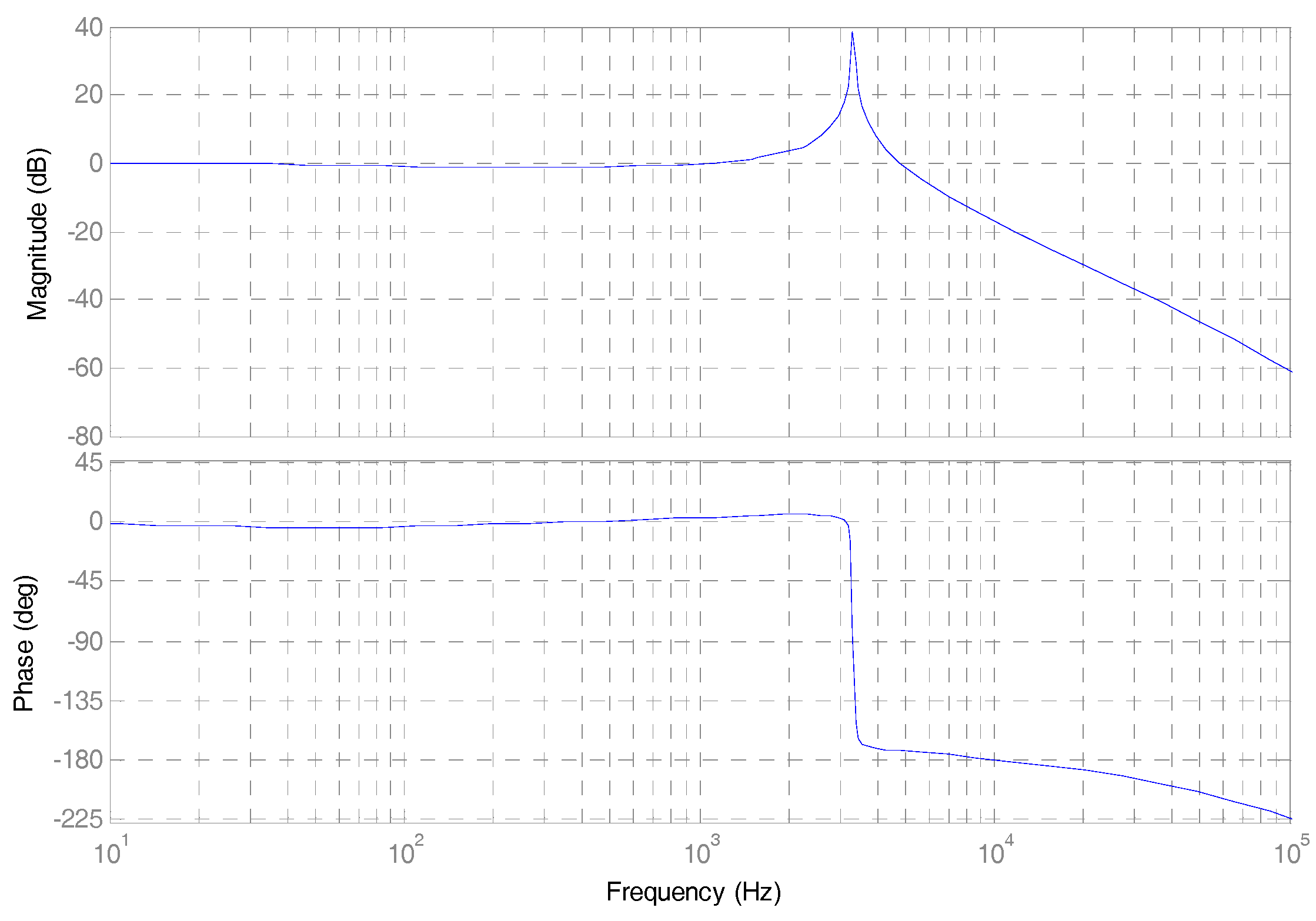
3.2. Resonance Analysis
4. Deviation Compensation Method
4.1. Random Integer Harmonic Detection
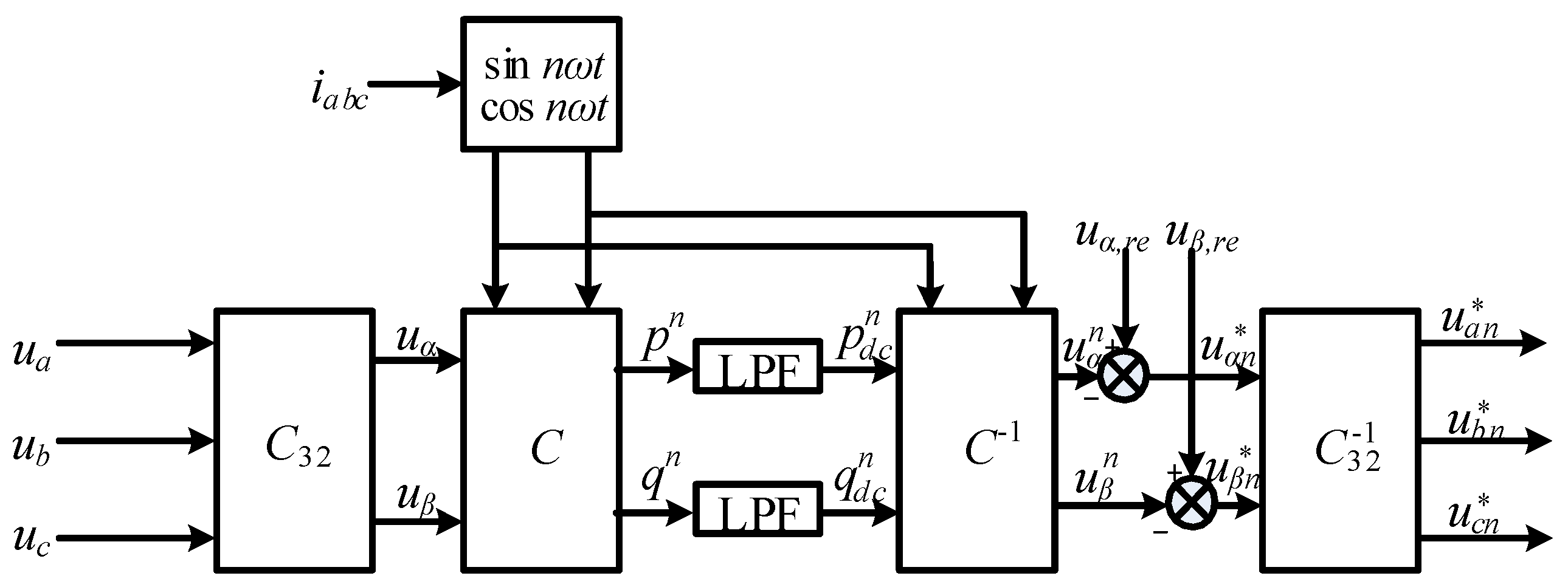
4.2. Control Algorithm of Deviation Compensation Method
5. Selective Harmonic Damping
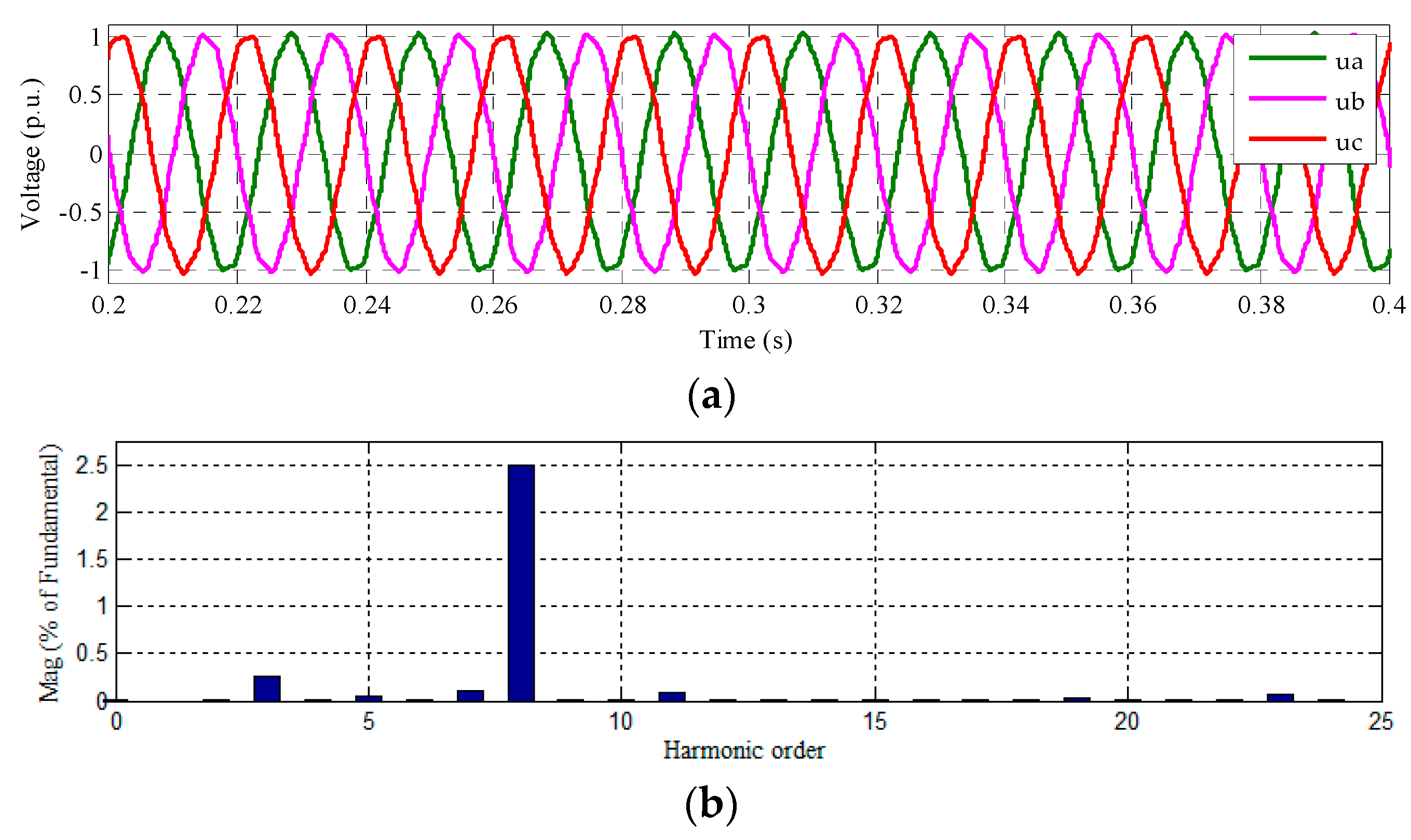
6. Simulation Results
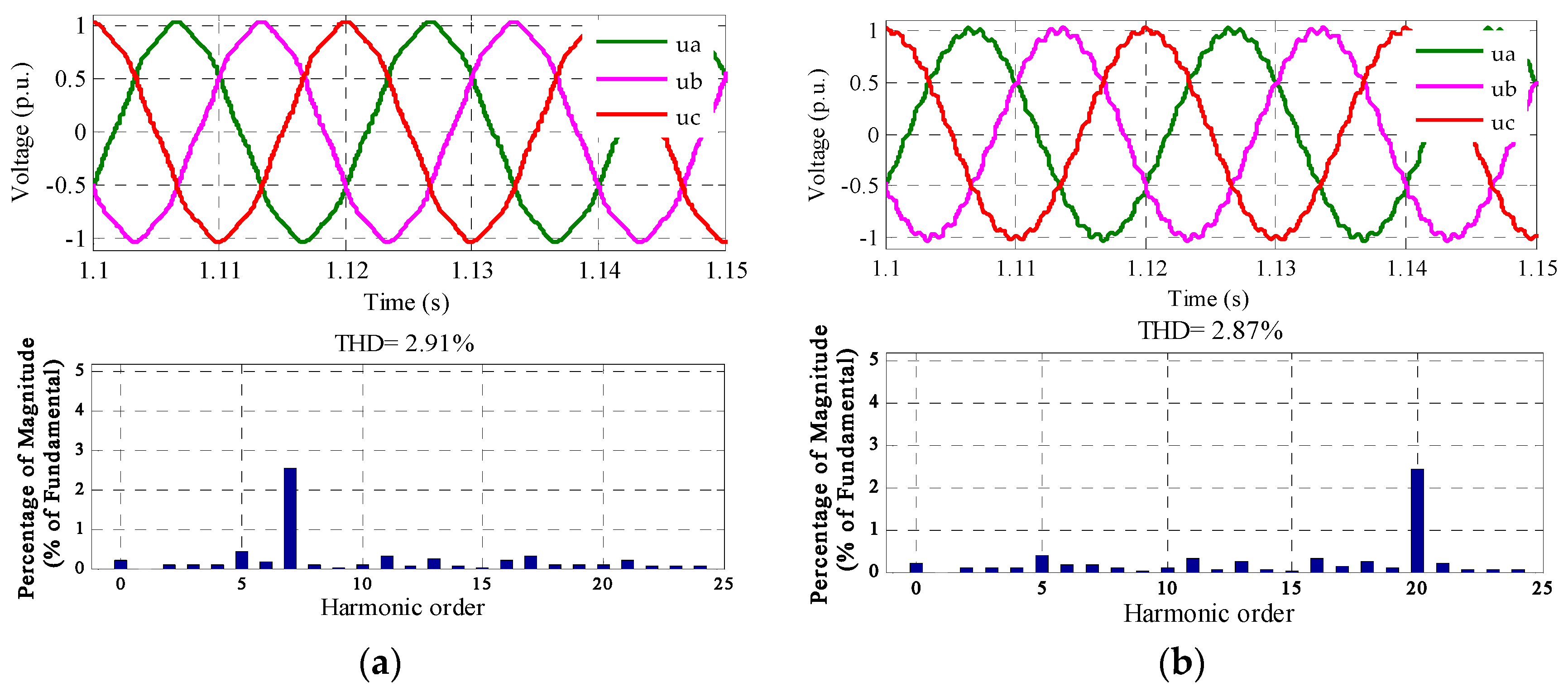
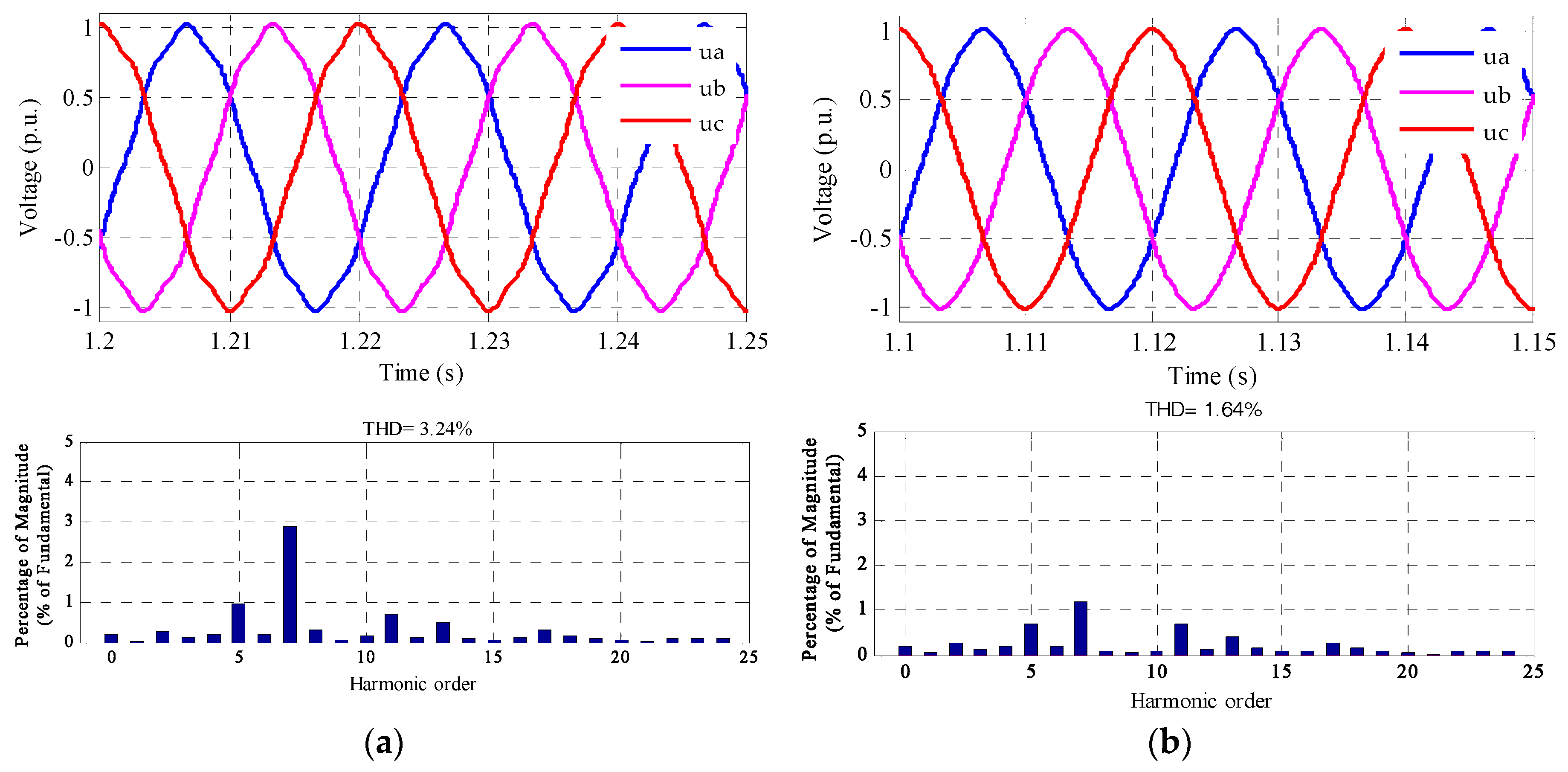
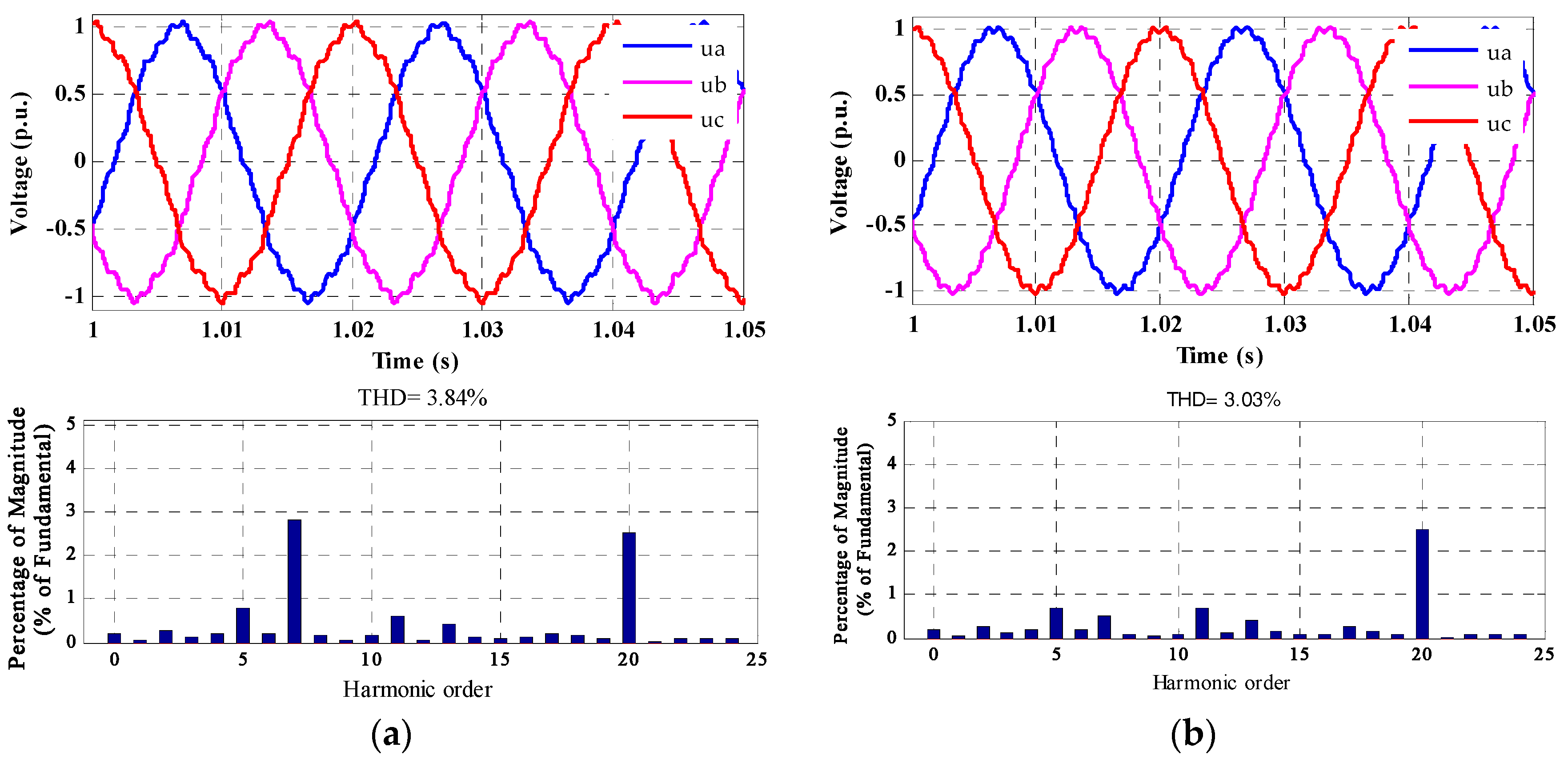
6.1. The Local Testing Method
6.2. Deviation Compensation Method
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Parameters | Electrical Values | |
|---|---|---|
| Sb | Rated power | 5 MW |
| Vs | Stator voltage (L-L) | 690 V |
| rs | Stator resistance | 0.003 p.u. |
| rr | Rotor resistance (referred to stator) | 0.004 p.u. |
| Lls | Stator leakage inductance | 0.125 p.u. |
| Llr | Rotor leakage inductance (referred to stator) | 0.05 p.u. |
| Lm | Magnetizing inductance | 2.5 p.u. |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Ll | 125 μH | VG | 480 V |
| Kprsc | 0.2 | VSR | 690 V |
| Kirsc | 2 | VPCC | 35 kV |
| Kpgsc | 0.05 | K1 | 2.03 |
| Kigsc | 2 | K2 | 1.55 |
| Sb | Vn | Uk% | I0% |
|---|---|---|---|
| 5500 kVA | 35 kV/690 V | 6.5 | 0.8 |
| Parameters | Values | Parameters | Values | ||
|---|---|---|---|---|---|
| Filter inductance | LfD | 3 mH | DC-link voltage | Vdc | 2.2 kV |
| Switching frequency | fsf | 20 kHz | PR controller | Kp_i | 30 |
| Kr_i | 600 | ||||
| DC-link voltage controller | Kp_dc | 0.05 | Resonant controller | Kr_v | 2 |
| Ki_dc | 0.5 | ωr | 750 | ||
| DC capacitor | Cdc | 10,000 μF | Sampling period | Ts | 50 μs |
References
- Santos-Mugica, M.; Robles, E.; Endegnanew, A.G.; Tedeschi, E.; Giebhardt, J. Grid integration and power quality testing of marine energy converters: Research activities in the MARINET project. In Proceedings of the 9th International Conference of Ecological Vehicles and Renewable Energies, Monte-Carlo, Monaco, 25–27 March 2014; pp. 1–9. [Google Scholar]
- Qi, Y.; Liu, Y. Wind Power Ramping Control Using Competitive Game. IEEE Trans. Sustain. Energy 2016, 7, 1516–1524. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, R.; Terzija, V. Power system restoration: A literature review from 2006 to 2016. J. Mod. Power Syst. Clean Energy 2016, 4, 332–341. [Google Scholar] [CrossRef]
- Li, S.; Qin, S.; Wang, R.; Li, Q.; Chen, C. Study on grid adaptability testing methodology for wind turbines. J. Mod. Power Syst. Clean Energy 2013, 1, 81–87. [Google Scholar] [CrossRef]
- Jiang, Z.; Kumar, M.; Liu, Y. A grid adaptability test method eliminating cable impacts for offshore wind turbines. In Proceedings of the 2016 China International Conference on Electricity Distribution, Xi’an, China, 10–13 August 2016; pp. 1–4. [Google Scholar]
- International Electro-technical Commission. IEC 61400-24 Wind Turbines-Part 21: Measurement and Assessment of Power Quality Characteristics of Grid Connected Wind Turbines; International Electro-technical Commission: Geneva, Switzerland, 2008. [Google Scholar]
- National Energy Administration of China. NB/T 31054 Test Procedure of Wind Turbine Grid Adaptability; National Energy Administration of China: Beijing, China, 2014. [Google Scholar]
- Ping, J.; Dai, C.B.; Wu, S.Y.; Jin, X.F. A scheme on adaption detection of large-capacity wind turbines to the power grid. In Proceedings of the International Conference of Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 900–905. [Google Scholar]
- Fan, L.; Yuvarajan, S.; Kavasseri, R. Harmonic analysis of a DFIG for a wind energy conversion system. IEEE Trans. Energy Convers. 2010, 25, 181–190. [Google Scholar]
- Zhao, W.; Xie, C.; Liu, Y. Resonance analysis of DFIG-based offshore wind farm. In Proceedings of the 2015 IEEE Region 10 Conference, Macau, China, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Song, Y.; Blaabjerg, F. Overview of DFIG-based wind power system resonances under weak networks. IEEE Trans. Power Electron. 2017, 32, 4370–4394. [Google Scholar] [CrossRef]
- Miao, Z. Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network. IEEE Trans. Energy Convers. 2012, 27, 984–991. [Google Scholar] [CrossRef]
- Vieto, I.; Sun, J. Sequence impedance modeling and analysis of type-III wind turbines. IEEE Trans. Energy Convers. 2017. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J. Voltage stability and control of offshore wind farms with AC collection and HVDC transmission. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1181–1189. [Google Scholar]
- Chien, C.H.; Bucknall, R.W.G. Theoretical aspects of the harmonic performance of subsea AC transmission systems for offshore power generation schemes. IET Proc. Gener. Transm. Distrib. 2006, 153, 599–609. [Google Scholar] [CrossRef]
- Liang, X.; Jackson, W.M. Influence of subsea cables on offshore power distribution systems. IEEE Trans. Ind. Appl. 2009, 45, 2136–2144. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, S.; Lu, X.; Ge, B.; Peng, F.Z. Resonance issues and damping techniques for grid-connected inverters with long transmission cable. IEEE Trans. Power Electron. 2014, 29, 110–120. [Google Scholar] [CrossRef]
- Luo, A.; Xu, Q.; Ma, F.; Chen, Y. Overview of power quality analysis and control technology for the smart grid. J. Mod. Power Syst. Clean Energy 2016, 4, 1–9. [Google Scholar] [CrossRef]
- Shuai, Z.K.; Liu, D.; Shen, J.; Tu, C.; Cheng, Y.; Luo, A. Series and parallel resonance problem of wideband frequency harmonic and its elimination strategy. IEEE Trans. Power Electron. 2014, 29, 1941–1952. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Lascu, C.; Hoseinzadeh, B.; Teodorescu, R.; Kocewiak, H.; Sørensen, T.; Jensen, C.F. Challenges with harmonic compensation at a remote bus in offshore wind power plant. In Proceedings of the 16th International Conference of Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Smith, K.S.; Ran, L. Active filter used as a controlled reactance to prevent harmonic resonance in interconnected offshore power systems. IEE Proc. Gener. Transm. Distrib. 1999, 146, 393–399. [Google Scholar] [CrossRef]
- Shen, H.; Yang, L.; Sun, X.; Li, Z.; Han, R.; Chen, Z. Active power filter equivalent to an infinite feeder for harmonic suppression in radial distribution systems. IET Power Electron. 2016, 9, 1331–1340. [Google Scholar] [CrossRef]
- Hasan, K.N.B.; Rauma, K.; Luna, A.; Candela, J.I.; Rodríguez, P. Harmonic compensation analysis in offshore wind power plants using hybrid filters. IEEE Trans. Ind. Appl. 2014, 50, 2050–2060. [Google Scholar] [CrossRef]
- Huali, C.; Yunlian, S.; Wei, C. Harmonic suppression of grid-connected distributed generation based on novel hybrid power filter. In Proceedings of the 4th IEEE Conference of International Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 2914–2918. [Google Scholar]
- Wang, T.X.; Choi, S.S.; Sng, E.K.K. Series compensation method to mitigate harmonics and voltage sags and swells. IET Gener. Transm. Distrib. 2007, 1, 96–103. [Google Scholar] [CrossRef]
- Shu, Z.; Lin, H.; Zhang, Z.; Yin, X.; Zhou, Q. Specific order harmonics compensation algorithm and digital implementation for multi-level active power filter. IET Power Electron. 2017, 10, 525–535. [Google Scholar] [CrossRef]
- Mattavelli, P. A closed-loop selective harmonic compensation for active filters. IEEE Trans. Ind. Appl. 2001, 37, 81–89. [Google Scholar] [CrossRef]
- Chen, X.; Dai, K.; Xu, C.; Li, P.; Zhang, Y. Harmonic compensation and resonance damping for SAPF with selective closed-loop regulation of terminal voltage. IET Power Electron. 2017, 10, 619–629. [Google Scholar] [CrossRef]
- Jianben, L.; Shaojun, D.; Qiaofu, C.; Kun, T. Modelling and industrial application of series hybrid active power filter. IET Power Electron. 2013, 6, 1707–1714. [Google Scholar] [CrossRef]
- Alali, M.A.E.; Chapuis, Y.-A.; Saadate, S.; Braun, F. Advanced common control method for shunt and series active compensators used in power quality improvement. IEE Proc. Electron. Power Appl. 2004, 151, 658–665. [Google Scholar] [CrossRef]
- Gupta, R.; Ghosh, A.; Joshi, A. Performance comparison of VSC-based shunt and series compensators used for load voltage control in distribution systems. IEEE Trans. Power. Deliv. 2011, 26, 268–278. [Google Scholar] [CrossRef]
- Ribeiro, E.R.; Barbi, I. Harmonic voltage reduction using a series active filter under different load conditions. IEEE Trans. Power Electron. 2006, 21, 1394–1402. [Google Scholar] [CrossRef]
- Inzunza, R.; Akagi, H. A 6.6-kV transformerless shunt hybrid active filter for installation on a power distribution system. IEEE Trans. Power Electron. 2005, 20, 893–900. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power-electronics-based AC systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Lisere, M. An active damper to suppress multiple resonances with unknown frequencies. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 16–20 March 2014; pp. 2184–2191. [Google Scholar]
- Rechka, S.; Ngandui, E.; Jianhong, X.; Sicard, P. Analysis of harmonic detection algorithms and their application to active power filters for harmonics compensation and resonance damping. Can. J. Electr. Comput. Eng. 2003, 28, 41–51. [Google Scholar] [CrossRef]
- Shi, Z.; Wei, S.; Wu, B.; Huang, Y. Research on the current detection algorithm for reactive and harmonic of active power filters. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–5. [Google Scholar]
- Yepes, A.G.; Freijedo, F.; Lopez, O.; Gandoy, J. High-performance digital resonant controllers implemented with two integrators. IEEE Trans. Power Electron. 2011, 26, 563–576. [Google Scholar] [CrossRef]
- Lavopa, E.; Zanchetta, P.; Sumner, M.; Cupertino, F. Real-time estimation of fundamental frequency and harmonics for active shunt power filters in aircraft electrical systems. IEEE Trans. Ind. Electron. 2009, 56, 2875–2884. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Li, C.; Liu, X.; Liu, Y.; Wang, R. Harmonic Adaptability Remote Testing Method for Offshore Wind Turbines. Energies 2017, 10, 1793. https://doi.org/10.3390/en10111793
Jiang Z, Li C, Liu X, Liu Y, Wang R. Harmonic Adaptability Remote Testing Method for Offshore Wind Turbines. Energies. 2017; 10(11):1793. https://doi.org/10.3390/en10111793
Chicago/Turabian StyleJiang, Zimin, Changgang Li, Xiaohao Liu, Yutian Liu, and Ruiming Wang. 2017. "Harmonic Adaptability Remote Testing Method for Offshore Wind Turbines" Energies 10, no. 11: 1793. https://doi.org/10.3390/en10111793
APA StyleJiang, Z., Li, C., Liu, X., Liu, Y., & Wang, R. (2017). Harmonic Adaptability Remote Testing Method for Offshore Wind Turbines. Energies, 10(11), 1793. https://doi.org/10.3390/en10111793




