Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies
Abstract
:1. Introduction
2. Methodology
2.1. Physical Experiments
2.1.1. Rheology Test
2.1.2. TPG Measurement and Its Critical Condition
- Experimental devices were connected according to the flow chart.
- The temperature of the thermotank was set to 30 °C, and the core with the saturated water was required to stand for at least 24 h.
- The heavy oil sample was used to displace the water in the core at a flow rate of 0.05 mL/min after bypassing the oil column tube #1. The displacing flow rate was increased to 0.5 mL/min when the water cut at the outlet was lower than 2% until the volume of injected heavy oil sample reached ten times the pore volume (PV) of the core, and there was no water production.
- The ISCO pump was stopped, and the height of the oil column in the oil column tube #2 was lowered to about 5 cm.
- The oil column tube #1 was put into use. The height of the oil column in the oil column tube #1 was raised to the same height as that in the oil column tube #2 by restarting the ISCO pump with the flow rate of 0.02 mL/min. The ISCO pump was stopped again, and this condition was kept for 24 h.
- The flow rate of 0.002 mL/min was used to displace and the height of the oil column in the oil column tube #1 increased gradually. The pressure gradient was the TPG of the heavy oil sample when the height of the oil column in the oil column tube #2 began to move.
- The TPG under the and was measured, where was the permeability, which started from , and is the viscosity, which started from .
- If the TPG existed under the and , a smaller than was used to replace and the TPG at the and was measured. If not, a larger than was used.
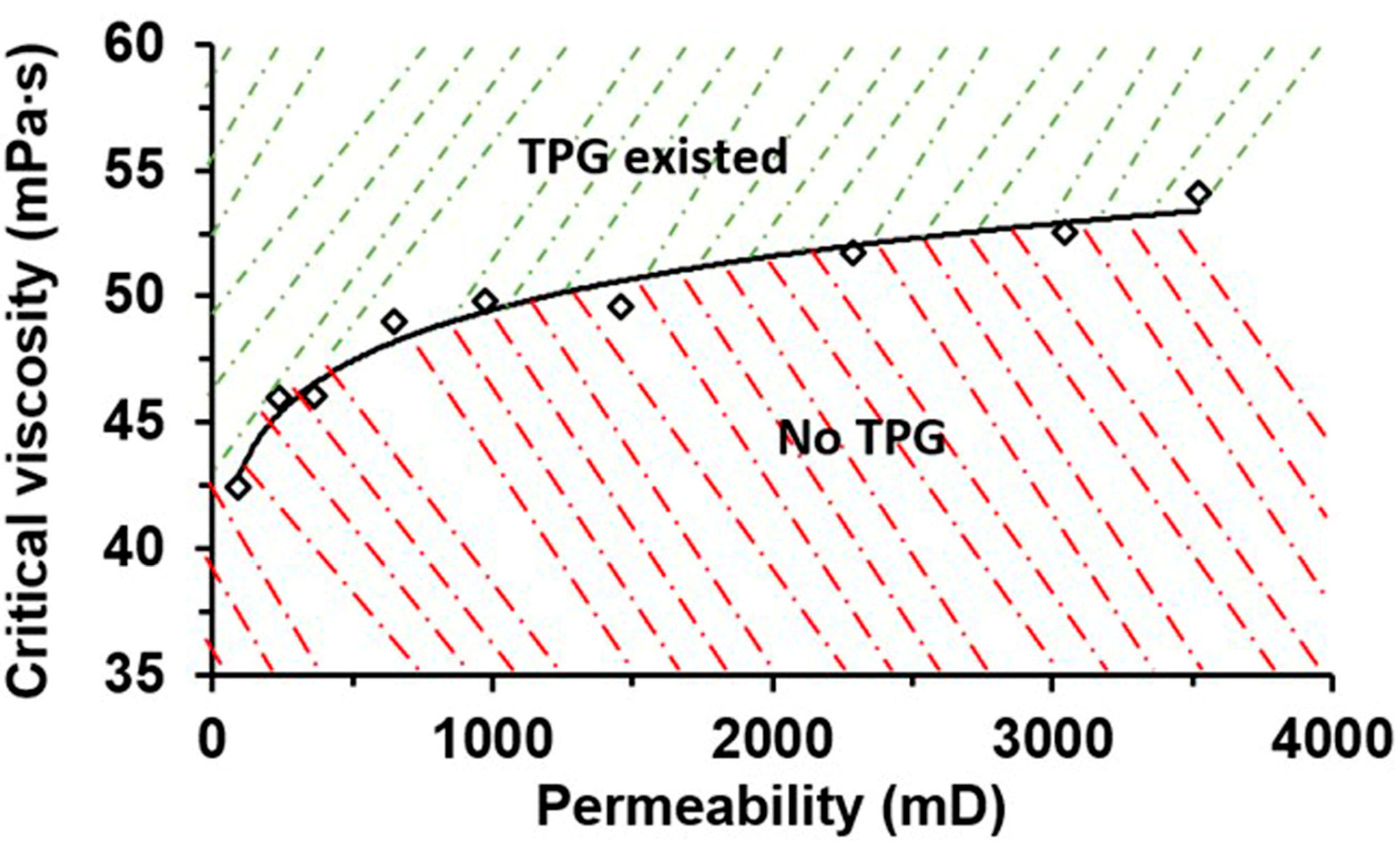
- The selection of was repeated until two cases for the inexistence of the TPG and four cases for the existence of the TPG were obtained. A curve of the relationship between the TPGs greater than 0 MPa/m and the corresponding viscosity was drawn. The intercept of the fitting curve on the viscosity axis was considered to be the critical viscosity () at the . Here, the TPG would be present for the specific permeability when the viscosity is higher than the critical viscosity (). Otherwise, the TPG no longer existed.
- The above steps were repeated until sets of permeability and the corresponding critical viscosities were obtained, where was determined by the requirements of the study.
2.1.3. Flow Experiments
2.2. Numerical Method
2.2.1. Corrected Darcy’s Law
2.2.2. Flow Model
- The corrected Darcy’s law of Equation (2) was applied.
- The model was 3D with two phases (the oil and water phases).
- The water component existed only in the water phase, which did not exchange its mass with the oil phase.
- The reservoir rock was compressible and anisotropic, while the fluid was compressible.
- The effects of the capillary force and gravity were taken into account.
2.2.3. IMPES
3. Results and Discussion
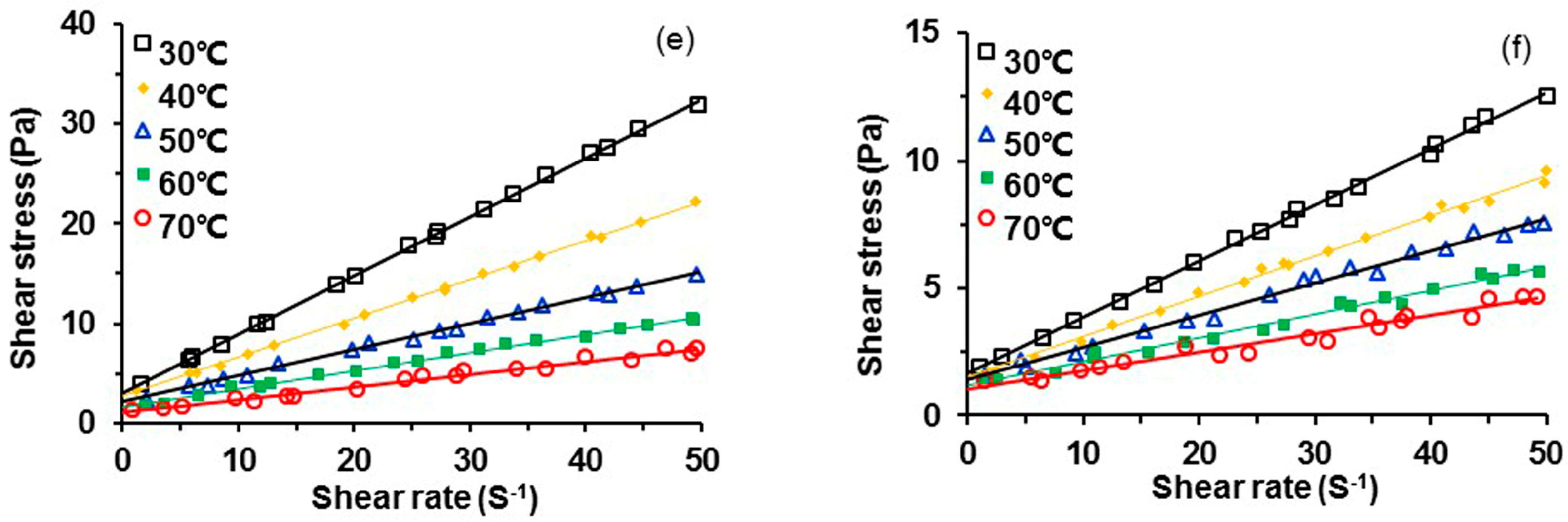
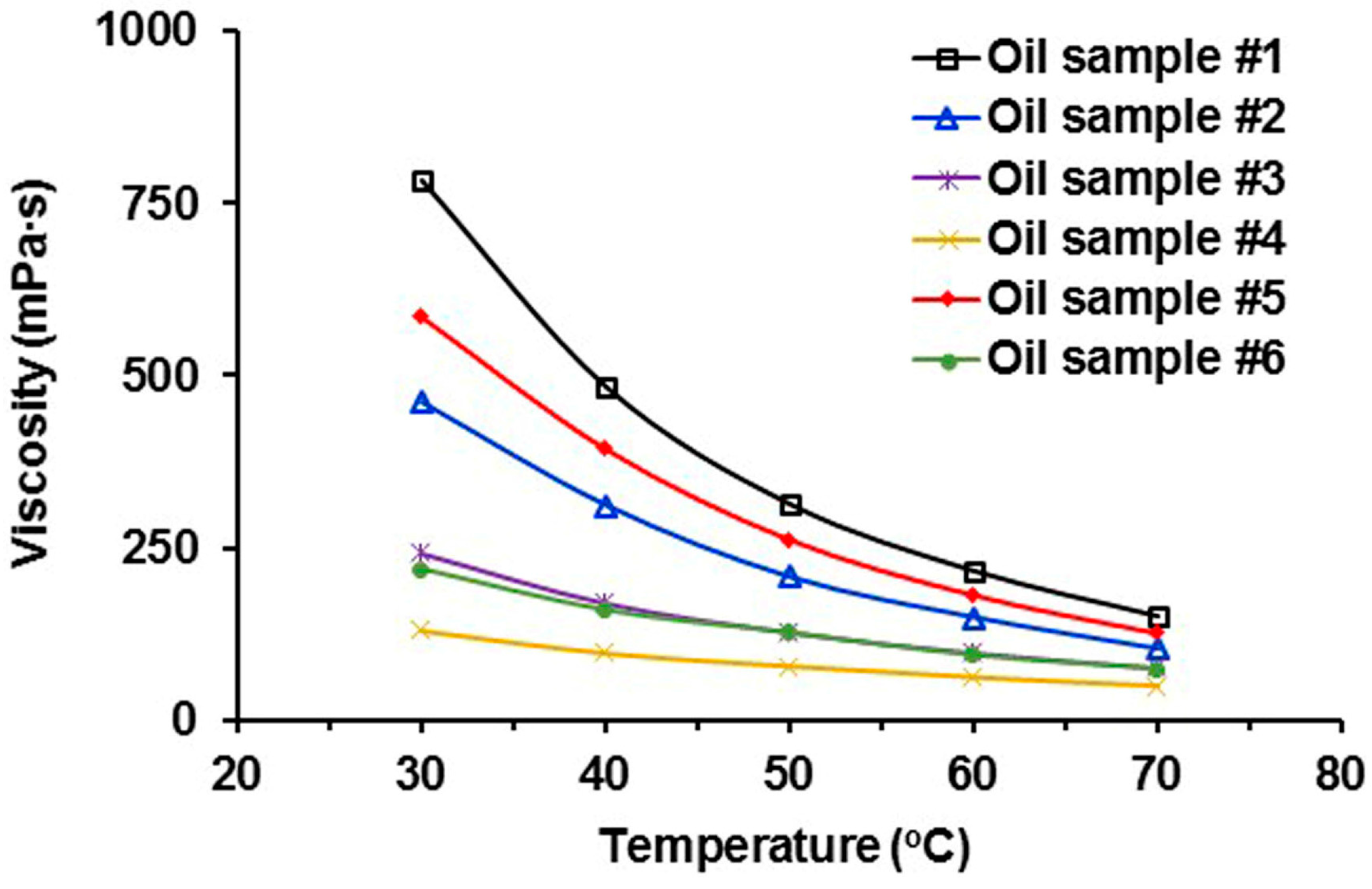
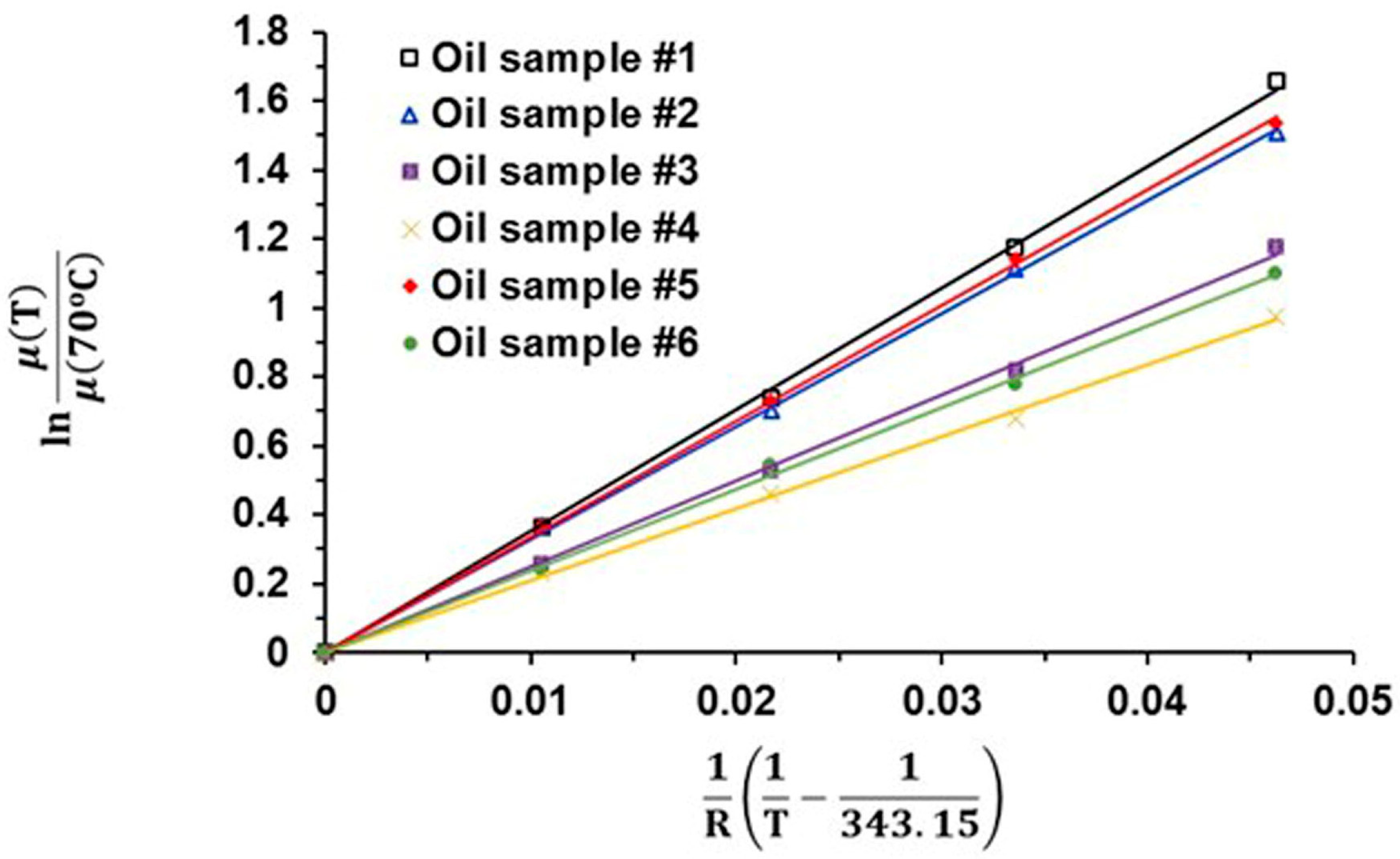
3.1. Rheology of Heavy Oil
3.2. Threshold Pressure Gradient (TPG)
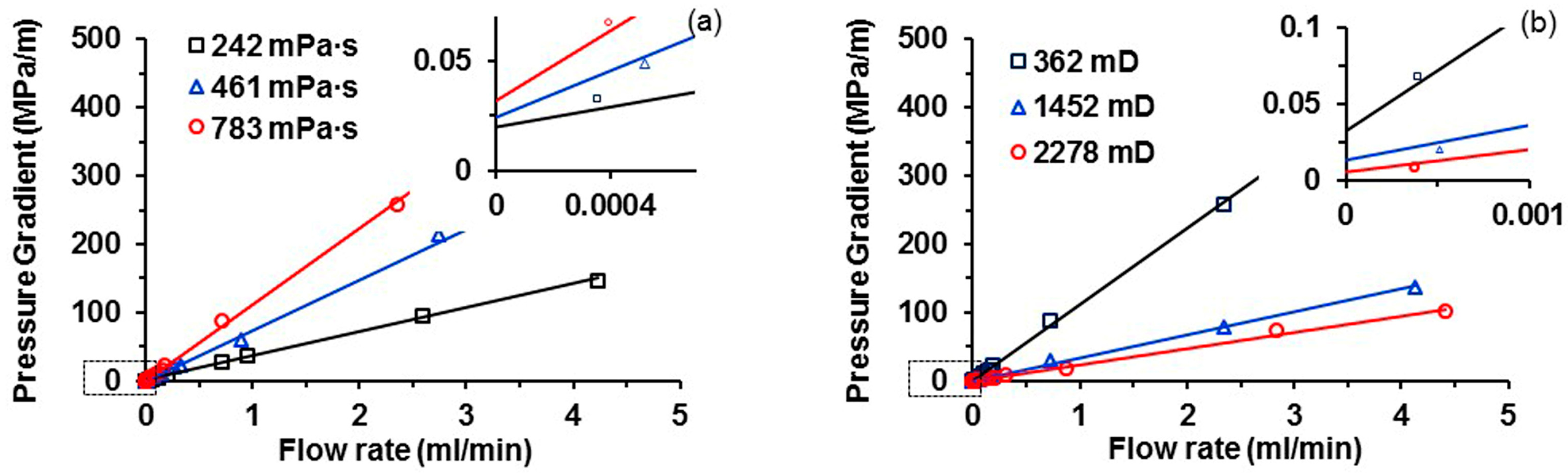
3.2.1. Impact of Flow Rate on TPG Measurement
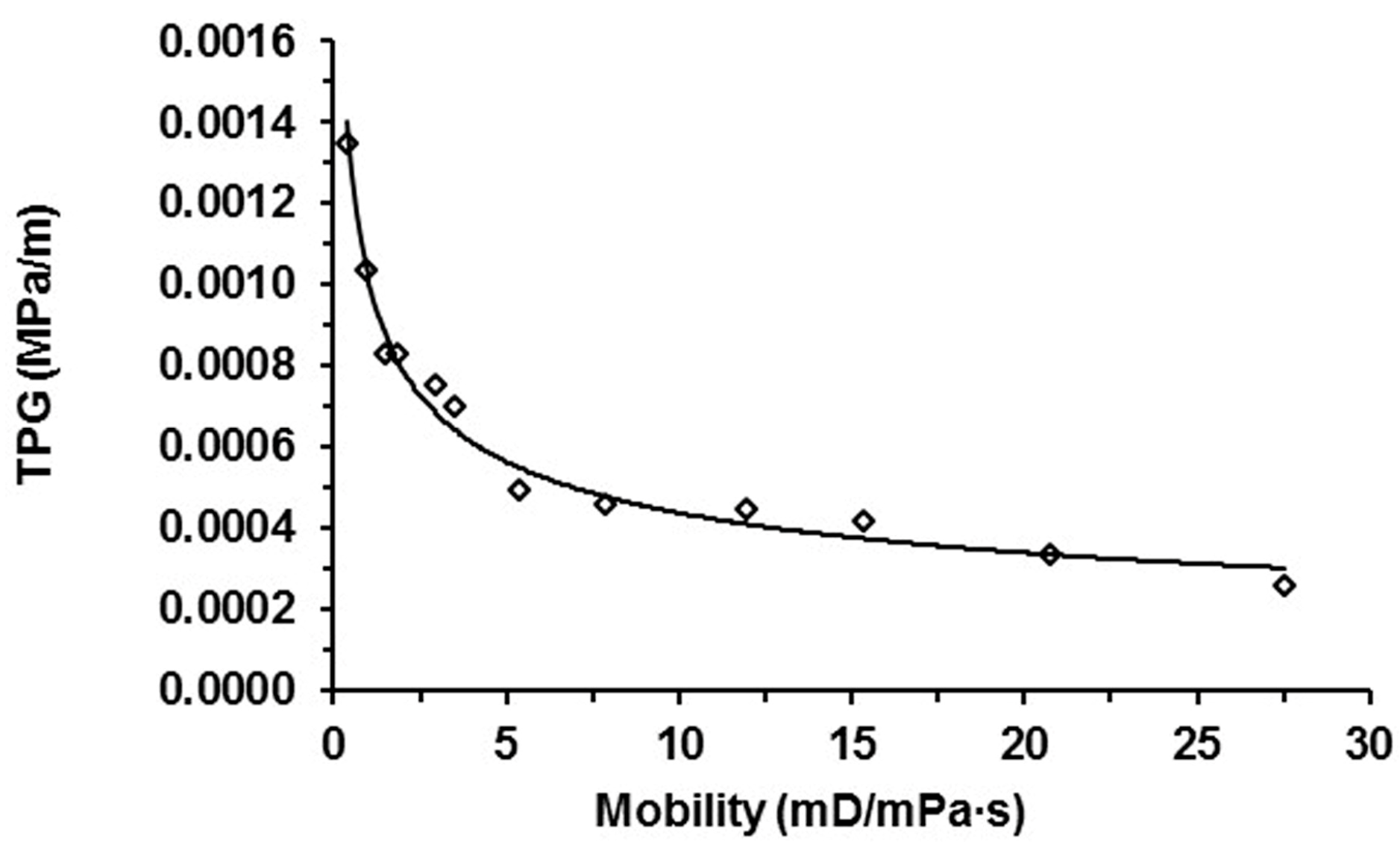
3.2.2. Relationship between TPG and Mobility
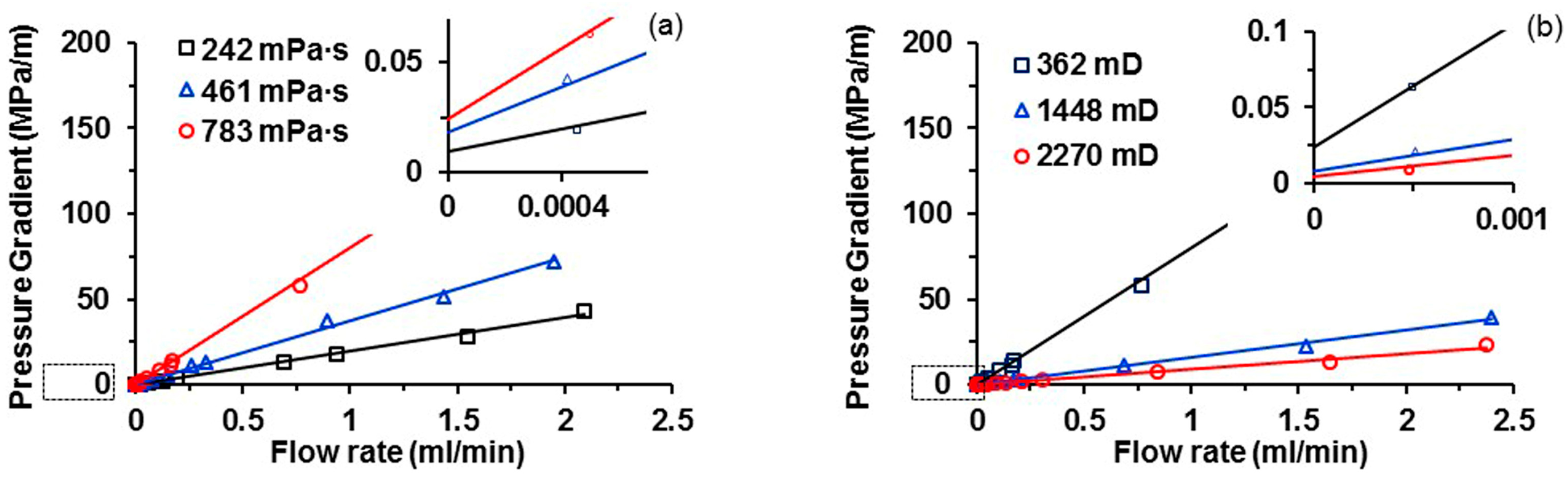
3.3. Flow Characteristics of Heavy Oil in Porous Media
3.4. Simulation
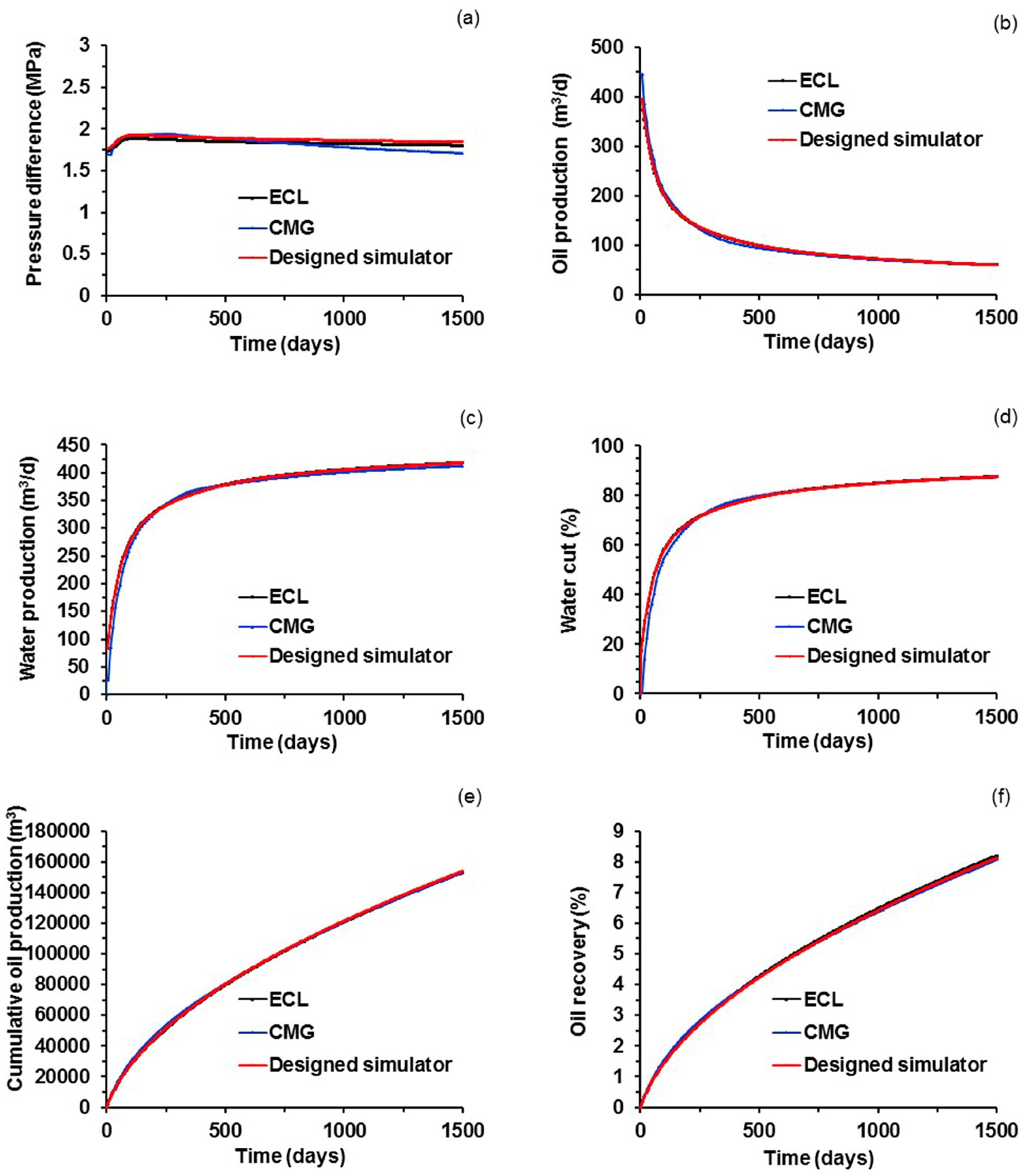
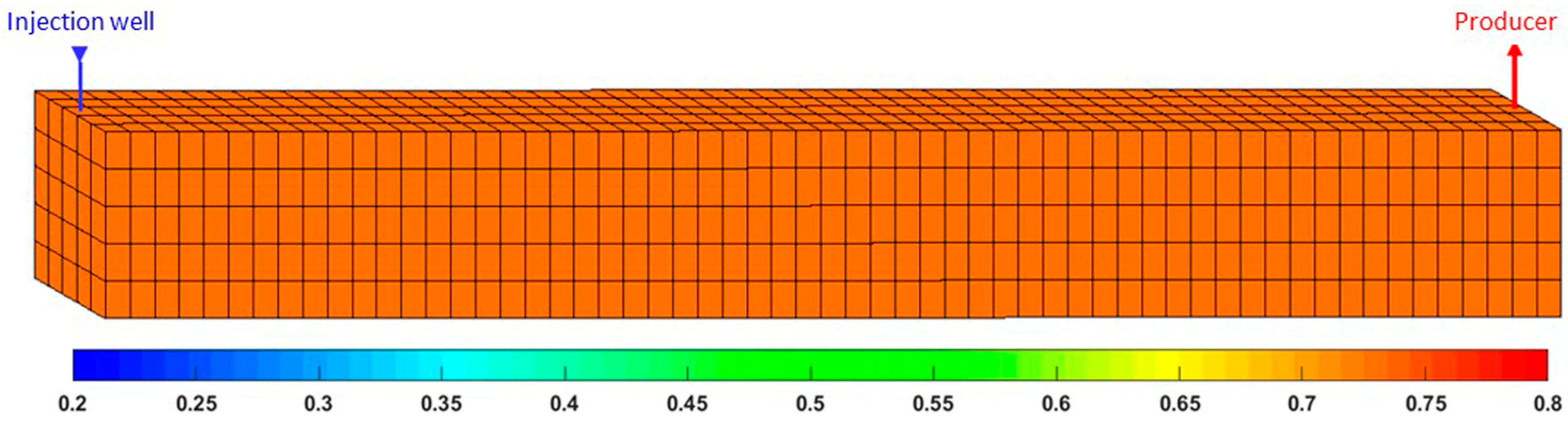
3.4.1. Validation
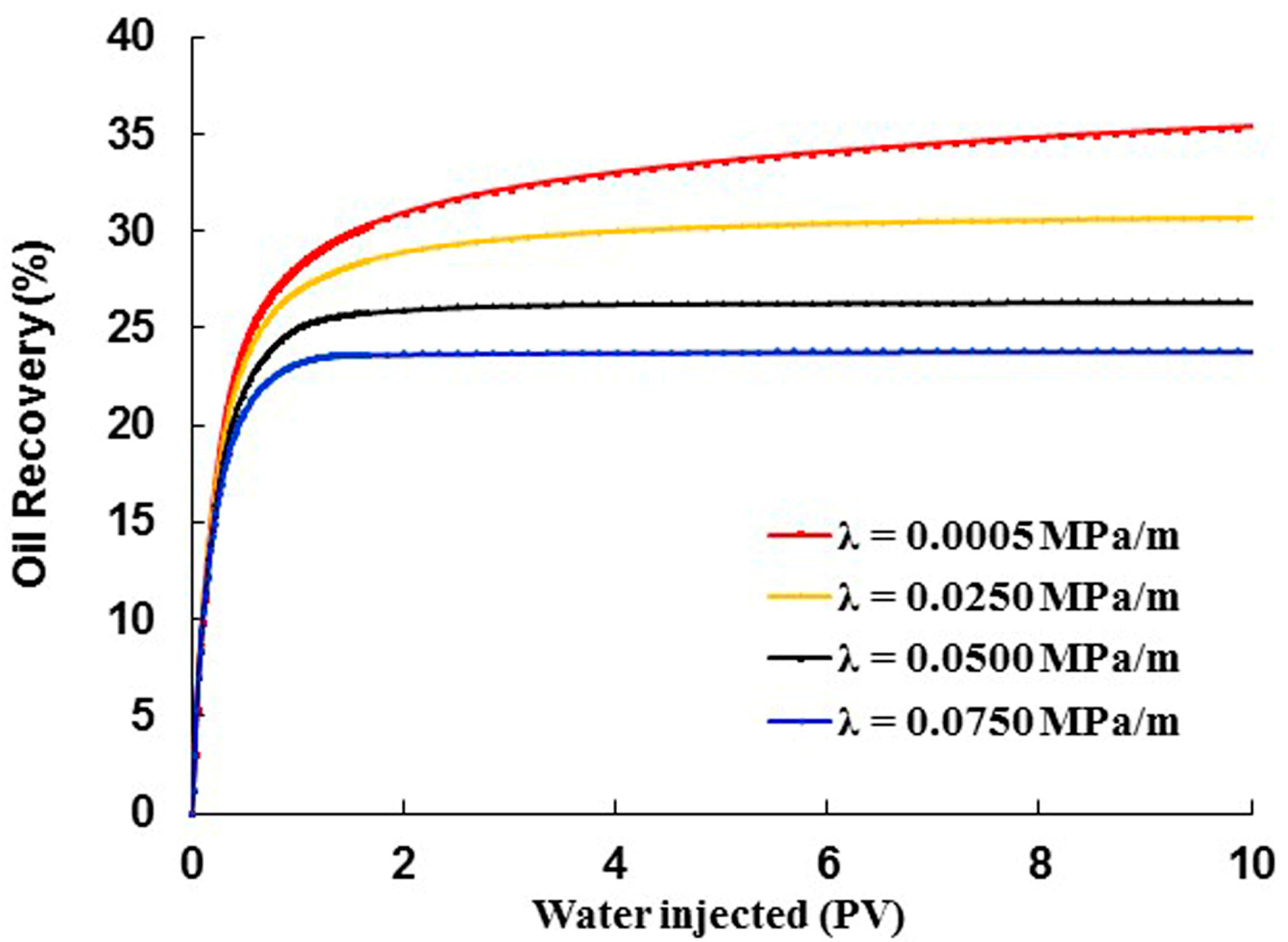
3.4.2. TPG Sensitivity
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Daily Demand for Crude Oil Worldwide from 2006 to 2016. Available online: https://www.statista.com/statistics/271823/daily-global-crude-oil-demand-since-2006/ (accessed on 25 October 2017).
- Lu, T.; Li, Z.; Zhou, Y. Flow Behavior and Displacement Mechanisms of Nanoparticle Stabilized Foam Flooding for Enhanced Heavy Oil Recovery. Energies 2017, 10, 560. [Google Scholar] [CrossRef]
- Huc, A.Y. Heavy Crude Oils: From Geology to Upgrading: An Overview; Editions Technip: Paris, France, 2011; p. 11. ISBN 978-2-7108-0890-9. [Google Scholar]
- Mai, A.; Bryan, J.; Goodarzi, N.; Kantas, A. Insights into Non-Thermal Recovery of Heavy Oil. J. Can. Pet. Technol. 2009, 48, 27. [Google Scholar] [CrossRef]
- Enrique, S.C.; Patsy, V.R.G.; Ulises, M.C.; Sergio, E.Q.C. Effect of the Temperature on the Non-Newtonian Behavior of Heavy Oils. Energy Fuels 2015, 29, 2883–2889. [Google Scholar]
- Ghannam, M.T.; Hasan, S.W.; Abu-Jdayil, B.; Esmail, N. Rheological Properties of Heavy & Light Crude Oil Mixtures for Improving Flowability. J. Pet. Sci. Eng. 2012, 81, 122–128. [Google Scholar]
- Luo, P.; Gu, Y. Effects of Asphaltene Content on the Heavy Oil Viscosity at Different Temperatures. Fuel 2007, 86, 1069–1078. [Google Scholar] [CrossRef]
- Ghanavati, M.; Shojaei, M.J.; Ramazani, R.S.A. Effects of Asphaltene Content and Temperature on Viscosity of Iranian Heavy Crude Oil: Experimental and Modeling Study. Energy Fuels 2013, 27, 7217–7232. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Civan, F. Experimental and Theoretical Investigation of the Zaoyuan Field Heavy Oil Flow through Porous Media. J. Pet. Sci. Eng. 2006, 50, 83–101. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2002; pp. 21–36. ISBN 0471410772. [Google Scholar]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; Wiley-VCH: Weinheim, Germany, 1994; pp. 92–101. ISBN 1560815795. [Google Scholar]
- Bassane, J.F.P.; Sad, C.M.S.; Neto, D.M.C.; Santos, M.F.P.; Santos, F.D. Study of the Effect of Temperature and Gas Condensate Addition on the Viscosity of Heavy Oils. J. Pet. Sci. Eng. 2016, 142, 163–169. [Google Scholar] [CrossRef]
- Mullins, O.C.; Sheu, E.Y. Structures and Dynamics of Asphaltenes; Plenum Press: New York, NY, USA, 1998; p. 15. ISBN 1560815795. [Google Scholar]
- Henaut, I.; Argillier, J.F.; Pierre, C.; Moan, M. Thermal Flow Properties of Heavy Oils. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2003. [Google Scholar]
- Ovalles, C.; Rogel, E.; Segerstrom, J. Improvement of Flow Properties of Heavy Oils Using Asphaltene Modifiers. In Proceedings of the SPE Annual Technical conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Yen, T.F.; Chilingarian, G.V. Asphaltenes and Asphalts, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 1994; pp. 249–295. ISBN 044488291X. [Google Scholar]
- Argillier, J.F.; Coustet, C.; Henaut, I. Heavy Oil Rheology as a Function of Asphaltene and Resin Content and Temperature. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium and International Horizontal Well Technology Conference, Calgary, AB, Canada, 4–7 November 2002. [Google Scholar]
- Malkin, A.Y.; Khadzhiev, S.N. On the Rheology of Oil (Review). Pet. Chem. 2016, 56, 541–551. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Xie, Y.; Ma, D.; Shi, X. Flow Characteristics of Heavy Oil through Porous Media. Energy Sources Part A 2012, 34, 347–359. [Google Scholar] [CrossRef]
- Chen, M.; Rossen, W.; Yortsos, Y.C. The Flow and Displacement in Porous Media of Fluids with Yield Stress. Chem. Eng. Sci. 2005, 60, 4183–4202. [Google Scholar] [CrossRef]
- Evdokimov, I.N.; Eliseev, N.Y.; Eliseev, D.Y. Rheological Evidence of Structural Phase Transitions in Asphaltene-Containing Petroleum Fluids. J. Pet. Sci. Eng. 2001, 30, 199–211. [Google Scholar] [CrossRef]
- Luo, Y.; Cheng, L.; Ding, Z. A Transient Flow Model of Non-Newtonian Heavy Oil under Different Bottom-hole Producing Pressure Conditions. Pet. Sci. Technol. 2014, 32, 505–512. [Google Scholar] [CrossRef]
- Dong, X.; Liu, H.; Wang, Q.; Pang, Z.; Wang, C. Non-Newtonian Flow Characterization of Heavy Crude Oil in Porous Media. J. Pet. Explor. Prod. Technol. 2013, 3, 43–53. [Google Scholar] [CrossRef]
- Laaber, P. Numerical Simulation of a Three-Dimensional Bingham Fluid Flow. Master’s Thesis, Johannes Kepler University Linz, Linz, Austria, March 2008. [Google Scholar]
- Boveta, E.; Chiaiaa, B.; Preziosib, L. A New Model for Snow Avalanche Dynamics Based on Bingham Fluids. Meccanica 2010, 45, 753–765. [Google Scholar] [CrossRef]
- Mirzajanzade, A.K.H.; Akhmedov, Z.M.; Gurbanov, R.S.; Amirov, A.D.; Barenblatt, G.I.; Entov, V.M.; Zaitsev, Y.V. On the Special features of Oil and Gas Field Development due to Effects of Initial Pressure Gradient. In Proceedings of the 8th World Petroleum Congress, Moscow, USSR, 13–18 June 1971. [Google Scholar]
- Zeng, B.; Cheng, L.; Hao, F. Experiment and Mechanism Analysis on Threshold Pressure Gradient with Different Fluids. In Proceedings of the 34th Annual SPE International Conference and Exhibition, Tinapa–Calabar, Nigeria, 31 July–7 August 2010. [Google Scholar]
- Ning, L. Experimental Method and Its Applications of Threshold Pressure Gradient of Heavy Oil in Porous Media. J. Pet. Univ. 2011, 24, 59–62. [Google Scholar]
- Lu, C.; Wang, J.; Sun, Z. An Experiment Study on Starting Pressure Gradient of Fluids Flow in Low Permeability Sandstone Porous Media. Pet. Explor. Dev. 2002, 29, 86–87. [Google Scholar]
- Wang, W.; Yu, G.; Ke, W.; Wang, Y.; Ge, Y. Experimental Study of Nonlinear Seepage for Heavy Oil. Pet. Geol. Exp. 2013, 35, 464–467. [Google Scholar]
- Pang, Z.; Liu, H. The Transient Method and Experimental Study on Threshold Pressure Gradient of Heavy Oil in Porous Media. Open Pet. Eng. J. 2012, 5, 7–13. [Google Scholar] [CrossRef]
- Sun, J. Threshold pressure gradient study on non-Newtonian flow of heavy oil reservoirs in Shengli oilfield. Pet. Geol. Recover. Effic. 2010, 17, 74–77. [Google Scholar]
- Zarivnyy, O. Investigation of the Two-and Three-Phase Relative Permeability Relation in Carbon Dioxide-Oil-Water Systems for Light and Heavy Oil Reservoirs. Master’s Thesis, University of Regina, Regina, SK, Canada, August 2011. [Google Scholar]
- Alizadeh, A.H.; Piri, M. Three-phase flow in porous media: A review of experimental studies on relative permeability. Rev. Geophys. 2014, 52, 468–521. [Google Scholar] [CrossRef]
- Yang, Q. Study on Relative Permeabilities in Condition of Two-Phase Flooding. Ph.D. Thesis, China University of Geosciences, Beijing, China, April 2012. [Google Scholar]
- Honarpour, M.; Mahmood, S.M. Relative-permeability measurements: An overview. J. Pet. Technol. 1988, 40, 963–966. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, J.; Gu, Y.; Leng, Y. Experimental Study on Threshold Pressure Gradient of Heavy Oil Reservoir. Xinjiang Pet. Geol. 2012, 33, 201–204. [Google Scholar]
- Wang, Z.; Zhang, D.; Yang, J.; Kou, G.; Yang, F. Experimental Study on Percolation Characteristics of Ordinary Heavy Oil Reservoirs: A Case Study from the Qigu Formation Reservoir in Nine-4 Block of Xinjiang Oilfield. Oil Gas Geol. 2012, 33, 302–306. [Google Scholar]
- Maini, B.; Coskuner, G.; Jha, K. A Comparison of Steady-State and Unsteady-State Relative Permeabilities of Viscocities Oil and Water in Ottawa Sand. J. Can. Pet. Technol. 1990, 29, 72–77. [Google Scholar] [CrossRef]
- Bian, X.; Zhou, L.; Zhang, J.; Zhang, S. Effect of Non-Darcy Flow on the Integral Fracturing Design of Low-Permeability Petroleum Reservoirs. Energy Technol. 2016, 4, 263–270. [Google Scholar] [CrossRef]
- Wang, J.; Dong, M.; Asghari, K. Effect of Oil Viscosity on Heavy Oil-Water Relative Permeability Curves. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006. [Google Scholar]
- Torabi, F.; Mosavat, N.; Zarivnyy, O. Predicting heavy oil/water relative permeability using modified Corey-based correlations. Fuel 2016, 163, 196–204. [Google Scholar] [CrossRef]
- Mai, A. Mechanisms of Heavy Oil Recovery by Waterflooding. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, April 2008. [Google Scholar]
- Doorwar, S.; Mohanty, K.K. Viscous-Fingering Function for Unstable Immiscible Flows. SPE J. 2017, 22, 19–31. [Google Scholar] [CrossRef]
- Saramito, P.; Wachs, A. Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 2017, 56, 211–230. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, C.; Feng, Y.; Sun, Q.; Jin, F. Three-dimensional simulations of Bingham plastic flows with the multiple-relaxation-time lattice Boltzmann model. Eng. Appl. Comput. Fluid Mech. 2016, 10, 346–358. [Google Scholar] [CrossRef]
- Sochi, T. Modelling the Flow of Yield-Stress Fluids in Porous Media. Transp. Porous Media 2010, 85, 489–503. [Google Scholar] [CrossRef]
- Balhoff, M.T.; Thompson, K.E. Modeling the Steady Flow of Yield-stress Fluids in Packed Beds. AIChE J. 2004, 50, 3034–3048. [Google Scholar] [CrossRef]
- Wu, Y.S.; Pruess, K.A. Numerical Method for Simulating non-Newtonian Fluid Flow and Displacement in Porous Media. Adv. Water Resour. 1998, 21, 351–362. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Li, B. An Improved IMPES Method for Two-Phase Flow in Porous Media. Transp. Porous Media 2004, 54, 361–376. [Google Scholar] [CrossRef]
- Ahmadpour, M.; Siavashi, M.; Doranehgard, M.H. Numerical Simulation of Two-phase Flow in Fractured Porous Media Using Streamline Simulation and IMPES Methods and Comparing Results with a Commercial Software. J. Cent. South Univ. 2016, 23, 2630–2637. [Google Scholar] [CrossRef]
- Chen, Z. Reservoir Simulation: Mathematical Techniques in Oil Recovery; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 94–101. ISBN 978-0-898716-40-5. [Google Scholar]
- Jo, G.; Kwak, D.Y. An IMPES Scheme for a Two-phase Flow in Heterogeneous Porous Media Using a Structured Grid. Comput. Methods Appl. Mech. Eng. 2017, 317, 684–701. [Google Scholar] [CrossRef]
- Salama, A.; Sun, S.; El-Amin, M. An Efficient Implicit-pressure/Explicit-saturation-method-based Shifting-matrix Algorithm to Simulate Two-phase, Immiscible Flow in Porous Media with Application to CO2 Sequestration in the Subsurface. SPE J. 2013, 18, 1092–1100. [Google Scholar] [CrossRef]
- Sheldon, J.W.; Cardwell, J.W.T. One-dimensional, Incompressible, Noncapillary, Two-phase Fluid Flow in a Porous Medium. Pet. Trans. AIME 1959, 216, 290–296. [Google Scholar]
- Stone, H.L.; Garder, J.A.O. Analysis of Gas-cap or Dissolved-gas Drive Reservoirs. Soc. Pet. Eng. J. 1961, 1, 92–104. [Google Scholar] [CrossRef]
- Wu, Y.S. Multiphase Fluid Flow in Porous and Fractured Reservoirs; Gulf Professional Publishing: Houston, TX, USA, 2015; pp. 127–166. ISBN 978-0-12-803848-2. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics, 7th ed.; Elsevier Publishing: Atlanta, GA, USA, 2014; pp. 163–194. ISBN 978-1-85617-635-4. [Google Scholar]
- Riber, S.; Valette, R.; Mesri, Y.; Hachem, E. Adaptive variational multiscale method for bingham flows. Comput. Fluids 2016, 138, 51–60. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; pp. 259–270. ISBN 978-0-89871-606-1. [Google Scholar]
- Viswanath, D.S.; Dutt, N.V.K.; Ghosh, T.K.; Prasad, D.H.L.; Rani, K.Y. Viscosity of Liquids: Theory, Estimation, Experiment, and Data; Springer: Dordrecht, The Netherlands, 2007; pp. 138–139. ISBN 978-1-4020-5481-5. [Google Scholar]
- Han, C.D. Rheology and Processing of Polymeric Materials; Oxford University Press: New York, NY, USA, 2007; pp. 206–207. ISBN 978-0-19-518782-3. [Google Scholar]
- Wu, Q.; Wu, J. Polymer Rheology; Higher Education Press: Beijing, China, 2002; pp. 44–47. ISBN 7-04-011582-4. [Google Scholar]
- Jia, H.; Liu, P.; Pu, W.; Ma, X.; Zhang, J.; Gan, L. In Situ Catalytic Upgrading of Heavy Crude Oil through Low-Temperature Oxidation. Pet. Sci. 2016, 13, 476–488. [Google Scholar] [CrossRef]
- Ke, W. Research on Nonlinear Percolation Law of Heavy Oil. Master’s Thesis, Yangtze University, Wuhan, China, May 2013. [Google Scholar]
- Nghiem, L.; Collins, D.A.; Sharma, R. Seventh SPE Comparative Solution Project: Modelling of Horizontal Wells in Reservoir Simulation. In Proceedings of the 11th SPE Symposium on Reservoir Simulation, Anaheim, CA, USA, 17–20 February 1991. [Google Scholar]
- Alvarado, V.; Manrique, E. Enhanced Oil Recovery: An Update Review. Energies 2010, 3, 1529–1575. [Google Scholar] [CrossRef]
- Xu, W.; Zhao, J.; Chen, Z.; Shan, J.; Sun, Y. Experimental and Simulation Studies on Steam Stimulation with Multiple Fluids for Offshore Heavy Oil Reservoirs. Int. J. Numer. Anal. Model.-B 2014, 5, 31–45. [Google Scholar]
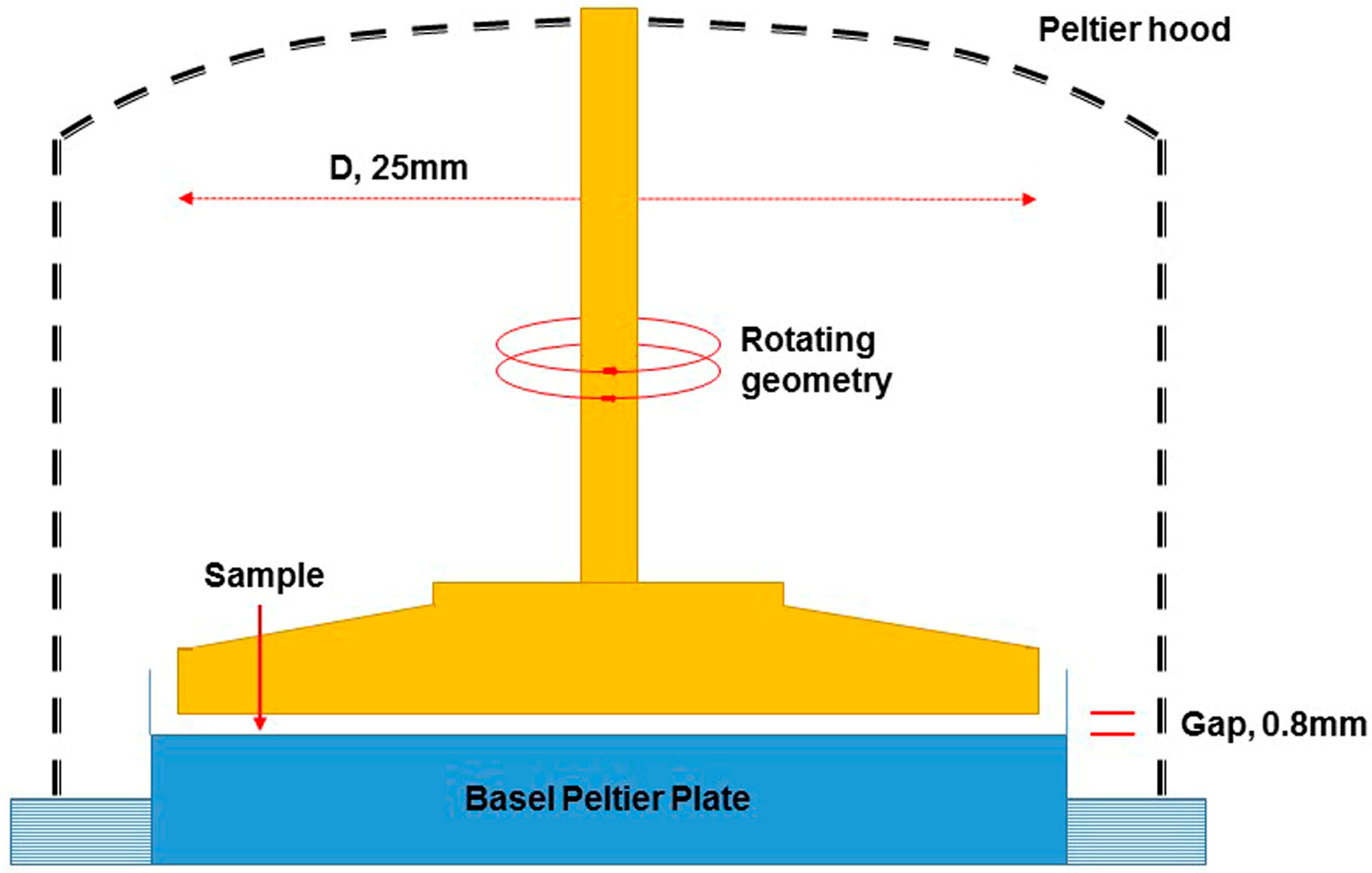
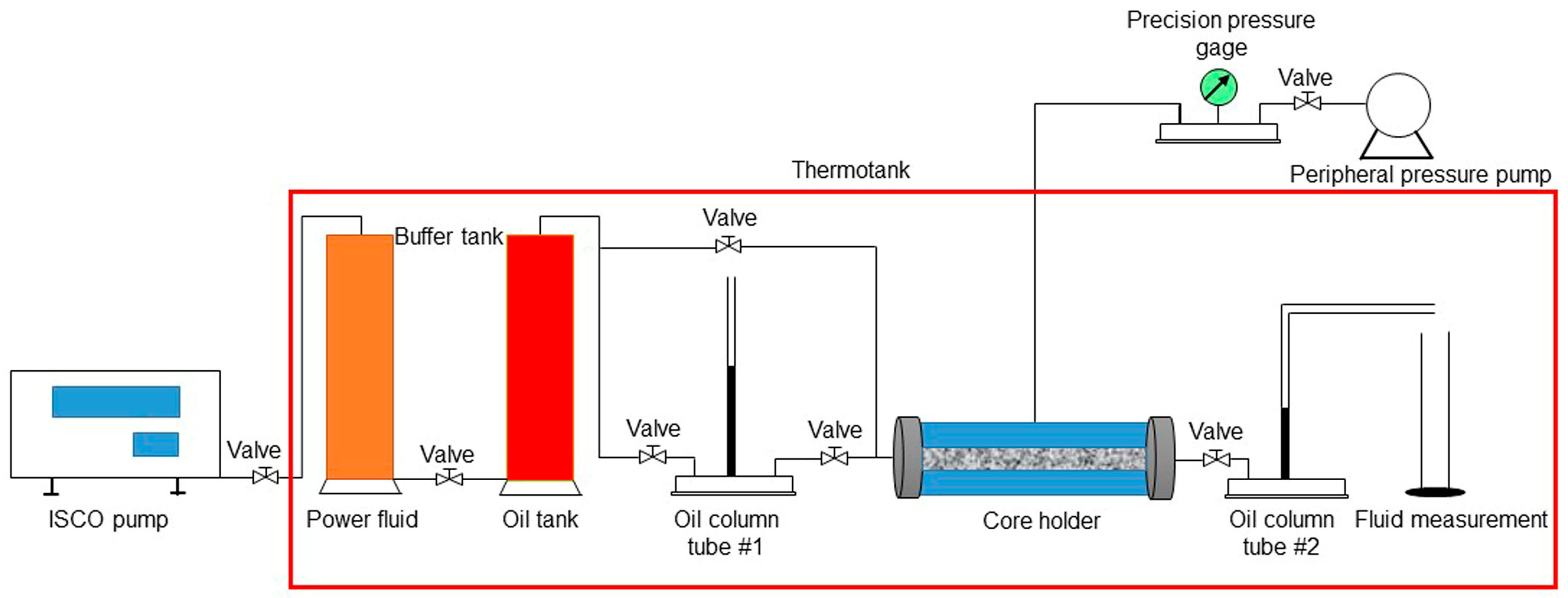

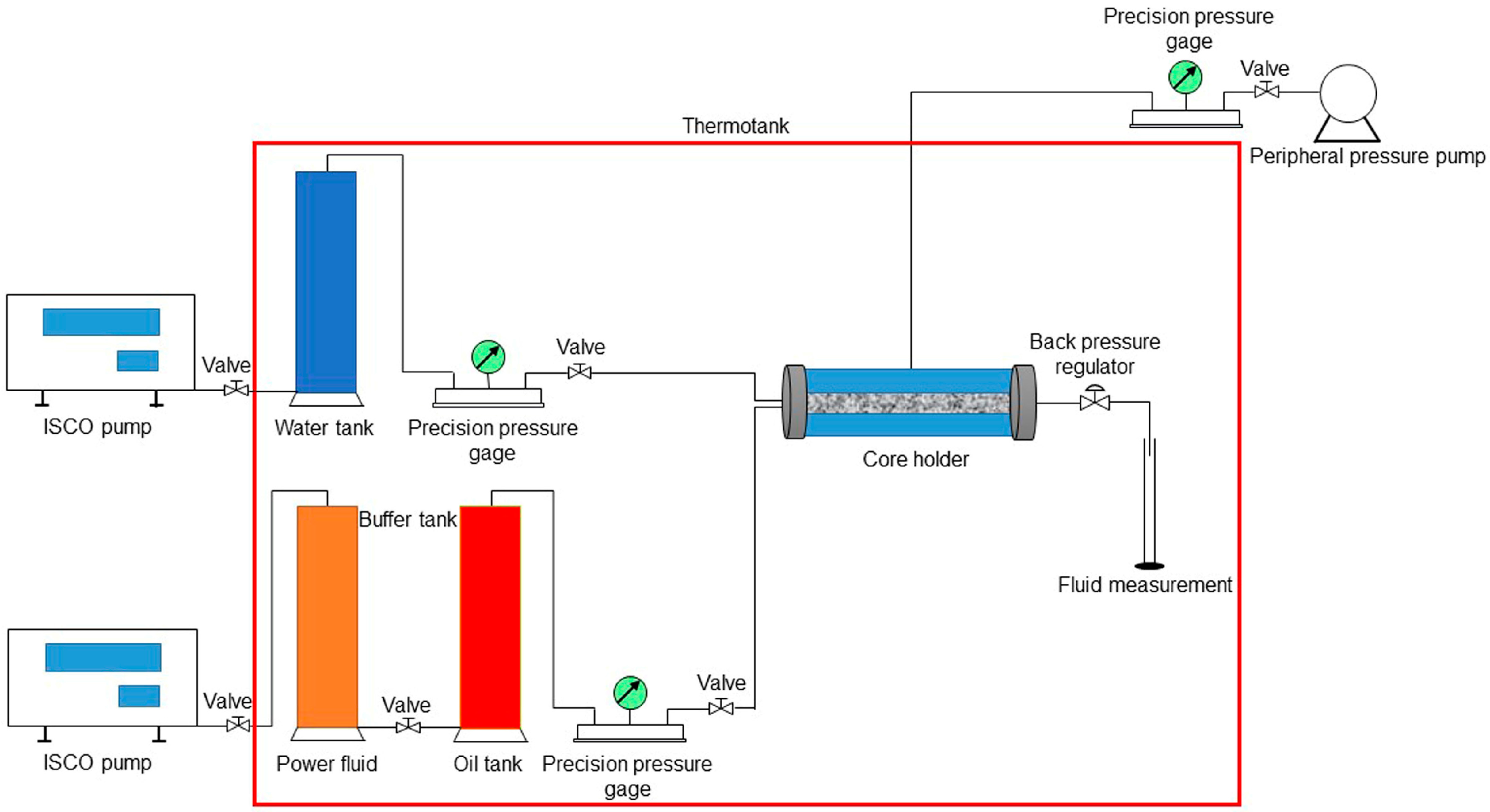
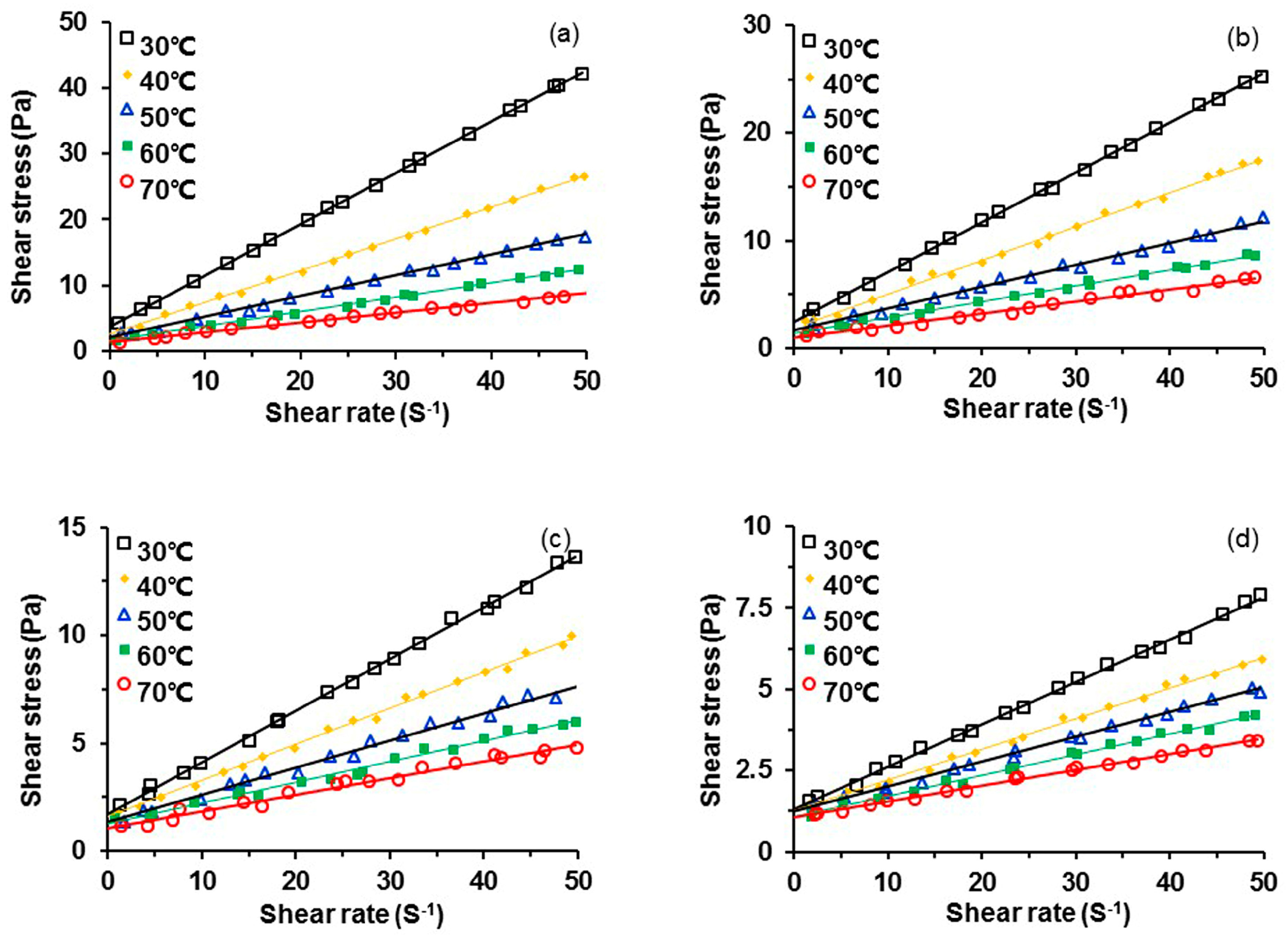



| Parameters | Heavy Oil Samples | ||||||
|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | ||
| Composition, mol.% | C3 | 0.12 | 0.09 | 0.03 | 0.01 | 0.00 | 0.00 |
| i-C4 | 0.21 | 0.15 | 0.06 | 0.04 | 0.00 | 0.00 | |
| n-C4 | 0.50 | 0.30 | 0.14 | 0.09 | 0.00 | 0.00 | |
| i-C5 | 0.82 | 0.54 | 0.32 | 0.23 | 0.00 | 0.00 | |
| n-C5 | 0.71 | 0.43 | 0.25 | 0.16 | 0.00 | 0.00 | |
| C6 | 0.50 | 0.33 | 0.24 | 0.16 | 0.00 | 0.00 | |
| C7 | 0.88 | 0.77 | 0.74 | 0.67 | 0.00 | 0.00 | |
| C8 | 3.34 | 2.98 | 2.81 | 2.63 | 0.24 | 0.34 | |
| C9 | 5.90 | 5.82 | 5.88 | 5.83 | 1.87 | 2.11 | |
| C10 | 17.65 | 18.42 | 18.88 | 19.07 | 13.12 | 13.97 | |
| C11 | 25.52 | 26.66 | 26.76 | 27.40 | 27.46 | 28.53 | |
| C12+ | 43.85 | 43.51 | 43.88 | 43.72 | 57.31 | 55.05 | |
| Asphaltene content, wt. % | 3.61 | 3.48 | 3.12 | 2.82 | 3.55 | 3.04 | |
| Density (30 °C), g/cm3 | 0.96 | 0.93 | 0.90 | 0.86 | 0.95 | 0.88 | |
| Viscosity (30 °C), mPa∙s | 783 | 461 | 242 | 129.78 | 586.8 | 218.97 | |
| Core Number | Length, cm | Dimension, cm | Porosity, % | Permeability, mD | Marks |
|---|---|---|---|---|---|
| #1 | 25.21 | 2.53 | 21.09 | 363 | Used to study the impact of flow rate on threshold pressure gradient (TPG) measurement. |
| #2 | 25.16 | 2.52 | 21.03 | 359 | |
| #3 | 25.18 | 2.49 | 21.07 | 360 | |
| #4 | 25.16 | 2.52 | 22.06 | 502 | |
| #5 | 25.05 | 2.50 | 23.58 | 946 | |
| #6 | 25.01 | 2.51 | 20.84 | 324 | Used to study the relationship between TPG and mobility. |
| #7 | 25.24 | 2.48 | 24.83 | 1465 | |
| #8 | 24.81 | 2.48 | 27.16 | 2765 | |
| #9 | 25.30 | 2.50 | 21.57 | 426 | |
| #10 | 25.00 | 2.53 | 26.68 | 2465 | |
| #11 | 24.92 | 2.51 | 28.56 | 3621 | |
| #12 | 24.62 | 2.48 | 21.04 | 361 | |
| #13 | 25.29 | 2.52 | 27.37 | 2894 | |
| #14 | 24.81 | 2.49 | 28.61 | 3710 | |
| #15 | 24.80 | 2.52 | 21.16 | 382 | |
| #16 | 25.32 | 2.48 | 27.06 | 2695 | |
| #17 | 24.86 | 2.53 | 28.51 | 3580 | |
| #18 | 25.07 | 2.49 | 19.37 | 92 | Used to determine the critical viscosity for the existence of TPG at a given permeability. |
| #19 | 24.79 | 2.51 | 20.30 | 238 | |
| #20 | 25.38 | 2.50 | 21.10 | 367 | |
| #21 | 24.67 | 2.48 | 22.92 | 647 | |
| #22 | 25.22 | 2.51 | 23.63 | 976 | |
| #23 | 25.09 | 2.49 | 24.85 | 1460 | |
| #24 | 25.26 | 2.50 | 26.41 | 2289 | |
| #25 | 24.96 | 2.51 | 27.52 | 3042 | |
| #26 | 24.75 | 2.48 | 28.49 | 3525 | |
| #27 | 25.19 | 2.49 | 21.09 | 362 | Used to study the flow characteristics of heavy oil. |
| #28 | 25.18 | 2.47 | 21.02 | 358 | |
| #29 | 25.21 | 2.52 | 21.05 | 360 | |
| #30 | 25.04 | 2.52 | 24.76 | 1452 | |
| #31 | 25.00 | 2.51 | 26.37 | 2278 | |
| #32 | 25.19 | 2.50 | 21.05 | 362 | |
| #33 | 25.17 | 2.48 | 21.03 | 358 | |
| #34 | 25.22 | 2.52 | 21.09 | 365 | |
| #35 | 25.07 | 2.51 | 24.62 | 1448 | |
| #36 | 24.97 | 2.50 | 26.28 | 2270 |
| Parameters | Value | |
|---|---|---|
| Composition, mg/L | Na+ and K+ | 3091.960 |
| Ca2+ | 276.17 | |
| Mg2+ | 156.68 | |
| CO32- | 11 | |
| HCO3− | 311.48 | |
| SO42− | 85.29 | |
| Cl- | 5436.34 | |
| TDS | 9374.12 | |
| Density (30 °C), g/cm3 | 1.046 | |
| Flow Rate, mL/min | Threshold Pressure Gradient, MPa/m | ||||
|---|---|---|---|---|---|
| Core Sample: #1 | Core Sample: #2 | Core Sample: #3 | Core Sample: #4 | Core Sample: #5 | |
| Oil Sample: #1 | Oil Sample: #2 | Oil Sample: #3 | Oil Sample: #4 | Oil Sample: #5 | |
| 0.001 | 0.00127 | 0.00110 | 0.00087 | 0.00114 | 0.00092 |
| 0.002 | 0.00127 | 0.00110 | 0.00087 | 0.00114 | 0.00092 |
| 0.003 | 0.00127 | 0.00110 | 0.00087 | 0.00114 | 0.00092 |
| 0.004 | 0.00133 | 0.00124 | 0.00092 | 0.00126 | 0.00099 |
| 0.005 | 0.00142 | 0.00140 | 0.00102 | 0.00134 | 0.00109 |
| 0.006 | 0.00164 | 0.00146 | 0.00103 | 0.00150 | 0.00114 |
| 0.008 | 0.00171 | 0.00158 | 0.00108 | 0.00162 | 0.00121 |
| 0.010 | 0.00186 | 0.00168 | 0.00114 | 0.00174 | 0.00128 |
| Core | Permeability, mD | Oil Sample | Viscosity, mPa∙s | TPG, MPa/m |
|---|---|---|---|---|
| #6 | 324 | #1 | 783 | 0.00135 |
| #7 | 1465 | #1 | 783 | 0.00083 |
| #8 | 2765 | #1 | 783 | 0.00070 |
| #9 | 426 | #2 | 461 | 0.00104 |
| #10 | 2465 | #2 | 461 | 0.00049 |
| #11 | 3621 | #2 | 461 | 0.00046 |
| #12 | 361 | #3 | 242 | 0.00083 |
| #13 | 2894 | #3 | 242 | 0.00045 |
| #14 | 3710 | #3 | 242 | 0.00042 |
| #15 | 382 | #4 | 130 | 0.00075 |
| #16 | 2695 | #4 | 130 | 0.00034 |
| #17 | 3580 | #4 | 130 | 0.00026 |
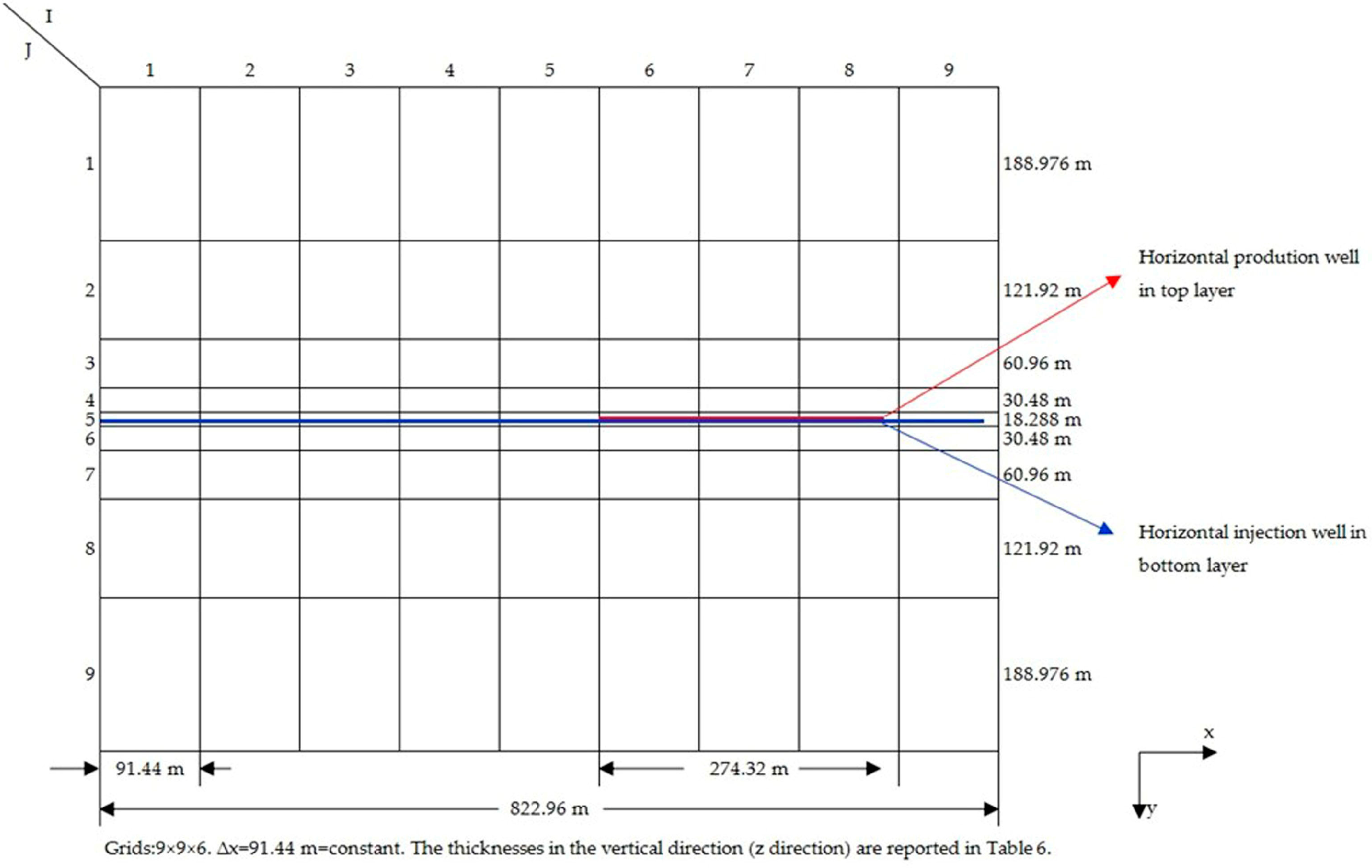
| Layer | Thickness ∆z, m | Depth to Center of Layer, m | Horizontal Permeability, mD | Vertical Permeability, mD | Porosity, Fraction | Initial Pressure, MPa | Initial oil Saturation, Fraction | Initial Water Saturation, Fraction |
|---|---|---|---|---|---|---|---|---|
| 1 (top) | 6.096 | 1097.280 | 300 | 30 | 0.2 | 24.822 | 0.711 | 0.289 |
| 2 | 6.096 | 1103.376 | 300 | 30 | 0.2 | 24.877 | 0.652 | 0.348 |
| 3 | 6.096 | 1109.472 | 300 | 30 | 0.2 | 24.932 | 0.527 | 0.473 |
| 4 | 6.096 | 1115.568 | 300 | 30 | 0.2 | 24.981 | 0.351 | 0.649 |
| 5 | 9.144 | 1123.188 | 300 | 30 | 0.2 | 25.050 | 0.131 | 0.869 |
| 6 (bottom) | 15.240 | 1135.380 | 300 | 30 | 0.2 | 25.167 | 0.000 | 1.000 |
| Parameters | Value |
|---|---|
| Stock tank oil density, g/cm3 | 0.721 |
| Initial oil viscosity, mPa∙s | 0.95 |
| Oil compressibility, MPa−1 | 1.45 × 10−3 |
| Oil formation volume factor | 1.11 |
| Initial water density, g/cm3 | 0.995 |
| Initial water viscosity, mPa∙s | 0.96 |
| Water compressibility, MPa−1 | 4.35 × 10−4 |
| Water formation volume factor | 1.014 |
| Rock compressibility, MPa−1 | 5.80 × 10−4 |
| Bottom hole pressure of injection well, MPa | 25.512 |
| Minimum bottom hole pressure of production well, MPa | 10.343 |
| Liquid rate of production well, m3/d | 477 |
| 0.2200 | 0.0000 | 1.0000 | 0.0434 |
| 0.3000 | 0.0700 | 0.4000 | 0.0248 |
| 0.4000 | 0.1500 | 0.1250 | 0.0186 |
| 0.5000 | 0.2400 | 0.0649 | 0.0155 |
| 0.6000 | 0.3300 | 0.0048 | 0.0124 |
| 0.8000 | 0.6500 | 0.0000 | 0.0062 |
| 0.9000 | 0.8300 | 0.0000 | 0.0031 |
| 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| Parameters of the Heavy Oil Displacement Experiment | Value | Input Parameters of the Designed Simulator | Value |
|---|---|---|---|
| Temperature, °C | 65 | Number of blocks along x | 59 |
| Oil sample number | #1 | Number of blocks along y | 5 |
| Core dimensions, cm | 29.5 × 4.5 × 4.5 | Number of blocks along z | 5 |
| Porosity, fraction | 0.246 | Length of the block along x, cm | 0.5 |
| Permeability, mD | 1200 | Length of the block along y, cm | 0.9 |
| Rock compressibility, MPa−1 | 2.6 × 10−4 | Length of the block along z, cm | 0.9 |
| Stock tank oil density, g/cm3 | 0.956 | Initial porosity, fraction | 0.246 |
| Oil viscosity, mPa∙s | 180 | Initial permeability in x direction, mD | 1200 |
| Oil compressibility, MPa−1 | 1.0 × 10−3 | Initial permeability in y direction, mD | 1200 |
| Oil formation volume factor | 1.066 | Initial permeability in z direction, mD | 120 |
| Water density, g/cm3 | 1 | Rock compressibility, MPa−1 | 2.6 × 10−4 |
| Water viscosity, mPa∙s | 0.52 | Stock tank oil density, g/cm3 | 0.956 |
| Water compressibility, MPa−1 | 4.6 × 10−4 | Initial oil viscosity, mPa∙s | 180 |
| Water formation volume factor | 1.012 | Oil compressibility, MPa−1 | 1.0 × 10−3 |
| Initial pressure, MPa | 2 | Oil formation volume factor | 1.066 |
| Water saturation, fraction | 0.272 | Initial water density, g/cm3 | 1 |
| Oil saturation, fraction | 0.728 | Water viscosity, mPa∙s | 0.52 |
| Bottom hole pressure of production well, MPa | 2 | Water compressibility, MPa−1 | 4.6 × 10−4 |
| Water rate of injection well, cm3/min | 0.5 | Water formation volume factor | 1.012 |
| TPG, MPa/m | 0.0005 | Initial pressure, MPa | 2 |
| initial water saturation, fraction | 0.272 | ||
| initial oil saturation, fraction | 0.728 | ||
| Bottom hole pressure of production well, MPa | 2 | ||
| Water rate of injection well, cm3 min−1 | 0.5 | ||
| TPG, MPa/m | 0.0005 |
| , MPa | |||
|---|---|---|---|
| 0.2720 | 0.0000 | 1.0000 | 0.1674 |
| 0.3014 | 0.0024 | 0.8531 | 0.1473 |
| 0.3308 | 0.0039 | 0.7156 | 0.1268 |
| 0.3602 | 0.0051 | 0.5877 | 0.1088 |
| 0.3896 | 0.0071 | 0.4692 | 0.0962 |
| 0.4190 | 0.0098 | 0.3578 | 0.0830 |
| 0.4484 | 0.0142 | 0.2583 | 0.0727 |
| 0.4778 | 0.0257 | 0.1659 | 0.0629 |
| 0.5072 | 0.0488 | 0.0723 | 0.0549 |
| 0.5366 | 0.0829 | 0.0213 | 0.0477 |
| 0.5660 | 0.1209 | 0.0118 | 0.0420 |
| 0.5954 | 0.1588 | 0.0088 | 0.0362 |
| 0.6248 | 0.1943 | 0.0071 | 0.0307 |
| 0.6542 | 0.2299 | 0.0061 | 0.0261 |
| 0.6836 | 0.2654 | 0.0052 | 0.0186 |
| 0.7130 | 0.3033 | 0.0038 | 0.0113 |
| 0.7424 | 0.3452 | 0.0012 | 0.0043 |
| 0.7718 | 0.3886 | 0.0000 | 0.0000 |
| Parameters | Simulation Number | ||||
|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | |
| Number of blocks along x | 15 | 31 | 59 | 71 | 81 |
| Number of blocks along y | 3 | 3 | 5 | 7 | 9 |
| Number of blocks along z | 3 | 3 | 5 | 7 | 9 |
| Length of the block along x, cm | 1.9667 | 0.9516 | 0.5 | 0.4155 | 0.3642 |
| Length of the block along y, cm | 1.5 | 1.5 | 0.9 | 0.6429 | 0.5 |
| Length of the block along z, cm | 1.5 | 1.5 | 0.9 | 0.6429 | 0.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; Li, Y.; Yu, G.; Wang, W.; Zhang, Z.; Zhang, M.; Ke, W.; Kong, D.; Wu, K.; Chen, Z. Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies. Energies 2017, 10, 1698. https://doi.org/10.3390/en10111698
Xin X, Li Y, Yu G, Wang W, Zhang Z, Zhang M, Ke W, Kong D, Wu K, Chen Z. Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies. Energies. 2017; 10(11):1698. https://doi.org/10.3390/en10111698
Chicago/Turabian StyleXin, Xiankang, Yiqiang Li, Gaoming Yu, Weiying Wang, Zhongzhi Zhang, Maolin Zhang, Wenli Ke, Debin Kong, Keliu Wu, and Zhangxin Chen. 2017. "Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies" Energies 10, no. 11: 1698. https://doi.org/10.3390/en10111698
APA StyleXin, X., Li, Y., Yu, G., Wang, W., Zhang, Z., Zhang, M., Ke, W., Kong, D., Wu, K., & Chen, Z. (2017). Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies. Energies, 10(11), 1698. https://doi.org/10.3390/en10111698







