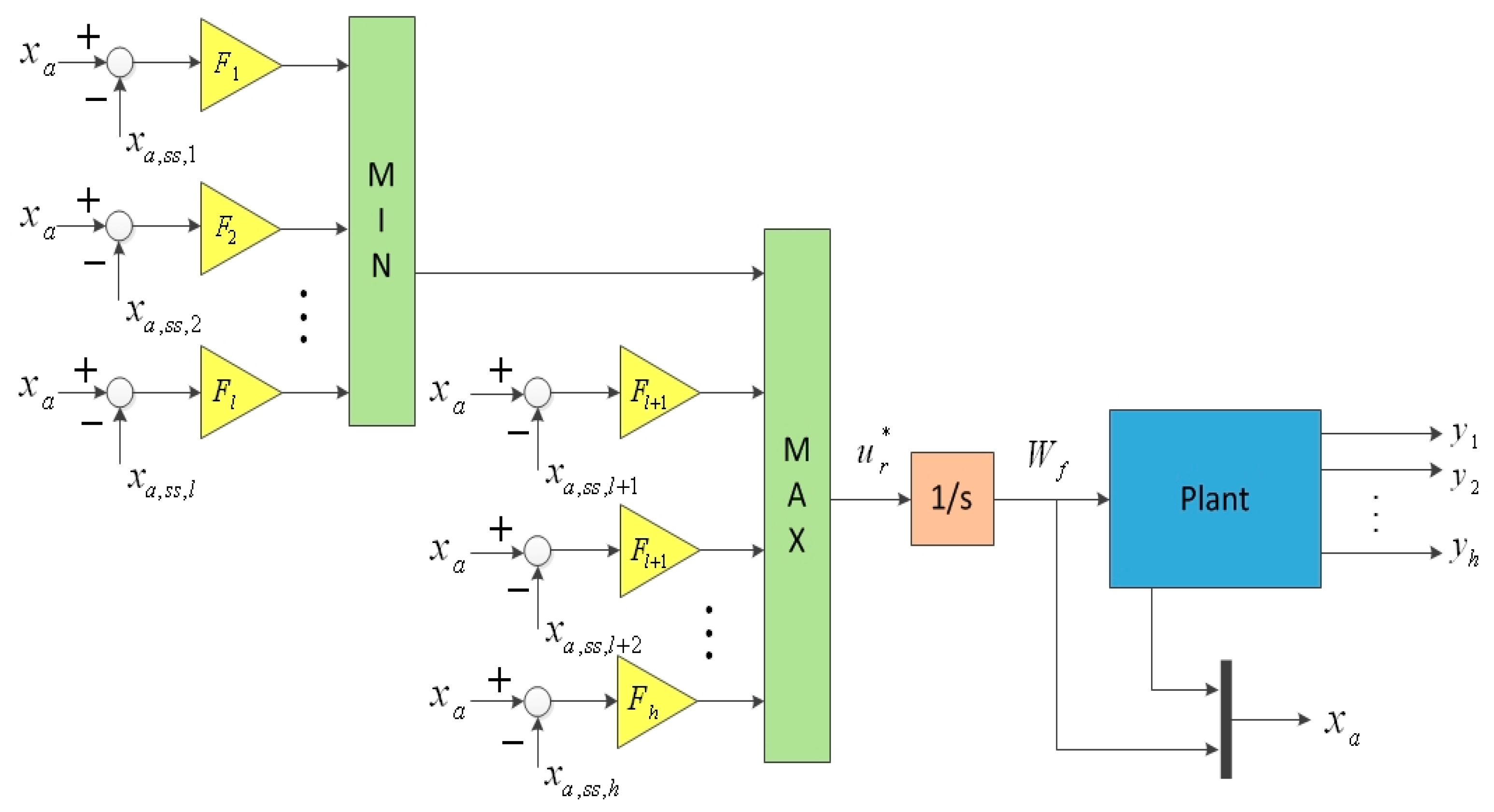
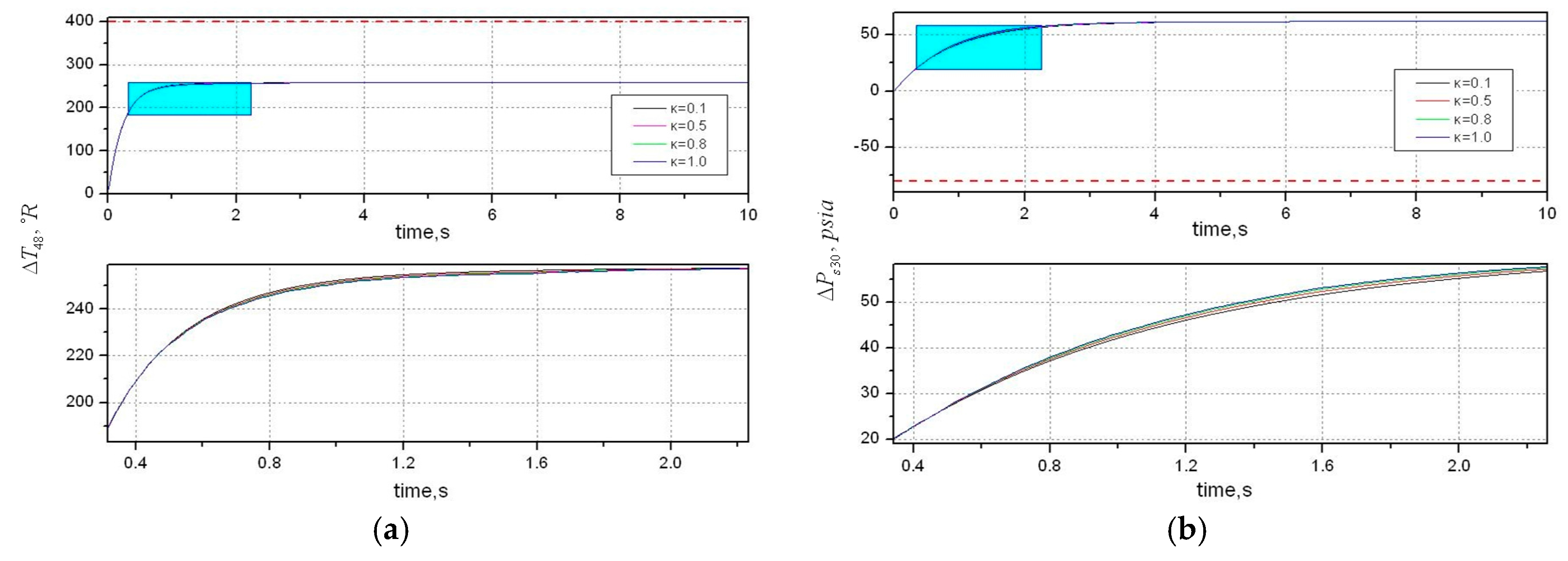
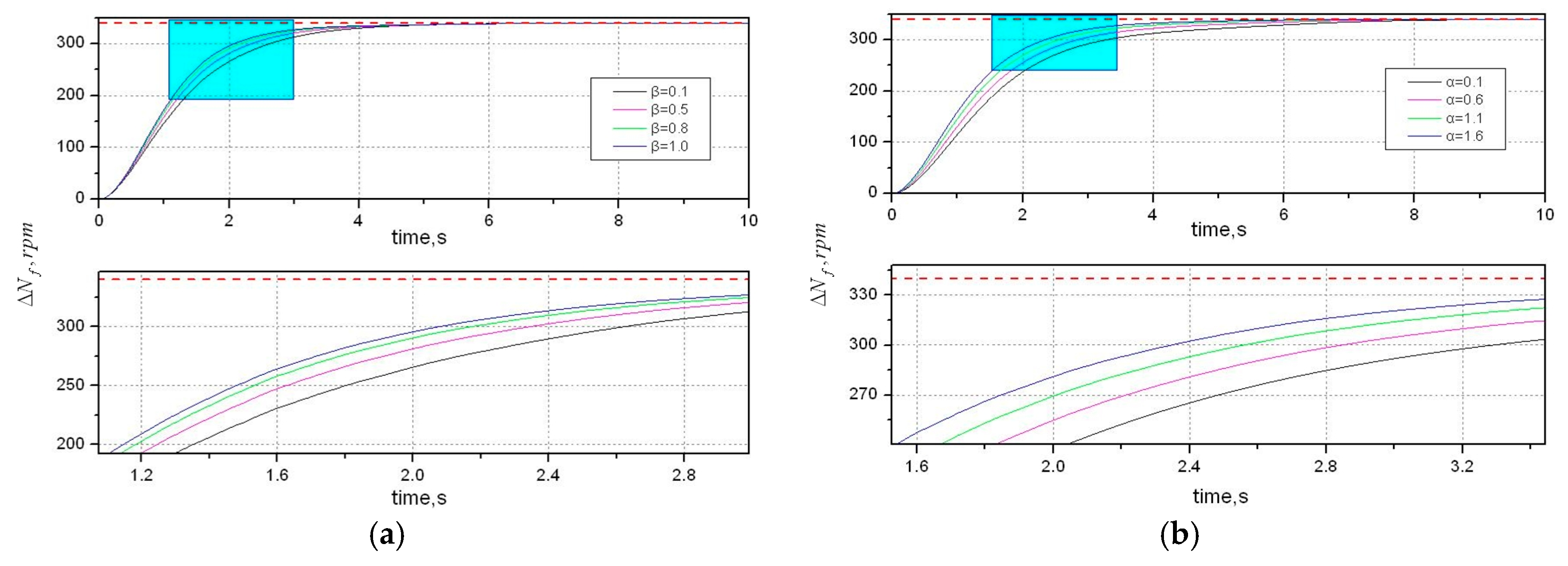
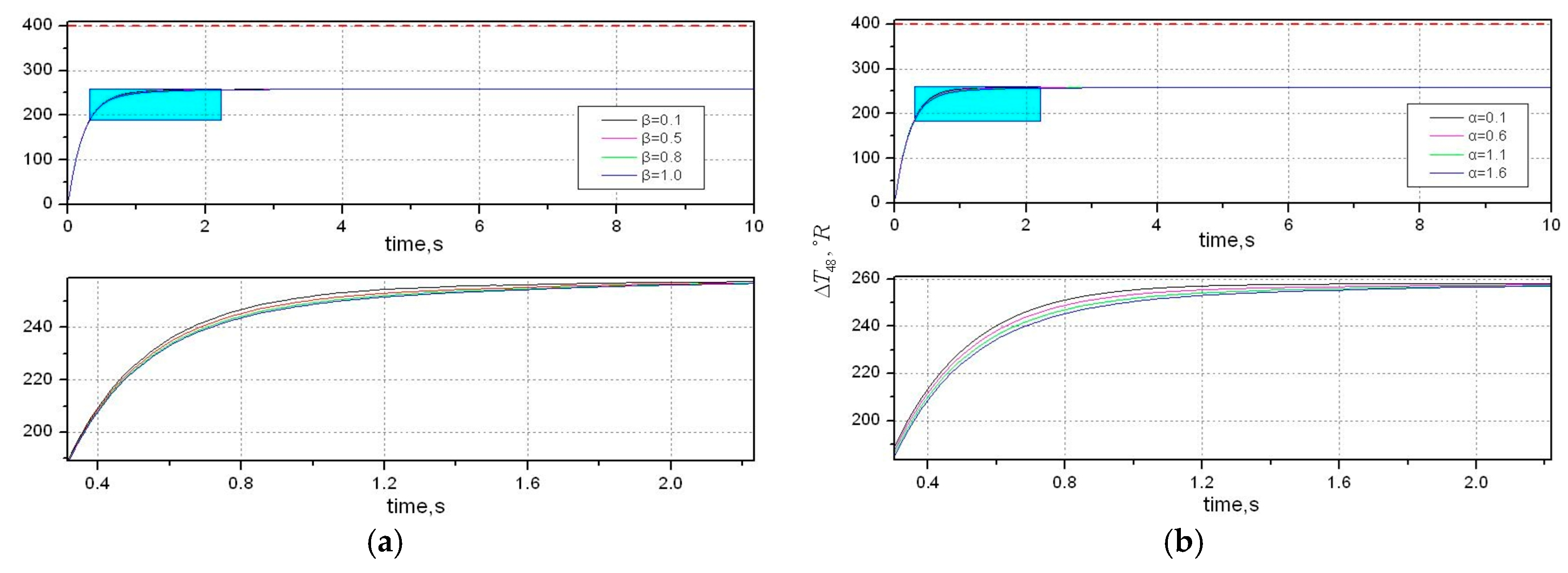
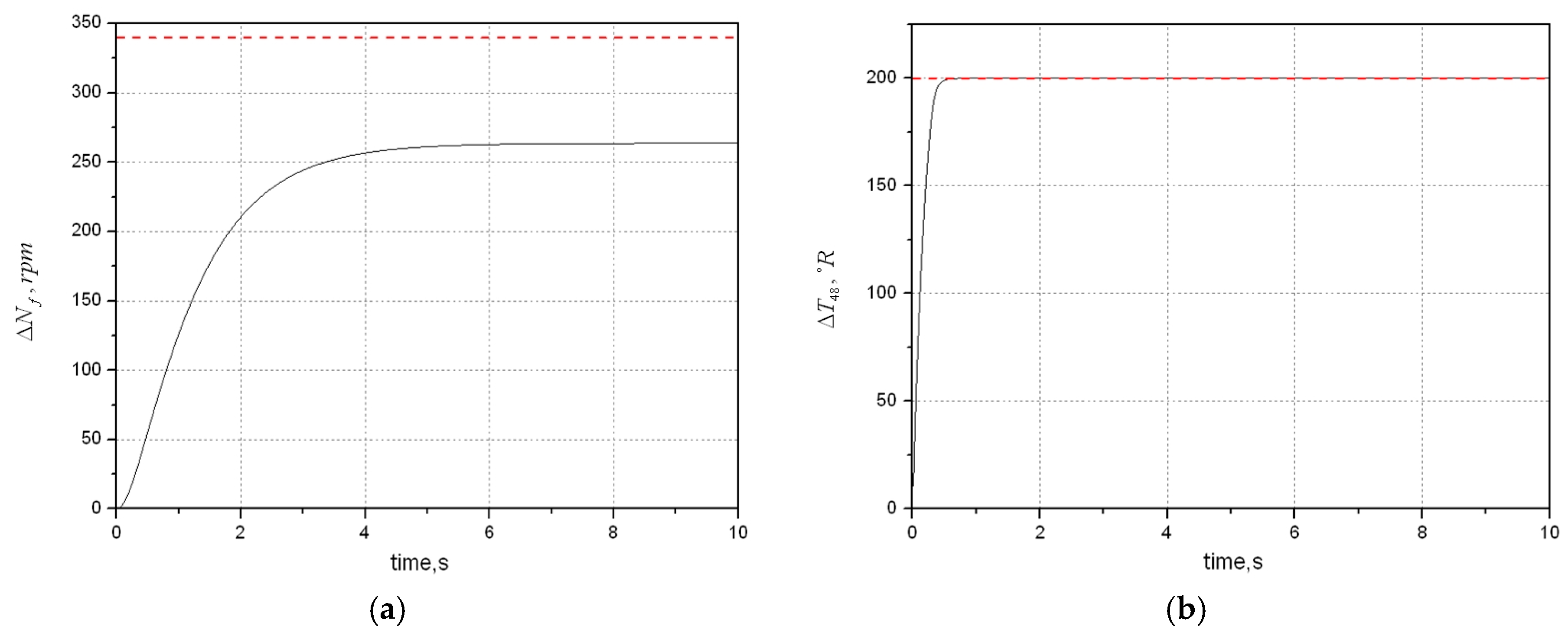
In this section, we discuss an augmented monotonic tracking controller applied for a non-square system with prescribed output constraints. To enhance robustness, a linear time-invariant system with input integration is considered.
2.1. Augmented Monotonic Tracking Controllers
Consider the linear time-invariant system:
where, for all
,
is the state,
is the control input,
is the output, and
,
,
and
are appropriate dimensional constant matrices. Assume that
has full column rank and
has full row rank. In this paper, the aircraft engine state variable model (SVM) in Equation (2) is extracted by using the Commercial Modular Aero-Propulsion System Simulation (CMAPSS). CMAPSS is a Simulink port and a database with a user-friendly graphical user interface (GUI) allowing the user to perform model extraction, elementary control design, and simulations without much effort [
13]. The linearization method used in CMAPSS for establishing engine SVM is a bias derivative method; for details, readers may refer to [
14].
As aircraft engines are often considered to be a single-input and multi-outputs plant, system
may be non-square. Then we decompose system
into two components: square system
and system
, which are governed by:
where
is a square system with main outputs
to be tracked and
is a system with the constrained auxiliary outputs
. The output vector
and appropriate dimensional constant matrices
and
of system
can be represented as:
where
stands for the
output of system
,
and
denote the
row vector of the output matrix
and
, respectively.
As we know, the monotonic tracking controller will result in zero steady-state error to a step reference for linear system with no uncertainty [
8], but in most real cases there are always some uncertainties in the plant parameters which cause the tracking error to be nonzero, and reduce the tracking accuracy of state feedback law for aircraft engines. One practicable method is to use integral control to obtain robust tracking. Then the ability to track references and reject uncertainties of the control system can be enhanced. To achieve integral control, the following augmented plant can be described as:
where
,
,
is the new control input which equals to
and the augmented state vector and system matrices are defined as:
The number of system outputs is:
The order of the system
is:
First, following assumptions are necessary to be adopted to design a monotonic tracking controller for system .
Assumption 1. System is right invertible and stabilizable, and has no invariant zeros at the origin.
Assumption 2. System is square.
Assumption 3. System has at least distinct invariant zeros in .
Next, the relationship between the invariant zeros of system and system is discussed.
Theorem 1. The invariant zeros of system is same as that of augmented system .
Proof. Let
denote the set of distinct invariant zeros of system
. Then, the rank of the system matrix pencil drops from its normal value for
. The system matrix pencil of system
is given by:
where
and
are the matrices formed by
,
and
, which can be expressed as:
where
,
,
and
are appropriate dimensional identity matrices. Properties of matrix elementary transformation implies
. Hence, the invariant zeros of system
and
are the same.□
For definiteness and without loss of generality, Assumption 3 is replaced by the following Assumption 4:
Assumption 4. System has at least distinct invariant zeros in .
The following method is developed to design a tracking controller such that
is stable for a step reference signal with state feedback gain matrix
. Let
and
denote the control input and the state at steady state, respectively. Then:
for any step reference
, where
and
is obtained by solving the following equation:
Let the tracking error vector and suppositional tracking error vector be defined as
and
, respectively, where suppositional tracking reference is defined as
. Applying the state feedback control law:
to Equation (5) and employing the change of variable
, we obtain the closed-loop autonomous system:
Since is stable, converges to , converges to and converges to as goes to infinity.
Definition 1. If the main output and the auxiliary output obtained from applying in Equation (13) are all monotonic, then we define this property as generalized monotonicity.
The following is the specific design method to shape the responses of the main output and auxiliary outputs. The key idea is the choice of a suitable closed loop eigenstructure, which is composed of eigenvalues
and eigenvectors
such that generalized monotonicity can be achieved. Firstly, decompose the set
into two parts. One part is the set of
distinct invariant zeros composed of
for
. Another part is the set composed of
for
, which may be freely chosen to be any distinct real stable modes. To obtain
, let
be such that:
where
is the canonical basis of
. Provided
is linearly independent, then sets
and
are obtained by solving the Rosenbrook matrix equation:
for
. The sets
,
and
all meet the requirements of Proposition 1 in [
13], then a gain matrix
can be obtained by use of the procedure given in that paper such that
has the desired eigenstructure. It is worth noting that when
is real,
, where
and
. Since
, the vectors in
satisfy:
Notation 1. For each , let:- (1)
and denote the eigenvectors in associated with canonical basis vector in Equation (15), and let and be the eigenvalues corresponding to and , ordered such that in each case;
- (2)
Let be the coordinate vector of in terms of . Then define:
Theorem 2. Assume that Assumptions 1, 2, and 4 are all satisfied. Let be a set of desired closed-loop poles, and assume that the set of associated eigenvectors obtained from solving Equation (16) with in Equation (15) is linearly independent. Let and be any step reference and any initial condition, respectively. Then, the output obtained from applying in Equation (13) to tracks monotonically if and only if for all .
Proof. The tracking error vector can be expressed as:
(Sufficiency). If
, then the following two possible situations should take into consideration:
If condition 1 holds,
increases monotonically with increasing
and takes its minimum value at
. The sign of
is determined by the sign of
as
is a positive constant. Then, we have
, which yields
for all
. It means that the feature of monotonicity of
is kept. Thus, the
component of the output
tracks
monotonically. The proof of condition 2 and condition 1 are similar. (Necessity). If
, we will concern about the following four possible situations:
If condition 1 holds, we have . In order to keep the sign of unchanged, only need to let the condition hold as increases monotonically with the increasing . The proof of condition 2 is similar to condition 1. If condition 3 holds, then . Thus, in either case does not change sign. The proof of condition 4 is similar to condition 3.
It can be known that the output converges to monotonically if and only if for all .
After obtaining the condition of how to achieve the monotonicity of
, then we think about how to keep the output
monotonic in order to obtain generalized monotonicity. The suppositional tracking error vector
is defined as:
where
is the
row vector of
,
for
,
and
for
. Then,
for
and
for
can be given by Equations (26) and (27), respectively. Then:
In Equations (26) and (27),
if
is odd and
if
is even. Let
denote the
component of the suppositional tracking error
for
. Then:
□
For the sake of ensuring the monotonicity of
for
, we should check whether
changes sign when the poles have been placed at the desired closed-loop poles positions. One approach is offered in [
15]. However, the results are conservative because this only provides a sufficient condition. The reason why no sufficient and necessary condition to be offered may be that it is difficult to find an analytical solution for high order systems. However, for low order systems, it is easier to obtain a condition with less conservativeness, even a sufficient and necessary condition. Therefore it is worth first thinking about the actual order of the aircraft engine system, and thereafter, to decide which method to employ. In fact, the dynamics of a turbine engine can be approximated by a set of low-order, linear model around operating points [
16]. There are three basic types of dynamic effects in gas turbine engines, namely, shaft dynamics caused by the inertial effect, pressure dynamics caused by the mass storage effect, and temperature dynamics caused by the energy storage as well as the heat transfer between the gas and the outer casing.
The shaft dynamics play the most important role in affecting gas turbine engines dynamic performance among the three dynamics, followed by temperature dynamics, and pressure dynamics in last. It is mainly because shaft speeds are directly linked with mass flow through the engine and thrust, which is the main output to be manipulated by the propulsion control system. Moreover, temperature dynamics of turbines, especially for high pressure turbine, are also considered in the analysis of dynamic performance. Pressure dynamics with minimal impact on dynamic performances are usually ignored for simplicity.
Shaft dynamics are generally considered in two-spool turbofan engines. Therefore, the number of state variables is 2, which means the model is second order. Now we take shaft dynamics of a two-spool aircraft engine into consideration. Thus, system is third order (the augmented state is combined with the rotor speeds and the fuel flow), and the following theorem provides a necessary and sufficient condition for ensuring the monotonicity of auxiliary outputs.
Theorem 3. Assume that is a third order system. Let be a real constant for all and , and let be sets of real numbers with .
There exists a state feedback control law (12) such that the output of system converges monotonically to the suppositional tracking reference signal if and only if one of the following conditions holds:- (1)
, and ;
- (2)
, and ;
- (3)
, and ;
- (4)
, and .
where and .
Proof. When
, the first order derivative of Equation (28) can be expressed by:
(Sufficiency). If condition 1 holds,
and
are all increases monotonically on
. Let:
In this case,
takes its minimum value
at
. This yields
for any
. The proof of condition 2 is similar to condition 1. For condition 3, calculate the first order derivative of
with respect to time, we have
as follows:
Let , then we have . Due to and , takes its maximum value at . If , then we have for any . The proof of condition 4 is similar to condition 3. The only difference is that takes its minimum value at and for any .
(Necessity).
converging to zero monotonically implies that it is necessary that
does not change sign. As shown in Equation (29), two parts dominate the sign, i.e.,
and
. Thereafter, the remaining consideration is the sign of
since
is always a positive number. Then
,
,
and
enumerate the ways in which this may occur:
For , it is clear that increases monotonically on and for all . Hence, it is known that takes its minimum value at . Then will not change sign if for any . The proofs of and are similar. For , it is easy to see that takes its maximum value at when and . If , then for any . For , it is easy to prove that takes its minimum value at and then if the condition holds.
Let
be the set of the closed-loop eigenvalues to be chosen for achieving generalized monotonicity, where
denotes the compact set that constitutes all the possible sets
. Let
and
denote the states at
and steady state respectively. Applying
and
to
yields the following two outputs:
□
Theorem 4. Assume that Assumptions 1, 2, and 4 are all satisfied and generalized monotonicity is achieved. Let compact set denote the constraints to be satisfied for output limit. The output of system is subjected to the constraint set if and only if: Proof. Assume that the number of output
is 1. Then the constraint set
turns into an interval, which can be represented as:
where
and
are all constants with respect to the limits. Suppose that
and
, and let
equal
for some
.
(Sufficiency). If condition (33) holds, it is known that:
Assume that is a monotonic increasing output, then , and hence . The same goes for a monotonic decreasing output .
(Necessity). If for any , then . Assume that is a monotonic increasing output, then . Then we have and . If is a monotonic decreasing output, the proof is similar. The aforementioned proof concerning single output can be easily generalized to multi outputs. □