Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting
Abstract
:1. Introduction
2. EMD and EEMD Based Signal Filtering
2.1. Empirical Mode Decomposition Based Signal Filtering
2.2. Ensemble Empirical Mode Decomposition Based Signal Filtering
2.3. Partial Auto Correlation Function (PACF)
3. The Processing Method of Waveform
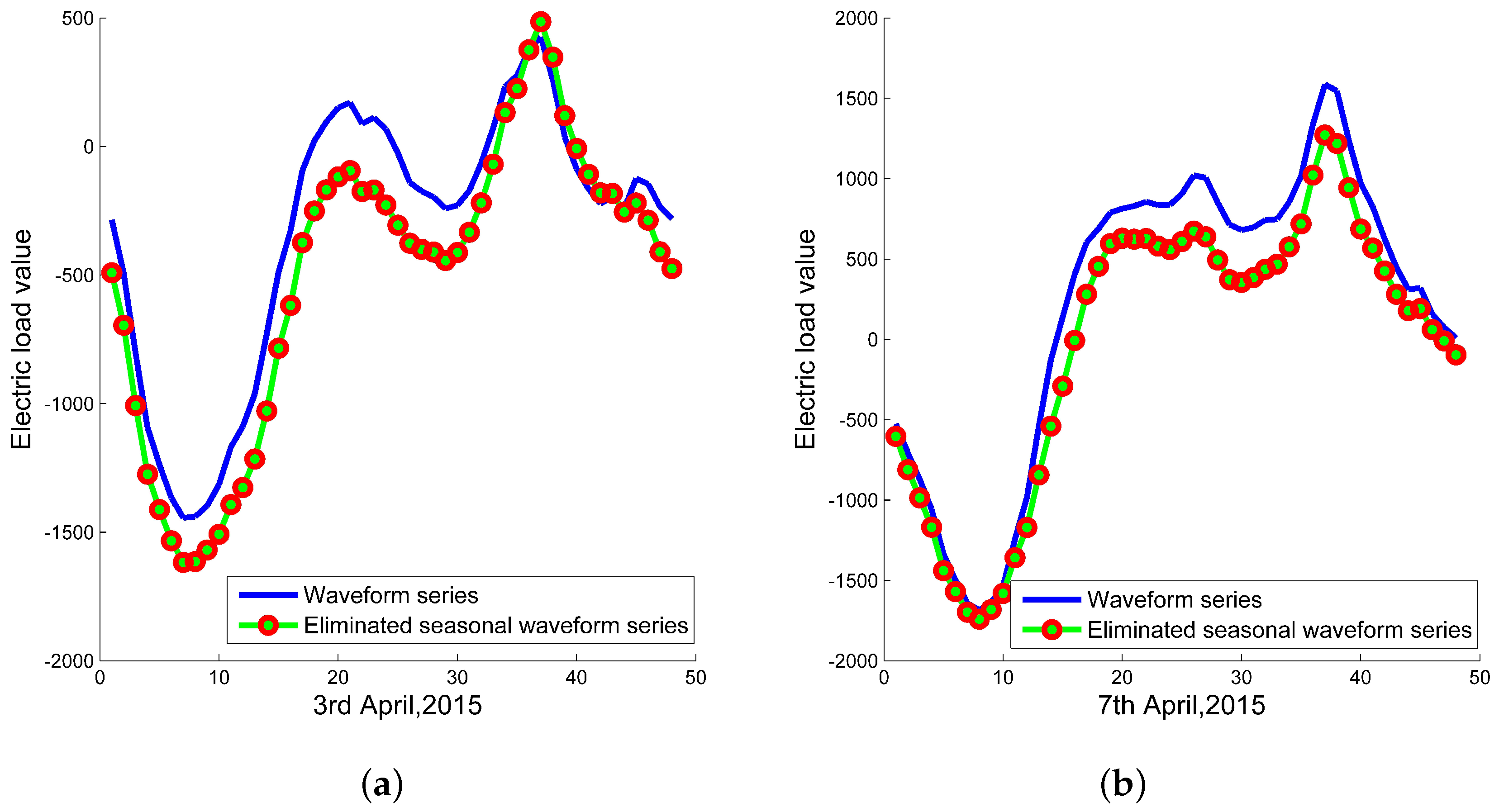
3.1. Seasonal Adjustment
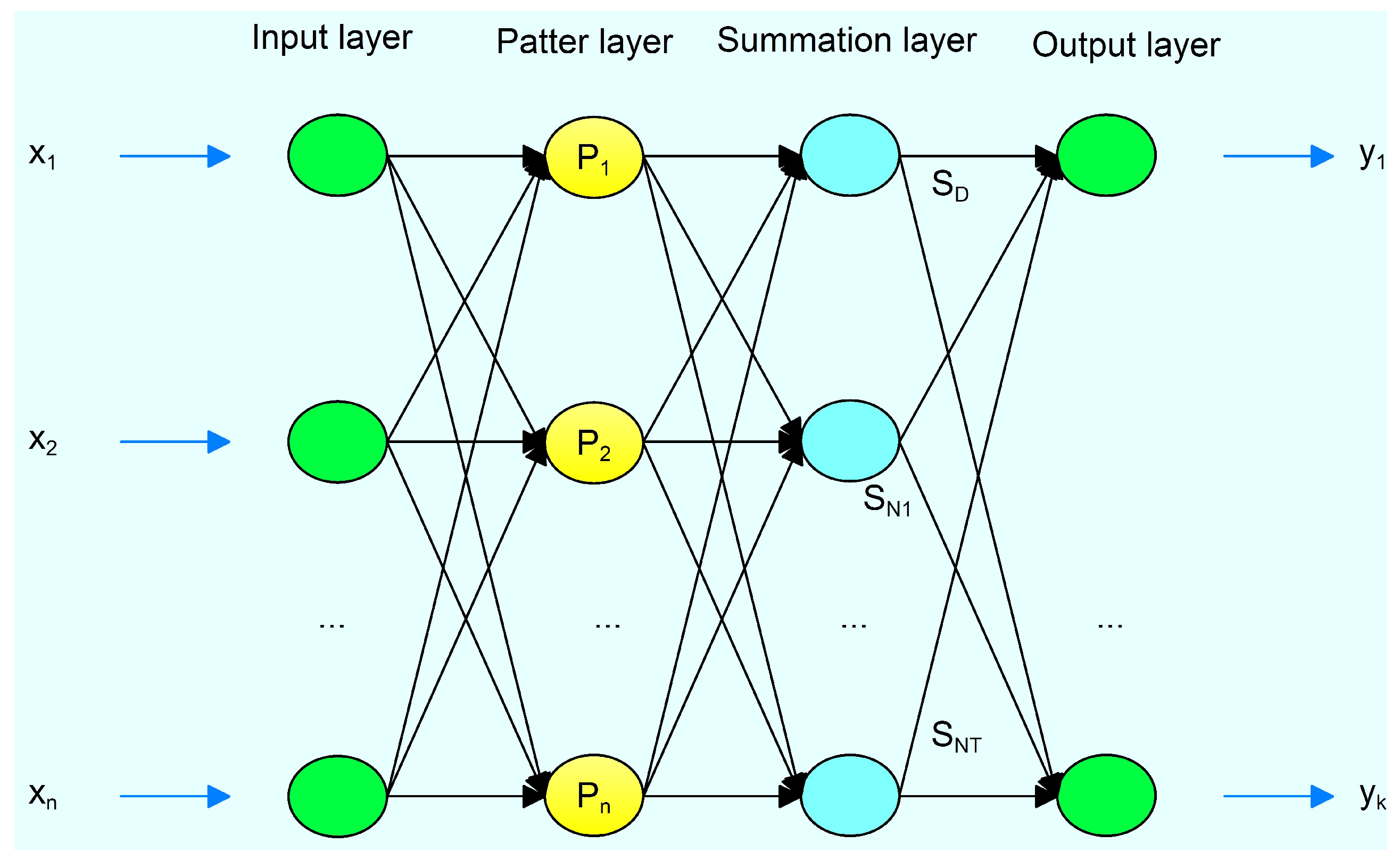
3.2. General Regression Neural Network (GRNN)
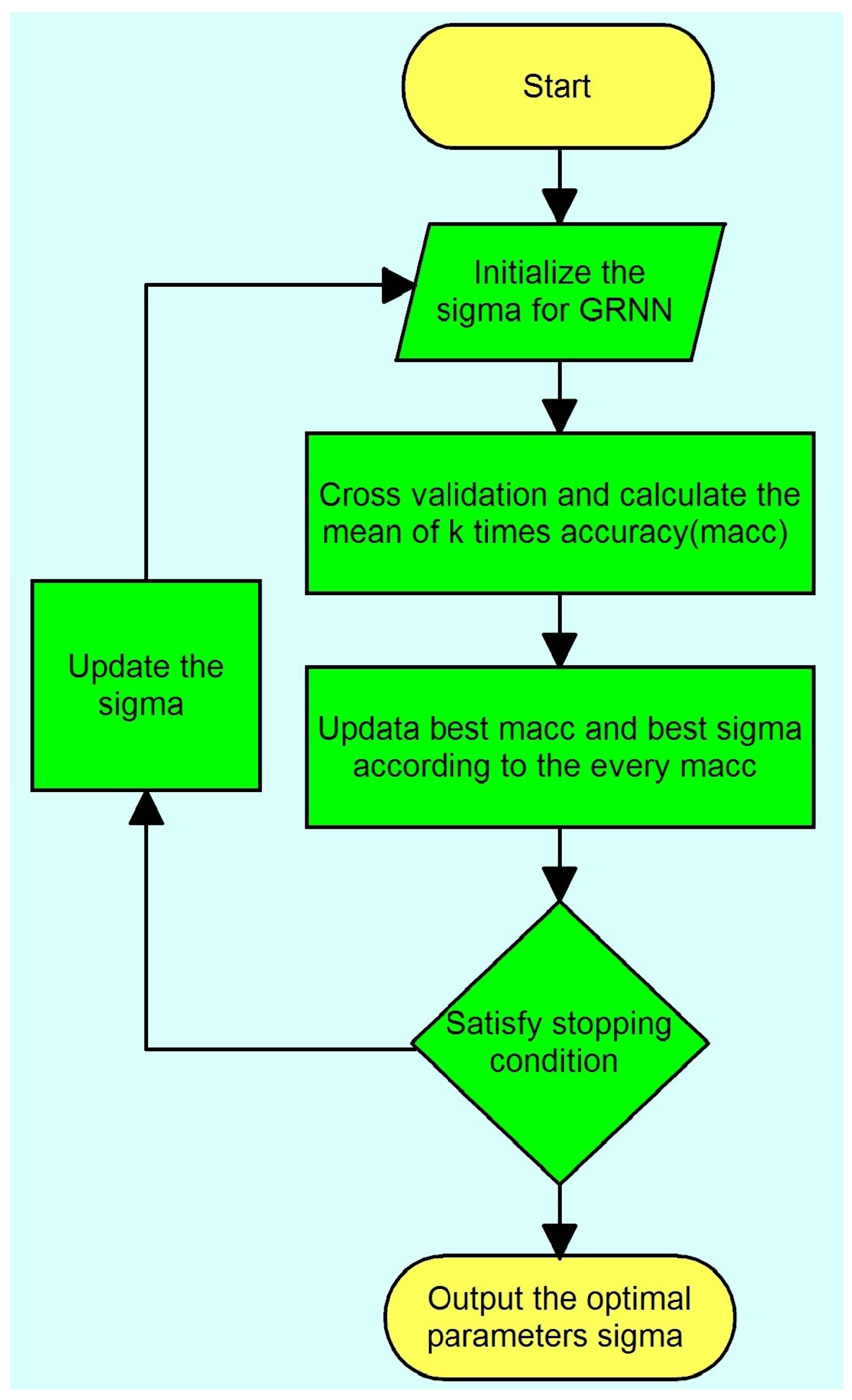
3.3. Cross Validation
3.4. General Regression Neural Network Optimized by CV
4. The Processing Method of Trend Component
4.1. Support Vector Regression Machine
4.2. Support Vector Regression Machine Optimized by Particle Swarm Optimization Algorithm
- Step 1
- Initialization. Randomly generate N particles to make up an original population. The initial position and velocity of each particle are randomly assigned.
- Step 2
- Fitness evaluation. Calculate the fitness value of each particle. The fitness function is calculated in the following equation:where and represent the actual values and prediction values by SVR respectively. Update the local best position and the globe best position .
- Step 3
- Update and generate new particles for the next generation.
- Step 4
- Check whether the termination criteria is satisfied. If not, go back to step 2, otherwise, output the result.
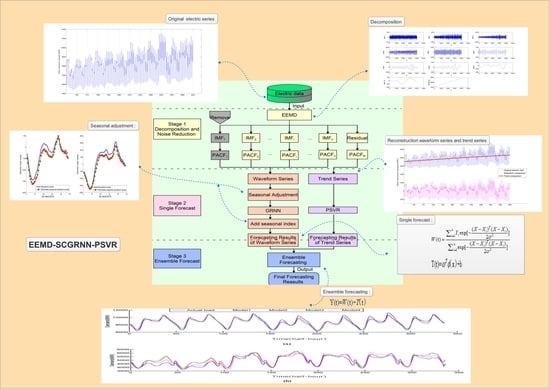
5. The Proposed Method
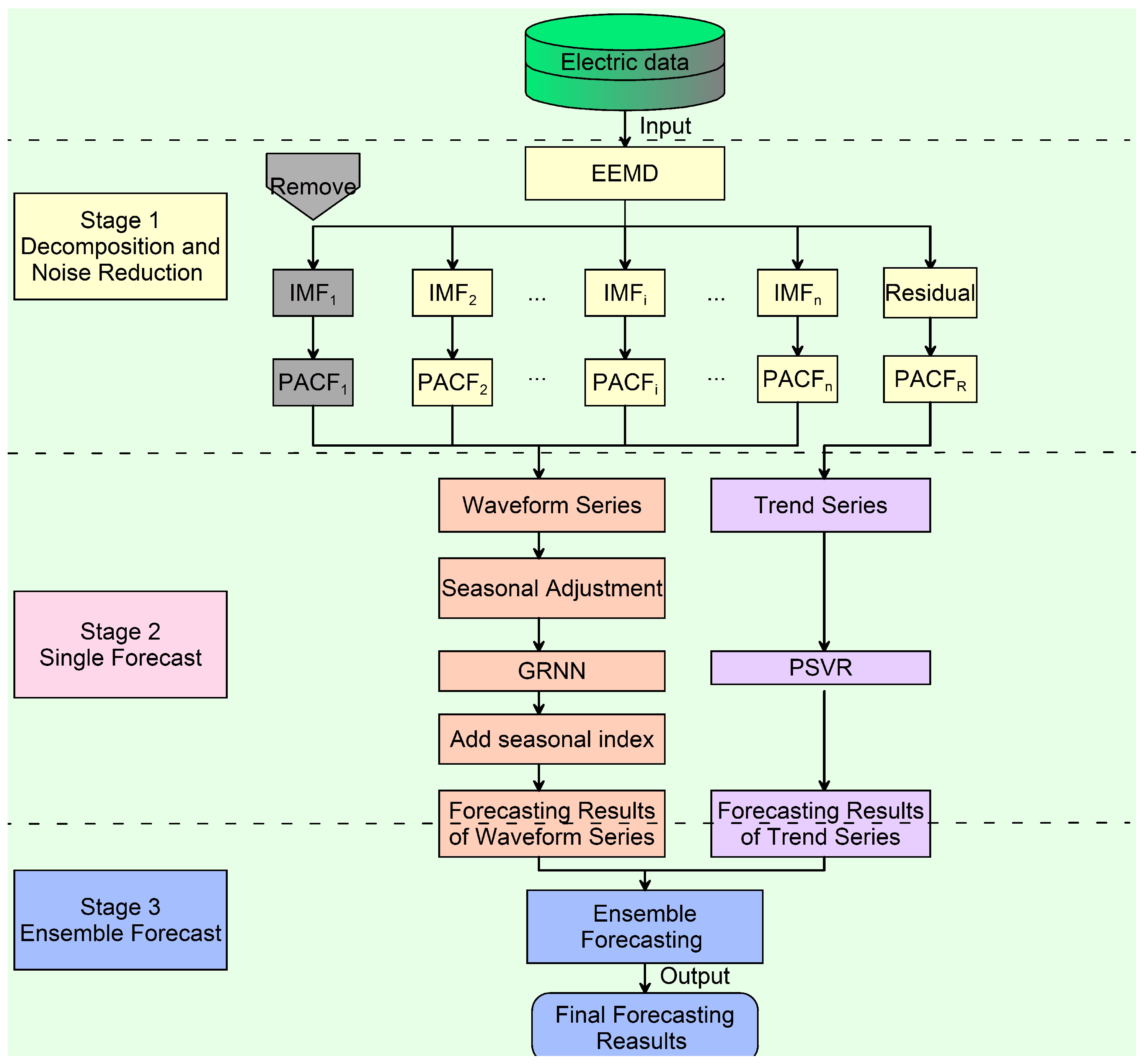
- Stage 1
- Decomposition and noise reduction: EEMD is used to decompose the original electric demand data into a series of IMFs and one residual series. Then, PACF is used to identify noise interference from a number of IMFs and one residual series. In general, the first IMF includes the noise. The rest of IMFs are considered as the waveform component and the residual is considered as the trend component.
- Stage 2
- Single forecasting: On the one hand, the strategy of seasonal adjustment is used to reduce cycle components, GRNN using CV to forecast the processed waveform component series. The CGRNN obtains the final waveform’s prediction by adding corresponding season indexes, and the waveform prediction is noted as W. On the other hand, PSVR is used to obtain the trend forecasting values (T).
- Stage 3
- Ensemble forecasting: These respective estimates of waveform and trend component are combined into the final electric demand forecasts using the principle of ensemble. Equation (15) is the ensemble forecasting formula.
6. Simulation
6.1. Data Collection
6.2. Statistical Measures of Forecasting Performance
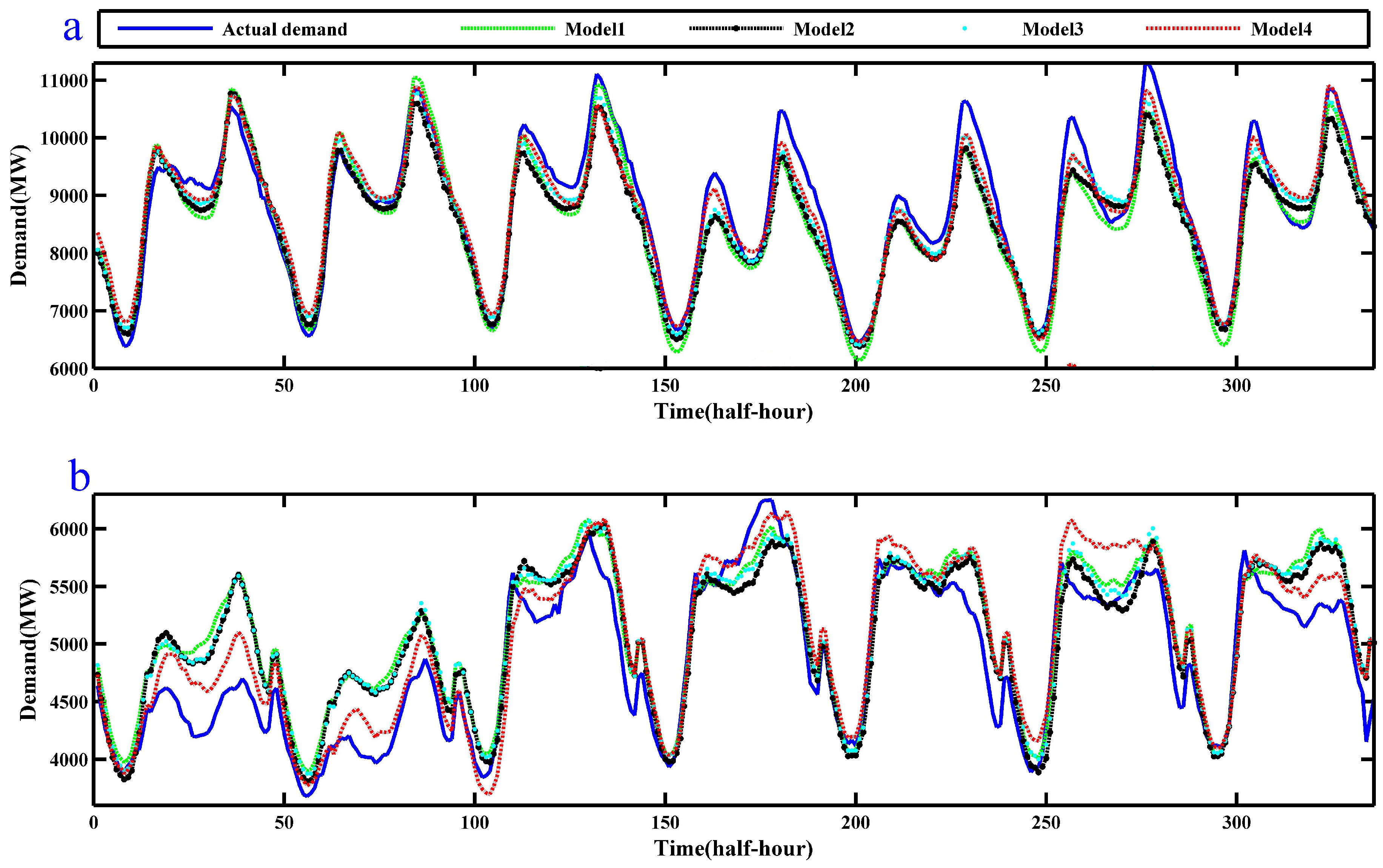
6.3. Different Processing Procedure of Four Predicted Models
6.4. Simulation and Experiment Result of EEMD-SCGRNN-PSVR in NSW
6.5. Comparative Analysis
6.5.1. Comparative Model Accuracy Analysis
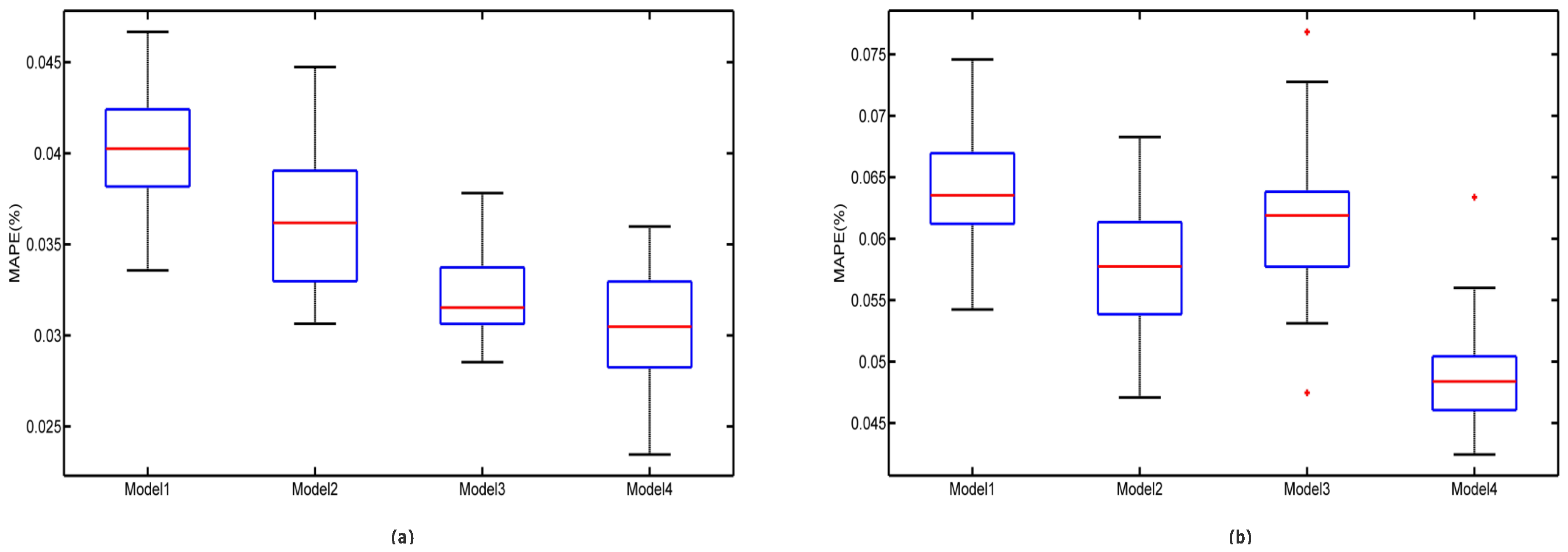
6.5.2. Comparative Model Robustness Analysis
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bunn, D.W.; Farmer, E.D. Comparative Models for Electrical Load Forecasting; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Zhu, S.; Wang, J.; Zhao, W.; Wang, J. A seasonal hybrid procedure for electricity demand forecasting in China. Appl. Energy 2011, 88, 3807–3815. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Hsu, C.C.; Chen, C.Y. Applications of improved grey prediction model for power demand forecasting. Energy Convers. Manag. 2003, 44, 2241–2249. [Google Scholar] [CrossRef]
- Xie, N.M.; Yuan, C.Q.; Yang, Y.J. Forecasting China’s energy demand and self-sufficiency rate by grey forecasting model and Markov model. Int. J. Electr. Power Energy Syst. 2015, 66, 1–8. [Google Scholar] [CrossRef]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Mohamed, N.; Ahmad, M.H.; Ismail, Z. Double seasonal ARIMA model for forecasting load demand. Matematika 2010, 2, 217–231. [Google Scholar]
- Tran, V. One week hourly electricity load forecasting using neuro-fuzzy and seasonal ARIMA models. In Proceedings of the Power Plants and Power Systems Control, Toulouse, France, 2–5 September 2012; pp. 97–102.
- Wang, Y.; Li, F.; Wan, Q.; Chen, H. Hybrid momentum TAR-GARCH models for short term load forecasting. In Proceedings of the Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011.
- Cifter, A. Forecasting electricity price volatility with the Markov-switching GARCH model: Evidence from the Nordic electric power market. Electr. Power Syst. Res. 2013, 102, 61–67. [Google Scholar] [CrossRef]
- Wang, J.; Chi, D.; Wu, J.; Lu, H.Y. Chaotic time series method combined with particle swarm optimization and trend adjustment for electricity demand forecasting. Expert Syst. Appl. 2011, 38, 8419–8429. [Google Scholar] [CrossRef]
- Hong, W.C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Gotman, N.; Shumilova, G.; Starceva, T. Electric Load Forecasting Using an Artificial Neural Networks; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2014. [Google Scholar]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Thanh, L.T. Short-term electric load forecasting using an artificial neural network: Case of Northern Vietnam. Int. J. Energy Res. 2004, 28, 463–472. [Google Scholar] [CrossRef]
- Hamid, M.A.; Rahman, T.A. Short term load forecasting using an artificial neural network trained by artificial immune system learning algorithm. In Proceedings of the Uksim, International Conference on Computer Modelling and Simulation, Cambridge, UK, 24–26 March 2010; pp. 408–413.
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Naguib, R.N.G.; Hamdy, F.C. A general regression neural network analysis of prognostic markers in prostate cancer. Neurocomputing 1998, 19, 145–150. [Google Scholar] [CrossRef]
- Nose-Filho, K.; Lotufo, A.D.P.; Minussi, C.R. Short-term multinodal load forecasting using a modified general regression neural network. IEEE Trans. Power Deliv. 2011, 26, 2862–2869. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Guo, X.C.; Liang, Y.C.; Wu, C.G.; Wang, H.Y. Electric load forecasting using SVMS. In Proceedings of the IEEE 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 4213–4215.
- Sun, W.; Liang, Y. Least-squares support vector machine based on improved imperialist competitive algorithm in a short-term load forecasting model. J. Energy Eng. 2014, 141, 04014037. [Google Scholar] [CrossRef]
- Bouzerdoum, M.; Mellit, A.; Pavan, A.M. A hybrid model (SARIMA–SVM) for short-term power forecasting of a small-scale grid-connected photovoltaic plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, J.; Lu, H. Combining forecasts of electricity consumption in China with time-varying weights updated by a high-order Markov chain model. Omega 2014, 45, 80–91. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, S.; Zhang, W.; Lu, H. Combined modeling for electric load forecasting with adaptive particle swarm optimization. Energy 2010, 35, 1671–1678. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Hong, W.C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2015, 173, 958–970. [Google Scholar] [CrossRef]
- Guo, Z.H.; Wu, J.; Lu, H.Y.; Wang, J.Z. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl.-Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Kran, M.S.; Ozceylan, E.; Gunduz, M.; Paksoy, T. A novel hybrid approach based on Particle Swarm Optimization and Ant Colony Algorithm to forecast energy demand of Turkey. Energy Convers. Manag. 2012, 53, 75–83. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, W. ARIMA model estimated by particle swarm optimization algorithm for consumer price index forecasting. In Proceedings of the Artificial Intelligence and Computational Intelligence, International Conference (AICI 2009), Shanghai, China, 7–8 November 2009; pp. 48–58.
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Cincotti, S.; Gallo, G.; Ponta, L.; Raberto, M. Modeling and forecasting of electricity spot-prices: Computational intelligence vs. classical econometrics. AI Commun. 2014, 27, 301–314. [Google Scholar]
- Amjady, N.; Keynia, F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power Energy Syst. 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948.
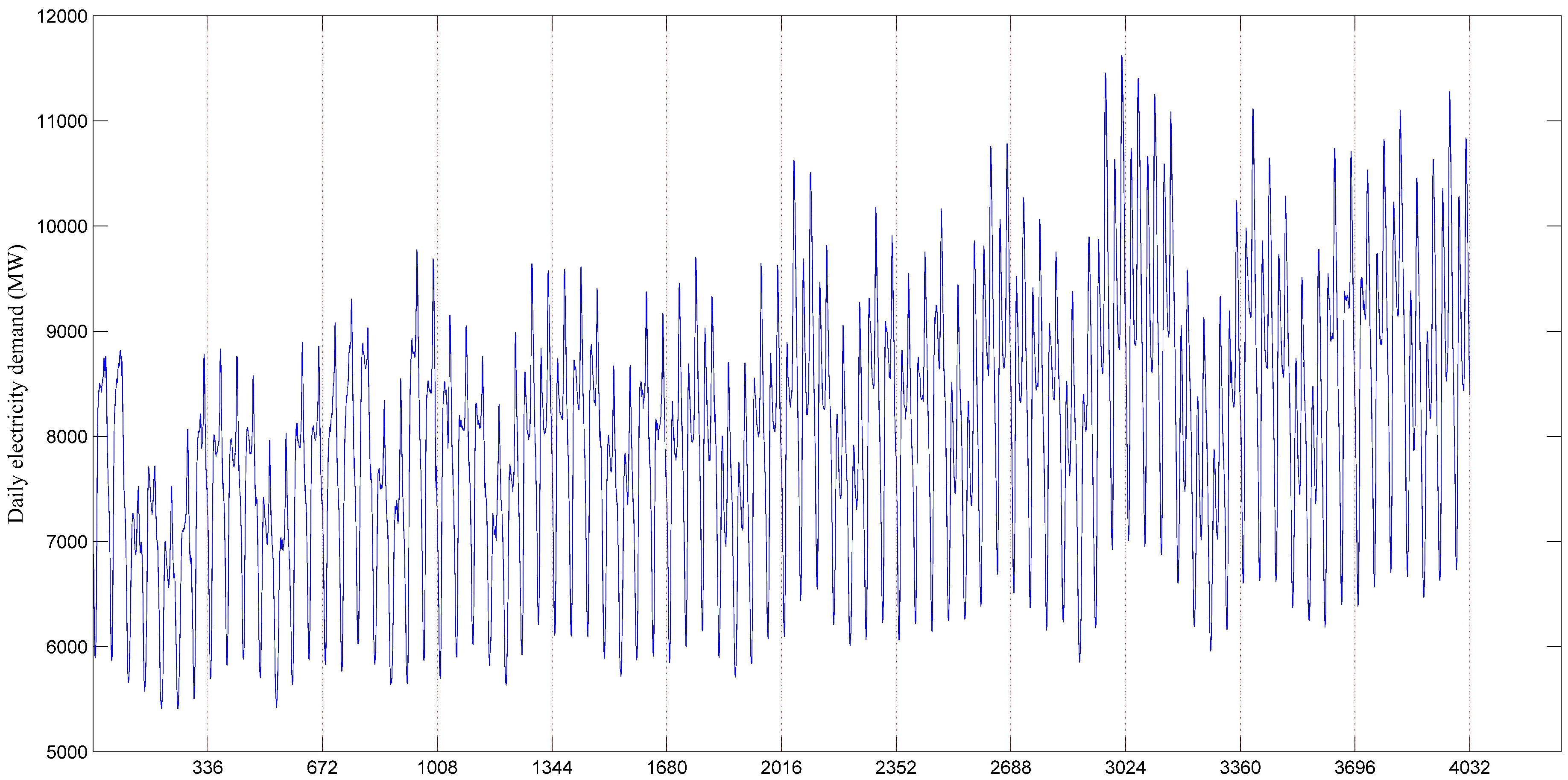
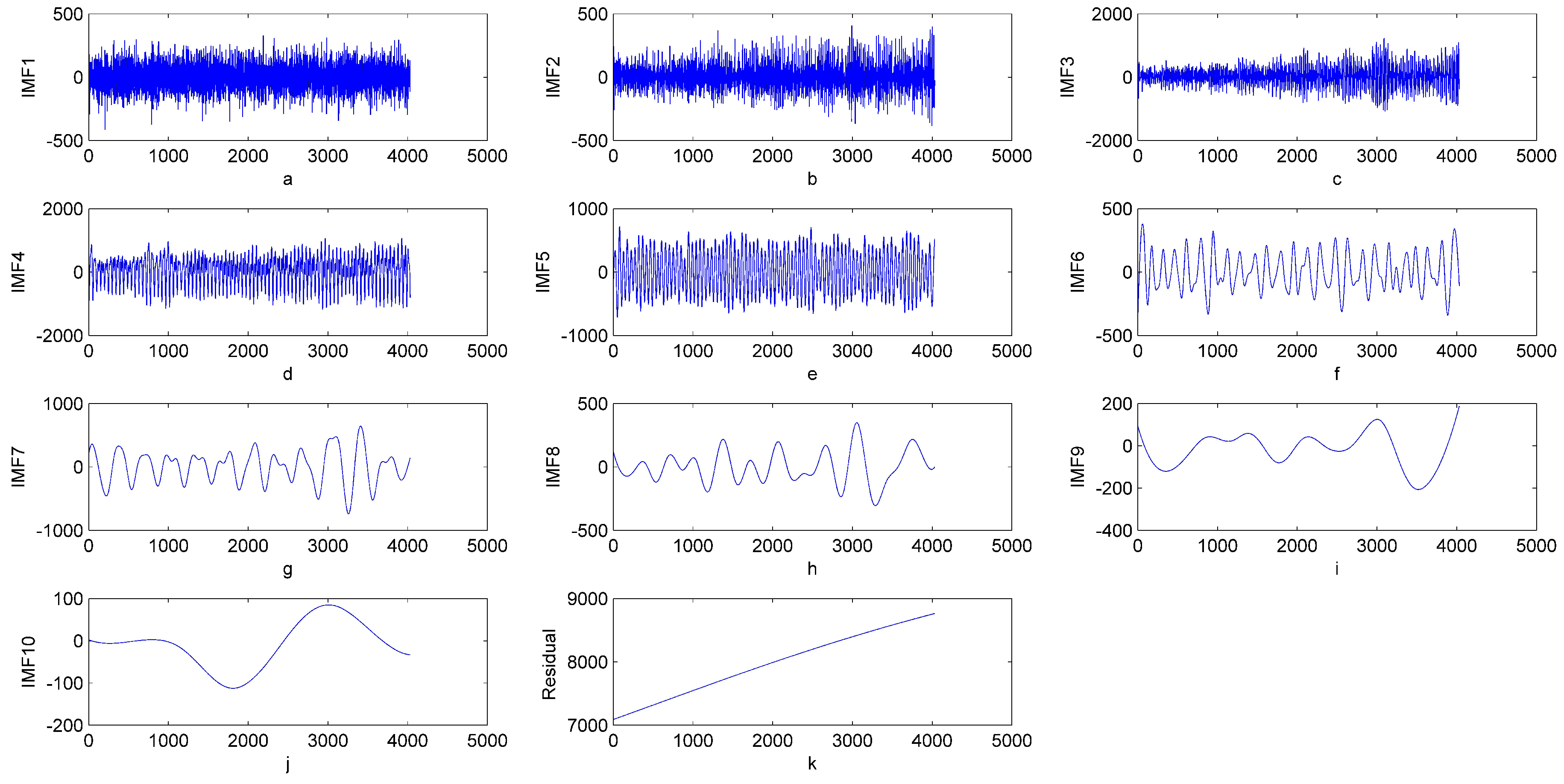
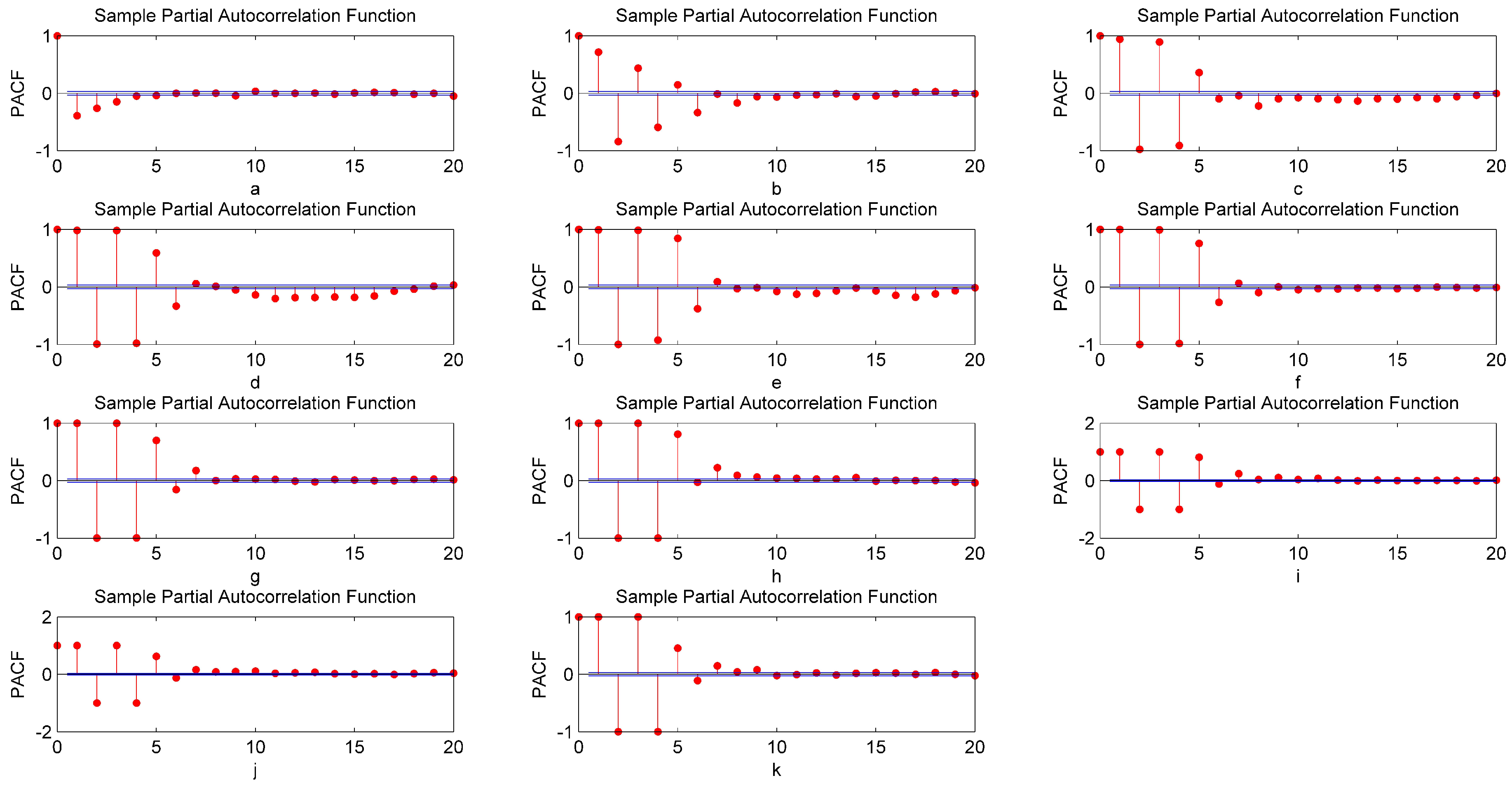
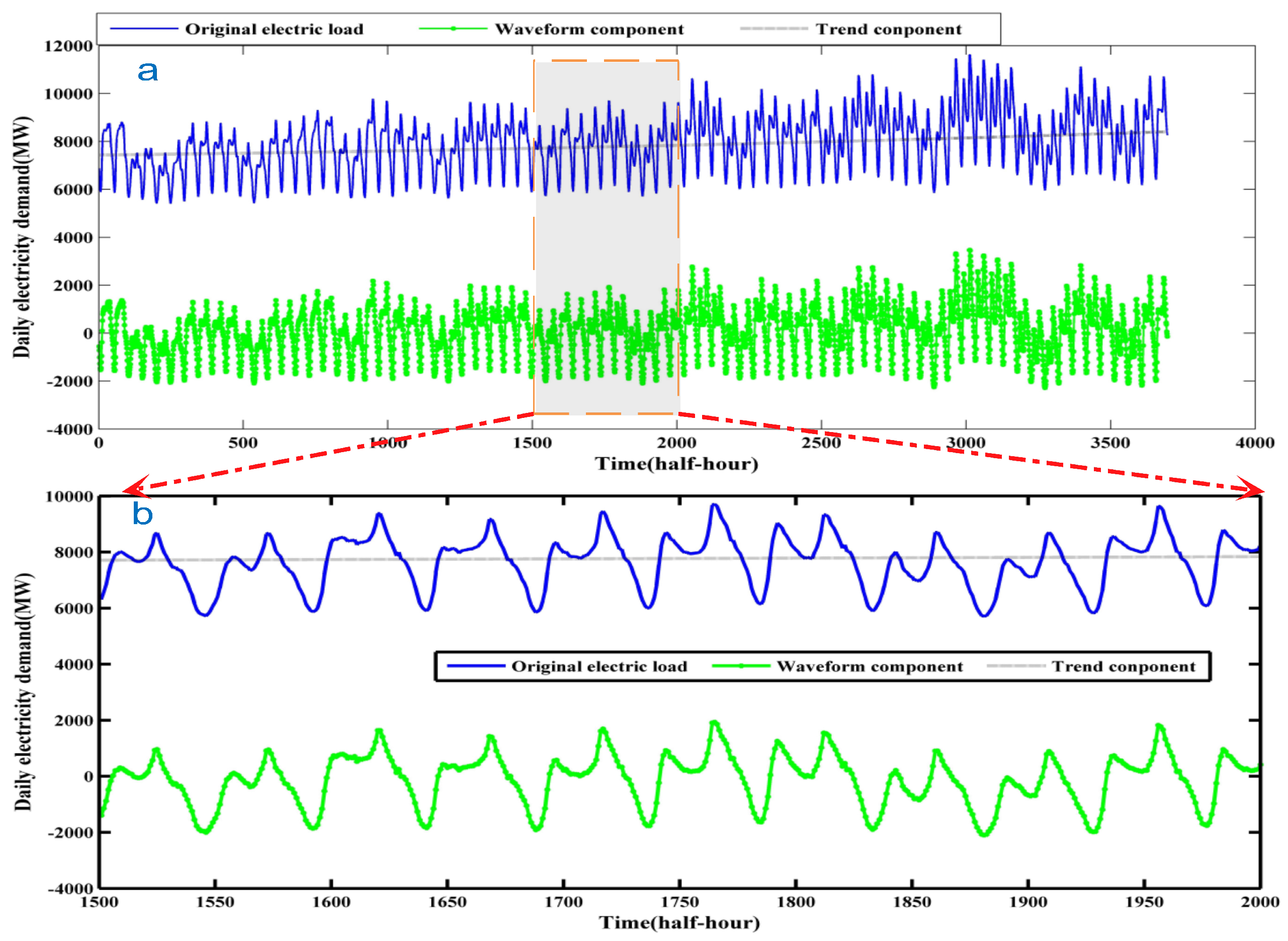
| Area ID | Data Set | Min (MW) | Max (MW) | Mean (MW) | Std (MW) |
|---|---|---|---|---|---|
| NSW | training set | 5407.55 | 11,625.47 | 7906.03 | 1143.13 |
| testing set | 6383.53 | 11,278.45 | 8796.39 | 1191.00 | |
| VIC | training set | 3479.24 | 7483.73 | 5246.76 | 794.51 |
| testing set | 3678.57 | 6250.54 | 4864.60 | 652.78 |
| Area ID | Criteria | Model1 | Model2 | Model3 | Model4 |
|---|---|---|---|---|---|
| NSW | RMSE | 391.17 | 359.71 | 301.22 | 276.84 |
| MAE | 293.38 | 283.78 | 253.36 | 229.63 | |
| MAPE (%) | 3.78 | 3.24 | 2.86 | 2.62 | |
| VIC | RMSE | 333.37 | 309.80 | 325.64 | 258.22 |
| MAE | 289.55 | 259.92 | 280.95 | 220.46 | |
| MAPE (%) | 6.18 | 5.49 | 5.96 | 4.54 |
| Training Period | NSW | VIC |
|---|---|---|
| 9 weeks | 3.30% | 4.77% |
| 10 weeks | 2.63% | 5.03% |
| 11 weeks | 2.62% | 4.54% |
| 12 weeks | 3.02% | 5.21% |
| 13 weeks | 2.88% | 4.69% |
| 14 weeks | 3.80% | 4.88% |
| Average | 3.04% | 4.85% |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Yang, X.; Li, H.; Su, L. Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting. Energies 2017, 10, 44. https://doi.org/10.3390/en10010044
Li W, Yang X, Li H, Su L. Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting. Energies. 2017; 10(1):44. https://doi.org/10.3390/en10010044
Chicago/Turabian StyleLi, Weide, Xuan Yang, Hao Li, and Lili Su. 2017. "Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting" Energies 10, no. 1: 44. https://doi.org/10.3390/en10010044
APA StyleLi, W., Yang, X., Li, H., & Su, L. (2017). Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting. Energies, 10(1), 44. https://doi.org/10.3390/en10010044