Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox
Abstract
:1. Introduction
2. Wind Turbine Drive Train
3. RUL Estimation of Bearings in Wind Turbine Gearbox
3.1. Neural Network for Short-Term Tendency Prediction
3.2. Procedure of Remaining Useful Life Estimation of Bearings
4. Case Study
4.1. Testing Conditions
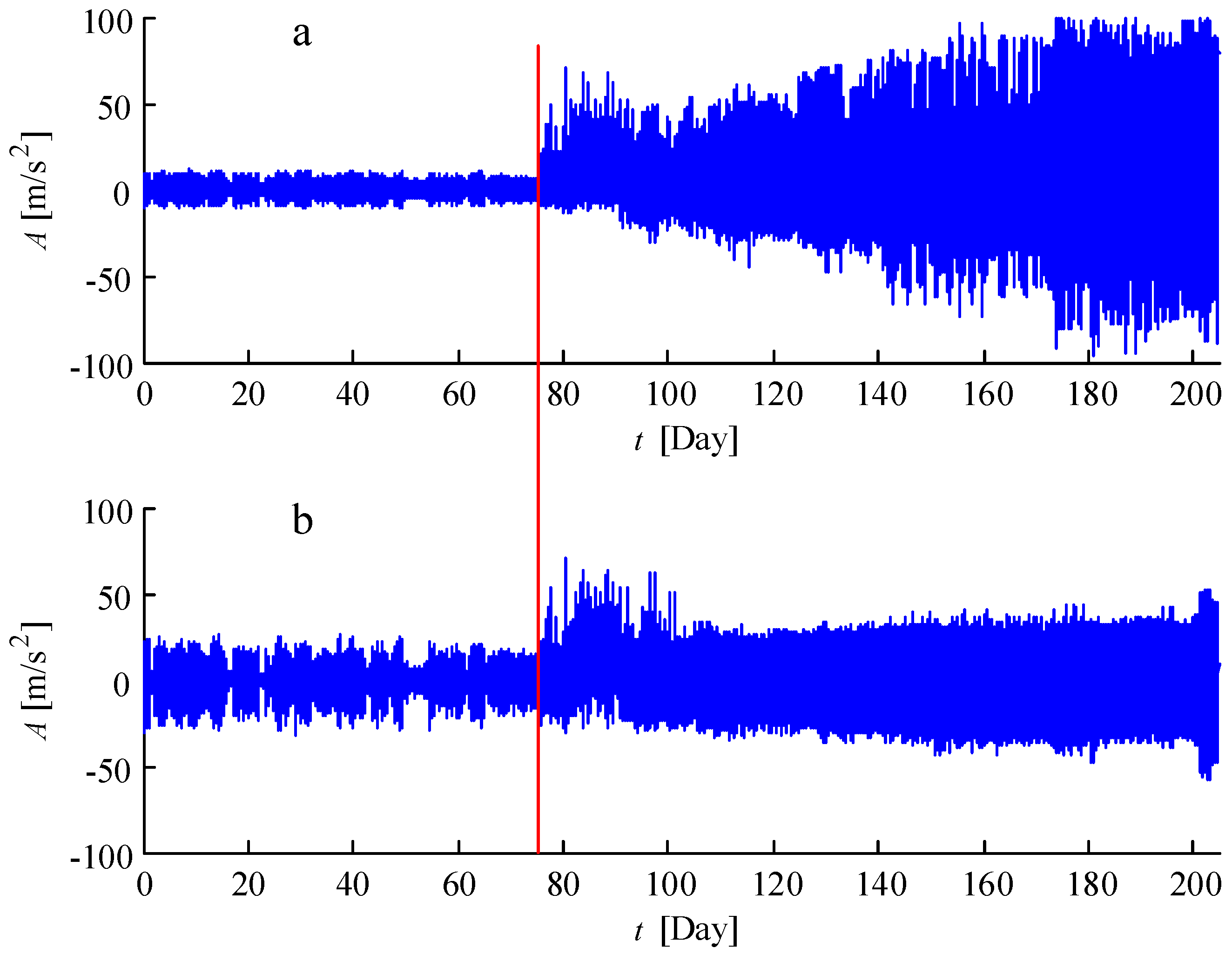
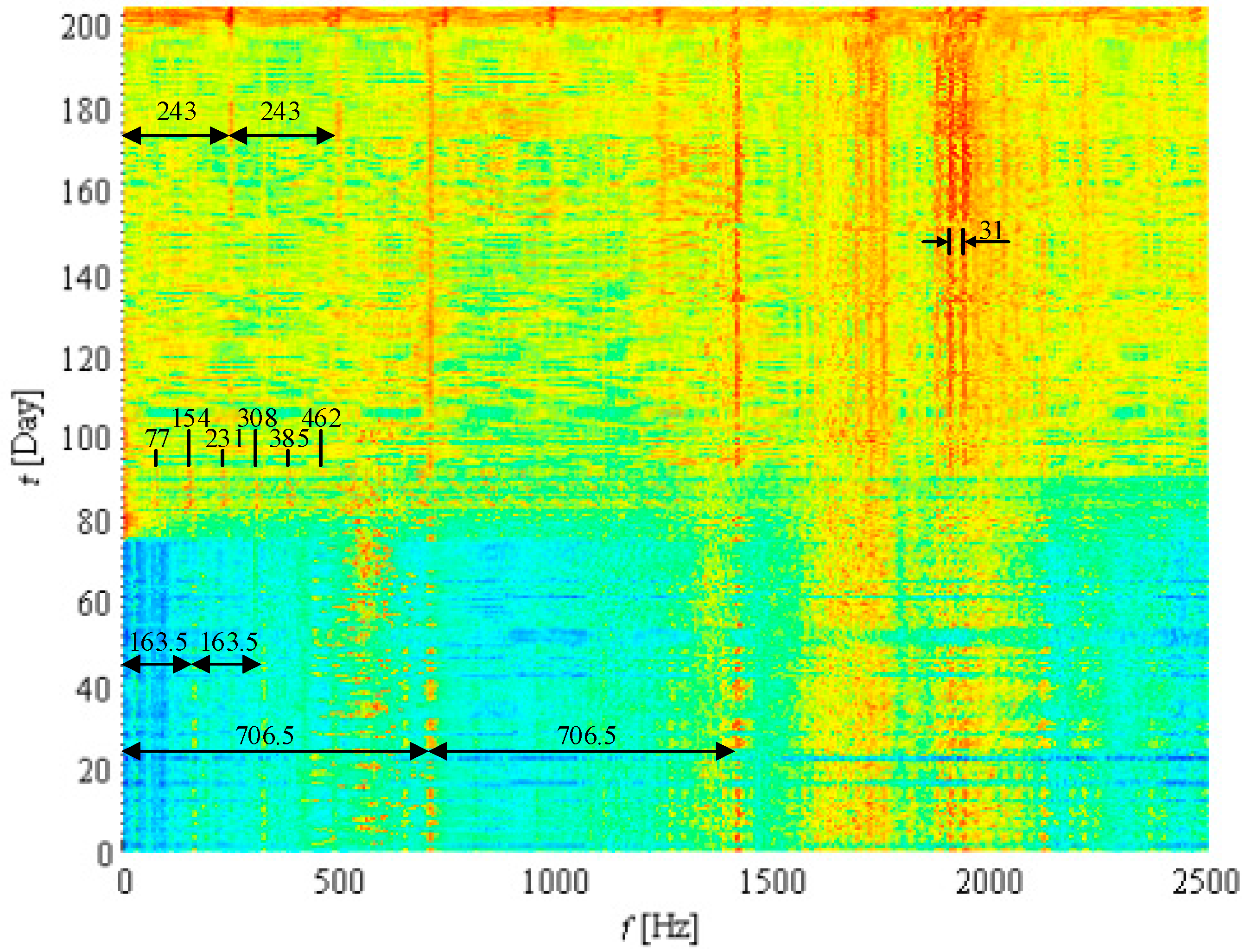
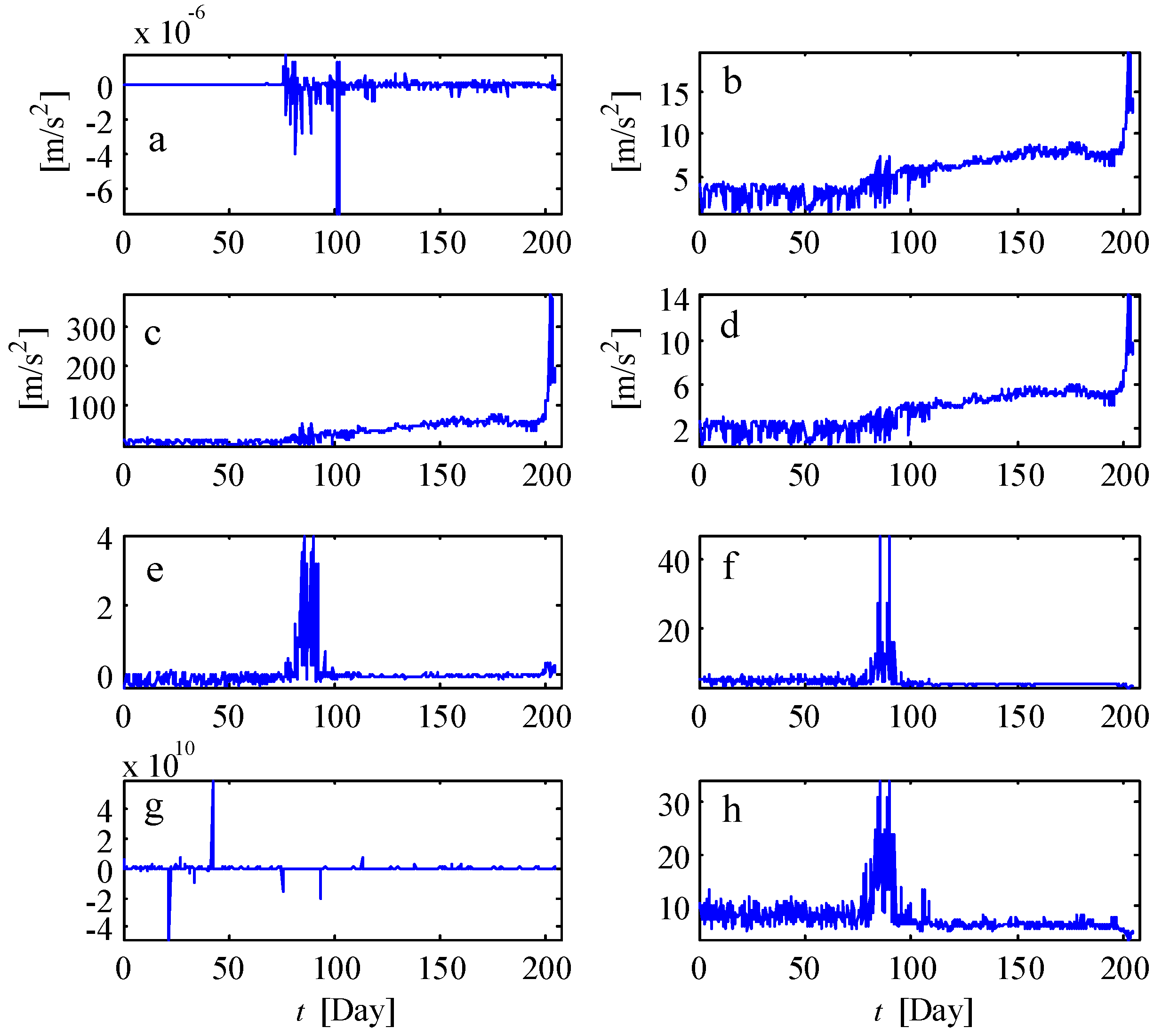
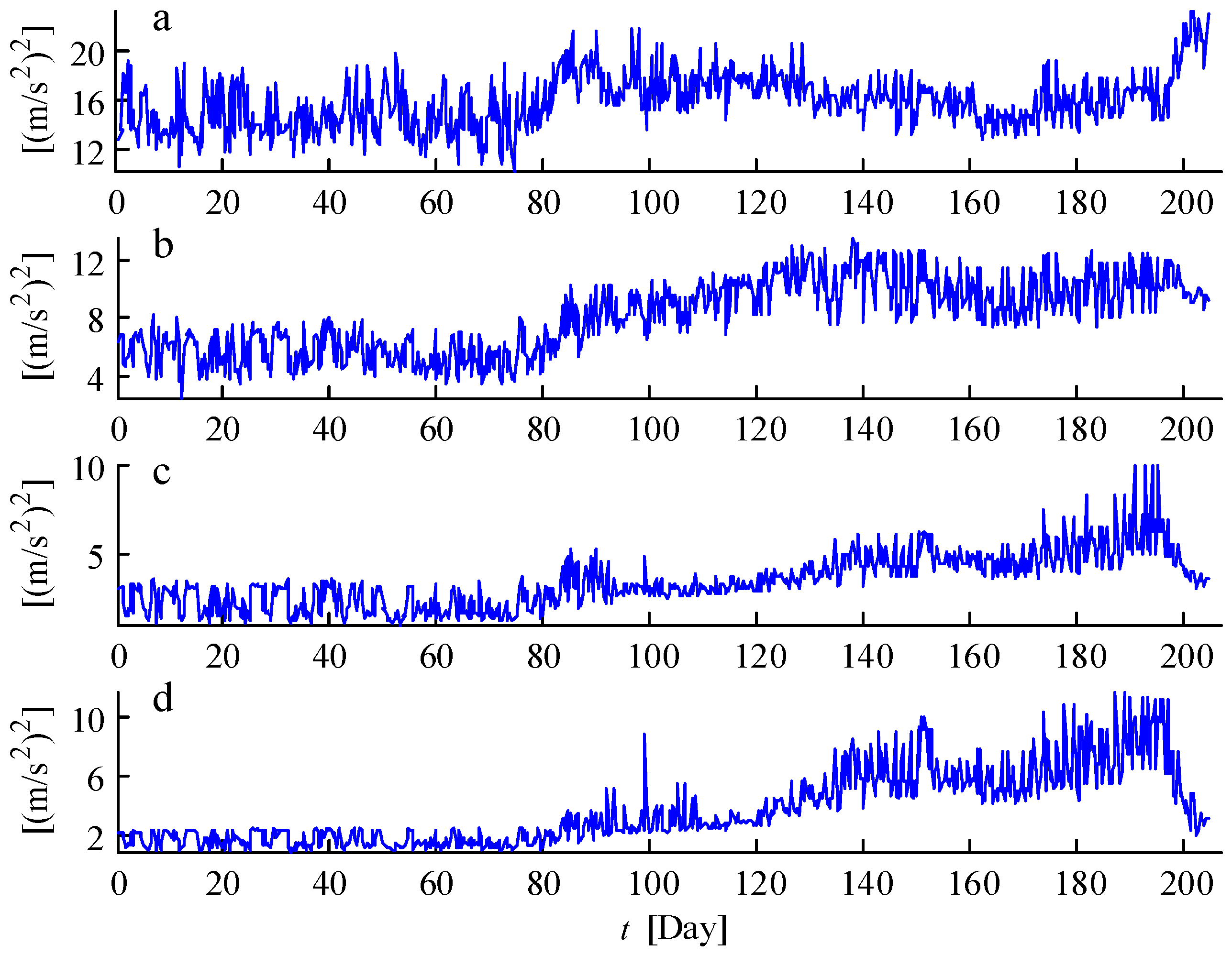
4.2. Fault Diagnosis for the Wind Turbine Gearbox
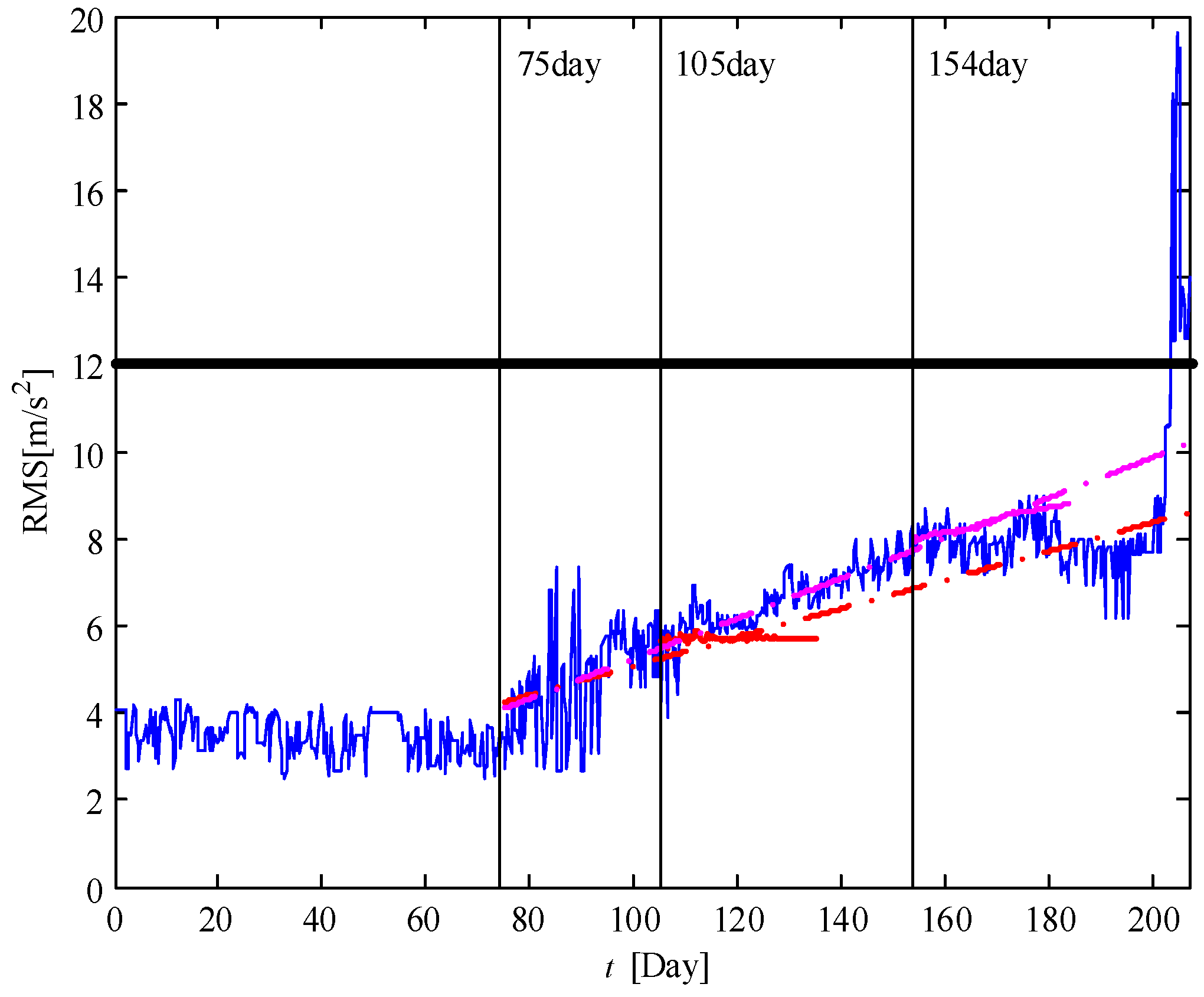
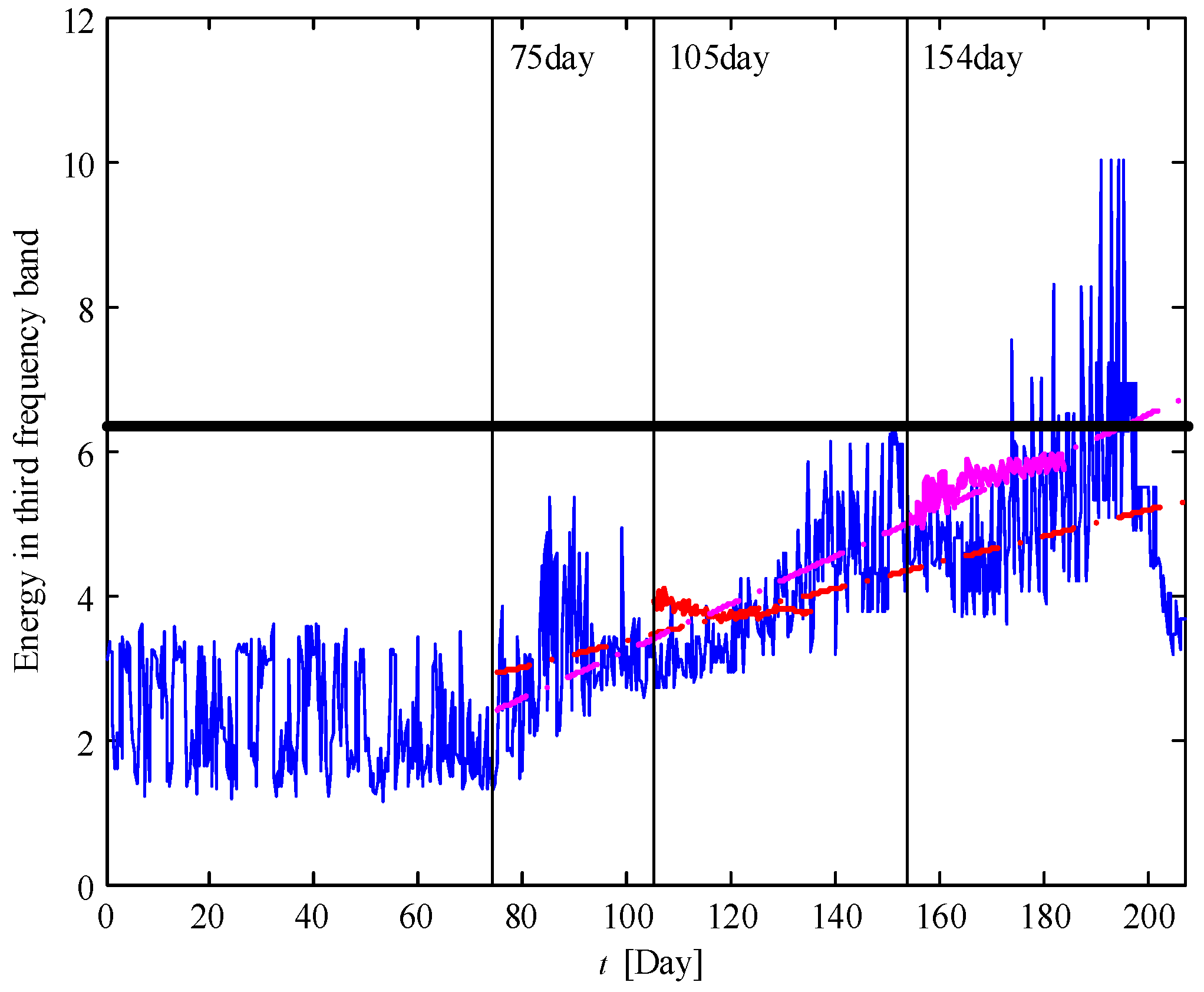
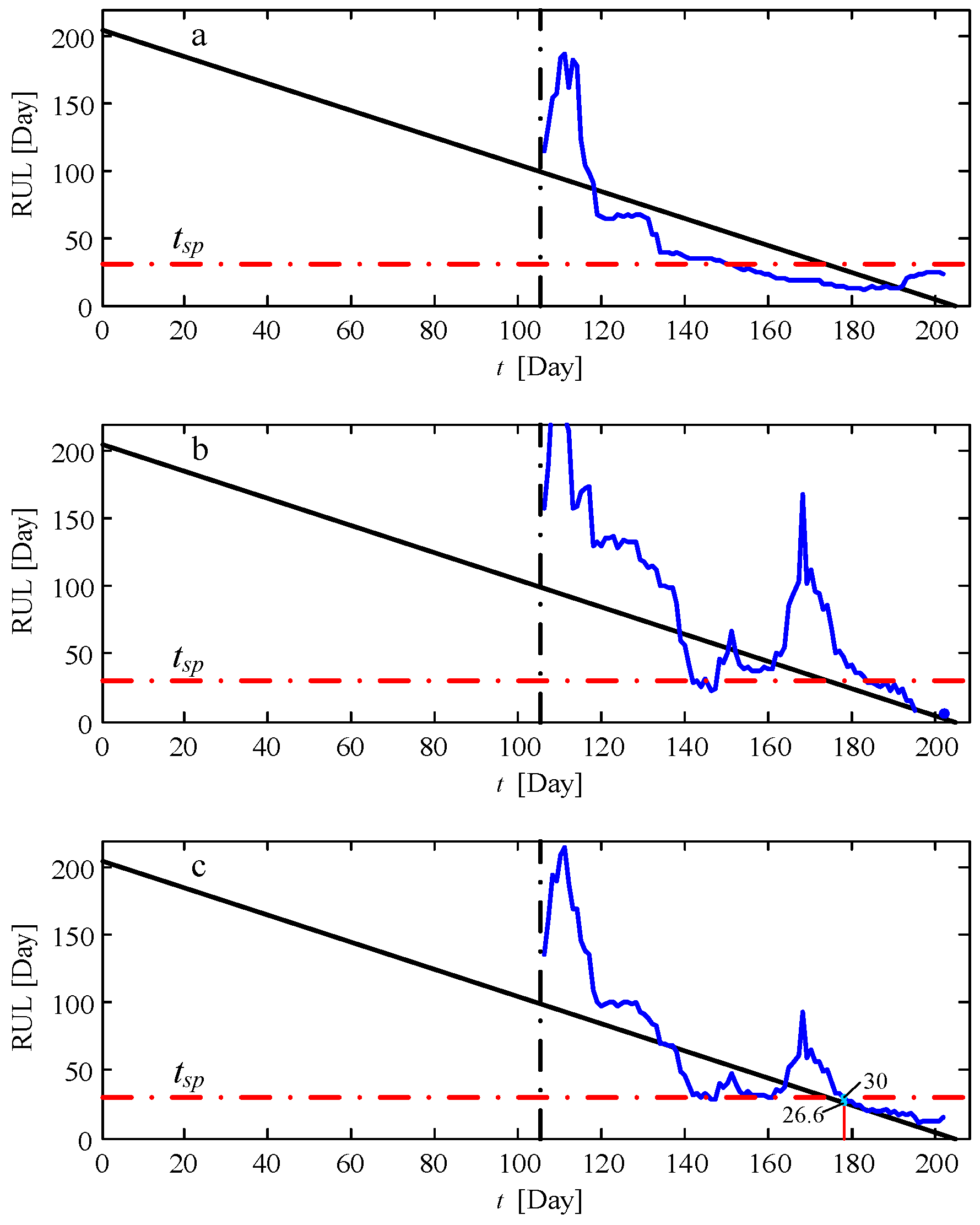
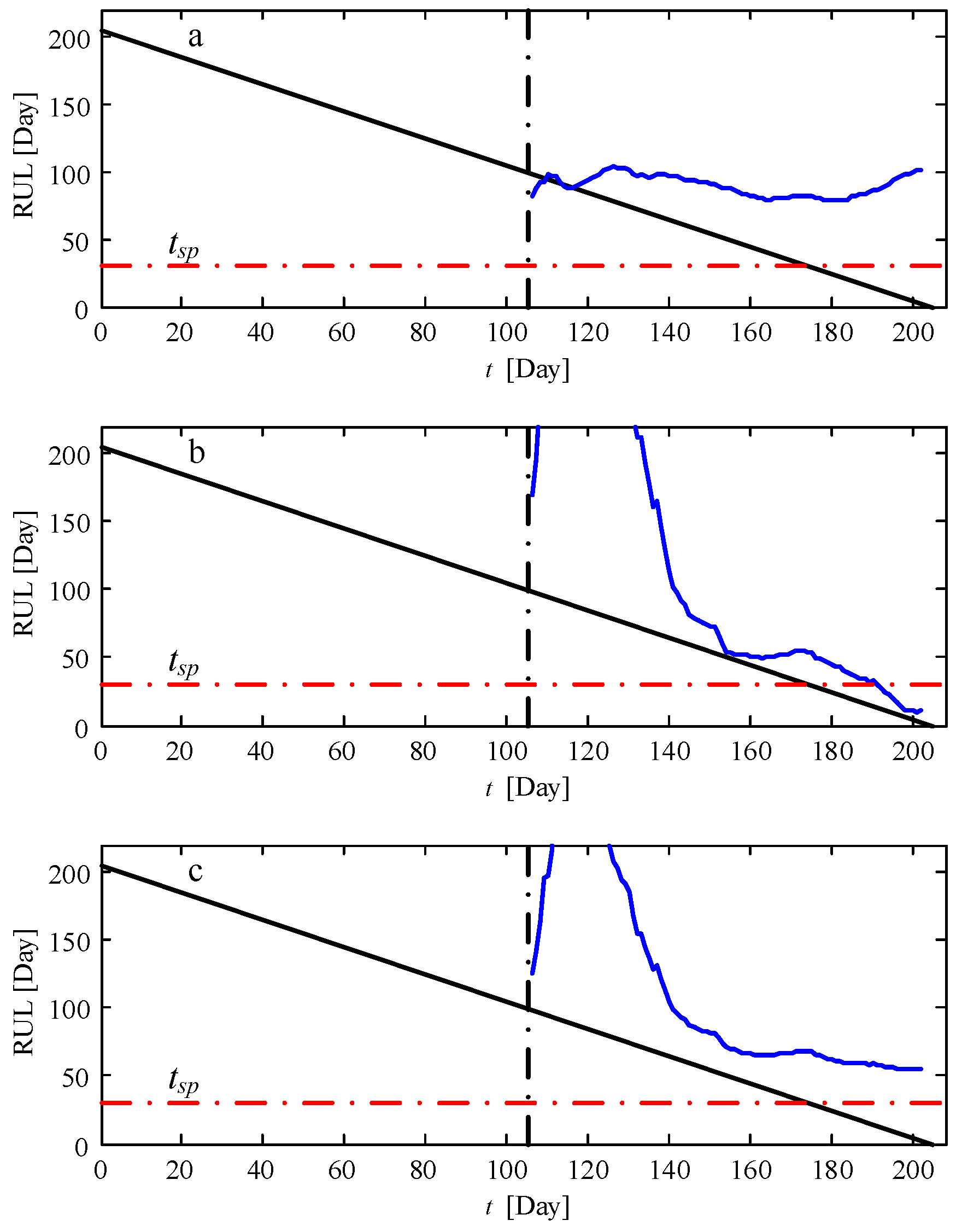
4.3. Prognosis of the Remaining Useful Life of the Faulty Bearing
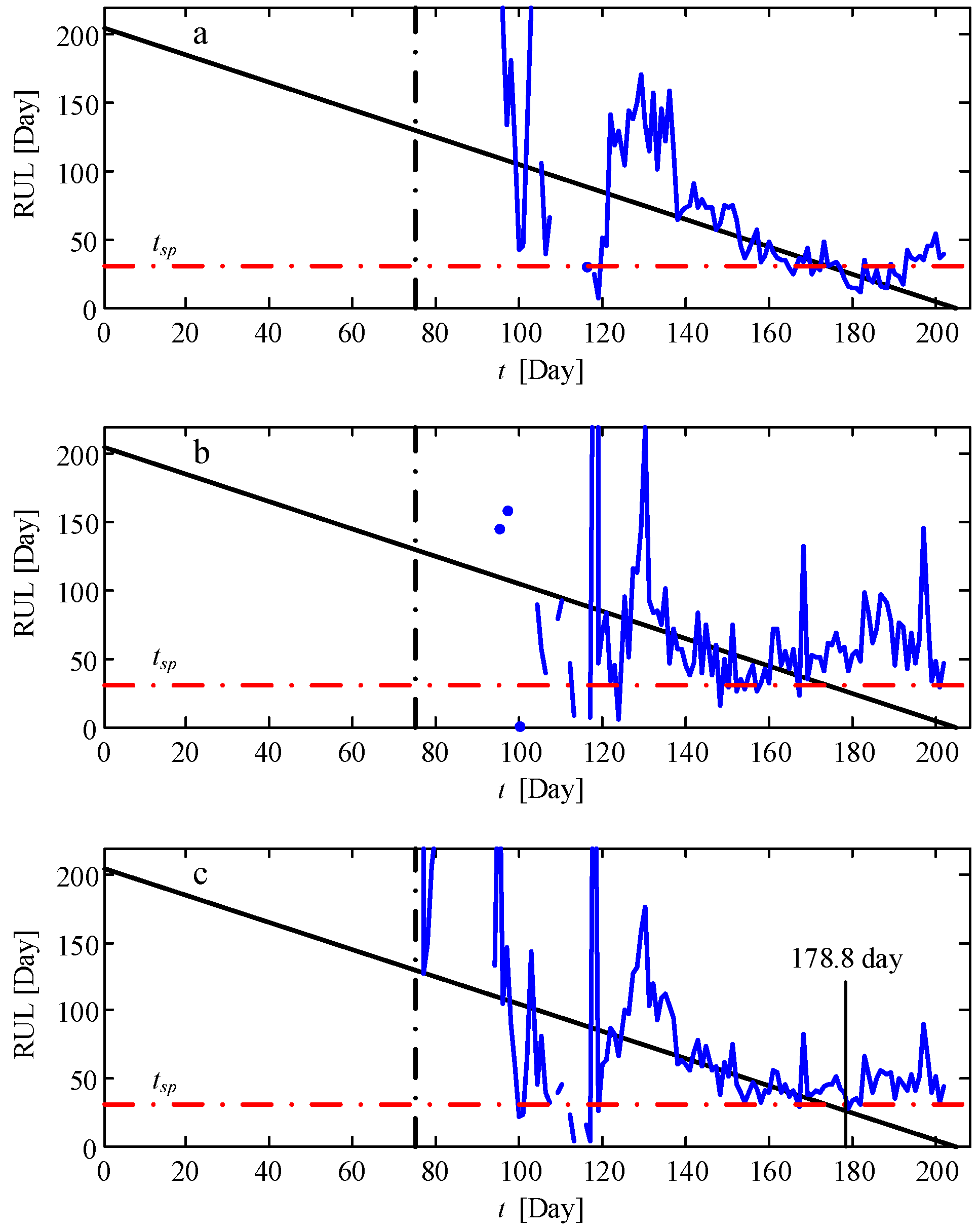
4.4. Comparision with Other Prognostic Method and Datasets
4.4.1. Echo State Network
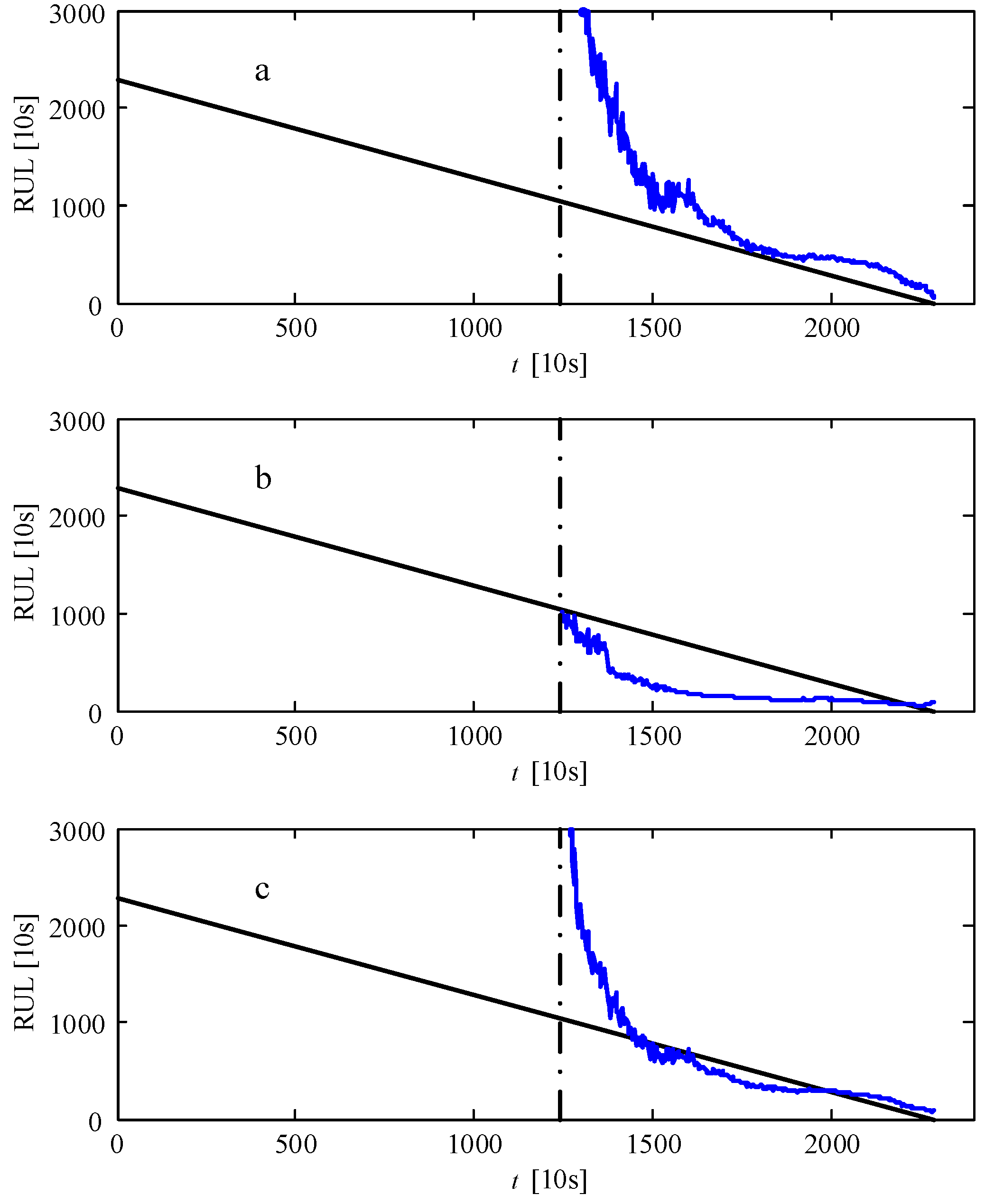
4.4.2. Application of the Presented Approach of Remaining Useful Life Estimation to Experimental Dataset
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tian, Z.; Jin, T.; Wu, B.; Ding, F. Condition based maintenance optimization for wind power generation systems under continuous monitoring. Renew. Energy 2011, 36, 1502–1509. [Google Scholar] [CrossRef]
- Byon, E.; Ntaimo, L.; Ding, Y. Optimal maintenance strategies for wind turbine systems under stochastic weather conditions. IEEE Trans. Reliab. 2010, 59, 393–404. [Google Scholar] [CrossRef]
- Sarker, B.R.; Faiz, T.I. Minimizing maintenance cost for offshore wind turbines following multi-level opportunistic preventive strategy. Renew. Energy 2016, 85, 104–113. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Court, R. An online technique for condition monitoring the induction generators used in wind and marine turbines. Mech. Syst. Signal Process. 2013, 38, 103–112. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Zhang, X.; Liu, Y.; Ma, Z. Multi-fault detection and failure analysis of wind turbine gearbox using complex wavelet transform. Renew. Energy 2016, 93, 591–598. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. Analyzing bearing faults in wind turbines: A data-mining approach. Renew. Energy 2012, 48, 110–116. [Google Scholar] [CrossRef]
- Dupuis, R. Application of oil debris monitoring for wind turbine gearbox prognostics and health management. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Portland, OR, USA, 10–16 October 2010.
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar]
- Tian, Z. An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring. J. Intell. Manuf. 2012, 23, 227–237. [Google Scholar] [CrossRef]
- Tian, Z.; Wong, L.; Safaei, N. A neural network approach for remaining useful life prediction utilizing both failure and suspension histories. Mech. Syst. Signal Process. 2010, 24, 1542–1555. [Google Scholar] [CrossRef]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowskib, S.; Fnaiecha, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar]
- Zio, E.; Peloni, G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components. Reliab. Eng. Syst. Saf. 2011, 96, 403–409. [Google Scholar] [CrossRef]
- Chen, C.; Vachtsevanos, G.; Orchard, M.E. Machine remaining useful life prediction: An integrated adaptive neuro-fuzzy and high-order particle filtering approach. Mech. Syst. Signal Process. 2012, 28, 597–607. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Remaining useful life estimation based on nonlinear feature reduction and support vector regression. Eng. Appl. Artif. Intell. 2013, 26, 1751–1760. [Google Scholar] [CrossRef]
- Maio, F.D.; Tsui, K.L.; Zio, E. Combining relevance vector machines and exponential regression for bearing residual life estimation. Mech. Syst. Signal Process. 2012, 31, 405–427. [Google Scholar] [CrossRef]
- Boskoski, P.; Gasperin, M.; Petelin, D.; Juricic, D. Bearing fault prognostics using Renyi entropy based features and Gaussian process models. Mech. Syst. Signal Process. 2015, 52–53, 327–337. [Google Scholar] [CrossRef]
- Sikorska, J.Z.; Hodkiewicz, M.; Ma, L. Prognostic modelling options for remaining useful life estimation by industry. Mech. Syst. Signal Process. 2011, 25, 1803–1836. [Google Scholar] [CrossRef]
- An, D.; Choi, J.H.; Kim, N.H. Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab. Reliab. Eng. Syst. Saf. 2013, 115, 161–169. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated life test. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012.
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006; Chapter 5. [Google Scholar]
- D’Addona, D.M.; Matarazzo, D.; Ullah, A.M.M.S.; Teti, R. Tool wear control through cognitive paradigms. Procedia CIRP 2015, 33, 221–226. [Google Scholar] [CrossRef]
- Measurement and Evaluation of the Mechanical Vibration of Wind Energy Turbines and Their Components—Onshore Wind Energy Turbines with Gears; VDI 3834; The Association of German Engineers: Duesseldorf, Germany, 2009.
- Lyons, L. Discovering the Significance of 5σ. Available online: https://arxiv.org/pdf/1310.1284v1.pdf (accessed on 7 October 2013).
- Le, B.; Andrew, J. Modelling wind turbine degradation and maintenance. Wind Energy 2016, 19, 571–591. [Google Scholar] [CrossRef]
- Jaeger, H. Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the “Echo State Network” Approach; GMD Report 159; German National Research Center for Information Technology: St. Augustin, Germany, 2002. [Google Scholar]
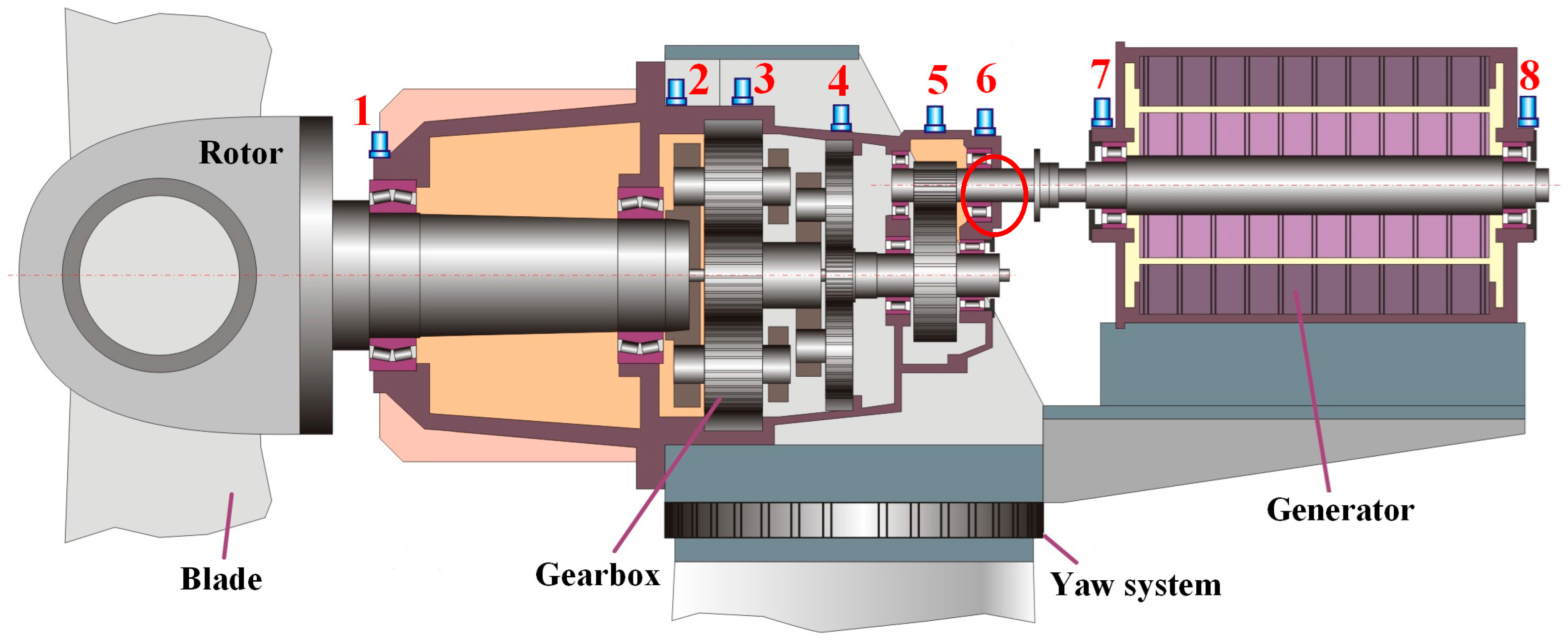






| Zp1 | Zs1 | Zr1 | Zp2 | Zs2 | Zr2 | Zhi | Zho |
|---|---|---|---|---|---|---|---|
| 40 | 23 | 104 | 37 | 27 | 102 | 92 | 23 |
| fa1 (Hz) | fs1 = fa2 (Hz) | fs2 (Hz) | fh (Hz) | fPS1 (Hz) | fPS2 (Hz) | fHSS (Hz) |
|---|---|---|---|---|---|---|
| 0.293 | 1.62 | 7.75 | 31.0 | 30.5 | 165.4 | 713 |
| Parts in the Bearing | Ratio to fr | Feature Frequency (Hz) |
|---|---|---|
| Cage fault | 0.401 | 12.43 |
| Rolling element fault | 2.43 | 75.3 |
| Outer race fault | 5.21 | 161.5 |
| Inner race fault | 7.79 | 241.7 |
| Features | Formulas |
|---|---|
| Mean () | |
| RMS () | |
| Variance () | |
| Square root of amplitude () | |
| Skewness factor | |
| Kurtosis factor | |
| Waveform factor | |
| Margin indicator | |
| Energy of 1st frequency band | |
| Energy of 2nd frequency band | |
| Energy of 3rd frequency band | |
| Energy of 4th frequency band |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, W.; Zhang, X.; Liu, Y.; Kusiak, A.; Ma, Z. Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox. Energies 2017, 10, 32. https://doi.org/10.3390/en10010032
Teng W, Zhang X, Liu Y, Kusiak A, Ma Z. Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox. Energies. 2017; 10(1):32. https://doi.org/10.3390/en10010032
Chicago/Turabian StyleTeng, Wei, Xiaolong Zhang, Yibing Liu, Andrew Kusiak, and Zhiyong Ma. 2017. "Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox" Energies 10, no. 1: 32. https://doi.org/10.3390/en10010032
APA StyleTeng, W., Zhang, X., Liu, Y., Kusiak, A., & Ma, Z. (2017). Prognosis of the Remaining Useful Life of Bearings in a Wind Turbine Gearbox. Energies, 10(1), 32. https://doi.org/10.3390/en10010032






