MTS Model Application to Materials Not Starting in the Annealed Condition
Abstract
:1. Introduction
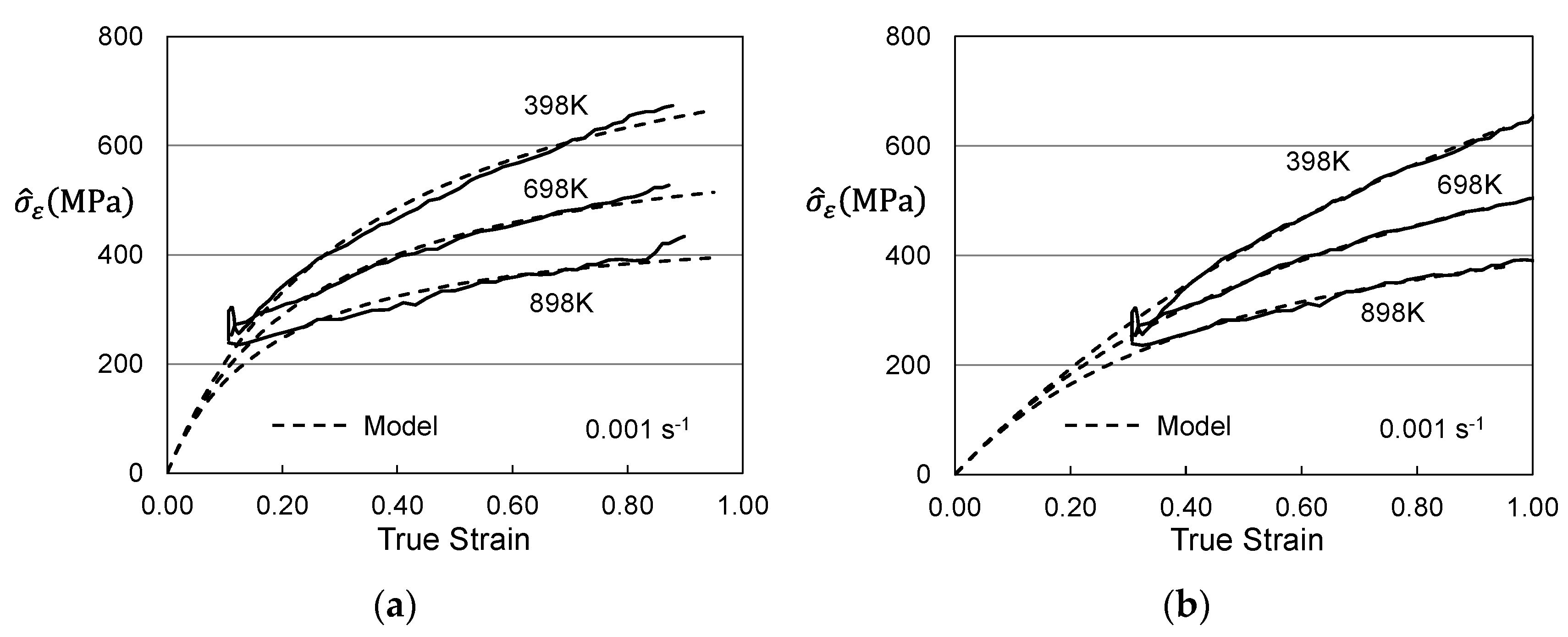
2. Analysis of Published Measurements in Molybdenum
3. Analysis of Hardening in Previously Worked Material
3.1. Hardening in Hot Worked Follyalloy
3.2. Additional Information on the Supplied Material
4. Analysis of Hardening in Molybdenum
5. Conclusions
- (1)
- Confound the analysis of the variation of the yield stress with temperature and strain rate. Equation (1) rather than Equation (3) is the governing kinetic equation. However, the researcher may not have sufficient information to assess the magnitude of the term in this Equation (1). The strengthening contribution due to the existing stored dislocation density would be mistakenly added to the strengthening contribution, for instance, due to solute additions. Then, mechanical threshold stress values and the normalized activation energies would not represent the true strengthening contributions.
- (2)
- Introduce errors in the analysis of continued structure evolution due to dislocation accumulation. The saturation threshold stress values and the activation energy due to dynamic recovery in Equation (5) would be under estimated.
- (1)
- Prior knowledge is available of the applicable activation energies for the operative strengthening mechanisms in Equation (1), and
- (2)
- The material supplier is able to report the strains introduced during the final warm-working process.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Follansbee, P.S.; Kocks, U.F. A Constitutive Description of the Deformation of Copper Based on the Use of the Mechanical Threshold Stress as an Internal State Variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Follansbee, P.S. Fundamentals of Strength: Principles, Experiment, and Applications of an Internal State Variable Constitutive Formulation, 2nd ed.; The Minerals, Metals, Materials Series; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Follansbee, P.S. On the Definition of State Variables for an Internal State Variable Constitutive Model Describing Metal Deformation. Mater. Sci. Appl. 2014, 5, 603–609. [Google Scholar] [CrossRef] [Green Version]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodynamics and Kinetics of Slip. In Progress in Materials Science; Chalmers, B., Christian, J.W., Massalski, T.B., Eds.; Pergamon Press: Oxford, UK, 1975; Volume 19. [Google Scholar]
- Follansbee, P.S. An Internal State Variable Constitutive Model for Deformation of Austenitic Stainless Steels. J. Eng. Mater.Technol. 2012, 134, 41007-1–41007-10. [Google Scholar] [CrossRef]
- Follansbee, P.S. Structure Evolution in Austenitic Stainless Steels. Mater. Sci. Appl. 2015, 6, 457–463. [Google Scholar]
- Follansbee, P.S. Analysis of Deformation in Inconel 718 When the Stress Anomaly and Dynamic Strain Aging Coexist. Metall. Mater. Trans. 2014, 47A, 4445–4466. [Google Scholar] [CrossRef]
- Follansbee, P.S. Application of the Mechanical Threshold Stress Model to Large Strain Processing. Mater. Sci. Appl. 2022, 13, 300–316. [Google Scholar] [CrossRef]
- Briggs, T.L.; Campbell, J.D. The Effect of Strain Rate and Temperature on the Yield and Flow of Polycrystalline Niobium and Molybdenum. Acta Metall. 1972, 20, 711–724. [Google Scholar] [CrossRef]
- Follansbee, P.S. Analysis of Deformation Kinetics in Seven BCC Metals Using a Two-Obstacle Model. Metall. Mater. Trans. A 2010, 41A, 3080–3090. [Google Scholar] [CrossRef]
- Cheng, J.; Nemat-Nasser, S.; Guo, W. A Unified Constitutive Model for Strain-Rate and Temperature Dependent Behavior of Molybdenum. Mech. Mater. 2001, 33, 603–616. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for Work Hardening and Low Temperature Creep. J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Varshni, Y.P. Temperature dependence of the elastic constants. Phys. Rev. B 1970, 2, 3952–3958. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Gray, G.T., III. An Analysis of the Low Temperature and Low and High Strain Rate Deformation of Ti-6Al-4V. Metall. Trans. A 1989, 20A, 863–874. [Google Scholar] [CrossRef]
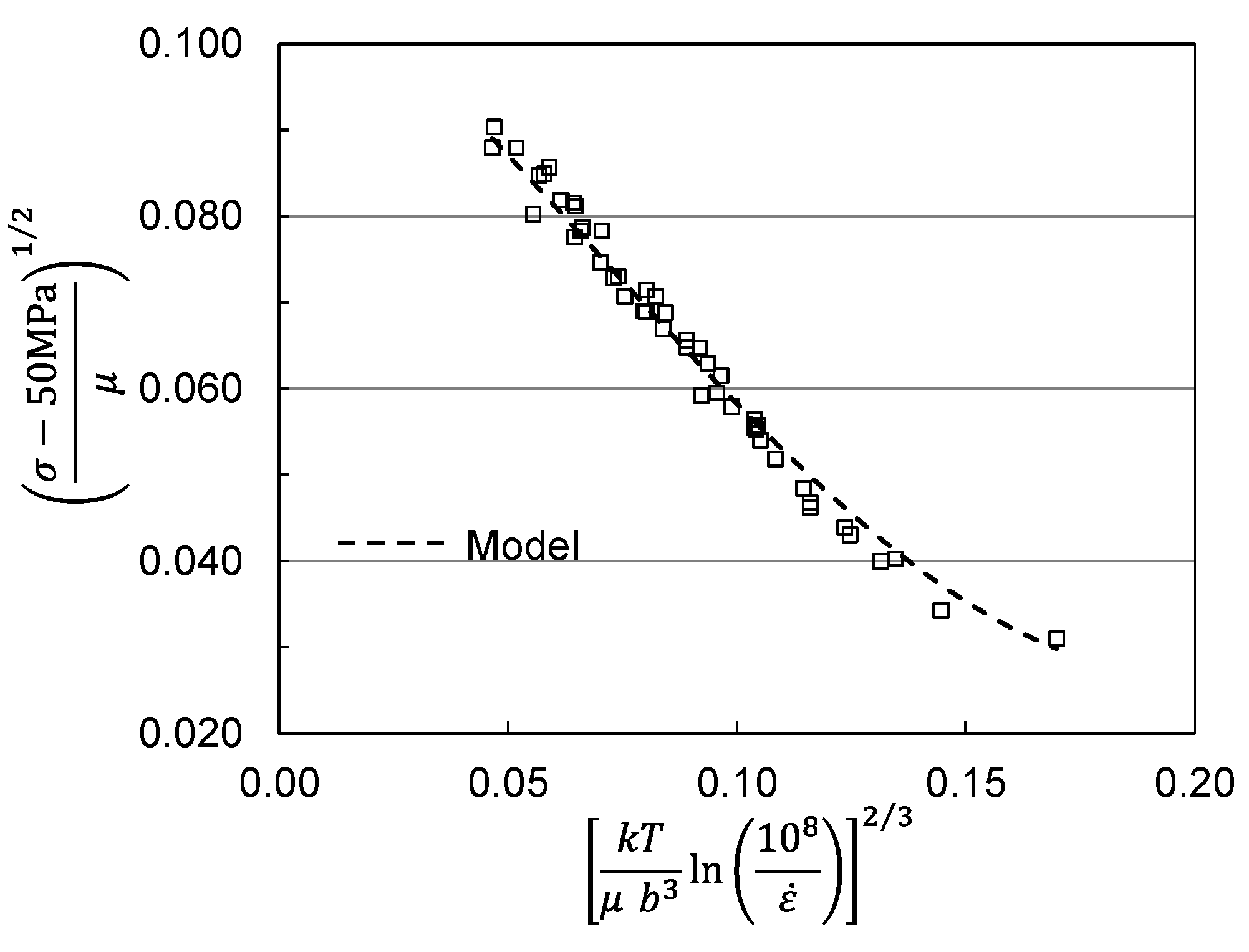

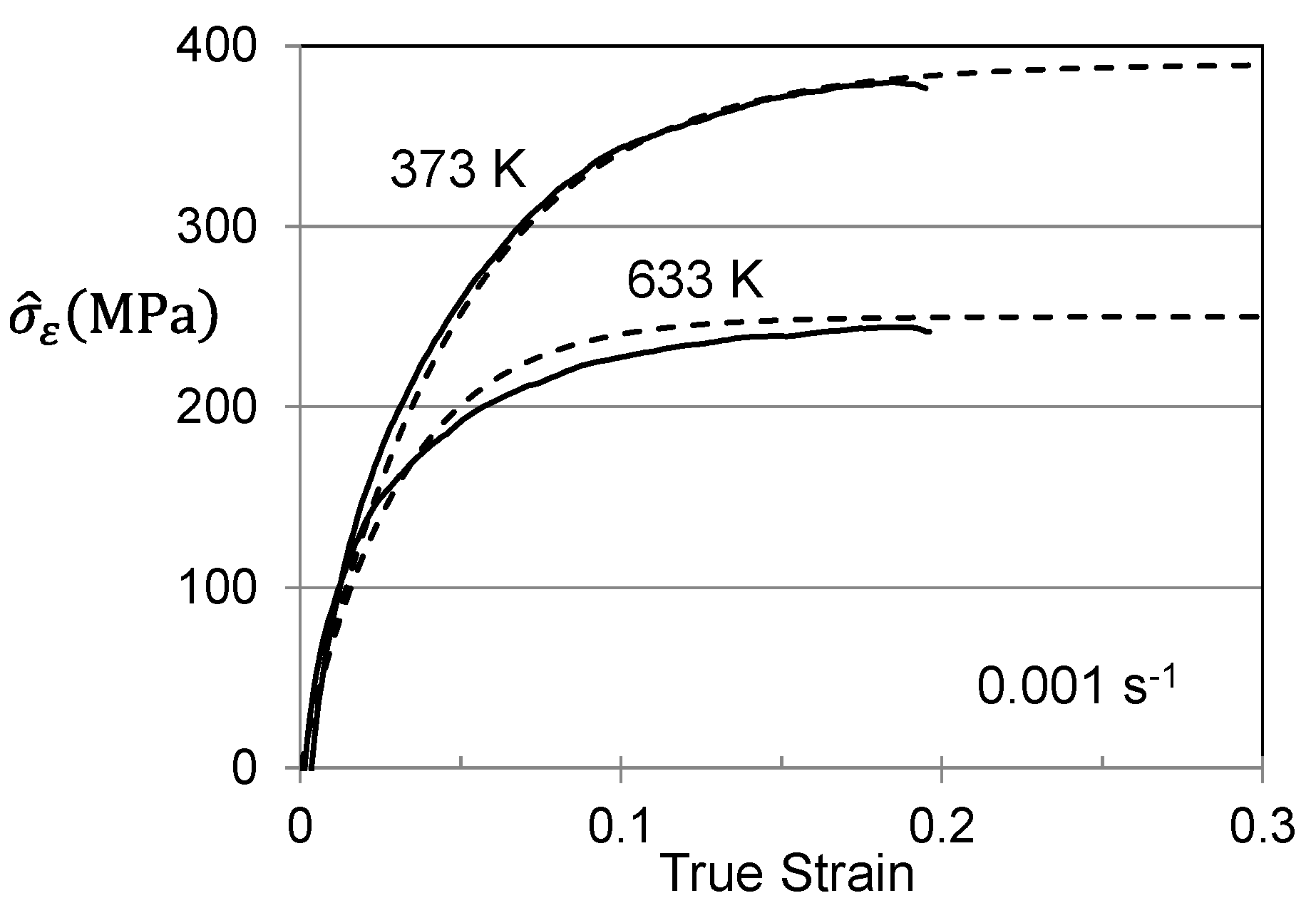
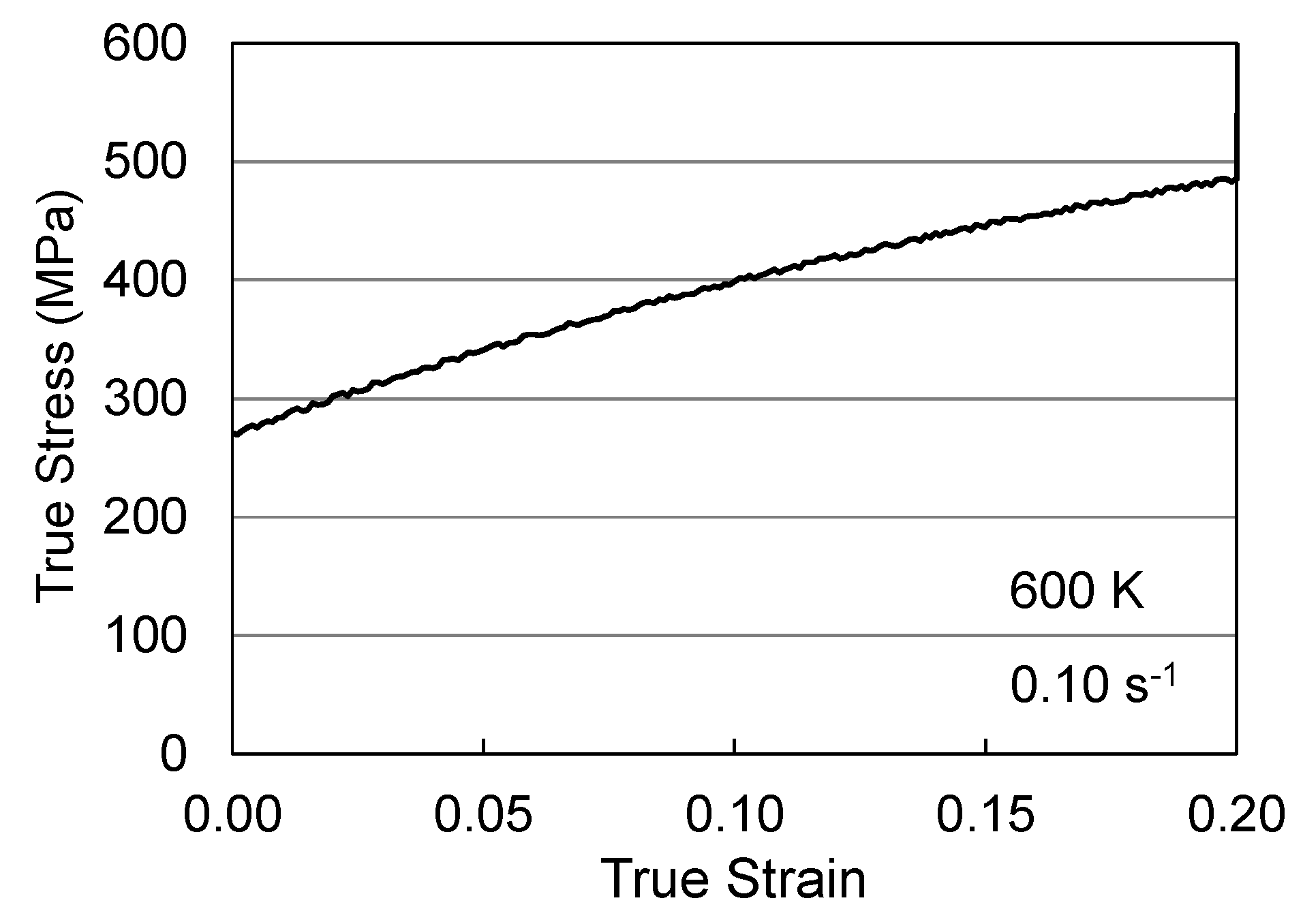
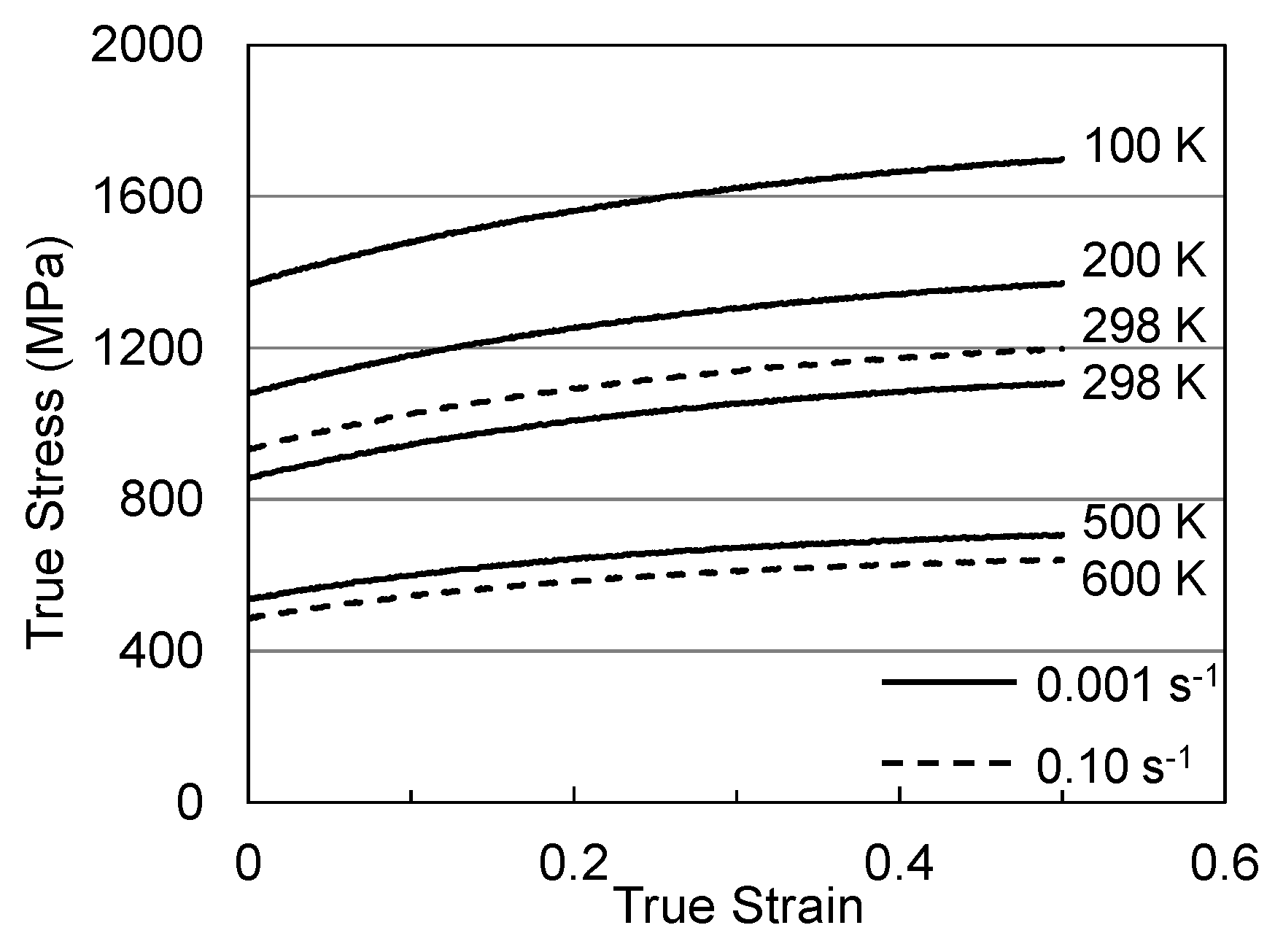

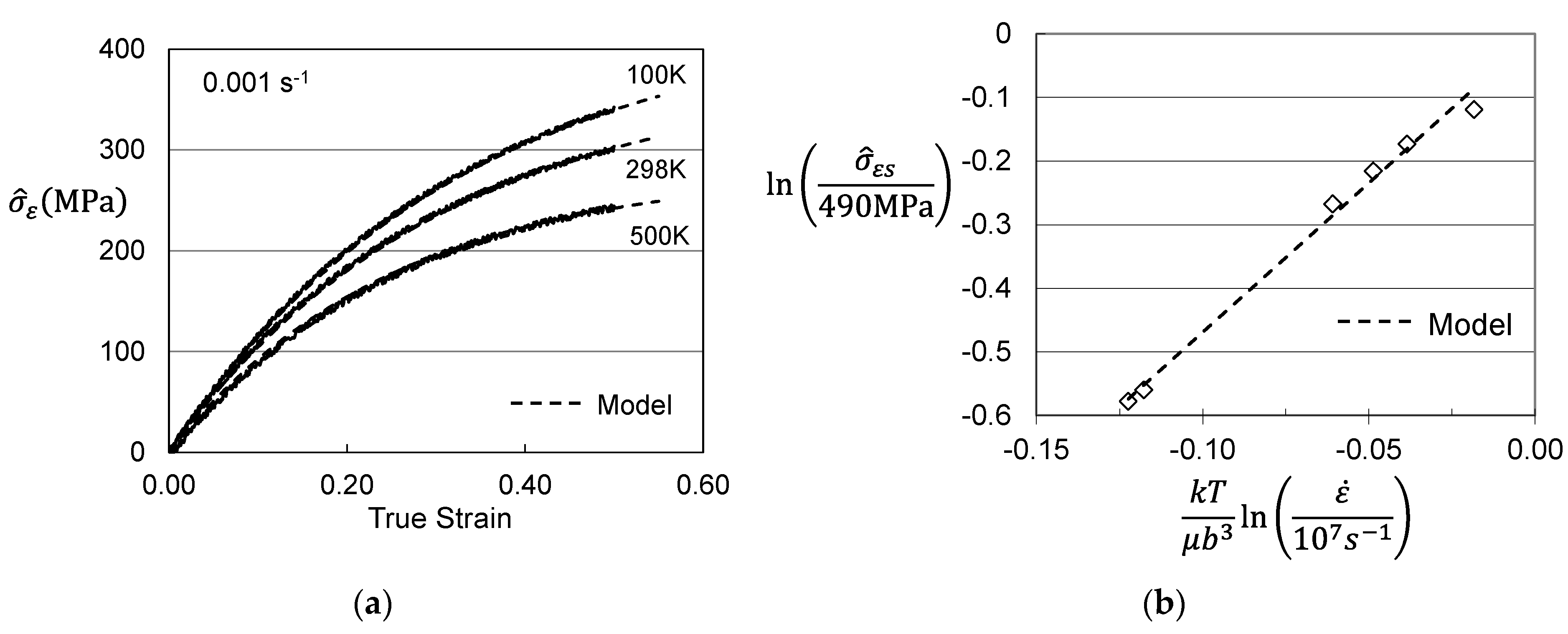
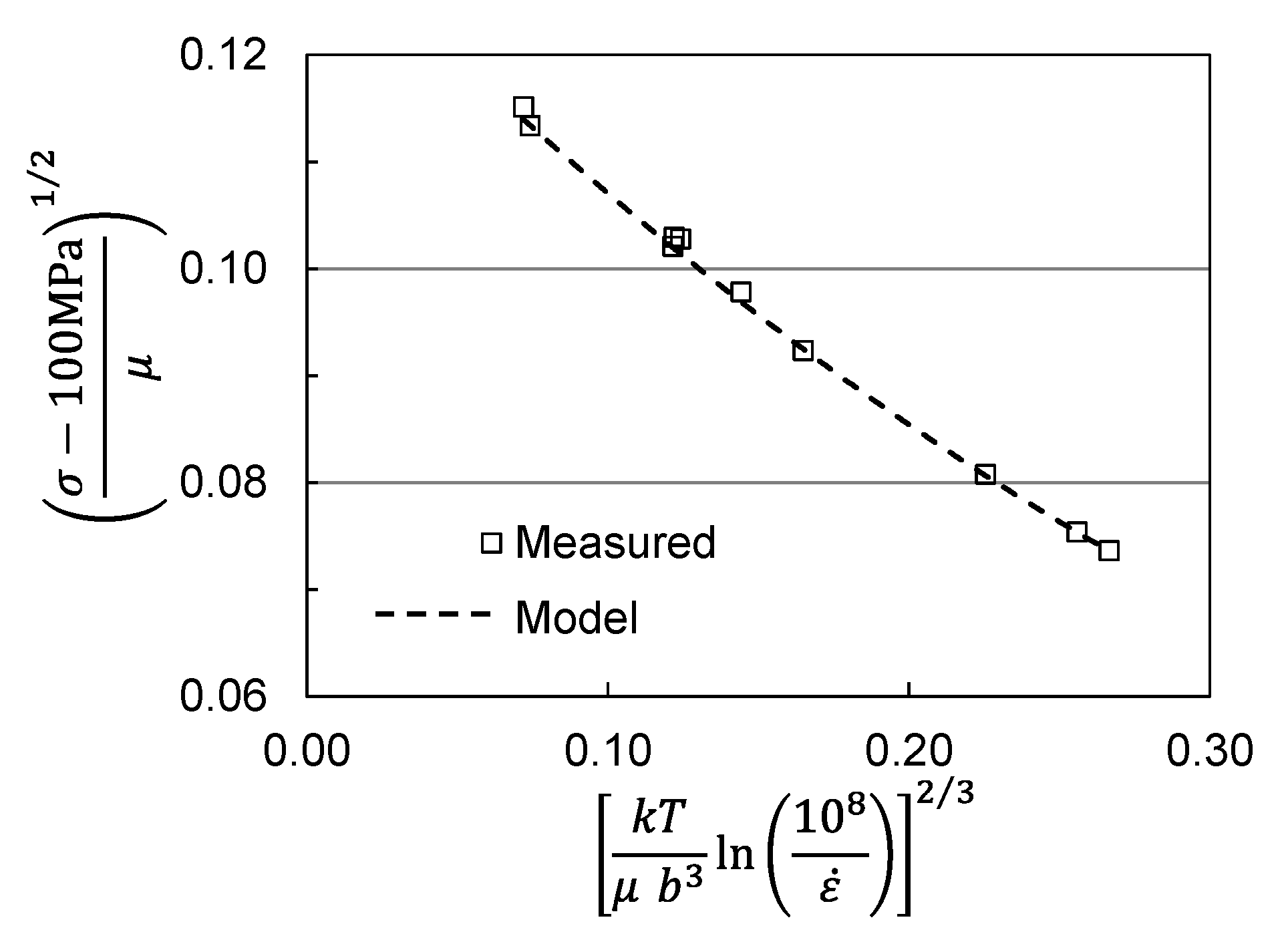
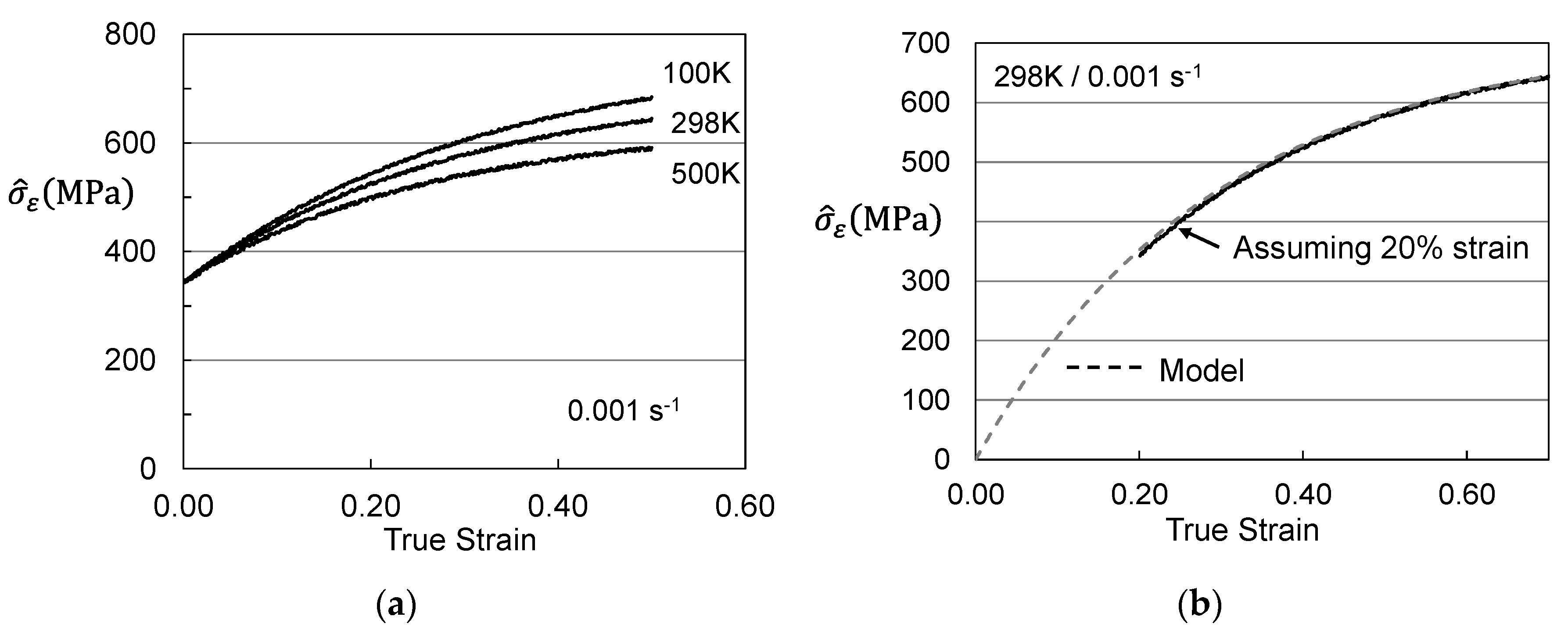
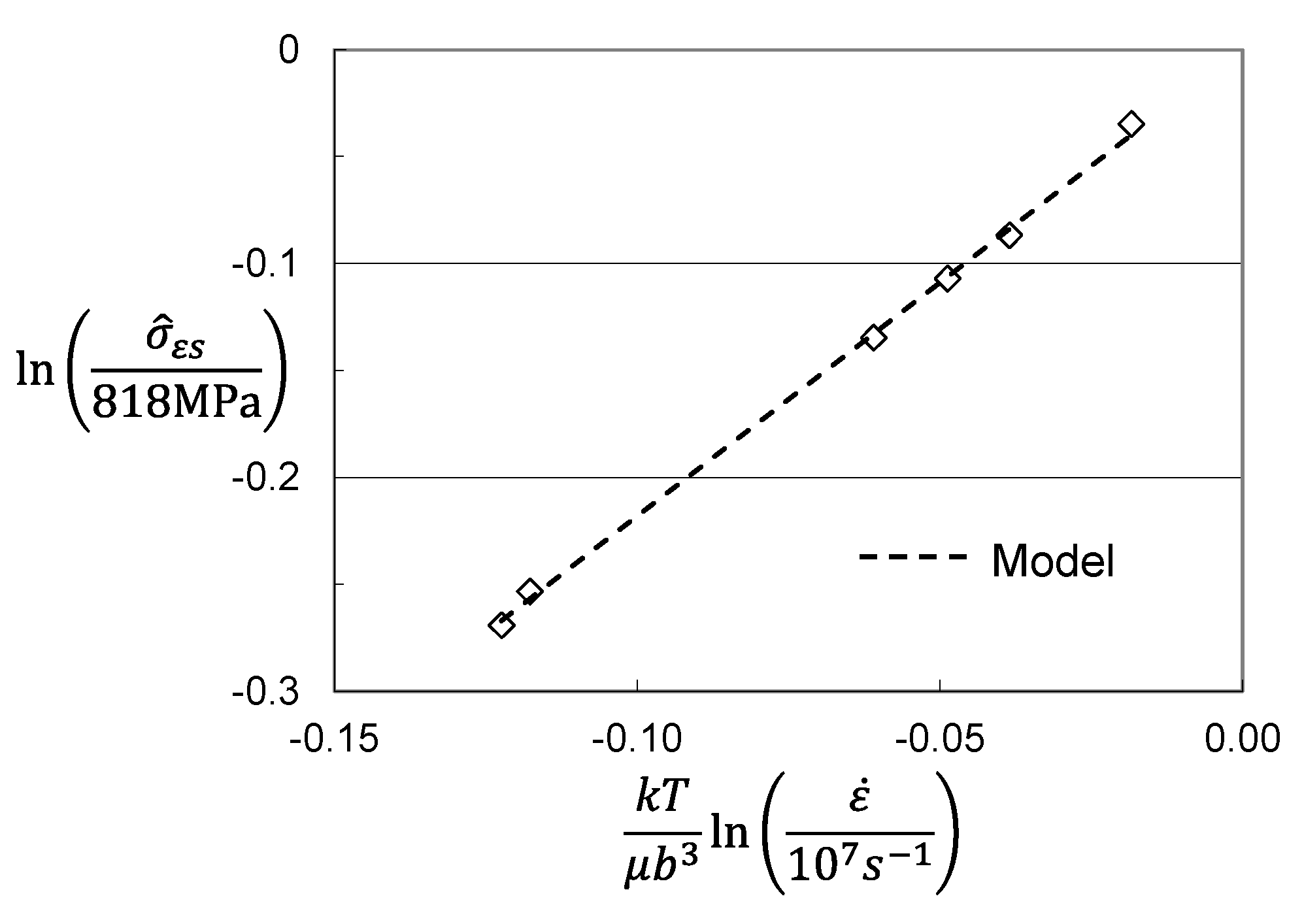


| Model Parameter | Briggs and Campbell [9] | Cheng et al. [11] | Cheng et al. [11] |
|---|---|---|---|
| Figure 1 | Figure 2a | Figure 2b | |
| σa | 50 MPa | 50 MPa | 50 MPa |
| 1541 MPa | 1712 MPa | 1541 MPa | |
| 0.07 | 0.07 | 0.07 | |
| 428 MPa | 600 MPa | 513 MPa | |
| 0.27 | 1.5 | 0.40 | |
| 0 | 0 | 228 MPa | |
| 1.6 | |||
| pp = pi = 0.5, qp = qi = 1.5, pε = 0.667, qε = 1, , | |||
| Equations (1) and (2) | |||||
|---|---|---|---|---|---|
| Obstacle | pj | qj | |||
| Athermal (a) | 100 | ||||
| Solute (i) | 400 | 0.8 | 0.5 | 1.5 | 1 × 108 |
| Peierls (p) | 1000 | 0.2 | 0.5 | 1.5 | 1 × 108 |
| Dislocations (ε) | 0 | 1.6 | 0.667 | 1 | 1 × 107 |
| Physical | Equation (7) | ||||
| b (nm) | (g/cm3) | µ0 (GPa) | D0 (GPa) | T0 (K) | |
| 0.26 | 19.3 | 100 | 15 | 250 | |
| Equations (4) and (6) | |||||
| ĸ | A0 (MPa) | A1 (MPa) | A2 (MPa s−1) | ||
| 1 | 2500 | 10 | 0 | ||
| Equation (5) | Equation (9) | ||||
| (MPa) | (s−1) | AC (J/g/kg) | B (J/g/K2) | C (JK/g) | |
| 800 | 0.5 | 1 × 107 | 0.1345 | 0 | 0 |
| Model Parameter | Material Supplied | Assumed Hot Worked |
|---|---|---|
| Figures 6 and 7a,b | Figures 9b and 10 | |
| σa | 100 MPa | 100 MPa |
| 1050 MPa | 1000 MPa | |
| 0.2 | 0.2 | |
| 700 MPa | 400 MPa | |
| 2.2 | 0.8 | |
| 0 | 343 MPa | |
| 1.6 | 1.6 | |
| 490 MPa | 818 MPa | |
| 0.214 | 0.458 | |
| A0 | 1210 MPa | 2410 MPa |
| A1 | 0 | 10 |
| pp = pi = 0.5, qp = qi = 1.5, pε = 0.667, qε = 1, , , ĸ = 1, = 107 s−1, A2 = 0 | ||
| Temp (K) | Strain Rate (s−1) | Figure 7a | Figure 9a | ||
|---|---|---|---|---|---|
| Material Supplied | Assumed Hot Worked | ||||
| Entry 1 | |||||
| 298 | 0.001 | 1230 | 375 | 2350 | 715 |
| 200 | 1270 | 412 | 2320 | 750 | |
| 100 | 1320 | 435 | 2290 | 790 | |
| 500 | 1120 | 280 | 2380 | 635 | |
| 298 | 0.10 | 1270 | 395 | 2340 | 735 |
| 600 | 1140 | 275 | 2430 | 625 | |
| ĸ = 1 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Follansbee, P. MTS Model Application to Materials Not Starting in the Annealed Condition. Materials 2022, 15, 7874. https://doi.org/10.3390/ma15227874
Follansbee P. MTS Model Application to Materials Not Starting in the Annealed Condition. Materials. 2022; 15(22):7874. https://doi.org/10.3390/ma15227874
Chicago/Turabian StyleFollansbee, Paul. 2022. "MTS Model Application to Materials Not Starting in the Annealed Condition" Materials 15, no. 22: 7874. https://doi.org/10.3390/ma15227874
APA StyleFollansbee, P. (2022). MTS Model Application to Materials Not Starting in the Annealed Condition. Materials, 15(22), 7874. https://doi.org/10.3390/ma15227874





