Inflation and Speculation in a Dynamic Macroeconomic Model
Abstract
:1. Introduction
2. The Keen Model
| Households | Firms | Banks | Sum | ||
|---|---|---|---|---|---|
| Balance Sheet | |||||
| Capital stock | |||||
| Deposits | 0 | ||||
| Loans | 0 | ||||
| Sum (net worth) | X | ||||
| Transactions | current | capital | |||
| Consumption | 0 | ||||
| Investment | 0 | ||||
| Accounting memo [GDP] | [] | ||||
| Wages | 0 | ||||
| Interest on deposits | 0 | ||||
| Interest on loans | 0 | ||||
| Financial Balances | Π | 0 | |||
| Flow of Funds | |||||
| Change in Capital Stock | |||||
| Change in Deposits | 0 | ||||
| Change in Loans | 0 | ||||
| Column sum | Π | ||||
| Change in net worth | |||||
3. Keen Model with Inflation
3.1. Specification and Equilibrium Points
3.2. Local Stability Analysis
3.2.1. Good Equilibrium
3.2.2. Bad Equilibrium
3.2.3. New Equilibria
4. Keen Model with Inflation and Speculation
4.1. Assumptions and Equilibria
4.2. Local Stability Analysis
4.2.1. Equilibria with Finite Debt
4.2.2. Equilibria with Infinite Debt and Finite Speculation
4.2.3. Bad Equilibria with Infinite Debt and Infinite Speculation
5. Numerical Simulations and Qualitative Analysis
5.1. Parameters, Equilibria and Stability
5.1.1. Basic Keen Model
5.1.2. Keen Model with Inflation
5.1.3. Keen Model with Inflation and Speculation
5.2. Dynamics and Behavior
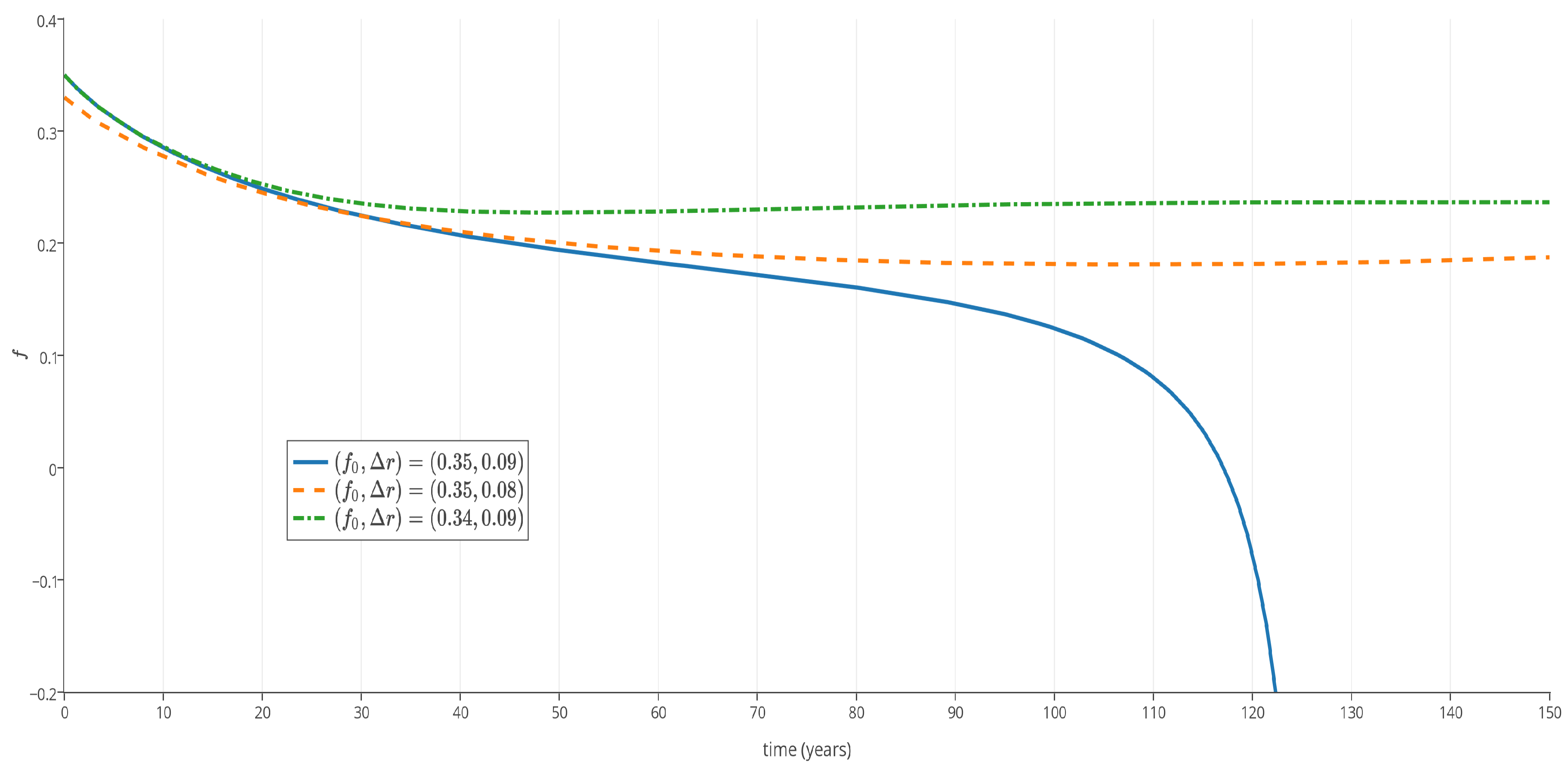
5.2.1. Keen Model with Inflation
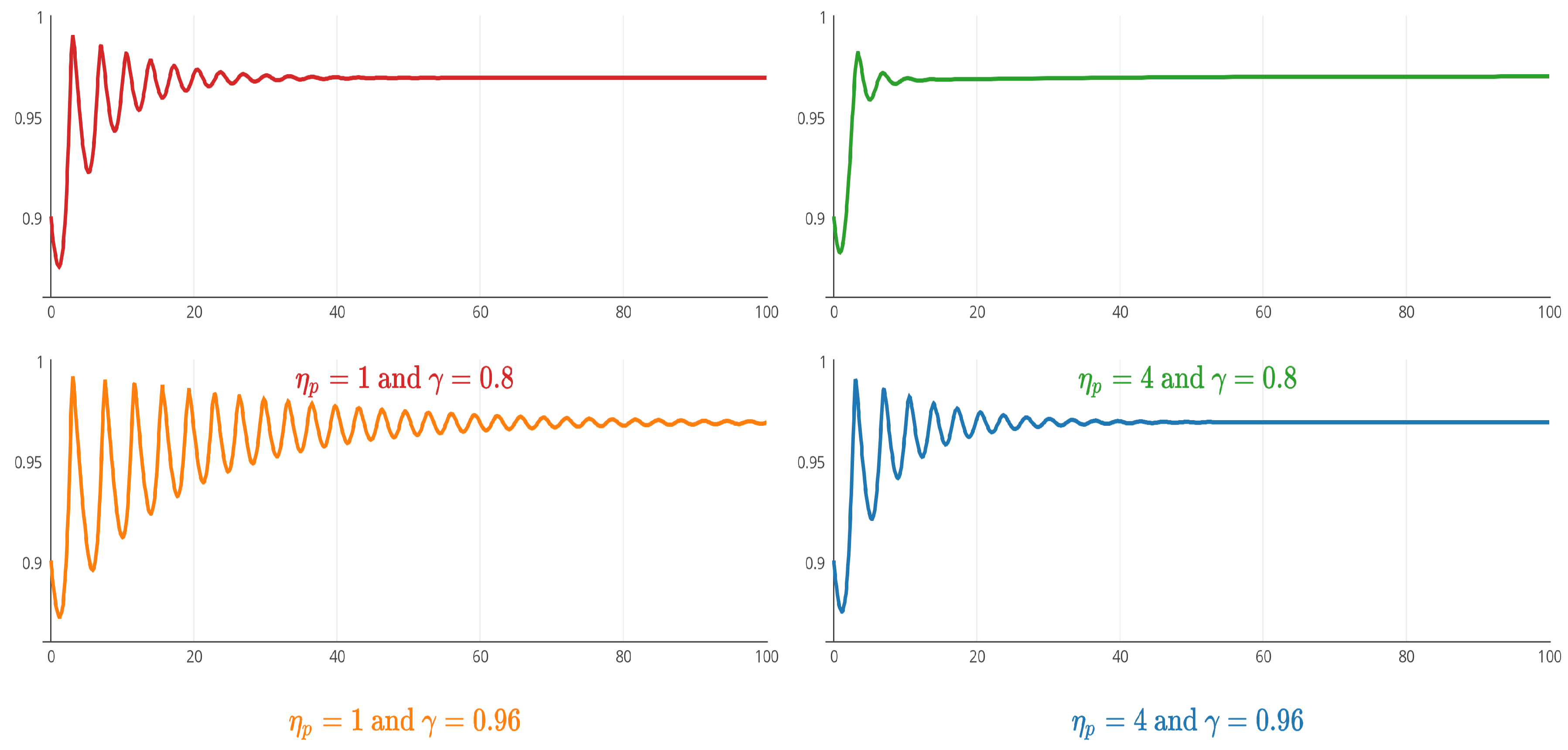
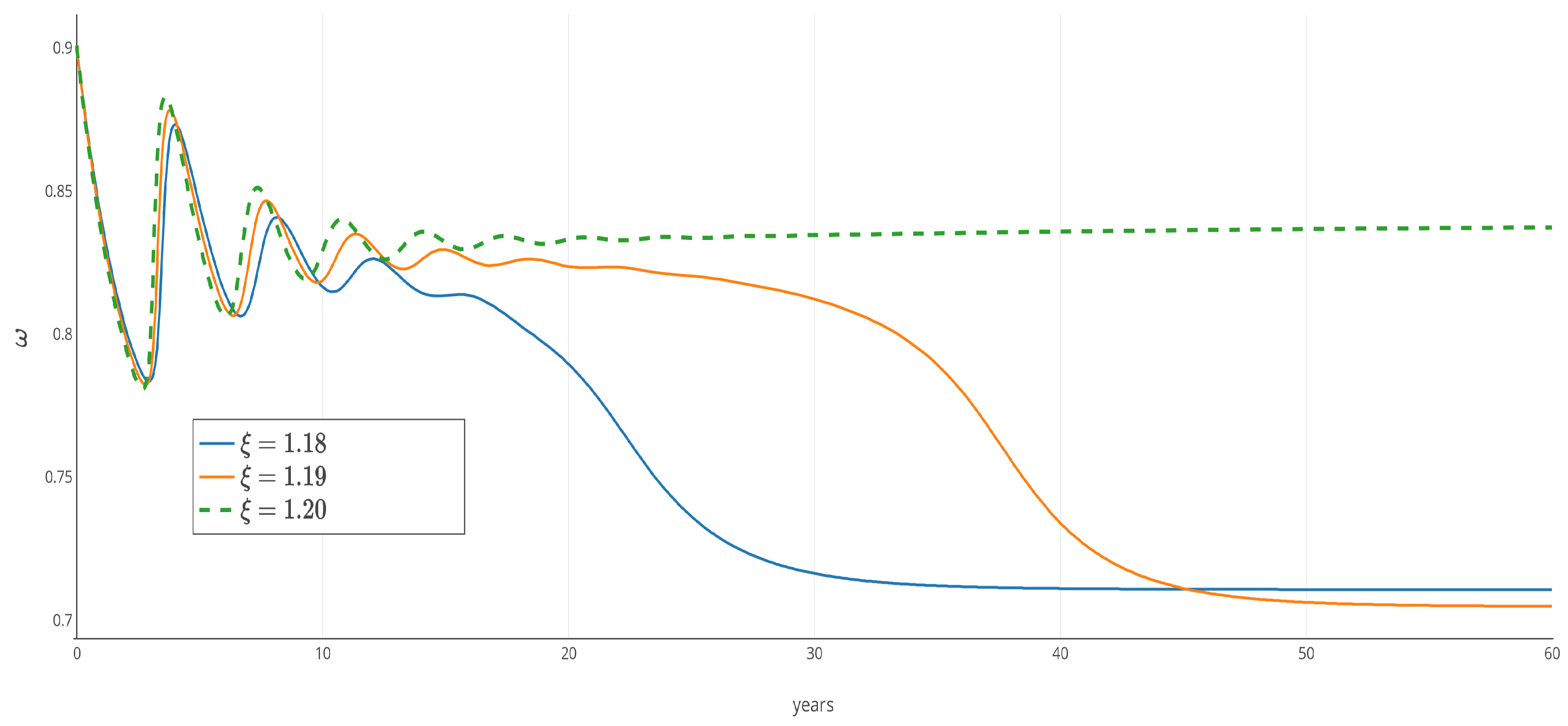
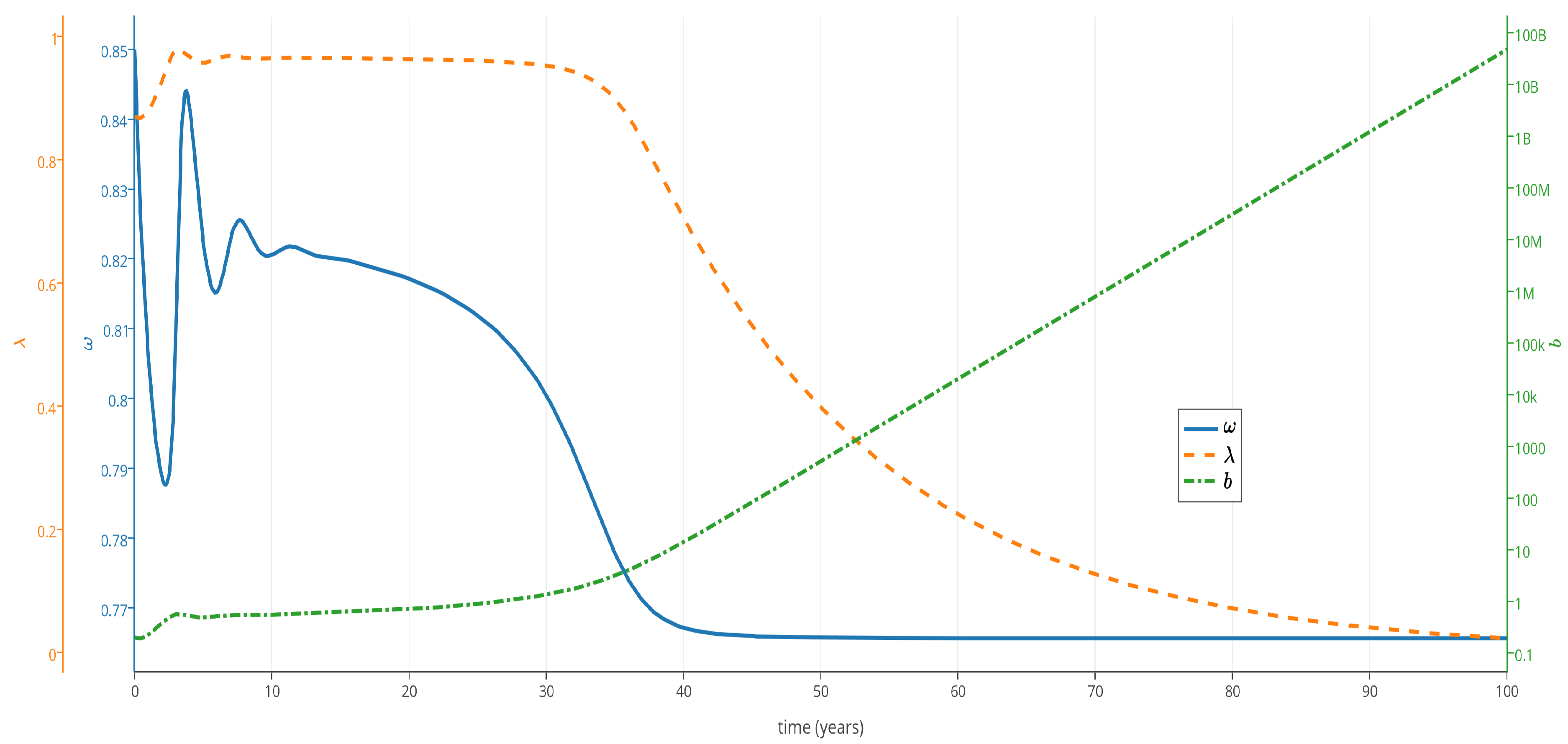
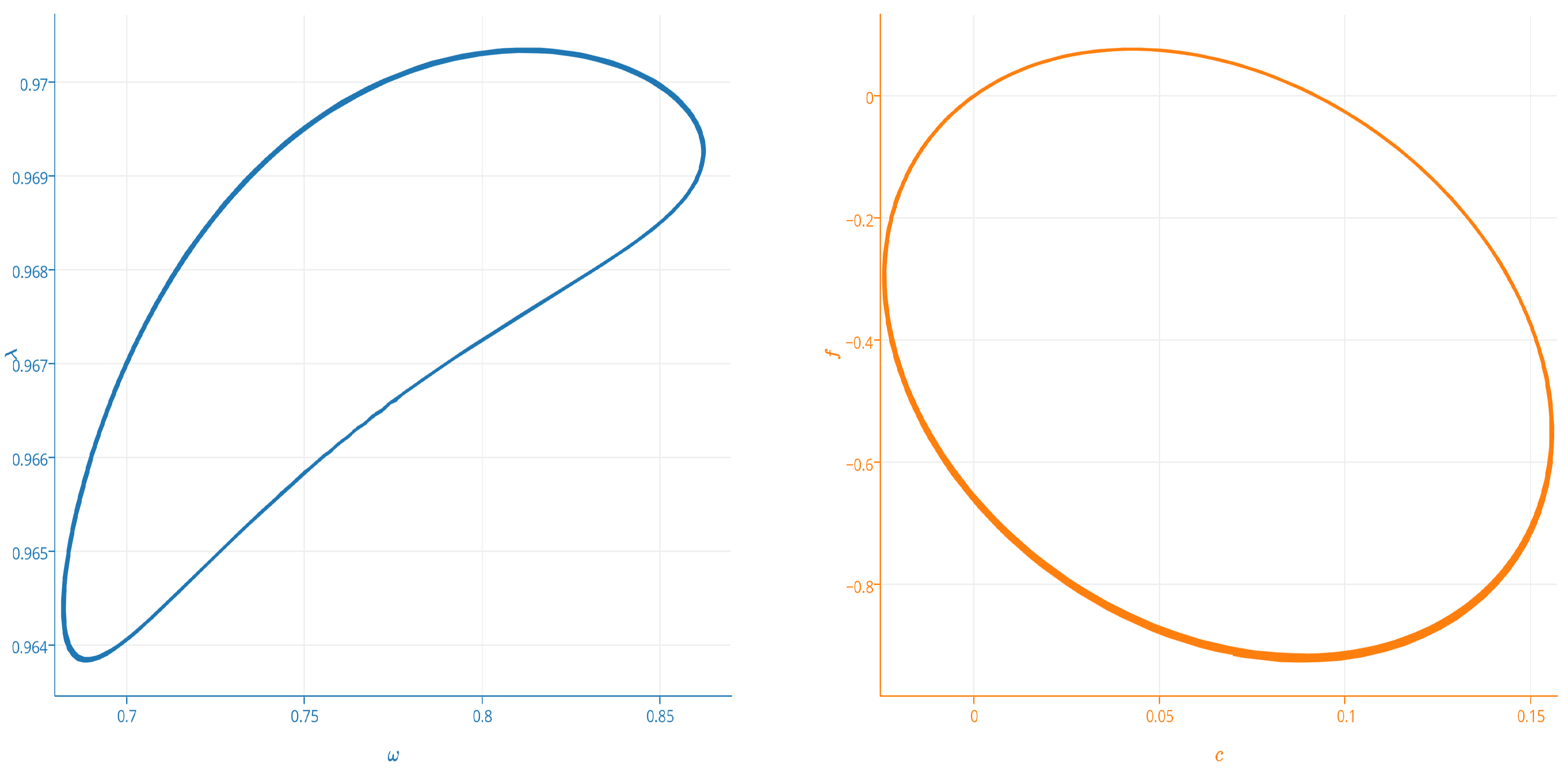
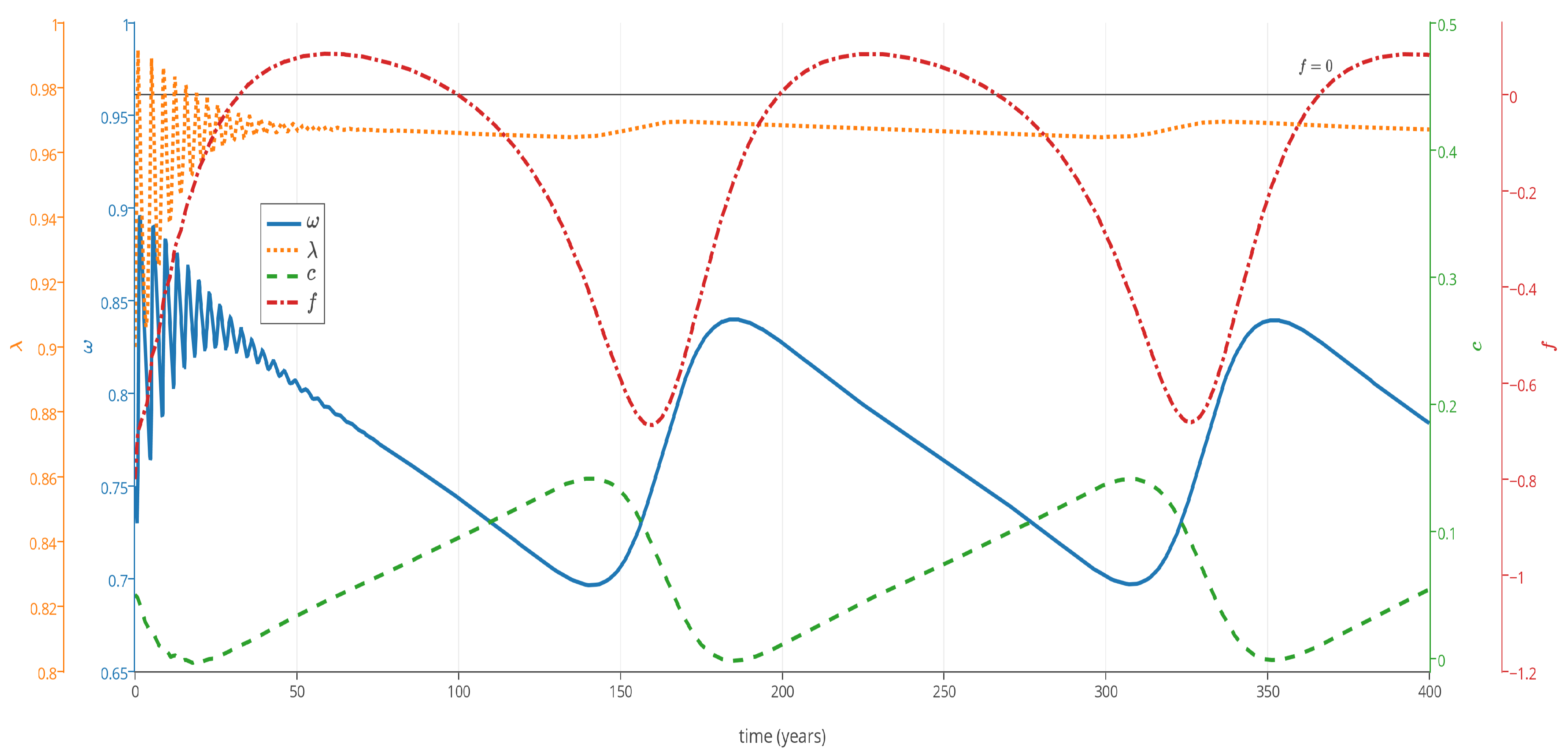
5.2.2. Keen Model with Inflation and Speculation
Acknowledgments
Author Contributions
Conflicts of Interest
References
- J. Hilsenrath, and B. Blackstone. “Risk of Deflation Feeds Global Fears.” Wall Street Journal, 2014. [Google Scholar]
- S. Keen. “Finance and Economic Breakdown: Modeling Minsky’s “Financial Instability Hypothesis”.” J. Post Keynes. Econ. 17 (1995): 607–635. [Google Scholar]
- R.M. Goodwin. “A Growth Cycle.” In Socialism, Capitalism and Economic Growth. Edited by C.H. Feinstein. London, UK: Cambridge University Press, 1967, pp. 54–58. [Google Scholar]
- M.R. Grasselli, and B. Costa Lima. “An analysis of the Keen model for credit expansion, asset price bubbles and financial fragility.” Math. Financ. Econ. 6 (2012): 191–210. [Google Scholar] [CrossRef]
- S. Keen. “A monetary Minsky model of the Great Moderation and the Great Recession.” J. Econ. Behav. Organ. 86 (2013): 221–235. [Google Scholar] [CrossRef]
- R. Franke. “A Metzlerian model of inventory growth cycles.” Struct. Change Econ. Dyn. 7 (1996): 243–262. [Google Scholar] [CrossRef]
- M.R. Grasselli, and A. Nguyen Huu. “Inventory dynamics in a debt-deflation model.” In preparation.
- M. Desai. “Growth cycles and inflation in a model of the class struggle.” J. Econ. Theory 6 (1973): 527–545. [Google Scholar] [CrossRef]
- J. Toporowski, and J. Michell. “The Stock-Flow Consistent Approach with Active Financial Markets.” In Contributions to Stock Flow Modelling: Essays in Honor of Wynne Godley. Edited by D. Papadimitriou and Z. Gennaro. London, UK: Palgrave Macmillan, 2011, pp. 173–196. [Google Scholar]
- J.M. Blatt. Dynamic Economic Systems: A post-Keynesian Approach. Armonk, NY, USA: ME Sharpe Inc., 1983. [Google Scholar]
- J.O. Martins, S. Scarpetta, and D. Pilat. Mark-up Ratios in Manufacturing Industries: Estimates for 14 OECD Countries. Technical Report; Paris, France: OECD Publishing, 1996. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grasselli, M.R.; Huu, A.N. Inflation and Speculation in a Dynamic Macroeconomic Model. J. Risk Financial Manag. 2015, 8, 285-310. https://doi.org/10.3390/jrfm8030285
Grasselli MR, Huu AN. Inflation and Speculation in a Dynamic Macroeconomic Model. Journal of Risk and Financial Management. 2015; 8(3):285-310. https://doi.org/10.3390/jrfm8030285
Chicago/Turabian StyleGrasselli, Matheus R., and Adrien Nguyen Huu. 2015. "Inflation and Speculation in a Dynamic Macroeconomic Model" Journal of Risk and Financial Management 8, no. 3: 285-310. https://doi.org/10.3390/jrfm8030285
APA StyleGrasselli, M. R., & Huu, A. N. (2015). Inflation and Speculation in a Dynamic Macroeconomic Model. Journal of Risk and Financial Management, 8(3), 285-310. https://doi.org/10.3390/jrfm8030285