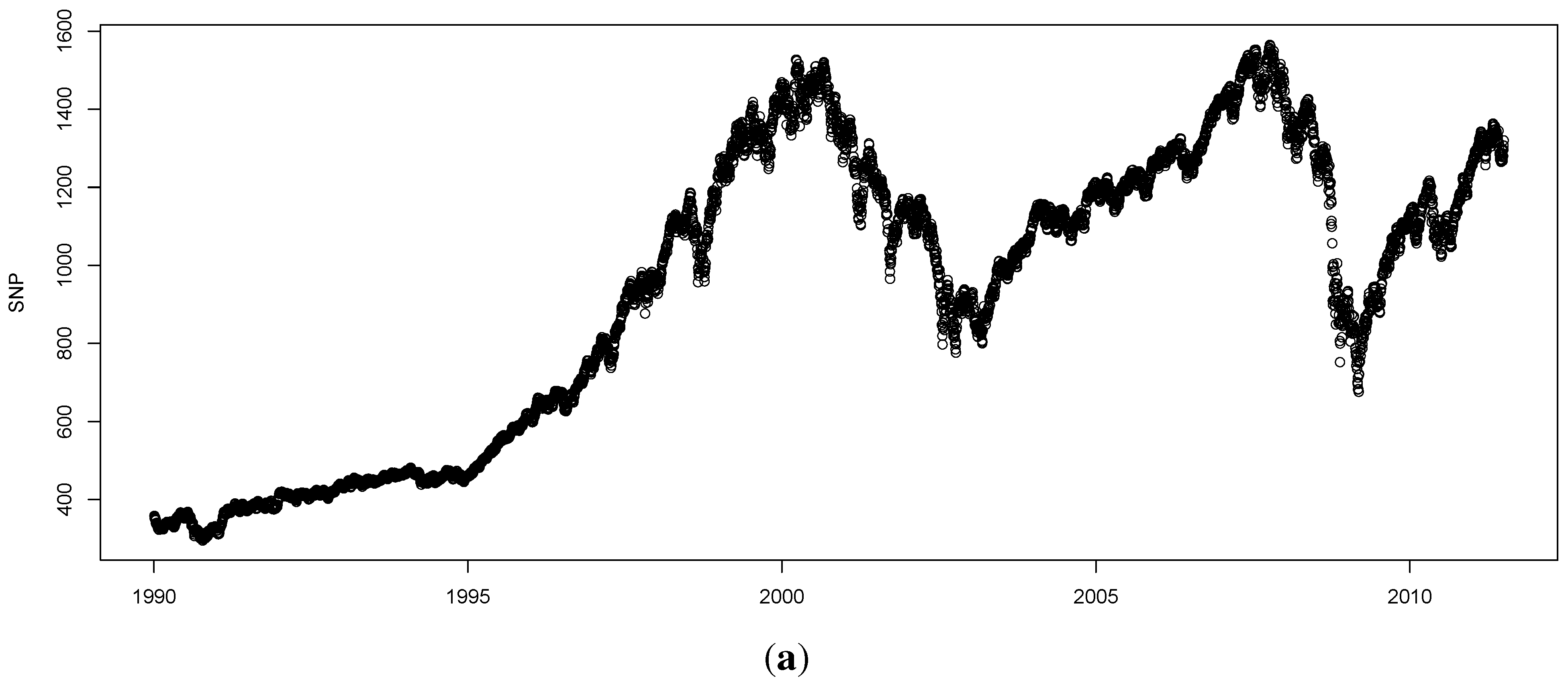
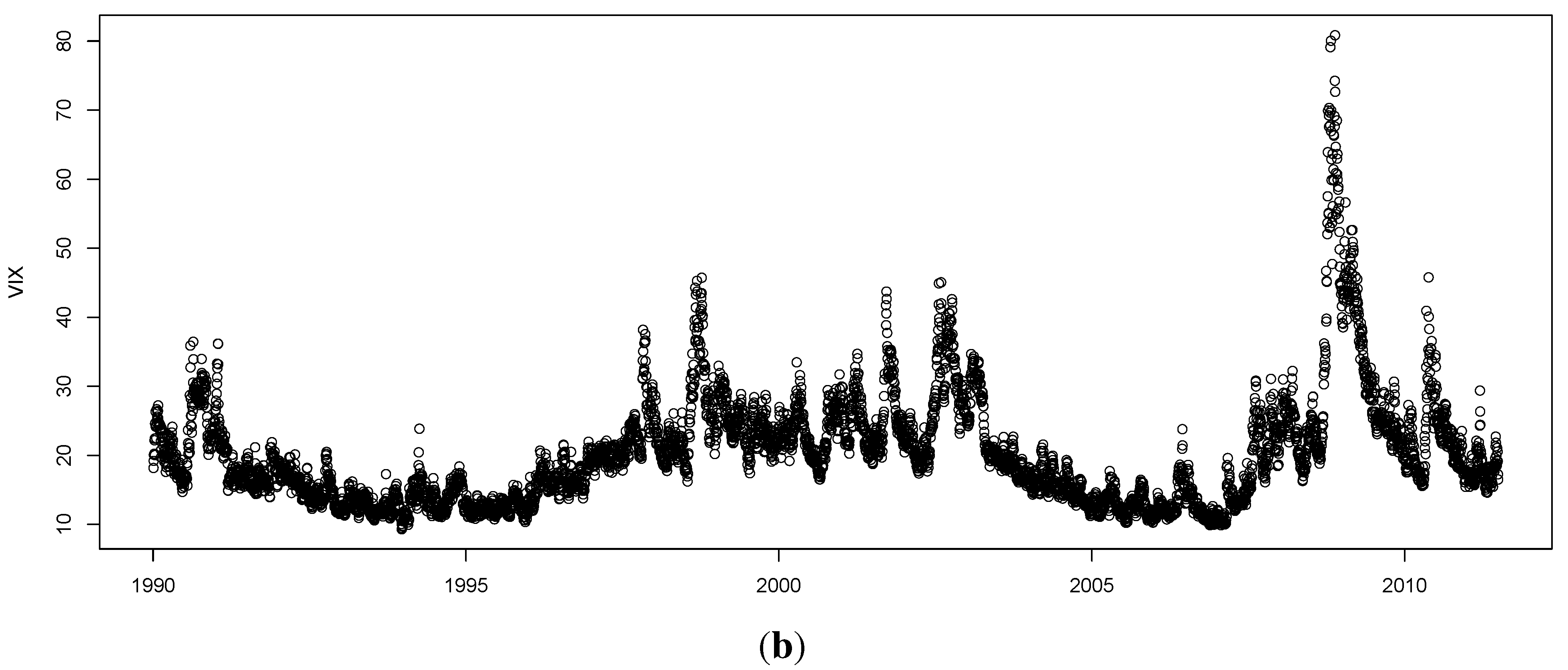
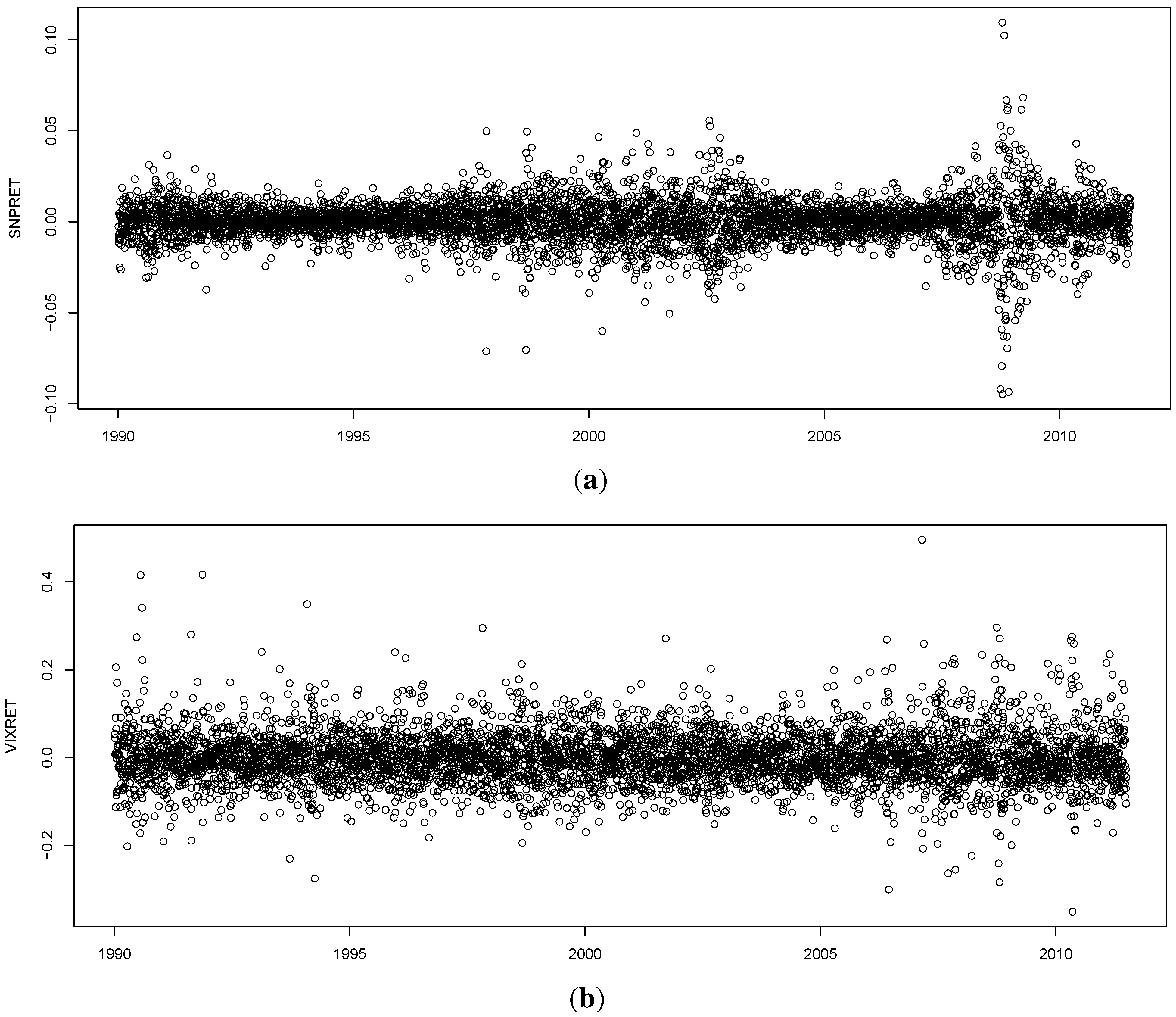
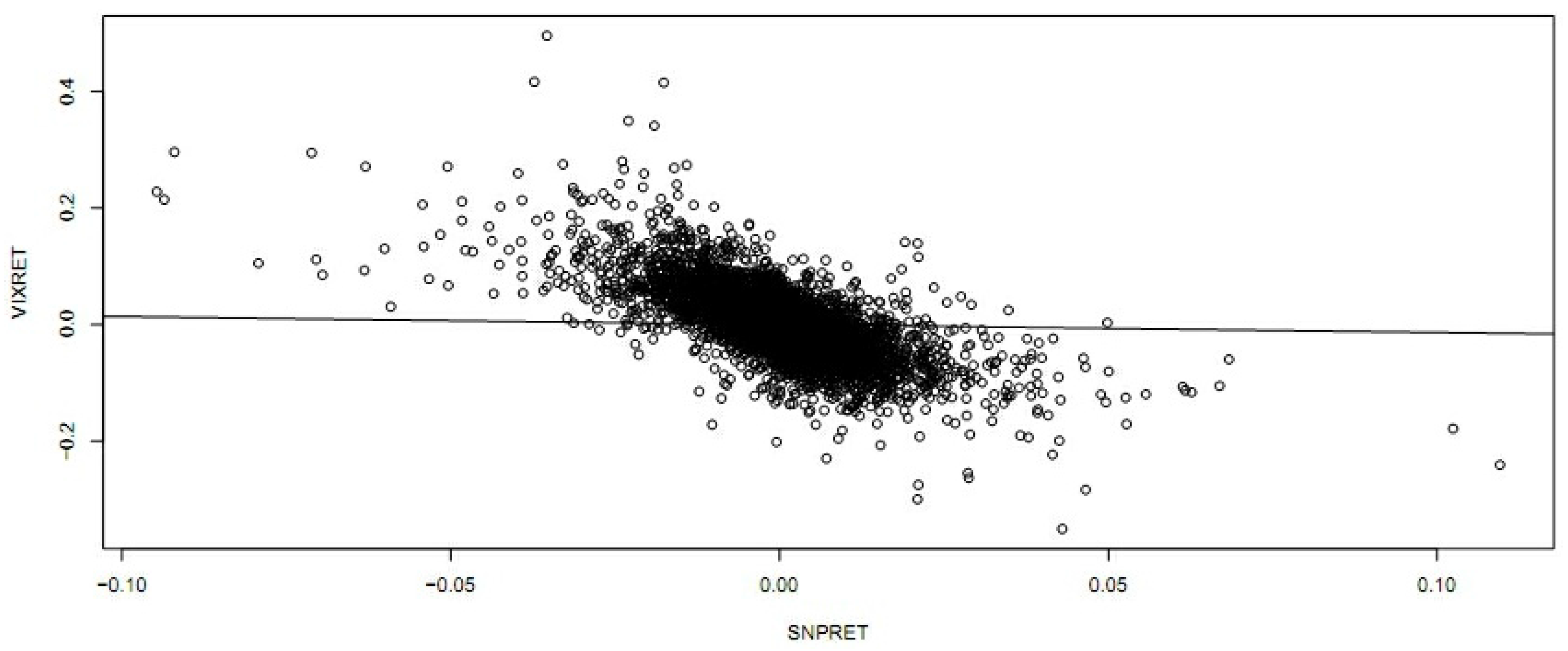
One attractive set of measures that are distribution free are based on entropy. The concept of entropy originates from physics in the 19th century; the second law of thermodynamics stating that the entropy of a system cannot decrease other way than by increasing the entropy of another system. As a consequence, the entropy of a system in isolation can only increase or remain constant over time. If the stock market is regarded as a system, then it is not an isolated system: there is a constant transfer of information between the stock market and the real economy. Thus, when information arrives from (leaves to) the real economy, then we can expect to see an increase (decrease) in the entropy of the stock market, corresponding to situations of increased (decreased) randomness.
Most often, entropy is used in one of the two main approaches, either as Shannon Entropy—in the discrete case, or as Differential Entropy—in the continuous time case. Shannon Entropy quantifies the expected value of information contained in a realization of a discrete random variable. Also, is a measure of uncertainty, or unpredictability: for a uniform discrete distribution, when all the values of the distribution have the same probability, Shannon Entropy reaches his maximum. Minimum value of Shannon Entropy corresponds to perfect predictability, while higher values of Shannon Entropy correspond to lower degrees of predictability. The entropy is a more general measure of uncertainty than the variance or the standard deviation, since the entropy depends on more characteristics of a distribution as compared to the variance and may be related to the higher moments of a distribution.
Secondly, both the entropy and the variance reflect the degree of concentration for a particular distribution, but their metric is different; while the variance measures the concentration around the mean, the entropy measures the diffuseness of the density irrespective of the location parameter. In information theory, entropy is a measure of the uncertainty associated with a random variable. The concept of entropy developed by Shannon [
17], which quantifies the expected value of the information contained in a message, frequently measured in units such as bits. In this context, a ‘message’ means a specific realization of the random variable. The USA National Science Foundation workshop ([
18], p. 4) pointed out that the, “Information Technology revolution that has affected Society and the world so fundamentally over the last few decades is squarely based on computation and communication, the roots of which are respectively Computer Science (CS) and Information Theory (IT)”. In [
17] provided the foundation for information theory. In the late 1960s and early 1970s, there were tremendous interdisciplinary research activities from IT and CS, exemplified by the work of Kolmogorov, Chaitin, and Solomonoff [
19,
20,
21], with the aim of establishing the algorithmic information theory. Motivated by approaching the Kolmogorov complexity algorithmically, A. Lempel (a computer scientist), and J. Ziv (an information theorist) worked together in later 1970s to develop compression algorithms that are now widely referred to as Lempel–Ziv algorithms. Today, these are a
de facto standard for lossless text compression; they are used pervasively in computers, modems, and communication networks. Shannon’s entropy represents an absolute limit on the best possible lossless compression of any communication, under certain constraints: treating messages to be encoded as a sequence of independent and identically-distributed random variables Shannon’s source coding theorem shows that, in the limit, the average length of the shortest possible representation to encode the messages in a given alphabet is their entropy divided by the logarithm of the number of symbols in the target alphabet. For a random variable
X with
n outcomes,
, the Shannon entropy is defined as:
where
is the probability mass function of outcome
. Usually logarithms base 2 are used when we are dealing with bits of information. We can also define the joint entropy of two random variables as follows:
The joint entropy is a measure of the uncertainty associated with a joint distribution. Similarly, the conditional entropy can be defned as:
where the conditional entropy measures the uncertainty associated with a conditional probability. Clearly, a generalized measure of uncertainty has lots of important implications across a wide number of disciplines. In the view of [
22], thermodynamic entropy should be seen as an application of Shannon’s information theory. Jaynes [
22] gathers various threads of modern thinking about Bayesian probability and statistical inference, develops the notion of probability theory as extended logic and contrasts the advantages of Bayesian techniques with the results of other approaches. Golan [
23] provides a survey of information-theoretic methods in econometrics, to examine the connecting theme among these methods, and to provide a more detailed summary and synthesis of the sub-class of methods that treat the observed sample moments as stochastic. Within the above objectives, this review focuses on studying the interconnection between information theory, estimation, and inference. Granger, Massoumi and Racine [
24] applied estimators based on this approach as a dependence metric for nonlinear processes. Pincus [
25] demonstrates the utility of approximate entropy (ApEn), a model-independent measure of sequential irregularity, via several distinct applications, both empirical data and model-based. He also considers cross-ApEn, a related two-variable measure of asynchrony that provides a more robust and ubiquitous measure of bivariate correspondence than does correlation, and the resultant implications for diversification strategies and portfolio optimization. A theme further explored by Bera and Park [
26]. Sims [
27] discusses information theoretic approaches that have been taken in the existing economics literature to applying Shannon capacity to economic modeling, whilst both critiquing existing models and suggesting promising directions for further progress.
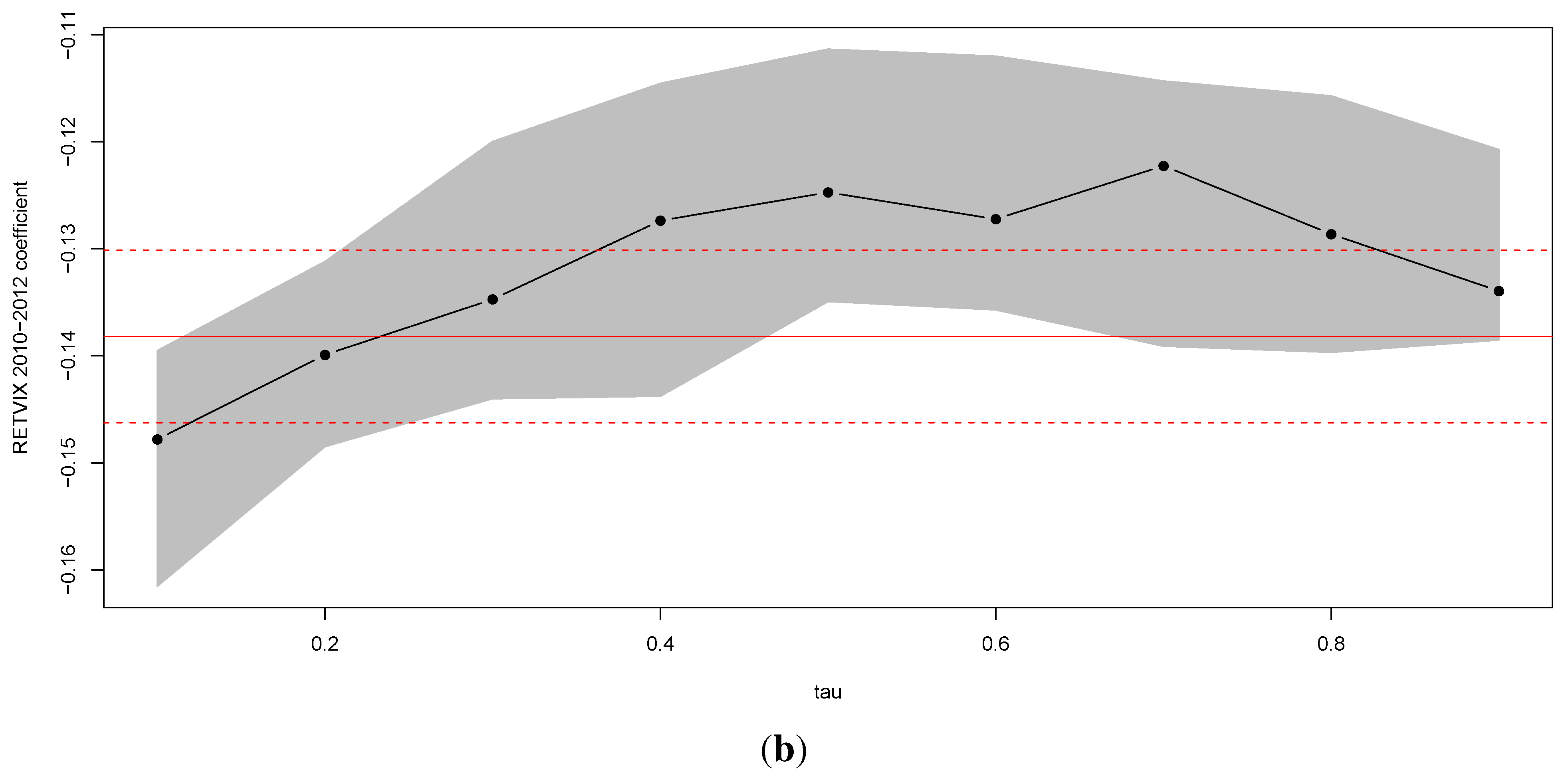
Usually, the variance is the central measure in the risk and uncertainty analysis in financial markets. However, the entropy measure can be used as an alternative measure of dispersion, and some authors consider that the variance should be interpreted as a measure of uncertainty with some precaution (see, e.g., [
28,
29]). Ebrahimi, Maasoumi and Soofi [
30] examined the role of the variance and entropy in ordering distributions and random prospects, and concluded that there is no general relationship between these measures in terms of ordering distributions. They found that, under certain conditions, the ordering of the variance and entropy is similar for transformations of continuous variables, and show that the entropy depends on many more parameters of a distribution than the variance. Indeed, a Legendre series expansion shows that the entropy is related to higher-order moments of a distribution and thus, unlike the variance, could offer a better characterization of
since it uses more information about the probability distribution than the variance (see [
30]).
To estimate entropy we used the “entropy package” in the R library. Hausser and Strimmer [
32], provide an explanation of how they develop their estimators: to define the Shannon entropy, they consider a categorical random variable with alphabet size
p and associated cell probabilities
with
and
. (By alphabet size the reference is to the source alphabet which consists of blocks of elementary symbols of equal size; which are typically of 8-bits in information theory applications, but in this case, are the number of categories used for estimation purposes). It is assumed that
p is fixed and known and in this case Shannon entropy in natural units is given by: