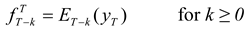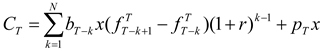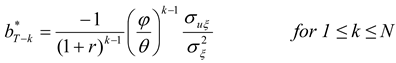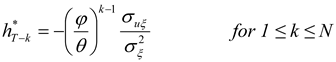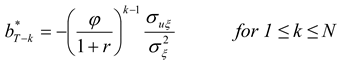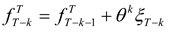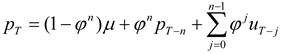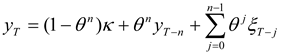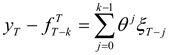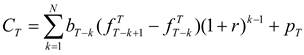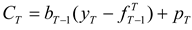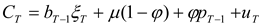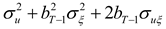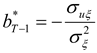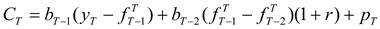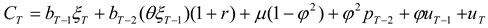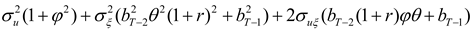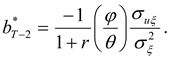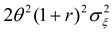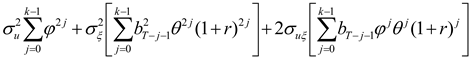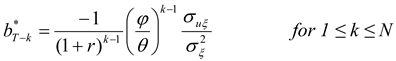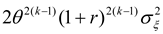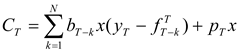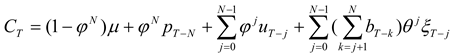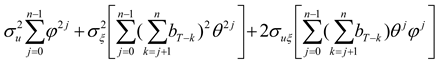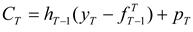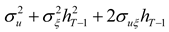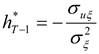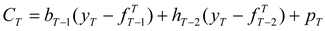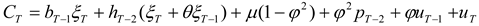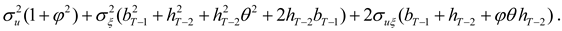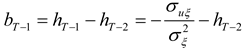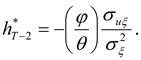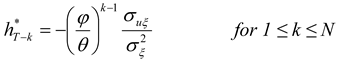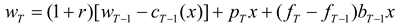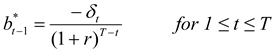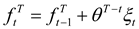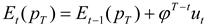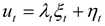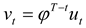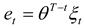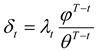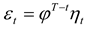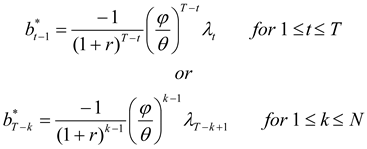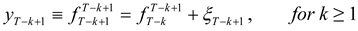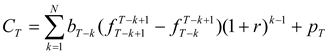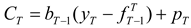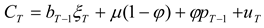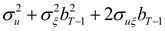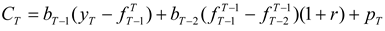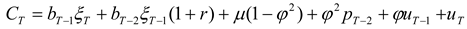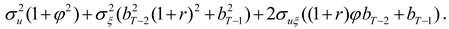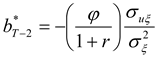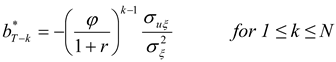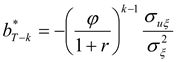ACKNOWLEDGEMENTS: I would like to thank Mike Sher and an anonymous referee for their comments on an earlier draft of this paper. Errors, of course, remain my own responsibility.
1. INTRODUCTION
Consider the hedging problem of a firm facing an uncertain future cash flow at a certain future time, T. The uncertain future cash flow (referred to as the hedged item) may arise from a fixed cash or spot position or, more generally, from revenues/costs/profits in a certain future period referred to as the terminal or target period. The hedging horizon (i.e. the time between now and the future terminal date T) is broken up into a series of discrete intervals, and the decisionmaker's task is to choose futures positions for each period so as to minimize the variance of the future cash flow. For example, the model may be applied to a commodity trader hedging a forward commitment or a firm hedging future input costs.
In a classic, widely-cited study, Howard and D’Antonio (1991), henceforth referred to as HD, derived the optimal hedging strategy in a framework of mean-reverting spot returns and unbiased futures markets. Their main result is that the optimal hedging strategy depends crucially on the rate of mean reversion of the spot process (i.e., the price process of the hedged item, also referred to as the “hedged process”). The current study extends the analysis by explicitly allowing for mean reversion in the price process of the underlying of the futures contract as well (referred to as the “hedging process”). In this extended framework, the HD model may be viewed as a special case in which hedging is carried out by rolling over a series of nearby contracts (“stack and roll” hedging, or just “stack” hedging). The current study considers hedging based on matched-maturity futures contracts (i.e., contracts maturing at the same time as the occurrence of the cash flow being hedged) as well as hedging based on nearby futures contracts. It is seen that if hedging is based on matched-maturity contracts, the optimal hedging strategy depends not so much on the absolute mean reversion rate of the hedged process (as in the case of hedging using nearby contracts), but rather on the relative mean reversion rates of the hedged and hedging processes.
The main contributions of the current paper are as follows. A simple, but empirically relevant setting of mean-reverting prices is used to illustrate matched-maturity hedging and compare it to stack hedging. However, the focus is not on determining if one is better than the other. Rather, the objective is to determine the optimal hedging path in each case. Possible multiperiod hedging paths can be grouped into three categories: (i) a static multiperiod hedge, wherein the hedge position is taken at the start of the hedging horizon and then kept unchanged until the terminal period, (ii) a myopic or single-period hedge, wherein the hedge position is initiated only at the start of the terminal period, and (iii) a dynamic hedge, wherein hedging is initiated at the start of the hedging horizon and updated each period. The focus is on the conditions under which each of these categories is optimal. It is shown that, in general, the optimal hedging path or pattern can be very different depending on whether hedging is carried out using matched-maturity or nearby futures contracts. The exception to this is when futures prices follow a random walk.
In addition to HD, another study to which the current paper has a strong relation is Myers and Hanson (1996), hereafter referred to as MH. Their paper deals with the same problem of hedging a fixed cash position in the presence of basis risk. They show that provided futures prices evolve as a martingale, it is possible to derive an optimal dynamic hedging strategy that is independent of risk preferences under fairly general assumptions about the relationship between spot and futures prices. As will be elaborated upon later, the current paper may be viewed as a special case of the MH model. As a result, the variance-minimizing hedge derived in the current study is also the expected-utility maximizing hedge.
The next section contains a review of the literature, the following section develops the model and discusses implications and the final section concludes with a brief summary of the main results.
2, LITERATURE REVIEW
Several studies have examined the hedging behavior of firms facing price or exchange rate uncertainty in input/output markets. A seminal study by Johnson (1960) analyzed the hedging decision as an optimal portfolio problem and derived the minimum variance hedge ratio. While Sandmo (1971) showed that a firm’s output decision would be affected by price uncertainty, Danthine (1978) and Holthausen (1979) showed that in the presence of a forward market to hedge away this uncertainty, the output decision would be independent of this risk and the firm’s risk preferences. Extensions and refinements were made by Losq (1982), Fishelson (1984) and Zilcha and Broll (1992) among many others. De Meza and von Ungern Sternberg (1980) derived the result that a monopolistic firm is more likely to hedge input risk than a competitive firm as volatile input prices will have a bigger impact on the profits of the former. Koppenhaver and Swidler (1996) investigated how the degree of market power enjoyed by a firm in the output market affects the extent to which the firm will hedge its input price risk. They concluded that lower the market power of the firm, more the importance of hedging. These studies are set in a single-period framework and focus on the relationship between hedging strategies and output decisions in the context of specific market structures. The decision-maker’s objective is typically assumed to be maximizing expected utility or minimizing the variance of end-of-period wealth. Examples of discrete-time, multi-period models investigating the dependency between the production and the hedging decision include Zilcha and Eldor (1991) and Donoso (1995). Among other things, these studies show that the firm will overhedge when current shocks can adversely affect future cash flows.
Another set of studies focuses on the optimal hedging strategy for a trader or producer who will liquidate a non-tradable cash position at a certain future time, T. The hedging horizon (i.e. the time between now and the future terminal date T) is broken up into a series of discrete intervals, and the decision-maker's task is to choose futures positions for each period so as to maximize expected utility of end-of-period wealth or minimize the variance of end-of-horizon wealth/cash flow. Some of these models ignore basis risk (Anderson and Danthine, 1983) and others assume negative exponential utility with a joint normal distribution for cash and futures price changes (Karp, 1987, Martinez and Zering, 1992, and Vukina and Anderson, 1993). A few studies have tackled the optimal dynamic hedging problem in a discrete-time setting without making restrictive assumptions either about risk preferences or the distribution of prices. Notable studies of this kind include HD and MH, mentioned earlier in the introduction and discussed in more detail in the next section. The interested reader is referred to Low, Muthuswamy, Sakar and Terry (2002) for a more extensive review.
While much of the discrete-time literature is based on expected utility maximization or variance minimization, some studies have explored alternative hedging objectives such as regret minimization and approaches based on the mean-extended Gini coefficient and the semivariance. Chen, Lee and Shrestha (2003) provide a fairly comprehensive review of these alternative theoretical approaches to hedging. Yet another branch is concerned with empirical testing of alternative estimation models and techniques, such as Ordinary Least Squares Regression, Cointegration and Error Correction models, Generalized Autoregressive Conditional Heteroscedasticity (GARCH) models and stochastic volatility models. The interested reader is referred to Lien and Tse (2002) for an excellent review of these various econometric approaches and estimation methods. Some noteworthy recent empirical studies include Hung and Lee (2007), who focus on minimizing down-side risk in the presence of volatility clustering and price jumps, Power and Vedenov (2008), who estimate a copula-GARCH model, Huang, Pan and Lo (2010), who compare a duration-dependent Markov-switching vector autoregression approach with GARCH models, Chan (2010), who employs a GARCH model that is modified to allow for jumps, Cao, Harris and Shen (2010), who use a non-parametric approach to estimate hedge ratios designed to minimize Value-at-Risk, and Chen and Tsay (2011), who use a novel approach to estimate a Markov regime-switching, Autoregressive Moving Average model.
There is also a vast literature that investigates optimal hedging in continuous-time. Early classics include Breeden (1984), Adler and Detemple (1988), Duffie and Jackson (1990) and Duffie and Richardson (1991). Breeden (1984) provides the dynamic optimal hedging strategy in terms of the value function for an agent maximizing expected utility of intertemporal consumption, while Adler and Detemple (1988) consider the problem of an agent hedging a nontraded spot position and maximizing logarithmic utility of terminal wealth, and derive an explicit, analytical solution for the case in which markets are complete. Duffie and Jackson (1990) and Duffie and Richardson (1991) consider the optimal hedging problem in a setting in which prices follow Geometric Brownian Motion (GBM) and derive explicit solutions for various mean-variance hedging objectives. Among recent studies, Basak and Chabakauri (2008) provide a good summary of this literature and also provide explicit, tractable solutions to the dynamic hedging problem of a non-tradable asset. Ankirchner and Heyne (2012) solve the problem for the case of stochastic correlation between the process being hedged and the hedging instrument, and Ankirchner, Dimitroff, Heyne and Pigorsch (2012), the case in which the (log) spread between the hedged and hedging processes is stationary (which is not the case when the two processes follow GBM).
As is apparent from the above, there is an extensive literature on dynamic hedging using futures. Below are described some recent studies (other than HD and MH) to which the current study is closely related and a summary of how the current study complements these prior studies.
Hilliard (1999) uses a continuous time setting in which prices follow Geometric Brownian motion to derive optimal hedging results using a “stack and roll” strategy. Neuberger (1999) studies a similar problem, but with a focus on “strip” hedges (i.e., hedging using futures contracts of multiple maturities). The model is based on assumptions about the cross-sectional character of futures prices of different maturities rather than assumptions about their time-series dynamics. In both these studies, the future commitment that is being hedged is far enough in the future so that hedging using a matched-maturity futures contract is either not possible or not economical. In contrast, the current study explicitly considers hedging based on matched-maturity contracts and is set in a different setting of discrete-time, autoregressive prices.
Another strand of research extends from a noteworthy study by Lien and Luo (1993) in which they derive the optimal multiperiod hedging strategy and apply it in a setting of cointegrated spot and futures prices. Their empirical results clearly show the superiority of multiperiod hedging over a myopic (single-period) strategy. Building on this work, Low et al (2002) study multiperiod hedging in a setting in which the futures price follows a cost of carry model. This allows them to capture the effect of the maturity of the futures contract on the spot-futures basis. Their empirical tests show that their “dynamic cost-of-carry hedge” outperforms other strategies such as the conventional (myopic) hedge, the cointegrated price hedge of Lien and Luo (1993), and the GARCH hedge of Kroner and Sultan (1993), although a static, cost-of-carry hedge is found to perform slightly better. Lien and Shaffer (2002) use a three period setting to compare the effectiveness of “strip” hedging with “stack” hedging in managing the risk of a forward commitment. They use a Vector Autoregressive framework to model spot and futures prices and show that “strip” hedging outperforms “stack” hedging especially when forward prices are subject to multiple risk factors. The current study is similar to these studies in that it investigates the same multiperiod hedging problem. However, it differs from these studies in some important respects. Firstly, the current study is set in a framework of mean-reverting rather than non-stationary prices. It is, of course, true that price processes of many assets – especially financial assets - have been determined to be non-stationary, as noted in the above studies. However, as concluded by Bessembinder, Coughenour, Smoller, and Seguin (1995) and noted in Schwartz (1997), a mean reverting process is a good description of the price dynamics of many commodities. Secondly, the main focus of the current study is different. Unlike these prior studies, the current paper does not attempt to assess the empirical performance of alternative hedging approaches. Instead, using a simple, but empirically useful framework, the paper makes clear (i) the connection between the relative rates of mean reversion of hedged and hedging processes on the one hand and the optimal multiperiod hedging strategy on the other, (ii) the conditions under which a single period (myopic) strategy, a static multiperiod strategy and a dynamic multiperiod strategy would each be optimal in this framework, and (iii) the difference in the optimal hedging path when hedging is based on matched-maturity as opposed to nearby contracts.
3. MODEL
Suppose that the hedger has a fixed cash position,
x. The hedger will liquidate this position at terminal time
T and faces the problem that the price of the hedged item as of time
T is uncertain. Suppose that the price process of the hedged item (the “hedged process”) is given by:
Above,
pt is the value of the process in period
t. If
ϕ = 1, then
pt follows a random walk. If
ϕ is strictly between 0 and 1,
µ is the long run mean of
pt and
(1-φ) is the speed of adjustment of
pt to the long run mean. If
ϕ = 0, then
pt is independently and identically distributed (i.i.d.) each period. Thus, higher the value of
ϕ, lower is the degree of mean reversion. Similar to the model in HD, it is assumed that
ut is i.i.d. with variance
. The process for
pt may be equivalently expressed as
Similarly, let
yt denote the price process of the underlying of the futures contract (the “hedging process”).
Above,
yt is the value of the process in period
t,
κ is the long run mean, and (1-
θ) is the rate of mean-reversion.
ξt is assumed to be i.i.d. with variance
. Further,
ut and
ξt are assumed to be contemporaneously correlated with covariance
σuξ, but all noncontemporaneous covariances are assumed to be zero.
Let
denote the futures price in period
T-k of the contract that matures in period
T. Similar to HD and MH, the current study assumes unbiased futures prices.
1 This assumption can be stated as follows:
where
Et is the expectations operator conditional on information available in period
t.
Take the hedger’s objective to be to minimize the variance of the cash flow at time T. (As discussed subsequently, the variance-minimizing hedge is also the strategy that maximizes the expected utility for any increasing, concave utility function.)
3.1 Hedging with Matched-Maturity contracts
The following assumes that the hedger uses matched-maturity futures contracts (i.e., contracts maturing at time T). The case of hedging with nearby futures contracts is considered later. Suppose that the earliest the hedger may initiate hedging is N periods prior to T. (This may be due to non-availability or lack of liquidity of longer-term futures contracts.) For 1 ≤ k ≤ N, let bT-k denote the hedge ratio (i.e., futures position per unit of the spot position).
The post-hedge cash flow in period
T is given by
Above, it is assumed that futures positions are marked-to-market each period, and
r is the constant, periodical interest rate used to compound intermediate, mark-to-market cash flows.
As in HD, the optimal hedge ratios can now be derived by working backwards from the terminal period. As derived in
Appendix A, the optimal hedge ratio at time
T-k is given by
The optimal hedging strategy derived above has several interesting features and implications. First, note that one period before the terminal date, the hedge ratio reduces to the standard single-period optimal hedge ratio,
σuξ/
, derived by Ederington (1979). Second, the hedging strategy derived above is dynamically optimal. Each period's hedge position is chosen after taking into account optimal hedging behavior in the future. Third, the model can be used to not only hedge a long or short cash position, but can also be readily adapted to hedging a future cash flow (such as a future period’s revenues or costs or operating cash flows) by letting the hedged process,
p, denote the relevant cash flow, setting the non-stochastic cash position
x equal to unity, and interpreting
bt as the futures position rather than the hedge ratio. Fourth, the model can be (obviously) used for hedging (either a fixed cash position or a future cash flow) not just on a one-time basis, but on an on-going basis. The optimal hedging strategy can then be viewed not just as minimizing the variance of a single future cash flow, but as minimizing the volatility of the time series of cash flows (provided the spot price process does not follow a random walk). For example, the model can be applied to a firm trying to minimize the volatility of its monthly foreign currency revenues (input costs) by hedging each month’s foreign currency receipts (consumption) over “
N” prior months. Fifth, the model can be readily adapted to hedging using forward contracts. As shown in part B of the
Appendix, the optimal, cumulative hedge ratio at time
T-k for hedging using forward contracts is given by
Sixth, this model can be shown to be a special case of the model developed in Myers and Hanson (1996), referred to as MH. In this paper, they show that provided futures prices evolve as a martingale, it is possible to derive an optimal dynamic hedging strategy that is independent of risk preferences under fairly general assumptions about the relationship between spot and futures prices. All they require of the utility function is that it should be increasing and strictly concave. As shown in part C of the
Appendix, the assumptions in the current model satisfy the conditions laid out in the MH framework. Consequently, the optimal hedging strategy derived in this study not only minimizes the variance of the net cash flow on the terminal date, but also maximizes the terminal date expected utility. This is related to the results in Lence (1995) and Rao (2000) derived in a single-period setting.
The points mentioned above are explicit or implicit in HD and/or in MH. The main point of the current paper is the following, which is a consequence of the additional structure imposed in the current study. As evident from (6), the optimal hedging strategy depends in an important manner on the relative magnitudes of
ϕ and
θ, which, as discussed below, may be influenced by the extent of market power enjoyed by the firm. The case
ϕ =
θ reflects the situation in which both the hedged process and the hedging process mean-revert with the same speed. This is likely to occur when the hedged and hedging processes are either the same or closely related (such as jet fuel and crude oil). If
ϕ <
θ, the hedged process mean-reverts at a
faster rate than the underlying of the futures contract. (Recall that the rate of mean reversion is one minus the autoregressive coefficient.) This is likely to be an empirically important case. For example, consider an airline hedging its operating cash flows against jet fuel price fluctuations using oil futures. In this case, the hedged process is the operating cash flow and the hedging process is oil price. Suppose that the firm is faced with an adverse shock, such as an increase in oil prices. If the firm has some degree of market power, it may be able to raise the price of its product at least partially and with a lag even if not immediately. As a result, its cash flows may recover (or revert to previous levels) quicker than the price of oil goes back down. In general, greater the pricing power of the firm, the better the firm can respond to adverse shocks, and therefore faster will be the mean reversion of its operating cash flows and hence smaller the ratio of
ϕ to
θ. Lastly, if
θ <
ϕ, the hedged series mean-reverts
slower than the underlying of the forward contract. This would, for example, reflect a situation in which operating cash flows take more time to return to pre-shock levels than the hedging process. Such cases are probably less common in the real world.
Table 1 illustrates how the optimal hedging strategy changes with the ratio of
ϕ to
θ. For ease of exposition,
σuξ/
(the ratio of the covariance between the shocks affecting the hedged and hedging processes to the variance of the hedged process) is set equal to unity. For simplicity, the interest rate,
r, is set equal to zero. Therefore, the results in the table may be interpreted as relating to hedging using forward contracts rather than futures. Thus, the table contains optimal, cumulative hedge positions in forward contracts for a few selected values of the ratio of
ϕ to
θ. It is assumed in the calculations that the number of prior periods over which hedging is possible is twelve (i.e.,
N = 12).
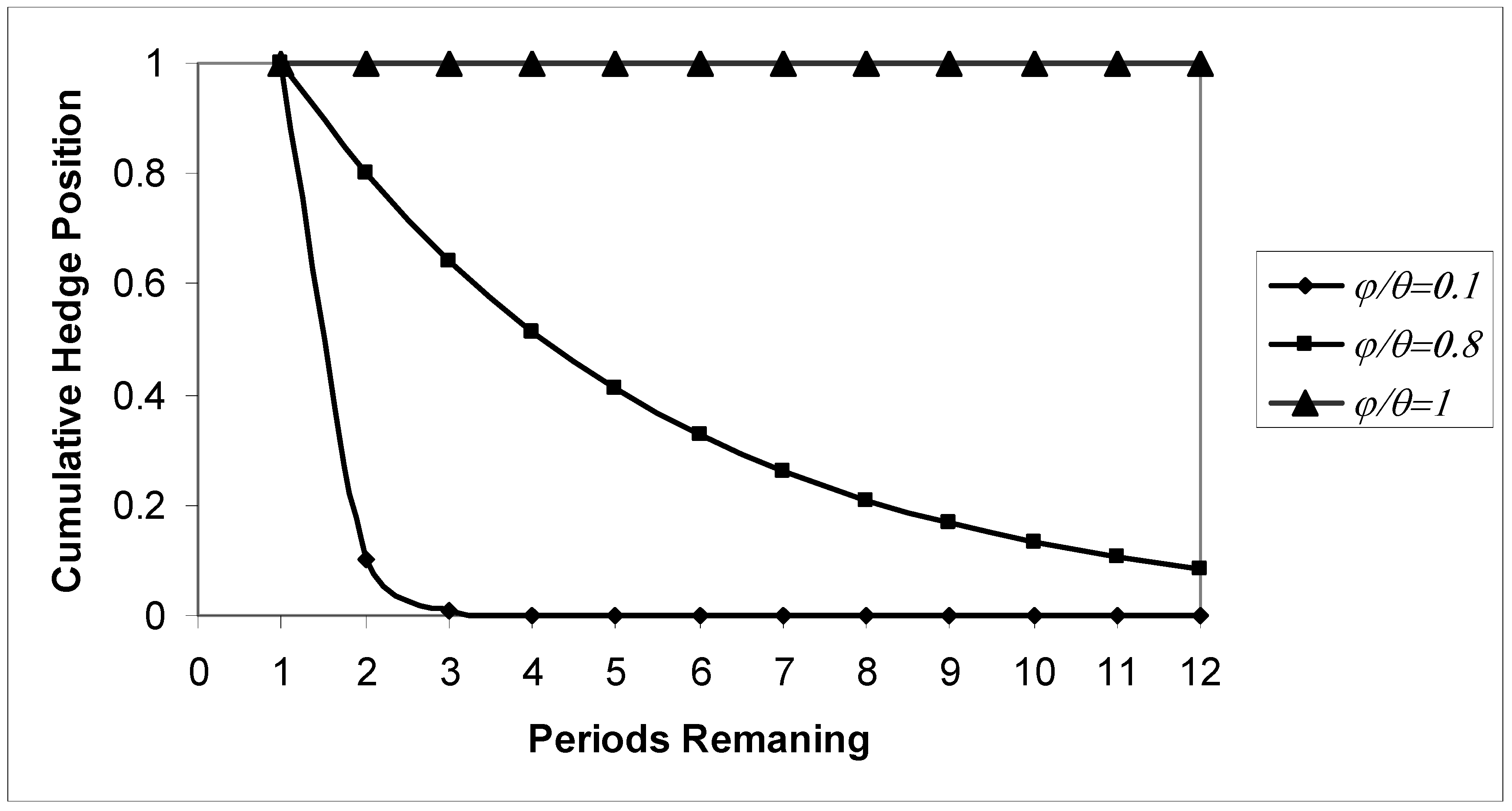
For convenience, define a “back-loaded” strategy as one in which substantial hedging positions are taken only in the period(s) just prior to the terminal date and a “front-loaded” strategy as one in which substantial hedging positions are taken well in advance of the terminal date. Now, consider the case,
ϕ/
θ=
1, in which both the hedged and hedging processes mean-revert at the same rate. In this case, the optimal strategy is seen to be a front-loaded strategy. In fact, the optimal strategy is essentially a static, multiperiod hedge – i.e., to undertake a complete hedge as far ahead as possible and retain this position until the terminal date. However, if the ratio is strictly between zero and one, then the optimal strategy is to spread the hedging activity over multiple periods. For example, if the ratio is 0.8, as shown in
Table 1, the hedger should enter into a partial hedge to the extent of 8.59% of the optimal single period hedge twelve periods prior to the terminal date. The hedger should gradually increase the hedge position each subsequent period such that it is 64% three periods prior to the terminal date and, of course, 100% one period prior. In general, both
Table 1 and
Graph 1 illustrate that smaller the ratio of
ϕ to
θ, smaller should be the size of the initial position with most of the hedging concentrated in the last few periods prior to the terminal date. Closer the ratio is to zero, more back-loaded the strategy should be. If the hedged process mean-reverts at a considerably faster rate than the hedging process (
ϕ <<
θ) perhaps as a consequence of the firm’s market power, distant shocks have a relatively small impact on the firm and only short-term shocks (i.e., shocks close to the terminal date) need to be hedged against. Indeed, if the ratio is zero, then a single period (myopic) hedging strategy (of entering into a hedge only at the start of the terminal period) would be perfectly appropriate. On the other hand, larger the ratio of
ϕ to
θ, larger should be the hedging positions taken in earlier periods. In fact, if it is the hedged process that mean-reverts
slower (
ϕ >
θ), then the optimal hedging strategy is to overhedge in the initial period, and then reverse out the excess position gradually as the terminal date draws near. This is illustrated in the last column of
Table 1.
3.2 Hedging using nearby contracts (stack hedging)
Now consider how the optimal hedging strategy will be different if hedging is carried out by rolling over a series of nearby contracts.
2 For simplicity, it is assumed that futures contracts are available for all expiration dates leading up to the terminal date.
As shown in part D of the
Appendix, the optimal hedging strategy is now given by
As may be seen, the autoregressive coefficient of the hedging process,
θ, plays no role. The result above is similar to the one derived by HD. (The result in HD is slightly different as in their model, the hedger is hedging not just one future cash flow but several. This paper considers the simpler problem of hedging just one future cash flow in order to simplify the exposition and ensure that a key point of the paper, namely the difference between hedging using nearby contracts and hedging using matched-maturity contracts, is made as clearly as possible.) If the autoregressive coefficient of the hedged process,
ϕ, is close to zero, then the optimal hedge ratio in all prior periods from
T-2 through
T-N would be close to zero; and the optimal hedge ratio one period prior to the terminal period (i.e., as of
T-1) would, of course, equal the standard single period optimal hedge. Thus, a single period (myopic) approach to hedging would be appropriate only in the case in which the hedged process is independently and identically distributed. Conversely, a front-loaded strategy of taking large hedging positions several periods prior to the terminal date is optimal only if
ϕ is close to unity – i.e., if the rate of mean reversion of the hedged process is so slow that the process is close to being a random walk. Note that the values in
Table 1 can be used to illustrate hedging using nearby contracts as well, with the difference that each column of
Table 1 should be taken to represent a particular value of
ϕ rather than the ratio of
ϕ to
θ.
3.3 Hedging using matched-maturity contracts v/s nearby contracts
From (3) and (4),
Thus, futures contracts of all maturities are perfectly correlated under the assumptions of our model, which is, of course, an immediate consequence of the fact that in this model, the entire term structure of futures price is driven by a single risk factor. Therefore, both hedging strategies – based on matched-maturity contracts and rolling over nearby contracts – will be equally effective (in the sense that both strategies will result in the same variance of terminal cash flow). However, as mentioned earlier, it is not the comparative effectiveness of these two strategies that is the focus of this paper, but rather the difference in the optimal hedging path and the conditions that determine the path in each of these cases.
The main differences between the two cases (hedging with matched-maturity v/s nearby futures) are summarized in
Table 2. It is clear that the optimal hedging strategy can be very different between hedging based on matched-maturity contracts and hedging based on nearby contracts. For example, if
ϕ =
θ < 1, then if hedging is based on matched-maturity contracts, the optimal strategy is a static multiperiod hedge, while if hedging is carried out by rolling over nearby futures, then the optimal strategy is either front-loaded or back-loaded depending on how close
ϕ is to zero. However, it is also apparent that if the price process of the underlying of the futures contract follows a random walk (i.e., if
θ = 1), then the optimal hedging path is the same regardless of whether hedging is based on matched-maturity or nearby contracts.
It may be noted that in the case of both hedging with nearby contracts and hedging with matched-maturity contracts, if the model is applied to hedging on an ongoing or rolling basis, the optimal hedging strategy may entail taking hedging positions that exceed the quantity required to hedge just a single future period’s cash flow. For example, suppose that the ratio of autoregression coefficients is 0.8, and consider a firm using matched-maturity forwards to hedge monthly cash flows on a rolling twelve-month basis. For this firm, the quantity of forward contracts held at any point in time would be 465% of the quantity required to hedge a single period’s cash flow. (4.65 is the sum of the hedge ratios in the appropriate column of
Table 1).
4. CONCLUSION
This study examines the multiperiod hedging decision relating to a stochastic future cash flow in a setting of mean-reverting price processes and unbiased futures markets. It is seen that the optimal multiperiod hedging strategy depends in an important way on whether hedging is carried out using nearby or matched-maturity contracts. The question of interest is the hedging path – whether it is optimal to undertake a back-loaded strategy (in which substantial hedge positions are taken only in the period(s) just prior to the terminal date) or a front-loaded strategy (in which substantial hedge positions are taken well in advance of the terminal date). In the case of hedging with nearby contracts, the answer depends on the rate of mean reversion of the hedged process. However, in the case of hedging with matched-maturity contracts, the optimal strategy depends crucially on the relative rates of mean reversion of the hedged and hedging processes. If both processes mean-revert at roughly the same rate, then the optimal strategy is a front-loaded path. However, higher the rate of mean reversion of the hedged process relative to that of the futures contract’s underlying, the greater the appropriateness of a back-loaded (myopic or single period) strategy.