Next Article in Journal
The Role of Financial Compensation Oversight Committees in Improving the Financial Performance Governance of Saudi Banks
Previous Article in Journal
Modeling Behavioral and Attitudinal Drivers of Life Insurance Selection and Premiums: Polynomial Approaches to Perceived Affordability in Term and Cash Value Products
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JRFM
Volume 18
Issue 9
10.3390/jrfm18090513
jrfm-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends

by
Sara Ali Alokley
Department of Finance, School of Business, King Faisal University, Al-Ahsa 31982, Saudi Arabia
J. Risk Financial Manag. 2025, 18(9), 513; https://doi.org/10.3390/jrfm18090513
Submission received: 3 August 2025 / Revised: 2 September 2025 / Accepted: 5 September 2025 / Published: 16 September 2025
(This article belongs to the Section Mathematics and Finance)
Browse Figures
Versions Notes

Abstract

This study presents a bibliometric analysis of the literature on financial options pricing. This study examined 1713 peer-reviewed journal articles published between January 2002 and January 2023. The literature on options pricing was analyzed using bibliometric methodologies and analysis techniques such as co-citation, citation networks, content, publication and keywords trends. The contribution of this study to the literature on options pricing lies in enhancing the understanding of the field by proposing ten clusters. These clusters will help investors, policymakers and researchers gain deeper insights on the topic and the research gaps and are crucial for the investment financial communities in light of institutions’ and society’s rising reliance on financial derivatives.

1. Introduction

Financial options are a type of derivative, defined as a financial instrument giving the right, but not the obligation, to buy or sell an underlying asset, such as a share or currency, for a predetermined price at a fixed future date. Kairys and Valerio (1997) state that options contracts date back as far as ancient Greece, and the options quotes were published weekly by the Commercial and Financial Chronicle in New York City during the period between 1873 and 1875. Since the word option has many definitions, studies in this field have used “financial option” and “option contract” interchangeably. Options rely on the underlying asset. The size of the option market has grown; in the USA, for example, exceeding 10.2 billion contracts in December 2024 (Market Watch, 2025). Today, investors and traders rely heavily on financial options to better manage their portfolios, which are primarily used as a hedging device; options contracts can provide investors with risk-reduction strategies.
Due to the importance of options in the financial sector, they have been studied since 1900; in the thesis of Bachelier (1900), he laid the foundation for options pricing by mathematically modeling the movement of the stock price and the pricing as a limit of random walks. During the 1960s, Paul Samuelson discovered Bachelier’s thesis, and it influenced his later work, including two significant articles published by (P. Samuelson, 1965; P. A. Samuelson, 1960). During this period, traders employed the Brownian motion technique until the Black and Scholes (1973) model was introduced. This model brought about a significant change in options pricing by providing a mathematical formula for determining the value of European options. The model offered a more convenient method for approximating the cost of an option under varying circumstances. Simultaneously, Merton (1973) expanded upon the Black–Scholes model by incorporating dividends. Merton’s contribution to the field is notable for its ability to account for dividends and for offering an alternative derivation of the Black–Scholes formula that can be applied under less strict assumptions, thus increasing its broader applicability. Subsequently, Cox and Ross (1976) researched the Black–Scholes model and a stock price model using Poisson jumps, proposing the notion of risk neutrality. The researchers hypothesized (without providing evidence) that, in a broad sense, the price of an option can be calculated using preferences (referred to as probabilities), so that the expected returns for both the stock and the option are equivalent to the returns under the risk-free rate. Hence, options provide returns that are equivalent to those obtained under the risk-free rate. Following this, Harrison and Kreps (1978) demonstrated that the model is feasible only if there is an analogous martingale measure. A redundant claim refers to a statement that can be duplicated by specific investment portfolios that consist of stocks and bank accounts. In the feasible model, a claim is considered redundant if it has an identical expectation under all equal martingale measures. Furthermore, in the case of a redundant claim, its arbitrage value corresponds to the widely anticipated outcome.
Many disciplines have used bibliometric methods, but only a few financial studies have utilized these methods. Here, we briefly overview the bibliometric studies carried out in the field of finance. Early financial studies using bibliometric methods included Merigó et al. (2015) and Khan et al. (2022). This was then followed by a study of supply chain finance by X. Xu et al. (2018). Subsequently, several studies have used the bibliometric method within the finance discipline; a noted author is J.W Goodell, who conducted several studies using bibliometric methods, including studies on portfolio diversification (Migliavacca et al., 2023), cultural finance (Goodell et al., 2023), investor attention (Goodell et al., 2022) and Machine Learning (ML) and Artificial Intelligence (AI) such as in Goodell et al. (2021). He also participated in a study focusing on COVID-19 and finance scholarships (Boubaker et al., 2023). Another notable author is Ashraf Khan; he has reviewed Sukuk (Paltrinieri et al., 2023) and has performed a bibliometric analysis on mergers and acquisitions (Chiaramonte et al., 2023). He has also conducted general research covering all finance areas, such as in Khan et al. (2022). Additionally, he participated in a review about Takaful (Nasir et al., 2021). Some studies focus on a single journal, such as Kumar et al. (2022) on the Journal of Behavioral and Experimental Finance, Baker et al. (2020) on Managerial Finance and Alshater et al. (2021) on the Journal of Sustainable Finance and Investment (JSF&I).
None of these earlier research studies attempted to cover all aspects of options pricing. Moreover, we were unable to find any literature examining the conceptual and intellectual combinations that underpin this expanding field of study. These limitations compelled us to integrate quantitative and qualitative approaches in order to synthesize the current literature and provide a guide for further investigation. This review and bibliometric analysis of options pricing is the first of its kind. The goal of this review is to eventually help practitioners, policymakers, educators, and academics by summarizing the latest developments in the field. This study examines studies on options pricing and current trends through bibliometric techniques and methods. This study analyses the intellectual status of options pricing by examining recent research trends derived from an analysis of current publications in the field. At last, this paper summarizes the key findings, conclusions and prospects.
The following are the research questions investigated during this study:
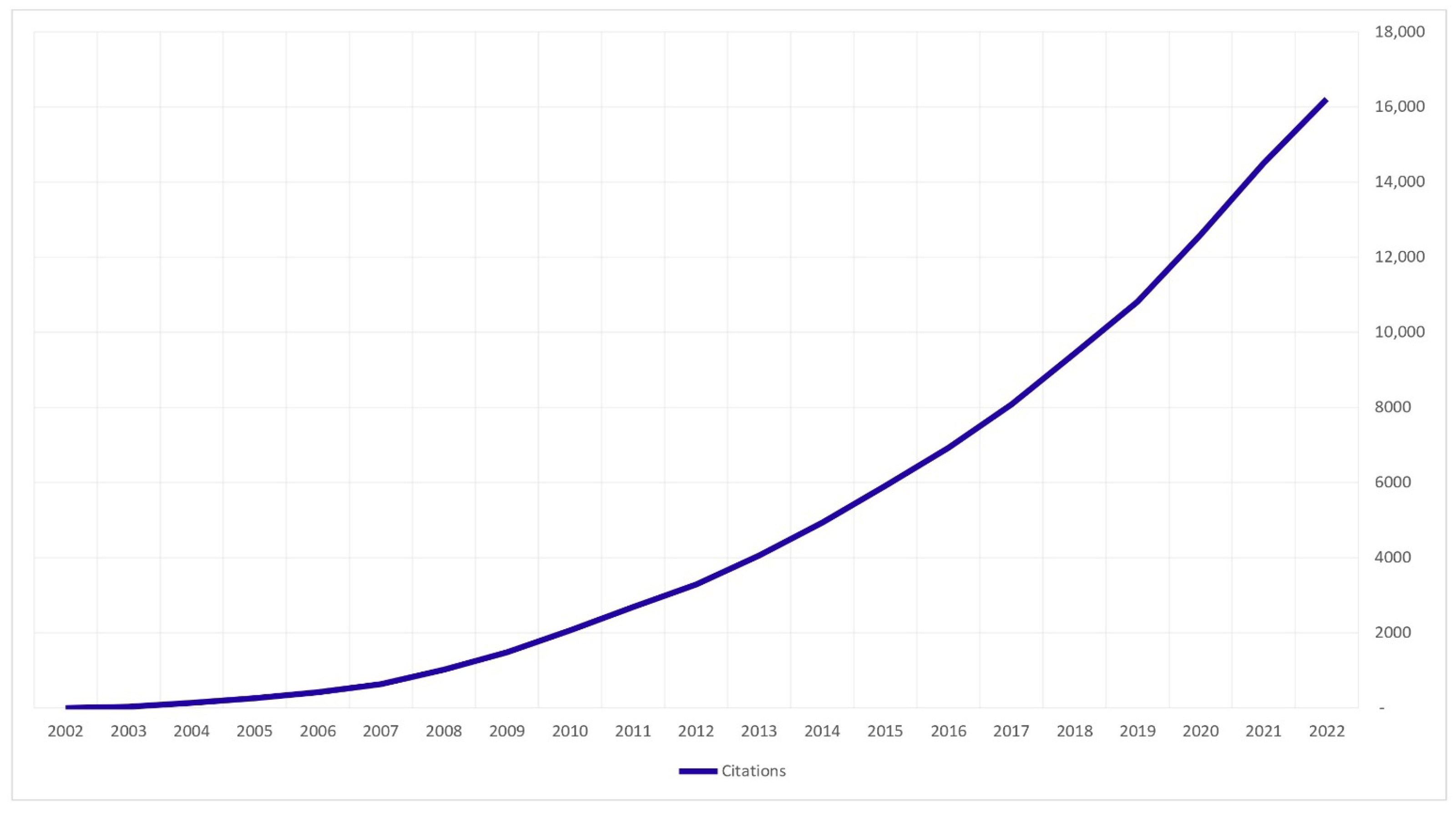
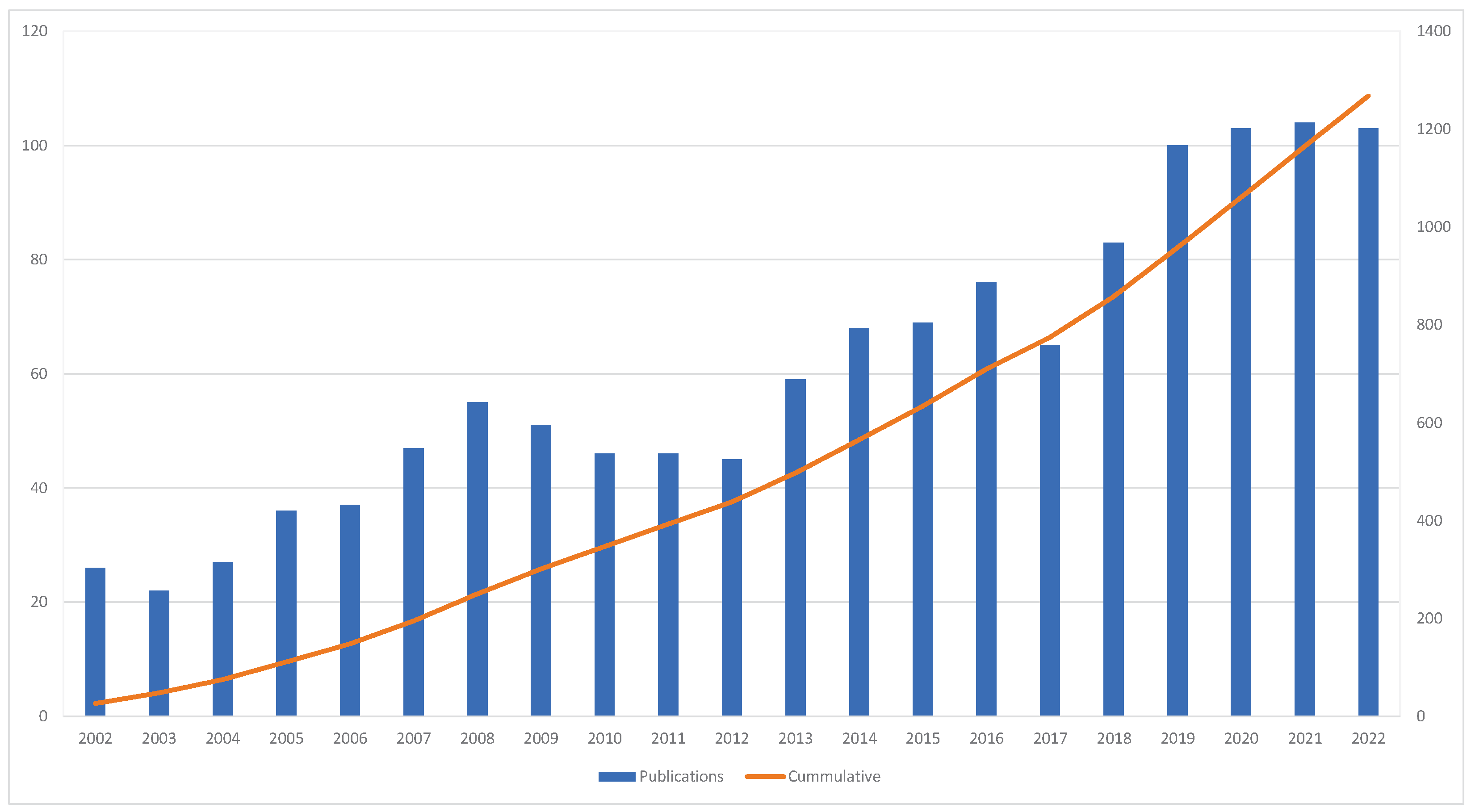
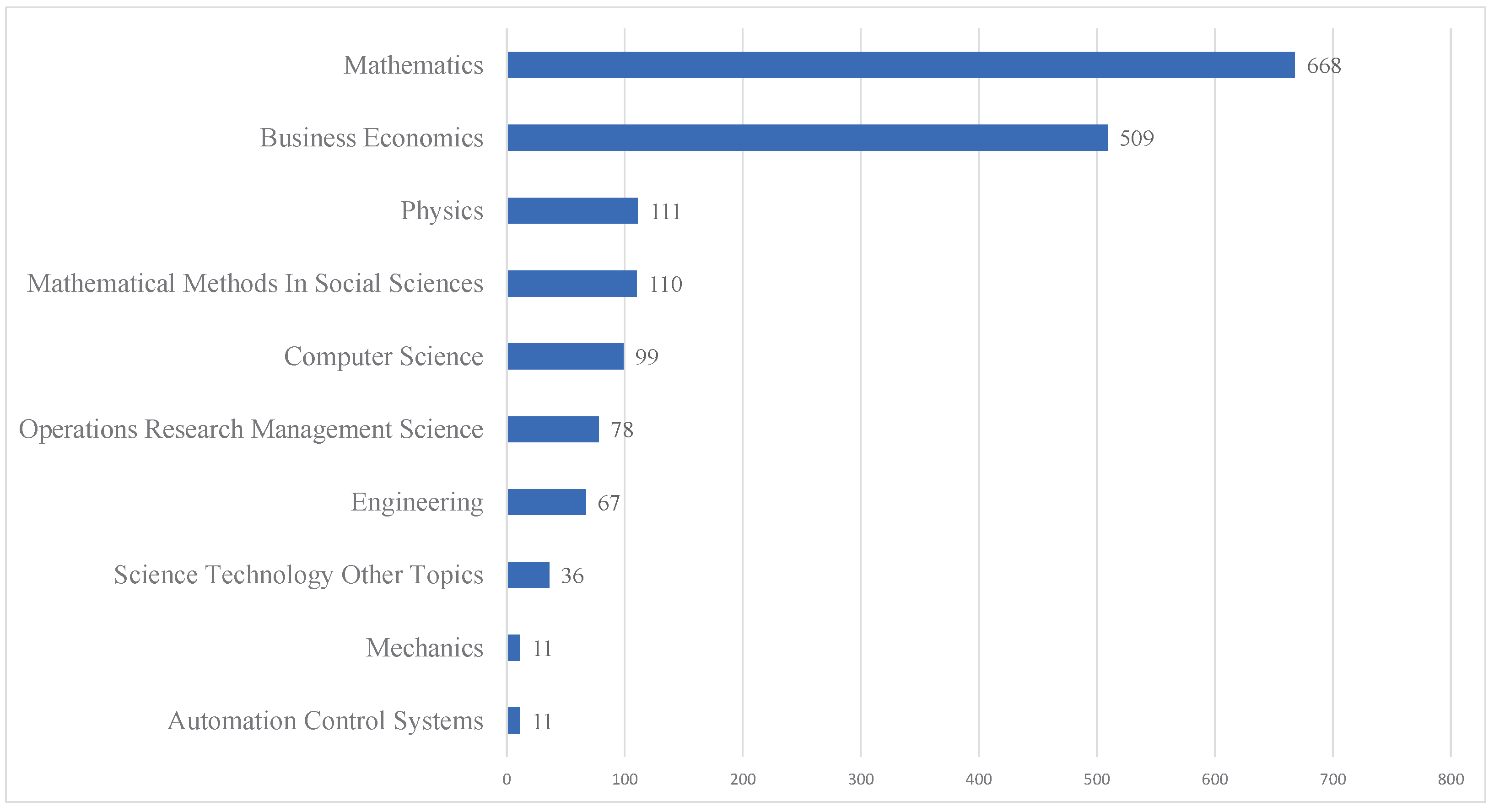
  • RQ1: What is the distribution of financial options pricing research from 2002 to 2022 based on the total number of publications and citations generated annually and the various research areas?
  • RQ2: In the field of research that focuses on financial options pricing, who are some of the most prominent authors, institutions, countries, high impact journals and notable publications?
  • RQ3: What advancements have been made in co-citation studies, and what significant clusters have emerged, specifically concerning the study’s research area?
  • RQ4: What are the most active research fields, the new research trends and the emerging themes in financial option pricing?
This study aims to identify the contributions made by researchers, institutions, nations, scientific journals and other possible avenues. In addition, the identified clusters shed light on the significance of options research and its potential applications in the future. In conclusion, the research study highlights the most active fields, emerging themes and new research trends.
The research’s subsequent sections are organized as follows: Section 2 presents a review of the materials and the methods of the data search. Section 3 analyzes the results of several aspects, such as historical and recent publication trends, active research fields, citation network and co-citation analysis and emerging themes. The discussion is contained within Section 4. Section 5 discusses potential future research directions concerning theory, methods and contexts. The conclusion of this study can be found in Section 6.

2. Materials and Methods

In this study, we employ bibliometric methods and techniques, which are the analysis of citation networks, co-citation, clustering, content, publishing trends, and keywords. A wide range of research fields have made extensive use of bibliometric analysis, including innovation (as discussed by (Randhawa et al., 2016)), strategic management (as discussed by (Vogel & Güttel, 2013)), entrepreneurship (as discussed by (Wu & Wu, 2017)) and fuzzy decision making (as discussed by (Blanco-Mesa et al., 2017)).
However, one of the most influential papers in business research is Donthu et al. (2021). In their study, they compared primary review methods. They argued that bibliometric analysis should be used when the scope of the review is broad and when the dataset is too large, which applies to this study topic. Bibliometrics equips academics with a powerful instrument for examining a specific research field, analyzing the literature and providing insights. We retrieved the data for this study from the core collection of Web of Science (WoS), considered the largest database of journal articles and citation records in the world. Both authors of Li et al. (2018) and W. Liu (2019) conducted their research using the WoS and they show the importance of the database.
Our research study took place in October 2022, and we gathered records for the period between January 2001 and January 2022. The investigation began with a search for “option”, “options” and “pricing” in the “Topic” field of the WoS database, generating 1342 initial results. To ensure that only relevant articles were included, we eliminated those that contained both “therapy” and “nursing.” The reason for this is that the word “option” is widely used in other fields, and therefore, using another word that would only be used in the field of study was crucial.
In addition, following other bibliometric studies, we examined articles published in journals. To ensure the inclusion of high-quality publications, we eliminated conference and proceedings papers, working papers, book chapters and communications. Also, we removed all duplicated articles. The search was then limited to English-language articles, giving 1331 hits. After reviewing the abstracts, 1331 full-length papers were selected for additional examination.
One of the tools this study used is the VOSviewer software 1.6.20 developed by Van Eck and Waltman (2010) to analyze the citation network and keyword analysis. This software offers researchers a powerful instrument that can be utilized for evaluating citations, geographical distribution and keyword analysis within a specific research field. Additionally, we utilized CiteSpace 6.1 R2 software, developed by Chen (2014), to carry out activities such as content analysis, co-citation and clustering to examine recent research trends.

3. Results

3.1. Descriptive Statistics

Figure 1 and Figure 2 show the distribution of research on options pricing according to the yearly number of publications and citations. The number of research papers published on options pricing has been steadily increasing, with more citations year after year, indicating the study’s relevance. After a comprehensive examination, our findings show that the articles which have been published are from 80 countries, which include China, USA, Australia, England, Taiwan and Republic of Korea.
In Figure 3, the significant fields of study in which over ten articles on options pricing have been published are shown. It is notable that options pricing has strong connections with mathematics. Because option pricing is based on the use of mathematical models, we can observe publications in various fields. However, it is worth noting that the business economics discipline in the Web of Science database includes finance and many other business fields.

3.2. Citation Network Analysis

The field of options pricing was analyzed using citation analysis, with a focus on identifying authors who have made significant contributions. The resulting dataset included 2026 authors affiliated with 1086 organizations in 80 countries. Table 1 displays the top authors in this field. Song-Ping Zhu holds the first position, with 17 publications, followed by Xingchun Wang, with 15 studies. Additionally, Song-Ping Zhu and Song Wang have received the highest number of citations, with 441 and 215, respectively. These two authors are recognized as experts in financial mathematics and work in Australian universities. They have authored several papers on the subject.
In the following step, a citation analysis was carried out in order to determine the 15 top institutions for articles contributions. The top university is the University of Wollongong which produced 32 articles, followed by the University of International Business and Economics with 17 and the Iran University of Science and Technology with 16 publications which are the most active universities working on research on options pricing. These institutions are not, as we would expect, in Western countries, but are instead located in Australia, Iran and China, which shows that interest in this topic is global.
Table 1 shows the top 15 countries that have published the most articles on this subject. China (248 articles), the US (203 articles) and Australia (104 articles) are the top three countries.
The citation analysis method was also utilized to investigate the journals that have been crucial in the publication of research on this topic. Various journals have made contributions to options pricing research, illustrating the extensive importance of the subject in the literature. A total of 1268 publications were examined across 395 journals. It was found that 64 of the 395 journals had published a minimum of five research studies in this domain. Table 2 shows the 15 most distinguished publications publishing research on options pricing. The most prolific platform is Physica A-Statistical Mechanics and Its Applications, with 61 articles published, followed by the Journal of Computational and Applied Mathematics.
A citation analysis of the publications was conducted to identify the most influential studies on options pricing. Among the 1268 papers, 66 studies were identified based on a minimum criterion of 50 citations. Table 3 summarizes the 15 most significant contributing papers. The research of (Kou, 2002) tops the list with 955 citations, followed by Hall and Murphy (2002) with 545 and Carr and Wu (2004) with 301 citations. The author of Kou (2002) integrated the concepts of Brownian motion and normal distribution to develop a novel, double-exponential jump-diffusion model. This model aimed to achieve a harmonious combination of realism and comprehensibility. Another study Hall and Murphy (2002) employed a certainty-equivalence approach to examine the cost, value and sensitivity of non-tradable options owned by risk-averse CEOs in relation to their performance-based compensation. Their analysis differentiated between the “value generated by executives” and the “cost incurred by the company”, offering valuable information on stock options usage and levels of executive compensation. Furthermore, in Carr and Wu (2004), the classic Black–Scholes options pricing model assumes that returns follow Brownian motion. However, it is recognized that return processes differ from this benchmark in three ways: asset prices jump, return volatilities vary stochastically over time and returns and their volatilities are correlated, often negatively, for equities. A time-changed Lévy process framework can address these three aspects, and it is easy to select and test a specific model using characteristic function technology.

3.3. Co-Citation Analysis

We could explain co-citation as the relationship between two articles that are both cited by a third piece. Furthermore, Small (1973) explained that the frequency with which one paper cites two other articles is termed co-citation. Co-citations imply that the two papers are intimately connected within their overarching scientific discipline (Culnan, 1987). Recently, researchers utilise Citespace software to conduct a co-citation analysis, identifying the most significant publications within a particular research field and clarifying the theoretical structure of the subject.

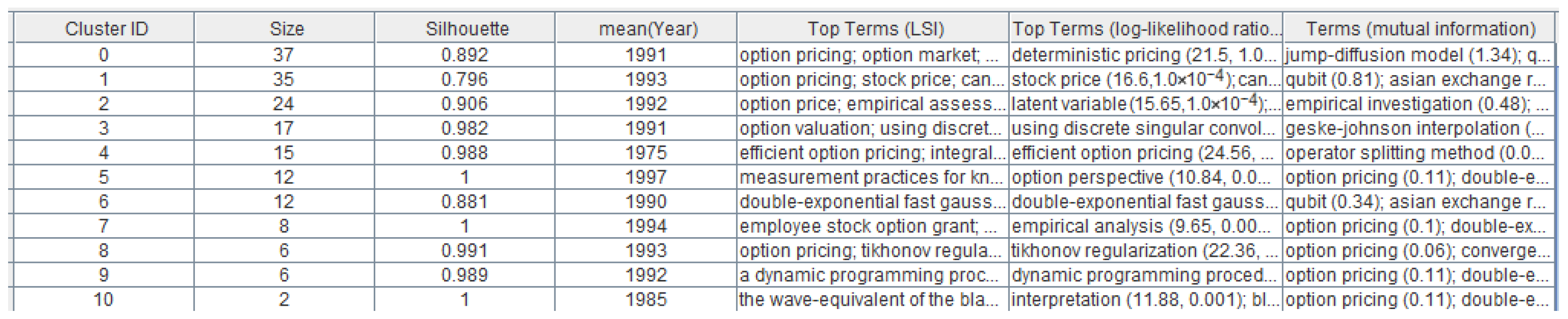
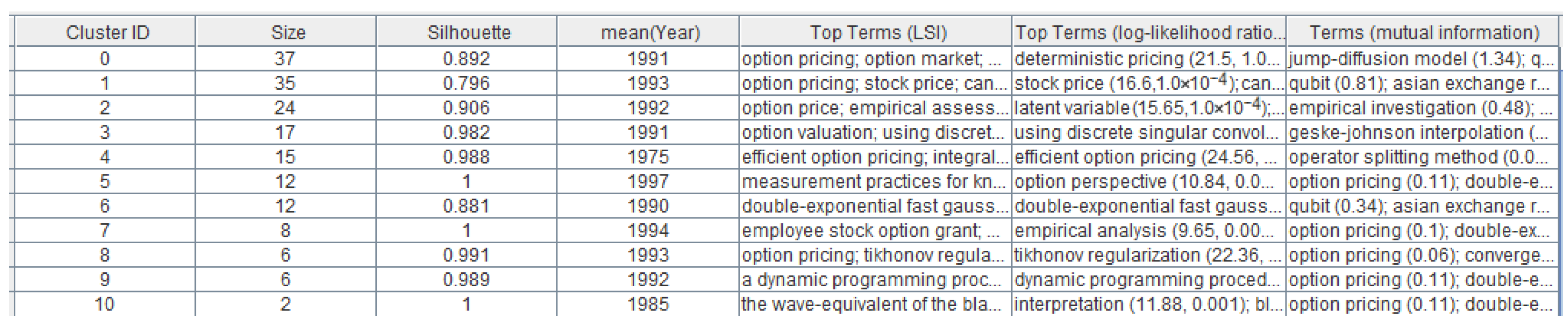
3.3.1. Clustering

Clustering is a technique that helped us to analyze the co-citation network thematically, as explained in Xu et al.’s work (S. Xu et al., 2018). A co-citation threshold of 5 was chosen based on previous empirical research by Trujillo and Long (2018), which indicated that this level strikes a balance between noise reduction and data retention, facilitating significant co-citation connections while maintaining adequate density for cluster identification. We observed ten major clusters using the CiteSpace software following Ansari et al. (2022); Cheng et al. (2023). These clusters were labeled automatically using the log-likelihood ratio (LLR) algorithm, a widely adopted method in bibliometric studies for meaningful and distinctive labeling (Kolani et al., 2023; Zhang et al., 2023). The clusters are presented in Figure 4.
The clustering setup quality is evaluated based on silhouette score Chen et al. (2010). This score measures the similarity between a point and other points in its cluster compared to points in other clusters; the range of this measure is between -1 and +1. A high score signifies a favorable match, whereas a low or negative score denotes an unfavorable match. The solution of clustering is suitable if the majority of points exhibit a high silhouette score. However, if many points have a low or negative score, it means that the clustering solution has many or few clusters (Madureira et al., 2017).
We can also assess the consistency of the cluster members using the silhouette column, shown in Figure 4. The higher the silhouette score, the more consistent the cluster members are. However, a high homogeneity score is not significant if the cluster size is small. Cluster 5, comprising just five members, yet possesses a silhouette score of 1.00, suggesting that the five references are likely citations from the same underlying author.
The timeline view exhibits a co-citation map of co-cited references derived from the citing patterns of authors who produced the articles that were selected. The clusters are arranged along a horizontal timeline, with the arrow indicating time pointing to the right.
Figure 5 displays the network’s signature in the top left corner, encompassing the modularity and silhouette scores. Modularity means the ease with which a network may be partitioned into several components or modules, serving as a benchmark for the overall clarity of network deconstruction. Modularity Q and mean silhouette scores are essential metrics that provide perspectives on the network’s general structural characteristics. The modularity Q of 0.6736 is not very high, which suggests that the network is, on average, partitioned into loosely connected clusters. The average silhouette value of 0.8602 indicates that these clusters exhibit a degree of homogeneity. The mean publication year of a cluster signifies whether it predominantly contains new or older works.
The clusters are numbered in descending order of cluster size, starting with the largest cluster 0, followed by the second-largest cluster 1, and continuing in this way. Deterministic pricing is the most prominent topic, with cluster 0 containing the most references, followed by stock price in cluster 1. The third type is latent variable in cluster 2, followed by using discrete singular convolution in cluster 3 and efficient options pricing in cluster 4. The smaller clusters cover topics such as option perspective, double-exponential fast Gaussian transform, empirical analysis, and Tikhonov regularization. Therefore, we now have a general oversight of options pricing research between 2002 and 2023.

3.3.2. Content Analysis

We carried out a content analysis of the top ten clusters using CiteSpace cluster explorer, as Figure 6 shows. The explorer clusters the most representative sentences by citing articles based on a sentence with high centrality, providing insights into common contexts.
The more cited the paper is, the larger the nodes are. Furthermore, the thickness of the line indicates the frequency with which interconnected nodes are referenced. Furthermore, 189 nodes, 762 links and 14 clusters are shown on the map (Figure 5). We chose ten clusters based on the Zhang et al. (2023) and Kolani et al. (2023). Clusters 5, 7, and 10 were not included in the content analysis due to their high silhouette value of 1. The reason for the omission of these clusters is that the high silhouette value could be due to the citation behaviors of a single paper, making them less representative.
  • Cluster 0: Deterministic Pricing
This cluster focuses on one of the widely used options pricing models. Deterministic pricing is a methodology that estimates the value of options based on fixed assumptions about market conditions and underlying asset behavior. Since the Black–Scholes model (Black & Scholes, 1973) is based on this mathematical model, it assumes that certain variables, such as volatility and interest rates, remain constant over time; therefore, these models provide closed-form solutions for pricing options. We expected this to be the most commonly used method in this study; this cluster was the largest, with the most papers, at 37 articles out of 174. Furthermore, an extension of the Black–Scholes model, which is the practitioner Black–Scholes (PBS), incorporates market insights and trading limits into the conventional Black–Scholes model. The original Black–Scholes model assumes constant volatility, whereas the PBS model incorporates implied volatility curves and market frictions (Christoffersen & Jacobs, 2004).
  • Cluster 1: Stock Price
The price of an option is determined by various factors, including the current share price and the time remaining until the option expires. In general, options obtain their value from an underlying asset, such as a stock. The literature on options pricing shows that the relationship between options pricing and stock prices is crucial in finance. This relationship provides insights into market behavior, investor attitude and financial instrument dynamics. For example, options pricing models, such as the Black–Scholes model (Black & Scholes, 1973), are based on the use of stock price, strike price and volatility. From the cluster (Figure 6) we can observe that 35 of 174 articles are listed under the term “stock price”, making this cluster the second largest.
  • Cluster 2: Latent Variable
In cluster 2, 24 out of 174 articles discuss latent variables. The link between these and options pricing is that latent variables improve options pricing models by providing a complex understanding of factors that affect option values, such as implied volatility and investor behavior, resulting in more accurate pricing. The model created in Heston (1993) is an example of these models.
  • Cluster 3: Discrete Singular Convolution
The discrete singular convolution algorithm (DSC) was first introduced in Wei (1999); the authors used one to solve the Fokker–Planck equation. The DSC algorithm is a general approach for numerically solving singular convolution problems. The DSC algorithm has been used in many other fields, but the first attempt to use it for options pricing was conducted in Zhao and Wei (2005), to solve the Black–Scholes equation for both European and American-style options. Therefore, we anticipated its connection to options pricing, as evidenced by the 17 articles out of 174 that rely on it.
  • Cluster 4: Efficient Option Pricing
As with any complicated problem, researchers aim to determine the best solutions. The question of which pricing methodology or solution is more efficient arises in the context of options pricing, given the abundance of available solutions. For example, the Black–Scholes model remains the most efficient in pricing European options under several assumptions. More complex options, such as American options pricing methods including Monte Carlo simulations, binomial trees and finite difference methods, might be more appropriate. These efforts are continuous, shown by the fact that 15 research studies out of 174 focused on efficiency. The most intuitive articles include Kairys and Valerio (1997), Cox et al. (1979), Kwok et al. (2011) and Figlewski and Gao (1999).
  • Cluster 6: Double-Exponential Fast Gaussian Transform
The double-exponential fast Gaussian transform (DE-FGT) is a numerical technique used in options pricing, particularly useful for pricing path-dependent options such as lookback options and for pricing options under the jump-diffusion model. The key features of this model are efficiency, accuracy and applicability. The model utilizes convolution using the Gaussian distribution, which results in a faster computation. This path of research has been studied thoroughly in Broadie and Yamamoto (2003), Broadie and Yamamoto (2005) and Yamamoto (2005).
  • Cluster 8: Tikhonov Regularization
This cluster shows that only 6 out of 174 articles used this method. Tikhonov regularization provides a robust way to stabilize ill-posed problems in options pricing, particularly in implied volatility, surface calibration, inverse options pricing, and high-dimensional pricing models. By introducing a penalty on the size of the model parameters, Tikhonov regularization helps prevent overfitting, improves the stability of the solution, and ensures more reliable and accurate pricing of options, even in the presence of noisy or sparse data. It is a powerful tool when dealing with stochastic volatility models, inverse problems, and high-dimensional systems in financial modeling; see Egger and Engl (2005) and Crepey (2003).
  • Cluster 9: Dynamic Programming
Dynamic programming is a powerful and efficient approach for options pricing, particularly in cases where early exercise is allowed (American options) or for path-dependent options. By breaking down the problem into smaller subproblems and using backward induction along with the Bellman equation, this method provides an exact solution to the options pricing problem. However, it can be computationally intensive, especially for high-dimensional problems or cases requiring a fine grid of asset prices. Dynamic programming is especially useful for American options, path-dependent options and other types of options where the optimal decision may depend on past prices or where early exercise is allowed. See Ben-Ameur et al. (2002), Myneni (1992) and Glasserman and Yu (2004).

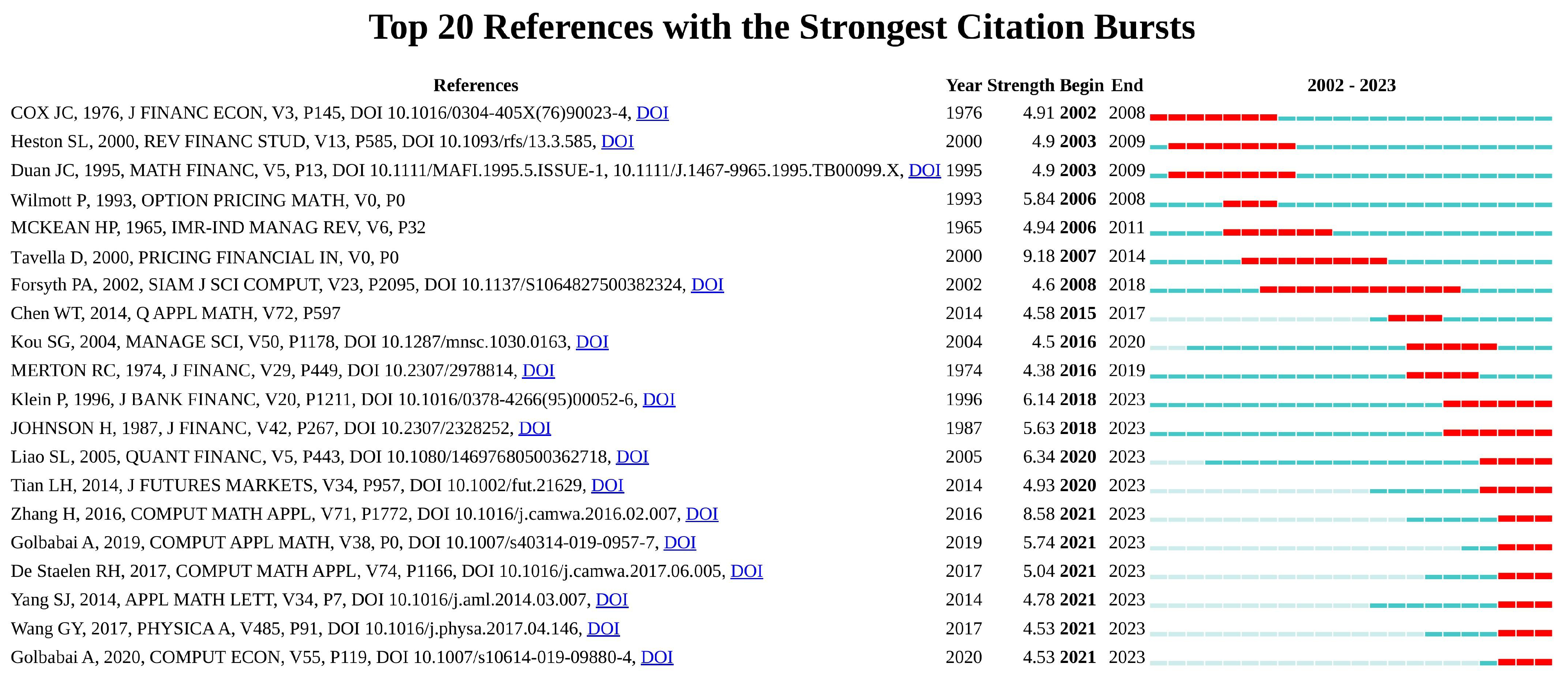
3.4. Research Trends, Active Research Areas and Emerging Themes

Citation bursts, which can last a single or multiple years, indicate an active research area. Clusters with high citation bursts indicate active study areas or recent trends. The Citation Burst History tool can produce a compilation of articles linked to citation bursts.
Figure 7 illustrates the references with the highest citation bursts and the timing of these occurrences. For instance, Cox and Ross (1976) has the most bursts among publications on options pricing, although their work was published in 1976. Notably, Aït-Sahalia and Lo (1998) had the highest second citation burst between 1998 and 2010. Some other notable references in the list include the following: Rubinstein (1994); Jackwerth and Rubinstein (1996); Duan (1995); Heston and Nandi (2000); and Jarrow and Rudd (1982).
The research articles’ themes are reflected in the author keywords. “Option pricing” ranks highest with 279 occurrences, as anticipated, suggesting that the term is used as a concept in the literature. Then, with 92 and 86 occurrences, respectively, “Black–Scholes model” and “Black–Scholes equation” are commonly used keywords. “American option” (86 occurrences), “stochastic volatility” (67 occurrences) and “implied volitality” (37 occurrences) are the other four most frequently used keywords. In the co-occurrence analysis, keywords that occurred ten times in the studies were used. A total of 122 keywords met this criterion, from which we selected the top 100 and grouped them into five clusters. By looking at the overlay visualization map of keyword co-occurrence analysis, it is clear that these keyword clusters give a notion of the subject linkages that are common in research projects. In Figure 8, it is evident that the clusters are connected and that the circles are close to each other, which indicates the researchers in related clusters are more likely to be cited in a similar situation. The overlay visualization map of keyword co-occurrence analysis identifies the year’s trending research topics. Option pricing trends are shifting towards Asian options, credit risk, implied volatility and schemes.
Table 4 summarizes current papers and research on option pricing from 2021 to 2024, organized into three major themes: (i) deep learning and hybrid neural networks, (ii) stochastic and rough volatility modeling and (iii) market frictions with xVA integration. First, data-driven approaches, such as deep neural networks (DNNs), forward-backwards stochastic differential equations (FBSDEs) and reinforcement learning, offer greater flexibility and precision in pricing and hedging in realistic trading environments. These strategies not only enhance the accuracy of calibration and hedging, but they also perform well in real-world trading situations (Ashok Naarayan & Parpas, 2024; Horvath et al., 2021; D. Liu, 2022). Their growing use shows a shift towards AI-based financial modeling. Second, volatility modeling advances beyond standard assumptions, using fractional Brownian motion and rough paths. This approach provides a more effective framework for capturing and reflecting market data, such as persistent volatility clustering and steep short-term smiles (Guo et al., 2023; Jang & Lee, 2019). These approaches establish rough volatility as a standard in theoretical modeling, where deep learning is often used to calibrate and simulate these models efficiently.
The third topic involves market frictions and valuation adjustments (xVA), such as transaction costs, liquidity constraints and credit valuation risks, which are incorporated into pricing frameworks. Neural-based methods show strong potential for handling challenges while maintaining traceability (Anderson & Ulrych, 2023; D. Liu, 2022).
Together, these research topics point to a clear path for integrating advanced mathematical models with machine learning to push beyond the traditional limits of option pricing. New trends, such as deep learning architectures and approximate volatility models, are not marginal but rather central to the next generation of option pricing models, as they offer practical improvements and deeper theoretical insights.

4. Discussion

The current research study investigated a theoretical research framework for different stages of investment planning and decision making involving options pricing. It corroborated previously held beliefs while contributing to the scientific literature on options pricing in the financial industry. It recommended and carried out a bibliometric analysis to discover the most significant studies in options pricing research, using citation and co-citation analysis.
This study’s first research question (RQ1) focused on the distribution of options pricing research, considering the annual frequency of citations and publications and the research themes spanning from 2002 to 2022. The investigation of RQ1 revealed a consistent upward trend in the annual publication of academic articles on options pricing, accompanied by a substantial number of citations, indicating the importance of the subject. The topic of options pricing appears to be multidisciplinary, as seen by its strong connections to several academic fields. Citation network analysis comprised the second research question (RQ2), and with 17 publications Song-Ping Zhu was the most influential author in this area. Interestingly, with 32 articles, the University of Wollongong was the top institution carrying out options pricing research. With 248 articles, China was the country contributing the most to options pricing research. Additionally, articles on options pricing can be found in economics, finance and mathematics journals. Options pricing research and development should adopt more interdisciplinary approaches to combine knowledge from various fields.
An additional paper citation analysis was carried out to investigate the most important options pricing studies. With 955 citations, a study by Kou (2002) was the most cited article. A study by Hall and Murphy (2002), which received 545 citations, came second. In third place was the study by Carr and Wu (2004), which received 301 citations.
The third research question asked how to advance co-citation studies to produce meaningful clusters. Our thematic analysis revealed the top ten clusters, each concentrating on a distinct facet of options pricing and ranging from concept to methodologies and industry application. Additionally, our thematic analysis illustrated the connections between the clusters and made a case for improved methods to advance options pricing strategies and their applications in financial and scientific contexts.
The fourth research question covered the most recent trends, emerging themes and the most active areas in options pricing research. Many current research domains, emerging themes and recent research trends have been identified. The overlay visualization map for keyword co-occurrence analysis identified each year’s most-discussed research topics. We also argued that options pricing has garnered considerable interest from scholars. This study demonstrates that collaboration between institutions and researchers has the potential to benefit both academia and industry. Scholars are devoting substantial efforts to expanding our understanding of the subject. Considerable potential exists for further theoretical development, contextual examination and methodological enhancements. The subject of options pricing possesses extensive ramifications for investments, and progress in this area could facilitate the development of financial markets that are more stable and competitive.

5. Limitations and Future Research

Some of the shortcomings of this study are listed below, as follows:
  • The research was based on an analysis of 1713 papers published on options pricing in the financial industry over the previous two decades. The research used a combination of keywords, and it is possible that various combinations of keywords would have produced different findings.
  • We acknowledged that relying solely on the Web of Science (WoS) may omit relevant studies indexed in Scopus. Therefore, future studies could combine two or three of the major indexing databases, such as Farooq (2023) and Sánchez et al. (2017).
  • In subsequent research on this subject, all ten clusters mentioned above should be included. As a result of these findings, additional investigation into this subject area is required.

6. Conclusions

This study utilized bibliometric analysis to conduct a literature review on financial options pricing research spanning the last 20 years (2002–2022). Every year, new scientific studies on various possibilities are produced, with citations that indicate the importance of the studies. This article examined the contributions to research on financial options pricing by researchers, institutions, countries, scientific journals and studies in the educational and financial sectors. Additionally, it offered researchers the chance to examine the knowledge gaps, technical competence, skill sets and innovation. It is crucial to investigate all ten identified options pricing clusters, including thoroughly deterministic pricing, stock price, latent variables, the use of discrete singular convolution, efficient options pricing, option perspective, double-exponential fast Gaussian transform, empirical analysis, Tikhonov regularization and dynamic programming, as this will ensure that investors have a wide range of options available to them. These clusters highlight the importance of options pricing research for improving investors’ performance. This study also identified the most active areas, recent research trends and emerging themes in the research field.
Finally, this article aimed to persuade scholars to conduct comprehensive examinations of the scientific literature, encompassing bibliometric methods, meta-analysis and literature reviews. In this study, we aimed to investigate the development of options pricing, and it is clear that more collaboration is needed for this research area to evolve and prosper. Additional research is required because financial options are an important topic today. Given the subject matter of options pricing, it is necessary to foster greater collaboration among scholars from several disciplines, including mathematics, economics and finance. There is an evident lack of research on this topic compared to other fields of study.
Based on the results obtained and from a practical standpoint, these conclusion leads to two future directions. Investors can improve risk management and option valuation in increasingly complex markets by implementing cutting-edge strategies such as deep learning and rough volatility models. To address unresolved issues in option pricing, researchers should enhance interdisciplinary collaboration and broaden the dataset beyond Web of Science in their future work.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data will be made available upon request.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Aït-Sahalia, Y., & Lo, A. W. (1998). Nonparametric estimation of state-price densities implicit in financial asset prices. The Journal of Finance, 53(2), 499–547. [Google Scholar] [CrossRef]
  2. Alshater, M. M., Atayah, O. F., & Hamdan, A. (2021). Journal of sustainable finance and investment: A bibliometric analysis. Journal of Sustainable Finance & Investment, 13(3), 1131–1152. [Google Scholar] [CrossRef]
  3. Anderson, D., & Ulrych, U. (2023). Accelerated american option pricing with deep neural networks. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4000756 (accessed on 1 February 2025).
  4. Ansari, Y., Albarrak, M. S., Sherfudeen, N., & Aman, A. (2022). A study of financial literacy of investors—A bibliometric analysis. International Journal of Financial Studies, 10(2), 36. [Google Scholar] [CrossRef]
  5. Ashok Naarayan, A., & Parpas, P. (2024, November 14–17). Stable multilevel deep neural networks for option pricing and xvas using forward-backward stochastic differential equations. ACM Transactions on Modeling and Computer Simulation (TOMACS), Brooklyn, NY, USA. [Google Scholar] [CrossRef]
  6. Bachelier, L. (1900). Théorie de la spéculation. In Annales scientifiques de l’école normale supérieure (Vol. 17, pp. 21–86). Gauthier-Villars. [Google Scholar]
  7. Baker, H. K., Kumar, S., & Pandey, N. (2020). A bibliometric analysis of managerial finance: A retrospective. Managerial Finance, 46(11), 1495–1517. [Google Scholar] [CrossRef]
  8. Barone-Adesi, G., Engle, R. F., & Mancini, L. (2008). A GARCH option pricing model with filtered historical simulation. The Review of Financial Studies, 21(3), 1223–1258. [Google Scholar] [CrossRef]
  9. Ben-Ameur, H., Breton, M., & L’Ecuyer, P. (2002). A dynamic programming procedure for pricing American-style Asian options. Management Science, 48(5), 625–643. [Google Scholar] [CrossRef]
  10. Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654. [Google Scholar] [CrossRef]
  11. Blanco-Mesa, F., Merigó, J. M., & Gil-Lafuente, A. M. (2017). Fuzzy decision making: A bibliometric-based review. Journal of Intelligent & Fuzzy Systems, 32(3), 2033–2050. [Google Scholar] [CrossRef]
  12. Bollerslev, T., Gibson, M., & Zhou, H. (2011). Dynamic estimation of volatility risk premia and investor risk aversion from option-implied and realized volatilities. Journal of Econometrics, 160(1), 235–245. [Google Scholar] [CrossRef]
  13. Borland, L. (2002). Option pricing formulas based on a non-Gaussian stock price model. Physical Review Letters, 89(9), 098701. [Google Scholar] [CrossRef] [PubMed]
  14. Boubaker, S., Goodell, J. W., Kumar, S., & Sureka, R. (2023). COVID-19 and finance scholarship: A systematic and bibliometric analysis. International Review of Financial Analysis, 85, 102458. [Google Scholar] [CrossRef]
  15. Broadie, M., Chernov, M., & Johannes, M. (2009). Understanding index option returns. The Review of Financial Studies, 22(11), 4493–4529. [Google Scholar] [CrossRef]
  16. Broadie, M., & Yamamoto, Y. (2003). Application of the fast Gauss transform to option pricing. Management Science, 49(8), 1071–1088. [Google Scholar] [CrossRef]
  17. Broadie, M., & Yamamoto, Y. (2005). A double-exponential fast Gauss transform algorithm for pricing discrete path-dependent options. Operations Research, 53(5), 764–779. [Google Scholar] [CrossRef]
  18. Carr, P., & Wu, L. (2004). Time-changed Lévy processes and option pricing. Journal of Financial Economics, 71(1), 113–141. [Google Scholar] [CrossRef]
  19. Cartea, A., & del Castillo-Negrete, D. (2007). Fractional diffusion models of option prices in markets with jumps. Physica A: Statistical Mechanics and Its Applications, 374(2), 749–763. [Google Scholar]
  20. Chen, C. (2014). The citespace manual. College of Computing and Informatics, 1, 1–84. [Google Scholar]
  21. Chen, C., Ibekwe-SanJuan, F., & Hou, J. (2010). The structure and dynamics of cocitation clusters: A multiple-perspective cocitation analysis. Journal of the American Society for Information Science and Technology, 61(7), 1386–1409. [Google Scholar] [CrossRef]
  22. Cheng, T.-Y., Ho, S. Y.-C., Chien, T.-W., Chow, J. C., & Chou, W. (2023). A comprehensive approach for clustering analysis using follower-leading clustering algorithm (FLCA): Bibliometric analysis. Medicine, 102(42), e35156. [Google Scholar] [CrossRef]
  23. Chiaramonte, L., Dreassi, A., Piserà, S., & Khan, A. (2023). Mergers and acquisitions in the financial industry: A bibliometric review and future research directions. Research in International Business and Finance, 64, 101837. [Google Scholar] [CrossRef]
  24. Christoffersen, P., Heston, S., & Jacobs, K. (2009). The shape and term structure of the index option smirk: Why multifactor stochastic volatility models work so well. Management Science, 55(12), 1914–1932. [Google Scholar] [CrossRef]
  25. Christoffersen, P., & Jacobs, K. (2004). The importance of the loss function in option valuation. Journal of Financial Economics, 72(2), 291–318. [Google Scholar] [CrossRef]
  26. Cox, J. C., & Ross, S. A. (1976). A survey of some new results in financial option pricing theory. The Journal of Finance, 31(2), 383–402. [Google Scholar] [CrossRef]
  27. Cox, J. C., Ross, S. A., & Rubinstein, M. (1979). Option pricing: A simplified approach. Journal of financial Economics, 7(3), 229–263. [Google Scholar] [CrossRef]
  28. Crepey, S. (2003). Calibration of the local volatility in a generalized black–scholes model using tikhonov regularization. SIAM Journal on Mathematical Analysis, 34(5), 1183–1206. [Google Scholar] [CrossRef]
  29. Culnan, M. J. (1987). Mapping the intellectual structure of MIS, 1980–1985: A co-citation analysis. Mis Quarterly, 11(3), 341–353. [Google Scholar] [CrossRef]
  30. Donthu, N., Kumar, S., Mukherjee, D., Pandey, N., & Lim, W. M. (2021). How to conduct a bibliometric analysis: An overview and guidelines. Journal of Business Research, 133, 285–296. [Google Scholar] [CrossRef]
  31. Duan, J.-C. (1995). The GARCH option pricing model. Mathematical Finance, 5(1), 13–32. [Google Scholar] [CrossRef]
  32. Egger, H., & Engl, H. W. (2005). Tikhonov regularization applied to the inverse problem of option pricing: Convergence analysis and rates. Inverse Problems, 21(3), 1027. [Google Scholar] [CrossRef]
  33. Farooq, R. (2023). Knowledge management and performance: A bibliometric analysis based on Scopus and WOS data (1988–2021). Journal of Knowledge Management, 27(7), 1948–1991. [Google Scholar] [CrossRef]
  34. Figlewski, S., & Gao, B. (1999). The adaptive mesh model: A new approach to efficient option pricing. Journal of Financial Economics, 53(3), 313–351. [Google Scholar] [CrossRef]
  35. Glasserman, P., & Yu, B. (2004). Number of paths versus number of basis functions in American option pricing. The Annals of Applied Probability, 14, 2090–2119. [Google Scholar] [CrossRef]
  36. Goodell, J. W., Kumar, S., Lahmar, O., & Pandey, N. (2023). A bibliometric analysis of cultural finance. International Review of Financial Analysis, 85, 102442. [Google Scholar] [CrossRef]
  37. Goodell, J. W., Kumar, S., Li, X., Pattnaik, D., & Sharma, A. (2022). Foundations and research clusters in investor attention: Evidence from bibliometric and topic modelling analysis. International Review of Economics & Finance, 82, 511–529. [Google Scholar] [CrossRef]
  38. Goodell, J. W., Kumar, S., Lim, W. M., & Pattnaik, D. (2021). Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. Journal of Behavioral and Experimental Finance, 32, 100577. [Google Scholar] [CrossRef]
  39. Guo, J., Kang, W., & Wang, Y. (2023). Option pricing under sub-mixed fractional Brownian motion based on time-varying implied volatility using intelligent algorithms. Soft Computing, 27, 15225–15246. [Google Scholar] [CrossRef]
  40. Hall, B. J., & Murphy, K. J. (2002). Stock options for undiversified executives. Journal of Accounting and Economics, 33(1), 3–42. [Google Scholar] [CrossRef]
  41. Harrison, J. M., & Kreps, D. M. (1978). Speculative investor behavior in a stock market with heterogeneous expectations. The Quarterly Journal of Economics, 92(2), 323–336. [Google Scholar] [CrossRef]
  42. Heston, S. L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies, 6(2), 327–343. [Google Scholar] [CrossRef]
  43. Heston, S. L., & Nandi, S. (2000). A closed-form GARCH option valuation model. The Review of Financial Studies, 13(3), 585–625. [Google Scholar] [CrossRef]
  44. Horvath, B., Muguruza, A., & Tomas, M. (2021). Deep learning volatility: A deep neural network perspective on pricing and calibration in (rough) volatility models. Quantitative Finance, 21(1), 11–27. [Google Scholar] [CrossRef]
  45. Ikonen, S., & Toivanen, J. (2004). Operator splitting methods for American option pricing. Applied Mathematics Letters, 17(7), 809–814. [Google Scholar] [CrossRef]
  46. Jackwerth, J. C., & Rubinstein, M. (1996). Recovering probability distributions from option prices. The Journal of Finance, 51(5), 1611–1631. [Google Scholar] [CrossRef]
  47. Jang, H., & Lee, J.-H. (2019). Generative Bayesian neural network model for risk-neutral pricing of American index options. Quantitative Finance, 19(11), 1783–1797. [Google Scholar] [CrossRef]
  48. Jarrow, R., & Rudd, A. (1982). Approximate option valuation for arbitrary stochastic processes. Journal of Financial Economics, 10(3), 347–369. [Google Scholar] [CrossRef]
  49. Kairys, J. P., Jr., & Valerio, N., III. (1997). The market for equity options in the 1870s. The Journal of Finance, 52(4), 1707–1723. [Google Scholar] [CrossRef]
  50. Khan, A., Goodell, J. W., Hassan, M. K., & Paltrinieri, A. (2022). A bibliometric review of finance bibliometric papers. Finance Research Letters, 47, 102520. [Google Scholar] [CrossRef]
  51. Knopf, J. D., Jr., Nam, J., & Thornton, J. H., Jr. (2002). The volatility and price sensitivities of managerial stock option portfolios and corporate hedging. The Journal of Finance, 57(2), 801–813. [Google Scholar] [CrossRef]
  52. Kolani, K., Wang, Y., Zhou, D., Nouyep Tchitchui, J. U., & Okolo, C. V. (2023). Passive building design for improving indoor thermal comfort in tropical climates: A bibliometric analysis using CiteSpace. Indoor and Built Environment, 32(6), 1095–1114. [Google Scholar] [CrossRef]
  53. Kou, S. G. (2002). A jump-diffusion model for option pricing. Management Science, 48(8), 1086–1101. [Google Scholar] [CrossRef]
  54. Kou, S. G., & Wang, H. (2004). Option pricing under a double exponential jump diffusion model. Management Science, 50(9), 1178–1192. [Google Scholar] [CrossRef]
  55. Kumar, S., Rao, S., Goyal, K., & Goyal, N. (2022). Journal of behavioral and experimental finance: A bibliometric overview. Journal of Behavioral and Experimental Finance, 34, 100652. [Google Scholar] [CrossRef]
  56. Kwok, Y. K., Leung, K. S., & Wong, H. Y. (2011). Efficient options pricing using the fast Fourier transform. In Handbook of computational finance (pp. 579–604). Springer. [Google Scholar]
  57. Li, K., Rollins, J., & Yan, E. (2018). Web of Science use in published research and review papers 1997–2017: A selective, dynamic, cross-domain, content-based analysis. Scientometrics, 115(1), 1–20. [Google Scholar] [CrossRef]
  58. Liu, D. (2022). Studies of issues on hybrid neural networks for pricing financial options. AI in Applications, 2(3), 331–339. [Google Scholar] [CrossRef]
  59. Liu, W. (2019). The data source of this study is web of science core collection? Not enough. Scientometrics, 121(3), 1815–1824. [Google Scholar] [CrossRef]
  60. Madureira, B., Pinto, T., Fernandes, F., & Vale, Z. (2017, June 18–22). Context analysis in energy resource management residential buildings. 2017 IEEE Manchester PowerTech (pp. 1–6), Manchester, UK. [Google Scholar]
  61. Market Watch. (2025). 2024 was another record-breaking year for options trading—What’s on tap for the industry in 2025? Available online: https://www.marketwatch.com/story/2024-was-another-record-breaking-year-for-options-trading-whats-on-tap-for-the-industry-in-2025-8f4a097c (accessed on 1 September 2025).
  62. Merigó, J. M., Yang, J.-B., & Xu, D.-L. (2015). A bibliometric overview of financial studies. In Scientific methods for the treatment of uncertainty in social sciences (pp. 245–254). Springer International Publishing. [Google Scholar]
  63. Merton, R. C. (1973). Theory of rational option pricing. The Bell Journal of Economics and Management Science, 141–183. [Google Scholar] [CrossRef]
  64. Migliavacca, M., Goodell, J. W., & Paltrinieri, A. (2023). A bibliometric review of portfolio diversification literature. International Review of Financial Analysis, 90, 102836. [Google Scholar] [CrossRef]
  65. Mordecki, E. (2002). Optimal stopping and perpetual options for Lévy processes. Finance and Stochastics, 6, 473–493. [Google Scholar] [CrossRef]
  66. Myneni, R. (1992). The pricing of the American option. The Annals of Applied Probability, 1–23. [Google Scholar] [CrossRef]
  67. Nasir, A., Farooq, U., & Khan, A. (2021). Conceptual and influential structure of Takaful literature: A bibliometric review. International Journal of Islamic and Middle Eastern Finance and Management, 14(3), 599–624. [Google Scholar] [CrossRef]
  68. Paltrinieri, A., Hassan, M. K., Bahoo, S., & Khan, A. (2023). A bibliometric review of sukuk literature. International Review of Economics & Finance, 86, 897–918. [Google Scholar] [CrossRef]
  69. Randhawa, K., Wilden, R., & Hohberger, J. (2016). A bibliometric review of open innovation: Setting a research agenda. Journal of Product Innovation Management, 33(6), 750–772. [Google Scholar] [CrossRef]
  70. Rubinstein, M. (1994). On the accounting valuation of employee stock options. Institute of Business and Economic Research, University of California, Berkeley. [Google Scholar]
  71. Samuelson, P. (1965). Rational theory of warrant pricing. Industrial Management Review, 6, 13–32. [Google Scholar]
  72. Samuelson, P. A. (1960). The St. Petersburg paradox as a divergent double limit. International Economic Review, 1(1), 31–37. [Google Scholar] [CrossRef]
  73. Sánchez, A. D., Del Río, M. d. l. C., & García, J. Á. (2017). Bibliometric analysis of publications on wine tourism in the databases Scopus and WoS. European Research on Management and Business Economics, 23(1), 8–15. [Google Scholar] [CrossRef]
  74. Small, H. (1973). Co-citation in the scientific literature: A new measure of the relationship between two documents. Journal of the American Society for information Science, 24(4), 265–269. [Google Scholar] [CrossRef]
  75. Trujillo, C. M., & Long, T. M. (2018). Document co-citation analysis to enhance transdisciplinary research. Science Advances, 4(1), e1701130. [Google Scholar] [CrossRef]
  76. Van Eck, N., & Waltman, L. (2010). Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics, 84(2), 523–538. [Google Scholar] [CrossRef]
  77. Vogel, R., & Güttel, W. H. (2013). The dynamic capability view in strategic management: A bibliometric review. International Journal of Management Reviews, 15(4), 426–446. [Google Scholar] [CrossRef]
  78. Wang, S. (2004). A novel fitted finite volume method for the Black–Scholes equation governing option pricing. IMA Journal of Numerical Analysis, 24(4), 699–720. [Google Scholar] [CrossRef]
  79. Wei, G. (1999). Discrete singular convolution for the solution of the Fokker–Planck equation. The Journal of Chemical Physics, 110(18), 8930–8942. [Google Scholar] [CrossRef]
  80. Wu, Y.-C. J., & Wu, T. (2017). A decade of entrepreneurship education in the Asia Pacific for future directions in theory and practice. Management Decision, 55(7), 1333–1350. [Google Scholar] [CrossRef]
  81. Xu, S., Liu, J., Zhai, D., An, X., Wang, Z., & Pang, H. (2018). Overlapping thematic structures extraction with mixed-membership stochastic blockmodel. Scientometrics, 117(1), 61–84. [Google Scholar] [CrossRef]
  82. Xu, X., Chen, X., Jia, F., Brown, S., Gong, Y., & Xu, Y. (2018). Supply chain finance: A systematic literature review and bibliometric analysis. International Journal of Production Economics, 204, 160–173. [Google Scholar] [CrossRef]
  83. Yamamoto, Y. (2005). Double-exponential fast Gauss transform algorithms for pricing discrete lookback options. Publications of the Research Institute for Mathematical Sciences, 41(4), 989–1006. [Google Scholar] [CrossRef]
  84. Zhang, J., Quoquab, F., & Mohammad, J. (2023). What do we know about plastic pollution in coastal/marine tourism? Documenting its present research status from 1999 to 2022. Sage Open, 13(4), 21582440231211706. [Google Scholar] [CrossRef]
  85. Zhao, S., & Wei, G.-W. (2005). Option valuation by using discrete singular convolution. Applied Mathematics and Computation, 167(1), 383–418. [Google Scholar] [CrossRef]
  86. Zhu, S.-P. (2006). An exact and explicit solution for the valuation of American put options. Quantitative Finance, 6(3), 229–242. [Google Scholar] [CrossRef]
Jrfm 18 00513 g001
Figure 1. The annual citation count from 2002 to 2022, as per WoS.
Figure 1. The annual citation count from 2002 to 2022, as per WoS.
Jrfm 18 00513 g001
Jrfm 18 00513 g002
Figure 2. The annual publication of papers in the period 2002–2022 retrieved from WOS.
Figure 2. The annual publication of papers in the period 2002–2022 retrieved from WOS.
Jrfm 18 00513 g002
Jrfm 18 00513 g003
Figure 3. Top research areas with more than ten published articles on options pricing acquired from WOS.
Figure 3. Top research areas with more than ten published articles on options pricing acquired from WOS.
Jrfm 18 00513 g003
Jrfm 18 00513 g004
Figure 4. A summary table of ten clusters based on silhouette values, generated using CiteSpace software.
Figure 4. A summary table of ten clusters based on silhouette values, generated using CiteSpace software.
Jrfm 18 00513 g004
Jrfm 18 00513 g005
Figure 5. A historical illustration of the clusters from 2001 to 2022, produced using CiteSpace software.
Figure 5. A historical illustration of the clusters from 2001 to 2022, produced using CiteSpace software.
Jrfm 18 00513 g005
Jrfm 18 00513 g006
Figure 6. A summary table of the clusters extracted from the abstracts of the articles by the explorer, prepared using CiteSpace software.
Figure 6. A summary table of the clusters extracted from the abstracts of the articles by the explorer, prepared using CiteSpace software.
Jrfm 18 00513 g006
Jrfm 18 00513 g007
Figure 7. The most intense citation burst between 2002 and 2022 was identified using the CiteSpace program.
Figure 7. The most intense citation burst between 2002 and 2022 was identified using the CiteSpace program.
Jrfm 18 00513 g007
Jrfm 18 00513 g008
Figure 8. Visualization map displaying the co-occurrence of keywords based on year, created using VOSviewer software.
Figure 8. Visualization map displaying the co-occurrence of keywords based on year, created using VOSviewer software.
Jrfm 18 00513 g008
Table 1. Notable authors, affiliated institutions and countries that publish articles on options pricing, as generated by VOSviewer software (TP = total publications; TC = total citations).
Table 1. Notable authors, affiliated institutions and countries that publish articles on options pricing, as generated by VOSviewer software (TP = total publications; TC = total citations).
Top AuthorsTop InstitutionsTop Countries
AuthorsTPTCInstitutionTPTCCountryTPTC
Zhu, Song-Ping17441University Wollongong32535China2482296
Wang, Xingchun15104University of International
Business and Economics		17108USA2036449
Wang, Song14215Iran University of
Science and Technology		16229Australia1041524
He, Xin-Jiang1170University Mauritius13199England871530
Chen, Wenting10187Columbia University111670Taiwan73909
Kim, Jeong-Hoon1098Jilin University11123Republic of Korea72435
Ballestra, Luca Vincenzo7205Southwestern University of
Finance and Economics		11102Iran70566
Company, Rafael7140Zhejiang University11191Italy67900
Company, R.672The University of Tabriz1024Germany59744
Jodar, L.672University of Western Australia9344Canada501007
Lu, Xiaoping662Polytechnic University of the
Marches		8213India48309
Zhang, Kai650Islamic Azad University744France43475
Bhuruth, M.5166University of Naples
Federico II		7224Spain29435
Jodar, Lucas577Fuzhou University5160Belgium24332
Xu, Xiang5156Queensland University
of Technology		5160Mauritius13199
Table 2. Leading journals publishing on option pricing using VOSviewer software.
Table 2. Leading journals publishing on option pricing using VOSviewer software.
Journal NameTPTCCPPJIFJCI
Physica A-Statistical Mechanics and Its Applications61936153.30.9
Journal of Computational and Applied Mathematics48874182.41.4
Journal of Futures Markets44457101.90.6
Quantitative Finance44619141.30.5
Computational Economics2618872.00.6
Computers & Mathematics with Applications26677262.91.7
Applied Mathematics and Computation25335134.02.3
North American Journal of Economics and Finance2411253.61.1
Chaos Solitons & Fractals1917097.82.5
International Journal of Computer Mathematics1711971.80.9
Journal of Computational Finance1712070.90.3
Journal of Economic Dynamics & Control12274231.90.6
Applied Mathematics Letters9223253.72.3
Mathematical Methods in The Applied Sciences92532.91.5
Management Science817192155.41.2
Table 3. Ranking of publications according to citation frequency, produced with VOSviewer software.
Table 3. Ranking of publications according to citation frequency, produced with VOSviewer software.
ReferenceArticle TitleJournalTimes Cited (WoS)
(Kou, 2002)A jump-diffusion model for option pricingManagement Science955
(Hall & Murphy, 2002)Stock options for undiversified executivesJournal Of Accounting & Economics545
(Carr & Wu, 2004)Time-changed Levy processes and option pricingJournal of Financial Economics301
(Kou & Wang, 2004)Option pricing under a double exponential jump diffusion modelManagement Science300
(Christoffersen et al., 2009)The Shape and Term Structure of the Index Option Smirk: Why Multifactor Stochastic Volatility Models Work So WellManagement Science267
(Cartea & del Castillo-Negrete, 2007)Fractional diffusion models of option prices in markets with jumpsPhysica A-Statistical Mechanics and Its Applications208
(Knopf et al., 2002)The volatility and price sensitivities of managerial stock option portfolios and corporate hedgingJournal of Finance196
(Bollerslev et al., 2011)Dynamic estimation of volatility risk premia and investor risk aversion from option-implied and realized volatilitiesJournal of Econometrics173
(Zhu, 2006)An exact and explicit solution for the valuation of American put optionsQuantitative Finance173
(Borland, 2002)Option pricing formulas based on a non-Gaussian stock price modelPhysical Review Letter162
(Wang, 2004)A novel fitted finite volume method for the Black-Scholes equation governing option pricingIMA Journal of Numerical Analysis129
(Mordecki, 2002)Optimal stopping and perpetual options for Levy processesFinance and Stochastics129
(Ikonen & Toivanen, 2004)Operator splitting methods for American option pricingApplied Mathematics Letters127
(Barone-Adesi et al., 2008)A GARCH option pricing model with filtered historical simulationReview of Financial Studies125
(Broadie et al., 2009)Understanding Index Option ReturnsReview of Financial Studies119
Table 4. Cited research themes in option pricing (Clarivate-Indexed, 2021–2024).
Table 4. Cited research themes in option pricing (Clarivate-Indexed, 2021–2024).
ThemeDescriptionReferences
Deep Learning and Hybrid Neural NetworksDeep learning models (DNN, LSTM, FBSDE) are widely used to price and hedge options under frictions. They offer improved calibration and performance over traditional models.(Ashok Naarayan & Parpas, 2024; Horvath et al., 2021)
Stochastic and Rough Volatility ModelingIncorporates rough paths, fractional Brownian motion and stochastic processes with ML to better match observed volatility surfaces.(Guo et al., 2023; Jang & Lee, 2019)
Market Frictions and xVA AdjustmentsModern pricing accounts for bid-ask spreads, liquidity constraints and valuation adjustments using neural strategies.(Anderson & Ulrych, 2023; D. Liu, 2022)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Alokley, S.A. Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. J. Risk Financial Manag. 2025, 18, 513. https://doi.org/10.3390/jrfm18090513

AMA Style

Alokley SA. Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. Journal of Risk and Financial Management. 2025; 18(9):513. https://doi.org/10.3390/jrfm18090513

Chicago/Turabian Style

Alokley, Sara Ali. 2025. "Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends" Journal of Risk and Financial Management 18, no. 9: 513. https://doi.org/10.3390/jrfm18090513

APA Style

Alokley, S. A. (2025). Financial Options Pricing: A Bibliometric Study and Cluster Analysis of Global Research Trends. Journal of Risk and Financial Management, 18(9), 513. https://doi.org/10.3390/jrfm18090513

Article Metrics

Back to TopTop